Global thermoacoustic oscillations in a thermally driven pulse tube

Abstract

We obtain linearized, BiGlobal thermoacoustic solutions in a pulse tube driven via an imposed mean temperature gradient. Here, the pulse tube is treated as a key unit of a thermoacoustic heat engine, in which the conversion of thermal energy to useful acoustic fluctuations occurs. A primary goal of this work is to understand the hydrodynamic efficiency of the energy conversion process and how it depends upon some of the important operating parameters, including the geometry of the device which in the limit of long length-to-diameter ratio approaches the so-called narrow tube approximation. As this limit is frequently imposed in the wave propagation analyses of thermoacoustic devices, it is critical to investigate the physical connections of such a model to more realistic finite-length pulse tube configurations, which we do here. The mean flow is quiescent with an analytic mean temperature profile that still models the necessary physical details of the hot heat exchanger and regenerator. The computed thermoacoustic oscillations are found to be globally stable, approaching neutral stability conditions at the narrow tube limit. In finite-length tubes, three distinct types of modes are identified and analyzed. Here, within a linear framework, radial modes do appear to act as key enablers for longitudinal modes to be the primary carriers of acoustic energy from the pulse tube section, while the identified boundary modes, essentially numerical constructs, are ignored in the analysis. Further, a disturbance energy-based efficiency metric is constructed that provides mechanistic understanding of some of the key parameters in pulse tube operation. For finite-length tubes, it shows oscillations of the first asymmetric mode to be the most efficient, while the axisymmetric perturbations dominate for longer tubes that eventually lead to the idealized plane wave propagation.

Appendices

A Validation of the BiGlobal solver

A reduced version of the TAE of Fig. 1, including only the PT of a specific $L^*/D^*$ ratio, subjected to a uniform temperature profile and classical boundary conditions are considered to verify the present BiGlobal algorithm. For such conditions, both analytical results, as well as results from another BiGlobal simulations [47] are available for us to compare with, which are shown in Table 2 and Fig. 17. Here, we simulate a zero Mach number case with $L^*/D^*= 5$ with $N_z \times N_r = 40 \times 40$, showing only the $m=0$ results. In this exercise, excellent match with the analytically obtained frequencies (in fact, better than the other BiGlobal results) are obtained in Table 2, while the corresponding mode shapes also matched well (see Fig. 17).

Elsewhere, our BiGlobal code has also been used to validate against configurations with a mean/base flow, e.g., compressible chevron jets, incompressible vortex rings, etc.

Table 2 Comparison of the first 5 modes from the present BiGlobal code with theoretical and numerical predictions of Majdalani et al. [47]

Fig. 17

Comparison of the pressure eigenfunctions between the present BiGlobal simulations (right column) with Majdalani et al. [47]

B The compatibility conditions for pulse tube

As discussed in Sect. 2.3, compatibility conditions are needed to avoid using ad hoc boundary conditions at the pulse tube ends. This procedure provides such conditions naturally via considering the travel of acoustic waves inside the TAE as a whole instead of treating the pulse tube in isolation. Here, for simplicity, we restrict ourselves to one-dimensional plane waves traveling through the TAE without any losses to form a standing-wave pattern.

Fig. 18

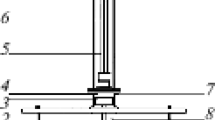
Same as in Fig. 1, but showing details of TAE components other than the pulse tube (PT) (shaded gray). The inlet and outlet of each component is labeled with the suffix “i” and “o,” respectively

The pressure and acoustic particle velocity for a one-dimensional standing wave are simply

$$\begin{aligned} {p}^{\prime }(z,t)= & {} A \exp \left\{ \mathrm {i}(\omega t - \kappa z)\right\} + B \exp \left\{ \mathrm {i}(\omega t + \kappa z)\right\} , \; \mathrm {and} \end{aligned}$$

(B1)

$$\begin{aligned} {v}^{\prime }(z,t)= & {} \frac{1}{Y_S} \left[ A \exp \left\{ \mathrm {i}(\omega t - \kappa z)\right\} + B \exp \left\{ \mathrm {i}(\omega t + \kappa z)\right\} \right] , \end{aligned}$$

(B2)

respectively, where $Y_S=1/S$ is a characteristic impedance and S is the cross-sectional area of a section of the TAE. Here, S is non-dimensionalized by the pulse tube cross-sectional area $S_{\mathrm{PT}}$ and ${v}^{\prime } = S{u}^{\prime }_z$. Next, with reference to Fig. 18, we apply the hard wall boundary conditions at $z = 0$ and $z = L_t$ to (B1) and (B2) to obtain the following relations at the resonator

$$\begin{aligned} {v}^{\prime }_{R_{\mathrm{o}}}(L_r,t) = -\frac{\mathrm {i}}{Y_r} \tan (\kappa L_r)\,{p}^{\prime }_{R_{\mathrm{o}}}(L_r,t), \end{aligned}$$

(B3)

and the compliance

$$\begin{aligned} {v}^{\prime }_{C_{\mathrm{i}}}(L_n,t) = \frac{\mathrm {i}}{Y_c} \tan (\kappa L_c)\,{p}^{\prime }_{C_{\mathrm{i}}}(L_n,t), \end{aligned}$$

(B4)

respectively, where $Y_r$ and $Y_c$ are the respective characteristic impedances for the resonator and compliance, while $L_n = L_r + L$ and the total length $L_t = L_n + L_c$. Similarly, for the inertance

$$\begin{aligned} {p}^{\prime }_{I_{\mathrm{o}}}(L_n,t)= & {} \cos (\kappa L) \, {p}^{\prime }_{I_{\mathrm{i}}}(L_r,t) - \mathrm {i}\,Y_i \sin (\kappa L) \, {v}^{\prime }_{I_{\mathrm{i}}}(L_r,t), \; \mathrm {and} \end{aligned}$$

(B5)

$$\begin{aligned} {v}^{\prime }_{I_{\mathrm{o}}}(L_n,t)= & {} -\frac{\mathrm {i}}{Y_i} \sin (\kappa L) \, {p}^{\prime }_{I_{\mathrm{i}}}(L_r,t) + \cos (\kappa L) \, {v}^{\prime }_{I_{\mathrm{i}}}(L_r,t), \end{aligned}$$

(B6)

where $Y_i$ is the characteristic impedance of the inertance. Further, continuity of pressure and mass at $z=L_r$ and $z=L_n$ yields

$$\begin{aligned}&{p}^{\prime }_{R_{\mathrm{o}}} = {p}^{\prime }_{I_{\mathrm{i}}} = {p}^{\prime }_{P_{\mathrm{o}}}, \qquad {p}^{\prime }_{C_{\mathrm{i}}} = {p}^{\prime }_{I_{\mathrm{o}}} = {p}^{\prime }_{P_{\mathrm{i}}},\, \mathrm {and} \end{aligned}$$

(B7)

$$\begin{aligned}&{v}^{\prime }_{R_{\mathrm{o}}} = {v}^{\prime }_{I_{\mathrm{i}}} + {v}^{\prime }_{P_{\mathrm{o}}}, \qquad {v}^{\prime }_{C_{\mathrm{i}}} = {v}^{\prime }_{P_{\mathrm{i}}} + {v}^{\prime }_{I_{\mathrm{o}}}. \end{aligned}$$

(B8)

Next, using (B7), (B8), (B3) and (B4) in (B5) and (B6), we get two equations involving the pressure and velocity at the pulse tube ends (${p}^{\prime }_{P_{\mathrm{i}}}$, ${p}^{\prime }_{P_{\mathrm{o}}}$, ${v}^{\prime }_{P_{\mathrm{i}}}$ and ${v}^{\prime }_{P_{\mathrm{o}}}$) along with a third equation

$$\begin{aligned} {u}^{\prime }_{z_{P_{\mathrm{i}}}}-\cos (\kappa L)\,{u}^{\prime }_{z_{P_{\mathrm{o}}}} = \mathrm {i}\sin (\kappa L)\, {p}^{\prime }_{P_{\mathrm{o}}} \end{aligned}$$

(B9)

when (B1) and (B2) are applied across the pulse tube. Two compatibility equations can now be derived for any end on eliminating the quantities at the other end to yield

$$\begin{aligned}&\left\{ \cot (\kappa L_c) \left[ \varSigma _c \cos (\kappa L) \tan (\kappa L_r) + \varSigma _c \sin (\kappa L) \right] + \cos (\kappa L) - \varSigma _i \sin (\kappa L) \tan (\kappa L_r) \right\} \nonumber \\&\quad \times \left( \bar{T} {\rho }^{\prime }_{P_{\mathrm{o}}} + \bar{\rho } {T}^{\prime }_{P_{\mathrm{o}}} \right) /\gamma + \mathrm {i}\left\{ \left( \varSigma _i - 1 \right) \sin (\kappa L) \right\} \, {u}^{\prime }_{z_{P_{\mathrm{o}}}} = 0, \end{aligned}$$

(B10)

at the PT outlet, where $S_r/S_c = \varSigma _c$, $S_r/S_i = \varSigma _i$, and

$$\begin{aligned}&\{ \cot (\kappa L_c) \left[ \varSigma _c \cos ^2(\kappa L)\, \tan (\kappa L_r) + \varSigma _c \sin (\kappa L)\,\cos (\kappa L) \right] + \cos ^2(\kappa L) \nonumber \\&\quad - \left( \varSigma _i - 1\right) \sin (\kappa L) - \varSigma _i \sin (\kappa L)\,\cos (\kappa L)\,\tan (\kappa L_r) \} \, \left( \bar{T} {\rho }^{\prime }_{P_{\mathrm{i}}} + \bar{\rho } {T}^{\prime }_{P_{\mathrm{i}}} \right) /\gamma \nonumber \\&\quad + \mathrm {i}\{\cot (\kappa L_c) \left[ \varSigma _c \sin ^2(\kappa L) + \varSigma _c \cos (\kappa L)\, \sin (\kappa L)\,\tan (\kappa L_r) \right] + \cos (\kappa L) \,\sin (\kappa L) \nonumber \\&\quad - \varSigma _i \sin ^2(\kappa L) \tan (\kappa L_r) + \left( \varSigma _i -1\right) \cos (\kappa L)\sin (\kappa L) \} \, {u}^{\prime }_{z_{P_{\mathrm{i}}}} = 0, \end{aligned}$$

(B11)

at the PT inlet, where $\gamma {p}^{\prime }= \bar{\rho }{T}^{\prime }+\bar{T}{\rho }^{\prime }$ is used. Equations (B10) and (B11) are of the same form as the boundary conditions of (2.16). For example, the benchmark case, whose spectrum is shown in Fig. 4 with $L^*/D^*= 2$ and $\bar{T}_{\mathrm{PT}} = 3.5$, has the following geometric parameters: $L_r = 20.62$, $L = 2$, $L_c = 0.96$, $\varSigma _c = 1$, $\varSigma _i = 56.16$ and the acoustic wavenumber $\kappa = 0.133$. The geometry of our TAE follows closely the Lycklama à Nijeholt configuration [20, 28]. For the other $L^*/D^*$ ratios of this work, the lengths are proportionally increased, keeping the cross-section identical.

C The stability equation operators

The elements of the matrices and of Eq. (2.6) are given in the following.

and

where

$$\begin{aligned} A_{11}&= \bar{u}_r \frac{\partial }{\partial r} + \bar{u}_z \frac{\partial }{\partial z} + \mathrm {i}\bar{u}_{\theta }\frac{m}{r} + \frac{\bar{u}_r}{r} + \bar{u}_{r,r} + \bar{u}_{z,z},\\ A_{12}&= \bar{\rho } \frac{\partial }{\partial r} + \bar{\rho }_{,r} + \frac{\bar{\rho }}{r},\\ A_{13}&= \mathrm {i}\bar{\rho }\frac{m}{r},\\ A_{14}&= \bar{\rho } \frac{\partial }{\partial z} +\bar{\rho }_{,z},\\ A_{15}&= 0,\\ A_{21}&= \frac{\bar{T}}{\gamma } \frac{\partial }{\partial r} + \frac{\bar{T}_{,r}}{\gamma }+ \bar{u}_r\,\bar{u}_{r,r}-\frac{{\bar{u}_{\theta }^2}}{r} + \bar{u}_z\,\bar{u}_{r,z},\\ A_{22}&= \bar{\rho }\,\bar{u}_r \frac{\partial }{\partial r} + \bar{\rho }\,\bar{u}_z \frac{\partial }{\partial z} + \mathrm {i}\bar{\rho }\,\bar{u}_{\theta }\frac{m}{r} + \frac{1}{Re}\frac{m^2}{r^2}+ \bar{\rho }\,\bar{u}_{r,r}-\frac{4}{3}\frac{1}{Re} \frac{\partial ^2 }{ \partial r^2} -\frac{1}{Re} \frac{\partial ^2 }{ \partial z^2} -\frac{4}{3}\frac{1}{r Re} \frac{\partial }{\partial r} + \frac{4}{3}\frac{Re_{,r}}{Re^2} \frac{\partial }{\partial r} \\&\quad +\frac{Re_{,z}}{Re^2} \frac{\partial }{\partial z} -\frac{2}{3}\frac{Re_{,r}}{Re^2}+\frac{4}{3}\frac{1}{r^2 Re},\\ A_{23}&= -\frac{\mathrm {i}}{3}\frac{m}{r Re} \frac{\partial }{\partial r} + \frac{7\mathrm {i}}{3}\frac{m}{r^2 Re} - \frac{2}{3}\frac{Re_{,r}}{r Re^2} - \frac{2\bar{\rho }\,\bar{u}_{\theta }}{r},\\ A_{24}&= -\frac{1}{3 Re} \frac{\partial ^2 }{ \partial r \partial z} +\bar{\rho }\,\bar{u}_{r,z}+\frac{Re_{,z}}{Re^2} \frac{\partial }{\partial r} -\frac{2}{3}\frac{Re_{,r}}{Re^2} \frac{\partial }{\partial z} ,\\ A_{25}&= \frac{\bar{\rho }}{\gamma } \frac{\partial }{\partial r} + \frac{\bar{\rho }_{,r}}{\gamma },\\ A_{31}&= \mathrm {i}\bar{T} \frac{m}{\gamma r} + \bar{u}_r\,\bar{u}_{\theta ,r} + \frac{\bar{u_{r}}\,\bar{u}_{\theta }}{r}+ \bar{u}_z\,\bar{u}_{\theta ,z},\\ A_{32}&= -\frac{\mathrm {i}}{3}\frac{m}{r Re} \frac{\partial }{\partial r} -\frac{7\mathrm {i}}{3}\frac{m}{r^2 Re} + \mathrm {i}\frac{m Re_{,r}}{r Re^2} + \bar{\rho }\,\bar{u}_{\theta ,r} + \frac{\bar{\rho }\,\bar{u}_{\theta }}{r},\\ A_{33}&= \bar{\rho }\,\bar{u}_r \frac{\partial }{\partial r} + \bar{\rho }\,\bar{u}_z \frac{\partial }{\partial z} + \mathrm {i}\bar{\rho }\,\bar{u}_{\theta }\frac{m}{r} + \frac{\bar{\rho }\,\bar{u}_r}{r}+ \frac{4}{3}\frac{m^2}{r^2 Re} -\frac{1}{Re} \frac{\partial ^2 }{ \partial r^2} -\frac{1}{Re} \frac{\partial ^2 }{ \partial z^2} - \frac{1}{r Re} \frac{\partial }{\partial r} -\frac{Re_{,r}}{Re^2} \frac{\partial }{\partial r} \\&\quad + \frac{Re_{,z}}{Re^2} \frac{\partial }{\partial z} + \frac{1}{r^2 Re} -\frac{Re_{,r}}{r Re^2}, \end{aligned}$$

$$\begin{aligned} A_{34}&= \mathrm {i}\frac{m Re_{,z}}{r Re^2} - \frac{\mathrm {i}}{3}\frac{m}{r Re} \frac{\partial }{\partial z} + \bar{\rho \,}\bar{u}_{\theta ,z},\\ A_{35}&= \mathrm {i}\bar{\rho } \frac{m}{\gamma r},\\ A_{41}&= \frac{\bar{T}}{\gamma } \frac{\partial }{\partial z} + \frac{\bar{T}_{,z}}{\gamma } + \bar{u}_r\,\bar{u}_{z,r} + \bar{u}_z\,\bar{u}_{z,z},\\ A_{42}&= -\frac{1}{3}\frac{1}{Re} \frac{\partial ^2 }{ \partial r \partial z} + \bar{\rho }\,\bar{u}_{z,r} - \frac{2}{3}\frac{Re_{,z}}{Re^2} \frac{\partial }{\partial r} - \frac{1}{3}\frac{1}{r Re} \frac{\partial }{\partial z} +\frac{Re_{,r}}{Re^2} \frac{\partial }{\partial z} - \frac{2}{3}\frac{Re_{,z}}{ r Re^2},\\ A_{43}&= -\frac{\mathrm {i}}{3}\frac{m}{r Re} \frac{\partial }{\partial z} -\frac{2\mathrm {i}}{3}\frac{m Re_{,z}}{r Re^2},\\ A_{44}&= \bar{\rho }\,\bar{u}_r \frac{\partial }{\partial r} + \bar{\rho }\,\bar{u}_z \frac{\partial }{\partial z} + \mathrm {i}\bar{\rho }\,\bar{u}_{\theta }\frac{m}{r} + \bar{\rho }\,\bar{u}_{z,z} + \frac{m^2}{r^2 Re} - \frac{1}{Re} \frac{\partial ^2 }{ \partial r^2} - \frac{4}{3}\frac{1}{Re} \frac{\partial ^2 }{ \partial z^2} - \frac{1}{r Re} \frac{\partial }{\partial r} + \frac{Re_{,r}}{Re^2} \frac{\partial }{\partial r} \qquad \quad \\&\quad + \frac{4}{3}\frac{Re_{,z}}{ Re^2} \frac{\partial }{\partial z} ,\\ A_{45}&= \frac{\bar{\rho }}{\gamma } \frac{\partial }{\partial z} + \frac{\bar{\rho }_{,z}}{\gamma },\\ A_{51}&= -\bar{u}_r\,\bar{T}\frac{\gamma -1}{\gamma } \frac{\partial }{\partial r} -\bar{u}_z\,\bar{T}\frac{\gamma -1}{\gamma } \frac{\partial }{\partial z} -\mathrm {i}\bar{u}_{\theta }\,\bar{T}\frac{\gamma -1}{\gamma }\frac{m}{r}+(\bar{u}_r\,\bar{T}_{,r} +\bar{u}_z\,\bar{T}_{,z})c_p\\&\quad -(\bar{u}_r\,\bar{T}_{,r}+\bar{u}_z\,\bar{T}_{,z})\frac{\gamma -1}{\gamma },\\ A_{52}&= -2\mathrm {i}\left( -\frac{\bar{u}_{\theta }}{r}+\bar{u}_{\theta ,r}\right) \frac{ (\gamma -1)m}{r Re} - 4 \bar{u}_{r,r}\frac{\gamma -1}{Re} \frac{\partial }{\partial r} + \left( \bar{u}_{r,r} +\frac{4}{3}\frac{\bar{u}_r}{r}+ \bar{u}_{z,z}\right) \frac{\gamma -1}{Re} \frac{\partial }{\partial r} \\&\quad - 4\bar{u}_r\frac{\gamma -1}{r^2 Re} - 2\left( \bar{u}_{r,z}+\bar{u}_{z,r}\right) \frac{\gamma -1}{Re} \frac{\partial }{\partial z} + \frac{4}{3}\left( \bar{u}_{r,r}+\frac{\bar{u}_r}{r}+ \bar{u}_{z,z}\right) \frac{\gamma -1}{r Re} +\bar{\rho }\,\bar{T}_{,r}c_p \\&\quad -\bar{p}_{,r}(\gamma -1),\\ A_{53}&= -4\mathrm {i}\bar{u}_r\frac{(\gamma -1)m}{r^2 Re}+ \frac{4\mathrm {i}}{3}\left( \bar{u}_{r,r}+\frac{\bar{u}_r}{r}+ \bar{u}_{z,z}\right) \frac{(\gamma -1)m}{r Re} - 2\left( \bar{u}_{\theta ,r}-\frac{\bar{u}_{\theta }}{r}\right) \frac{\gamma -1}{Re} \frac{\partial }{\partial r} \\&\quad -2\bar{u}_{\theta ,z}\frac{\gamma -1}{Re} \frac{\partial }{\partial z} - 2\left( \frac{\bar{u}_{\theta }}{r}-\bar{u}_{\theta ,r}\right) \frac{\gamma -1}{r Re},\\ A_{54}&= -2\mathrm {i}\bar{u}_{\theta ,z}\frac{(\gamma -1) m}{r Re} - 2 \left( \bar{u}_{z,r}+\bar{u}_{r,z}\right) \frac{\gamma -1}{Re} \frac{\partial }{\partial r} - \frac{4}{3}\bar{u}_{z,z}\frac{\gamma -1}{Re} \frac{\partial }{\partial z} + c_p\bar{\rho }\,\bar{T}_{,z}-(\gamma -1)\bar{p}_{,z}\\&\quad +\frac{4}{3}\left( \bar{u}_{r,r} +\bar{u}_{z,z}+\frac{\bar{u}_r}{r}\right) \frac{\gamma -1}{Re} \frac{\partial }{\partial z} , \\ A_{55}&= \bar{\rho }\,\bar{u}_r c_p \frac{\partial }{\partial r} - \bar{\rho }\,\bar{u}_r\frac{\gamma -1}{\gamma } \frac{\partial }{\partial r} + \bar{\rho }\,\bar{u}_z c_p \frac{\partial }{\partial z} - \bar{\rho }\,\bar{u}_z\frac{\gamma -1}{\gamma } \frac{\partial }{\partial z} + \mathrm {i}\bar{\rho }\,\bar{u}_{\theta }\frac{m c_p}{r} - \mathrm {i}\bar{\rho }\,\bar{u}_{\theta }\frac{(\gamma -1)m}{\gamma r}\\&\quad +\frac{m^2}{r^2 Pe} -\Big (\bar{u}_r\bar{\rho }_{,r}+ \bar{u}_z\bar{\rho }_{,z}\Big ) \frac{\gamma -1}{\gamma }-\frac{1}{Pe} \frac{\partial ^2 }{ \partial r^2} -\frac{1}{Pe} \frac{\partial ^2 }{ \partial z^2} -\frac{1}{r Pe} \frac{\partial }{\partial r} + \frac{Pe_{,r}}{Pe^2} \frac{\partial }{\partial r} +\frac{Pe_{,z}}{Pe^2} \frac{\partial }{\partial z} , \end{aligned}$$

with $a_{,b} = \dfrac{\partial a}{\partial b}$ being used to denote partial derivatives.