An advanced shell model for the analysis of geometrical and material nonlinear shells

Abstract

In this paper layered shells subjected to static loading are considered. The displacements of the Reissner–Mindlin theory are enriched by a an additional part. These so-called fluctuation displacements include warping displacements and thickness changes. They lead to additional terms for the material deformation gradient and the Green–Lagrangian strain tensor. Within a nonlinear multi-field variational formulation the weak form of the boundary value problem accounts for the equilibrium of stress resultants and couple resultants, the local equilibrium of stresses, the geometrical field equations and the constitutive equations. For the independent shell strains an ansatz with quadratic shape functions is chosen. This leads to a significant improved convergence behaviour especially for distorted meshes. Elimination of a set of parameters on element level by static condensation yields an element stiffness matrix and residual vector of a quadrilateral shell element with the usual 5 or 6 nodal degrees of freedom. The developed model yields the complicated three-dimensional stress state in layered shells for elasticity and elasto-plasticity considering geometrical nonlinearity. In comparison with fully 3D solutions present 2D shell model requires only a fractional amount of computing time.

1 Introduction

Shell elements which account for the layer sequence of a laminated structure are able to predict the deformation behaviour of the reference surface in an accurate way. Also the assumption of a linear shape of the in-plane strains through the thickness is sufficient, if the shell is not too thick. In contrast to that only constant transverse shear strains through the thickness are obtained within the Reissner–Mindlin theory. As a consequence only the average of the transverse shear stresses is accurate. Neither the shape of the stresses is correct nor the boundary conditions at the outer surfaces are fulfilled. Within the Kirchhoff theory the transverse shear strains are set to zero. By assumption the thickness normal stresses are neglected in a standard shell theory. This is necessary to avoid unphysical stresses due to inextensibility assumptions in thickness direction.

In several publications the equilibrium equations are exploited within post-processing procedures to obtain the interlaminar stresses, e.g. [1, 2] for the transverse shear stresses and e.g. [3] for the thickness normal stresses. In a standard version first and second derivatives of the in-plane stresses require bi-quadratic or bi-cubic shape functions. The essential restriction of the approach is the fact that these stresses are not embedded in the variational formulation and an immediate extension to geometrical and physical nonlinearity is not possible.

The standard displacement field is enhanced by layer-wise (zig-zag) functions through the thickness in e.g. [4,5,6]. An enhanced modeling approach for multilayer anisotropic plates based on the dimension reduction method is presented in [7]. An assessment of the variable separation method is discussed in [8].

Higher order plate and shell formulations and layerwise approaches represent a wide class of advanced models, e.g. [9,10,11,12,13,14,15]. For geometrical nonlinear formulations we refer to e.g. [16, 17]. These theories are associated with layerwise degrees of freedom in an associated FE formulation.

The use of brick elements or so-called solid shell elements represents a computationally expensive approach, e.g. [18, 19]. For a sufficient accurate evaluation of the interlaminar stresses each layer must be discretized with several elements ($\approx$4–10) in thickness direction. Especially for large scale industrial problems with a multiplicity of load steps and several iterations in each load step this is not a feasible approach.

The purpose of this paper is to present a shell model which is able to compute the load-deflection behaviour and the complicated three-dimensional stress-state of geometrical nonlinear, elasto-plastic, layered shells. It is based on Refs. [20,21,22]. Present work delivers essential new developments.

• (i) The displacements of the Reissner–Mindlin kinematics are enriched by warping displacements and thickness changes. This yields additional terms for the material deformation gradient, the Green–Lagrangian strain tensor and associated variation. The thickness integration of the local equilibrium equations are extended to elasto-plasticity.

• (ii) The proposed nonlinear variational formulation leads to Euler-Lagrange equations which include besides the usual shell equations in terms of stress resultants, the local equilibrium in terms of stresses, a constraint which enforces the correct shape of the displacement fluctuations through the thickness, the geometric field equations and the constitutive equations.

• (iii) A new ansatz for the independent shell strains with quadratic shape functions is proposed. It leads to a significant improved convergence behaviour especially for distorted meshes. Furthermore, quadratic functions allow the computation of second derivatives. These are necessary when rewriting the local equilibrium equation for the thickness direction with the derivatives of the transverse shear strains.

• (iv) Elimination of a certain set of parameters by static condensation from the resulting system of equations yields the element stiffness matrix and the element residual vector. The derived four-node element possesses the usual 5 or 6 nodal degrees of freedom. This is an essential feature since standard geometrical boundary conditions can be applied and the element is applicable also to shell intersection problems. In comparison with fully 3D discretizations present 2D shell model requires only a fractional amount of computing time.

The paper is organized as follows. In Sect. 2 the shell theory is derived. The associated finite element formulation is presented in Sect. 3. Several geometrical and physical nonlinear examples are presented in Sect. 4. The computed displacements and stresses of the developed model are compared with costly 3D computations. Furthermore, we compare with the displacements and stresses computed with Reissner–Mindlin shell elements.

2 Governing equations

2.1 Shell kinematics

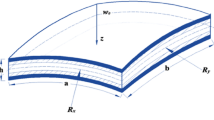
Let ${\mathcal B}_0$ be the three-dimensional Euclidean space occupied by the shell with thickness h in the undeformed configuration. The position vector ${\mathbf{X}}$ of any point $P \in {\mathcal B}_0$ is parametrized with convected coordinates $\xi ^i$

$$\begin{aligned} \begin{array}{rcl} {\mathbf{X}} (\xi ^1,\xi ^2,\xi ^3) &{}=&{} {\mathbf{X}}_0(\xi ^1, \xi ^2) + \xi ^3 \, {\mathbf{N}} (\xi ^1, \xi ^2) \\ |{\mathbf{N}} (\xi ^1, \xi ^2)| &{}=&{} 1 \,, \end{array} \end{aligned}$$

(1)

where ${\mathbf{X}}_0$ and ${\mathbf{N}}$ denote the position vector and normal vector of the reference surface $\Omega$, respectively. The thickness coordinate $\xi ^3$ is defined in the range $h^-\le \xi ^3 \le h^+$, where $h^-$ and $h^+$ denote the coordinates of the outer surfaces. The coordinate on the boundary $\Gamma = \Gamma _u \cup \Gamma _\sigma$ of $\Omega$ is s. The usual summation convention is used, where Latin indices range from 1 to 3 and Greek indices range from 1 to 2. Commas denote partial differentiation with respect to the coordinates $\xi ^i$.

The kinematic assumption for the position vector of the deformed shell space $\mathcal B$ reads

$$\begin{aligned} \begin{array}{rll} {\mathbf{x}}(\xi ^1, \xi ^2, \xi ^3) &{}=&{} {\mathbf{x}}_0(\xi ^1,\xi ^2) + \xi ^3 \, {\mathbf{d}}(\xi ^1,\xi ^2) + \tilde{{\mathbf{u}}} (\xi ^3)\\ |{\mathbf{d}} (\xi ^1, \xi ^2)| &{}=&{} 1 \,. \end{array} \end{aligned}$$

(2)

Here, ${\mathbf{x}}_0$ describes the position vector of the current reference surface $\Omega _t$. The director vector ${\mathbf{d}}({{\varvec{\varphi }}})$ of the current configuration is not perpendicular to the deformed reference surface, thus shear deformations are accounted for. We introduce the vector field ${\mathbf{v}}(\xi ^1, \xi ^2) =[{\mathbf{u}}, {{\varvec{\varphi }}}]^T$, where ${\mathbf{u}} = {\mathbf{x}}_0 - {\mathbf{X}}_0$ and ${{\varvec{\varphi }}}$ contains rotational parameters. In Eq. (2) the assumptions of the Reissner–Mindlin theory are extended by the displacement fluctuation field

$$\begin{aligned} \tilde{{\mathbf{u}}}(\xi ^3) = {\varvec{\Phi }}(\xi ^3) \, {{\varvec{\alpha }}}\,. \end{aligned}$$

(3)

For this purpose the shell is subdivided in thickness direction in M numerical layers. For laminated shells M usually corresponds to the number of physical layers. The vector ${{\varvec{\alpha }}}$ contains displacements at nodes in thickness direction and is element-wise constant. The matrix ${\varvec{\Phi }}$ contains layer-wise cubic hierarchic functions

$$\begin{aligned} \begin{array}{l} {\varvec{\Phi }}(\xi ^3) = \left[ \begin{array}{cccc} \phi _1 \, {\mathbf{1}}_3 &{} \phi _2 \, {\mathbf{1}}_3 &{} \phi _3 \, {\mathbf{1}}_3 &{} \phi _4 \, {\mathbf{1}}_3 \end{array} \right] \, {\mathbf{a}}^i \\ \begin{array}{ll} \phi _1 = \displaystyle \frac{1}{2}\,(1-\zeta ) &{} \phi _2 = 1-\zeta ^2 \\ \phi _3 = \displaystyle \frac{8}{3}\,\zeta \, (1-\zeta ^2) \qquad &{} \phi _4 = \displaystyle \frac{1}{2}\,(1+\zeta ) \,, \end{array} \end{array} \end{aligned}$$

(4)

where ${\mathbf{a}}^i$ is an assembly matrix, which relates the 12 degrees of freedom of layer i to the K components of ${{\varvec{\alpha }}}$. For M layers this leads to $K = 9 \cdot M + 3$. Furthermore, $\zeta$ is a normalized coordinate of layer i defined in the range $-1 \le \zeta \le 1$ and ${\mathbf{1}}_n$ denotes a unit matrix of order n.

With the parametrization of the shell (1) and kinematic assumption (2) one can express the material deformation gradient as

$$\begin{aligned} {\mathbf{F}} = {\mathbf{g}}_i \otimes {\mathbf{G}}^i {\mathbf{g}}_i = {\mathbf{x}},_i {\mathbf{G}}_i = {\mathbf{X}},_i {\mathbf{G}}^i = G^{ij} \, {\mathbf{G}}_j \end{aligned}$$

(5)

with the contravariant metric coefficients $G^{ij}$ and

$$\begin{aligned} \begin{array}{rcl} {\mathbf{X}},_\alpha &{}=&{} {\mathbf{X}}_0,_\alpha + \xi ^3 \, {\mathbf{N}},_\alpha \\ {\mathbf{X}},_3 &{}=&{} {\mathbf{N}} \\ {\mathbf{x}},_\alpha &{}=&{} {\mathbf{x}}_0,_\alpha + \xi ^3 \, {\mathbf{d}},_\alpha \\ {\mathbf{x}},_3 &{}=&{} {\mathbf{d}} + \tilde{{\mathbf{u}}},_3 \,. \end{array} \end{aligned}$$

(6)

The vector $\tilde{{\mathbf{u}}},_3$ follows from $\tilde{{\mathbf{u}}},_3 = {\varvec{\Phi }},_3 {{\varvec{\alpha }}}$ with

$$\begin{aligned} \begin{array}{lcl} {\varvec{\Phi }},_3 &{}=&{} \left[ \phi _1,_3 {\mathbf{1}}_3 \;, \phi _2,_3 {\mathbf{1}}_3 \;, \phi _3,_3 {\mathbf{1}}_3 \;, \phi _4,_3 {\mathbf{1}}_3 \right] \, {\mathbf{a}}^i \\ \\ \phi _j,_3 &{}=&{} \dfrac{\,\text {d}\phi _j}{\,\text {d}\zeta } \; \dfrac{2}{h^i} \,, \end{array} \end{aligned}$$

(7)

where $h^i$ denotes the thickness of layer i.

Inserting the deformation gradient into the Green–Lagrangian tensor ${\mathbf{E}}_g = \frac{1}{2} \, ({\mathbf{F}}^T {\mathbf{F}} -{\mathbf{1}})$ yields

$$\begin{aligned} {\mathbf{E}}_g = E_{ij} \, {\mathbf{G}}^i \otimes {\mathbf{G}}^j \qquad E_{ij} = \dfrac{1}{2} ({\mathbf{x}},_i \cdot {\mathbf{x}},_j - {\mathbf{X}},_i \cdot {\mathbf{X}},_j) \,, \end{aligned}$$

(8)

where the index g refers to geometrical strains. The components read with (6) considering ${\mathbf{d}} \cdot {\mathbf{d}} = {\mathbf{N}} \cdot {\mathbf{N}} = 1$ as well as ${\mathbf{N}},_\alpha \cdot {\mathbf{N}} = {\mathbf{d}},_\alpha \cdot {\mathbf{d}} = 0$

$$\begin{aligned} \begin{array}{rcl} E_{\alpha \beta } &{}=&{} \varepsilon _{\alpha \beta } + \xi ^3 \, \kappa _{\alpha \beta } +( \xi ^3)^2 \, \rho _{\alpha \beta } \\ 2 E_{\alpha 3} &{}=&{} \gamma _\alpha + {\mathbf{g}}_\alpha \cdot \tilde{{\mathbf{u}}},_3 \\ E_{33} &{}=&{} \tilde{{\mathbf{g}}}_3 \cdot \tilde{{\mathbf{u}}},_3 \end{array} \end{aligned}$$

(9)

with

$$\begin{aligned} \begin{array}{rcl} \varepsilon _{\alpha \beta } &{}=&{} \dfrac{1}{2}({\mathbf{x}}_0,_\alpha \cdot {\mathbf{x}}_0,_\beta - {\mathbf{X}}_0,_\alpha \cdot {\mathbf{X}}_0,_\beta ) \\ \kappa _{\alpha \beta } &{}=&{} \dfrac{1}{2}({\mathbf{x}}_0,_\alpha \cdot {\mathbf{d}},_\beta + {\mathbf{x}}_0,_\beta \cdot {\mathbf{d}},_\alpha - {\mathbf{X}}_0,_\alpha \cdot {\mathbf{N}},_\beta - {\mathbf{X}}_0,_\beta \cdot {\mathbf{N}},_\alpha ) \\ \rho _{\alpha \beta } &{}=&{} \dfrac{1}{2}({\mathbf{d}},_\alpha \cdot {\mathbf{d}},_\beta - {\mathbf{N}},_\alpha \cdot {\mathbf{N}},_\beta ) \\ \gamma _\alpha &{}=&{} {\mathbf{x}}_0,_\alpha \cdot {\mathbf{d}} - {\mathbf{X}}_0,_\alpha \cdot {\mathbf{N}} \\ \tilde{{\mathbf{g}}}_3 &{}=&{} {\mathbf{d}} + \dfrac{1}{2} \, {\varvec{\Phi }},_3 {{\varvec{\alpha }}}\,. \end{array} \end{aligned}$$

(10)

The higher order curvatures $\rho _{\alpha \beta }$ are neglected. This is admissible for sufficiently thin structures with $L/h \gg 1$, see e.g. [23, 24]. Here, L is a characteristic length of a plate or lowest curvature radius of a shell. Hence, the in-plane strains $\{E_{11},E_{22},$ $2 E_{12}\}$ are linear functions of $\xi ^3$. Our numerical investigations show that for $L/h \ge 10$ this is a good approximation. Using Voigt notation the Green-Lagrangian strains of a point in shell space with coordinate $\xi ^3$ are obtained with

$$\begin{aligned} {\mathbf{E}}_g = {\mathbf{A}}_1 \, {{\varvec{\varepsilon }}}_g + \tilde{{\mathbf{A}}}_2 \, {{\varvec{\alpha }}}\end{aligned}$$

(11)

where

$$\begin{aligned} \begin{array}{rcl} {{\varvec{\varepsilon }}}_g ({\mathbf{v}}) &{}=&{} [\varepsilon _{11},\varepsilon _{22},2 \varepsilon _{12}, \kappa _{11},\kappa _{22},2 \kappa _{12},\gamma _{1},\gamma _{2}]^T \\ {\mathbf{E}}_g &{}=&{} \left[ \begin{array}{r} E_{11}\\ E_{22}\\ E_{33}\\ 2E_{12}\\ 2E_{13}\\ 2E_{23}\\ \end{array} \right] \\ {\mathbf{A}}_1 &{}=&{} \left[ \begin{array}{ccccccccc} 1 &{} 0 &{} 0&{} \xi ^3 &{} 0&{} 0 &{} 0 &{} 0 \\ 0 &{} 1 &{} 0&{} 0 &{} \xi ^3 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0&{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 1&{} 0 &{} 0 &{} \xi ^3 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0&{} 0 &{} 0 &{} 0 &{} 1 &{} 0 \\ 0 &{} 0 &{} 0&{} 0 &{} 0 &{} 0 &{} 0 &{} 1 \end{array} \right] \tilde{{\mathbf{A}}}_2 = \left[ \begin{array}{c} {\mathbf{0}} \\ {\mathbf{0}} \\ \tilde{{\mathbf{g}}}^T_3 \\ {\mathbf{0}} \\ {\mathbf{g}}^T_1 \\ {\mathbf{g}}^T_2 \end{array} \right] {\varvec{\Phi }},_3\,. \end{array} \end{aligned}$$

(12)

The components of ${\mathbf{F}}$ and ${\mathbf{E}}_g$ are transformed to the element-wise constant Cartesian element coordinate system ${\mathbf{t}}_i$, see Sect. 3. The transformations are standard and therefore are not displayed here.

For the below described variational formulation the virtual Green–Lagrangian strain tensor has to be specified

$$\begin{aligned} \begin{array}{rcl} \delta {\mathbf{E}}_g &{}=&{} \delta E_{ij} \, {\mathbf{G}}^i \otimes {\mathbf{G}}^j \\ \delta E_{ij} &{}=&{} \dfrac{1}{2} (\delta {\mathbf{x}},_i \cdot {\mathbf{x}},_j + \delta {\mathbf{x}},_j \cdot {\mathbf{x}},_i) \\ \delta {\mathbf{x}},_\alpha &{}=&{} \delta {\mathbf{x}}_0,_\alpha + \xi ^3 \, \delta {\mathbf{d}},_\alpha \\ \delta {\mathbf{x}},_3 &{}=&{} \delta {\mathbf{d}} + {\varvec{\Phi }},_3 \, \delta {{\varvec{\alpha }}}\,. \end{array} \end{aligned}$$

(13)

Using Voigt notation it holds

$$\begin{aligned} \begin{array}{rclrcl} \delta {\mathbf{E}}_g &{}=&{} {\mathbf{A}}_1 \, \delta {{\varvec{\varepsilon }}}_g + {\mathbf{A}}_2 \, \delta {{\varvec{\alpha }}}\\ \delta {\mathbf{E}}_g &{}=&{} \left[ \begin{array}{r} \delta E_{11}\\ \delta E_{22}\\ \delta E_{33}\\ 2\delta E_{12}\\ 2\delta E_{13}\\ 2\delta E_{23}\\ \end{array} \right] &{}{\mathbf{A}}_2 &{}=&{} \left[ \begin{array}{c} {\mathbf{0}} \\ {\mathbf{0}} \\ {\mathbf{g}}^T_3 \\ {\mathbf{0}} \\ {\mathbf{g}}^T_1 \\ {\mathbf{g}}^T_2 \\ \end{array} \right] {\varvec{\Phi }},_3 \end{array} \end{aligned}$$

(14)

with

$$\begin{aligned} \begin{array}{rcl} \delta {{\varvec{\varepsilon }}}_g &{}=&{} [\delta \varepsilon _{11},\delta \varepsilon _{22},2 \delta \varepsilon _{12}, \delta \kappa _{11},\delta \kappa _{22}, 2 \delta \kappa _{12},\delta \gamma _{1},\delta \gamma _{2}]^T \\ \delta \varepsilon _{\alpha \beta } &{}=&{} \dfrac{1}{2}(\delta {\mathbf{x}}_0,_\alpha \cdot {\mathbf{x}}_0,_\beta + \delta {\mathbf{x}}_0,_\beta \cdot {\mathbf{x}}_0,_\alpha ) \\ \delta \kappa _{\alpha \beta } &{}=&{} \dfrac{1}{2}(\delta {\mathbf{x}}_0,_\alpha \cdot {\mathbf{d}},_\beta + \delta {\mathbf{x}}_0,_\beta \cdot {\mathbf{d}},_\alpha \\ &{}&{} + \delta {\mathbf{d}},_\alpha \cdot {\mathbf{x}}_0,_\beta + \delta {\mathbf{d}},_\beta \cdot {\mathbf{x}}_0,_\alpha ) \\ \delta \gamma _\alpha &{}=&{} \delta {\mathbf{x}}_0,_\alpha \cdot \, {\mathbf{d}} + \delta {\mathbf{d}} \cdot {\mathbf{x}}_0,_\alpha \,. \end{array} \end{aligned}$$

(15)

The below presented finite element equations are iteratively solved. To maintain quadratic convergence in the Newton-Raphson scheme the vectors $[{\mathbf{d}}, {\mathbf{g}}_1, {\mathbf{g}}_2]$ of the last converged load increment are used in $\tilde{{\mathbf{A}}}_2$ and ${\mathbf{A}}_2$. In order to assess the effect of this approximation a variation of the load step size has to be performed. This is done by means of the numerical examples in Sect. 4.

In this context also the second variation of the Green–Lagrangian strains has to be derived. One obtains

$$\begin{aligned} \begin{array}{rcl} \Delta \delta {\mathbf{E}}_g &{}=&{} \Delta \delta {\mathbf{E}}^1_g + \Delta \delta {\mathbf{E}}^2_g \\ \Delta \delta {\mathbf{E}}^1_g &{}=&{} {\mathbf{A}}_1 \, \Delta \delta {{\varvec{\varepsilon }}}_g\\ \Delta \delta {\mathbf{E}}^2_g &{}=&{} [0,0,\Delta \delta E_{33},0,0,0]^T\\ \Delta \delta E_{33}&{}=&{} \delta {{\varvec{\alpha }}}^T ({\varvec{\Phi }}^T\!\!,_3 {\varvec{\Phi }},_3) \, \Delta {{\varvec{\alpha }}}\,. \end{array} \end{aligned}$$

(16)

The linearized virtual shell strains $\Delta \delta {{\varvec{\varepsilon }}}_g$ are specified e.g. in Ref. [25].

2.2 Equilibrium equations and a constraint

This part follows Ref. [22] considering the new relations of Sect. 2.1. Furthermore, the extension to elasto-plastic material behaviour is derived. In this section we use Voigt notation. The components of the stresses, strains and material laws refer to the element-wise constant Cartesian coordinate system ${\mathbf{t}}_i$, see Sect. 3.

2.2.1 Definition of stress resultants

The transformation of the Second Piola–Kirchhoff stress tensor ${\mathbf{S}} = {\mathbf{S}} ^T$ to the First Piola–Kirchhoff stress tensor ${\mathbf{P}}$ is obtained in a standard way by ${\mathbf{P}} = {\mathbf{F}} \, {\mathbf{S}}$. Thus, with ${\mathbf{P}} = P^{ij} \, {\mathbf{t}}_i \otimes {\mathbf{t}}_j$ and ${\mathbf{F}} = F_{ij} \, {\mathbf{t}}_i \otimes {\mathbf{t}}_j$, where $F_{ij} = {\mathbf{t}}_i \cdot {\mathbf{g}}_j = F^i_{\,\, j}$ with ${\mathbf{t}}_i = {\mathbf{t}}^i$, it holds

$$\begin{aligned} P^{ij} = F^i_{\, \,k} \, S^{kj} \,. \end{aligned}$$

(17)

Figure 1 depicts static loading $p^-$ and $p^+$ acting at the outer surfaces of the shell with coordinates $\xi ^3 = h^-$ and $\xi ^3 = h^+$, respectively. The stress boundary conditions at the outer surfaces read

$$\begin{aligned} \begin{array}{rcl} P^{\alpha 3}(h^-) &{}=&{} 0 \\ P^{\alpha 3}(h^+) &{}=&{} 0 \\ P^{33}(h^+) &{}=&{} p^+ \\ P^{33}(h^-) &{}=&{} -p^- \,. \end{array} \end{aligned}$$

(18)

Fig. 1

Surface loading of the shell

The components of the Second Piola–Kirchhoff stress tensor are organized in a vector using Voigt notation

$$\begin{aligned} {\mathbf{S}} = \left[ \begin{array}{c} S^{11} \\ S^{22} \\ S^{33} \\ S^{12} \\ S^{13} \\ S^{23} \end{array} \right] \,. \end{aligned}$$

(19)

In an analogous way the physical strains ${\mathbf{E}}$ and associated variations $\delta {\mathbf{E}}$ are introduced. The components are organized in vectors as the geometrical counterparts in Eqs. (12) and (14).

Now, the relation of ${\mathbf{S}}$ to the stress resultants is defined by thickness integration of the internal virtual work per unit area. This yields with $\delta {\mathbf{E}} = {\mathbf{A}}_1 \, \delta {{\varvec{\varepsilon }}}+ {\mathbf{A}}_2 \, \delta {{\varvec{\alpha }}}$, where $\delta {{\varvec{\varepsilon }}}$ is the vector of the virtual independent shell strains

$$\begin{aligned} \int \limits _{h^-}^{h^+} \delta {\mathbf{E}}^T {\mathbf{S}} \, \bar{\mu }\,\text {d}\xi ^3 = \delta {{\varvec{\varepsilon }}}^T {\partial {}_{{\varvec{\varepsilon }}}W} + \delta {{\varvec{\alpha }}}^T {\partial {}_{{\varvec{\alpha }}}W} \end{aligned}$$

(20)

with the determinant of the shifter tensor $\bar{\mu }$ and

$$\begin{aligned} {\partial {}_{{\varvec{\varepsilon }}}W} := \int \limits _{h^-}^{h^+} {\mathbf{A}}_1^T \, {\mathbf{S}} \, \bar{\mu }\,\text {d}\xi ^3 {\partial {}_{{\varvec{\alpha }}}W} := \int \limits _{h^-}^{h^+} {\mathbf{A}}_2^T \, {\mathbf{S}} \, \bar{\mu }\,\text {d}\xi ^3 \,. \end{aligned}$$

(21)

The components of ${\partial {}_{{\varvec{\varepsilon }}}W} =[n^{11}, n^{22}, n^{12}, m^{11}, m^{22}, m^{12}, q^{1}, q^{2}]^T$ are membrane forces, bending moments and shear forces, whereas the components of ${\partial {}_{{\varvec{\alpha }}}W}$ are higher order stress resultants.

Remark: In contrast to the independent stress resultants denoted by ${{\varvec{\sigma }}}$, we use for the stress resultants (21) computed with ${\mathbf{S}}$ via the constitutive law the notation ${\partial {}_{{\varvec{\varepsilon }}}W}$. Thus, the notation ${\partial {}_{{\varvec{\varepsilon }}}W}$ and ${\partial {}_{{\varvec{\alpha }}}W}$ has for nonlinear material laws not the meaning of derivatives of a strain energy density with respect to ${{\varvec{\varepsilon }}}$ and ${{\varvec{\alpha }}}$.

2.2.2 Thickness integration of the equilibrium equations

Neglecting body forces the component representation of the equilibrium equation $\text{ Div } \, {\mathbf{P}} = P^{kl}\!\!,_l \, {\mathbf{t}}_k = {\mathbf{0}}$ reads

$$\begin{aligned} \left[ \begin{array}{l} P^{11}\!\!,_1 + P^{12}\!\!,_2 + P^{13}\!\!,_3 \\ P^{21}\!\!,_1 + P^{22}\!\!,_2 + P^{23}\!\!,_3 \\ P^{31}\!\!,_1 + P^{32}\!\!,_2 + P^{33}\!\!,_3 \end{array} \right] := {\mathbf{f}} = {\mathbf{0}} \quad \text { in } \mathcal{B}_0 \,. \end{aligned}$$

(22)

Subsequently, the integral form of ${\mathbf{f}} = {\mathbf{0}}$ is derived. This is done in two steps. At first the derivatives of the stresses $P^{i \alpha }$ are reformulated. In a second step the terms $P^{i3}\!\!,_3$ are treated.

The derivatives of the stresses $P^{i \alpha }$ with respect to $\xi ^\alpha$ using (17) yield

$$\begin{aligned} \begin{array}{l} \left[ \begin{array}{l} P^{11}\!\!,_1 + P^{12}\!\!,_2 \\ P^{21}\!\!,_1 + P^{22}\!\!,_2 \\ P^{31}\!\!,_1 + P^{32}\!\!,_2 \end{array} \right] = {\mathbf{F}} \left[ \begin{array}{l} S^{11}\!\!,_1 + S^{12}\!\!,_2 \\ S^{21}\!\!,_1 + S^{22}\!\!,_2 \\ S^{31}\!\!,_1 + S^{32}\!\!,_2 \end{array} \right] + \left[ \begin{array}{l} \hat{p}^*_1 \\ \hat{p}^*_2 \\ \hat{p}^*_3 \end{array} \right] \\ \left[ \begin{array}{l} \hat{p}^*_1 \\ \hat{p}^*_2 \\ \hat{p}^*_3 \end{array} \right] = \left[ \begin{array}{cccccc} F_{11},_1&{}F_{12},_2&{} 0 &{}F_{11},_2+F_{12} ,_1&{}F_{13} ,_1 &{}F_{13},_2 \\ F_{21},_1&{}F_{22},_2&{} 0 &{}F_{21},_2+F_{22} ,_1&{}F_{23} ,_1 &{}F_{23},_2 \\ F_{31},_1&{}F_{32},_2&{} 0 &{}F_{31},_2+F_{32} ,_1&{}F_{33} ,_1 &{}F_{33},_2 \end{array} \right] {\mathbf{S}} \,. \end{array} \end{aligned}$$

(23)

In-plane stresses $S^{\alpha \beta }$ as well as transverse shear stresses $S^{3 \alpha }$ enter in this equation.

In the following the term $S^{31}\!\!,_1 + S^{32}\!\!,_2$ is reformulated. For this purpose the first two equations of (22) are rewritten with (17) and (23) as follows

$$\begin{aligned} \begin{array}{l} \hat{{\mathbf{F}}} \left[ \begin{array}{l} S^{11}\!\!,_1 + S^{12}\!\!,_2 + S^{13}\!\!,_3 \\ S^{21}\!\!,_1 + S^{22}\!\!,_2 + S^{23}\!\!,_3 \end{array} \right] + \left[ \begin{array}{l} p_{1} \\ p_{2} \end{array} \right] = \left[ \begin{array}{l} 0 \\ 0 \end{array} \right] \\ \hat{{\mathbf{F}}}= \left[ \begin{array}{cc} F_{11} &{} F_{12} \\ F_{21} &{} F_{22} \end{array} \right] \\ p_\alpha =\hat{p}^*_\alpha + F_{\alpha i},_3 \, S^{3i} + F_{\alpha 3} \, S^{3i}\!\!,_i \end{array} \end{aligned}$$

(24)

For arbitrary $\hat{{\mathbf{F}}} \ne {\mathbf{0}}$ and $p_\alpha \ll \hat{p}^*_3$ the transverse shear stresses follow from (24) as

$$\begin{aligned} \begin{array}{lcl} S^{13} &{}=&{} S^{31} = -\displaystyle \int \limits _{h^-}^{\xi ^3} (S^{11}\!\!,_1 + S^{12}\!\!,_2 )\,\text {d}\bar{\xi }^3 \\ S^{23} &{}=&{} S^{32} = - \displaystyle \int \limits _{h^-}^{\xi ^3} (S^{21}\!\!,_1 + S^{22}\!\!,_2 )\,\text {d}\bar{\xi }^3 \end{array} \end{aligned}$$

(25)

and the sum of the derivatives yields

$$\begin{aligned} S^{31}\!\!,_1 + S^{32}\!\!,_2 = -\int \limits _{h^-}^{\xi ^3} (S^{11}\!\!,_{11} + 2 \,S^{21}\!\!,_{12} +S^{22}\!\!,_{22})\,\text {d}\bar{\xi }^3 \,. \end{aligned}$$

(26)

In a first step we assume elastic orthotropic material behaviour. Hence, the strain energy density $\Psi ({\mathbf{E}})=\frac{1}{2} \, {\mathbf{E}}^T \, {\mathbf{C}} \, {\mathbf{E}}$ can be written in terms of the constant elasticity matrix ${\mathbf{C}}$ and the physical strains ${\mathbf{E}}$. They are obtained with the physical shell strains ${{\varvec{\varepsilon }}}$ via ${\mathbf{E}} = {\mathbf{A}}_1 \, {{\varvec{\varepsilon }}}+ \tilde{{\mathbf{A}}}_2 \, {{\varvec{\alpha }}}\,.$ Hence, the constitutive equation may be written in the following standard form

$$\begin{aligned} \begin{array}{rcl} {\partial {}_{\mathbf{E}} \Psi } = {\mathbf{S}} &{}=&{} {\mathbf{C}} \; {\mathbf{E}} \\ \left[ \begin{array}{c} S^{11} \\ S^{22} \\ S^{33} \\ S^{12} \\ S^{13} \\ S^{23} \end{array} \right] &{}=&{} \left[ \begin{array}{cccccc} C_{11} &{} C_{12} &{} C_{13} &{} C_{14} &{}0&{} 0 \\ C_{21} &{} C_{22} &{} C_{23} &{} C_{24} &{}0&{} 0 \\ C_{31} &{} C_{32} &{} C_{33} &{} C_{34} &{}0&{} 0 \\ C_{41} &{} C_{42} &{} C_{43} &{} C_{44} &{}0&{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{}C_{55}&{} C_{56} \\ 0 &{} 0 &{} 0 &{} 0 &{}C_{65}&{} C_{66} \end{array} \right] \left[ \begin{array}{r} E_{11} \\ E_{22} \\ E_{33} \\ 2E_{12} \\ 2E_{13} \\ 2E_{23} \\ \end{array} \right] _{\,.} \end{array} \end{aligned}$$

(27)

Due to the varying fibre orientation in laminated shells the constants $C_{ij} = C_{ji}$ differ for each individual layer. For the in-plane stresses holds with ${\mathbf{E}} = {\mathbf{A}}_1 \, {{\varvec{\varepsilon }}}+ \tilde{{\mathbf{A}}}_2 \, {{\varvec{\alpha }}}$ and Eq. (27)

$$\begin{aligned} \left[ \begin{array}{c} S^{11} \\ S^{22} \\ S^{12} \end{array} \right] \!=\! \left[ \! \begin{array}{ccc} C_{11} &{} C_{12} &{} C_{14} \\ C_{21} &{} C_{22} &{} C_{24} \\ C_{41} &{} C_{42} &{} C_{44} \end{array} \!\right] \!\!\left[ \! \begin{array}{r} \varepsilon _{11} + \xi ^3 \, \kappa _{11} \\ \varepsilon _{22} + \xi ^3 \, \kappa _{22} \\ 2 \varepsilon _{12} + \xi ^3 \, 2 \kappa _{12} \end{array} \!\right] \!+\! \left[ \begin{array}{c} C_{13} \\ C_{23} \\ C_{43} \end{array} \right] E_{33} \,. \end{aligned}$$

(28)

We introduce the matrices

$$\begin{aligned} \begin{array}{rcl} {\mathbf{C}}^1_{23} &{}=&{} \left[ \begin{array}{cccccc} C_{11} &{} C_{12} &{} C_{14} &{}C_{41} &{} C_{42} &{} C_{44} \\ C_{41} &{} C_{42} &{} C_{44} &{}C_{21} &{} C_{22} &{} C_{24} \end{array} \right] \\ {\mathbf{C}}^{2\; T}_{23} &{}=&{} - \displaystyle \int \limits _{h^-}^{\xi ^3} \left[ \begin{array}{r} C_{11}\\ C_{12}\\ C_{14}\\ C_{21}\\ C_{22}\\ C_{24}\\ 2 \, C_{41}\\ 2 \, C_{42}\\ 2 \, C_{44} \end{array} \right] \, \hat{\xi }^3 \, \,\text {d}\bar{\xi }^3 \end{array} \end{aligned}$$

(29)

with $\hat{\xi }^3 = \bar{\xi }^3 - \xi ^3_{ij}$. The constants $\xi ^3_{ij}$ are computed for every $C_{ij} \in \{C_{11},C_{12}, C_{14}, C_{22}, C_{24}, C_{44}\}$

$$\begin{aligned} \xi ^3_{ij} = \frac{\int \limits _{h^-}^{h^+} C_{ij} \, \xi ^3 \,\text {d}\xi ^3 }{\int \limits _{h^-}^{h^+} C_{ij} \,\text {d}\xi ^3} \text {with} \int \limits _{h^-}^{h^+} C_{ij} \,\text {d}\xi ^3 \ne 0 \,. \end{aligned}$$

(30)

For a symmetric shape of $C_{ij}$ through the thickness and $h^- = -h/2$ as well as $h^+ = h/2$ one obtains $\xi ^3_{ij} = 0$. With layerwise constant $C_{ij}$ the integration in (29)$_2$ and (30) can be done by summation over layers and analytical integration in each layer.

The derivatives of the stresses $P^{i \alpha }$ (23) yield with (26)–(30)

$$\begin{aligned} \begin{array}{rcl} \left[ \begin{array}{l} P^{11}\!\!,_1 + P^{12}\!\!,_2 \\ P^{21}\!\!,_1 + P^{22}\!\!,_2 \\ P^{31}\!\!,_1 + P^{32}\!\!,_2 \end{array} \right] &{}=&{} {\mathbf{F}} \left[ \begin{array}{ccc} {\mathbf{C}}^1_{23} &{} \xi ^3 \, {\mathbf{C}}^1_{23} &{} {\mathbf{0}} \\ {\mathbf{0}} &{} {\mathbf{0}} &{} {\mathbf{C}}^2_{23} \end{array} \right] \left[ \begin{array}{c} {{\varvec{\lambda }}}_{\varepsilon 1} \\ {{\varvec{\lambda }}}_{\kappa 1} \\ {{\varvec{\lambda }}}_{\kappa 2} \end{array} \right] + \left[ \begin{array}{l} p^*_1 \\ p^*_2 \\ p^*_3 \end{array} \right] \\ &{}=&{} {\mathbf{C}}_{23} \; {{\varvec{\lambda }}}+ {\mathbf{p}}^* , \end{array} \end{aligned}$$

(31)

where

$$\begin{aligned} {\mathbf{p}}^* = \left[ \begin{array}{l} \hat{p}^*_1 \\ \hat{p}^*_2 \\ \hat{p}^*_3 \end{array} \right] + {\mathbf{F}} \left[ \begin{array}{l} C_{13} \, E_{33},_1 + C_{43} \, E_{33},_2 \\ C_{43} \, E_{33},_1 + C_{23} \, E_{33},_2 \\ 0 \end{array} \right] _{\,.} \end{aligned}$$

(32)

The derivatives of $E_{33}$ follows from (9)$_3$ and yield $E_{33},_\beta = \tilde{{\mathbf{g}}}_3,_\beta \cdot \tilde{{\mathbf{u}}}_3 = {\mathbf{d}},_\beta \cdot \tilde{{\mathbf{u}}}_3$. However, the numerical tests show that the second part in (32) leads to negligible contributions. The vector ${{\varvec{\lambda }}}$ contains derivatives of the membrane strains and curvatures

$$\begin{aligned} \begin{array}{lcllcl} {{\varvec{\lambda }}}&{}=&{} \left[ \begin{array}{c} {{\varvec{\lambda }}}_{\varepsilon 1} \\ {{\varvec{\lambda }}}_{\kappa 1} \\ {{\varvec{\lambda }}}_{\kappa 2} \end{array} \right] &{} {{\varvec{\lambda }}}_{\varepsilon 1} &{}=&{} \left[ \begin{array}{r} \varepsilon _{11},_1 \\ \varepsilon _{22},_1 \\ 2 \varepsilon _{12},_1 \\ \varepsilon _{11},_2 \\ \varepsilon _{22},_2 \\ 2 \varepsilon _{12},_2 \end{array} \right] \\ {{\varvec{\lambda }}}_{\kappa 1} &{}=&{} \left[ \begin{array}{r} \kappa _{11},_1 \\ \kappa _{22},_1 \\ 2 \kappa _{12},_1 \\ \kappa _{11},_2 \\ \kappa _{22},_2 \\ 2 \kappa _{12},_2 \end{array} \right] &{} {{\varvec{\lambda }}}_{\kappa 2} &{}=&{} \left[ \begin{array}{rcl} \kappa _{11},_{11} \\ \kappa _{22},_{11} \\ 2 \kappa _{12},_{11} \\ \kappa _{11},_{22} \\ \kappa _{22},_{22} \\ 2 \kappa _{12},_{22} \\ \kappa _{11},_{12} \\ \kappa _{22},_{12} \\ 2\kappa _{12},_{12} \\ \end{array} \right] _{\,.} \end{array} \end{aligned}$$

(33)

Next we introduce

$$\begin{aligned} \begin{array}{lrl} {\partial {}_{{\varvec{\alpha }}}W} &{}=&{} -\displaystyle \int \limits _{h^-}^{h^+} {\varvec{\Phi }}^T \left[ \begin{array}{l} P^{13}\!\!,_3 \\ P^{23}\!\!,_3 \\ P^{33}\!\!,_3 \end{array} \right] \, \bar{\mu }\, \,\text {d}\xi ^3 + {\mathbf{q}} \\ {\mathbf{D}}_{23} &{}:=&{} - \displaystyle \int \limits _{h^-}^{h^+} {\varvec{\Phi }}^T {\mathbf{C}}_{23} \, \bar{\mu }\,\text {d}\xi ^3 \,, \end{array} \end{aligned}$$

(34)

where the reformulation of ${\partial {}_{{\varvec{\alpha }}}W}$ with $\bar{\mu }= 1$ according to (21)$_2$ is obtained with integration by parts. Here, one needs the relation

$$\begin{aligned} {\mathbf{A}}^{T}_2 \, {\mathbf{S}} = {\varvec{\Phi }}^T\!\!,_3 \left[ \begin{array}{c} P^{13} \\ P^{23} \\ P^{33} \end{array} \right] _{\,,} \end{aligned}$$

(35)

with ${\mathbf{A}}_2$ and $P^{i3}$ from (14) and (17), respectively. Considering the stress boundary conditions (18) one obtains for the boundary term

$$\begin{aligned} {\mathbf{q}} = \left[ \begin{array}{c} {\mathbf{p}}^-, \; {\mathbf{0}}_{M-6} , \; {\mathbf{p}}^+ \end{array} \right] ^T \,, \end{aligned}$$

(36)

where ${\mathbf{p}}^- = p^- \, {\mathbf{N}}$ and ${\mathbf{p}}^+ = p^+ \, {\mathbf{N}}$. Furthermore, ${\mathbf{0}}_n$ denotes a zero vector with n components.

The weighted integral of ${\mathbf{p}}^*$ is constant as is taken from the last load increment. Therefore it can be summarized with ${\mathbf{q}}$

$$\begin{aligned} \bar{{\mathbf{q}}} := {\mathbf{q}} + {\mathbf{q}}^* {\mathbf{q}}^* = \displaystyle \int \limits _{h^-}^{h^+} {\varvec{\Phi }}^T {\mathbf{p}}^* \, \bar{\mu }\, \,\text {d}\xi ^3 \,. \end{aligned}$$

(37)

Now the integral form of ${\mathbf{f}} = {\mathbf{0}}$ (22) is formulated with $\delta \tilde{{\mathbf{u}}} = {\varvec{\Phi }} \, \delta {{\varvec{\alpha }}}$ and Eqs. (31)–(37)

$$\begin{aligned} \int \limits _{h^-}^{h^+} \delta \tilde{{\mathbf{u}}}^T \, {\mathbf{f}} \, \bar{\mu }\,\text {d}\xi ^3 = - \delta {{\varvec{\alpha }}}^T ({\partial {}_{{\varvec{\alpha }}}W} + {\mathbf{D}}_{23} \, {{\varvec{\lambda }}}- \bar{{\mathbf{q}}}) = 0 \,. \end{aligned}$$

(38)

With $\delta {{\varvec{\alpha }}}\ne {\mathbf{0}}$ one obtains the equilibrium of higher order stress resultants

$$\begin{aligned} {\partial {}_{{\varvec{\alpha }}}W} + {\mathbf{D}}_{23} \, {{\varvec{\lambda }}}- \bar{{\mathbf{q}}} = {\mathbf{0}} \,. \end{aligned}$$

(39)

2.2.3 Thickness integration of a constraint

The displacement field $\tilde{{\mathbf{u}}}$ must fulfill a constraint. To specify this equation we introduce the equilibrium of virtual stresses $\delta P^{i \alpha }$. As ${\mathbf{C}}_{23}$ and ${\mathbf{p}}^*$ are constant in Eq. (31) one obtains

$$\begin{aligned} \left[ \begin{array}{l} \delta P^{11}\!\!,_1 + \delta P^{12}\!\!,_2 \\ \delta P^{21}\!\!,_1 + \delta P^{22}\!\!,_2 \\ \delta P^{31}\!\!,_1 + \delta P^{32}\!\!,_2 \\ \end{array} \right] = {\mathbf{C}}_{23} \, \delta {{\varvec{\lambda }}}:= \delta {\mathbf{f}}_1 = {\mathbf{0}} \,. \end{aligned}$$

(40)

The integral form of $\delta {\mathbf{f}}_1 = {\mathbf{0}}$ yields with $\tilde{{\mathbf{u}}} = {\varvec{\Phi }} \, {{\varvec{\alpha }}}$

$$\begin{aligned} \int \limits _{h^-}^{h^+} \delta {\mathbf{f}}^T_1 \tilde{{\mathbf{u}}} \, \bar{\mu }\, \,\text {d}\xi ^3 = \delta {{\varvec{\lambda }}}^T \int \limits _{h^-}^{h^+} {\mathbf{C}}_{23}^T \, {\varvec{\Phi }} \, \bar{\mu }\, \,\text {d}\xi ^3 \, {{\varvec{\alpha }}}= 0 \,. \end{aligned}$$

(41)

With

$$\begin{aligned} {\mathbf{D}}_{32} = - \int \limits _{h^-}^{h^+} {\mathbf{C}}_{23}^T \, {\varvec{\Phi }} \, \bar{\mu }\,\,\text {d}\xi ^3 = {\mathbf{D}}_{23}^T \end{aligned}$$

(42)

Eq. (41) reads $-\delta {{\varvec{\lambda }}}^T {\mathbf{D}}_{32} \, {{\varvec{\alpha }}}= 0$ where $\delta {{\varvec{\lambda }}}\ne {\mathbf{0}}$. One obtains the constraint

$$\begin{aligned} {\mathbf{g}}({{\varvec{\alpha }}}) = {\mathbf{D}}_{32} \, {{\varvec{\alpha }}}= {\mathbf{0}} \,, \end{aligned}$$

(43)

which enforces the correct shape of the displacements $\tilde{{\mathbf{u}}}$ through the thickness. It has the descriptive meaning that the superposed warping displacements and thickness changes must not lead to additional stress resultants.

2.2.4 Extension to elasto-plastic material behaviour

The extension to elasto-plastic material behaviour is possible. In the following we consider small strain plasticity with an additive decomposition of the total strains ${\mathbf{E}} = {\mathbf{E}}^{el} + {\mathbf{E}}^{pl}$ in elastic and plastic part and Eq. (27) is replaced by

$$\begin{aligned} {\mathbf{S}} = {\mathbf{C}} \, ({\mathbf{E}} - {\mathbf{E}}^{pl}) \,. \end{aligned}$$

(44)

The vector ${\mathbf{E}}^{pl}= \left[ E^{pl}_{11} , E^{pl}_{22} , E^{pl}_{33} , 2E^{pl}_{12} , 2E^{pl}_{13} , 2E^{pl}_{23} \right] ^T$ leads to further contributions in ${\mathbf{p}}^*$ according to (32). It has to be replaced by

$$\begin{aligned} \begin{array}{rcl} {\mathbf{p}}^* &{}=&{} \left[ \begin{array}{l} \hat{p}^*_1 \\ \hat{p}^*_2 \\ \hat{p}^*_3 \end{array} \right] + {\mathbf{F}} \left[ \begin{array}{l} C_{13} \, E_{33},_1 + C_{43} \, E_{33},_2 \\ C_{43} \, E_{33},_1 + C_{23} \, E_{33},_2 \\ 0 \end{array} \right] - {\mathbf{F}} \left[ \begin{array}{l} p^{pl}_1 \\ p^{pl}_2 \\ 0 \end{array} \right] \\ p^{pl}_1 &{}=&{} C_{11} \, E^{pl}_{11},_1 + C_{12} \, E^{pl}_{22},_1 + C_{13} \, E^{pl}_{33},_1 + 2 \, C_{14} \, E^{pl}_{12},_1 \\ &{}+&{} C_{41} \, E^{pl}_{11},_2 + C_{42} \, E^{pl}_{22},_2 + C_{43} \, E^{pl}_{33},_2 + 2 \, C_{44} \, E^{pl}_{12},_2 \\ p^{pl}_1 &{}=&{} C_{41} \, E^{pl}_{11},_1 + C_{42} \, E^{pl}_{22},_1 + C_{43} \, E^{pl}_{33},_1 + 2 \, C_{44} \, E^{pl}_{12},_1 \\ &{}+&{} C_{21} \, E^{pl}_{11},_2 + C_{22} \, E^{pl}_{22},_2 + C_{23} \, E^{pl}_{33},_2 + 2 \, C_{24} \, E^{pl}_{12},_2 \,. \end{array} \end{aligned}$$

(45)

The vector ${\mathbf{p}}^*$ depends on the deformation. To maintain quadratic convergence in the Newton iteration process, the constant values of the last load increment are used. As already written above this requires a variation of the load step size to assess this approximation.

2.3 Linearized weak form of the boundary value problem

In the following the weak form of the boundary value problem and associated linearization is derived. For a compact representation the vector ${{\varvec{\theta }}}$ and admissible variation $\delta {{\varvec{\theta }}}$ are introduced

$$\begin{aligned} \begin{array}{rclrcl} {{\varvec{\theta }}}&{}:=&{} \left[ \begin{array}{c} {{\varvec{\varepsilon }}}_g ({\mathbf{v}}) \\ {{\varvec{\sigma }}}\\ {{\varvec{\vartheta }}}\end{array} \right] \quad &{} \delta {{\varvec{\theta }}}&{}:=&{} \left[ \begin{array}{c} \delta {{\varvec{\varepsilon }}}_g ({\mathbf{v}},\delta {\mathbf{v}}) \\ \delta {{\varvec{\sigma }}}\\ \delta {{\varvec{\vartheta }}}\end{array} \right] \\ {{\varvec{\vartheta }}}&{}:=&{}\left[ \begin{array}{c} {{\varvec{\varepsilon }}}\\ {{\varvec{\alpha }}}\\ {{\varvec{\lambda }}}\end{array} \right] &{} \delta {{\varvec{\vartheta }}}&{}:=&{}\left[ \begin{array}{c} \delta {{\varvec{\varepsilon }}}\\ \delta {{\varvec{\alpha }}}\\ \delta {{\varvec{\lambda }}}\end{array} \right] \,. \end{array} \end{aligned}$$

(46)

Furthermore,

$$\begin{aligned} {{\varvec{\psi }}}:= \left[ \begin{array}{c} {\partial {}_{{\varvec{\varepsilon }}}W} - {{\varvec{\sigma }}}\\ {\partial {}_{{\varvec{\alpha }}}W} + {\mathbf{D}}_{23} \, {{\varvec{\lambda }}}- \bar{{\mathbf{q}}} \\ {\mathbf{D}}_{32} \, {{\varvec{\alpha }}}\end{array} \right] = {\mathbf{0}} \end{aligned}$$

(47)

summarizes the constitutive equation, the equilibrium of higher order stress resultants (39) and the constraint (43).

Hence, the weak form of the boundary value problem can be written as

$$\begin{aligned} g({{\varvec{\theta }}}, \delta {{\varvec{\theta }}}) = \displaystyle \int \limits _{\Omega } \, \left[ \begin{array}{c} \delta {{\varvec{\varepsilon }}}_g \\ \delta {{\varvec{\sigma }}}\\ \delta {{\varvec{\vartheta }}}\\ \end{array} \right] ^T \left[ \begin{array}{c} {{\varvec{\sigma }}}\\ {{\varvec{\varepsilon }}}_g - {{\varvec{\varepsilon }}}\\ {{\varvec{\psi }}}\end{array} \right] \,\text {d}A + g_{ext} = 0 \,. \end{aligned}$$

(48)

The shell is loaded statically by surface loads ${\mathbf{p}}^+ = p^+ \, {\mathbf{N}}$ and ${\mathbf{p}}^- = p^- \,{\mathbf{N}}$ acting at the outer surfaces, see Fig. 1 and by boundary forces $\bar{{\mathbf{t}}}$ on the boundary $\Gamma _\sigma$. Hence, the virtual work of the external forces reads

$$\begin{aligned} g_{ext} = \displaystyle -\int \limits _{\Omega } (\bar{{\mathbf{p}}} \cdot \delta {\mathbf{u}} + \bar{{\mathbf{m}}} \cdot \delta {\mathbf{d}} ) \,\text {d}A -\int \limits _{\Gamma _\sigma } \bar{{\mathbf{t}}} \cdot \delta {\mathbf{u}} \,\text {d}s \end{aligned}$$

(49)

with surface loads $\bar{{\mathbf{p}}} = {\mathbf{p}}^+ + {\mathbf{p}}^-$ and couple loads $\bar{{\mathbf{m}}} = h^+ \, {\mathbf{p}}^+ + h^- \, {\mathbf{p}}^-$.

With application of integration by parts to the integral of $\delta {{\varvec{\varepsilon }}}_g^T \, {{\varvec{\sigma }}}$ in Eq. (48) and use of standard arguments of variational calculus one obtains as Euler–Lagrange equations the equilibrium of stress resultants and couple resultants, the geometric field equation ${{\varvec{\varepsilon }}}_g - {{\varvec{\varepsilon }}}= {\mathbf{0}}$ and ${{\varvec{\psi }}}= {\mathbf{0}}$ in $\Omega$ along with the static boundary conditions ${\mathbf{t}} = \bar{{\mathbf{t}}}$ on $\Gamma _\sigma$.

The associated nonlinear finite element equations are iteratively solved using Newton’s method. For this purpose variational equation (48) is linearized. With ${\mathbf{A}}_2= {\mathbf{A}}_2({{\varvec{\alpha }}})$ one has to consider Eq. (16). The following matrices are introduced

$$\begin{aligned} \begin{array}{l} \dfrac{\partial {{\varvec{\psi }}}}{\partial {{\varvec{\vartheta }}}} := {\mathbf{D}} = \left[ \begin{array}{ccc} {\mathbf{D}}_{11} &{} {\mathbf{D}}_{12} &{} {\mathbf{0}} \\ {\mathbf{D}}_{21} &{} {\mathbf{D}}_{22} &{} {\mathbf{D}}_{23} \\ {\mathbf{0}} &{} {\mathbf{D}}_{32} &{} {\mathbf{0}} \\ \end{array} \right] {\mathbf{I}} := \left[ \begin{array}{r} -{\mathbf{1}} \\ {\mathbf{0}} \\ {\mathbf{0}} \end{array} \right] \\ {\mathbf{D}}_{\alpha \beta } = \displaystyle \int \limits _{h^-}^{h^+} \, {\mathbf{A}}_\alpha ^T \, {\mathbf{C}}_T \, {\mathbf{A}}_\beta \, \bar{\mu }\, \,\text {d}\xi ^3 \alpha \beta \in \{11,12,21\} \\ {\mathbf{D}}_{22} = \displaystyle \int \limits _{h^-}^{h^+} \, ({\mathbf{A}}_2^T \, {\mathbf{C}}_T \, {\mathbf{A}}_2 + S^{33} \, {\varvec{\Phi }}^T\!\!,_3 {\varvec{\Phi }},_3 )\, \bar{\mu }\, \,\text {d}\xi ^3 \end{array} \end{aligned}$$

(50)

and ${\mathbf{D}}_{23}$ according to (34). The matrix ${\mathbf{C}}_T = {\partial {}_{\mathbf{E}} {\mathbf{S}}}$ denotes the algorithmic tangent matrix. The singular matrix ${\mathbf{D}} = {\mathbf{D}}^T$ is of order $29 + K$. The integration of the submatrices ${\mathbf{D}}_{ij}$ is performed by summation over M layers and three point Gauss integration for each layer. With $\,\text {d}\xi ^3 = \frac{h^i}{2} \,\text {d}\zeta$ one obtains

$$\begin{aligned} {\mathbf{D}}_{ij} \approx \sum _{i=1}^M \sum _{j=1}^3 {\mathbf{C}}_{ij} (\zeta _j) \, \bar{\mu }\, \dfrac{h^i}{2} \, W_j \,, \end{aligned}$$

(51)

where ${\mathbf{C}}_{ij}$ denotes the respective integrand of ${\mathbf{D}}_{ij}$. Furthermore, $\zeta _j$ and $W_j$ are the normalized thickness coordinate and weighting factor of the particular Gauss point, respectively. For the determinant of the shifter tensor the first approximation $\bar{\mu }= 1$ is taken. In case of linear elasticity ${\mathbf{C}}_T$ is constant and the numerical integration is exact.

With displacement independent loads $\bar{{\mathbf{p}}}$, $\bar{{\mathbf{m}}}$, $\bar{{\mathbf{t}}}$ and consideration of (50) one obtains the linearized weak form

$$\begin{aligned} \begin{array}{l} \,\text {L}[g({{\varvec{\theta }}}, \delta {{\varvec{\theta }}}), \Delta {{\varvec{\theta }}}] = g_{ext} \!+\!\displaystyle \int \limits _{\Omega }\! \bar{{\mathbf{m}}} \cdot \Delta \delta {\mathbf{d}} \,\text {d}A \!+ \!\displaystyle \int \limits _{\Omega }\! \Delta \delta {{\varvec{\varepsilon }}}_g^T {{\varvec{\sigma }}}\,\text {d}A \\ + \displaystyle \int \limits _{\Omega } \left[ \begin{array}{c} \delta {{\varvec{\varepsilon }}}_g \\ \delta {{\varvec{\sigma }}}\\ \delta {{\varvec{\vartheta }}}\\ \end{array} \right] ^T \left\{ \left[ \begin{array}{c} {{\varvec{\sigma }}}\\ {{\varvec{\varepsilon }}}_g - {{\varvec{\varepsilon }}}\\ {{\varvec{\psi }}}\end{array} \right] + \left[ \begin{array}{ccc} {\mathbf{0}} &{} {\mathbf{1}} &{} {\mathbf{0}} \\ {\mathbf{1}} &{} {\mathbf{0}} &{} {\mathbf{I}}^T \\ {\mathbf{0}} &{} {\mathbf{I}} &{} {\mathbf{D}} \\ \end{array} \right] \, \left[ \begin{array}{c} \Delta {{\varvec{\varepsilon }}}_g \\ \Delta {{\varvec{\sigma }}}\\ \Delta {{\varvec{\vartheta }}}\end{array} \right] \right\} \,\text {d}A \,. \end{array} \end{aligned}$$

(52)

The second variation $\Delta \delta {\mathbf{d}}$ of the current director vector has been derived e.g. in Ref. [25].

3 Finite element formulation

The approximation of initial and current geometry of the shell reference surface applying the isoparametric concept for 4-node elements is specified in detail in Refs. [25, 26]. Bilinear functions $N_I(\xi , \eta )$ are used, where for the coordinates of the unit square $-1\le \{\xi , \eta \} \le 1$ holds. The local orthonormal element coordinate system is denoted by $[{\mathbf{t}}_1,{\mathbf{t}}_2,{\mathbf{t}}_3]$ , where ${\mathbf{t}}_3$ is normal vector of the approximated shell surface at the element center. With the vectors of nodal coordinates ${\mathbf{X}}_i \; (i=1...4)$ it holds

$$\begin{aligned} \begin{array}{rclcrcl} \bar{{\mathbf{d}}}_1 &{}=&{} {\mathbf{X}}_3 - {\mathbf{X}}_1 \qquad &{} {\mathbf{ \widehat{d}_1}} &{}=&{} \bar{{\mathbf{d}}}_1 / |\bar{{\mathbf{d}}}_1 | \\ \bar{{\mathbf{d}}}_2 &{}=&{} {\mathbf{X}}_2 - {\mathbf{X}}_4 \qquad &{} {\mathbf{ \widehat{d}_2}} &{}=&{} \bar{{\mathbf{d}}}_2 / |\bar{{\mathbf{d}}}_2 | \\ {\mathbf{t}}_1 &{}=&{} ({\mathbf{ \widehat{d}_1}} + {\mathbf{ \widehat{d}_2}})/|{\mathbf{ \widehat{d}_1}} + {\mathbf{ \widehat{d}_2}}| \\ {\mathbf{t}}_2 &{}=&{} ({\mathbf{ \widehat{d}_1}} - {\mathbf{ \widehat{d}_2}})/|{\mathbf{ \widehat{d}_1}} - {\mathbf{ \widehat{d}_2}}| \\ {\mathbf{t}}_3 &{}=&{} {\mathbf{t}}_1 \times {\mathbf{t}}_2 \,. \end{array} \end{aligned}$$

(53)

Hence, the Jacobian matrix ${\mathbf{J}}$ reads

$$\begin{aligned} {\mathbf{J}} = \left[ \begin{array}{cc} J_{11} &{} J_{12} \\ J_{21} &{} J_{22} \\ \end{array} \right] = \left[ \begin{array}{cc} {\mathbf{X}}^h_0,_\xi \cdot {\mathbf{t}}_1 &{} {\mathbf{X}}^h_0,_\xi \cdot {\mathbf{t}}_2 \\ {\mathbf{X}}^h_0,_\eta \cdot {\mathbf{t}}_1 &{} {\mathbf{X}}^h_0,_\eta \cdot {\mathbf{t}}_2 \\ \end{array} \right] _{\,.} \end{aligned}$$

(54)

The superscript h refers to the finite element approximation of the particular quantity, and commas denote the partial derivative with respect to $\xi$ or $\eta$.

The shape of the quantities $\delta {{\varvec{\theta }}}^h$ is chosen as follows

$$\begin{aligned} \delta {{\varvec{\theta }}}^h := \left[ \begin{array}{c} \delta {{\varvec{\varepsilon }}}^h_g \\ \delta {{\varvec{\sigma }}}^h \\ \delta {{\varvec{\vartheta }}}^h \end{array} \right] = \left[ \begin{array}{ccc} {\mathbf{B}} &{} {\mathbf{0}}&{} {\mathbf{0}} \\ {\mathbf{0}} &{} {\mathbf{N}}_\sigma &{} {\mathbf{0}} \\ {\mathbf{0}} &{} {\mathbf{0}}&{} {\mathbf{N}}_\vartheta \\ \end{array} \right] \left[ \begin{array}{c} \delta \hat{{\mathbf{v}}} \\ \delta \hat{{\varvec{\sigma }}}\\ \delta \hat{{\varvec{\vartheta }}}\end{array} \right] _{\,.} \end{aligned}$$

(55)

To avoid shear locking, ansatz functions of the assumed strain method [27] are incorporated in ${\mathbf{B}}$, see Ref. [25].

The matrix ${\mathbf{N}}_\sigma$ for the interpolation of $\delta {{\varvec{\sigma }}}^h = {\mathbf{N}}_\sigma \, \delta \hat{{\varvec{\sigma }}}$ as well as ${{\varvec{\sigma }}}^h$ is chosen as follows

$$\begin{aligned} \begin{array}{rcl} {\mathbf{N}}_\sigma &{}=&{} \left[ \begin{array}{ccc ccc} {\mathbf{1}}_3 &{} {\mathbf{0}} &{} {\mathbf{0}} &{} {\mathbf{N}}^m_\sigma &{} {\mathbf{0}} &{} {\mathbf{0}} \\ {\mathbf{0}} &{} {\mathbf{1}}_3 &{} {\mathbf{0}} &{} {\mathbf{0}} &{} {\mathbf{N}}^b_\sigma &{} {\mathbf{0}} \\ {\mathbf{0}} &{} {\mathbf{0}} &{} {\mathbf{1}}_2 &{} {\mathbf{0}} &{} {\mathbf{0}} &{} {\mathbf{N}}^s_\sigma \\ \end{array} \right] \\ {\mathbf{N}}^m_\sigma &{}=&{} {\mathbf{N}}^b_\sigma = {\mathbf{T}}^0_\sigma \, \left[ \begin{array}{cc} \eta -\bar{\eta }&{} 0 \\ 0 &{} \xi -\bar{\xi }\\ 0 &{} 0 \\ \end{array} \right] \\ {\mathbf{N}}^s_\sigma &{}=&{} \tilde{{\mathbf{T}}}^0_\sigma \, \left[ \begin{array}{cc} \eta -\bar{\eta }&{} 0 \\ 0 &{} \xi -\bar{\xi }\\ \end{array} \right] _{\,.} \end{array} \end{aligned}$$

(56)

The coefficient matrices ${\mathbf{T}}^0_\sigma$, $\tilde{{\mathbf{T}}}^0_\sigma$ describe a transformation of contravariant tensor components to the constant base system ${\mathbf{t}}_i$. The matrices and the constants $\bar{\xi }$ and $\bar{\eta }$ are specified in [25]. The parameter vectors $\hat{{\varvec{\sigma }}}$ and $\delta \hat{{\varvec{\sigma }}}$ contain 8 parameters for the constant part and 6 parameters for the varying part of the stress field. The interpolation of the membrane forces and bending moments corresponds to the membrane part in Ref. [28]. The original approach for plane stress problems was published in Ref. [29]. Regarding requirements on the interpolation functions to fulfill the patch test and to ensure stability of the discrete system of equations we refer to the discussion in Ref. [25].

The interpolation for ${{\varvec{\vartheta }}}$ and equivalent $\delta {{\varvec{\vartheta }}}$ is chosen as follows

$$\begin{aligned} \begin{array}{rcl} \left[ \begin{array}{c} {{\varvec{\varepsilon }}}^h \\ {{\varvec{\alpha }}}^h \\ {{\varvec{\lambda }}}^h \end{array} \right] &{}=&{} \left[ \begin{array}{ccccc} {\mathbf{N}}^1_\varepsilon &{}{\mathbf{N}}^2_\varepsilon &{} {\mathbf{0}} &{} {\mathbf{0}} &{} {\mathbf{N}}^3_\varepsilon \\ {\mathbf{0}} &{}{\mathbf{0}} &{} {\mathbf{0}} &{} {\mathbf{N}}_\alpha &{} {\mathbf{0}} \\ {\mathbf{0}} &{}{\mathbf{0}} &{} {\mathbf{N}}^2_\lambda &{} {\mathbf{0}} &{} {\mathbf{N}}^3_\lambda \end{array} \right] \left[ \begin{array}{c} \hat{{\varvec{\varepsilon }}}\\ \hat{{\varvec{\lambda }}}_1 \\ \hat{{\varvec{\lambda }}}_2 \\ \hat{{\varvec{\alpha }}}\\ \hat{{\varvec{\lambda }}}_3 \end{array} \right] \\ {{\varvec{\vartheta }}}^h &{}=&{} {\mathbf{N}}_\vartheta \; \hat{{\varvec{\vartheta }}}\,, \end{array} \end{aligned}$$

(57)

where $\hat{{\varvec{\varepsilon }}}\in \mathbb {R}^{8}, \hat{{\varvec{\lambda }}}_1 \in \mathbb {R}^{6}, \hat{{\varvec{\lambda }}}_2 \in \mathbb {R}^{4}, \hat{{\varvec{\lambda }}}_3 \in \mathbb {R}^{l}, l=n+9$ and $\hat{{\varvec{\alpha }}}\in \mathbb {R}^K$. The submatrices associated with ${{\varvec{\varepsilon }}}^h$ read

$$\begin{aligned} \begin{array}{rcl} {\mathbf{N}}^1_\varepsilon &{}=&{} {\mathbf{1}} _8 \\ {\mathbf{N}}_\varepsilon ^2 &{}=&{} \left[ \begin{array}{ccc} {\mathbf{N}}^{m2}_\varepsilon &{} {\mathbf{0}} &{} {\mathbf{0}} \\ {\mathbf{0}} &{} {\mathbf{N}}^{b2}_\varepsilon &{} {\mathbf{0}} \\ {\mathbf{0}} &{} {\mathbf{0}} &{} {\mathbf{N}}^{s2}_\varepsilon \end{array} \right] _{8 \times 6} \\ {\mathbf{N}}_\varepsilon ^3 &{}=&{} \left[ \begin{array}{cc} \frac{j_0}{j} \, ({\mathbf{T}}^0_\sigma )^{-T} \, {\mathbf{M}}^m_n &{} {\mathbf{0}} \\ {\mathbf{0}} &{} \frac{j_0}{j} \, ({\mathbf{T}}^0_\sigma )^{-T} \, {\mathbf{M}}^b \\ {\mathbf{0}} &{} {\mathbf{0}} \end{array} \right] _{8 \times l} \end{array} \end{aligned}$$

(58)

with $j_0 = j \, (\xi = 0, \eta = 0)$ where $j=|\,{\mathbf{X}}^h_0,_\xi \times {\mathbf{X}}^h_0,_\eta |$. The submatrices of ${\mathbf{N}}^2_\varepsilon$ read

$$\begin{aligned} \begin{array}{rcl} {\mathbf{N}}^{m2}_\varepsilon &{}=&{} {\mathbf{N}}^{b2}_\varepsilon = {\mathbf{T}}^0_\varepsilon \left[ \begin{array}{cc} \eta - \bar{\eta }&{} 0 \\ 0 &{} \xi - \bar{\xi }\\ 0 &{} 0 \end{array} \right] \\ {\mathbf{N}}^{s2}_\varepsilon &{}=&{} \tilde{{\mathbf{T}}}^0_\varepsilon \, \left[ \begin{array}{cc} \eta - \bar{\eta }&{} 0 \\ 0 &{} \xi - \bar{\xi }\end{array} \right] _{\,.} \end{array} \end{aligned}$$

(59)

The coefficient matrices ${\mathbf{T}}^0_\varepsilon$ and $\tilde{{\mathbf{T}}}^0_\varepsilon$

$$\begin{aligned} \begin{array}{rcl} {\mathbf{T}}^0_\varepsilon &{}=&{} \left[ \begin{array}{ccc} J^0_{11} \, J^0_{11} &{} J^0_{21}\,J^0_{21} &{} J^0_{11}\,J^0_{21} \\ J^0_{12} \, J^0_{12} &{} J^0_{22}\,J^0_{22} &{} J^0_{12}\,J^0_{22} \\ 2 \, J^0_{11} \, J^0_{12} &{} ~2 \, J^0_{21}\,J^0_{22}~&{} J^0_{11}\,J^0_{22} + J^0_{12}\,J^0_{21} \\ \end{array} \right] \\ \tilde{{\mathbf{T}}}^0_\varepsilon &{}=&{} \left[ \begin{array}{cc} J^0_{11} &{} J^0_{21} \\ J^0_{12} &{} J^0_{22} \\ \end{array} \right] \end{array} \end{aligned}$$

(60)

cause a transformation of contravariant tensor components to the constant element base system ${\mathbf{t}}_i$. The entries $J_{\alpha \beta }^0$ are the components of ${\mathbf{J}}$ according to (54) evaluated at the element center. Detailed investigations on the use of ansatz functions for contravariant stress and strain components in the framework of a Hu-Washizu functional are contained in Ref. [30].

The interpolation matrix ${\mathbf{M}}^m_n$ is chosen as

$$\begin{aligned} {\mathbf{M}}^m_n \!\!=\!\! \left[ \begin{array}{ccccccccccc} \xi &{} 0 &{}0&{}0 &{}\xi \eta &{}0&{}0 &{} (\xi ^2-c)\, \eta &{} 0 &{}\eta ^2 \,\xi &{}0 \\ 0 &{} \eta &{}0&{}0 &{}0 &{}\xi \eta &{} 0 &{}0&{} (\eta ^2-c)\,\xi &{}0&{} \xi ^2 \,\eta \\ 0 &{} 0 &{}\xi &{} \eta &{}0&{}0&{} \xi \eta &{}0&{}0 &{}0&{}0 \end{array} \right] _{,} \end{aligned}$$

(61)

where the index $n \in \{0,2,4,6,7,9,11\}$ has the meaning that optionally the first n columns are taken. With $n=0$ the matrix is omitted. Due to the factor $j_0/j$ and the constant coefficient matrix ${\mathbf{T}}^0_\varepsilon$ the integrals of the functions $(\xi , \eta , \xi \, \eta , \xi ^2 \, \eta , \eta ^2 \,\xi )$ in ${\mathbf{N}}^2_{\varepsilon }$ over the element domain $\Omega _e$ vanish.

The shape factor c considers the deviation of the element geometry from a square and warping of the particular element. For this purpose the metric coefficients $G_{\alpha \beta }$ of the initial reference surface are evaluated at the element center

$$\begin{aligned} \begin{array}{l} {\mathbf{G}}_0 =\left[ \begin{array}{cc} G_{11} &{} G_{12} \\ G_{21} &{} G_{22} \end{array} \right] \\ \begin{array}{rclrcl} G_{11} &{}=&{} {\mathbf{X}}_0,_\xi \cdot {\mathbf{X}}_0,_\xi \ \qquad &{} G_{12} &{}=&{} {\mathbf{X}}_0,_\xi \cdot {\mathbf{X}}_0,_\eta \\ G_{22} &{}=&{} {\mathbf{X}}_0,_\eta \cdot {\mathbf{X}}_0,_\eta \qquad &{} G_{21} &{}=&{} G_{12} \,. \end{array} \end{array} \end{aligned}$$

(62)

A principal axis analysis leads to

$$\begin{aligned} \begin{array}{l} \widehat{{\mathbf{G}}}_0 =\left[ \begin{array}{cc} \lambda ^2_\text {min} &{} 0 \\ 0 &{} \lambda ^2_\text {max} \end{array} \right] \\ \lambda ^2_{\text {max},\text {min}} = \frac{1}{2} \, (G_{11}+G_{22} ) \pm \sqrt{\frac{1}{4} (G_{11}-G_{22})^2+G_{12}^2} \end{array} \end{aligned}$$

(63)

with $\lambda ^2_\text {min} > 0$, as ${\mathbf{G}}_0$ is positive definite.

Fig. 2

a Inscribed ellipse in a distorted element (flat projection $\Omega ^h_0$), b element warping

Introducing $\hat{{\mathbf{x}}} =[\hat{x}, \hat{y} ]^T$ one obtains for the quadratic form $\hat{{\mathbf{x}}}^T \, \widehat{{\mathbf{G}}}^0 \, \hat{{\mathbf{x}}} := r^2 = \hat{x}^2 \, \lambda ^2_\text {min} +\hat{y}^2 \, \lambda ^2_\text {max}$ and thus the equation of an ellipse

$$\begin{aligned} \frac{\hat{x}^2}{a^2} + \frac{\hat{y}^2}{b^2} = 1 \text {with} a = \frac{r}{\lambda _\text {min}} \qquad b = \frac{r}{\lambda _\text {max}} \,. \end{aligned}$$

(64)

Here, a and b $(a \ge b)$ denote the semiaxes of the ellipse which can be inscribed in the flat projection $\Omega ^h_0$ of a distorted element, see Fig. 2a. Furthermore, the element warping d according to Fig. 2b is computed. One obtains

$$\begin{aligned} \begin{array}{lrl} d &{}=&{} | {\mathbf{X}}_d \cdot {\mathbf{t}}_3| \\ {\mathbf{X}}_d &{}:=&{} {\mathbf{X}}_0,_{\xi \eta } = \frac{1}{4}({\mathbf{X}}_1 - {\mathbf{X}}_2 + {\mathbf{X}}_3 - {\mathbf{X}}_4) \end{array} \end{aligned}$$

(65)

with the position vectors ${\mathbf{X}}_i$ of the four nodes and the normal vector ${\mathbf{t}}_3$. Hence, c is defined as

$$\begin{aligned} c = \sqrt{ \Big (\dfrac{a}{b}\Big )^2 + \Big (\dfrac{d}{h}\Big )^2 } \text {with} \frac{a}{b} = \frac{\lambda _\text {max}}{\lambda _\text {min}} \qquad \end{aligned}$$

(66)

as well as d and the shell thickness h. The part a/b considers the in-plane distortion and d/h the out-of-plane distortion of the particular element. For a flat square element holds $c=1$. The impact of c on the element convergence behaviour is demonstrated by means of the numerical examples.

The matrix ${\mathbf{M}}^b$, associated with the curvatures, reads

$$\begin{aligned} {\mathbf{M}}^b = \left[ \begin{array}{ccccccccc} \xi &{} 0 &{}0&{}0 &{}\xi \, \eta &{}0&{}0 &{} \xi ^2 \, \eta &{} 0 \\ 0 &{} \eta &{}0&{}0 &{}0 &{}\xi \eta &{} 0 &{}0&{} \eta ^2 \,\xi \\ 0 &{} 0 &{}\xi &{} \eta &{}0&{}0&{} \xi \eta &{}0&{}0 \end{array} \right] _{3 \times 9 \,.} \end{aligned}$$

(67)

With ${\mathbf{N}}_\alpha = {\mathbf{1}}_K$ the vector ${{\varvec{\alpha }}}^h$ is constant within each element. Considering Eq. (57) the interpolation for ${{\varvec{\lambda }}}^h = [{{\varvec{\lambda }}}^h_{\varepsilon 1}, {{\varvec{\lambda }}}^h_{\kappa 1}, {{\varvec{\lambda }}}^h_{\kappa 2}]^T$ is performed with ${{\varvec{\lambda }}}^h = {\mathbf{N}}^2_\lambda \, \hat{{\varvec{\lambda }}}_2 + {\mathbf{N}}^3_\lambda \, \hat{{\varvec{\lambda }}}_3$ using the matrices

$$\begin{aligned} {\mathbf{N}}_\lambda ^2 = \left[ \begin{array}{cc} {\mathbf{N}}_\lambda ^{21} &{} {\mathbf{0}} \\ {\mathbf{0}} &{} {\mathbf{N}}_\lambda ^{21} \\ {\mathbf{0}} &{} {\mathbf{0}} \end{array} \right] _{21 \times 4} {\mathbf{N}}_\lambda ^3 = \left[ \begin{array}{cc} {\mathbf{N}}_\lambda ^{311} &{} {\mathbf{0}} \\ {\mathbf{N}}_\lambda ^{312} &{} {\mathbf{0}} \\ {\mathbf{0}} &{} {\mathbf{N}}_\lambda ^{321} \\ {\mathbf{0}} &{} {\mathbf{N}}_\lambda ^{322} \\ {\mathbf{0}} &{} {\mathbf{N}}_\lambda ^{323} \\ {\mathbf{0}} &{} {\mathbf{N}}_\lambda ^{324} \\ {\mathbf{0}} &{} {\mathbf{N}}_\lambda ^{325} \end{array} \right] _{21 \times l} \end{aligned}$$

(68)

where

$$\begin{aligned} \begin{array}{rcl} {\mathbf{N}}_\lambda ^{21} &{}=&{} \left[ \begin{array}{cccccc} 1&{}0 \\ 1&{}0 \\ 0&{}1 \\ 0&{}1 \\ 0&{}1 \\ 1&{}0 \\ \end{array} \right] \\ {\mathbf{N}}_\lambda ^{311} &{}=&{} {\mathbf{T}}^0_\varepsilon \left[ \begin{array}{ccccccccccc} 1 &{} 0 &{}0 &{} 0 &{} \eta &{} 0 &{} 0 &{} 2 \,\xi \, \eta &{}0 &{} \eta ^2 &{} 0 \\ 0 &{} 0 &{}0 &{} 0 &{} 0 &{} \eta &{} 0 &{} 0 &{} \eta ^2-c &{} 0 &{} 2 \,\xi \,\eta \\ 0 &{} 0 &{}1 &{} 0 &{} 0 &{} 0 &{} \eta &{} 0 &{} 0 &{} 0 &{} 0 \\ \end{array} \right] \dfrac{2}{\ell } \\ {\mathbf{N}}_\lambda ^{312} &{}=&{} {\mathbf{T}}^0_\varepsilon \left[ \begin{array}{ccccccccccc} 0 &{} 0 &{}0 &{} 0 &{} \xi &{} 0 &{} 0 &{} \xi ^2-c &{}0 &{} 2 \, \xi \, \eta &{} 0 \\ 0 &{} 1 &{}0 &{} 0 &{} 0 &{} \xi &{} 0 &{} 0 &{} 2 \, \xi \,\eta &{} 0 &{} \xi ^2 \\ 0 &{} 0 &{}0 &{} 1 &{} 0 &{} 0 &{} \xi &{} 0 &{} 0 &{} 0 &{} 0 \\ \end{array} \right] \dfrac{2}{\ell }\\ {\mathbf{N}}_\lambda ^{321} &{}=&{} {\mathbf{T}}^0_\varepsilon \left[ \begin{array}{ccccccccc} 1 &{} 0 &{}0 &{} 0 &{} \eta &{} 0 &{} 0 &{} 2 \,\xi \, \eta &{}0 \\ 0 &{} 0 &{}0 &{} 0 &{} 0 &{} \eta &{} 0 &{} 0 &{} \eta ^2 \\ 0 &{} 0 &{}1 &{} 0 &{} 0 &{} 0 &{} \eta &{} 0 &{} 0 \\ \end{array} \right] \dfrac{2}{\ell }\\ {\mathbf{N}}_\lambda ^{322} &{}=&{} {\mathbf{T}}^0_\varepsilon \left[ \begin{array}{ccccccccc} 0 &{} 0 &{}0 &{} 0 &{} \xi &{} 0 &{} 0 &{} \xi ^2 &{}0 \\ 0 &{} 1 &{}0 &{} 0 &{} 0 &{} \xi &{} 0 &{} 0 &{} 2 \, \xi \, \eta \\ 0 &{} 0 &{}0 &{} 1 &{} 0 &{} 0 &{} \xi &{} 0 &{} 0 \\ \end{array} \right] \dfrac{2}{\ell } \\ {\mathbf{N}}_\lambda ^{323} &{}=&{} {\mathbf{T}}^0_\varepsilon \left[ \begin{array}{ccccccccc} 0 &{} 0 &{}0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 2 \, \eta &{} 0 \\ 0 &{} 0 &{}0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{}0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ \end{array} \right] \dfrac{2}{\ell } \\ {\mathbf{N}}_\lambda ^{324} &{}=&{} {\mathbf{T}}^0_\varepsilon \left[ \begin{array}{ccccccccccc} 0 &{} 0 &{}0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{}0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 2 \,\xi \\ 0 &{} 0 &{}0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ \end{array} \right] \dfrac{2}{\ell } \\ {\mathbf{N}}_\lambda ^{325} &{}=&{} {\mathbf{T}}^0_\varepsilon \left[ \begin{array}{ccccccccccc} 0 &{} 0 &{}0 &{} 0 &{} 1 &{} 0 &{} 0 &{} 2 \, \xi &{} 0 \\ 0 &{} 0 &{}0 &{} 0 &{} 0 &{} 1 &{} 0 &{} 0 &{} 2 \, \eta \\ 0 &{} 0 &{}0 &{} 0 &{} 0 &{} 0 &{} 1 &{} 0 &{} 0 \\ \end{array} \right] \dfrac{2}{\ell } _{\,.} \end{array} \end{aligned}$$

(69)

Concerning the predefinition $\ell =100 \, h$ we refer to the investigations in Ref. [20].

The FE approximation of the external virtual work of $\bar{{\mathbf{p}}}, \bar{{\mathbf{m}}}$ and $\bar{{\mathbf{t}}}$ leads to

$$\begin{aligned} g^{eh}_{ext} = - \sum _{e=1}^{numel} \delta \hat{{\mathbf{v}}}^{T} \, {\mathbf{f}}^{a}. \end{aligned}$$

(70)

Here, numel denotes the total number of finite shell elements to discretize the problem and ${\mathbf{f}}^{a}$ corresponds to the element load vector of a standard displacement formulation. Furthermore, it holds

$$\begin{aligned} \displaystyle \int \limits _{\Omega } \bar{{\mathbf{m}}} \cdot \Delta \delta {\mathbf{d}} \,\text {d}A + \displaystyle \int \limits _\Omega \Delta \delta {{\varvec{\varepsilon }}}^{hT}_g \, {{\varvec{\sigma }}}^h \,\text {d}A = \sum _{e=1}^{numel} \delta \hat{{\mathbf{v}}}^T {\mathbf{K}}_g \Delta \hat{{\mathbf{v}}} \,, \end{aligned}$$

(71)

where for the special case $\bar{{\mathbf{m}}}\cdot \Delta \delta {\mathbf{d}} = 0$ the matrix ${\mathbf{K}}_g$ is specified in detail in Ref. [25]. For the general case the term $\bar{{\mathbf{m}}} \cdot \Delta \delta {\mathbf{d}} \ne 0$ leads to a symmetric contribution in ${\mathbf{K}}_g$. The second variation of ${\mathbf{d}}$ has been derived in e.g. Ref. [25] such that the consideration of the load term is standard.

Hence, inserting eq. (55) and the corresponding equation for $\Delta {{\varvec{\theta }}}^h$ into the linearized variational equation (52) yields

$$\begin{aligned} \begin{array}{l} \,\text {L}\, [g({{\varvec{\theta }}}^h, \delta {{\varvec{\theta }}}^h), \Delta {{\varvec{\theta }}}^h] = \displaystyle \sum _{e=1}^{numel} \, \\ \left[ \begin{array}{c} \delta \hat{{\mathbf{v}}} \\ \delta \hat{{\varvec{\sigma }}}\\ \delta \hat{{\varvec{\vartheta }}}\end{array} \right] ^T \left\{ \left[ \begin{array}{c} {\mathbf{f}}^i - {\mathbf{f}}^a \\ {\mathbf{f}}^s \\ {\mathbf{f}}^e \\ \end{array} \right] + \left[ \begin{array}{ccc} {\mathbf{K}}_g &{} {\mathbf{G}}^T &{} {\mathbf{0}} \\ {\mathbf{G}} &{} {\mathbf{0}} &{} {\mathbf{L}}^T \\ {\mathbf{0}} &{} {\mathbf{L}} &{} {\mathbf{H}} \end{array} \right] \, \left[ \begin{array}{c} \Delta \hat{{\mathbf{v}}} \\ \Delta \hat{{\varvec{\sigma }}}\\ \Delta \hat{{\varvec{\vartheta }}}\\ \end{array} \right] \right\} \end{array} \end{aligned}$$

(72)

with

$$\begin{aligned} \begin{array}{rclrcl} {\mathbf{f}}^i &{}=&{} \displaystyle \int \limits _{\Omega _e} \, {\mathbf{B}}^T {{\varvec{\sigma }}}^h \, \,\text {d}A &{} {\mathbf{L}} &{}=&{} \displaystyle \int \limits _{\Omega _e} \, {\mathbf{N}}^T_\vartheta \, {\mathbf{I}} \, {\mathbf{N}}_\sigma \, \,\text {d}A \\ {\mathbf{f}}^s &{}=&{} \displaystyle \int \limits _{\Omega _e} \, {\mathbf{N}}_\sigma ^T \, {{\varvec{\varepsilon }}}_g^{h} \,\text {d}A + {\mathbf{L}}^T \hat{{\varvec{\varepsilon }}}&{} {\mathbf{G}} &{}=&{} \displaystyle \int \limits _{\Omega _e} \, {\mathbf{N}}^T_\sigma \, {\mathbf{B}} \, \,\text {d}A \\ {\mathbf{f}}^e &{}=&{} \displaystyle \int \limits _{\Omega _e} \, {\mathbf{N}}_\vartheta ^T \, \hat{{\varvec{\psi }}}^h \, \,\text {d}A + {\mathbf{L}} \, \hat{{\varvec{\sigma }}}&{} {\mathbf{H}} &{}=&{} \displaystyle \int \limits _{\Omega _e} \, {\mathbf{N}}^T_\vartheta \, {\mathbf{D}} \, {\mathbf{N}}_\vartheta \, \,\text {d}A \,. \end{array} \end{aligned}$$

(73)

The vector $\hat{{\varvec{\psi }}}$ corresponds to ${{\varvec{\psi }}}$ according to (47) without vector ${{\varvec{\sigma }}}$. The integrals in (73) are computed numerically applying a $3 \times 3$ Gauss integration scheme considering $\,\text {d}A = |{\mathbf{X}}^h_0, _\xi \times {\mathbf{X}}^h_0,_\eta | \, \,\text {d}\xi \,\text {d}\eta$. It is important to note, that although ${\mathbf{D}}$ is singular, ${\mathbf{H}}$ is regular. The matrix ${\mathbf{L}}$ is expressed with (57)

$$\begin{aligned} {\mathbf{L}} = - \int \limits _{\Omega _e} \, \left[ \begin{array}{c} {\mathbf{N}}^{1T}_\varepsilon \\ {\mathbf{N}}^{2T}_\varepsilon \\ {\mathbf{0}} \\ {\mathbf{0}} \\ {\mathbf{N}}^{3T}_\varepsilon \\ \end{array} \right] {\mathbf{N}}_\sigma \,\text {d}A = \left[ \begin{array}{c} {\mathbf{L}}_1 \\ {\mathbf{L}}_2 \\ {\mathbf{0}} \\ {\mathbf{0}} \\ {\mathbf{L}}_3 \end{array} \right] _{\,.} \end{aligned}$$

(74)

The columns with quadratic shape functions in ${\mathbf{N}}^3_\varepsilon$ are not orthogonal to columns 9–12 of ${\mathbf{N}}_\sigma$ and thus lead to entries in ${\mathbf{L}}_3$. They are consistently omitted when setting ${\mathbf{L}}_3 = {\mathbf{0}}$ in ${\mathbf{L}}$, ${\mathbf{f}}^e$ and ${\mathbf{f}}^s$.

We continue with $\; \,\text {L}[g({{\varvec{\theta }}}^h, \delta {{\varvec{\theta }}}^h ), \Delta {{\varvec{\theta }}}^h] = 0\;$, where $\;\delta {{\varvec{\theta }}}^h \ne {\mathbf{0}}\;$ and obtain for each element

$$\begin{aligned} \left[ \begin{array}{ccc} {\mathbf{K}}_g &{} {\mathbf{G}}^T &{} {\mathbf{0}} \\ {\mathbf{G}} &{} {\mathbf{0}} &{} {\mathbf{L}}^T \\ {\mathbf{0}} &{} {\mathbf{L}} &{} {\mathbf{H}} \\ \end{array} \right] \, \left[ \begin{array}{cc} \Delta \hat{{\mathbf{v}}} \\ \Delta \hat{{\varvec{\sigma }}}\\ \Delta \hat{{\varvec{\vartheta }}}\\ \end{array} \right] + \left[ \begin{array}{cc} {\mathbf{f}}^i - {\mathbf{f}}^a \\ {\mathbf{f}}^s \\ {\mathbf{f}}^e \end{array} \right] = \left[ \begin{array}{cc} {\mathbf{r}} \\ {\mathbf{0}} \\ {\mathbf{0}} \\ \end{array} \right] \end{aligned}$$

(75)

where ${\mathbf{r}}$ denotes the vector of element nodal forces. Since ${{\varvec{\sigma }}}$ and ${{\varvec{\vartheta }}}$ are interpolated discontinuously across the element boundaries the parameters $\Delta \hat{{\varvec{\sigma }}}$ and $\Delta \hat{{\varvec{\vartheta }}}$ can be eliminated from the set of equations. This is done applying a standard Gaussian elimination procedure [31] to the system of equations (75).

One obtains the tangential element stiffness matrix ${\mathbf{k}}^e_T$, the element residual vector $\hat{{\mathbf{f}}}^e$ and (72) reduces to

$$\begin{aligned} \,\text {L}\, [g({{\varvec{\theta }}}^h, \delta {{\varvec{\theta }}}^h), \Delta {{\varvec{\theta }}}^h] = \displaystyle \sum _{e=1}^{numel} \, \delta \hat{{\mathbf{v}}}^T( {\mathbf{k}}^e_T \, \Delta \hat{{\mathbf{v}}} + \hat{{\mathbf{f}}}^e) \,. \end{aligned}$$

(76)

The element possesses 5 or 6 degrees of freedom (dofs) at the nodes. At nodes on intersections 6 dofs (3 global displacements and 3 global rotations) and at the remaining nodes 5 dofs (3 global displacements and 2 local rotations) are present. For the back substitution of $\Delta \hat{{\varvec{\sigma }}}$ and $\Delta \hat{{\varvec{\vartheta }}}$ the corresponding matrices have to be stored or to be recalculated. Present element formulation has been implemented in an extended version of the general finite element program FEAP [32]. The linear element stiffness matrix possesses with six zero eigenvalues the correct rank. Furthermore, the membrane and bending patch tests, suggested in [33], are fulfilled.

Remark: The derivatives of the plastic strains $E^{pl}_{ij}$ in Eq. (45) with respect to the coordinates $\xi ^\alpha$ are computed as follows

$$\begin{aligned} \left[ \begin{array}{c} E^{pl}_{ij},_1 \\ E^{pl}_{ij},_2 \\ \end{array} \right] = {\mathbf{J}}_0^{-1} \left[ \begin{array}{c} E^{pl}_{ij},_\xi \\ E^{pl}_{ij},_\eta \\ \end{array} \right] _{\,,} \end{aligned}$$

(77)

where ${\mathbf{J}}_0$ denotes the Jacobian matrix (54) evaluated at the element center. The derivatives of $E^{pl}_{ij}(\xi , \eta )$ with respect to $\xi$ and $\eta$ are approximated using a central difference scheme

$$\begin{aligned} \begin{array}{rcl} E^{pl}_{ij},_\xi &{}\approx &{} \dfrac{E^{pl}_{ij}(\Delta \xi , 0) - E^{pl}_{ij}(-\Delta \xi , 0) }{ 2 \, \Delta \xi } \\ E^{pl}_{ij},_\eta &{}\approx &{} \dfrac{E^{pl}_{ij}(0,\Delta \eta ) - E^{pl}_{ij}(0, -\Delta \eta ) }{ 2 \, \Delta \eta } \end{array} \end{aligned}$$

(78)

and thus are elementwise constant. Here, $\Delta \xi = \Delta \eta = \sqrt{0.6}$ are the coordinates of the applied $3 \times 3$ Gauss integration scheme.

Remark: The derivatives of the deformation gradient in (23) with respect to the coordinates $\xi ^\alpha$ require the computation of second derivatives of the displacements. Thus, at least bi-quadratic shape functions for the displacements have to be used. This means that for 4-node elements with bi-linear shape functions the derivatives $F_{ij},_\alpha$ cannot be obtained in a standard way. However, numerical investigations show that for small strain problems $R_{ij},_\alpha$ provides a good approximation for the required quantities. Here, $R_{ij}$ denote components of a rotation tensor ${\mathbf{R}}$. For small strain problems the polar decomposition of the deformation gradient ${\mathbf{F}} = {\mathbf{R}} \, {\mathbf{U}}$ leads with $| {\mathbf{U}} | \approx 1$ to ${\mathbf{F}} \approx {\mathbf{R}}$. Hence, for ${\mathbf{R}}$ the rotation tensor which transforms the initial normal vector ${\mathbf{N}}$ via ${\mathbf{d}} = {\mathbf{R}} \, {\mathbf{N}}$ can be used. For quadrilateral shell elements ${\mathbf{R}}$ is interpolated with bi-linear functions $N_I$ and nodal rotations ${\mathbf{R}}_I$, thus the required first derivatives of $R_{ij}$ are computable. It is well-known, that for shells undergoing moderate or even finite rotations the strains still may be small, if the structure is sufficiently thin.

4 Examples

The displacements and stresses obtained with present 4-node shell element are compared with 3D reference solutions. For this purpose we use the 8-noded solid shell element [18] with a sufficient number of elements in thickness direction of the plate or shell. We add results computed with shell element [34]. It is based on standard Reissner–Mindlin kinematic assumptions along with thickness strains which have a constant and linear shape through the thickness. This leads to an interface for three-dimensional constitutive laws. The element was designed for homogeneous shell structures. With application to layered shells it leads to restraints especially for the thickness normal stresses. Furthermore, we compare with literature results. These were obtained with the 4-node shells elements [35] and [36]. The used notation of the different element formulations is summarized in Table 1.

Table 1 Notation of the different element formulations

4.1 Comparison of relative computing times

A simply supported square plate subjected to a constant load is considered. The length and thickness of the plate are $L=1000$ mm and $h = 20$ mm, respectively. We consider symmetric angle ply laminates $[45^\circ /-45^\circ / \ldots /45^\circ /-45^\circ /45^\circ ]$ with $M=5, 10$ and 20 layers of equal thickness as well as 8 different meshes. Assuming transversal isotropy the material parameters for carbon fiber reinforced polymers (CFRP) are chosen as follows

$$\begin{aligned} \begin{array}{rcllrcll} E_{1} &{}=&{} 125000 \, &{}\text {N/mm}^2 \qquad &{} G_{12} &{}=&{} 4800 \, &{}\text {N/mm}^2 \\ E_{2} &{}=&{} 7400 \, &{}\text {N/mm}^2 &{} G_{23} &{}=&{} 2700 \, &{}\text {N/mm}^2 \\ \nu _{12} &{}=&{} 0.34 \,. \end{array} \end{aligned}$$

(79)

In Table 2 relative computing times (stiffness computation and solution of the system of equations) using present 2D shell element and the 3D solid shell element are displayed. The 3D meshes are generated with 4 elements in thickness direction of each layer. This is necessary to map the complicated shape of the stresses through the thickness, see [37]. A fast direct parallel solver is used along with a Windows PC (1 Intel i9-7900X CPU, 10 cores, 3.3 GHz). In each row of the table the 3D times are normalized with respect to the 2D times. The 3D times for the finest meshes are not computable with the used hardware. This shows that fully 3D computations are costly, which restricts the applicability to small problems.

Table 2 Comparison of relative computing times

4.2 Element convergence behaviour

4.2.1 Hemispherical shell

Fig. 3

Hemispherical shell: a $12 \times 12$ regular mesh, b principal mesh distortion for a $4 \times 4$ mesh, c $12 \times 12$ distorted mesh

The first problem is the hemispherical shell with an 18$^\circ$ cutout subjected to alternating radial point loads P at its equator, shown in Fig. 3a. This geometrically non-linear example is often cited as a benchmark problem for shell elements. It is a test for the ability to model rigid body modes and inextensible bending, [33]. Geometrical and material data are $R=10,\,\varphi =18^\circ$, thickness $h=0.04$ and $E=6.825\cdot 10^7,\, \nu =0.3$. Considering symmetry one quarter of the structure corresponding to the region ABCD in Fig. 3a is discretized using regular and distorted meshes. Here, the principal mesh distortion is described in Fig. 3b for a $4 \times 4$ mesh. Each edge is discretized using the aspect ratios L$_1$: L$_2$: L$_3$: ... : L$_N = 1: 2: 3: ... : N$, where N denotes the number of elements per direction. A $12 \times 12$ distorted mesh is illustrated in Fig. 3c. We employ the boundary conditions $u_y=\beta =0$ on $\overline{\text {AD}}$, $u_x=\beta =0$ on $\overline{\text {BC}}$ and $u_z=0$ at a point on $\overline{\text {AB}}$, e.g. at A. Fig. 4 shows load displacement curves for the regular and distorted mesh $8 \times 8$. The defined converged solution is computed with a $128 \times 128$ mesh. Results are only presented for $P- u_{xA}$; similar output can be obtained for $P-u_{yB}$. For comparison we add results from Ref. [35] using the MITC4+ element.

Fig. 4

Hemispherical shell: $P- u_{xA}$ for the regular (top) and distorted (bottom) $8 \times 8$ mesh

The convergence behaviour of the displacement $u_{xA}$ at $P=400$ versus the number of elements N is depicted in Fig. 5 for both meshes. It is obvious that $n=11$ leads to a significant improvement of the element behaviour. The results for $n=9$ are close to those for $n=11$. In this context we compare the effort to setup the tangential stiffness matrix for different parameters n. The computing time T is normalized to $T=1$ for the case $n=0$. The comparison with the further parameters leads to $T=1.21$ for $n=7$, $T=1.28$ for n=9 and $T=1.32$ for $n=11$. The numbers prove that the effort especially for the last two cases is comparable. Within the following examples the parameter $n=9$ is not considered. Finally a plot of the shape factor c according to Eq. (66) is shown for a regular and distorted $16 \times 16$ mesh in Fig. 6.

Fig. 5

Hemispherical shell: $u_{xA} - N$ for regular (top) and distorted (bottom) meshes

Fig. 6

Hemispherical shell: distribution of shape factor c for the regular (top) and distorted (bottom) $16 \times 16$ mesh

4.2.2 Twisted beam

The twisted beam problem according to Fig. 7 was originally introduced in [33]. Geometrical and material data are $L=12,\,b=1.1$,  thickness $h=0.0032$ and $E=29\cdot 10^6,\, \nu =0.22$, respectively. The cantilever beam is clamped at one end and is loaded by an out-of-plane acting load P at point A. A regular and a distorted $4 \times 24$ mesh is chosen for the solution. The distorted mesh is depicted in Fig. 8. Here, a ratio $L_{max}/L_{min}=2$ is chosen, where $L_{max}$ and $L_{min}$ denote the longest and shortest element length in the flat projection, respectively.

Fig. 7

Twisted beam: problem and $4 \times 24$ regular mesh

Fig. 8

Twisted beam: distorted $4 \times 24$ mesh, a perspective view, b perspective view of the flat projection

Figure 9 depicts load deflection curves for the regular mesh and the distorted mesh using different parameters n . Available results using the MITC4+ element [35] are added. The converged solution is obtained employing a $32 \times 192$ regular mesh. Again, the quadratic terms in Eq. (61) $(n=11)$ are necessary to produce accurate results.

Fig. 9

Twisted beam: $P-u_{yA}$ for the regular (top) and the distorted (bottom) $4 \times 24$ mesh

For the distorted mesh the convergence behaviour of the final displacements $u_{yA}$ and $-u_{zA}$ versus the number of elements N in width direction is presented in Figs. 10 and 11, respectively. Again, $n=11$ leads to a significant improvement of the element behaviour. This is only obtained with the shape factor c according to Eq. (66), as the comparison with the curves $n=11\, (c=0)$ shows.

Fig. 10

Twisted beam: $u_{yA} - N$ for the distorted mesh

Fig. 11

Twisted beam: $-u_{zA} - N$ for the distorted mesh

4.2.3 Hook problem

Next, we consider the hook problem shown in Fig. 12, referred to in linear analysis as the Raasch challenge, [38]. For the FE-discretization we use $N \times 2\,N \times 3\,N$ elements with N elements in width direction, $2\,N$ elements for the first arch (radius $R_1$) and $3\,N$ elements for the second arch (radius $R_2$), see Fig. 12.

Fig. 12

Hook problem: geometry and a 4 $\times$ 8 $\times$ 12 regular mesh

Geometrical and material data are $R_1=14,\,\varphi _1=60^\circ ,\,R_2=46,\,\varphi _2=150^\circ ,\,b=20$, thickness $h=0.02$ and $E=3.3\cdot 10^3,\, \nu =0.3$, respectively. The structure is fully clamped at one end and is loaded by a shear load P applied as a uniformly distributed traction at the free end. For the solution, we use a regular and a distorted 4 $\times$ 8$\times$ 12 mesh. The principal distorted mesh is shown in Fig. 13 with respect to a flat projection together with a perspective view of the structure. Following [36], $L_{max}/L_{min} = 1.5$ is chosen for the first arch and $L_{max}/L_{min} = 2.0$ for the second arch.

Fig. 13

Hook problem: distorted mesh and flat projection for a 4 $\times$ 8 $\times$ 12 mesh

Figure 14 shows the resulting load-displacement curves $P- u_{zA}$ of point A . The displacements using the MITC4+ element [35] are included. Similar results can be found for the +HW element (see Fig. 12b, 13b of [36]). The defined converged solutions are obtained with a 32 $\times$ 64 $\times$ 96 regular mesh.

Fig. 14

Hook problem: $P-u_{zA}$ for the regular (top) and distorted (bottom) 4 $\times$ 8 $\times$ 12 mesh

Figure 15 shows the convergence behaviour of the final displacement $u_{zA}$ of point A versus the number of elements N in width direction. Results for the elements MITC4, MITC4+ and +HW are taken from Fig. 12a and 13a in [36]. The superior behaviour of present element ($n=11$) for $N \ge 8$ is demonstrated.

Fig. 15

Hook problem: convergence behaviour $u_{zA}-N$ for regular (top) and distorted (bottom) meshes

4.3 Inelasticity, layered shells and intersections

4.3.1 Elasto-plastic analysis of a square plate

A simply supported square plate (soft support) subjected to a constant load is considered. The length and thickness of the plate are $L=200$ cm and $h = 4$ cm, respectively. The origin of the $(x,y,z)-$ coordinate system is chosen at the center of the plate. The material parameters are the elastic constants E and $\nu$ as well as yield stress $y_0$ and linear hardening parameter $\xi$ for $J_2$-plasticity. They are chosen as follows

$$\begin{aligned} \begin{array}{rcllrcll} E &{}=&{} 21000 \, &{}\text {kN/cm}^2 \\ \nu &{}=&{} 0.3 \, &{} \\ y_0 &{}=&{} 36 \, &{}\text {kN/cm}^2 \\ \xi &{}=&{} 420 \, &{}\text {kN/cm}^2 \,. \end{array} \end{aligned}$$

(80)

The plate is loaded by a constant load $\lambda \, \bar{p}$ with $\bar{p}$ = 1 N/cm$^2$ which is applied one half each via the lower and upper surface. With respect to symmetry one quarter of the plate is discretized with a mesh of 20$\times$20 quadrilateral elements. Present element and the Reissner–Mindlin shell element [34] are used with $N=5$ layers of equal thickness. For the 3D reference solution of the stresses the mesh has to be refined to obtain sufficient accurate results. We choose a $40 \times 40 \times 20$ mesh. Besides the symmetry conditions the boundary conditions are $u_z=0$ at (L/2, y, z) and (x, L/2, z).

Geometrical linear and material nonlinear calculations are performed. Load deflection curves for the center displacement $w=-u_z(0,0)$ are shown in Fig. 16. Both shell results agree with the 3D reference solution. The yield line theory, which assumes elasto-plasticity without hardening, predicts a bearing load $\bar{p}_{ylt}=6\cdot y_0\cdot (h/L)^2$ which leads to a load factor $\bar{\lambda }=86.4$.

For the maximum load the normal stresses $S_{xx}$ and $S_{zz}$ are evaluated near the plate center at the coordinates $(x_{p1},y_p) =(2.5,2.5)$ cm and are plotted as function of the thickness coordinate in Figs. 17 and 18. The transverse shear stresses, evaluated at the coordinates $(x_{p2},y_p) =(22.5,2.5)$ cm, are shown in Fig. 19 . The diagrams show, that there is good agreement of present model with the reference solution. In Figs. 20, 21 and 22 the Reissner–Mindlin solutions are shown. The stresses are computed in the elastic range ($\lambda = 50$) and in the plastic range ($\lambda =100$). Only in the elastic range there is agreement of the in-plane stress $S_{xx}$ with the reference solution. For elasto-plasticity the stresses fulfill the yield condition but not the equilibrium equations in terms of stresses. This holds for all components. The integrals of the stresses lead to correct stress resultants and thus to correct load deflection curves for sufficient fine meshes.

Fig. 16

Elasto-plastic square plate: $\lambda - w$

Fig. 17

Elasto-plastic square plate: $S_{xx} (x_{p1}, y_p, z)$

Fig. 18

Elasto-plastic square plate: $S_{zz} (x_{p1}, y_p, z)$

Fig. 19

Elasto-plastic square plate: $S_{xz} (x_{p2}, y_p, z)$

Fig. 20

Elasto-plastic square plate: $S_{xx} (x_{p1}, y_p, z)$ for $\lambda =50$ (top) and $\lambda =100$ (bottom)

Fig. 21

Elasto-plastic square plate: $S_{zz} (x_{p1}, y_p, z)$ for $\lambda =50$ (top) and $\lambda =100$ (bottom)

Fig. 22

Elasto-plastic square plate: $S_{xz} (x_{p2}, y_p, z)$ for $\lambda =50$ (top) and $\lambda =100$ (bottom)

Fig. 23

Sandwich plate: cross section (not to scale)

4.3.2 Elasto-plastic analysis of a sandwich plate

The next example is a square sandwich plate with a layup according to Fig. 23. The origin of the (x, y, z)-coordinate system lies in the center of the plate. The thickness of the core is $t_c$ and the thickness of one face layer is $t_f$. All edges are simply supported (soft support). A constant load $\lambda \, \bar{p}$ with $\bar{p} = 10^{-3} \, \text {N/mm}^2$ is applied at the upper surface. The material properties for isotropy are $E_c, \nu _c$ for the elastic core and $E_f, \nu _f$ for the elasto-plastic face layers with yield stress $y_0$ and linear hardening parameter $\xi$ for a $J_2$-plasticity model. One quarter is discretized with a mesh of $N \times N$ elements considering symmetry. Two layers are used for the core and one for each face layer. For the 3D solution 6 elements are used in thickness direction of the core and one element for each face layer. All data are summarized as follows.

(81)

The geometrical and material nonlinear computations are carried out load controlled with mesh parameter $N=40$. The displacements w are computed for load factors $\lambda = 1, 2, ... , 12$ and subsequently for unloading with $\lambda = 12, 11, ... , 0$, see Fig. 24. The Reissner–Mindlin solution without shear correction $(k=1)$ is to stiff in the elastic range. With shear correction factor $k=0.03$, computed with element formulation [37], there is good agreement in the elastic range. For inelasticity the factor is applied to the algorithmic tangent matrix. This leads in the inelastic range to a response which is to soft.

Fig. 24

Sandwich plate: $\lambda -w$

The stresses are evaluated for load factor $\lambda = 12$. To obtain sufficient accurate results especially for the thickness normal stresses the 3D mesh is refined with $N = 80$. The normal stresses $S_{xx}$ and $S_{zz}$ are computed near the plate center at $x_{p1} = y_p = L/80$. They are plotted as function of z in Figs. 25 and 26, respectively. The transverse shear stresses are computed at $x_{p2} = 61/80 \cdot L , y_p = L/80$ and are shown in Fig. 27. In all diagrams there is good agreement between present 2D and the 3D results. This holds for the displacements and the computed stresses. The Reissner–Mindlin results for the stresses are not included in the diagrams. As already shown with the previous example only for the in-plane stresses and elasticity one obtains usable results. Here, even the load deflection behaviour is not correct in the inelastic range.

Fig. 25

Sandwich plate: $S_{xx}(x_{p1},y_p,z)$

Fig. 26

Sandwich plate: $S_{zz}(x_{p1},y_p,z)$

Fig. 27

Sandwich plate: $S_{xz}(x_{p2}, y_p,z)$

4.3.3 Clamped plate with angle ply laminate

A clamped plate according to Fig. 28 is considered. The clamping is applied at $x=y=0$, whereas the other edges are free. The geometrical data are $L = 1000 \text { mm}$ and $h = 20 \text { mm}$. The constant loading $\bar{p} = 0.25 \text { N/mm}^2$ is applied at the upper surface. The plate consists of an eight layer angle ply laminate with a $[45^\circ / -45^\circ / 45^\circ / -45^\circ ]_s$ stacking sequence. The material data for CFRP-layers (79) are taken. The discretization is performed with a mesh of $24 \times 24$ elements. To obtain a sufficient accurate reference solution for the interlaminar stresses the 3D mesh has to be refined. We choose a $72 \times 72 \times 16$ mesh of solid shell elements.

Fig. 28

Clamped plate with angle ply laminate

The geometrical nonlinear computation is performed applying the load in one single step. The maximum displacement computed with the different models amounts to $u_z = -145.7 \text { mm}$. The stresses $S_{xx},S_{zz},S_{xz}$ and $S_{yz}$ are evaluated at the coordinates $x_p = 13/48 \cdot L, y_p = 5/48 \cdot L$. They are plotted as function of the thickness coordinate z in Figs. 29, 30, 31, and 32. The transverse shear stress $S_{yz}$ according to Fig. 32 shows a very complicate shape. Even the sign of the stresses changes several times. There is a good agreement of present 2D solution with the 3D reference stresses. For comparison we add the results based on the Reissner–Mindlin theory. As already written in the previous examples only the in-plane stresses agree with the reference solution. The interlaminar stresses deviate considerable form the reference solution. The integrals through the thickness lead to correct stress resultants within the chosen mesh density. Finally, the deformed configuration is depicted in Fig. 33.

Fig. 29

Clamped plate: $S_{xx}(x_p,y_p,z)$

Fig. 30

Clamped plate: $S_{zz}(x_p,y_p,z)$

Fig. 31

Clamped plate: $S_{xz}(x_p,y_p,z)$

Fig. 32

Clamped plate: $S_{yz}(x_p,y_p,z)$

Fig. 33

Clamped plate: displacements $-u_z$ in [mm]

Fig. 34

Stiffened cylindrical shell and finite element mesh

4.3.4 Stiffened cylindrical shell

As last example the stiffened cylindrical shell according to Fig. 34 is investigated. The figure shows a cross-section of the shell and a coarse finite element mesh of half the structure accounting for symmetry conditions. Radius and length of the cylinder are $R=1000\, \text {mm}$, $L=2000\, \text {mm}$ and the shell thickness is $h = 10 \,\text {mm}$. The shell is free at $x_2=x_3=0$ and clamped at $x_2=L$. A concentrated force F acts at the coordinates $(x_1,x_2,x_3)=(0,0,R)$. The skin of the structure consists of a [$0^{^{\circ }}/90^{^{\circ }}/0^{^{\circ }}$] lay-up, where $0^{^{\circ }}$ refers to the tangential direction and $90^{^{\circ }}$ to the length direction of the cylinder. The stiffeners with measurements $d=50\, \text {mm}$ and $h=10\, \text {mm}$ are arranged in radial direction. In the symmetry axis a thickness $2\, h$ is present. The stiffeners are homogeneous and the fibre direction coincides with the length direction. The material data for CFRP-layers (79) are taken. The mesh density is denoted by $l \times m \times n$, where in Fig. 34$l=12$ is the number of elements in circumferential direction, $m=8$ the number in length direction and $n=2$ the number of elements for a stiffener in radial direction. The laminate of the skin is modeled with 6 numerical layers, whereas 3 layers are used for the homogeneous stiffeners. A mesh density of $l \times m \times n = 48 \times 32 \times 4$ elements is chosen.

Comparative results are computed with a 3D discretization of the skin. In thickness direction of the skin each physical layer is discretized with 2 elements. To obtain sufficient accurate results for the thickness normal stresses an in-plane refined mesh with $l \times m \times n = 144 \times 96 \times 4$ is used. For the discretization of the stiffeners present shell element is used.

Fig. 35

Stiffened cylindrical shell: $F-w$

Fig. 36

Stiffened cylindrical shell: $S_{11}(\xi ^1_p,\xi ^2_p , z)$

Fig. 37

Stiffened cylindrical shell: $S_{33}(\xi ^1_p,\xi ^2_p , z)$

Fig. 38

Stiffened cylindrical shell: $S_{13}(\xi ^1_p,\xi ^2_p , z)$

Fig. 39

Stiffened cylindrical shell: final deformed configuration computed with a $24 \times 16 \times 2$ mesh

The geometrical nonlinear computations are performed with displacement control and a step size $\Delta w = 20$ mm. In Fig. 35 load F is plotted versus the prescribed displacement w.

For two deformed configurations $w=200$ mm and $w=400$ mm the stresses $S_{11}, S_{33}$ and $S_{13}$ at a point P of the reference surface with coordinates $\xi ^1_p = (13/96 \cdot \pi /2) \cdot R$, $\xi ^2_p = x_{2p}= 7/64 \cdot L$ are displayed in Figs. 36, 37 and 38 in dependence of $z=\xi ^3$. In all diagrams there is good agreement of present element with the reference solution.

For comparison results of the Reissner–Mindlin model are added. Again, one obtains good results for the in-plane stress $S_{11}$, whereas this is not the case for $S_{33}$ and $S_{13}$. Figure 39 shows the final deformed configuration computed with present element formulation.

5 Conclusions

An advanced 2D shell model for layered shell structures is presented. With the developed finite element formulation the load deflection behaviour of geometrical and material nonlinear shell problems and the complicated three-dimensional stress state in layered shells can be computed. The matrices $\tilde{{\mathbf{A}}}_2$ and ${\mathbf{A}}_2$ (Eqs. (12) and (14) ) are evaluated with the displacements of the last converged load step. This also holds for ${\mathbf{D}}_{23}$ and ${\mathbf{p}}^*$ (Eqs. (34)$_2$ and (45) ). All computed examples show by a variation of the load step size that no visible differences in the load deflection curves occur, which means that the applied approximation is admissible.

The proposed ansatz for the independent shell strains with quadratic functions leads to a significant improved convergence behaviour especially when meshes with distorted elements are used. The computed displacements and stresses are in good agreement with the results of 3D comparative models. For structures with many layers present 2D shell model requires only a fractional amount of the computing time in comparison with fully 3D discretizations.

The numerical examples furthermore show, that shell elements based on the Reissner–Mindlin theory are able to predict the correct shape of the in-plane stresses only for the case of elasticity. For elasto-plasticity the stresses fulfill the yield condition but not the equilibrium equations in terms of stresses. This holds for all components. As the weak form of equilibrium in terms of stress resultants is basis of the finite element formulation, the integrals of the stresses lead to correct stress resultants and thus to correct load deflection curves for sufficient fine meshes. For sandwich plates and shells the load deflection behaviour can only be predicted with a shear correction factor in the elastic range.