Abstract
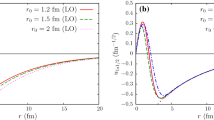
We compute the momentum-space probability density of \({}^6\)He at leading order in Halo EFT. In this framework, the \({}^6\)He nucleus is treated as a three-body problem with a \({}^4\)He core (\(c\)) and two valence neutrons (\(n\)). This requires the \(nn\) and \(n c\) t-matrices as well as a \(cnn\) force as input in the Faddeev equations. Since the \(n c\) t-matrix corresponds to an energy-dependent potential, we consider the consequent modifications to the standard normalization and orthogonality conditions. We find that these are small for momenta within the domain of validity of Halo EFT. In this regime, the \({}^6\)He probability density is regulator independent, provided the cutoff is significantly above the EFT breakdown scale.



Similar content being viewed by others
Notes
Note that we abbreviate the spin states in the following way:
$$\begin{aligned} \left| {L, -M}\right\rangle _{n}^{}&= \left| {\left( \frac{1}{2}, 0\right) \frac{1}{2},\frac{1}{2}; L, -M}\right\rangle _{n}^{} , \\ \left| {0, 0}\right\rangle _{c}^{}&= \left| {\left( \frac{1}{2}, \frac{1}{2}\right) 0,0; 0, 0}\right\rangle _{c}^{} , \end{aligned}$$where the notation \(\left| {\left( \nu _j,\nu _k\right) s_i, \sigma _i; S, M_S}\right\rangle _{i}^{} \) from [15] is used.
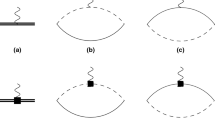
We put it in quotation marks, since it is actually only an approximation for the potential energy density. The potential energy density of \(V_i\) is defined as \(P_{\varvec{p},\varvec{q}} V_i\), where \(P_{\varvec{p},\varvec{q}}\) projects on the Jacobi momenta, \(\varvec{p}\) and \(\varvec{q}\). The formula above represents the expectation value of this product of operators in the case of potentials which are not energy dependent. Otherwise, correction terms exist.
We define the following measure for the numerical uncertainty:
$$\begin{aligned} \frac{ \max _{i,j}{\left( \left| \rho _{ij}^{\left( 2n\right) } - \rho _{ij}^{\left( n\right) } \right| \right) } }{ \max _{i,j}{\left( \left| \rho _{ij}^{\left( 2n\right) } \right| \right) }/2 } , \end{aligned}$$where the \(\rho _{ij}\) is the probability density evaluated on a grid. We put a number proportional to the number of mesh points for the discretization of both the integral equations and the angular integration in the brackets in the superscript of the \(\rho _{ij}\). These two numerical techniques—as well as others—generally use different numbers of mesh points, but the common proportionality factor enables us to change the overall precision. Accordingly this measure is the maximum absolute difference of the result with fixed numbers of mesh points and the result obtained with twice as many mesh points, divided by a “typical” density value. For the latter we choose the half of the maximum of the absolute values.
Note that we make a small error by using the analytic results for the \(\lambda _i\) as given in Sect. 2.2, since in these calculations the three-body cutoff \(\varLambda \) is neglected.
References
S. Ulrych, H. Müther, Nucl. Phys. A 641, 499 (1998). https://doi.org/10.1016/S0375-9474(98)00537-5
I. Yaron, J. Alster, L. Frankfurt, E. Piasetzky, M. Sargsian, M. Strikman, Phys. Rev. C 66, 024601 (2002). https://doi.org/10.1103/PhysRevC.66.024601
O. Benhar, D. Day, I. Sick, Rev. Mod. Phys. 80, 189 (2008). https://doi.org/10.1103/RevModPhys.80.189
R. Haag, Phys. Rev. 112, 669 (1958). https://doi.org/10.1103/PhysRev.112.669
S. Kamefuchi, L. O’Raifeartaigh, A. Salam, Nucl. Phys. 28, 529 (1961). https://doi.org/10.1016/0029-5582(61)91075-6
J.S.R. Chisholm, Nucl. Phys. 26(3), 469 (1961). https://doi.org/10.1016/0029-5582(61)90106-7
R.J. Furnstahl, H.W. Hammer, Phys. Lett. B 531, 203 (2002). https://doi.org/10.1016/S0370-2693(01)01504-0
S.N. More, S.K. Bogner, R.J. Furnstahl, Phys. Rev. C 96(5), 054004 (2017). https://doi.org/10.1103/PhysRevC.96.054004
A.S. Jensen, K. Riisager, D.V. Fedorov, E. Garrido, Rev. Mod. Phys. 76, 215 (2004). https://doi.org/10.1103/RevModPhys.76.215
E. Braaten, H.W. Hammer, Phys. Rep. 428, 259 (2006). https://doi.org/10.1016/j.physrep.2006.03.001
C. Bertulani, H.W. Hammer, U. van Kolck, Nucl. Phys. A 712(1), 37 (2002). https://doi.org/10.1016/S0375-9474(02)01270-8
P. Bedaque, H.W. Hammer, U. van Kolck, Phys. Lett. B 569(3), 159 (2003). https://doi.org/10.1016/j.physletb.2003.07.049
H.W. Hammer, C. Ji, D.R. Phillips, J. Phys. G44(10), 103002 (2017)
J. Rotureau, U. van Kolck, Few-Body Syst. 54, 725 (2013). https://doi.org/10.1007/s00601-012-0455-6
C. Ji, C. Elster, D.R. Phillips, Phys. Rev. C 90, 044004 (2014). https://doi.org/10.1103/PhysRevC.90.044004
D.V. Fedorov, A.S. Jensen, J. Phys. A 34(30), 6003 (2001). https://doi.org/10.1088/0305-4470/34/30/311
D.V. Fedorov, A.S. Jensen, Nucl. Phys. A 697, 783 (2002). https://doi.org/10.1016/S0375-9474(01)01266-0
H. Hebach, P. Henneberg, H. Kümmel, Phys. Lett. 24B, 134 (1967). https://doi.org/10.1016/0370-2693(67)90501-1
M.S. Shah, A.N. Mitra, Phys. Rev. C 1, 35 (1970). https://doi.org/10.1103/PhysRevC.1.35
A. Ghovanlou, D.R. Lehman, Phys. Rev. C 9, 1730 (1974). https://doi.org/10.1103/PhysRevC.9.1730
M.V. Zhukov, L.V. Chulkov, B.V. Danilin, A.A. Korsheninnikov, Nucl. Phys. A 533, 428 (1991). https://doi.org/10.1016/0375-9474(91)90526-C
M.V. Zhukov, B.V. Danilin, D.V. Fedorov, J.M. Bang, I.J. Thompson, J.S. Vaagen, Phys. Rep. 231, 151 (1993). https://doi.org/10.1016/0370-1573(93)90141-Y
W. Glöckle, The Quantum Mechanical Few-Body Problem. Texts and Monographs in Physics (Springer, Berlin, 1983)
L.D. Faddeev, Sov. Phys. JETP 12, 1014 (1961). [Zh. Eksp. Teor. Fiz. 39, 1459 (1960)]
I.R. Afnan, A.W. Thomas, Top. Curr. Phys. 2, 1 (1977)
E. Ryberg, C. Forssn, L. Platter, Few-Body Syst. 58(4), 143 (2017). https://doi.org/10.1007/s00601-017-1307-1
E.P. Wigner, Phys. Rev. 73, 1002 (1948). https://doi.org/10.1103/PhysRev.73.1002
W.N. Polyzou, W. Glöckle, Few-Body Syst. 9(2), 97 (1990). https://doi.org/10.1007/BF01091701
B.H.J. Mckellar, C.M. Mckay, Aust. J. Phys. 36, 607 (1983). https://doi.org/10.1071/PH830607
J. Formánek, R.J. Lombard, J. Mareš, Czechoslov. J. Phys. 54(3), 289 (2004). https://doi.org/10.1023/B:CJOP.0000018127.95600.a3
L. Pricoupenko, Phys. Rev. Lett. 96, 050401 (2006). https://doi.org/10.1103/PhysRevLett.96.050401
L. Pricoupenko, Phys. Rev. A 73, 012701 (2006). https://doi.org/10.1103/PhysRevA.73.012701
S.R. Beane, M.J. Savage, Nucl. Phys. A 694, 511 (2001). https://doi.org/10.1016/S0375-9474(01)01088-0
D.B. Kaplan, Nucl. Phys. B 494, 471 (1997). https://doi.org/10.1016/S0550-3213(97)00178-8
D.R. Phillips, Czechoslov. J. Phys. 52, B49 (2002). https://doi.org/10.1007/s10582-002-0079-z
M. Brodeur, T. Brunner, C. Champagne, S. Ettenauer, M.J. Smith, A. Lapierre, R. Ringle, V.L. Ryjkov, S. Bacca, P. Delheij, G.W.F. Drake, D. Lunney, A. Schwenk, J. Dilling, Phys. Rev. Lett. 108, 052504 (2012). https://doi.org/10.1103/PhysRevLett.108.052504
D.E. Gonzalez Trotter, F.S. Meneses, W. Tornow, C.R. Howell, Q. Chen, A.S. Crowell, C.D. Roper, R.L. Walter, D. Schmidt, H. Witała, W. Glöckle, H. Tang, Z. Zhou, I. Šlaus, Phys. Rev. C 73, 034001 (2006). https://doi.org/10.1103/PhysRevC.73.034001
R.A. Arndt, D.D. Long, L. Roper, Nucl. Phys. A 209(3), 429 (1973). https://doi.org/10.1016/0375-9474(73)90837-3
H. Feshbach, Ann. Phys. 5, 357 (1958). https://doi.org/10.1016/0003-4916(58)90007-1
G.P. Lepage, Phys. Rev. A 16, 863 (1977). https://doi.org/10.1103/PhysRevA.16.863
J. Adam Jr., F. Gross, C. Savkli, J.W. Van Orden, Phys. Rev. C 56, 641 (1997). https://doi.org/10.1103/PhysRevC.56.641
Acknowledgements
DRP and CJ thank Charlotte Elster for useful discussions during the early stages of this work. DRP thanks Jerry Yang for drawing his attention to Ref. [29]. MG thanks Wael Elkamhawy and Fabian Hildenbrand for useful discussions during the early stages of this work. The work of DRP was supported by the US Department of Energy under Contract DE-FG02-93ER-40756 and by the ExtreMe Matter Institute EMMI at the GSI Helmholtzzentrum für Schwerionenphysik, Darmstadt, Germany. HWH and MG were supported by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) under Project Number 279384907 – SFB 1245. HWH was also supported by the Bundesministerium für Bildung und Forschung (BMBF) through Contract 05P18RDFN1.
Author information
Authors and Affiliations
Corresponding author
Additional information
In memory of Ludwig Faddeev.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This article belongs to the Topical Collection “Ludwig Faddeev Memorial Issue”.
Appendices
Alternative Derivation of the Normalization Condition
In this appendix we give an alternative derivation of the normalization condition in the presence of an energy-dependent potential. This derivation focuses on the resolvent of H(E). It is equivalent to the normalization conditions obtained for two-particle vertex functions in relativistic bound-state equations in Refs. [40, 41].
The resolvent of H(E) is:
This contrasts with the resolvent of the energy-independent Hamiltonian obtained by evaluating H(E) at \(E=E_\alpha \), \({\bar{H}} :=H(E_\alpha )\). Denoting that resolvent by \({\bar{G}}(E)\) we have:
By construction, \({\bar{H}}\) and H(E) both have \(|\psi _\alpha \rangle \) as a right eigenstate corresponding to energy \(E_\alpha \). The rest of \({\bar{H}}\)’s spectrum will, however, be different. And, while the eigenstate \(|\psi _\alpha \rangle \) is common to the spectrum of both operators, it is not guaranteed that it should be normalized in the same way. Indeed, we will show here that it should not be.
Expanding H(E) around \(E=E_\alpha \) yields:
where \('\) denotes differentiation with respect to E. This, in turn, allows us to write:
Since \({\bar{G}}(E)\) is the resolvent of an energy-independent Hermitian operator it has a standard spectral representation. If \(E_\alpha \) is an isolated bound state then that is:
where we have used \(|{\bar{\psi }}_\alpha \rangle \) to emphasize that this eigenstates of \({\bar{H}}\) obey the standard normalization condition \(\langle {\bar{\psi }}_\beta |{\bar{\psi }}_\alpha \rangle =\delta _{\beta \alpha }\), since \({\bar{H}}\) is an energy-independent, Hermitian, operator. As discussed at length in Sect. 3 the states \(|\psi _\alpha \rangle \) do not obey this condition, although for \(\beta \ne \alpha \) this is not a surprise, since the spectrum of \({\bar{H}}\) differs from that of H apart from the one state at \(E=E_\alpha \). But for that particular state we must write:
with \(\mathcal{Z}\) an additional wave function renormalization associated with the energy dependence of V(E).
To fix \(\mathcal{Z}\) we insert Eq. (108) in Eq. (107) and sum the geometric series. This yields:
The factor in the denominator here ensures that the consistency condition:
is satisfied. The spectral decomposition (110) will then take the standard form:
provided we identify:
In practice this means that we solve the Hamiltonian eigenvalue problem at \(E=E_\alpha \), thereby obtaining an eigenvector that is, prior to normalization, proportional to both \(|{\bar{\psi }}_\alpha \rangle \) and \(|\psi _\alpha \rangle \). Then, if we wish to compute the latter, we must normalize such that:
instead of using the standard
Additional Formulas for the Probability Density
1.1 Transformation of Jacobi Coordinates
For the evaluation of overlaps of the type \( {}^{}_{i}\! \left\langle {\varvec{p},\varvec{q}}\vert {\varvec{p^{\prime }},\varvec{q^{\prime }}}\right\rangle _{j}^{} \) the following functions are useful, since they abbreviate many expressions:
The transformations can be summarized by the expression
which defines \(\varvec{\kappa }_{ijk}{\left( \varvec{p},\varvec{q}\right) }\) with \(i,j \in \{n,c\}\), \(i \ne j\) and \(k \in \{p,q\}\). The functions \(\varvec{\kappa }_{ijk}\) are given by
Furthermore, we define the functions \(\varvec{\kappa }^\prime _{ijk}{\left( \varvec{p},\varvec{q}\right) }\) with \(i,j \in \{n,c\}\) and \(k \in \{p,q\}\) by
where the spatial part of the \(nn\) permutation operator \(\mathcal {P}_{nn}\) is given by \(\mathcal {P}_{nn}^\mathrm {(spatial)}\). The used functions of the type \(\varvec{\kappa }^\prime _{ijk}\) read
1.2 Simplification of Certain Combinations of Coupled Spherical Harmonics
In this appendix identities simplifying the angular dependence of the probability density are given. The angle \(\gamma \) between two vectors \(\varvec{v}_1\) and \(\varvec{v}_2\) is defined by
Expressed in terms of the angles of the two vectors it reads
In fact, the angular dependence of the coupled spherical harmonic \(\mathcal {Y}_{11}^{00}\) is captured entirely by this angle \(\gamma \).
Also the following combination of coupled spherical harmonics can be purely expressed in terms of relative angles:
Although these relative angles are angles between different vectors, their use simplifies the probability density a lot. If the identity is applied to our probability density all these relative angles will be only functions of \(p\), \(q\) and \(\theta _{pq}\). Therefore angular integrations over the probability density simplify significantly. Instead of four angular integrals only the one over \(\theta _{pq}\) has to be carried out numerically.
1.3 Numerical Calculation of \(X_{ij}\)
In the following expressions for the numerical calculation of the \(X_{ij}\) are given for any type of form factor. In a first step the expression for \(X_{nn}\) is derived using the identity
The calculation yields
where \(\delta ^{(\varOmega )}{\left( \varvec{p}- \varvec{p^{\prime }}\right) } :=\delta {\left( \varphi -\varphi ^\prime \right) } \frac{\delta {\left( \theta -\theta ^\prime \right) }}{\sin {\theta }}\) holds. In order to evaluate this expression only one angular integral has to be computed numerically by using the identities given in “Appendix B.2”.
The calculation of \(X_{nc}\) is based on an identity similar to Eq. (134):
With it one obtains
where the definition \(\theta _{\varvec{a},\varvec{b}} :=\arccos { \left( \varvec{a} \cdot \varvec{b}/\left( ab\right) \right) }\) holds. Note that
holds. This can be shown using that \( {}^{}_{n}\! \left\langle {p,q;\varOmega _n}\vert {p^{\prime },q^{\prime };\varOmega _c}\right\rangle _{c}^{} \) is real.
The implementation of these results was checked by evaluating the expressions for Heaviside form factors, for which the analytic expressions have been calculated in [15]. As in the derivation of the analytic expressions the Heaviside form factors have been neglected, discrepancies from the numerical results can occur at momenta of the order of the regularization scale.
1.4 Overlaps in Partial Wave Basis
In the following expressions for the overlaps of partial wave states with different spectators are derived. Also matrix elements of the \(nn\) permutation operator \(\mathcal {P}_{nn}= \mathcal {P}_{nn}^\mathrm {(spatial)}\otimes \mathcal {P}_{nn}^\mathrm {(spin)}\) are given in this basis. We obtain
Rights and permissions
About this article
Cite this article
Göbel, M., Hammer, HW., Ji, C. et al. Momentum-Space Probability Density of \({}^6\)He in Halo Effective Field Theory. Few-Body Syst 60, 61 (2019). https://doi.org/10.1007/s00601-019-1528-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00601-019-1528-6