Hostname: page-component-8448b6f56d-jr42d Total loading time: 0 Render date: 2024-04-23T16:02:07.754Z Has data issue: false hasContentIssue false
  • English
  • Français

ON 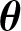$\boldsymbol{\theta} $-CONGRUENT NUMBERS OVER REAL NUMBER FIELDS

Part of: Algebraic number theory: global fields Arithmetic algebraic geometry

Published online by Cambridge University Press:  09 September 2020

SHAMIK DAS Open the ORCID record for SHAMIK DAS [Opens in a new window]  and
ANUPAM SAIKIA Open the ORCID record for ANUPAM SAIKIA [Opens in a new window]
SHAMIK DAS*
Affiliation:
Department of Mathematics, Indian Institute of Technology Guwahati, Guwahati-781039, Assam, India
ANUPAM SAIKIA
Affiliation:
Department of Mathematics, Indian Institute of Technology Guwahati, Guwahati-781039, Assam, Indiaa.saikia@iitg.ac.in
*
e-mail: shamikdas@iitg.ac.in
Get access Rights & Permissions [Opens in a new window]

Abstract

The notion of 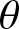$\theta $ -congruent numbers is a generalisation of congruent numbers where one considers triangles with an angle 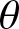$\theta $ such that 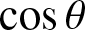$\cos \theta $ is a rational number. In this paper we discuss a criterion for a natural number to be 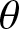$\theta $ -congruent over certain real number fields.

Keywords

congruent numberelliptic curve

MSC classification

Primary: 11G05: Elliptic curves over global fields
Secondary: 11R21: Other number fields 11R16: Cubic and quartic extensions
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 103 , Issue 2 , April 2021 , pp. 218 - 229
Check for updates
Copyright
© 2020 Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The first author has been supported by a Senior Research Fellowship from IIT Guwahati and the second author has been supported by a Professional Development Allowance from IIT Guwahati.

References

Cremona, J. E. and Serf, P., ‘Computing the rank of elliptic curves over real quadratic number fields of class number 1’, Math. Comp. 68(227) (1999), 1187–1200.CrossRefGoogle Scholar
Daniels, H. B. and González-Jiménez, E., ‘On the torsion of rational elliptic curves over sextic fields’, Math. Comp. 89(321) (2020), 411–435.CrossRefGoogle Scholar
Fujiwara, M., ‘θ-congruent numbers’, in: Number Theory: Diophantine, Combinatorial and Algebraic Aspects (eds. Győry, K., Pethő, A. and Sós, V.) (de Gruyter, Berlin, 1998), 235–241.Google Scholar
Girondo, E., González-Diez, G., González-Jiménez, E., Steuding, R. and Steuding, J., ‘Right triangles with algebraic sides and elliptic curves over number fields’, Math. Slovaca 59(3) (2009), 299–306.CrossRefGoogle Scholar
González-Jiménez, E., ‘Complete classification of the torsion structures of rational elliptic curves over quintic number fields’, J. Algebra 478 (2017), 484–505.CrossRefGoogle Scholar
González-Jiménez, E. and Najman, F., ‘Growth of torsion groups of elliptic curves upon base change’, Math. Comp. 89(323) (2020), 1457–1485.CrossRefGoogle Scholar
González-Jiménez, E., Najman, F. and Tornero, J. M., ‘Torsion of rational elliptic curves over cubic fields’, Rocky Mountain J. Math. 46(6) (2016), 1899–1917.CrossRefGoogle Scholar
Janfada, A. S. and Salami, S., ‘On $\theta$-congruent numbers on real quadratic number fields’, Kodai Math. J. 38(2) (2015), 352–364.CrossRefGoogle Scholar
Jędrzejak, T., ‘Congruent numbers over real number fields’, Colloq. Math. 128(2) (2012), 179–186.CrossRefGoogle Scholar
Kan, M., ‘ $\theta$ -congruent numbers and elliptic curves’, Acta Arith. 94(2) (2000), 153–160.CrossRefGoogle Scholar
Knapp, A. W., Elliptic Curves, Mathematical Notes, 40 (Princeton University Press, Princeton, NJ, 1992).Google Scholar
Koblitz, N., Introduction to Elliptic Curves and Modular Forms, Graduate Texts in Mathematics, 97 (Springer-Verlag, New York, 1984).CrossRefGoogle Scholar
Monsky, P., ‘Mock Heegner points and congruent numbers’, Math. Z. 204(1) (1990), 45–67.CrossRefGoogle Scholar
Najman, F., ‘Torsion of rational elliptic curves over cubic fields and sporadic points on ${X}_1(n)$’, Math. Res. Lett. 23(1) (2016), 245–272.CrossRefGoogle Scholar
Prasad, D. and Yogananda, C. S., ‘Bounding the torsion in CM elliptic curves’, C. R. Math. Acad. Sci. Soc. R. Can. 23(1) (2001), 1–5.Google Scholar
Qiu, D. and Zhang, X., ‘Elliptic curves and their torsion subgroups over number fields of type $\left(2,2,\dots, 2\right)$’, Sci. China Ser. A 44(2) (2001), 159–167.CrossRefGoogle Scholar
Silverberg, A., ‘Points of finite order on abelian varieties’, in: p-Adic Methods in Number Theory and Algebraic Geometry, Contemporary Mathematics, 133 (American Mathematical Society, Providence, RI, 1992), 175–193.Google Scholar
Tada, M., ‘Congruent numbers over real quadratic fields’, Hiroshima Math. J. 31(2) (2001), 331–343.CrossRefGoogle Scholar
Tian, Y., ‘Congruent numbers and Heegner points’, Camb. J. Math. 2(1) (2014), 117–161.CrossRefGoogle Scholar
Tunnell, J. B., ‘A classical Diophantine problem and modular forms of weight 3/2’, Invent. Math. 72(2) (1983), 323–334.CrossRefGoogle Scholar