Viscoelastic Wave Simulation with High Temporal Accuracy Using Frequency-Dependent Complex Velocity

Abstract

In recent decades, the study of seismic attenuation has received more and more concerns because it can stimulate the development of wave propagation simulation and improve the accuracy of structure imaging and reservoir prediction. In this paper, we review the attenuation theory and the development of high temporal accuracy wave simulation. The conventional mathematical models to describe the characteristics of viscoelastic are based on constant-Q model or standard linear solids theory. However, these approaches possess some noticeable shortcomings. Therefore, we introduce a frequency-dependent complex velocity to derive the novel viscoelastic wave equations with decoupled amplitude dissipation and phase dispersion. To obtain high temporal accuracy viscoelastic wave simulation, we adopt the normalized pseudo-Laplacian to compensate for the temporal dispersion errors caused by the second-order finite-difference discretization in the time domain. During the implementation, we incorporate the normalized pseudo-Laplacian into the optimized staggered-grid finite-difference coefficients. Therefore, it can greatly reduce the times of low-rank decomposition and Fourier transform and largely improve the computational efficiency. Based on this strategy, we can implement the high temporal accuracy viscoelastic wavefield extrapolation by comprehensively exploiting the staggered-grid finite-difference scheme, pseudo-spectral method and low-rank decomposition algorithm. Meanwhile, a linear velocity model is employed to evaluate the accuracy of low-rank approximation. Furthermore, we use several numerical examples to carry out the comparison between our scheme and other conventional methods. The numerical results reveal that our proposed scheme can effectively compensate for temporal dispersion errors and help generate high temporal accuracy viscoelastic wave solutions.

Appendices

Appendix A. Phase velocity analysis in isotropic media

Substituting plane wave into viscoelastic wave equations can generate the Christoffel equation in attenuative media. This equation is widely used in phase velocity analysis. First, the displacement of a harmonic plane wave in attenuative media can be written as:

$${\tilde{\mathbf{u}}} = {\tilde{\mathbf{U}}}\exp \left[ {i\left( {\omega t - {\tilde{\mathbf{k}}\mathbf{x}}} \right)} \right],$$

(49)

where ${\tilde{\mathbf{U}}}$ denotes the polarization vector, ${\tilde{\mathbf{k}}} = {\mathbf{k}}_{R} - i{\mathbf{k}}_{I}$ is the wave vector that becomes complex in the presence of attenuation, ${\mathbf{k}}_{R}$ is the real part of wavenumber and ${\mathbf{k}}_{I}$ is the imaginary part of the wave vector. Substituting the plane wave of Eq. (49) into viscoelastic equations, we can obtain the corresponding Christoffel equation as follows:

$$\left[ {{\tilde{\mathbf{k}}}^{2} {\mathbf{G}} - \rho \omega^{2} {\mathbf{I}}} \right]{\tilde{\mathbf{U}}} = 0,$$

(50)

where ${\mathbf{G}}$ is the complex Christoffel matrix and ${\mathbf{I}}$ is the identity matrix.

1.1 SH-Wave Phase Velocity Analysis

For the wave vector of SH-wave, the Christoffel equation has the following form ($\tilde{k} = \left| {{\tilde{\mathbf{k}}}} \right|$):

$$\tilde{c}_{66} \tilde{k}_{1}^{2} + \tilde{c}_{55} \tilde{k}_{3}^{2} - \rho \omega^{2} = 0.$$

(51)

Substituting the complex stiffness coefficients $\tilde{c}_{ij} { = }c_{ij}^{R} + {{i}}c_{ij}^{I}$ into Eq. (51) yields

$$\left( {c_{66}^{R} + ic_{66}^{I} } \right)\left( {k_{R} \sin \theta - ik_{I} \sin \theta } \right)^{2} + \left( {c_{55}^{R} + ic_{55}^{I} } \right)\left( {k_{R} \cos \theta - ik_{I} \cos \theta } \right)^{2} - \rho \omega^{2} = 0.$$

(52)

In weakly attenuative media, we have

$$\gamma_{P,S} = {{\arctan \left( {\frac{1}{{Q_{P,S} }}} \right)} \mathord{\left/ {\vphantom {{\arctan \left( {\frac{1}{{Q_{P,S} }}} \right)} \pi }} \right. \kern-0pt} \pi } \approx \frac{1}{{\pi Q_{P,S} }}.$$

(53)

Because of the truncated TE of $\left| {{\omega \mathord{\left/ {\vphantom {\omega {\omega_{0} }}} \right. \kern-0pt} {\omega_{0} }}} \right|^{2\gamma } \approx 1{ + }2\gamma \ln \left| {{\omega \mathord{\left/ {\vphantom {\omega {\omega_{0} }}} \right. \kern-0pt} {\omega_{0} }}} \right|$, the complex moduli are rewritten in the forms

$$C_{\lambda } = M_{0} \left( {\left| {\frac{\omega }{{\omega_{0} }}} \right|^{{2\gamma_{P} }} - \frac{{i\text{sgn} \left( \omega \right)}}{{Q_{P} \left( {\mathbf{x}} \right)}}} \right),$$

(54)

$$C_{\mu } = \mu_{0} \left( {\left| {\frac{\omega }{{\omega_{0} }}} \right|^{{2\gamma_{S} }} - \frac{{i\text{sgn} \left( \omega \right)}}{{Q_{S} \left( {\mathbf{x}} \right)}}} \right).$$

(55)

After some simplifications, the imaginary part of Eq. (52) can be formulated as (assume $\text{sgn} \left( \omega \right) = - 1$):

$$\frac{{\mu_{0} }}{{Q_{S} }}\left( {k_{R}^{2} - k_{I}^{2} } \right) - 2\mu_{0} \left| {\frac{\omega }{{\omega_{0} }}} \right|^{{2\gamma_{S} }} k_{R} k_{I} = 0.$$

(56)

The only physically meaningful solution of equation is given by

$$\frac{{k_{I} }}{{k_{R} }} = \sqrt {1 + Q_{S}^{2} \left| {\frac{\omega }{{\omega_{0} }}} \right|^{{4\gamma_{S} }} } - Q_{S} \left| {\frac{\omega }{{\omega_{0} }}} \right|^{{2\gamma_{S} }} \approx \frac{1}{{2Q_{S} }}\left| {\frac{\omega }{{\omega_{0} }}} \right|^{{ - 2\gamma_{S} }} .$$

(57)

The real part of Eq. (52) then reduces to

$$\mu_{0} \left| {\frac{\omega }{{\omega_{0} }}} \right|^{{2\gamma_{S} }} \left( {k_{R}^{2} - k_{I}^{2} } \right) + \frac{{\mu_{0} }}{{Q_{S} }}2k_{R} k_{I} - \rho \omega^{2} = 0.$$

(58)

The phase velocity of SH-waves is found as

$$V_{SH} = \frac{\omega }{{k_{R} }} = V_{S0} \sqrt {\left| {{\omega \mathord{\left/ {\vphantom {\omega {\omega_{0} }}} \right. \kern-0pt} {\omega_{0} }}} \right|^{{2\gamma_{S} }} + \frac{3}{{4Q_{S}^{2} }}\left| {{\omega \mathord{\left/ {\vphantom {\omega {\omega_{0} }}} \right. \kern-0pt} {\omega_{0} }}} \right|^{{ - 2\gamma_{S} }} } \approx V_{S0} \left| {{\omega \mathord{\left/ {\vphantom {\omega {\omega_{0} }}} \right. \kern-0pt} {\omega_{0} }}} \right|^{{\gamma_{S} }} .$$

(59)

1.2 P- and SV-Wave Phase Velocity Analysis

For P- and SV-waves, the Christoffel equation can be written as

$$\left( {\tilde{c}_{11} \tilde{k}_{1}^{2} + \tilde{c}_{55} \tilde{k}_{3}^{2} - \rho \omega^{2} } \right)\left( {\tilde{c}_{55} \tilde{k}_{1}^{2} + \tilde{c}_{33} \tilde{k}_{3}^{2} - \rho \omega^{2} } \right) - \left[ {\left( {\tilde{c}_{13} + \tilde{c}_{55} } \right)\tilde{k}_{1} \tilde{k}_{3} } \right]^{2} = 0.$$

(60)

On the basis of $\tilde{c}_{ij} { = }c_{ij}^{R} + {{i}}c_{ij}^{I}$ and ${{c_{M,\mu }^{R} } \mathord{\left/ {\vphantom {{c_{M,\mu }^{R} } {c_{M,\mu }^{I} }}} \right. \kern-0pt} {c_{M,\mu }^{I} }}{ = }Q_{P,S} \left( {1{ + }\frac{2}{{\pi Q_{P,S} }}\ln \left| {\frac{\omega }{{\omega_{0} }}} \right|} \right) \approx Q_{P,S} \left| {\frac{\omega }{{\omega_{0} }}} \right|^{{2\gamma_{P,S} }}$, Eq. (60) can be reformulated as

$$\begin{aligned} & \left[ {\left( {c_{11}^{I} \sin^{2} \theta + c_{55}^{I} \cos^{2} \theta } \right)\mathcal{K}_{1} - \rho \omega^{2} + {{i}}\left( {c_{11}^{I} \sin^{2} \theta + c_{55}^{I} \cos^{2} \theta } \right)\mathcal{K}_{2} } \right] \\ & \quad \times {\kern 1pt} \left[ {\left( {c_{55}^{I} \sin^{2} \theta + c_{33}^{I} \cos^{2} \theta } \right)\mathcal{K}_{1} - \rho \omega^{2} + {{i}}\left( {c_{55}^{I} \sin^{2} \theta + c_{33}^{I} \cos^{2} \theta } \right)\mathcal{K}_{2} } \right] - \left[ {\left( {c_{13}^{I} + c_{55}^{I} } \right)\sin \theta \cos \theta \left( {\mathcal{K}_{1} + {{i}}\mathcal{K}_{2} } \right)} \right]^{2} = 0, \\ \end{aligned}$$

(61)

where

$$\begin{array}{*{20}c} {\mathcal{K}_{1} { = }Q_{P,S} \left| {\frac{\omega }{{\omega_{0} }}} \right|^{{2\gamma_{P,S} }} \left( {k_{R}^{2} - k_{I}^{2} } \right) + 2k_{R} k_{I} ,} & {\mathcal{K}_{2} { = }\left( {k_{R}^{2} - k_{I}^{2} } \right) - Q_{P,S} \left| {\frac{\omega }{{\omega_{0} }}} \right|^{{2\gamma_{P,S} }} 2k_{R} k_{I} } \\ \end{array} .$$

(62)

The physically meaningful solution of the imaginary part of Eq. (61) is $\mathcal{K}_{2} { = 0}$, which then yields

$$\frac{{k_{I} }}{{k_{R} }} = \sqrt {1 + Q_{P,S}^{2} \left| {\frac{\omega }{{\omega_{0} }}} \right|^{{4\gamma_{P,S} }} } - Q_{P,S} \left| {\frac{\omega }{{\omega_{0} }}} \right|^{{2\gamma_{P,S} }} \approx \frac{1}{{2Q_{P,S} }}\left| {\frac{\omega }{{\omega_{0} }}} \right|^{{ - 2\gamma_{P,S} }} .$$

(63)

After some mathematical manipulations, the real part of Eq. (61) is simplified as follows:

$$\left( {\rho \omega^{2} - \frac{{\mu_{0} }}{{Q_{S} }}\mathcal{K}_{1} } \right)\left( {\rho \omega^{2} - \frac{{M_{0} }}{{Q_{P} }}\mathcal{K}_{1} } \right) = 0.$$

(64)

Solving Eq. (64) can obtain the phase velocities in the following form

$$V_{P,SV} \approx V_{P0,S0} \left| {{\omega \mathord{\left/ {\vphantom {\omega {\omega_{0} }}} \right. \kern-0pt} {\omega_{0} }}} \right|^{{\gamma_{P,S} }} .$$

(65)

Based on Eqs. (59) and (65), we can theoretically calculate the P- and S-wave phase velocities.

1.3 Accuracy analysis for

$$\omega \approx \left| {\mathbf{k}} \right|v_{P0,S0}$$

Inserting $\omega \approx \left| {\mathbf{k}} \right|v_{P0,S0}$ into Eq. (65) produces

$$V_{P,SV} \approx V_{P0,S0} \left| {\frac{{\left| {\mathbf{k}} \right|v_{P0,S0} }}{{\omega_{0} }}} \right|^{{\gamma_{P,S} }} .$$

(66)

Therefore, we can use Eq. (66) to evaluate the accuracy of real phase velocity after adopting the approximation of $\omega \approx \left| {\mathbf{k}} \right|v_{P0,S0}$. To evaluate quantitatively the accuracy of phase velocity, the relative error is defined as follows:

$${\text{REL}} = {{\left( {{\text{RX}} - {\text{RY}}} \right)} \mathord{\left/ {\vphantom {{\left( {{\text{RX}} - {\text{RY}}} \right)} {\text{RX}}}} \right. \kern-0pt} {\text{RX}}},$$

(67)

where RX is the accurate solution and RY is the approximate value.

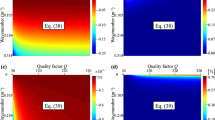
Based on Eqs. (65) and (66), we calculate the accurate and approximate phase velocities. Figure 11 describes the phase velocity variations with reference velocities, wavenumbers and quality factors. It can be seen that even in a strongly attenuative media ($Q = 10$), the phase velocity relative errors are as small as 0.0041. Based on the above analysis, we can conclude that the approximation of $\omega \approx \left| {\mathbf{k}} \right|v_{P0,S0}$ has a very small influence on phase velocity. Therefore, introducing this approximation to solve viscoelastic wave equations is reasonable.

Fig. 11

Phase velocity variations with reference velocities, wavenumbers and quality factors. a Computed by Eq. (65), considered as an accurate solution. b The difference between the approximation, computed by Eq. (66), and the accurate value. c The relative error computed by Eq. (67)

Appendix B. Phase Velocity Analysis in Anisotropic Media

In this section, we perform SH-, SV- and P-waves phase velocity analysis in VTI attenuative media.

2.1 SH-Wave Phase Velocity Analysis

Based on the complex modulus expression in anisotropic attenuative media (Eq. 41), the real and imaginary stiffness coefficients can be written as (assume $\text{sgn} \left( \omega \right) = - 1$)

$$c_{ij}^{R} = c_{ij} \left| {\frac{\omega }{{\omega_{0} }}} \right|^{{2\gamma_{ij} }} ,$$

(68)

$$c_{ij}^{I} = {{c_{ij} } \mathord{\left/ {\vphantom {{c_{ij} } {Q_{ij} }}} \right. \kern-0pt} {Q_{ij} }}.$$

(69)

Substituting Eqs. (68) and (69) into Eq. (52), we can derive the following real and imaginary parts, respectively.

$$c_{66} \sin^{2} \theta \left[ {\left| {\frac{\omega }{{\omega_{0} }}} \right|^{{2\gamma_{66} }} \left( {k_{R}^{2} - k_{I}^{2} } \right) + \frac{1}{{Q_{66} }}2k_{R} k_{I} } \right] + c_{55} \cos^{2} \theta \left[ {\left| {\frac{\omega }{{\omega_{0} }}} \right|^{{2\gamma_{55} }} \left( {k_{R}^{2} - k_{I}^{2} } \right) + \frac{1}{{Q_{55} }}2k_{R} k_{I} } \right] - \rho \omega^{2} = 0,$$

(70)

$$c_{66} \sin^{2} \theta \left[ {\frac{1}{{Q_{66} }}\left( {k_{R}^{2} - k_{I}^{2} } \right) - \left| {\frac{\omega }{{\omega_{0} }}} \right|^{{2\gamma_{66} }} 2k_{R} k_{I} } \right] + c_{55} \cos^{2} \theta \left[ {\frac{1}{{Q_{55} }}\left( {k_{R}^{2} - k_{I}^{2} } \right) - \left| {\frac{\omega }{{\omega_{0} }}} \right|^{{2\gamma_{55} }} 2k_{R} k_{I} } \right] = 0.$$

(71)

Substituting the relationship $c_{66} = c_{55} \left( {1 + 2\gamma } \right)$ into Eq. (71) and making some simplifications produce

$$k_{R}^{2} - k_{I}^{2} - 2Q_{55} \alpha k_{R} k_{I} = 0,$$

(72)

where

$$\alpha { = }\frac{{\left( {1{ + 2}\gamma } \right)\left| {\frac{\omega }{{\omega_{0} }}} \right|^{{2\gamma_{66} }} \sin^{2} \theta { + }\left| {\frac{\omega }{{\omega_{0} }}} \right|^{{2\gamma_{55} }} \cos^{2} \theta }}{{\left( {1{ + 2}\gamma } \right)\frac{{Q_{55} }}{{Q_{66} }}\sin^{2} \theta + \cos^{2} \theta }}.$$

(73)

The physically meaningful solution of Eq. (72) is

$$\frac{{k_{I} }}{{k_{R} }} = \sqrt {1 + \left( {Q_{55} \alpha } \right)^{2} } - Q_{55} \alpha .$$

(74)

Then, the real part can be simplified as

$$\left( {c_{66} \sin^{2} \theta + c_{55} \cos^{2} \theta } \right)\left( {k_{R}^{2} - k_{I}^{2} + \frac{{2k_{R} k_{I} }}{{Q_{55} \alpha }}} \right) - \rho \omega^{2} = 0.$$

(75)

The phase velocity of SH-wave can be calculated by

$$V_{\text{SH}} = \frac{\omega }{{k_{R} }} = \xi_{Q} V_{\text{SH}}^{\text{elastic}} ,$$

(76)

where

$$V_{\text{SH}}^{\text{elastic}} = \sqrt {\frac{{\left( {c_{66} \sin^{2} \theta + c_{55} \cos^{2} \theta } \right)}}{\rho }} ,$$

(77)

and

$$\xi_{Q} = \sqrt {\frac{{2\left( {\sqrt {1 + \left( {Q_{55} \alpha } \right)^{2} } - Q_{55} \alpha } \right)\left( {1 + \left( {Q_{55} \alpha } \right)^{2} } \right)}}{{Q_{55} \alpha }}} .$$

(78)

For weakly attenuative media, $\xi_{Q} \approx 1 { + }\frac{1}{{2\left( {Q_{55} \alpha } \right)^{2} }}.$

2.2 P- and SV-Wave Phase Velocity Analysis

In VTI attenuative media, Eq. (60) has the following form

$$\begin{aligned} & \left\{ {\left[ {\left( {c_{11}^{R} + {{i}}c_{11}^{I} } \right)\sin^{2} \theta + \left( {c_{55}^{R} + {{i}}c_{55}^{I} } \right)\cos^{2} \theta } \right]\left( {k_{R} - ik_{I} } \right)^{2} - \rho \omega^{2} } \right\} \\ & \quad \times {\kern 1pt} \left\{ {\left[ {\left( {c_{55}^{R} + ic_{55}^{I} } \right)\sin^{2} \theta + \left( {c_{33}^{R} + ic_{33}^{I} } \right)\cos^{2} \theta } \right]\left( {k_{R} - ik_{I} } \right)^{2} - \rho \omega^{2} } \right\} - \left\{ {\left[ {\left( {c_{13}^{R} + c_{55}^{R} } \right) + i\left( {c_{13}^{I} + c_{55}^{I} } \right)} \right]\sin \theta \cos \theta k_{R} k_{I} } \right\}^{2} . \\ \end{aligned}$$

(79)

Combining Eqs. (68) and (69), Eq. (79) can be simplified as follows:

$$\begin{aligned} & \left[ {\left( {c_{11}^{I} \sin^{2} \theta \mathcal{K}_{1}^{11} + c_{55}^{I} \cos^{2} \theta \mathcal{K}_{1}^{55} } \right) - \rho \omega^{2} + i\left( {c_{11}^{I} \sin^{2} \theta \mathcal{K}_{2}^{11} + c_{55}^{I} \cos^{2} \theta \mathcal{K}_{2}^{55} } \right)} \right] \\ & \quad \times {\kern 1pt} \left[ {\left( {c_{55}^{I} \sin^{2} \theta \mathcal{K}_{1}^{55} + c_{33}^{I} \cos^{2} \theta \mathcal{K}_{1}^{33} } \right) - \rho \omega^{2} + i\left( {c_{55}^{I} \sin^{2} \theta \mathcal{K}_{2}^{55} + c_{33}^{I} \cos^{2} \theta \mathcal{K}_{2}^{33} } \right)} \right] \\ & \quad - {\kern 1pt} \left[ {\left( {c_{13}^{I} \mathcal{K}_{1}^{13} + c_{55}^{I} \mathcal{K}_{1}^{55} } \right) + i\left( {c_{13}^{I} \mathcal{K}_{2}^{13} + c_{55}^{I} \mathcal{K}_{2}^{55} } \right)} \right]^{2} \sin^{2} \theta \cos^{2} \theta = 0, \\ \end{aligned}$$

(80)

where

$$\begin{array}{*{20}c} {\mathcal{K}_{1}^{ij} { = }Q_{ij} \left| {\frac{\omega }{{\omega_{0} }}} \right|^{{2\gamma_{ij} }} \left( {k_{R}^{2} - k_{I}^{2} } \right) + 2k_{R} k_{I} ,} & {\mathcal{K}_{2}^{ij} { = }\left( {k_{R}^{2} - k_{I}^{2} } \right) - Q_{ij} \left| {\frac{\omega }{{\omega_{0} }}} \right|^{{2\gamma_{ij} }} 2k_{R} k_{I} } \\ \end{array} .$$

(81)

To make Eq. (80) meaningful, we set $\mathcal{K}_{2}^{ij} { = 0}$, which yields

$$\frac{{k_{I} }}{{k_{R} }} = \sqrt {1 + Q_{ij}^{2} \left| {\frac{\omega }{{\omega_{0} }}} \right|^{{4\gamma_{ij} }} } - Q_{ij} \left| {\frac{\omega }{{\omega_{0} }}} \right|^{{2\gamma_{ij} }} \approx \frac{1}{{2Q_{ij} }}\left| {\frac{\omega }{{\omega_{0} }}} \right|^{{ - 2\gamma_{ij} }} .$$

(82)

For weak attenuation ($k_{R} \gg k_{I}$), thus we have

$$\mathcal{K}_{1}^{ij} \approx Q_{ij} \left| {\frac{\omega }{{\omega_{0} }}} \right|^{{2\gamma_{ij} }} k_{R}^{2} .$$

(83)

Therefore, Eq. (80) can be simplified as follows:

$$\left[ {\left( {c_{11}^{R} \sin^{2} \theta + c_{55}^{R} \cos^{2} \theta } \right)k_{R}^{2} - \rho \omega^{2} } \right]\left[ {\left( {c_{55}^{R} \sin^{2} \theta + c_{33}^{R} \cos^{2} \theta } \right)k_{R}^{2} - \rho \omega^{2} } \right] - \left[ {\left( {c_{13}^{R} + c_{55}^{R} } \right)\sin \theta \cos \theta k_{R}^{2} } \right]^{2} = 0.$$

(84)

Solving Eq. (84) can obtain the P- or SV-wave phase velocity in VTI attenuative media:

$$V_{P,SV} = \frac{\omega }{{k_{R} }} \approx \frac{1}{{\sqrt {2\rho } }}\left\{ {\frac{{\left( {c_{11}^{R} + c_{55}^{R} } \right)\sin^{2} \theta + \left( {c_{33}^{R} + c_{55}^{R} } \right)\cos^{2} \theta }}{{ \pm {\kern 1pt} \sqrt {\left[ {\left( {c_{11}^{R} - c_{55}^{R} } \right)\sin^{2} \theta - \left( {c_{33}^{R} - c_{55}^{R} } \right)\cos^{2} \theta } \right]^{2} + 4\left( {c_{13}^{R} + c_{55}^{R} } \right)^{2} \sin^{2} \theta \cos^{2} \theta } }}} \right..$$

(85)

Appendix C. Accuracy Analysis for Incorporating Normalized Pseudo-Laplacian into Optimized SGFD Coefficients

To efficiently solve the new high temporal accuracy viscoelastic wave equations, a critical technology of incorporating normalized pseudo-Laplacian into optimized SGFD coefficients has been proposed. To investigate the accuracy of this operation, we compare the difference between $\sqrt {\hat{F}\left( {\mathbf{k}} \right)} \sum\nolimits_{m = 1}^{M} {c_{m} \sin \left[ {\left( {m - 0.5} \right)kh} \right]}$ and $\sum\nolimits_{m = 1}^{M} {c^{\prime}_{m} \sin \left[ {\left( {m - 0.5} \right)kh} \right]}$ with a simple linear velocity model. $c_{m}$ and $c^{\prime}_{m}$ stand for the conventional and optimized SGFD coefficients, respectively, computed by Eqs. (28) and (29) through minimizing the square error between the left- and right-hand sides.

First, the velocity and wavenumber are formulated as:

$$\begin{array}{*{20}c} {v\left( x \right) = 1500 + 2x} & {\left( {0 \le x < N} \right),} \\ \end{array}$$

(86)

$$k\left( x \right) = \left\{ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {{{2\pi x} \mathord{\left/ {\vphantom {{2\pi x} {\left( {Nh} \right)}}} \right. \kern-0pt} {\left( {Nh} \right)}},} \\ {{{2\pi \left( {N - x} \right)} \mathord{\left/ {\vphantom {{2\pi \left( {N - x} \right)} {\left( {Nh} \right)}}} \right. \kern-0pt} {\left( {Nh} \right)}},} \\ \end{array} } & {\begin{array}{*{20}c} {0 \le x < {N \mathord{\left/ {\vphantom {N 2}} \right. \kern-0pt} 2}} \\ {{N \mathord{\left/ {\vphantom {N 2}} \right. \kern-0pt} 2} \le x < N} \\ \end{array} } \\ \end{array} } \right.,$$

(87)

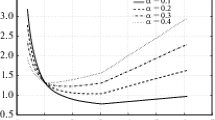
where x is the grid number and N is the grid length. Figure 12 plots some results of $\sqrt {\hat{F}\left( {\mathbf{k}} \right)} \sum\nolimits_{m = 1}^{M} {c_{m} \sin \left[ {\left( {m - 0.5} \right)kh} \right]}$, $\sum\nolimits_{m = 1}^{M} {c^{\prime}_{m} \sin \left[ {\left( {m - 0.5} \right)kh} \right]}$ and their differences with different time steps. For a small time step, the differences between two expressions are very small. With the increase in time step, the absolute errors are also growing (Fig. 12a–d). To avoid numerical instability, the spatial interval usually should increase with the time step. Using a large spatial spacing, the approximation errors may decrease a lot (Fig. 12d–f). Overall, the maximal error is relatively small and can be accepted during the computation.

Fig. 12

Comparisons between reference (black line) and approximation (red line) computed by $\sqrt {\hat{F}\left( {\mathbf{k}} \right)} \sum\nolimits_{m = 1}^{M} {c_{m} \sin \left[ {\left( {m - 0.5} \right)k_{x} h} \right]}$ and $\sum\nolimits_{m = 1}^{M} {c^{\prime}_{m} \sin \left[ {\left( {m - 0.5} \right)k_{x} h} \right]}$ with different time steps and spatial intervals. Note that $c_{m}$ and $c^{\prime}_{m}$ stand for the conventional and optimized SGFD coefficients, respectively, which are computed by Eqs. (28) and (29) through minimizing the square error between the left- and right-hand sides