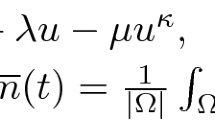Can Fluid Interaction Influence the Critical Mass for Taxis-Driven Blow-up in Bounded Planar Domains?

Abstract

In a bounded planar domain $\varOmega$ with smooth boundary, the initial-boundary value problem of homogeneous Neumann type for the Keller-Segel-fluid system

$$\begin{aligned} \left \{ \textstyle\begin{array}{l@{\quad }l} n_{t} + \nabla \cdot (nu) = \Delta n - \nabla \cdot (n\nabla c), & x\in \varOmega , \ t>0, \\ 0 = \Delta c -c+n, & x\in \varOmega , \ t>0, \end{array}\displaystyle \right . \end{aligned}$$

is considered, where $u$ is a given sufficiently smooth velocity field on $\overline {\varOmega }\times [0,\infty )$ that is tangential on $\partial \varOmega$ but not necessarily solenoidal.

It is firstly shown that for any choice of $n_{0}\in C^{0}(\overline {\varOmega })$ with $\int _{\varOmega}n_{0}<4\pi$, this problem admits a global classical solution with $n(\cdot ,0)=n_{0}$, and that this solution is even bounded whenever $u$ is bounded and $\int _{\varOmega}n_{0}<2\pi$. Secondly, it is seen that for each $m>4\pi$ one can find a classical solution with $\int _{\varOmega}n(\cdot ,0)=m$ which blows up in finite time, provided that $\varOmega$ satisfies a technical assumption requiring $\partial \varOmega$ to contain a line segment.

In particular, this indicates that the value $4\pi$ of the critical mass for the corresponding fluid-free Keller-Segel system is left unchanged by any fluid interaction of the considered type, thus marking a considerable contrast to a recent result revealing some fluid-induced increase of critical blow-up masses in a related Cauchy problem in the entire plane.

1 Introduction

Understanding possible effects of fluid interaction on chemotaxis systems has been the objective of considerable efforts in the mathematical literature during the past decade. Motivated by experimentally obtained results reporting significant influences of corresponding transport mechanisms on the structure-enhancing potential of aggregation due to attractive cross-diffusion ([23]), a noticeable literature has been concerned with various types of associated chemotaxis-fluid systems. Even in the most complex case in which, according to the modeling approach presented in [23], the fluid velocity itself is an unknown system variable according to buoyancy-induced feedback effects of cells on the fluid flow, beyond establishing basic solution theories ([3, 4, 7, 8, 12, 21, 24, 25, 27, 29, 31]) it has been possible to address aspects related to qualitative solution behavior in some situations ([4, 5, 14, 28, 30, 32, 33, 35]).

While the latter class of findings seems yet limited to results identifying conditions under which spatial homogeneity ultimately prevails due to dominance of various dissipative mechanisms, somewhat deeper insight with regard to genuine structure formation could be gained upon renouncing any feedback of the considered population on the fluid evolution, thus considering the fluid flow as an externally given system ingredient. Examples in this direction address corresponding variants of classical Keller-Segel systems which in their fluid-free two- and higher-dimensional versions are known to exhibit blow-up phenomena due to the aggregation-enhancing interplay of chemotactic attraction to a signal produced by the cells themselves ([1, 10, 17, 19]). The results reported in [11], for instance, indicate that in two- and three-dimensional cases, any such explosion can be suppressed by an appropriately chosen, and hence data-dependent, incompressible fluid velocity field.

Even a class of very simple and explicit fluid fields has recently been found to substantially influence the critical mass phenomenon known as the probably most striking characteristic feature of the Cauchy problem for the unperturbed parabolic-elliptic Keller-Segel system in the whole plane: Namely, it has been shown in [9] that for each $m\in (0,16\pi )$ there exist $A>0$ and some initial data $n_{0}$ fulfilling $\int _{\mathbb {R}^{2}} n_{0}=m$ such that with $u(x):=A\cdot (-x_{1},x_{2})$, $x=(x_{1},x_{2})\in \mathbb {R}^{2}$, the problem

$$ \left \{ \textstyle\begin{array}{l@{\quad }l} n_{t} + \nabla \cdot (nu) = \Delta n - \nabla \cdot (n\nabla c), & x\in \mathbb {R}^{2}, \ t>0, \\ 0 = \Delta c+n, & x\in \mathbb {R}^{2}, \ t>0, \\ n(x,0)=n_{0}(x), & x\in \mathbb {R}^{2}, \end{array}\displaystyle \right . $$

(1.1)

possesses a globally defined smooth solution. As the corresponding fluid-free analogue with $u\equiv 0$ is well-known to allow for global solutions only when $\int _{\mathbb {R}^{2}} n_{0} \le 8\pi$, whereas any choice of reasonably regular $n_{0}$ with $\int _{\mathbb {R}^{2}}n_{0}>8\pi$ enforces finite-time blow-up of the associated solution ([19, 20]), this demonstrates that fluid transport in fact can increase the value of the critical mass in this Cauchy problem, which appears to be in quite good accordance with the predictions formulated as conclusions from the numerical simulations in [16].

The intention of the present work is to show that this considerably changes when the considered physical region is a bounded domain $\varOmega \subset \mathbb {R}^{2}$ with smooth boundary, rather than the entire plane. For this purpose, let us recall that in the case $u\equiv 0$, the Neumann initial-boundary value problem

$$ \left \{ \textstyle\begin{array}{l@{\quad }l} n_{t} + \nabla \cdot (nu) = \Delta n - \nabla \cdot (n\nabla c), & x\in \varOmega , \ t>0, \\ 0 = \Delta c -c+n, \qquad & x\in \varOmega , \ t>0, \\ \frac{\partial n}{\partial \nu } = \frac{\partial c}{\partial \nu }=0, & x\in \partial \varOmega , \ t>0, \\ n(x,0)=n_{0}(x), & x\in \varOmega , \end{array}\displaystyle \right . $$

(1.2)

still exhibits a critical mass phenomenon with respect to finite-time blow-up, but that this slightly differs from the above in its nature: It is well-known, namely, that whenever $n_{0}$ is sufficiently regular with $\int _{\varOmega}n_{0}< m_{c}:=4\pi$, then (1.2) admits a global classical solution, while for any $m>4\pi$ it is possible to find at least some smooth $n_{0}$ such that $\int _{\varOmega}n_{0}=m$, but that (1.2) possesses a solution blowing up in finite time with respect to the spatial $L^{\infty }$ norm of the component $n$ ([1, 17, 20]). Indeed, a role of $m_{c}$ equally strict to that of the number $8\pi$ in the context of (1.1) cannot be expected in (1.2) due to the presence of the constant steady states $(n,c)\equiv (\frac{m}{|\varOmega |}, \frac{m}{|\varOmega |})$ at arbitrary mass levels $m>0$.

As we shall see below, in this slightly modified form the criticality of $m_{c}=4\pi$ remains untouched when allowing for widely arbitrary $u$ in (1.2), not even requiring solenoidality. To substantiate this, throughout the sequel we shall assume that

$$ u\in C^{2,1} \bigl(\overline {\varOmega }\times [0,\infty \bigr);\mathbb {R}^{2} ) \ \text{is such that} \ u\cdot \nu =0 \text{ on } \partial \varOmega \times (0, \infty ), $$

(1.3)

and that

$$ n_{0}\in C^{0}(\overline {\varOmega }) \ \text{is nonnegative with } n_{0}\not \equiv 0. $$

(1.4)

Then the first of our main results shows that any such fluid interaction cannot decrease the critical mass in the sense described above:

Theorem 1.1

Let $\varOmega \subset \mathbb {R}^{2}$ be a bounded domain with smooth boundary, and suppose that $u$ satisfies (1.3). Then for any choice of $n_{0}$ fulfilling (1.4) as well as $\int _{\varOmega}n_{0}<4\pi$, the problem (1.2) possesses a uniquely determined global classical solution $(n,c)$ such that

$$\begin{aligned} \left \{ \textstyle\begin{array}{l} n\in C^{0}(\overline {\varOmega }\times [0,\infty )) \cap C^{2,1}(\overline {\varOmega }\times (0, \infty )) \quad \textit{and} \\ c\in C^{2,1}(\overline {\varOmega }\times (0,\infty )), \end{array}\displaystyle \right . \end{aligned}$$

and that $n>0$ and $c>0$ in $\overline {\varOmega }\times (0,\infty )$.

All these solutions are even bounded whenever $u$ is bounded and $\int _{\varOmega}n_{0}<2\pi$:

Theorem 1.2

Suppose that $\varOmega \subset \mathbb {R}^{2}$ is a bounded domain with smooth boundary, and that $u$ satisfies (1.3) as well as

$$ \sup_{t>0} \big\| u(\cdot ,t)\big\| _{L^{\infty }(\varOmega )} < \infty . $$

(1.5)

Then for arbitrary $n_{0}$ fulfilling (1.4) with $\int _{\varOmega}n_{0}<2\pi$, the global classical solution of (1.2) from Theorem 1.1is bounded in the sense that there exists $C>0$ such that

$$ \big\| n(\cdot ,t)\big\| _{L^{\infty }(\varOmega )} \le C \quad \textit{for all } t>0. $$

(1.6)

On the other hand, under the mere assumption (1.3) any such fluid flow does as well not increase the critical mass in the following sense:

Theorem 1.3

Suppose that $\varOmega \subset \mathbb {R}^{2}$ is a bounded domain, the smooth boundary of which contains a line segment in the sense that

$$ \left \{ \textstyle\begin{array}{l} \varOmega \subset \{ (x,y)\in \mathbb {R}^{2}) \mid y>0 \} \quad \textit{with} \\ \partial \varOmega \subset [-r,r] \times \{0\} \end{array}\displaystyle \right . $$

(1.7)

for some $r>0$, and that $u$ satisfies (1.3). Then for all $m>4\pi$ one can find $\mu (m)>0$ with the property that whenever $n_{0}$ complies with (1.4) and is such that $\int _{\varOmega}n_{0}=m$ and

$$ \int _{\varOmega}|x|^{2} n_{0}(x) dx \le \mu (m), $$

(1.8)

the corresponding solution of (1.2) blows up in finite time in the sense that there exist $T>0$ and uniquely determined functions

$$ \left \{ \textstyle\begin{array}{l} n\in C^{0}(\overline {\varOmega }\times [0,T)) \cap C^{2,1}(\overline {\varOmega }\times (0,T)) \quad \textit{and} \\ c\in C^{2,1}(\overline {\varOmega }\times (0,T)), \end{array}\displaystyle \right . $$

(1.9)

with $n>0$ and $c>0$ in $\overline {\varOmega }\times (0,T)$, which solve (1.2) in the classical sense in $\varOmega \times (0,T)$ and for which we have

$$ \big\| n(\cdot ,t)\big\| _{L^{\infty }(\varOmega )} \to \infty \quad \textit{as } t \nearrow T_{\mathit {max}}. $$

(1.10)

We remark that at the cost of additional technical efforts based on the refined analysis in [20, Chap. 5] it is possible to remove the restriction (1.7) on $\partial \varOmega$; in order to keep the presentation conveniently simple, however, we refrain from detailing this here.

2 Preliminaries

2.1 Local Existence and Upper Bounds for the Increase of Energy

To begin with, let us state a basic result on local existence and extensibility that can be obtained by adapting standard arguments from the existence theories of parabolic-elliptic Keller-Segel type systems to the present situation; we may therefore refrain from giving details here, and rather refer to the literature (see [13, 15] or [6], for instance).

Lemma 2.1

Let $\varOmega \subset \mathbb {R}^{2}$ be a bounded domain with smooth boundary, and assume (1.3) and (1.4). Then there exist $T_{\mathit {max}}\in (0,\infty ]$ and a uniquely determined pair $(n,c)$ of functions

$$ \left \{ \textstyle\begin{array}{l} n\in C^{0}(\overline {\varOmega }\times [0,T_{\mathit {max}})) \cap C^{2,1}(\overline {\varOmega }\times (0,T_{\mathit {max}})) \quad \textit{and} \\ c\in C^{2,1}(\overline {\varOmega }\times (0,T_{\mathit {max}})) \end{array}\displaystyle \right . $$

(2.1)

such that $n>0$ and $c>0$ in $\overline {\varOmega }\times (0,T_{\mathit {max}})$, that $(n,c)$ solves (1.2) in the classical sense in $\varOmega \times (0,T_{\mathit {max}})$, and that

$$ \textit{if}\ T_{\mathit {max}}< \infty , \quad \textit{then} \quad \big\| n(\cdot ,t)\big\| _{L^{\infty }( \varOmega )} \to + \infty \quad \textit{as } t\nearrow T_{\mathit {max}}. $$

(2.2)

Moreover, this solution has the property that

$$ \int _{\varOmega}n(x,t)dx = \int _{\varOmega}c(x,t) dx = \int _{\varOmega}n_{0}(x)dx \quad \textit{for all } t \in (0,T_{\mathit {max}}). $$

(2.3)

The following observation provides some information on how the evolution of the natural Lyapunov functional associated with the unperturbed Keller-Segel system is influenced by the presence of a fluid flow. Here a control of the corresponding additional contribution will be achieved by making appropriate use of the dissipation rate functional $\int _{\varOmega}|\frac{\nabla n}{\sqrt{n}}-\sqrt{n}\nabla c|^{2}$ which, due to its complicated coupling of both solution components, is only trivially estimated in most places in the literature.

Lemma 2.2

Assume (1.3) and (1.4). Then the function ${\mathcal {F}}\in C^{1}((0,T_{\mathit {max}}))$ defined by

$$\begin{aligned} & {\mathcal {F}}(t):=\frac{1}{2} \int _{\varOmega}\big|\nabla c(\cdot ,t)\big|^{2} + \frac{1}{2} \int _{\varOmega}c^{2}( \cdot ,t) - \int _{\varOmega}n(\cdot ,t)c(\cdot ,t) + \int _{\varOmega}n(\cdot ,t)\ln n(\cdot ,t), \\ & \quad t \in (0,T_{\mathit {max}}), \end{aligned}$$

(2.4)

satisfies

$$ {\mathcal {F}}'(t) \le \frac{1}{4} \big\| u(\cdot ,t)\big\| _{L^{\infty }(\varOmega )}^{2} \cdot \int _{\varOmega}n_{0} \qquad \textit{for all } t\in (0,T_{\mathit {max}}). $$

(2.5)

Proof

We use (2.3) and integrate by parts in (1.2) to compute

$$\begin{aligned} {\mathcal {F}}'(t) =& \int _{\varOmega}\nabla c\cdot \nabla c_{t} + \int _{\varOmega}cc_{t} - \int _{\varOmega}nc_{t} \\ &{} - \int _{\varOmega}\nabla \cdot ( \nabla n - n\nabla c -nu ) c + \int _{\varOmega}\nabla \cdot ( \nabla n - n\nabla c -nu ) \ln n \\ =& \int _{\varOmega}c_{t} (-\Delta c+c ) - \int _{\varOmega}nc_{t} \\ &{} + \int _{\varOmega}\nabla n\cdot \nabla c - \int _{\varOmega}n|\nabla c|^{2} - \int _{\varOmega}n (u \cdot \nabla c) \\ &{} - \int _{\varOmega}\frac{|\nabla n|^{2}}{n} + \int _{\varOmega}\nabla n\cdot \nabla c + \int _{\varOmega}u \cdot \nabla n \\ =& - \int _{\varOmega}\bigg| \frac{\nabla n}{\sqrt{n}}-\sqrt{n}\nabla c \bigg|^{2} + \int _{\varOmega}u\cdot (\nabla n-n\nabla c ) \quad \text{for all } t\in (0, T_{\mathit {max}}). \end{aligned}$$

Therefore, (2.5) follows upon observing that by Young’s inequality and (2.3),

$$\begin{aligned} \int _{\varOmega}u\cdot (\nabla n-n\nabla c ) \le & \int _{\varOmega}\bigg| \frac{\nabla n}{\sqrt{n}}- \sqrt{n}\nabla c \bigg|^{2} + \frac{1}{4} \int _{\varOmega}|u|^{2} n \\ \le & \int _{\varOmega}\bigg|\frac{\nabla n}{\sqrt{n}}- \sqrt{n}\nabla c \bigg|^{2} + \frac{1}{4} \|u\|_{L^{\infty }(\varOmega )}^{2} \int _{\varOmega}n \\ \le & \int _{\varOmega}\bigg|\frac{\nabla n}{\sqrt{n}}- \sqrt{n}\nabla c \bigg|^{2} + \frac{1}{4} \|u\|_{L^{\infty }(\varOmega )}^{2} \int _{\varOmega}n_{0} \end{aligned}$$

for all $t\in (0,T_{\mathit {max}})$. □

2.2 Deriving $L^{\infty }$ Estimates from Bounds in $L\log L$

In order to substantiate our goals in connection with Theorem 1.1 and Theorem 1.2, let us next perform a variant of a standard bootstrap procedure to make sure that similar to the situation in the original parabolic-elliptic Keller-Segel system, also in the presence of a suitably regular fluid flow a supposedly available bound for $\int _{\varOmega}n\ln n$ already implies a corresponding $L^{\infty }$ estimate.

Lemma 2.3

Let $B>0$. Then there exists $C(B)>0$ with the property that if (1.3) and (1.4) hold with $\|n_{0}\|_{L^{\infty }(\varOmega )} \le B$, and if $T\in (0,T_{\mathit {max}}]$ is such that

$$ \int _{\varOmega}n(\cdot ,t)\ln n(\cdot ,t) \le B \quad \textit{and} \quad \big\| u(\cdot ,t) \big\| _{L^{\infty }(\varOmega )} \le B \quad \textit{for all } t\in (0,T), $$

(2.6)

then

$$ \big\| n(\cdot ,t)\big\| _{L^{\infty }(\varOmega )} \le C(B) \quad \textit{for all } t \in (0,T). $$

(2.7)

Proof

Proceeding in a standard manner, we first use $n^{3}$ as a test function in the first equation from (1.2) to see that since $\frac{\partial n}{\partial \nu }=\frac{\partial c}{\partial \nu }=u \cdot \nu =0$ on $\partial \varOmega \times (0,T_{\mathit {max}})$,

$$\begin{aligned} & \frac{d}{dt} \int _{\varOmega}n^{4} + \int _{\varOmega}n^{4} \\ & \quad = - 12 \int _{\varOmega}n^{2} |\nabla n|^{2} + 12 \int _{\varOmega}n^{3} \nabla n\cdot \nabla c + 12 \int _{\varOmega}n^{3} (u\cdot \nabla n) + \int _{\varOmega}n^{4} \\ &\quad = - 12 \int _{\varOmega}n^{2} |\nabla n|^{2} + 3\int _{\varOmega}n^{5} - 3 \int _{\varOmega}n^{4} c + 12 \int _{\varOmega}n^{3} (u\cdot \nabla n) + \int _{\varOmega}n^{4} \\ &\quad \le - 6\int _{\varOmega}n^{2}|\nabla n|^{2} + 3\int _{\varOmega}n^{5} + 6\int _{\varOmega}n^{4} |u|^{2} + \int _{\varOmega}n^{4} \\ &\quad \le - \frac{3}{2} \int _{\varOmega}\big|\nabla n^{2}\big|^{2} + 10 \int _{\varOmega}n^{5} + \bigl\{ 6 \|u\|_{L^{\infty }(\varOmega )}^{10}+1 \bigr\} \cdot |\varOmega | \\ & \qquad \text{for all } t\in (0,T_{\mathit {max}}) \end{aligned}$$

(2.8)

due to Young’s inequality. Now assuming (2.6) as well as $\|n_{0}\|_{L^{\infty }(\varOmega )} \le B$, we may invoke a well-known variant of the Gagliardo-Nirenberg inequality ([2], [22, Lemma A.5]) to find $C_{1}>0$ such that

$$\begin{aligned} 16 \int _{\varOmega}n^{5} = 16\big\| n^{2}\big\| _{L^{\frac{5}{2}}(\varOmega )}^{\frac{5}{2}} \le & \frac{3}{2} \cdot \frac{1}{2B+\frac{4|\varOmega |}{e}} \big\| \nabla n^{2}\big\| _{L^{2}( \varOmega )}^{2} \big\| n^{2}\ln ^{2} n^{2}\big\| _{L^{\frac{1}{2}}(\varOmega )}^{\frac{1}{2}}\\ &{} + C_{1} \big\| n^{2}\big\| _{L^{\frac{1}{2}}(\varOmega )}^{\frac{5}{2}} + C_{1} \\ \le & \frac{3}{2} \big\| \nabla n^{2}\big\| _{L^{2}(\varOmega )}^{2} + C_{1} B^{5} |\varOmega |^{5} + C_{1} \quad \text{for all } t\in (0,T), \end{aligned}$$

because $\|n^{2}\|_{L^{\frac{1}{2}}(\varOmega )}^{\frac{5}{2}}=\|n_{0}\|_{L^{1}( \varOmega )}^{5} \le \|n_{0}\|_{L^{\infty }(\varOmega )}^{5} |\varOmega |^{5}$ for all $t\in (0,T_{\mathit {max}})$, and because

$$\begin{aligned} \big\| n^{2}\ln ^{2} n^{2}\big\| _{L^{\frac{1}{2}}(\varOmega )}^{\frac{1}{2}} =& 2\int _{\varOmega}n| \ln n| = 2\int _{\varOmega}n\ln n - 4 \int _{\{n< 1\}} n\ln n\\ \le & 2\int _{\varOmega}n\ln n + \frac{4|\varOmega |}{e} \quad \text{for all } t\in (0,T_{\mathit {max}}) \end{aligned}$$

according to the fact that $\xi \ln \xi \ge -\frac{1}{e}$ for all $\xi >0$. As a consequence of (2.8), we thus obtain that with some $C_{2}(B)>0$ we have

$$\begin{aligned} \frac{d}{dt} \int _{\varOmega}n^{4} + \int _{\varOmega}n^{4} \le C_{2}(B) \quad \text{for all } t\in (0,T) \end{aligned}$$

and hence, by an ODE comparison,

$$ \int _{\varOmega}n^{4} \le C_{3}(B):=\max \bigl\{ C_{2}(B) , B^{4}|\varOmega | \bigr\} \quad \text{for all } t\in (0,T) $$

(2.9)

thanks to the inequality $\int _{\varOmega}n_{0}^{4} \le \|n_{0}\|_{L^{\infty }(\varOmega )}^{4} |\varOmega |$.

Now since (2.9) together with standard elliptic regularity theory warrants the existence of $C_{4}(B)>0$ such that

$$\begin{aligned} \big\| \nabla c(\cdot ,t)\big\| _{L^{\infty }(\varOmega )} \le C_{4}(B) \quad \text{for all }t\in (0,T), \end{aligned}$$

we may next invoke well-known smoothing estimates for the Neumann heat semigroup $(e^{t\Delta })_{t\ge 0}$ on $\varOmega$ ([26]) to see that with some $C_{5}>0$, once more due to (2.6) we have

$$\begin{aligned} \big\| n(\cdot ,t)\big\| _{L^{\infty }(\varOmega )} =& \Bigg\| e^{t(\Delta -1)} n_{0} - \int _{0}^{t} e^{(t-s)(\Delta -1)} \nabla \cdot \bigl\{ n( \cdot ,s)\nabla c(\cdot ,s) \bigr\} ds \\ &{} - \int _{0}^{t} e^{(t-s)(\Delta -1)} \nabla \cdot \bigl\{ n(\cdot ,s) u(\cdot ,s) \bigr\} ds + \int _{0}^{t} e^{(t-s)(\Delta -1)} n(\cdot ,s) ds \Bigg\| _{L^{\infty }(\varOmega )} \\ \le & \|n_{0}\|_{L^{\infty }(\varOmega )} + C_{5} \int _{0}^{t} \bigl(1+(t-s)^{- \frac{3}{4}} \bigr) e^{-(t-s)} \big\| n(\cdot ,s)\nabla c(\cdot ,s)\big\| _{L^{4}( \varOmega )} ds \\ & {} + C_{5} \int _{0}^{t} \bigl(1+(t-s)^{-\frac{3}{4}} \bigr) e^{-(t-s)} \big\| n(\cdot ,s)u(\cdot ,s)\big\| _{L^{4}(\varOmega )} ds \\ &{} + C_{5} \int _{0}^{t} \bigl(1+(t-s)^{-\frac{1}{4}} \bigr) e^{-(t-s)} \big\| n(\cdot ,s)\big\| _{L^{4}(\varOmega )} ds \\ \le & B + C_{3}(B) C_{4}(B) C_{5} \int _{0}^{\infty }\bigl(1+\sigma ^{- \frac{3}{4}} \bigr) e^{-\sigma } d\sigma \\ &{} + C_{3}(B) C_{5} B \int _{0}^{\infty }\bigl(1+\sigma ^{-\frac{3}{4}} \bigr) e^{- \sigma } d\sigma \\ &{} + C_{3}(B) C_{5} \int _{0}^{\infty }\bigl(1+\sigma ^{-\frac{1}{4}} \bigr) e^{- \sigma } d\sigma \quad \text{for all } t\in (0,T), \end{aligned}$$

and conclude. □

2.3 Two Functional Inequalities Resulting from the Moser-Trudinger Inequality

Now in subsequently deriving estimates for $\int _{\varOmega}n\ln n$ on the basis of Lemma 2.2, we shall rely on the following consequence of the Moser-Trudinger inequality observed in [34, Lemma 2.2]:

Lemma 2.4

For all $\varepsilon >0$ there exists $M=M(\varepsilon ,\varOmega )>0$ such that if $0\not \equiv \varphi \in C^{0}(\overline {\varOmega })$ is nonnegative and $\psi \in W^{1,2}(\varOmega )$, then for each $a>0$,

$$\begin{aligned} \int _{\varOmega}\varphi |\psi | \le & \frac{1}{a} \int _{\varOmega}\varphi \ln \frac{\varphi }{\overline {\varphi }} + \frac{(1+\varepsilon )a}{8\pi } \cdot \bigg\{ \int _{\varOmega}\varphi \bigg\} \cdot \int _{\varOmega}|\nabla \psi |^{2} \\ &{} + Ma\cdot \bigg\{ \int _{\varOmega}\varphi \bigg\} \cdot \biggl\{ \int _{\varOmega}|\psi | \biggr\} ^{2} + \frac{M}{a} \int _{\varOmega}\varphi , \end{aligned}$$

(2.10)

where $\overline {\varphi }:=\frac{1}{|\varOmega |} \int _{\varOmega}\varphi$.

As a first and quite well-known consequence thereof, as usual we can make sure that the crucial quantity $\int _{\varOmega}n\ln n$ is essentially dominated by the energy functional from (2.4) whenever $\int _{\varOmega}n_{0}<4\pi$ (cf. also [18, Lemma 3.4]).

Corollary 2.5

Assume (1.3) and (1.4) with $\int _{\varOmega}n_{0}<4\pi$. Then there exists $C>0$ such that

$$ {\mathcal {F}}(t) \ge \frac{1}{C} \int _{\varOmega}n(\cdot ,t)\ln n( \cdot ,t) - C \quad \textit{for all } t \in (0,T_{\mathit {max}}). $$

(2.11)

Proof

As our assumption on $m:=\int _{\varOmega}n_{0}$ warrants that $\frac{4\pi }{m}>1$, we can pick some suitably $\varepsilon >0$ such that $a:=\frac{4\pi }{(1+\varepsilon )m}$ satisfies $a>1$. An application of Lemma 2.4 then shows that with $M=M(\varepsilon ,\varOmega )$ as accordingly provided there we have

$$\begin{aligned} {\mathcal {F}}(t) \ge & \frac{1}{2} \int _{\varOmega}|\nabla c|^{2} - \int _{\varOmega}nc + \int _{\varOmega}n\ln n \\ \ge & \frac{1}{2} \int _{\varOmega}|\nabla c|^{2} - \biggl\{ \frac{1}{a} \int _{\varOmega}n\ln \frac{|\varOmega | n}{m} + \frac{(1+\varepsilon )am}{8\pi } \int _{\varOmega}|\nabla c|^{2} + Mam\bigg\{ \int _{\varOmega}c \bigg\} ^{2} + \frac{Mm}{a} \biggr\} \\ &{} + \int _{\varOmega}n\ln n \\ =& \frac{a-1}{a} \int _{\varOmega}n\ln n - Mam^{3} - \frac{Mm}{a} + \frac{1}{a} m \ln \frac{m}{|\varOmega |} \quad \text{for all } t\in (0,T_{\mathit {max}}), \end{aligned}$$

because of (2.3). As $a>1$, this establishes (2.11) if we let $C:=\max \{\frac{a}{a-1} , Mam^{3} + \frac{Mm}{a} -\frac{1}{a} m \ln \frac{m}{|\varOmega |}\}>0$. □

As documented in [34, Lemma 2.3], Lemma 2.4 furthermore entails the following functional inequality, to be used in Lemma 4.1, which solely involves a single function.

Lemma 2.6

Let $0\not \equiv \varphi \in C^{0}(\overline {\varOmega })$ be nonnegative. Then for any choice of $\varepsilon >0$,

$$\begin{aligned} \int _{\varOmega}\varphi \ln (\varphi +1) \le & \frac{1+\varepsilon }{2\pi } \cdot \bigg\{ \int _{\varOmega}\varphi \bigg\} \cdot \int _{\varOmega}\frac{|\nabla \varphi |^{2}}{(\varphi +1)^{2}} \\ &{} + 4M \cdot \bigg\{ \int _{\varOmega}\varphi \bigg\} ^{3} + \biggl\{ M - \ln \frac{1}{|\varOmega |} \int _{\varOmega}\varphi \biggr\} \cdot \int _{\varOmega}\varphi , \end{aligned}$$

(2.12)

where $M=M(\varepsilon ,\varOmega )>0$ is as in Lemma 2.4.

3 Global Existence when $\int _{\varOmega}n_{0}<4\pi$. Proof of Theorem 1.1

Now since the growth rate of ℱ is favorably controlled on finite time intervals by Lemma 2.2, for all subcritical-mass data we may rely on a combination of Corollary 2.5 and Lemma 2.3 to draw the claimed conclusion on global existence:

Lemma 3.1

Assume (1.3) and (1.4) with $\int _{\varOmega}n_{0}<4\pi$. Then $T_{\mathit {max}}=\infty$.

Proof

If $T_{\mathit {max}}$ was finite, then Lemma 2.2 together with (1.3) would entail the existence of $C_{1}>0$ such that

$$\begin{aligned} {\mathcal {F}}'(t) \le C_{1} \quad \text{for all } t\in (0,T_{\mathit {max}}), \end{aligned}$$

so that

$$\begin{aligned} {\mathcal {F}}(t) \le {\mathcal {F}}\biggl(\frac{1}{2}T_{\mathit {max}}\biggr) + \frac{C_{1}}{2}T_{\mathit {max}}\quad \text{for all } t\in \biggl( \frac{1}{2}T_{\mathit {max}},T_{\mathit {max}}\biggr). \end{aligned}$$

In light of Corollary 2.5 and Lemma 2.1, this would imply that with some $C_{2}>0$,

$$\begin{aligned} \int _{\varOmega}n\ln n \le C_{2} \quad \text{for all } t\in (0,T_{\mathit {max}}), \end{aligned}$$

so that Lemma 2.3 would apply so as to provide $C_{3}>0$ fulfilling

$$\begin{aligned} \|n(\cdot ,t)\|_{L^{\infty }(\varOmega )} \le C_{3} \quad \text{for all } t \in (0,T_{\mathit {max}}), \end{aligned}$$

which however contradicts (2.2). □

We have thereby already established the first of our main results:

Proof of Theorem 1.1

The statement directly results from Lemma 3.1 and Lemma 2.1. □

4 Boundedness for $\int _{\varOmega}n_{0}<2\pi$. Proof of Theorem 1.2

In order to next address the boundedness property claimed in Theorem 1.2, let us now make use of the functional inequality from Lemma 2.6 in discovering a second quasi-dissipative structure under the more restrictive assumption that $\int _{\varOmega}n_{0}<2\pi$. Here unlike our analysis of (2.5), our subsequent exploitation of (4.1) will exclusively refer to the dissipation rate $\int _{\varOmega}n\ln n$ appearing therein.

Lemma 4.1

Assume (1.5) and (1.4) with $\int _{\varOmega}n_{0}<2\pi$. Then there exists $C>0$ such that

$$ - \frac{d}{dt} \int _{\varOmega}\ln (n+1) + \frac{1}{C} \int _{\varOmega}n\ln (n+1) \le C \quad \textit{for all } t>0. $$

(4.1)

Proof

We use (1.2) and integrate by parts to see that for all $t>0$,

$$\begin{aligned} - \frac{d}{dt} \int _{\varOmega}\ln (n+1) =& - \int _{\varOmega}\frac{1}{n+1} \nabla \cdot \{ \nabla n-n\nabla c-nu \} \\ =& - \int _{\varOmega}\frac{|\nabla n|^{2}}{(n+1)^{2}} + \int _{\varOmega}\frac{n}{(n+1)^{2}} \nabla n \cdot \nabla c \\ &{} + \int _{\varOmega}\frac{n}{(n+1)^{2}} (u\cdot \nabla n), \end{aligned}$$

(4.2)

where another integration by parts shows that

$$\begin{aligned} \int _{\varOmega}\frac{n}{(n+1)^{2}} \nabla n\cdot \nabla c =& \int _{\varOmega}\nabla \biggl\{ \ln (n+1) + \frac{1}{n+1} \biggr\} \cdot \nabla c \\ =& - \int _{\varOmega}\biggl\{ \ln (n+1) + \frac{1}{n+1} \biggr\} \Delta c \\ \le & \int _{\varOmega}n\ln (n+1) + \int _{\varOmega}\frac{n}{n+1} \\ \le & \int _{\varOmega}n\ln (n+1) + |\varOmega | \quad \text{for all } t>0, \end{aligned}$$

(4.3)

because $-\Delta c\le n$ by (1.2). Now since our hypotheses warrant that $m:=\int _{\varOmega}n_{0}$ satisfies $m<2\pi$, we can pick $\varepsilon \in (0,1)$ suitably small such that $C_{1}:=\frac{(1-\varepsilon ) \cdot 2\pi }{m}-1$ is positive, and apply Lemma 2.6 along with (2.3) to obtain $C_{2}>0$ such that

$$\begin{aligned} \int _{\varOmega}n\ln (n+1) =& \frac{(1-\varepsilon )\cdot 2\pi }{m} \int _{\varOmega}n\ln (n+1) - C_{1} \int _{\varOmega}n\ln (n+1) \\ \le & \bigl(1-\varepsilon ^{2}\bigr) \int _{\varOmega}\frac{|\nabla n|^{2}}{(n+1)^{2}} + C_{2} - C_{1} \int _{\varOmega}n\ln (n+1) \quad \text{for all } t>0, \end{aligned}$$

so that from (4.3) and (4.2) we infer that

$$\begin{aligned} &{} -\frac{d}{dt} \int _{\varOmega}\ln (n+1) + \varepsilon ^{2} \int _{\varOmega}\frac{|\nabla n|^{2}}{(n+1)^{2}} + C_{1} \int _{\varOmega}n\ln (n+1)\\ &\quad \le C_{2} + |\varOmega | + \int _{\varOmega}\frac{n}{(n+1)^{2}} (u\cdot \nabla n) \end{aligned}$$

for all $t>0$. As, by Young’s inequality,

$$\begin{aligned} \int _{\varOmega}\frac{n}{(n+1)^{2}} (u\cdot \nabla n) \le & \varepsilon ^{2} \int _{\varOmega}\frac{|\nabla n|^{2}}{(n+1)^{2}} + \frac{1}{4\varepsilon ^{2}} \int _{\varOmega}\frac{n^{2}}{(n+1)^{2}} |u|^{2} \\ \le & \varepsilon ^{2} \int _{\varOmega}\frac{|\nabla n|^{2}}{(n+1)^{2}} + \frac{|\varOmega |}{4\varepsilon ^{2}} \|u\|_{L^{\infty }(\varOmega )}^{2} \quad \text{for all } t>0, \end{aligned}$$

in view of the assumed boundedness property of $u$ this establishes (4.1). □

Indeed, this implies a spatio-temporal $L\log L$ estimate for $n$:

Corollary 4.2

Assume (1.5) and (1.4) with $\int _{\varOmega}n_{0}<2\pi$. Then there exists $C>0$ such that

$$ \int _{t}^{t+1} \int _{\varOmega}n\ln (n+1) \le C \quad \textit{for all } t > 0. $$

(4.4)

Proof

This directly follows on integrating (4.1) in time and using that $0\le \ln (n+1) \le \int _{\varOmega}n=\int _{\varOmega}n_{0}$ for all $t>0$ by (2.3). □

As a consequence, under such smallness conditions the energy from (2.4) is bounded in its temporal average in the following sense.

Lemma 4.3

Assume (1.5) and (1.4) with $\int _{\varOmega}n_{0}<2\pi$. Then there exists $C>0$ such that

$$ \int _{t}^{t+1} {\mathcal {F}}(s) ds \le C \quad \textit{for all } t> 0. $$

(4.5)

Proof

As from (1.2) we know that

$$\begin{aligned} \int _{\varOmega}|\nabla c|^{2} + \int _{\varOmega}c^{2} = \int _{\varOmega}nc \quad \text{for all } t>0 \end{aligned}$$

and that hence

$$\begin{aligned} {\mathcal {F}}(t)=-\frac{1}{2} \int _{\varOmega}nc + \int _{\varOmega}n\ln n \le \int _{\varOmega}n\ln (n+1) \quad \text{for all } t>0, \end{aligned}$$

this is an immediate consequence of Corollary 4.2. □

Along with Lemma 2.2, this shows that in fact ℱ must remain bounded for large times:

Lemma 4.4

Assume (1.5) and (1.4) with $\int _{\varOmega}n_{0}<2\pi$. Then there exists $C>0$ such that

$$ {\mathcal {F}}(t) \le C \quad \textit{for all } t>1. $$

(4.6)

Proof

Relying on (1.5), from Lemma 2.2 we infer the existence of $C_{1}>0$ such that

$$ {\mathcal {F}}'(t) \le C_{1} \quad \text{for all } t>0, $$

(4.7)

whereas Lemma 4.3 asserts that

$$\begin{aligned} \int _{t}^{t+1} {\mathcal {F}}(s) ds \le C_{2} \quad \text{for all } t> 0 \end{aligned}$$

with some $C_{2}>0$. Therefore, given any $t>1$ we can find $t_{\star }(t)\in (t-1,t)$ such that ${\mathcal {F}}(t_{\star }(t))\le C_{2}$, and that thus, by (4.7), indeed

$$\begin{aligned} {\mathcal {F}}(t) \le {\mathcal {F}}\bigl(t_{\star }(t)\bigr) + C_{1} \cdot \bigl(t-t_{\star }(t)\bigr) \le C_{2} + C_{1} \cdot \bigl(t-t_{\star }(t)\bigr) \le C_{2}+C_{1}, \end{aligned}$$

because $t-t_{\star }(t)<1$. □

Again thanks to Corollary 2.5 and Lemma 2.3, this implies our main result on boundedness under the assumption that $\int _{\varOmega}n_{0}<2\pi$:

Proof of Theorem 1.2

We first combine Lemma 4.4 with Corollary 2.5 and Lemma 2.1 to find $C_{1}>0$ such that

$$\begin{aligned} \int _{\varOmega}n\ln n \le C_{1} \quad \text{for all } t>0, \end{aligned}$$

whereupon once more relying on (1.5) we may employ Lemma 2.3 to obtain (1.6). □

5 Occurrence of Blow-up when $\int _{\varOmega}n_{0}>4\pi$. Proof of Theorem 1.3

Finally concerned with the blow-up result announced in Theorem 1.3, we shall see that the present framework involving a given fluid flow in fact allows for an appropriate adaptation of the classical argument from [17] based on the analysis of functionals that can be viewed as certain localized variants of second moments. In order to keep our presentation compact here, let us import from [17] two preparatory observations, the first of which summarizes some elementary features of said localization procedure.

Lemma 5.1

Let $r_{1}>0$, $r_{2}>r_{1}$ and

$$ \varPhi (x) \equiv \varPhi ^{(r_{1},r_{2})}(x):= \left \{ \textstyle\begin{array}{l@{\quad }l} |x|^{2} & \textit{if } |x|< r_{1}, \\ -\frac{r_{1}}{r_{2}-r_{1}} |x|^{2} + \frac{2r_{1}r_{2}}{r_{2}-r_{1}} |x| - \frac{r_{1}^{2} r_{2}}{r_{2}-r_{1}} & \textit{if } r_{1}\le |x| \le r_{2}, \\ r_{1} r_{2} & \textit{if } |x|>r_{2}. \end{array}\displaystyle \right . $$

(5.1)

Then $\varPhi \in W^{2,\infty }(\mathbb {R}^{2})$ with $0\le \varPhi (x)\le |x|^{2}$ and $|\nabla \varPhi (x)|\le 2\sqrt{\varPhi (x)}$ for all $x\in \mathbb {R}^{2}$.

Proof

Noting that $\varphi (r):=- \frac{r_{1}}{r_{2}-r_{1}} + \frac{2r_{1} r_{2}}{r_{2}-r_{1}} \cdot \frac{1}{r} - \frac{r_{1}^{2} r_{2}}{r_{2}-r_{1}} \cdot \frac{1}{r^{2}}$, $r\in [r_{1},r_{2}]$, is nonincreasing with $\varphi (r_{1})=1$ and $\varphi (r_{2})=\frac{r_{1}}{r_{2}} \in (0,1)$, we readily verify the inequalities $\varPhi (x) \le |x|^{2}$ and $\varPhi (x)\ge 0$ for all $x\in \mathbb {R}^{2}$. The observations concerning regularity and the estimate $|\nabla \varPhi |\le 2\sqrt{\varPhi }$ have been documented in [17, p. 41] already. □

We next recall some information on the behavior of the diffusive and cross-diffusive contributions to the first equation in (1.2) when tested against one particular among these functions, with the latter being chosen in such a way that, inter alia, its center of symmetry is located at the line segment of the boundary of $\varOmega$ addressed in the hypothesis (1.7) from Theorem 1.3.

Lemma 5.2

Suppose that $\varOmega$ satisfies (1.7) for some $r>0$. Then there exists $K(r)>0$ with the property that if $\varPhi \equiv \varPhi ^{(\frac{r}{4},\frac{r}{2})}$ is as defined in (5.1) with $r_{1}:=\frac{r}{4}$ and $r_{2}:=\frac{r}{2}$, whenever $u$ and $n_{0}$ satisfy (1.3) and (1.4), the corresponding solution of (1.2) has the property that

$$\begin{aligned} \int _{\varOmega}\varPhi \Delta n - \int _{\varOmega}\varPhi \nabla \cdot (n\nabla c) \le & 2\int _{\varOmega}n_{0} - \frac{1}{ 2\pi } \cdot \bigg\{ \int _{\varOmega}n_{0} \bigg\} ^{2} \\ &{} + K(r) \cdot \bigg\{ \int _{\varOmega}n_{0} \bigg\} \cdot \int _{\varOmega}\varPhi n \\ &{} + K(r) \cdot \bigg\{ \int _{\varOmega}n_{0} \bigg\} ^{\frac{3}{2}} \cdot \bigg\{ \int _{\varOmega}\varPhi n \bigg\} ^{\frac{1}{2}} \end{aligned}$$

(5.2)

for all $t\in (0,T_{\mathit {max}})$.

Proof

This has been shown in [17, Lemma 3.1 and Proof of Theorem 3.2]. □

As a consequence of this and an adequate estimation of the respective contribution due to the fluid field, the evolution of the corresponding moment-type functional can be described as follows.

Lemma 5.3

Assume that $\varOmega$ satisfies (1.7) with some $r>0$, and let $\varPhi \equiv \varPhi ^{(\frac{r}{4},\frac{r}{2})}$ be taken from (5.1) and $K(r)$ be as accordingly provided by Lemma 5.2. Then whenever (1.3) and (1.4) hold, the function $y\in C^{0}([0,T_{\mathit {max}})) \cap C^{1}((0,T_{\mathit {max}}))$ defined by letting

$$ y(t):=\int _{\varOmega}\varPhi (x) n(x,t) dx, \quad t\in [0,T_{\mathit {max}}), $$

(5.3)

has the property that for any choice of $\varepsilon >0$,

$$\begin{aligned} y'(t) \le & (2+\varepsilon )m - \frac{m^{2}}{ 2\pi } \\ &{} + \biggl\{ K(r)m + \frac{1}{\varepsilon } \big\| u(\cdot ,t)\big\| _{L^{\infty }( \varOmega )}^{2} \biggr\} \cdot y(t) \\ &{} + K(r) m^{\frac{3}{2}} y^{\frac{1}{2}}(t) \quad \textit{for all }t\in (0,T_{\mathit {max}}), \end{aligned}$$

(5.4)

where $m:=\int _{\varOmega}n_{0}$.

Proof

As $u\cdot \nu =0$ on $\partial \varOmega \times (0,\infty )$, using (1.2) and (5.2) and integrating by parts we see that

$$\begin{aligned} y'(t) =& \int _{\varOmega}\varPhi \Delta n - \int _{\varOmega}\varPhi \nabla \cdot (n\nabla c) + \int _{\varOmega}nu\cdot \nabla \varPhi \\ \le & 2m - \frac{m^{2}}{{ 2\pi }} + K(r)m y(t) + K(r) m^{\frac{3}{2}} y^{\frac{1}{2}}(t) \\ &{} + \int _{\varOmega}nu\cdot \nabla \varPhi \quad \text{for all } t \in (0,T_{\mathit {max}}). \end{aligned}$$

(5.5)

Since $|\nabla \varPhi |\le 2\sqrt{\varPhi }$ by Lemma 5.1, and since thus for all $\varepsilon >0$ we can estimate

$$\begin{aligned} \int _{\varOmega}nu\cdot \nabla \varPhi \le & 2\|u\|_{L^{\infty }(\varOmega )} \int _{\varOmega}\sqrt{ \varPhi } n \\ \le & \varepsilon \int _{\varOmega}n + \frac{1}{\varepsilon } \|u\|_{L^{\infty }(\varOmega )}^{2} \int _{\varOmega}\varPhi n \\ =& \varepsilon m + \frac{1}{\varepsilon }\|u\|_{L^{\infty }(\varOmega )}^{2} y(t) \quad \text{for all } t\in (0,T_{\mathit {max}}) \end{aligned}$$

due to Young’s inequality and (2.3), from (5.5) we directly obtain (5.4). □

Now since the mere assumption (1.3) enables us to favorably control the effect of the fluid flow on (5.4), by straightforward ODE comparison we readily arrive at the claimed result on finite-time blow-up at arbitrary mass levels beyond $4\pi$:

Proof of Theorem 1.3

Given $m>4\pi$, we fix $\varepsilon >0$ small enough such that $C_{1}:=\frac{m^{2}}{{ 2\pi }}-(2+\varepsilon )m$ is positive, and we claim that then the intended conclusion holds if we fix $\varPhi \equiv \varPhi ^{(\frac{r}{4},\frac{r}{2})}$ and $K(r)>0$ as in Lemma 5.2 and take $\mu (m)>0$ suitably small fulfilling

$$ \biggl\{ K(r) m + \frac{1}{\varepsilon } \|u \|_{L^{\infty }(\varOmega \times (0,1))}^{2} \biggr\} \cdot \mu (m) \le \frac{C_{1}}{4} $$

(5.6)

and

$$ K(r) m^{\frac{3}{2}} \mu ^{\frac{1}{2}}(m) \le \frac{C_{1}}{4} $$

(5.7)

as well as

$$ \frac{2}{C_{1}} \cdot \mu (m) < 1. $$

(5.8)

To verify this, we assume on the contrary that for some $n_{0}$ satisfying (1.4) and (1.8) with $\int _{\varOmega}n_{0}=m$, we have $T_{\mathit {max}}=\infty$. Then, in particular, the function $y$ introduced in (5.3) would belong to $C^{0}([0,1]) \cap C^{1}((0,1))$ with

$$ y'(t) \le -C_{1} + \biggl\{ K(r) m + \frac{1}{\varepsilon }\|u\|_{L^{\infty }( \varOmega \times (0,1))}^{2} \biggr\} \cdot y(t) + K(r) m^{\frac{3}{2}} y^{\frac{1}{2}}(t) \quad \text{for all } t\in (0,1) $$

(5.9)

by (5.4), and

$$ y(0) = \int _{\varOmega}\varPhi (x) n_{0}(x) dx \le \int _{\varOmega}|x|^{2} n_{0}(x) dx \le \mu (m) $$

(5.10)

due to (1.8) and the fact that $\varPhi (x) \le |x|^{2}$ for all $x\in \mathbb {R}^{2}$ by Lemma 5.1. From (5.6) and (5.7) we would thus obtain that at $t=0$ we have

$$\begin{aligned} & - C_{1} + \biggl\{ K(r) m + \frac{1}{\varepsilon }\|u \|_{L^{\infty }(\varOmega \times (0,1))}^{2} \biggr\} \cdot y(t) + K(r) m^{\frac{3}{2}} y^{\frac{1}{2}}(t) \\ &\quad {} \le - C_{1} + \frac{C_{1}}{4}+ \frac{C_{1}}{4}=- \frac{C_{1}}{2}, \end{aligned}$$

(5.11)

so that a first comparison argument applied to (5.9) would show that $y(t)\le y(0)$ for all $t\in (0,1)$ and that therefore (5.11) actually holds for all $t\in [0,1]$. But then (5.9) would entail that $y' \le -\frac{C_{1}}{2}$ for all $t\in (0,1)$ and hence $0\le y(1) \le y(0)-\frac{C_{1}}{2}$, which in view of (5.10) and (5.8) is absurd. □