1 Introduction

In recent years there has been an increasing interest in multi-phase models applied to tumour growth. Traditionally, tumour growth was modelled using a single equation describing the evolution of the abnormal cell density. This paper is dedicated to studying the two-species model

$$\begin{aligned} \left \{ \textstyle\begin{array}{rl} \displaystyle \frac {\partial n^{(i)}_{k}}{\partial t} - \nabla \cdot \left (n^{(i)}_{k} \nabla W_{k}\right ) &= \displaystyle n^{(i)}_{k} G^{(i)}(p _{k}), \\ \displaystyle -\nu \Delta W_{k} +W_{k} &= \displaystyle p_{k}, \end{array}\displaystyle \right . \end{aligned}$$

where \(n^{(i)}\) represents the normal (resp. abnormal) cells, for \(i=1,2\), and \(k\in {\mathbb {N}}\) is a given constant modelling the stiffness of the total population pressure, \(p_{k}\), which is generated by both species, i.e.,

$$\begin{aligned} p_{k} := \frac{k}{k-1}\left (n_{k}^{(1)} + n^{(2)} _{k}\right )^{k-1}. \end{aligned}$$

In addition, \(\nu >0\) is a fixed positive constant that is understood as a measure of viscosity. The elliptic equation linking the macroscopic velocity potential, \(W_{k}\), with the pressure \(p_{k}\) is typically referred to as Brinkman’s law, for instance cf. [1]. The growth of the two densities is assumed to be modulated by two functions \(G^{(i)}\), for \(i=1,2\), that are assumed to be decreasing in their variable, \(p_{k}\), similar to [7, 20].

Throughout, we shall use the shorthand notation \(n_{k} := n^{(1)} _{k} + n_{k}^{(2)} \), in order to denote the total population. Upon adding up the two equations for the individual species, we obtain an equation for the total population density, \(n_{k}\), i.e.,

(1)

where \(r_{k}\) is the population fraction \(r_{k}:= n_{k}^{(1)} / n_{k}\). Related models have been extensively studied in the past. We refer to [17, 19], and references therein, for a treatise of the incompressible limit for a single-species visco-elastic tumour model. As above, the velocity potential is given by an elliptic equation involving the pressure that, in their case, is just given by a power of the sole species. Introducing the coupling of the two equations for the individual species drastically changes the behaviour and the same tool employed in [19] cannot be applied, at least not in a straightforward manner, and a different strategy has to be found. Even in the case \(\nu = 0\) corresponding to the inviscid case, the system nature of the problem gives rise to a whole range of difficulties, cf. [6, 8, 13]. At first glance, the pressure gains in regularity, however, it gains just enough regularity to obtain compactness of its gradient, requiring a minute derivation of suitable estimates. Let us stress that the same type of difficulties are also encountered when the pressure is not given as a power law, cf. [11, 12, 14]. A key tool in obtaining existence results and stable (with respect to the parameter \(k\)) estimates is to devise and manipulate the equation satisfied by the (joint) population pressure, cf. [6, 8, 11–14, 16, 18, 19]. In this work we shall follow this path. An easy application of the chain rule in conjunction with Eq. (1) leads to

$$\begin{aligned} \frac {\partial p_{k}}{\partial t} - \nabla p_{k} \cdot \nabla W_{k} =\frac{k-1}{\nu }p _{k} \left [W_{k} - p_{k} + \nu r_{k} G^{(1)} (p_{k}) + \nu (1-r_{k})G^{(2)} (p_{k})\right ], \end{aligned}$$

where the population fraction \(r_{k}\) satisfies

$$\begin{aligned} \frac {\partial r_{k}}{\partial t} -\nabla r_{k} \cdot \nabla W_{k} = r_{k} (1-r_{k}) \left [G^{(1)} (p_{k}) - G^{(2)} (p_{k})\right ]. \end{aligned}$$

The change to these new variables was first introduced in [2–4] in the context of a two-species system where the two species avoid overcrowding. In a way, their works paved the way for more modern approaches to tumour models linked through Darcy’s law, cf. [5, 6, 8, 13, 18].

The rest of this paper is organised as follows. In the subsequent section we set up precisely the problem and state our assumptions. In Sect. 3 we establish existence of solutions to the main system under consideration, Eqs. (2a), (2b), and discuss their regularity necessary for our purposes. Section 4 is dedicated to establishing a range of a priori estimates necessary in the analysis of the incompressible limit. Section 5 is devoted to establishing the strong compactness of the pressure, which is key in passing to the stiff limit. Finally, with all information at hand, we pass to the incompressible limit in the pressure equation and derive the so-called complementarity relation in Sect. 6. We round off the analytical results in Sect. 7 by presenting some numerical simulations for different parameter choices.

2 Preliminaries and Statement of the Main Results

We study the system

$$\begin{aligned} \left \{ \textstyle\begin{array}{rl} \displaystyle \frac {\partial n^{(1)}_{k}}{\partial t} - \frac {\partial }{\partial x} \left (n^{(1)} _{k} \frac {\partial W_{k}}{\partial x}\right ) &= \displaystyle n^{(1)} _{k} G^{(1)} (p_{k}), \\ \displaystyle \frac {\partial n^{(2)}_{k}}{\partial t} - \frac {\partial }{\partial x} \left (n^{(2)} _{k} \frac {\partial W_{k}}{\partial x}\right ) &= \displaystyle n^{(2)} _{k} G^{(2)} (p_{k}), \end{array}\displaystyle \right . \end{aligned}$$
(2a)

posed on the whole domain ℝ. It is coupled through the Brinkman law

$$\begin{aligned} \displaystyle -\nu \frac{\partial ^{2}}{\partial x^{2}} W_{k} +W_{k} &= \displaystyle p _{k}. \end{aligned}$$
(2b)

The system is equipped with non-negative initial data

$$\begin{aligned} n^{(i)}_{0,k} \in L^{1}({\mathbb {R}}) \cap L^{\infty }({\mathbb {R}}), \end{aligned}$$
(3a)

for any integer \(k\geq 2\). Moreover, we assume that there exists a constant, \(C>0\), such that

(3b)

for \(i=1,2\), and every \(k\geq 2\). As before, the pressure is given in form of a power of the joint population, i.e.,

$$\begin{aligned} p_{k} := \frac{k}{k-1} \left (n_{k}^{(1)} + n_{k}^{(2)} \right )^{k-1} = \frac{k}{k-1} n_{k}^{k-1}. \end{aligned}$$

Recall that the pressure satisfies

$$\begin{aligned} \frac {\partial p_{k}}{\partial t} - \frac {\partial p_{k}}{\partial x} \frac {\partial W_{k}}{\partial x} =\frac{k-1}{ \nu }p_{k} \left [W_{k} - p_{k} + \nu r_{k} G^{(1)} (p_{k}) + \nu (1-r_{k})G^{(2)} (p_{k})\right ], \end{aligned}$$
(4)

with the population fraction, \(r_{k} := n^{(1)} _{k} / n_{k}\), given by

$$\begin{aligned} \frac {\partial r_{k}}{\partial t} -\frac {\partial r_{k}}{\partial x} \frac {\partial W_{k}}{\partial x} = r_{k} (1-r _{k})\left [G^{(1)} (p_{k}) - G^{(2)} (p_{k})\right ]. \end{aligned}$$
(5)

Throughout the paper we assume the following regularity and properties of the growth functions \(G^{(i)}\), \(i=1,2\),

$$\begin{aligned} G^{(i)}\in C^{1}({\mathbb {R}}), \quad G^{(i)}_{p} \leq -\alpha < 0, \quad \text{as well as }G^{(i)}(p_{M}) = 0, \end{aligned}$$
(6)

for some \(p_{M} > 0\), where \(G^{(i)}_{p}\) denotes the derivative of the function \(G^{(i)}\). The pressure \(p_{M}\) is often called the homeostatic pressure.

Recall that a solution \(W_{k}\) to Brinkman’s equation \(-\nu \partial ^{2}_{x} W_{k} + W_{k} = p_{k}\) can be written as \(W_{k} = K\star p _{k}\), where \(K\) is the fundamental solution to the equation \(-\nu {\partial _{x}^{2} K} + K = \delta _{0}\), i.e.,

(7)

Then \(K\geq 0\), and \(K, \partial _{x}{K} \in L^{q}({\mathbb {R}})\) for \(1\leq q \leq \infty \). By the elliptic regularity theory we have \(W_{k}(t,\cdot )\in W^{2,q}({\mathbb {R}})\), for any \(t\in [0,T]\), \(1\leq q\leq \infty \).

Below we formulate the main results of this work.

Theorem 2.1

(Existence of Solutions)

For any initial data satisfying (3a), (3b), system (2a), (2b) admits a unique solution \(n_{k}^{(1)} , n_{k}^{(2)} \in L^{\infty }(0,T; \mathit{BV}({\mathbb {R}}) \cap L^{\infty }({\mathbb {R}}))\).

We highlight the fact that solutions are essentially bounded since these bounds are not a consequence of the BV-bounds. Rather, they are obtained independently. This may prove useful for an extension to higher dimensions in future works.

Theorem 2.2

(Incompressible Limit and Complementarity Relation)

We may pass to the limit \(k\to \infty \)in the pressure equation, Eq. (4). This yields the so-called complementarity relation

$$\begin{aligned} 0 = p_{\infty } \left (W_{\infty }- p_{\infty }+ \nu n^{(1)} _{\infty }G^{(1)} (p_{\infty }) + \nu n^{(2)} _{\infty }G^{(2)} (p_{\infty })\right ), \end{aligned}$$

in the distributional sense, where \(n^{(i)}_{\infty }\), \(i=1,2\), satisfies

$$\begin{aligned} \left \{ \textstyle\begin{array}{rl} \displaystyle \frac {\partial n^{(i)}_{\infty}}{\partial t} - \frac {\partial }{\partial x}{\left (n^{(i)}_{\infty }\frac {\partial W_{\infty}}{\partial x}\right )} &=\displaystyle n^{(i)}_{\infty }G^{(i)}(p_{\infty }), \\ \displaystyle -\nu \frac{\partial ^{2} W_{\infty }}{\partial x^{2}} + W_{ \infty }&=\displaystyle p_{\infty }. \end{array}\displaystyle \right . \end{aligned}$$

Moreover, the following holds true

$$\begin{aligned} p_{\infty }(n_{\infty }- 1) = 0. \end{aligned}$$

The subsequent sections are concerned with the proof of the two main theorems.

3 Existence of Solutions and Regularity

This section is dedicated to proving the existence of solutions to the \((p,r)\)-system. The proof is based on an application of Banach’s fixed point theorem. Let \(k\geq 2\) be fixed throughout this section. Further, assume for now, that the initial data \(u_{0}^{(i)}\) are Lipschitz continuous. For given functions \(p,r \in L^{\infty }(0,T; L^{\infty }({\mathbb {R}}))\) we construct solutions \(u^{(i)}\) to the linearised system, \(i=1,2\),

$$\begin{aligned} \displaystyle \frac {\partial u}{\partial t}^{(i)}- \frac {\partial u^{(i)}}{\partial x} \frac {\partial W}{\partial x} =\displaystyle \frac{k-1}{ \nu } f^{(i)}(p,r), \end{aligned}$$
(8)

where

$$\begin{aligned} f^{(1)}(p,r) = K\star p - p + \nu r G^{(1)} (p) + \nu (1-r)G^{(2)} (p), \end{aligned}$$

and

For the fixed \(p\) from above, we may construct the backward flow

We readily observe that

\(i=1,2\), solve the linearised system (8). Now, considering another element \((\tilde{p},\tilde{r})\) in \(L^{\infty }(0,T; L^{\infty }({\mathbb {R}}))\), we observe that

Thus, upon passing to the supremum, we obtain the following stability estimate for two solutions

In particular, for \(T_{1}>0\) small enough the estimate gives rise to a contraction in the Banach space \(L^{\infty }(0,T_{1}; L^{\infty }({\mathbb {R}}))\), which is sufficient to infer the existence of a unique fixed point, by an application of Banach’s fixed point theorem. Since the supremum norm of the solution does not blow up, a finite number of iterations of the above argument leads to existence of a unique solution for all times \(T>0\).

For the subsequent analysis, let us call this fixed point \((u^{(1)} _{ \ast }, u^{(2)} _{\ast })\). It remains to prove the expected BV-regularity of solutions. This is an easy consequence of the “transport nature” of the system, i.e.,

$$\begin{aligned} \frac {\partial }{\partial t} \frac {\partial u^{(i)}_{\ast}}{\partial x} &= \frac {\partial u^{(i)}_{\ast}}{\partial x} \frac {\partial W}{\partial x} + \frac{k-1}{\nu } \left [ f^{(i)}_{p}(u^{(1)} _{\ast }, u^{(2)} _{\ast }) \frac {\partial u^{(1)}_{\ast}}{\partial x} +f^{(i)}_{r}(u^{(1)} _{\ast }, u^{(2)} _{\ast }) \frac {\partial u^{(2)}_{\ast}}{\partial x} \right ]. \end{aligned}$$

Multiplying by \(\mathrm {sign}(\partial_{x} u^{(i)}_{\ast })\) and adding the two equations, for \(i=1,2\), we obtain, after integrating

where the constant \(C>0\) depends only on the Lipschitz constants of the functions \(f^{(i)}\) and the \(L^{\infty }\)-bounds on the fixed point. In particular, from Gronwall’s inequality we deduce a control on the BV-seminorm and, more importantly, the existence of solutions even in cases where \(u^{(i)}_{0}\) is not Lipschitz continuous but only of bounded variation.

Using the fact that

$$ n^{(1)} = \left (\frac{k-1}{k}u^{(1)} _{*}\right )^{\frac{1}{k-1}}u_{*}^{(2)} ,\quad \text{and } \quad n^{(2)} = \left (\frac{k-1}{k}u^{(1)} _{*}\right )^{ \frac{1}{k-1}}\left (1-u_{*}^{(2)} \right ), $$

the existence and uniqueness result transfers to the original system for \(n^{(i)}_{k}\), \(i=1,2\).

Remark 3.1

(Extension to Higher Dimensions)

Let us remark here that the same strategy can be easily extended to higher dimensions since the transport nature is the same in any dimension. In fact, the only “problematic” point in our strategy is the contraction argument which depends on . However, this norm is finite in any dimension, and therefore our existence result holds in any dimension.

4 A Priori Estimates

In this section we derive some bounds for the main quantities of interests, uniformly in \(k\). These will be vital when passing to the limit with \(k\to \infty \).

Lemma 4.1

(A priori estimates I)

The following hold uniformly in \(k\)for any \(T>0\).

  1. (i)

    \(n_{k} \in L^{\infty } (0,T; L^{1}({\mathbb {R}}))\),

  2. (ii)

    \(p_{k} \in L^{\infty } (0,T; L^{\infty }({\mathbb {R}}))\),

  3. (iii)

    \(n_{k} \in L^{\infty } (0,T; L^{\infty }({\mathbb {R}}))\),

  4. (iv)

    \(p_{k} \in L^{\infty } (0,T; L^{1}({\mathbb {R}}))\), and

  5. (v)

    \(n_{k}^{(i)}\in L^{\infty } (0,T; L^{\infty }({\mathbb {R}}))\), for \(i=1,2\).

Proof

Clearly when \(n_{k}(t=0)\geq 0\), then \(n_{k}\) stays non-negative at all times. Integrating Eq. (1) in space and time we deduce that \(n_{k}\in L^{\infty } (0,T; L^{1}({\mathbb {R}}))\) uniformly in \(k\). By the maximum principle we have the bound \(0\leq p_{k} \leq p _{M}\). Then using \(n_{k} \simeq p^{\frac{1}{k-1}}\) we deduce \(n_{k} \in L^{\infty } (0,T; L^{\infty }({\mathbb {R}}))\) uniformly. Writing we see that \(p_{k} \in L^{\infty } (0,T; L^{1}({\mathbb {R}}))\). Finally, we use that \(n^{(1)} _{k} = r_{k} n_{k}\) and \(0\leq r_{k}\leq 1\) to deduce the last bounds. □

Using the above Lemma and the boundedness of \(W_{k}\), we have the following result.

Lemma 4.2

(Integrability and Segregation)

If both species are segregated initially, i.e.,

then there holds

for all times \(0\leq t \leq T\). In particular, \(r_{k}^{0}(1-r_{k}^{0}) \in L^{1}({\mathbb {R}})\)implies \(r_{k}(1-r_{k}) \in L^{\infty }(0,T; L ^{1}({\mathbb {R}}))\).

Proof

Here and henceforth we shall employ the notation

The supremum is taken only up to \(p_{M}\), because in principle the functions \(G^{(i)}\) can decrease arbitrarily. The uniform bound obtained in the previous proof shows however, that only the range \(0\leq p_{k}\leq p_{M}\) is relevant.

Using the equation for the population fraction and boundedness of the growth functions \(G^{(i)}\), we obtain

Using Brinkman’s law (2b), we obtain

having used the a priori bounds on the pressure, \(p_{k}\). □

The following lemma establishes an \(L^{1}\)-bound on the right-hand side of the pressure equation.

Lemma 4.3

(A priori estimates II)

The following estimate holds for any \(T>0\)

for a constant \(C(T)>0\), independent of \(k\). Furthermore, the following bounds hold uniformly in \(k\):

  1. (i)

    \(\displaystyle \frac {\partial W_{k}}{\partial t} \in L^{1}(0,T;L^{q}({\mathbb {R}}))\), for \(1\leq q\leq \infty \),

  2. (ii)

    \(\displaystyle \frac {\partial }{\partial t}{\frac {\partial W_{k}}{\partial x}} \in L^{1}(0,T;L^{q}({\mathbb {R}}))\), for \(1< q <\infty \).

Proof

Let us introduce the following notation

and follow the strategy of [19]. Using

$$ \frac {\partial W_{k}}{\partial t} = K \star \left [\frac {\partial p_{k}}{\partial x}\frac {\partial W_{k}}{\partial x} + \frac{k-1}{\nu }p_{k} Q_{k}\right ], $$
(9)

we derive the equation

$$ \begin{aligned} \frac {\partial Q_{k}}{\partial t} &- \frac {\partial Q_{k}}{\partial x} \frac {\partial W_{k}}{\partial x} + \frac{k-1}{ \nu }p_{k}Q_{k} \left [1-\nu r_{k} G^{(1)} _{p}(p_{k})-\nu \left (1-r_{k}\right ) G^{(2)} _{p}(p_{k})\right ]\\ &= - \left \lvert \frac {\partial W_{k}}{\partial x}\right \rvert ^{2} + K \star \left [\frac {\partial p_{k}}{\partial x}\frac {\partial W_{k}}{\partial x} + \frac{k-1}{\nu }p_{k} Q_{k}\right ] + \nu \left (G^{(1)} (p_{k}) - G^{(2)} (p_{k})\right )^{2}r_{k}(1-r_{k}), \end{aligned} $$

and consequently,

$$ \begin{aligned} &\frac {\partial \left \lvert Q_{k}\right \rvert }{\partial t} - \frac {\partial \left \lvert Q_{k}\right \rvert }{\partial x} \frac {\partial W_{k}}{\partial x} + \frac{k-1}{\nu }p_{k}\left \lvert Q_{k}\right \rvert \left [1-\nu r_{k} G^{(1)} _{p}(p_{k})-\nu(1-r_{k}) G^{(2)} _{p}(p_{k})\right ]\\ & \quad \leq - \left \lvert \frac {\partial W_{k}}{\partial x}\right \rvert ^{2} + \left \lvert K \star \left [\frac {\partial p_{k}}{\partial x}\frac {\partial W_{k}}{\partial x} + \frac{k-1}{\nu }p_{k} \left \lvert Q_{k}\right \rvert \right ]\right \rvert \\ & \qquad {} + \nu \left (G^{(1)} (p_{k}) - G^{(2)} (p_{k})\right )^{2}r_{k}\left (1-r_{k}\right ). \end{aligned} $$

Integrating in space-time and using the assumption that \(|G^{(i)}_{p}|\geq \alpha > 0\), we obtain

The first three terms on the right-hand side are controlled uniformly, as is the very last term. For the remaining two terms we write

which, for \(k\) large enough, is controlled by the left-hand side of the last inequality, and

$$ \begin{aligned}[b] K \star \left [\frac {\partial p_{k}}{\partial x}\frac {\partial W_{k}}{\partial x}\right ] &= \frac {\partial K}{\partial x} \star \left [p_{k}\frac {\partial W_{k}}{\partial x}\right ] - K \star \left [p_{k}\frac{\partial ^{2} W_{k}}{\partial x^{2}}\right ] \\&= \frac {\partial K}{\partial x} \star \left [p_{k} \frac {\partial K}{\partial x}\star p_{k}\right ] - K \star \left [p_{k}\frac{\partial ^{2} W_{k}}{\partial x^{2}}\right ]. \end{aligned} $$

Using Lemma 4.1, we see that the right-hand side is uniformly bounded in \(L^{\infty }(0,T;L^{q}({\mathbb {R}}))\), \(1\leq q \leq \infty \). It follows that

as desired.

Now, using Eq. (9) and the above computations, it is clear that \(\partial _{t}{W_{k}}\) is uniformly bounded in \(L^{\infty }(0,T;L ^{q}({\mathbb {R}}))\), for \(1\leq q\leq \infty \). Finally we write

$$ \frac {\partial }{\partial t}\frac {\partial W_{k}}{\partial x} = \frac{\partial ^{2} K}{\partial x^{2}} \star \left (p_{k}\frac {\partial W_{k}}{\partial x}\right ) - \frac {\partial K}{\partial x}\star \left (p_{k}\frac{\partial ^{2} W_{k}}{\partial x^{2}}\right ) + \frac{k-1}{ \nu }\frac {\partial K}{\partial x}\star \left (p_{k} Q_{k}\right ), $$

and use the definition of \(K\), cf. Eq. (7), to conclude the proof. □

Remark 4.4

All the results of this section remain valid in any spatial dimension \(d\geq 1\), see for example [19] for the a priori estimates, and the \(L^{1}\)-bound on the quantity \(\mathit{kp}_{k} Q_{k}\).

5 Strong Compactness of the Pressure

This section is solely dedicated to the derivation of suitable estimates in order to obtain strong compactness of the pressure, \(p_{k}\). A key step in this pursuit is the following BV-estimate on the individual species as well as the total population.

Lemma 5.1

(Regularity of \(n^{(i)}_{k}\) and \(n_{k}\))

For \(i=1,2\), we have the following

$$\begin{aligned} \left \lvert \frac {\partial n^{(i)}_{k}}{\partial x}\right \rvert , \left \lvert \frac {\partial n_{k}}{\partial x}\right \rvert \in L^{ \infty }(0,T; L^{1}({\mathbb {R}})), \end{aligned}$$

uniformly in \(k\geq 2\).

Proof

For \(i=1,2\), we consider

$$\begin{aligned} \frac {\partial n_{k}^{(i)}}{\partial t} = \frac {\partial }{\partial x} \left ( n^{(i)}_{k} \frac {\partial W_{k}}{\partial x}\right ) + n^{(i)}_{k} G^{(i)}(p_{k}). \end{aligned}$$

Upon differentiating in space, we obtain

$$\begin{aligned} \frac {\partial }{\partial t} \frac {\partial n^{(i)}_{k}}{\partial x} = \frac {\partial }{\partial x} \left (\frac {\partial n^{(i)}_{k} }{\partial x} \frac {\partial W}{\partial x}\right ) + \frac {\partial }{\partial x} \left (n^{(i)}_{k} \frac{\partial ^{2} W}{\partial x ^{2}}\right ) + \frac {\partial n^{(i)}_{k}}{\partial x} G^{(i)}(p_{k}) + n^{(i)}_{k} G_{p}^{(i)}(p _{k}) \frac {\partial p_{k}}{\partial x}, \end{aligned}$$
(10)

for \(i=1,2\). Upon adding up both equations we get

$$\begin{aligned} \frac {\partial }{\partial t} \frac {\partial n_{k}}{\partial x} = \frac {\partial }{\partial x} \left (\frac {\partial n_{k}}{\partial x} \frac {\partial W_{k}}{\partial x}\right ) + \frac {\partial }{\partial x} \left (n_{k} \frac{\partial ^{2} W_{k}}{\partial x^{2}}\right ) + \sum _{i=1,2} \frac {\partial n^{(i)}_{k}}{\partial x} G^{(i)}(p_{k}) + n^{(i)}_{k} G_{p}^{(i)}(p _{k}) \frac {\partial p_{k}}{\partial x}. \end{aligned}$$
(11)

Multiplying the equation for the individual species by \(\sigma ^{(i)}:=\mathrm {sign}{(\partial _{x}n_{k}^{(i)})}\) and the equation for the total population by \(\sigma :=\mathrm {sign}{(\partial _{x}n_{k})}\), we get, upon adding the two equations in Eq. (10) and the one in Eq. (11), and integrating in space

First we notice that the exact derivatives vanish and the estimate simplifies to

Next, we notice that all the terms involving the pressure gradient cancel due to opposite signs, whence

Thus we are left with

(12)

Using the fact that

$$\begin{aligned} - \nu \frac{\partial ^{2} W_{k}}{\partial x^{2}} + W_{k} = p_{k}, \end{aligned}$$

the integrand of the last line of Eq. (12) may be simplified to

(13)

Using the fact that and exploiting the bounds

$$\begin{aligned} n_{k}^{(i)}, n_{k} \in L^{\infty }(0,T; L^{1}({\mathbb {R}})), \quad \text{and} \quad \frac {\partial W_{k}}{\partial x} \in L^{\infty }(0,T; L^{\infty }({\mathbb {R}})), \end{aligned}$$

we may bound the terms of Eq. (13), and the last line of Eq. (12) becomes

(14)

The last integral in Eq. (14) vanishes due to the fact that \(n_{k} = n^{(1)} _{k} + n^{(2)} _{k}\). Thus, substituting Eq. (14) into Eq. (12), an application of Gronwall’s lemma yields the BV-estimate in space. □

Corollary 5.2

From the proof of the preceding lemma we deduce

where \(C>0\)is independent of \(k\).

Proof

Let us revisit the equation for \(\partial _{t} {n_{k}}\), i.e.,

Now we use the bounds \(G^{(i)}_{p}\leq -\alpha <0\), for \(i=1,2\), and integrate in time to see that

where

$$\begin{aligned} R:= \left \lVert \frac {\partial n_{k}}{\partial x}\right \rVert _{L^{\infty }(0,T; L^{1}({\mathbb {R}}))}+ \left \lVert \frac {\partial n^{(1)}_{k}}{\partial x}\right \rVert _{L^{\infty }(0,T; L^{1}({\mathbb {R}}))}+ \left \lVert \frac {\partial n^{(2)}_{k}}{\partial x}\right \rVert _{L^{\infty }(0,T; L^{1}({\mathbb {R}}))}+1. \end{aligned}$$

Thus we infer that \(n_{k}\partial _{x}{p_{k}}\) is uniformly bounded in \(L^{1}(0,T;L^{1}({\mathbb {R}}))\). □

Lemma 5.3

(Strong Compactness of the Pressure)

There exists a function

$$ p_{\infty }\in L^{\infty } \left (0,T; L^{1}({\mathbb {R}}) \cap L^{\infty }({\mathbb {R}})\right ), $$

such that, up to a subsequence, there holds

$$\begin{aligned} p_{k} \longrightarrow p_{\infty }, \end{aligned}$$

in \(L_{\mathrm{loc}}^{p}(0,T; L^{q}({\mathbb {R}}))\), as \(k\rightarrow \infty \)for any \(2\leq p\), \(q<\infty \). In addition, the convergence also holds in the almost everywhere sense.

Proof

Let us write the quantity \(n_{k}\left \lvert \partial _{x} p_{k}\right \rvert \) as a spatial derivative of a non-decreasing function of the pressure. We compute as follows

$$\begin{aligned} n_{k} \left \lvert \frac {\partial p_{k}}{\partial x}\right \rvert = \left (\frac{k-1}{k}\right )^{\frac{k}{k-1}}\mathrm {sign}{\left (\frac {\partial p_{k}}{\partial x}\right )}\frac {\partial }{\partial x}\left (p^{\frac{k}{k-1}}\right ) = \left (\frac{k-1}{k}\right )^{\frac{k}{k-1}} \left \lvert \frac {\partial }{\partial x}\left (p^{\frac{k}{k-1}}\right )\right \rvert . \end{aligned}$$

Let . Then

i.e., \(\partial _{x}{\phi _{k}}(p_{k}) \in L^{1}(0,T;L^{1}({\mathbb {R}}))\), uniformly in \(k\). Moreover, we have the same \(L^{1}\)-bound for the time derivative of \(\phi _{k}(p_{k})\). Indeed

$$\begin{aligned} \frac {\partial \phi _{k}}{\partial t}(p_{k}) &= \phi _{k}'(p_{k})\frac {\partial p_{k}}{\partial t} \\ &= \phi _{k}'(p_{k}) \left (\frac {\partial p_{k}}{\partial x}\frac {\partial W_{k}}{\partial x} + \frac{k-1}{\nu }p_{k} Q_{k}\right ) \\ &= \frac {\partial \phi _{k}}{\partial x}(p_{k})\frac {\partial W_{k}}{\partial x} + \frac{k}{k-1}\frac{k-1}{ \nu }p_{k}^{\frac{1}{k-1}}p_{k} Q_{k}, \end{aligned}$$

and therefore

where we have used Lemma 4.3.

We conclude that the sequence \((\phi _{k}(p_{k}))_{k}\) converges strongly in \(L^{2}((0,T)\times {\mathbb {R}})\). On the other hand, from the uniform bounds on \(p_{k}\) we infer that \(p_{k}\rightharpoonup p_{\infty }\), weakly in \(L^{2}((0,T)\times {\mathbb {R}})\), up to the subsequence. We can therefore apply Lemma 8.1 to conclude that

$$ \phi _{k}(p_{k}) \rightarrow p_{\infty }, $$

strongly in \(L_{\mathrm{loc}}^{2}((0,T)\times {\mathbb {R}})\). We claim that this in fact implies strong convergence of the sequence of pressures \((p_{k})_{k}\) itself. Indeed, using the triangle inequality yields

and

with the right-hand side of the last line converging to zero. We conclude that

$$ p_{k} \rightarrow p_{\infty }, $$

strongly in \(L_{\mathrm{loc}}^{2}((0,T)\times {\mathbb {R}})\). In combination with the \(L^{\infty }\)-bounds, we deduce that this convergence holds strongly in \(L_{\mathrm{loc}}^{p}(0,T;L^{q}({\mathbb {R}}))\), for any \(2\leq p\), \(q<\infty \), using the dominated convergence theorem. Moreover, the convergence is also true almost everywhere. □

6 Incompressible Limit and Complementarity Relation

We have garnered all information necessary to pass to the incompressible limit in the pressure equation (4) and prove Theorem 2.2.

Proof of Theorem 2.2

Having established strong convergence of the sequence \((p_{k})_{k}\), and weak convergence of \((n_{k})_{k}\) due to the a priori estimates, we can pass to the limit in the relation

$$ n_{k} p_{k} = \left (\frac{k-1}{k}\right )^{\frac{1}{k-1}}p_{k}^{ \frac{k}{k-1}}, $$
(15)

to deduce the relation \((1-n_{\infty })p_{\infty }= 0\), almost everywhere. For a test function \(\varphi \in C_{c}^{1}((0,T)\times {\mathbb {R}})\), let us recall the weak formulation of the equation for the pressure

Due to the uniform bounds on the right-hand side, cf. Lemma 4.3, we may divide by \(k-1\) to obtain

Note that, writing \(n^{(1)} _{k} = n_{k} r_{k}\) and expressing \(n_{k}\) in terms of \(p_{k}\), in a fashion similar to Eq. (15), we may readily pass to the limit in all of these terms due to the strong convergence of the pressure and the a priori bounds of Lemma 4.1. We thus obtain

$$ 0 = p_{\infty } \left (W_{\infty }- p_{\infty }+ \nu n^{(1)} _{\infty }G^{(1)} (p_{\infty }) + \nu n^{(2)} _{\infty }G^{(2)} (p_{\infty })\right ), $$

in the weak sense, where \(n^{(i)}_{\infty }\) satisfies

$$ \frac {\partial n^{(i)}_{\infty}}{\partial t} - \frac {\partial }{\partial x}{\left (n^{(i)}_{\infty }\frac {\partial W_{\infty}}{\partial x}\right )} = n^{(i)}_{\infty }G^{(i)}(p_{\infty }), $$

for \(i=1,2\). Indeed these equations follow by passing to the limit in the weak formulation of (2a), (2b)

where \(\varphi \in C_{c}^{1}((0,T)\times {\mathbb {R}})\). □

Remark 6.1

In fact, using the strategy of the previous section, i.e., the BV-bounds in space, in conjunction with a control on the time derivative obtained from bounding the right-hand side of the equation for the individual species, one can deduce also strong convergence of the sequence \((n_{k})_{k}\). As a consequence, the limit functions \(n_{\infty }\), \(n^{(i)}_{\infty }\) are of bounded variation in time and space.

7 Numerical Investigations

In this section, we revisit the results from the preceding sections and showcase certain properties of the system. The numerical simulations are performed using the positivity-preserving upwind finite volume scheme proposed for a system of two interacting species in [9, 10] where the reaction terms are computed on each finite volume cell as simple ODEs. The implementation hinges on the fact that the elliptic Brinkman law (2b) can be solved using the integral representation (7).

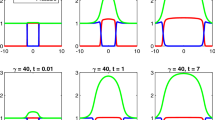
Figure 1 displays the role of the viscosity parameter, \(\nu \). The same initial data

$$\begin{aligned} n_{k,0}^{(1)} (x) = m (x-4.5)(6.5 - x) , \quad \text{and} \quad n_{k,0}^{(2)} (x) = m(x-8.5)(10.5-x), \end{aligned}$$

are used in both cases and \(m>0\) is chosen to normalise the initial mass to 1. In both cases we used \(k=100\), as we are interested in the incompressible regime. In addition, we chose \(G^{(i)}(p)= 1-p\), for \(i=1,2\), corresponding to a homeostatic pressure of \(p_{M} = 1\), cf. Eq. (6). In both cases we observe the propagation of segregation in agreement with Lemma 4.2. Moreover, we observe a drastic drop in the pressure in Fig. 1(b). This was already observed in the one species case, cf. [19], where the fact was exploited that the limiting pressure has an integral representation formula. In stark contrast, Fig. 1(d) shows an almost smooth transition of the pressure indicating a much higher regularity. This is in perfect alignment with the findings of [6], as the case \(\nu =0\) yields, at least formally, the system studied in the latter. As a matter of fact, the pressure gradient was shown to be square-integrable in the Darcy case, i.e., \(\nu =0\). We conclude, by remarking that the front propagation is much faster in the regime of small \(\nu \), another fact that was already observed in the single-species case.

Fig. 1
figure 1

We run the simulation for the same initial data for two different values of \(\nu \), i.e., \(\nu = 1\) in the upper row and \(\nu = 0.01\) in the bottom row. In both cases, we chose \(k=100\) since we are interested in the limiting behaviour. The individual species are represented by solid lines in red and blue, the pressure is superimposed as a black dotted line. In the upper row the pressure drops to zero immediately, whereas in the bottom row we can see an almost smooth transition

Full size image

In Fig. 2 we present the effect of different growth terms of the tumour cells and healthy tissue. To be more precise, we choose the same initial condition as above but use

$$\begin{aligned} G^{(1)} (p) = 2 - p, \quad \text{and} \quad G^{(2)} (p) = 1 - p, \end{aligned}$$

as growth terms for the two species. We see that the first species, \(n_{k}^{(1)} \), proliferates much faster compared to the second one. More interestingly, we see that the pressure not only has a jump at the boundaries of the support of the total population, but also at the internal layer.

Fig. 2
figure 2

We run the simulation for the same initial data for two different growth functions, \(G^{(i)}(p)\). In both cases, we chose \(k=100\) and the individual species are represented by solid lines in red and blue, the pressure is superimposed as a black dotted line, as before. The pressure drops not only at the boundary of its support. We also observe jumps in internal layers

Full size image

Figure 3 shows the evolution of system (2a), (2b) for initial data representing a regime where healthy tissue has already been intruded by cancerous cells, i.e.,

$$\begin{aligned} n_{k,0}^{(1)} (x) = m (x-6.5)(8.5 - x) , \quad \text{and} \quad n_{k,0}^{(2)} (x) = m(x-6)(9-x), \end{aligned}$$

where, again, \(m>0\) normalises the mass. In addition, we choose the same unequal growth functions, \(G^{(i)}\), as before, thus promoting the tumour growth compared to the normal tissue.

Fig. 3
figure 3

The simulation shows the invasion of abnormal cells surrounded by healthy tissue. As time evolves, the tumour spreads and the density of normal cells is diminished and nearly vanishes, cf. Figure 3(d). As before, \(\nu =1\) and \(k=100\)

Full size image

8 Conclusions

The goal of the paper was twofold. We extended an established tumour growth model to an interaction system of two cell populations, i.e., normal and abnormal cells. The interaction is given through the Brinkman flow, an elliptic equation that yields the velocity potentials for each cell population. In the first part of this paper we proved the existence of solutions to the interaction system, cf. Theorem 2.1. Building upon this result, we passed to the “incompressible” limit in the pressure equation, Eq. (4), and obtained the limiting equation, also referred to as complementarity relation, cf. Theorem 2.2. This way we were able to derive a geometric model from the cell-density model we presented.

Note that both the existence result and the incompressible limit rely on strategies different from the ones adapted for related models (either in the parabolic two-species case when Brinkman’s law is replaced by Darcy’s law (\(\nu =0\)) or the one-species model with Brinkman flow). The results are complemented with a numerical investigation showcasing the segregation result, the discontinuities in the pressure and the two individual population densities which is why we do not expect better regularity than bounded variation.

In summary, this paper extends known results in the literature to two species. As far as the existence of solutions is concerned, no additional difficulties are expected in the multi-dimensional case. However, when it comes to the stiff limit not only our method fails but also the kinetic reformulation that was employed in the one-species case, cf. [19], would need a serious make-over that is, at this stage, far from clear — even in one dimension. New singularities appear at internal layers when the two species meet and it seems that different tools are required, such as the extension of the kinetic reformulation to systems, which, to our knowledge, does not exist. The exploration of such a technique is left for future works.

In addition, the rigorous inviscid limit, \(\nu \rightarrow 0\), remains an open question that is left for future work.