Abstract
We investigate input-to-state stability (ISS) of infinite-dimensional collocated control systems subject to saturated feedback. Here, the unsaturated closed loop is dissipative and uniformly globally asymptotically stable. Under an additional assumption on the linear system, we show ISS for the saturated one. We discuss the sharpness of the conditions in light of existing results in the literature.
Similar content being viewed by others
1 Introduction
In this note we continue the study of the stability of systems of the form

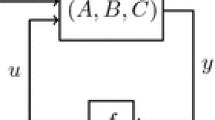
derived from the linear collocated open-loop system
by the nonlinear feedback law \(u(t)=-\sigma (y(t)+d(t))\). Here X and U are Hilbert spaces, \(A:D(A)\subset X\rightarrow X\) is the generator of a strongly continuous contraction semigroup, and B is a bounded linear operator from U to X, i.e. \(B\in \mathcal {L}(U,X)\). The function \(\sigma :U\rightarrow U\) is locally Lipschitz continuous and maximal monotone with \(\sigma (0)=0\). Of particular interest is the case in which \(\sigma \) is even linear in a neighbourhood of 0. The open-loop system is called collocated as the output operator \(B^*\) equals the adjoint of the input operator B. In the following, we are interested in stability with respect to both the initial value \(x_{0}\), that is, internal stability, and the disturbance d, external stability. This is combined in the notion of input-to-state stability (ISS), which has recently been studied for infinite-dimensional systems e.g. in [7, 9, 19, 20] and particularly for semilinear systems in [5, 6, 23], see also [18] for a survey. The effect of feedback laws acting (approximately) linearly only locally is known in the literature as saturation and first appeared in [24, 25] in the context of stabilization of infinite-dimensional linear systems, see also [10]. There, internal stability of the closed-loop system was studied using nonlinear semigroup theory, a natural tool to establish existence and uniqueness of solutions for equations of the above type, see also the more recent works [11, 15, 16]. The simultaneous study of internal stability and the robustness with respect to additive disturbances in the saturation seems to be rather recent. This notion clearly includes uniform global (internal) stability, which is far from being trivial for such nonlinear systems. In [22], this was studied for a wave equation, and in [14] Korteweg–de Vries type equation was rigorously discussed, building on preliminary works in [12, 13], see also [11].
The combination of saturation and ISS was initiated in [15] and, as for internal stability, complemented in [16]. For the rich finite-dimensional theory on ISS for related semilinear systems, we refer e.g. to [5, 6] and the references therein. For (infinite-dimensional) nonlinear systems, ISS is typically assessed by Lyapunov functions, see e.g. [3, 8, 17, 20, 23]. These are often constructed by energy-based \(L^{2}\) norms, but also Banach space methods exist [20], which are much easier to handle in the sense of \(L^{\infty }\)-estimates as present in ISS. We will use some of these constructions here.
In this note, we investigate the question whether internal stability of the linear undisturbed system, that is, (\(\varSigma _{SLD}\)) with \(\sigma (u)=u\) and \(d\equiv 0\), implies input-to-state stability of (\(\varSigma _{SLD}\)). In doing so, we try to shed light on limitations of existing results. Because the linear system has a bounded input operator, the above question is equivalent to asking whether ISS of the linear system yields that (\(\varSigma _{SLD}\)) is ISS, see e.g. [9]. For nonlinear systems, uniform global asymptotic (internal) stability is only a necessary condition for ISS, which, however, may fail in the presence of saturation. Indeed, the following saturated transport equation will serve as a model for a counterexample which we shall discuss in this note in detail, see Theorem 7,

where
2 ISS for saturated systems
Definition 1
We call \(\sigma :U\rightarrow U\) an admissible feedback function if
-
(i)
\(\sigma (0) = 0\),
-
(ii)
\(\sigma \) is locally Lipschitz continuous, i.e. for every \(r>0\) there exists a \(k_r>0\) such that
$$\begin{aligned} \Vert \sigma (u)-\sigma (v)\Vert _U \le k_r\Vert u-v\Vert _U \quad \forall \ u,v \in U \text { with } \Vert u\Vert _U,\Vert v\Vert _U\le r, \end{aligned}$$ -
(iii)
\(\sigma \) is maximal monotone, i.e. \(\mathfrak {R}\langle \sigma (u)-\sigma (v),u-v\rangle _U \ge 0 \quad \forall \ u,v\in U\).
If additionally a Banach space S is continuously, densely embedded in U with dual space \(S'\) such that
-
(iv)
\(\Vert \sigma (u)-u\Vert _{S'}\le \mathfrak {R}\langle \sigma (u),u\rangle _U \quad \forall \ u\in U\), and
-
(v)
there exists \(C_0>0\) such that
$$\begin{aligned} \mathfrak {R}\langle u,\sigma (u+v)-\sigma (u)\rangle _U \le C_0\Vert v\Vert _U \quad \forall \ u,v\in U, \end{aligned}$$
then we call \(\sigma \) a saturation function. Here \(U\subset S'\) is understood in the sense of rigged Hilbert spaces, i.e. an element u in U is identified with the functional \(s\mapsto \langle s,u\rangle _U\) in \(S'\).
It seems that the notion of a saturation function appeared first in the context of infinite-dimensional systems in [24, 25]. Note that the precise definition—in particular which properties it should include—has varied in the literature since then. Our definition here matches the one in [15], except for the fact that, in addition, it is required that \(\Vert \sigma (u)\Vert _{S}\le 1\). We distinguish between “admissible feedback functions” and “saturation functions” in order to point out which (minimal) assumptions are needed in the following results.
Example 2
Let \(\mathrm {sat}_{\mathbb {R}}\) be the function from (1). It is easy to see that the function
is an admissible feedback function. Moreover, for \(S=L^\infty (0,1)\) we have that
As Property (v) from Definition 1 follows similarly, \(\mathfrak {sat}\) is a saturation function. Note that this example is well known in the literature, see [15, 16] and the references therein.
Let \(\sigma \) be an admissible feedback function. In the rest of the paper, we will be interested in the following two types of systems: The unsaturated system,

and the disturbed saturated system

with \(d\in L^\infty (0,\infty ;U)\). We abbreviate
By the Lumer–Phillips theorem, \({\widetilde{A}}\) generates a strongly continuous semigroup of contractions \(({\widetilde{T}}(t))_{t\ge 0}\) as \(-BB^*\in L(X)\) is dissipative. Moreover, the nonlinear operator \(A-B\sigma (B^{*}\cdot )\) generates a nonlinear semigroup of contractions [26, Thm. 1] since, obviously, \(B\sigma (B^{*}\cdot ):X\rightarrow X\) is continuous and monotone, i.e.
Clearly, (\(\varSigma _L\)) is a special case of (\(\varSigma _{SLD}\)) with \(d=0\), as \(\sigma (u)=u\) is an admissible feedback function.
Definition 3
Let \(x_{0}\in X\), \(d\in L_{\mathrm {loc}}^\infty (0,\infty ;U)\) and \(t_{1}>0\). A continuous function \(x:[0,t_{1}]\rightarrow X\) satisfying
is called a mild solution of (\(\varSigma _{SLD}\)) on \([0,t_{1}]\), and we may omit the reference to the interval. If \(x:[0,\infty )\rightarrow X\) is such that the restriction \(x|_{[0,t_{1}]}\) is a mild solution for every \(t_{1}>0\), then x is called a global mild solution.
By our assumptions, (\(\varSigma _{SLD}\)) has a unique mild solution (on some maximal interval) for any \(x_{0}\in X\) and \(d\in L^\infty (0,\infty ;U)\), [21, Thm. 6.1.4]Footnote 1. In order to introduce the external stability notions, the following well-known comparison functions are needed,
where \(C({\mathbb {R}}_+,{\mathbb {R}}_{+})\) refers to the continuous functions from \({\mathbb {R}}_{+}\) to \({\mathbb {R}}_{+}\).
Definition 4
-
(i)
(\(\varSigma _{SLD}\)) is called globally asymptotically stable (GAS) if every mild solution x for \(d=0\) is global and the following two properties hold; \(\lim _{t\rightarrow \infty }\Vert x(t)\Vert _X=0\) for every initial condition \(x_{0}\in X\) and there exist \(\sigma \in \mathcal {K}_{\infty }\) and \(r>0\) such that \(\Vert x(t)\Vert \le \sigma (\Vert x_{0}\Vert )\) for every \(x_{0}\in X\) with \(\Vert x_0\Vert \le r\), \(d=0\) and \(t\ge 0\).
-
(ii)
(\(\varSigma _{SLD}\)) is called semi-globally exponentially stable in D(A) if for \(d=0\) and any \(r>0\) there exist \(\mu (r)>0\) and \(K(r)>0\) such that any mild solution x with initial value \(x_0\in D(A)\) is global and satisfies
$$\begin{aligned} \Vert x(t)\Vert _X \le K(r)\mathrm {e}^{-\mu (r)t}\Vert x_0\Vert _X \qquad \forall t\ge 0 \end{aligned}$$for \(\Vert x_0\Vert _{D(A)} :=\Vert x_0\Vert _X + \Vert Ax_0\Vert _X \le r\).
-
(iii)
(\(\varSigma _{SLD}\)) is called locally input-to-state stable (LISS) if there exist \(r>0\), \(\beta \in \mathcal {KL}\) and \(\rho \in \mathcal {K}_\infty \) such that every mild solution x with initial value satisfying \(\Vert x_0\Vert _X\le r\) and disturbance d with \(\Vert d\Vert _{L^{\infty }(0,\infty ;U)}\le r\) is global and for all \(t\ge 0\) we have that
$$\begin{aligned} \Vert x(t)\Vert _X \le \beta (\Vert x_0\Vert _X,t)+\rho (\Vert d\Vert _{L^\infty (0,t;U)}). \end{aligned}$$(2)(\(\varSigma _{SLD}\)) is called input-to-state stable (ISS) if \(r=\infty \). System (\(\varSigma _{SLD}\)) is called LISS with respect to \(C(0,\infty ;U)\) if the above holds for continuous disturbances only. If (2) holds for (\(\varSigma _{SLD}\)) with \(d\equiv 0\) and \(r=\infty \), the system is called uniformly globally asymptotically stable (UGAS), where the uniformity is with respect to the initial values.
Note that in our notation “UGAS” refers to “0-UGAS” and “GAS” refers to “0-GAS” more commonly used in the literature. The System (\(\varSigma _{SLD}\)) is globally asymptotically stable if and only if for every mild solution x for \(d=0\) we have \(\lim _{t\rightarrow \infty }\Vert x(t)\Vert _X=0\). This directly follows from the fact that the mild solutions of (\(\varSigma _{SLD}\)) with \(d=0\) can be represented by a (nonlinear) contraction semigroup, which implies that \(\Vert x(t)\Vert \le \Vert x_{0}\Vert \) for all \(t\ge 0\), \(x_{0}\in X\). Compared to the other notions, semi-global exponential stability in D(A) seems to be less common in the literature, but appeared already in the context of saturated systems in [16]. The notion of semi-global exponential stability in X was studied in [14]. Note that for the linear System (\(\varSigma _L\)) UGAS is equivalent to the existence of constants \(M,\omega >0\) such that \(\Vert {\widetilde{T}}(t)\Vert _X\le M\mathrm {e}^{-\omega t}\) for all \(t\ge 0\), see [4, Proposition V.1.2]. Clearly, if (\(\varSigma _{SLD}\)) is UGAS, then it is globally asymptotically stable. We note that semi-global exponential stability in D(A) implies global asymptotical stability since D(A) is dense in X and by the above-mentioned fact that the mild solutions are described by a nonlinear contraction semigroup. Moreover, using again the denseness of D(A) in X, the System (\(\varSigma _L\)) is UGAS if and only if it is semi-globally exponentially stable in D(A).
Next we investigate the question whether (semi-)global exponential stability in D(A) or UGAS of System (\(\varSigma _L\)) implies (semi-)global exponential stability in D(A) or UGAS of System (\(\varSigma _{SLD}\)).
In [11, Theorem 2], it is shown that global asymptotic stability of (\(\varSigma _L\)) implies global asymptotic stability of (\(\varSigma _{SLD}\)) if
-
D(A) equipped with the norm \(\Vert \cdot \Vert _{D(A)}= \Vert \cdot \Vert _X + \Vert A\cdot \Vert _X\) is a Banach space compactly embedded in X and
-
\(\sigma \) is an admissible feedback function with the additional properties that for all \(u\in U\), \(\mathfrak {R}\langle u,\sigma (u)\rangle =0\) implies \(u=0\).
Note that the other assumptions of [11, Theorem 2] are satisfied in our situation if \(\sigma \) is globally Lipschitz; this follows again by the fact that the mild solutions are represented by a nonlinear semigroup. In [19, Section V], it is shown that under these conditions and in finite dimensions, i.e. \(X={\mathbb {R}}^n\) and \(U={\mathbb {R}}^m\), (\(\varSigma _{SLD}\)) is UGAS.
Here we are interested in results for general admissible feedback functions and saturation functions. The following result was proved in [16] and [15].
Proposition 5
[[15, Theorem 1], [16, Theorem 2]] Let (\(\varSigma _L\)) be UGAS and \(\sigma :U\rightarrow U\) be a globally Lipschitz saturation function.
-
(i)
If \(S=U\), then (\(\varSigma _{SLD}\)) is ISS.
-
(ii)
If there exists a bounded self-adjoint operator P which maps D(A) to D(A) and solves
$$\begin{aligned} \langle \widetilde{A}x,Px\rangle +\langle Px,\widetilde{A}x\rangle \le -\langle x,x\rangle ,\qquad \forall x\in D(\widetilde{A})=D(A), \end{aligned}$$(3)and if
$$\begin{aligned} \exists c>0 \, \forall x\in D(A):\quad \Vert B^*x\Vert _S \le c\Vert x\Vert _{D(A)}, \end{aligned}$$(4)then (\(\varSigma _{SLD}\)) is semi-globally exponentially stable in D(A).
Note that in the second part of Proposition 5, the existence of a bounded, self-adjoint operator P satisfying (3) always follows from the assumption that (\(\varSigma _L\)) is UGAS. However, the property that such P leaves \(D(\widetilde{A})\) invariant does not hold in general. For instance, this is satisfied if there exists \(\alpha >0\) such that \(\mathfrak {R}\langle Ax,x\rangle \le -\alpha \Vert x\Vert ^{2}\) all \(x\in D(A)\), which follows directly from dissipativity. On the other hand, it is not hard to construct examples where this invariance is not satisfied. We will comment on this condition also in Remark 10(ii). We will show next that Proposition 5(ii) does not hold without assuming (4) and, moreover, that (4) does neither imply UGAS nor ISS for (\(\varSigma _{SLD}\)).
Proposition 6
Let \(X=U=L^2(0,1)\), \(S=L^\infty (0,1)\), \(A=0\), \(B=I\) and \(\sigma =\mathfrak {sat}\). Then, System (\(\varSigma _L\)) is UGAS and System (\(\varSigma _{SLD}\)) is neither semi-globally exponentially stable in D(A), nor UGAS nor ISS.
Proof
As System (\(\varSigma _L\)) is given by \(\dot{x}(t)=-x(t)\), it is UGAS. System (\(\varSigma _{SLD}\)) s given by
with the unique mild solution \(x\in C([0,\infty );L^2(0,1))\)
which can be derived by solving (5) for fixed \(\xi \) as simple ODE. We will show that there exists a sequence \((f_n)_n\in L^2(0,1)\) with \(\Vert f_n\Vert _{D(A)} = \Vert f_n\Vert _{L^2(0,1)} = 1\) such that for all \(t>0\) there exists an \(n\in \mathbb {N}\) such that \(\Vert x_n(t)\Vert _{L^2(0,1)}>\frac{1}{2}\) where \(x_n\) denotes the corresponding solution of (5) with initial function \(f_n\). For this purpose, we will only consider the restriction of \(x_n\) to \(\{\xi \in [0,1] \ | \ f(\xi )\ge 1+t\}\) and define
with \(\alpha _n:=\frac{1}{2}\left( 1-\frac{1}{n}\right) \). Clearly, \(f_n\in L^2(0,1)\), \(\Vert f_{n}\Vert _{L^{2}}=1\) and \(f_n\) is decreasing. Note that the equation \(f_{n}(\xi )=1+t\) has a unique solution \(\xi \) for fixed n and t which is given by
Therefore, \(\{\xi \in [0,1] \ | \ f_n(\xi )\ge 1+t\} = \{\xi \in [0,1] \ | \ \xi \le \xi _{t,n}\}\). Hence,
Taking the limit \(n\rightarrow \infty \), we conclude
Thus, the solution of System (5) does not converge uniformly to 0 with respect to the norm or graph norm of the initial value, so the system is neither semi-globally exponentially stable in D(A) nor UGAS. \(\square \)
Note that System (\(\varSigma _{SLD}\)) from Proposition 6 is (GAS) for \(d=0\) by [11, Theorem 2]. After we have seen that (4) is necessary to conclude semi-global exponential stability in D(A) in Proposition 5(ii), one may ask whether “more stability” can in fact be expected. The following theorem shows that UGAS of System (\(\varSigma _L\)) together with the hypotheses in Proposition 5(ii) is not sufficient to guarantee UGAS of System (\(\varSigma _{SLD}\)).
Theorem 7
Let \(X=U=L^2(0,1)\), \(B=I\), \(S=L^\infty (0,1)\), \(\sigma =\mathfrak {sat}\) and
Then, the following assertions hold.
-
(i)
System (\(\varSigma _L\)) is UGAS and the hypothesis of Proposition 5(ii) holds,
-
(ii)
System (\(\varSigma _{SLD}\)) is semi-globally exponentially stable in D(A),
-
(iii)
System (\(\varSigma _{SLD}\)) is neither UGAS nor ISS.
We note that System (\(\varSigma _{SLD}\)) of Theorem 7 equals (\(\varSigma _\mathfrak {sat}\)). Further, in [15, Thm. 1] it has been wrongly stated that the saturated system is UGAS.
Proof
It is easy to see that System (\(\varSigma _L\)) is UGAS. Since A is dissipative, it follows that \(P=I\) solves (3) for \(\tilde{A}=A-BB^*=A-I\). Trivially, P maps D(A) to D(A). Condition (4) is satisfied because \(H^1(0,1)\) is continuously embedded in \(L^\infty (0,1)\). Hence, (\(\varSigma _{SLD}\)) is semi-globally exponentially stable in D(A) by Proposition 5 and the fact that \(\sigma \) is globally Lipschitz continuous. This shows Assertions (i) and (ii). To see (iii), note that A generates the periodic shift semigroup on \(L^2(0,1)\). By extending the initial function f periodically to \({\mathbb {R}}_+\), the unique mild solution \(y\in C([0,\infty );L^2(0,1))\) of (\(\varSigma _{SLD}\)) is given by
where x is defined in (6). By the particular form of (6), this implies that
holds for all \(t\ge 0\). We can therefore choose the same sequence \((f_n)_n\in L^2(0,1)\) with \(\Vert f_n\Vert _{L^2(0,1)}=1\) as in the proof of Proposition 6 in order to conclude
This shows that System (\(\varSigma _{SLD}\)) is not UGAS and thus not ISS. \(\square \)
An important tool for the verification of ISS of System (\(\varSigma _{SLD}\)) are ISS Lyapunov functions.
Definition 8
Let \(U_{r}=\{x\in X:\Vert x\Vert \le r\}\) and \(r\in (0,\infty ]\). Let \(\mathcal {U}\) be either \(C(0,\infty ;U)\) or \(L_{\mathrm{loc}}^{\infty }(0,\infty ;U)\). A continuous function \(V:U_{r}\rightarrow {\mathbb {R}}_{\ge 0}\) is called an LISS Lyapunov function for (\(\varSigma _{SLD}\)) with respect to \(\mathcal {U}\), if there exists \(\psi _1,\psi _2,\alpha ,\rho \in \mathcal {K}_\infty \), such that for all \(x_0\in U_{r}\), \(d\in \mathcal {U}\), \(\Vert d\Vert _{L^\infty (0,\infty ;U)}\le r\),
and
where x is the mild solution of (\(\varSigma _{SLD}\)) with initial value \(x_0\) and disturbance d. If \(r=\infty \), then V is called an ISS Lyapunov function.
Note that our definition of an ISS Lyapunov function corresponds to the one of a “coercive ISS Lyapunov function in dissipative form” in the literature, [18]. By [3, Thm. 1], see also [18, Thm. 2.18], the existence of an (L)ISS Lyapunov implies (L)ISS for a large class of control systems which, in particular, have to satisfy the “boundedness-implies-continuation” property (BIC). System (\(\varSigma _{SLD}\)) with an admissible feedback function and continuous, or, more generally, piecewise continuous disturbances d belongs to this class, which allows to infer (L)ISS from the existence of a Lyapunov function. To see this, note in particular that the (BIC) property is satisfied by classical results on semilinear equations, [1, Prop. 4.3.3] or [21, Thm. 6.1.4].In the following, we will infer ISS by constructing Lyapunov functions.
Theorem 9
Suppose that there exists \(\alpha >0\) such that \(\Vert T(t)\Vert \le \mathrm {e}^{-\alpha t}\) for all \(t>0\) and let \(\sigma \) be an admissible feedback function. Then, the function
is an ISS Lyapunov function for (\(\varSigma _{SLD}\)) with respect to \(C(0,\infty ;U)\) and System (\(\varSigma _{SLD}\)) is ISS with respect to \(C(0,\infty ;U)\).
Proof
Let \(x\in C(0,t_1;X)\) be the mild solution of (\(\varSigma _{SLD}\)) with initial value \(x_0\in D(A)\) and disturbance \(d\in C(0,\infty ;U)\). Let \(y\in C(0,t_2;X)\) be the mild solution of the system
with \(\tilde{d}\in C(0,\infty ;U)\) and \(y_0\in X\). Then there exists an \(r>0\) such that
because x, y, d and \(\tilde{d}\) are continuous. Thus, we have for \(t\in [0,\min \{t_1,t_2\})\)
Applying Gronwall’s inequality yields
Let us for a moment assume that d is Lipschitz continuous with Lipschitz constant L. We will prove that x is right differentiable. For \(0<h<t_1-t\), we can write \(x(t+h)\) in the form
Thus, x at time \(t+h\) equals the mild solution y of
at time t. Hence, by (8) we obtain
Note that
converges to \(Ax_0-B\sigma \big (B^*x_0+d(0)\big )\) as \(h\searrow 0\) since \(x_0\in D(A)\) and \(\sigma \), x and d are continuous. Therefore, by (10), we deduce
By the definition of the mild solution, we have that
Again by continuity of \(\sigma \), x and d, we have that
Combining this with (11) shows that
which means that x(t) is an element of the Favard space of the semigroup, and because X is reflexive, we can conclude that \(x(t)\in D(A)\), [4, Cor. II.5.21]. This implies that x is right differentiable at t with
As \(V(x) = \Vert x\Vert ^2\), we hence obtain for the Dini derivative
that
where we used that \(-\mathfrak {R}\langle \sigma (B^{*}x),B^{*}x\rangle \le 0\) by Property (i) and (ii) of admissible feedback functions and the local Lipschitz condition for \(\sigma \). By [2, Cor. A.5.45], we obtain
From (8), we derive
and therefore, the mild solution of (\(\varSigma _{SLD}\)) depends continuously on the initial data and the disturbance. Hence, by understanding \(x(t+h)\) again as the solution of (9) at time t, (13) holds for all \(x_0\in X\) and \(d\in C(0,\infty ;U)\) which leads to
for all \(x_{0}\in X\), \(d\in C(0,\infty ;U)\) and \(\varepsilon >0\). Choosing \(\varepsilon <2\alpha \), this shows that V is an ISS-Lyapunov function for (\(\varSigma _{SLD}\)) which implies that (\(\varSigma _{SLD}\)) is ISS by [18, Thm. 2.18]. \(\square \)
Remark 10
-
(i)
Recall that the semigroup generated by A in Theorem 7 was not exponentially stable. Theorem 9 shows that this is not accidental.
-
(ii)
Note that the assumption on the semigroup made in Theorem 9 is strictly stronger than the condition that \((T(t))_{t\ge 0}\) is an exponentially stable contraction semigroup as can be seen e.g. for a nilpotent shift semigroup on \(X=L^{2}(0,1)\). It is a simple consequence of the Lumer–Phillips theorem that the following assertions are equivalent for a semigroup \((T(t))_{t\ge 0}\) generated by A and some constant \(\omega >0\).
-
(a)
\(\mathfrak {R}\langle Ax,x\rangle \le -\omega \Vert x\Vert ^{2}\) all \(x\in D(A)\).
-
(b)
\(\sup _{t>0}\Vert e^{\omega t}T(t)\Vert \le 1\).
-
(c)
\(P=\frac{1}{\omega } I\) solves \(\mathfrak {R}\langle Ax,Px\rangle \le -\langle x,x\rangle \), for all \(x\in D(A)\).
However, we also remark that the above condition is satisfied for a large class of examples, such as in the case when A is a normal operator.
-
(a)
-
(iii)
It is natural to ask whether Theorem 9 holds when A is merely assumed to generate an exponentially stable semigroup. However, it is unclear how to use the structural assumptions on \(\sigma \) in the general case. On the other hand, the assumption on the semigroup in Theorem 9 implies that \(P=I\) satisfies (3) in Proposition 5(ii).
-
(iv)
An inspection of the proof shows that Theorem 9 can be generalized to piecewise continuous or regulated functions \(d:[0,\infty )\rightarrow U\).
Locally linear admissible feedback functions yield LISS Lyapunov functions.
Theorem 11
Let (\(\varSigma _L\)) be UGAS with \(M,\omega >0\) such that \(\Vert {\widetilde{T}}(t)\Vert \le M\mathrm {e}^{-\omega t}\) for all \(t\ge 0\) and let \(\sigma \) be an admissible feedback function with \(\sigma (u) = u\) for all \(\Vert u\Vert _U\le \delta \) and some \(\delta >0\). Then, (\(\varSigma _{SLD}\)) is LISS with Lipschitz continuous LISS Lyapunov function \(V(x):=\max _{s\ge 0}\Vert \mathrm {e}^{\frac{\omega }{2} s}{\widetilde{T}}(s)x\Vert _X\).
Proof
Let \(\Vert x_0\Vert _X\le \Vert B\Vert ^{-1}\delta \) and \(r:=\max \{\Vert B^*x(s)\Vert _U,\Vert B^*x(s)+d(s)\Vert _U \mid s\in [0,t]\}\) for some \(t>0\). We can rewrite (\(\varSigma _{SLD}\)) in the form
Hence, the mild solution satisfies
Denoting the integral by \(I_{h}\), we have
where the continuity of x, the Lipschitz continuity of \(\sigma \) as well as the condition \(\sigma (u)=u\) if \(\Vert u\Vert \le \delta \) have been used.
With \(\Vert x\Vert \le V(x)\le M\Vert x\Vert \) and \(V\big ({\widetilde{T}}(t)x\big ) \le \mathrm {e}^{-\frac{\omega }{2} t}V(x)\) for all \(x\in X\) we obtain
for every \(\varepsilon >0\). The Lipschitz continuity of V follows from
for all \(x,y\in X\). Applying [17, Theorem 4] yields local input-to-state stability of (\(\varSigma _{SLD}\)). \(\square \)
Note that Property (iii) of Definition 1 has not been used in the proof of Theorem 11.
3 Conclusion
In this note we have continued the study of ISS for saturated feedback connections of linear systems. Theorem 7 states that ISS cannot be concluded from uniform exponential stability of the unsaturated closed-loop and stability of the (undisturbed) open-loop linear system
(i.e. the semigroup generated by A is bounded). However, the conclusion does hold under more assumptions on A; namely, that \(\mathfrak {R}\langle Ax,x\rangle \le -\alpha \Vert x\Vert ^{2}\) for some \(\alpha >0\) and all \(x\in D(A)\), see Theorem 9. The latter property can be seen as some kind of quasi-contractivtiy of the semigroup combined with exponential stability. This condition seems to be crucial for the proof, see Remark 10. The question remains whether the result could be generalized to more general semigroups, e.g. such as contractive semigroups which are exponentially stable, but do not satisfy the above mentioned quasi-contractivity. Note, however, that the assumption that A generates a contraction semigroup seems to be essential to employ dissipativity of the nonlinear system.
Another task for future research is the step towards unbounded operators B, prominently appearing in boundary control systems. As our techniques and also the ones used in existing results for ISS on saturated systems seem to heavily rely on the boundedness of B, this may require a different approach or more structural assumptions on A.
Change history
05 February 2021
A Correction to this paper has been published: https://doi.org/10.1007/s00498-021-00278-y
Notes
A careful look at the proof reveals that the continuity of the nonlinearity in t required in [21, Thm. 6.1.2] can be dropped in our setting.
References
Cazenave T, Haraux A (1998) An introduction to semilinear evolution equations, Oxford Lecture Series in Mathematics and its Applications, vol 13. The Clarendon Press, Oxford University Press, New York
Curtain R, Zwart H (2020) Introduction to infinite-dimensional systems theory: a state-space approach, Texts in applied mathematics, vol 71. Springer, New York, NY
Dashkovskiy S, Mironchenko A (2013) Input-to-state stability of infinite-dimensional control systems. Math Control Signals Syst 25(1):1–35
Engel KJ, Nagel R (2000) One-parameter semigroups for linear evolution equations, Graduate Texts in Mathematics, vol 194. Springer, New York. With contributions by S. Brendle, M. Campiti, T. Hahn, G. Metafune, G. Nickel, D. Pallara, C. Perazzoli, A. Rhandi, S. Romanelli and R. Schnaubelt
Grüne L (1999) Input-to-state stability of exponentially stabilized semilinear control systems with inhomogeneous perturbations. Syst Control Lett 38(1):27–35
Guiver C, Logemann H (2020) A circle criterion for strong integral input-to-state stability. Automatica J IFAC 111:108641
Guiver C, Logemann H, Opmeer MR (2019) Infinite-dimensional Lur’e systems: input-to-state stability and convergence properties. SIAM J Control Optim 57(1):334–365
Jacob B, Mironchenko A, Partington JR, Wirth F (2019) Non-coercive Lyapunov functions for input-to-state stability of infinite-dimensional systems. arXiv: 1911.01327
Jacob B, Nabiullin R, Partington JR, Schwenninger F (2018) Infinite-dimensional input-to-state stability and Orlicz spaces. SIAM J Control Optim 56(2):868–889
Lasiecka I, Seidman T (2003) Strong stability of elastic control systems with dissipative saturating feedback. Syst Control Lett 48:243–252
Marx S, Andrieu V, Prieur C (2017) Cone-bounded feedback laws for \(m\)-dissipative operators on Hilbert spaces. Math Control Signals Syst 29(4), Art. 18, 32
Marx S, Cerpa E, Prieur C, Andrieu V (2015) Stabilization of a linear Korteweg-de Vries equation with a saturated internal control. In: 14th annual European Control Conference (ECC15). Linz, Austria
Marx S, Cerpa E, Prieur C, Andrieu V (2016) Global stabilization of a Korteweg-de Vries equation with a distributed control saturated in \(L_2\)-norm. In: 10th IFAC symposium on nonlinear control systems (NOLCOS 2016). Monterey, CA, USA
Marx S, Cerpa E, Prieur C, Andrieu V (2017) Global stabilization of a Korteweg-de Vries equation with saturating distributed control. SIAM J Control Optim 55(3):1452–1480
Marx S, Chitour Y, Prieur C (2018) Stability results for infinite-dimensional linear control systems subject to saturations. In: 16th European control conference (ECC 2018). Limassol, Cyprus
Marx S, Chitour Y, Prieur C (2020) Stability analysis of dissipative systems subject to nonlinear damping via lyapunov techniques. IEEE Trans Autom Control 65(5):2139–2146
Mironchenko A (2016) Local input-to-state stability: characterizations and counterexamples. Syst Control Lett 87:23–28
Mironchenko A, Prieur C (2019) Input-to-state stability of infinite-dimensional systems: recent results and open questions. arXiv: 1910.01714
Mironchenko A, Wirth F (2018) Characterizations of input-to-state stability for infinite-dimensional systems. IEEE Trans Automat Control 63(6):1602–1617
Mironchenko A, Wirth F (2018) Lyapunov characterization of input-to-state stability for semilinear control systems over Banach spaces. Syst Control Lett 119:64–70
Pazy A (1983) Semigroups of linear operators and applications to partial differential equations, Applied Mathematical Sciences, vol 44. Springer, New York
Prieur C, Tarbouriech S, Gomes da Silva JM (2016) Wave equation with cone-bounded control laws. IEEE Trans Automat Control 61(11):3452–3463
Schwenninger FL (2020) Input-to-state stability for parabolic boundary contrl: Linear and semi-linear systems. In: Kerner J, Laasri H, Mugnolo D (eds) Control theory of infinite-dimensional systems. Birkhäuser, 83–116
Seidman TI, Li H (2001) A note on stabilization with saturating feedback. Discrete Contin Dyn Syst 7(2):319–328
Slemrod M (1989) Feedback stabilization of a linear control system in Hilbert space with an a priori bounded control. Math Control Signals Syst 2(3):265–285
Webb GF (1972) Continuous nonlinear perturbations of linear accretive operators in Banach spaces. J Funct Anal 10:191–203
Acknowledgements
The authors thank Hans Zwart for fruitful discussions on the proof of Proposition 6 during a visit of the third author at the University of Twente.
Funding
Open Access funding provided by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Jacob, B., Schwenninger, F.L. & Vorberg, L.A. Remarks on input-to-state stability of collocated systems with saturated feedback. Math. Control Signals Syst. 32, 293–307 (2020). https://doi.org/10.1007/s00498-020-00264-w
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00498-020-00264-w