Hostname: page-component-76fb5796d-qxdb6 Total loading time: 0 Render date: 2024-04-25T19:58:20.251Z Has data issue: false hasContentIssue false
  • English
  • Français

On some threshold-one attractive interacting particle systems on homogeneous trees

Part of: Special processes

Published online by Cambridge University Press:  04 September 2020

Y. X. Mu  and
Y. Zhang
Y. X. Mu*
Affiliation:
Peking University
Y. Zhang*
Affiliation:
Peking University
*
*Postal address: School of Mathematical Sciences, Peking University, Beijing 100871, P. R. China. Email address: muyingxin@pku.edu.cn
*Postal address: School of Mathematical Sciences, Peking University, Beijing 100871, P. R. China. Email address: muyingxin@pku.edu.cn
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider the threshold-one contact process, the threshold-one voter model and the threshold-one voter model with positive spontaneous death on homogeneous trees 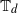$\mathbb{T}_d$ , 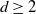$d\ge 2$ . Mainly inspired by the corresponding arguments for the contact process, we prove that the complete convergence theorem holds for these three systems under strong survival. When the system survives weakly, complete convergence may also hold under certain transition and/or initial conditions.

Keywords

Complete convergence theoremthreshold-one processeshomogeneous trees

MSC classification

Primary: 60K35: Interacting random processes; statistical mechanics type models; percolation theory
Type
Research Papers
Information
Journal of Applied Probability , Volume 57 , Issue 3 , September 2020 , pp. 866 - 898
Check for updates
Copyright
© Applied Probability Trust 2020

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aizenman, M. andJung, P. (2007). On the critical behavior at the lower phase transition of the contact process. ALEA, Lat. Am. J. Probab. Math. Stat. 3, 301–320.Google Scholar
Andjel, E. D., Liggett, T. M. andMountford, T. (1992). Clustering in one-dimensional threshold voter models. Stoch. Process. Appl. 42, 73–90.10.1016/0304-4149(92)90027-NCrossRefGoogle Scholar
Bramson, M., Ding, W. D. andDurrett, R. (1991). Annihilating branching processes. Stoch. Process. Appl. 37, 1–17.10.1016/0304-4149(91)90056-ICrossRefGoogle Scholar
Cox, J. T. andDurrett, R. (1991). Nonlinear voter models. In Random Walks, Brownian Motion, and Interacting Particle Systems. Birkhäuser, Boston, pp. 189–201.10.1007/978-1-4612-0459-6_8CrossRefGoogle Scholar
Cranston, M., Mountford, T., Mourrat, J. C. andValesin, D. (2014). The contact process on finite homogeneous trees revisited. ALEA, Lat. Am. J. Probab. Math. Stat. 11, 385–408.Google Scholar
Durrett, R. (2010). Probability: Theory and Examples, 4th edn. Cambridge University Press.10.1017/CBO9780511779398CrossRefGoogle Scholar
Durrett, R. andSchinazi, R. (1995). Intermediate phase for the contact process on a tree. Ann. Prob. 23, 668–673.10.1214/aop/1176988283CrossRefGoogle Scholar
Griffeath, D. (1978). Limit theorems for nonergodic set-valued Markov processes. Ann. Prob. 6, 379–387.10.1214/aop/1176995524CrossRefGoogle Scholar
Handjani, S. J. (1999). The complete convergence theorem for coexistent threshold voter models. Ann. Prob. 27, 226–245.10.1214/aop/1022677260CrossRefGoogle Scholar
Lalley, S. P. (1999). Growth profile and invariant measures for the weakly supercritical contact process on a homogeneous tree. Ann. Prob. 27, 206–225.10.1214/aop/1022677259CrossRefGoogle Scholar
Liggett, T. M. (1985). Interacting Particle Systems. Springer, New York.10.1007/978-1-4613-8542-4CrossRefGoogle Scholar
Liggett, T. M. (1995). Improved upper bounds for the contact process critical value. Ann. Prob. 23, 697–723.10.1214/aop/1176988285CrossRefGoogle Scholar
Liggett, T. M. (1996). Multiple transition points for the contact process on the binary tree. Ann. Prob. 24, 1675–1710.Google Scholar
Liggett, T. M. (1999). Stochastic Interacting Systems: Contact, Voter and Exclusion Processes. Springer, Berlin.10.1007/978-3-662-03990-8CrossRefGoogle Scholar
Louidor, O., Tessler, R. andVandenberg-Rodes, A. (2014). The Williams–Bjerknes model on regular trees. Adv. Appl. Prob. 24, 1889–1917.10.1214/13-AAP966CrossRefGoogle Scholar
Morrow, G. J., Schinazi, R. B. andZhang, Y. (1994). The critical contact process on a homogeneous tree. J. Appl. Prob. 31, 250–255.10.2307/3215251CrossRefGoogle Scholar
Mountford, T. andSchonmann, R. H. (2009). The survival of large-dimensional threshold contact processes. Ann. Prob. 37, 1483–1501.10.1214/08-AOP440CrossRefGoogle Scholar
Pemantle, R. (1992). The contact process on trees. Ann. Prob. 20, 2089–2116.10.1214/aop/1176989541CrossRefGoogle Scholar
Penrose, M. D. (1996). The threshold contact process: a continuum limit. Prob. Theory Relat. Fields 104, 77–95.10.1007/BF01303804CrossRefGoogle Scholar
Salzano, M. andSchonmann, R. H. (1998). A new proof that for the contact process on homogeneous trees local survival implies complete convergence. Ann. Prob. 26, 1251–1258.Google Scholar
Stacey, A. (2001). The contact process on finite homogeneous trees. Prob. Theory Relat. Fields 121, 551–576.10.1007/s004400100149CrossRefGoogle Scholar
Stacey, A. M. (1996). The existence of an intermediate phase for the contact process on trees. Ann. Prob. 24, 1711–1726.Google Scholar
Xue, X. F. (2015). Asymptotic behavior of critical infection rates for threshold-one contact processes on lattices and regular trees. J. Theoret. Prob. 28, 1447–1467.10.1007/s10959-014-0544-1CrossRefGoogle Scholar
Xue, X. F. (2016). Convergence rates for subcritical threshold-one contact processes on lattices. J. Statist. Phys. 162, 371–386.10.1007/s10955-015-1419-2CrossRefGoogle Scholar
Zhang, Y. (1996). The complete convergence theorem of the contact process on trees. Ann. Prob. 3, 1408–1443.10.1214/aop/1065725187CrossRefGoogle Scholar
Ziezold, H. andGrillenberger, C. (1988). On the critical infection rate of the one-dimensional basic contact process: numerical results. J. Appl. Prob. 25, 1–8.10.2307/3214228CrossRefGoogle Scholar