An Improved Tobit Kalman Filter with Adaptive Censoring Limits

Abstract

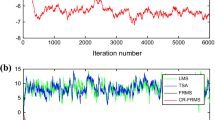
This paper deals with the Tobit Kalman filtering (TKF) process when the measurements are correlated and censored. The case of interval censoring, i.e., the case of measurements which belong to some interval with given censoring limits, is considered. Two improvements of the standard TKF process are proposed, in order to estimate the hidden state vectors. Firstly, the exact covariance matrix of the censored measurements is calculated by taking into account the censoring limits. Secondly, the probability of a latent (normally distributed) measurement to belong in or out of the uncensored region is calculated by taking into account the Kalman filter residual. The designed algorithm is tested using both synthetic and real data sets. The real data set includes human skeleton joints’ coordinates captured by the Microsoft Kinect II sensor. In order to cope with certain real-life situations that cause problems in human skeleton tracking, such as (self)-occlusions, closely interacting persons, etc., adaptive censoring limits are used in the proposed TKF process. Experiments show that the proposed method outperforms other filtering processes in minimizing the overall root-mean-square error for synthetic and real data sets.

Appendices

Appendix A: The Censored Mean Value

In what follows, the proof of Proposition 2 is provided:

Proof of Proposition 2, Sect. 3.3

For a discrete random variable $z_i \sim B(p_i)$ (Bernoulli distribution) in Lemma 1, it is derived that

$$\begin{aligned} {{\,\mathrm{\mathbb {E}}\,}}(x,z_i) = {{\,\mathrm{\mathbb {E}}\,}}(x|z_i=1)\cdot p_i. \end{aligned}$$

(42)

The censored measurement, $y_i$, can be written in terms of Bernoulli distributions; therefore, the censored mean value is written by (42) as,

$$\begin{aligned} {{\,\mathrm{\mathbb {E}}\,}}(y_i)=\sum _{j=1}^{3^{n-1}}\!{{\,\mathrm{\mathbb {E}}\,}}(y^*_i|a_i<y^*_i<b_i, R_j)P((a_i,b_i),R_j)+ a_iP(y^*_i\le a_i)+b_iP(y^*_i \ge b_i), \qquad \end{aligned}$$

(43)

where the first term is the sum of all possible mean values of ${{\,\mathrm{\mathbb {E}}\,}}(y_i|a_i<y_i<b_i)$ given that the rest variables lie in a region $R_j = [(L_1,U_1),\ldots ,(L_{i-1},U_{i-1}),(L_{i+1},U_{i+1}),\ldots ,(L_n,U_n)]$, where

$$\begin{aligned} (L_k,U_k)= {\left\{ \begin{array}{ll} (-\infty ,a_k) \quad or\\ (a_k, b_k) \quad \; \; \; or\\ (b_k, \infty ) \end{array}\right. } \end{aligned}$$

where j=1,...,$3^{n-1}$. $P((a_i,b_i),R_j)$ denotes the probability of variable $\mathbf{y }^*$ to lie in a region $[(a_i,b_i),R_j].$ It is derived by (5) that

$$\begin{aligned} \begin{aligned} {{\,\mathrm{\mathbb {E}}\,}}(y_i)&= \sum _{j=1}^{3^{n-1}}\Big (\mu _i + \sum _{k=1}^n \sigma _{i,k}\big (F_{k}(L_k)-F_{k}(U_k)\big )_{R_j} \Big )P(R_j)+ a_iP(y^*_i\le a_i)\\&\quad + b_iP(y^*_i \ge b_i)\\&= \sum _{k=1}^n\sum _{j=1}^{3^{n-1}}\sigma _{i,k}\big (F_{k}(L_k)-F_{k}(U_k)\big )_{R_j}P(R_j)+\mu _iP(a_i<y^*_i<b_i)\\&\quad + a_iP(y^*_i\le a_i) + b_iP(y^*_i \ge b_i), \end{aligned} \end{aligned}$$

(44)

where $\big (F_{k}(L_k)-F_{k}(U_k)\big )_{R_j}$ is the difference of functions (6) given that the variable $\mathbf{y }^*$ lies in the region $R_j \cup (a_i,b_i)$. In the case where $k \ne i$, it is derived that:

$$\begin{aligned} \sum _{j=1}^{3^{n-1}}\sigma _{i,k}\big (F_{k}(L_k)-F_{k}(U_k)\big )_{R_j}P(R_j)= & {} \sum _{j=1}^{3^{n-2}}\sigma _{i,k}\big (F_{k}(-\infty )-F_{k}(a_k)\big )_{V_j}P(V_j)\nonumber \\&+\sum _{j=1}^{3^{n-2}}\sigma _{i,k}\big (F_{k}(a_k)-F_{k}(b_k)\big )_{V_j}P(V_j)\nonumber \\&+\sum _{j=1}^{3^{n-2}}\sigma _{i,k}\big (F_{k}(b_k)-F_{k}(\infty )\big )_{V_j}P(V_j)=0, \nonumber \\ \end{aligned}$$

(45)

where $V_j$ is the region

$$\begin{aligned}{}[(L_1,U_1),\ldots ,(L_{k-1},U_{k-1}),(L_{k+1},U_{k+1}),\ldots ,(a_i,b_i),\ldots ,(L_n,U_n)]. \end{aligned}$$

In the case where $k = i$, it is derived that,

$$\begin{aligned}&\sum _{j=1}^{N}\sigma _{i,k}\big (F_{k}(L_k)-F_{k}(U_k)\big )_{R_j}P(R_j)\nonumber \\&\quad \begin{aligned}&=\sum _{j=1}^{N}\sigma _{i,i}\big (F_{i}(a_i)-F_{i}(b_i)\big )_{R_j}P(R_j)\\&=\sigma _{i,i}\big (f_{i}(a_i)-f_{i}(b_i)\big ), \end{aligned} \end{aligned}$$

(46)

where $f_i(y^*_i)$ is the normal distribution of $y^*_i \sim N(\mu _i, \sigma _{i,i})$. Thus, by (44)-(46) arises

$$\begin{aligned} {{\,\mathrm{\mathbb {E}}\,}}(y_i)=\mu _iP(a_i<y^*_i<b_i) + \sigma _{i,i}(f_i(a_i)-f_i(b_i)) +a_iP(y^*_i\le a_i) + b_iP(y^*_i \ge b_i). \nonumber \\ \end{aligned}$$

(47)

$\square$

Appendix B: The Censored Covariance Matrix

In what follows, the proof of Proposition 3 is provided:

Proof of Proposition 3, Sect. 3.3

In the same way as for the censored mean (“Appendix A”), it is proved that the second moment of $y_i$ depends on the censoring limits {$a_i$, $b_i$}. Therefore, it is derived by Lemma 1 that

$$\begin{aligned} \begin{aligned} {{\,\mathrm{\mathbb {E}}\,}}\big (y_i^2\big ) = {{\,\mathrm{\mathbb {E}}\,}}(y^{*2}_i|a_i<y^*_i<b_i)P(a_i<y^*_i<b_i) + a^2_iP(y^*_i \le a_i) + b^2_iP(y^*_i \ge b_i), \end{aligned} \end{aligned}$$

where the first term [31] is equal with

$$\begin{aligned} \begin{aligned} {{\,\mathrm{\mathbb {E}}\,}}(y^{*2}_i|a_i<y^*_i<b_i)&= \sigma _{i,i} + \mu _i^2 + 2\mu _i\sigma _{i,i}\frac{f_i(a_i)-f(b_i) }{P(a_i<y^*_i<b_i)} \\&\quad +\sigma _{i,i}\frac{(a_i-\mu _i)f_i(a_i)- (b_i-\mu _i)f_i(b_i) }{P(a_i<y^*_i<b_i)}. \end{aligned} \end{aligned}$$

(48)

Therefore, it is derived by (48) that,

$$\begin{aligned} \begin{aligned} {{\,\mathrm{\mathbb {E}}\,}}\big (y_i^2\big )&= (\sigma _{i,i} + \mu _i^2)P(a_i<y^*_i<b_i) \\&\quad + \sigma _{i,i}\big ((a_i-\mu _i)f_i(a_i)- (b_i-\mu _i)f_i(b_i)\big )\\&\quad + 2\mu _i\sigma _{i,i}(f_i(a_i)-f(b_i)) + a^2_iP(y^*_i \le a_i) + b^2_iP(y^*_i \ge b_i). \end{aligned} \end{aligned}$$

(49)

Finally, the censored variance is given by

$$\begin{aligned} \begin{aligned} Var(y_i)&= \mu _i^2(1-P_{un}^i)P_{un}^i + \sigma _{i,i}P_{un}^i + a^2_i(1-P_{a}^i)P_{a}^i \\&\quad + b^2_i(1-P_{b}^i)P_{b}^i-2a_ib_iP_{a}^iP_{b}^i - \sigma _{i,i}^2(f(a_i)-f(b_i))\\&\quad +2\mu _i\sigma _{i,i}(f_i(a_i)-f(b_i))(1-P_{un}^i)\\&\quad +\sigma _{i,i}\big ((a_i-\mu _i)f_i(a_i)- (b_i-\mu _i)f_i(b_i)\big ) \\&\quad -2\Big ( \mu _iP_{un}^i + \sigma _{i,i}\big (f_i(a_i)-f(b_i)\big )\Big )\Big (a_iP_{a}^i + b_iP_{b}^i \Big ),\\ \end{aligned} \end{aligned}$$

(50)

where $P_{un}^i = P(a_i<y^*_i<b_i)$, $P_{a}^i= P(y^*_i \le a_i)$ and $P_{b}^i = P(y^*_i \ge b_i)$.

The expectation value of $y_i \cdot y_j$ is written by Lemma 1 as:

$$\begin{aligned} \begin{aligned} {{\,\mathrm{\mathbb {E}}\,}}(y_{i}y_{j})&=a_ib_j P(1) +b_ib_j P(3) + a_ia_jP(7) + b_ia_jP(9)\\&\quad + b_j\sum _{k=1}^{3^{n-2}}{{\,\mathrm{\mathbb {E}}\,}}(y^*_{i}|a_i< y^*_{i}<b_i, y^*_j \ge b_j, G_{k})P(G_{k})\\&\quad + a_i\sum _{k=1}^{3^{n-2}}{{\,\mathrm{\mathbb {E}}\,}}(y^*_{j}|a_j< y^*_{j}<b_j, y^*_i \le a_i, G_{k})P(G_{k})\\&\quad +\sum _{k=1}^{3^{n-2}}{{\,\mathrm{\mathbb {E}}\,}}(y_{i}y^*_{j}|a_i< y^*_{i}< b_i, a_j< y^*_{j}<b_j, G_{k})P(G_{k})\\&\quad + b_i\sum _{k=1}^{3^{n-2}}{{\,\mathrm{\mathbb {E}}\,}}(y^*_{j}|a_j< y^*_{j}<b_j, y^*_i \ge b_i, G_{k})P(G_{k})\\&\quad + a_j\sum _{k=1}^{3^{n-2}}{{\,\mathrm{\mathbb {E}}\,}}(y^*_{i}|a_i< y^*_{i} <b_i, y^*_j \le a_j, G_{k})P(G_{k}),\\ \end{aligned} \end{aligned}$$

(51)

where

$$\begin{aligned} \begin{aligned}&P(1)= P(y^*_i\le a_i, y^*_j\ge b_j),P(3)= P(y^*_i\ge b_i, y^*_j\ge b_j),\\&P(7)= P(y^*_i\le a_i, y^*_j\le a_j), P(9)= P(y^*_i\ge b_i, y^*_j\le a_j), \end{aligned} \end{aligned}$$

and $G_k$ for $k=1,\ldots ,3^{n-2}$ denote a region (as in the case of the censored mean) where the multi-variable, $\mathbf{y }^*_{-i-j}$, lies on.

Concerning the last five terms of (51), it is proved (as in case of second moment) that they depend only on the censoring limits {$a_i$, $b_i$, $a_j$, $b_j$}; thus, (51) can be written as

$$\begin{aligned} \begin{aligned} {{\,\mathrm{\mathbb {E}}\,}}(y_{i}y_{j})&=a_ib_j P(1) +b_ib_j P(3) + a_ia_jP(7) + b_ia_jP(9)\\&\quad + b_j{{\,\mathrm{\mathbb {E}}\,}}(y^*_{i}|a_i< y^*_{i}<b_i, y^*_j \ge b_j)P(2)\\&\quad + a_i{{\,\mathrm{\mathbb {E}}\,}}(y^*_{j}|a_j< y^*_{j}<b_j, y^*_i \le a_i)P(4)\\&\quad +{{\,\mathrm{\mathbb {E}}\,}}(y^*_{i}y^*_{j}|a_i< y^*_{i}< b_i, a_j< y^*_{j}<b_j)P(5)\\&\quad + b_i{{\,\mathrm{\mathbb {E}}\,}}(y^*_{j}|a_j< y^*_{j}<b_j, y^*_i \ge b_i)P(6)\\&\quad + a_j{{\,\mathrm{\mathbb {E}}\,}}(y^*_{i}|a_i< y^*_{i} <b_i, y^*_j \le a_j)P(8),\\ \end{aligned} \end{aligned}$$

(52)

where

$$\begin{aligned} \begin{aligned}&P(2)= P(a_i<y^*_i< b_i, y^*_j\ge b_j),\\&P(4)= P(y^*_i\le a_i, a_j<y^*_j<b_j),\\&P(5)= P(a_i<y^*_i<b_i, a_j<y^*_j< b_j),\\&P(6)= P(y^*_i\ge b_i, a_j<y^*_j< b_j),\\&P(8)= P(a_i<y^*_i< b_i, y^*_j\le a_j). \end{aligned} \end{aligned}$$

At this point, it should be noted that the truncated moments ${{\,\mathrm{\mathbb {E}}\,}}(y^*_{i}|\cdot )$ and ${{\,\mathrm{\mathbb {E}}\,}}(y^*_{i}y^*_{j}|\cdot )$ in (52) are calculated by (5) and (5), respectively. Although the functions (6), (7) in our case (censoring measurements) are defined only for the variables $y^*_i$ and $y^*_j$, i.e.,:

$$\begin{aligned} F_i(x)=\frac{\int _{a_j}^{b_j}f_{Y^*_i,Y^*_j}(x,y^*_j)dy^*_{j}}{P(a_j<y^*_j<b_j, a_i<y^*_i<b_i)}, \end{aligned}$$

and

$$\begin{aligned} F_{i,j}(x,y)=\frac{f_{Y^*_i,Y^*_j}(x,y)}{P(a_j<y^*_j<b_j, a_i<y^*_i<b_i)}. \end{aligned}$$

Therefore, the covariance matrix can be defined by the terms (47), (50) and (52). $\square$

Appendix C: Evaluation of the Probabilities of the Latent Measurement to Belong to the Censored or Uncensored Region

In what follows, the proofs for (13)–(15) are provided.

The mean of the latent measurement $\mathbf{y }^*_{k}$ given the saturated measurement $\mathbf{y }_{k-1}$ is

$$\begin{aligned} \mathbf{m }_k={{\,\mathrm{\mathbb {E}}\,}}(\mathbf{H }_k\mathbf{x }_k+\mathbf{v }_k|\mathbf{y }_{k-1})=\mathbf{H }_k{{\,\mathrm{\mathbb {E}}\,}}(\mathbf{x }_k|\mathbf{y }_{k-1})=\mathbf{H }_k\hat{\mathbf{x }}^-_{k}. \end{aligned}$$

(53)

The covariance matrix of $\mathbf{y }^*_{k}-\mathbf{H }_k\hat{\mathbf{x }}^-_{k}$ is

$$\begin{aligned} \begin{aligned} \mathbf{S }_k=\mathrm {Cov}(\mathbf{y }^*_{k}-\mathbf{H }_k\hat{\mathbf{x }}^-_{k})&=\mathrm {Cov}(\mathbf{H }_k\mathbf{x }_k+\mathbf{v }_k-\mathbf{H }_k\hat{\mathbf{x }}^-_{k})\\&=\mathrm {Cov}\big (\mathbf{H }_k(\mathbf{x }_k-\hat{\mathbf{x }}^-_{k}))+\mathrm {Cov}(\mathbf{v }_k) \end{aligned} \end{aligned}$$

thus,

$$\begin{aligned} \mathbf{S }_{k}=\mathbf{H }_k\mathbf{P }^-_{k}\mathbf{H }_k^T+\mathbf{R }_k. \end{aligned}$$

(54)

By (53) and (54), it is clear that $\mathbf{y }^*_{k}|\mathbf{y }_{k-1}\sim ~N(\mathbf{m }_k, \mathbf{S }_k)$. The probability $P^i_{\mathbf{a },k}$ of the $i{\mathrm{th}}$ component of the latent measurement $\mathbf{y }^*_k$ to be equal or less than $a_i$ is

$$\begin{aligned} P^i_{\mathbf{a },k}= P( y^*_{k,i}\le a_i )= & {} P\Bigg (\frac{y^*_{k,i}-m_{k,i}}{\sqrt{s_{(i,i),k}}}\le \frac{a_i-m_{k,i}}{\sqrt{s_{(i,i),k}}} \Bigg ) \nonumber \\= & {} \varPhi \Bigg ( \frac{a_i-m_{k,i}}{\sqrt{s_{(i,i),k}}} \Bigg ). \end{aligned}$$

(55)

Following the same procedure, the probability $P^i_{\mathbf{b },k}$ of the $i{\mathrm{th}}$ component of the latent measurement $\mathbf{y }^*_k$ to be equal or bigger than $b_i$ is

$$\begin{aligned} P^i_{\mathbf{b },k}=1-\varPhi \Bigg ( \frac{b_i-m_{k,i}}{\sqrt{s_{(i,i),k}}} \Bigg ). \end{aligned}$$

(56)

Finally, the probability of the $i{\mathrm{th}}$ component of the latent measurement $\mathbf{y }^*_k$ to lie in the uncensored region $(a_i, b_i)$ is

$$\begin{aligned} P^i_{un,k}=1-P^i_{\mathbf{a },k}-P^i_{\mathbf{b },k} . \end{aligned}$$

(57)

$\square$