Modelling and parameter identification of steel–concrete composite beams in 3D rigid finite element method

Abstract

This study presents spatial vibration modelling of steel–concrete composite beams. Structures of this type are commonly used as elements of composite floors and primary carrying girders in bridge structures. Two-dimensional models used to date did not enable analysis of all eigenmodes, specifically torsional, flexural horizontal, and distortional. A discrete computational model was developed in the convention of the rigid finite element method, the so-called RFEM model. It was assumed that the concrete slab and the steel I-section would be modelled separately. This approach realistically reflects the actual performance of the connection, comprising studs connecting the concrete slab and the steel section. The model was used to analyse two steel–concrete composite beams with different connector spacings. The paper presents the results of experiments conducted on the two composite beams. Their dynamic characteristics, including frequency and vibration modes, were determined with impulse response methods. Based on experimental research, identification of connection parameters with substitute longitudinal moduli of elasticity of reinforced concrete was conducted. A comparison of experimental results with those calculated with the model confirmed their good agreement.

1 Introduction

A composite element is created when two or more construction elements, made of materials of different properties, are permanently connected. An example of such a structure is a steel–concrete composite beam. The concept of composite beams is understood as an element comprising a (rolled or welded) steel section with a reinforced concrete slab resting on it (Fig. 1). Steel connecting elements welded to the upper flange of the steel I-section before the concrete slab is casted enable cooperation of both components. Beams of this type are often used in floors in civil engineering, and as primary carrying girders in bridge structures.

Fig. 1

Steel–concrete composite beam—general arrangement

One of the major components of the sustainable development is durability and reliability of both designed and already existing structures. One of the particularly susceptible example are Bridges which are exposed to environmental conditions. The object is often located on hardly accessible grounds which increases the problems with proper maintenance. Modern increase in vehicle count and overall traffic requires new approach towards monitoring, particularly in case of strategic objects such as bridges on main routes. Negligence can cause to catastrophe, which was seen in case of Genoa overpass that collapsed in August 2018. Periodic visual inspections does not guarantee finding of all problems. Strategic objects are often controlled by measuring systems that determine the static deformation and low frequency vibrations. The Structural Health Monitoring (SHM) systems often take measures in real time which requires huge computing power.

The Rigid Finite Elements Method used in this paper is a method already established in 1970s [1]. During the years, numerous researchers used it to analyse the structural vibrations in shipbuilding industry, offshore structures or construction, the latter considered in the article [2,3,4]. The main advantage of the method is the compatibility of the calculated results to experimental finding with relatively low number of degrees of freedom. The compatibility of the results acquired from RFEM with the results acquired from the classical FEM was verified by the authors of the articles as well as many other researchers. It is worth remembering that regardless of chosen method, a reliable numerical model requires identification of initial parameters, particularly if the method is designed for SHM.

2 Vibration of composite beams

Figure 2 presents possible vibration state of composite girder presented in Fig. 1. Following vibration types can be seen: vertical bending vibration, torsion vibrations and distorted vibrations. Other forms of vibration can be obtained by adding the above-mentioned types.

Fig. 2

Modes of vibration of composite beam: a vertical flexural, b horizontal flexural, c torsional, d distortional

The fundamental mode shapes of composite beams to be analysed are modes of vertical flexural vibrations as the beam moves in the X–Z plane. Given that, a 2D model can be used, where the reinforced concrete slab is treated as a beam with a rectangular cross section. However, a 2D model cannot determine modes and frequencies of torsional vibrations that lie in the same frequency range (Fig. 3), which have a significant impact on the dynamic properties of these structures. Figure 3 shows a comparison of frequency response functions for a certain steel–concrete composite beam. The blue solid line shows the FRF obtained in the Z-axis direction, for point 1, in response to excitation at point A in the same direction. The black dotted line shows the FRF obtained in the same point 1 in response to excitation at point B. The symbols used to identify the points and axes are shown in Fig. 1.

Fig. 3

Comparison of frequency response functions in Z direction at point 1, with excitation at A (blue solid) and B (black dotted) in Z direction

Both FRFs were recorded as responses in the same direction, and at the same point. While analysing the FRF with excitation at point B (black dotted), both flexural and torsional vibration frequencies can be clearly seen. Only flexural vibration frequencies were obtained for the FRF with excitation at point A (blue solid). As can be seen, to analyse torsional vibration modes, a spatial 3D model needs to be defined.

Modelling of spatial vibrations is of particular importance in the analysis of bridges, whose spans comprise two or more girders connected with a reinforced concrete slab. In the case of double-track railway bridges, forces generated by a moving train typically have an asymmetric effect on the structure. Therefore, a bridge span is subjected to not only bending, but also twisting. Torsion of a bridge span also occurs in analyses of structures bent in the plane, where the centrifugal forces generated by a fast-moving train are applied in the eccentricity, relative to the centre of gravity of the span, generating torque that twists the span.

3 Beam’s computational model

While developing a rigid finite element (RFE) model of composite beam, it was assumed that the reinforced concrete slab and the steel beam would be modelled separately, and then connected with spring-damping elements (SDE) that would model the connection. Figure 4a shows a schematic of a composite beam with length L, divided into n segments with length ΔL, in the X direction. A reinforced concrete slab with a width B was divided into m segments with length ΔB, in the Y direction. No divisions were made for the steel I-section in the Y direction. For every segment created as a result of the primary division, an SDE was defined. Each SDE for the steel section had spring-damping properties of the I-section , and each SDE for the reinforced concrete slab had spring-damping properties of the slab . Rigid finite elements of length resulting from the secondary division (Fig. 4b) were placed between the SDEs, separately for the concrete slab and for the steel I-section. For elements at the edge, the length of each element was ΔL/2 in the X direction and ΔB/2 in the Y direction (for the slab), and the lengths of the other elements were ΔL and ΔB, respectively. Finally, the model was fitted with SDEs modelling the connection . They connect the edges in RFEs of the slab and the steel I-section.

Fig. 4

RFE model of composite beam: a primary division into segments; b secondary division into RFEs connected by SDEs

Each RFE with a number i has its own independent reference system ${X}_{RFE}^{(i)}$, ${Y}_{RFE}^{(i)}$, and ${Z}_{RFE}^{(i)}$. The system is selected such that it overlaps the central system of inertia of the relevant RFE. To define any given RFE, it is necessary to know masses and mass moments of inertia given by a diagonal mass matrix (1):

$${\mathbf{M}}^{(i)}=\mathrm{diag}\left[{m}^{(i)},{m}^{(i)},{m}^{(i)},{J}_{X}^{(i)},{J}_{Y}^{(i)},{J}_{Z}^{(i)}\right],$$

(1)

where the first three terms of the matrix are equivalent to the mass of an RFE, and the other three are the mass moments of inertia for an RFE relative to the axes ${X}_{\mathrm{RFE}}^{(i)}$, ${Y}_{\mathrm{RFE}}^{(i)}$, and ${Z}_{\mathrm{RFE}}^{(i)}$.

The primary parameters which describe an SDE of k number are coefficients defining its spring and damping properties. Each SDE has its own independent coordinate system of ${X}_{\mathrm{SDE}}^{(k)}$, ${Y}_{\mathrm{SDE}}^{(k)}$, and ${Z}_{\mathrm{SDE}}^{(k)}$. Damping properties are negligible while solving the problem of natural vibration of a structure. Spring properties are described by means of a stiffness matrix which comprises three coefficients of translational stiffness ${k}_{T,j}^{(k)}$, and three coefficients of rotational stiffness ${k}_{R,j}^{(k)}$. The stiffness matrix ${\mathbf{K}}^{(k)}$ takes the form of a 6 × 6 diagonal matrix (2):

$${\mathbf{K}}^{(k)}=\mathrm{diag}\left[{k}_{T,X}^{(k)},{k}_{T,Y}^{(k)},{k}_{T,Z}^{(k)},{k}_{R,X}^{(k)},{k}_{R,Y}^{(k)},{k}_{R,Z}^{(k)}\right].$$

(2)

The global stiffness matrix K is based on the stiffness matrix ${\mathbf{K}}^{(k)}$ for each successive EST, and the inertia matrix M is based on the mass matrix ${\mathbf{M}}^{(i)}$ for each successive RFE. The methods of their development are described in detail in other studies [5,6,7].

As mentioned earlier, the modelling of continuous elements in rigid finite element method begins with primary division. For the slab, division must be conducted in two directions, n segments (ΔL long each) in the longitudinal X-axis direction and m segments (ΔB long each) in the transverse Y-axis direction. The slab can be divided into segments of equal or comparable lengths. The primary division of a slab is shown in Fig. 5a. An SDE is then placed at the centre of gravity of each segment. Each SDE is then broken down into four smaller SDEs so that it is possible to connect the corners of four adjacent rigid finite elements, which is secondary division. In each set of four SDEs, two are parallel to the main X axis and the other two are parallel to the main Y axis. In the classic approach [5, 6], spring properties of respective elements are reflected by SDEs spaced as shown in Fig. 5b (left), i.e. at the point where four RFE corners meet. Using this method, elements with three degrees of freedom are used for modelling. Elements are displaced in the Z-axis direction and relative to rotation in the X- and Y-axis directions. The classic approach neglects rotational stiffness in the Z-axis direction. With this approach, the modelling did not provide consistent torsional vibration frequencies. Analysis revealed that this lack of consistency resulted from the way SDEs were distributed. If SDEs are fixed at the corners, it blocks the freedom of successive RFEs to turn relative to the X and Y axes. Modification was to move SDEs so that they connected the centres of successive RFEs, as shown in Fig. 5b (right). A similar solution was presented elsewhere [8].

Fig. 5

RFE model of reinforced concrete slab: a primary division; b secondary division—classical position of SDE (left) and modified position of SDE (right)

The approach present in this study uses a slab model defined with six degrees of freedom, three translational and three rotational, which will be combined with a steel I-section model with six degrees of freedom. Modification required introduction of an additional SDE rotational stiffness coefficient relative to the Z axis. The coefficient was determined by treating slab elements as prismatic beams with rectangular cross sections.

The inertia coefficients in the diagonal matrix ${\mathbf{M}}^{(i)}$ for the RFEs modelling the inside of the slab, were determined as follows (3–6):

$${m}^{(i)}={h}_{c}\bullet \Delta L\bullet \Delta B\bullet {\rho }_{c},$$

(3)

where:

${h}_{c}$ is the thickness of the reinforced concrete slab, and, ${\rho }_{c}^{(i)}$ is the mass density of material.

$${J}_{X}^{(i)}=\frac{{m}^{\left(i\right)}}{12}\left({\Delta L}^{2}+{{h}_{c}}^{2}\right),$$

(4)

$${J}_{Y}^{(i)}=\frac{{m}^{\left(i\right)}}{12}\left({\Delta B}^{2}+{{h}_{c}}^{2}\right),$$

(5)

$${J}_{Z}^{(i)}=\frac{{m}^{\left(i\right)}}{12}\left({\Delta L}^{2}+{\Delta B}^{2}\right).$$

(6)

The primary axes of an SDE have a property whereby forces acting on an SDE in a direction compatible with these axes result in its translational deformations, which occur only in the direction where these forces are applied.

The values of translational and rotational stiffness coefficients were determined according to the following rules (7–18):

(a) for SDEs parallel to the main axis X.

$$k_{T,X - X}^{(k)} = \frac{{E_{c} \cdot h_{c,eff} \cdot \Delta B}}{\Delta L},$$

(7)

$$k_{T,Y - X}^{(k)} = \frac{{G_{c} \cdot h_{c,eff} \cdot \Delta B}}{\Delta L \cdot \chi },$$

(8)

$$k_{T,Z - X}^{(k)} = \frac{{G_{c} \cdot h_{c,eff} \cdot \Delta B}}{\Delta L \cdot \chi },$$

(9)

$$k_{R,X - X}^{(k)} = \frac{{G_{c} \cdot h_{c,eff}^{3} \cdot \Delta B}}{6 \cdot \Delta L},$$

(10)

$$k_{R,Y - X}^{(k)} = \frac{{E_{c} \cdot h_{c,eff}^{3} \cdot \Delta B}}{{12 \cdot \left( {1 - \nu_{c}^{2} } \right) \cdot \Delta L}},$$

(11)

$$k_{T,Z - X}^{(k)} = \frac{{E_{c} \cdot h_{c,eff} \cdot \Delta B^{3} }}{12 \cdot \Delta L},$$

(12)

(b) for SDEs parallel to the main axis Y

$$k_{T,X - Y}^{(k)} = \frac{{G_{c} \cdot h_{c,eff} \cdot \Delta L}}{\Delta B \cdot \chi },$$

(13)

$$k_{T,Y - Y}^{(k)} = \frac{{E_{c} \cdot h_{c,eff} \cdot \Delta L}}{\Delta B},$$

(14)

$$k_{T,Z - Y}^{(k)} = \frac{{G_{c} \cdot h_{c,eff} \cdot \Delta L}}{\Delta B \cdot \chi },$$

(15)

$$k_{R,X - Y}^{(k)} = \frac{{E_{c} \cdot h_{c,eff}^{3} \cdot \Delta L}}{{12 \cdot \left( {1 - \nu_{c}^{2} } \right) \cdot \Delta B}},$$

(16)

$$k_{R,Y - Y}^{(k)} = \frac{{G_{c} \cdot h_{c,eff}^{3} \cdot \Delta L}}{6 \cdot \Delta B},$$

(17)

$$k_{T,Z - Y}^{(k)} = \frac{{E_{c} \cdot h_{c,eff} \cdot \Delta L^{3} }}{12 \cdot \Delta B},$$

(18)

where, ${E}_{c}$ is the substitute dynamic longitudinal modulus of elasticity of the reinforced concrete slab, ${G}_{c}$ is the substitute dynamic transverse modulus of elasticity of the reinforced concrete slab, ${\nu }_{c}$ is the Poisson's ratio of concrete, and $\chi$ is the Timoshenko coefficient of cross-section shape [9, 10].

The discrete model of the steel I-section was developed using the RFE method. The steel I-section was divided in a classic way into n segments along its length in the X direction. The classic approach, described in the literature, was used.

Finally, the connection between the reinforced concrete slab and the steel I-section was modelled. In the composite beam model, the primary division of the slab in the transverse direction was done into an even number of segments. This type of division always results in an odd number of RFEs in the secondary division across the slab. As a result, the middle RFE was placed directly above the RFE modelling the steel I-section. An example of a division with 7 elements in the transverse direction (secondary division) is shown in Fig. 6. In the first approach to modelling of the connection, two SDEs were placed in the model at the points where steel studs were placed in the real composite beam (variant I—Fig. 6).

Fig. 6

RFE model—variant I of connection model: a primary division; and b secondary division

Analysing the modes of torsional vibrations (Fig. 7) with such an approach to connection modelling, it can be seen that beam components were turning in the same direction relative to the X axis. For comparison purposes, Fig. 8 shows the same vibration modes obtained in the experiment. Analysis showed that the steel section behaved differently relative to the slab during torsional vibrations.

Fig. 7

Torsional vibration modes in RFE model of composite beam with variant I of connection model: a second torsional vibration mode; b third torsional vibration mode

Fig. 8

Torsional vibration modes of composite beam obtained in experiment: a second torsional vibration mode; b third torsional vibration mode

A comparison of torsional vibration modes for the composite beam model with those obtained in experiments, showed that the proposed model of the connection (variant I) did not provide the correct representation of the interaction between the slab and the steel beam.

Having analysed the contact point between the steel beam and the slab, it was decided that the connection would be modelled as a single SDE (variant II—Fig. 9). The stiffness of a single SDE took into account the influence of stiffness of: steel studs, a fragment of the reinforced concrete slab, and the slab–beam contact point.

Fig. 9

Spatial RFE model—variant II of connection model: a primary division; and b secondary division

When the modification was introduced, the connection model produced similar vibration modes to those obtained experimentally (Fig. 10).

Fig. 10

Torsional vibration modes in RFE model of composite beam with variant II of connection model: a second torsional vibration mode; b third torsional vibration mode

Therefore, stiffness of the connecting element has a decisive effect on the representation of natural vibration modes. Stiffness of the connecting element was defined with axial stiffness in the Z direction expressed with coefficient K_v, and shear stiffness in the X and Y directions expressed with coefficient K_h. The term ‘axial stiffness’ is understood to be the direction of loading of the steel studs, i.e. vertically, as the load is applied to the studs along their axes. The term ‘shear stiffness’ is understood to be the stiffness of connecting elements preventing slipping at the steel–concrete interface. This stiffness acts tangentially to the contact plane between slab and beam. The same shear stiffness value was used in both directions parallel to the contact plane. Because of the method of modelling the connection as a single SDE (variant II, Fig. 9), it was necessary to define an additional parameter as rotational stiffness relative to the X axis, denoted as K_R,X. A single SDE accounts for stud (axial and shear) stiffness, stiffness of the interface between the slab and the steel beam along the length of connected RFEs, and cooperation between a stud and concrete.

Stiffness matrices ${\mathbf{K}}_{\mathrm{CONNECTION}}$ take the form of a diagonal matrix, 6 × 6 in size (19).

$${\mathbf{K}}_{\mathrm{CONNECTION}}=\mathrm{diag}\left[{K}_{h},{K}_{h},{K}_{v},{K}_{R,X},\mathrm{0,0} \right],$$

(19)

where, ${K}_{h}$ is the stiffness of a SDE in the direction of the X and Y axes, ${K}_{v}$ is the stiffness of a SDE in the Z direction, and ${K}_{R,X}$ is the rotational stiffness of a SDE relative to the X axis.

To determine the division density for the analysis, numerical experiments were conducted to determine the number of elements required, precision of the solution, computation time, and the position of the steel connector studs.

4 Verification and validation of the RFE model

When the computational model being well-known conceptually is to be used for widening the state of the art, the credibility of such a model needs to be subjected to a verification and validation exercise that is nowadays a standard method of the credibility assessment in engineering sciences. Practical problems associated with verification and validation of computational models were presented in [11]. Verification is supposed to deliver evidence that mathematical models are properly implemented and that the numerical solution is correct with respect to the mathematical model. Verification uses comparison of computational solutions with highly accurate numerical solutions (e.g. FEM) or exact analytical solutions; whereas, validation compares the numerical solution with the experimental data.

The subject of this paper is the steel–concrete composite beams that are a combination of a steel I-beam with a uniform cross section and a rectangular isotropic concrete slab of constant thickness. Verification of the RFEM composite beam model should be preceded by verification of the models of its individual components, i.e. beam and slab.

Verification of a rectangular beam model with a uniform cross section is presented in [5] and [6]. The verification was carried out by comparing the frequencies of natural vibrations determined using the 2D RFEM model with the frequencies obtained with the analytical method [12] taking into account the influence of shear stresses and the influence of kinetic energy of rotational motion, i.e. taking into account the assumptions of Timoshenko's beam theory [13]. The verification showed very high compliance of the results obtained by both methods.

Verification of the steel I-beam model has been presented in [14]. The results obtained from the 3D RFEM model were compared with the results obtained using FEM (deformable Finite Element Method). The FEM model was developed in the Abaqus program. One-dimensional B31 beam elements were used. Very high compliance of results was obtained. Both frequencies (differences below 1%) and vibration modes were compared. Flexural, axial and torsional modes of vibrations were analysed.

Verification of the steel I-beam model was also presented in [15]. Also here, the FEM model developed in Abaqus was used. This time, S8R shell elements were used to create the model. High compliance of frequencies and modes of vibrations was obtained. Flexural, axial and torsional vibrations were analysed. In the case of torsional vibrations, the basic mode of vibration was analysed. In [15], apart from verification, the 3D RFEM model was also validated using the results of experimental tests [14]. A 3.24-m-long beam made of IPE 160 profile made of S235 steel was tested. Very high compliance of results was obtained.

The 2D RFEM model of a rectangular plate was verified in [6]. The comparison was made with the results obtained with the method which took into account the continuous distribution of mass and stiffness [16]. A thin plate with dimensions L = 1000 mm, B = 700 mm and thickness h = 10 mm was analysed. Good compliance of results was obtained, i.e. the frequencies and modes of vibrations.

Verification of 3D RFEM models of moderately thick rectangular plates is presented in [15]. Rectangular plates with L/B ranging from 0.6 to 2.5 were analysed. During the research, it was investigated how discretization density affects the results. Plates of various thickness were analysed—h/B changed in the range from 0.001 to 0.2. Various combinations of boundary conditions were analysed: C—clamped, S—simply supported and F—free. The results obtained with the use of RFEM models were compared with an exact solution for the problem of plate natural vibrations, taking into account the influence of rotatory inertia and shear deformations [17]. Very good consistency of results was obtained for both frequencies and the modes of vibrations.

The paper [18] presents the results of validation of the 3D RFEM plate model with the results of experimental tests carried out on a 2200 × 600 × 60-mm concrete slab. The slab dimensions were deliberately chosen so that it was clearly longer in one direction. Both experimental tests and numerical calculations were carried out for a flat plate slab with free edges. This allowed to avoid the uncertainty associated with determining the rigidity of the supports at the edges of the slab. High compliance was obtained for both frequencies and the modes of vibrations.

In the aforementioned work [15], the 3D RFEM model of an aluminium rectangular plate stiffened with beams was also verified and validated. The reference results of experimental tests and numerical calculations presented in [19] were used for the analysis. The rectangular plate was stiffened from below with one or two beams. The plate–beam connection was non-deformable. The results obtained from the RFEM model were compared with the numerical results of several independent scholars (various methods were used, including DFEM) and the results of experimental studies. High compliance was obtained for both frequencies and the modes of vibrations.

Verification was also carried out for steel–concrete composite beam models with a deformable beam-slab connection. Verification of 2D RFEM models of three composite beams with various types of connection is presented in [20] and [21]. The results obtained using RFEM models were compared with the results of continuous analytical models developed in accordance with the Euler beam theory (two models) and Timoshenko beam theory (one model). The results of the 2D RFEM model were also compared with the 3D DFEM model developed in the Cosmos/M system. In each case, high compliance of results was obtained. Positive verification results also allowed for validation of the RFEM model using the results of previous experimental studies.

As the above examples show, the RFEM method has been repeatedly verified using both deformable FEM models and analytical models that take into account continuous weight and stiffness distribution. The verification concerned simple elements such as beam or plate/slab, as well as complex systems where plates and beams are connected with each other in a rigid or flexible manner. Verification and validation of spatial more complex 3D RFEM models, e.g. the composite steel–concrete span of a double-girder composite bridge, is presented in [15]. As before, high compliance of RFEM and FEM results was obtained.

The positive results of verification and validation of both 2D and 3D RFEM models incline towards further development of discussed method and search for optimal applications for it using its undoubted advantages.

5 Experimental studies

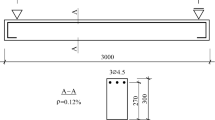
Two composite beams were studied. Each beam comprised an IPE 160 I-beam, of S235JRG2 steel, connected to a reinforced concrete slab which was 60-mm thick and 600-mm wide. The concrete mix for the reinforced concrete slab was made of cement-based class 42.5, with the addition of a BV plasticiser. The W/C ratio was 0.64 with the consistency of S3, C25/30 concrete class. The maximum size of aggregate was reduced to 8 mm because of the relatively small size of the studied elements. Ribbed steel bars, 6 mm in diameter made from A-I steel, were used as concrete reinforcement. Longitudinal reinforcement was placed every 75 mm, and transverse reinforcement every 150 mm. Reinforcing fabric was used on the top and bottom. The slab was connected to the I-beam with steel studs. A ductile connection was made using headed studs manufactured by KÖCO: SD type, 10 mm in diameter and 50 mm long, made of S235J2G3 steel.

The connecting studs were spaced every 200 mm for beam C1, and every 100 mm for beam C3. The total length of the beam was 3200 mm. The beam arrangements are shown in Fig. 11. The geometric characteristics of the composite beams were determined on the basis of in situ measurements.

Fig. 11

Analysed steel–concrete composite beam: a isometric view; b cross section A–A; c beam C1 and b beam C3

Dynamic tests were conducted in a free beam scheme. The experimental stand comprised two steel bearers spaced 2 m apart. The bearers were braced with angle sections. During dynamic tests, the beam was suspended on bearers with four 3-mm steel wires, and in this way, a free beam scheme was implemented. Bearer deformability and its effect on obtained results are considered to be negligible in the scheme. Rope deformability was selected so that frequency vibrations typical for solid bodies in motion were beyond the range of the investigated beam free vibration frequencies. The points where the ropes were fixed to the beam were selected to overlap with the theoretical nodes of fundamental modes of flexural vibrations. A diagram of the test stand and the suspended beam is presented in Fig. 12a.

Fig. 12

Experimental stand: a suspended beam; b excitation points; and c mesh of measurement points

The aim of this study was to determine the fundamental dynamic characteristics of the beams: frequency of natural vibration, damping, and frequency response function. As high-frequency results were expected, it was deemed necessary to measure vibration acceleration, which was considered to be the response of a system. Impulse excitation was used, with a modal hammer used to excite a structure into vibration. Acceleration was measured using nine PCB 356A01 triaxial piezoelectric sensors, which were attached with special wax provided by the manufacturer to circular steel washers, 25 mm in diameter, placed on the reinforced concrete slab (Fig. 13a). The washers were attached with modified epoxy resin.

Fig. 13

Measurement equipment: a triaxial piezoelectric sensor; b modal hammer

Impulses were studied with excitation generated at three points on the structure (Fig. 12b): 2 − Z vertical impact in the middle of the slab; 1 − Z vertical impact on the edge of the slab; and 2 + X horizontal impact on the face of slab. The various excitation points were used to produce different vibration modes of the beam: point 1 − Z—vertical flexural, torsional and distortional modes; point 2 − Z—vertical flexural modes; point 2 + X—axial modes.

A mesh of 36 evenly distributed measurement points was defined for the tests: 27 points on the slab and 9 on the lower flange of the I-section (Fig. 12c). The number of points required tests to be carried out in stages, with sensors being placed at different points measuring acceleration. The impulse excitation was performed using a modal hammer KISLER 9726A20000 (500 g) (Fig. 13b), with a KISLER 9904A steel head covered with polyoxymethylene, which can excite vibrations of frequencies up to 600 Hz.

Table 1 presents a comparison of the flexural and torsional modes for the tested composite beams. The parameter ${\Delta }_{{\varvec{i}},{\varvec{C}}1/{\varvec{C}}3}$ presents the difference between the natural frequencies of C1 and C3 beams. Beams differ only in the spacing of connectors (steel studs). The value of index ${\Delta }_{{\varvec{i}},{\varvec{C}}1/{\varvec{C}}3}$ presented in the tables was calculated using the following equation (20):

Table 1 Frequencies of natural vibrations and modal damping for beams C1 and C3: flexural, torsional, and axial vibrations

$${\Delta }_{{\varvec{i}},{\varvec{C}}1/{\varvec{C}}3}=\frac{{{\varvec{f}}}_{{\varvec{i}}}^{{\varvec{e}}{\varvec{x}}{\varvec{p}},{\varvec{C}}1}-{{\varvec{f}}}_{{\varvec{i}}}^{{\varvec{e}}{\varvec{x}}{\varvec{p}},{\varvec{C}}3}}{{{\varvec{f}}}_{{\varvec{i}}}^{{\varvec{e}}{\varvec{x}}{\varvec{p}},{\varvec{C}}3}}.$$

(20)

The frequencies and modal damping are different for composite beams C1 and C3. The reduction of the steel stud distribution to 100 mm for beam C3 had a significant effect on the stiffness of the beam, which changed the frequencies obtained. The frequency decrease was observed for both flexural (3–8%) and torsional modes (1–3%). While comparing obtained axial vibration frequency values for the tested beams, it must be borne in mind that they are affected by the axial stiffness of the beam, which is a function of its cross-sectional area and material stiffness expressed by the longitudinal modulus of elasticity. Forces generated in the connection are low, and have a negligible effect on the frequency. The distribution density of the connection does not have a significant impact on the axial stiffness of the beam, which is observed in the small difference of axial frequency of 1%.

Analysis of measured mode shapes of the beams revealed additional distortional modes of vibration—movement of the bottom flange of the I-section in the X–Y plane (Fig. 2d and Fig. 14).

Fig. 14

Composite beam with steel bottom flange marked

The vibrations were excited at point 1 − Z. During analysis, five distortional vibration modes were determined. The frequencies of natural vibration and modal damping coefficients are presented in Table 2.

Table 2 Frequencies of natural vibrations and modal damping for beams C1 and C3: distortional vibrations, for excitation 1-Z

The fundamental distortional vibration mode (with the lowest frequency) was denoted as ‘1_dist’. This represents movement of the I-section relative to the slab (Figs. 2d, 15). All distortional vibration modes have a common feature, in that elements of vibration mode vectors determined for points on the surface of the slab are many times smaller than those determined for the bottom flange of the steel I-section. The reinforced concrete slab exhibits marginal movement relative to the transversely vibrating bottom flange of the steel beam.

Fig. 15

First distortional vibration mode (${{\varvec{f}}}_{{1}_{{\varvec{d}}{\varvec{i}}{\varvec{s}}{\varvec{t}}}}^{{\varvec{e}}{\varvec{x}}{\varvec{p}}}=92.03 Hz$) – beam C1

During tests, the bottom flange of the I-section was not supported in any manner, as there were no supports for the beam. Because of the flexural stiffness of the I-section web (bending in the X axis) and certain flexibility of the steel–concrete interface for rotation along the X axis, it was possible to observe such vibration modes.

While comparing the vibration frequencies determined for the two tested beams, corresponding to successive distortional vibration modes, it can be seen that differences are not highly significant, and that they tend to decrease with increasing vibration frequency. The difference between the fundamental frequencies is approximately 3%, which is approximately 0.6% for the highest frequency. Higher frequencies were recorded for the beam with more densely spaced connectors, which means that the type and distribution of connectors have a certain effect on the examined vibration modes.

6 Estimation of model parameters

In the RFE model of beam C1, the slab and the steel section in the X direction were divided into 32 segments of 100-mm long. The complete model comprised 33 RFEs modelling the steel section, 33 × 7 RFEs modelling the reinforced concrete slab, 16 SDEs modelling the connection (studs spaced every 200 mm required introduction of SDEs on every second RFE), 32 SDEs modelling the connection for RFEs of the steel section, 32 × 7 SDEs in the X direction, and 33 × 6 SDEs in the Y direction, for a total of 422 SDEs. In beam C3, the slab and the steel section in the X direction were divided into 33 segments of 100-mm long. The complete model comprised 33 RFEs modelling the steel section, 33 × 7 RFEs modelling the reinforced concrete slab, 31 SDEs modelling the connection (studs spaced every 100 mm), 32 SDEs modelling the connection for RFEs of the steel section, 32 × 7 SDEs in the X direction, and 33 × 6 SDEs in the Y direction, for a total of 422 SDEs.

Parameter estimation was based on the natural frequencies and vibration modes. The following parameters were estimated: stiffness of connecting elements K_h, K_v, and K_R,X, and substitute dynamic longitudinal modulus of elasticity of concrete, E_c. The effect of external forces acting on the beam and damping was considered to be negligible. The differential equation of motion can be given by (21):

$$\mathbf{M}\ddot{\mathbf{q}}+\mathbf{K}\mathbf{q}=0,$$

(21)

where, q is the vector of generalised coordinates.

Methods of solving the above equation to determine natural vibration frequencies and corresponding vibration modes were described in more detail in the literature [22].

An original program was developed in MATLAB to perform estimations [23,24,25]. It can be used to solve this problem, and to analyse forced vibrations of the structure.

For parameter estimation, the following minimisation criterion was used (22):

$$\mathrm{J}={w}_{f}\bullet S+{w}_{\varphi }\bullet Z,$$

$${w}_{f}+{w}_{\varphi }=1,$$

(22)

where, ${w}_{f}$ is the weight function of the fit of natural vibration frequency, and, ${w}_{\varphi }$ is the weight function of the fit of natural vibration modes.

This approach enabled simultaneous minimisation of indices S (the fit of natural vibration frequency) and Z (the fit of natural vibration modes). To account for the fit of frequency and mode of natural vibrations in the estimations, appropriate weights, w_f and w_φ, were used for frequency and modes of natural vibrations, respectively. To use the weights, it was necessary to determine validity in the fit of vibration frequency and natural vibration modes. A similar solution was proposed by Mordini [26].

The index S (23) is the sum of squares of relative deviations of the first n numerical frequencies of flexural natural vibrations, m numerical frequencies of torsional natural vibrations, and one frequency of axial natural vibrations from the same frequencies determined in the experiments.

$$\mathrm{S}=\sum_{i=1}^{n}{\left(\frac{{f}_{i\_flex}^{num}-{f}_{i\_flex}^{exp}}{{f}_{i\_flex}^{exp}}\right)}^{2}+\sum_{i=1}^{m}{\left(\frac{{f}_{i\_tors}^{num}-{f}_{i\_tors}^{exp}}{{f}_{i\_tors}^{exp}}\right)}^{2}+{\left(\frac{{f}_{1\_long}^{num}-{f}_{1\_long}^{exp}}{{f}_{1\_long}^{exp}}\right)}^{2}.$$

(23)

The index Z (24) is an average complement of modal assurance criterion (MAC) (25). Therefore, the fit of natural vibration modes was accounted for in the process of estimation [27].

$$Z=\frac{1}{n}\sum_{i=1}^{n}\left(1-MAC\left({\varphi }_{{i}_{flex},Z}^{num},{\varphi }_{{i}_{flex},Z}^{exp}\right)\right)+\frac{1}{m}\sum_{i=1}^{m}\left(1-MAC\left({\varphi }_{{i}_{tors},Z}^{num},{\varphi }_{{i}_{tors},Z}^{exp}\right)\right).$$

(24)

The value of MAC (25) is bounded between 0 and 1, the latter denoting full consistency, and it is a criterion of consistency of mode shapes determined experimentally and numerically.

$$MAC\left({\varphi }_{i,Z}^{num}, {\varphi }_{i,Z}^{exp}\right)=\frac{\left|{{\varphi }_{i,Z}^{num}}^{T}\bullet {\varphi }_{i,Z}^{exp}\right|}{\left({{\varphi }_{i,Z}^{exp}}^{T}\bullet {\varphi }_{i,Z}^{exp}\right)\bullet \left({{\varphi }_{i,Z}^{num}}^{T}\bullet {\varphi }_{i,Z}^{num}\right)}.$$

(25)

Only natural vibration modes in the Z direction were taken into consideration in the process of estimation.

The only defined equality constraint was the condition of experimental and numerical consistency, zero frequency of distortional vibration (26):

$${f}_{{1}_{dist}}^{exp}={f}_{{1}_{dist}}^{num}.$$

(26)

This constraint has the greatest effect on the estimation of rotational stiffness in the X direction, K_R,X of the SDEs modelling the connection. In the proposed procedure of identification algorithm I, the value of K_R,X will be determined primarily based on the fit of frequency of fundamental distortional mode of vibration ${f}_{{1}_{dist}}^{exp}$. Analysis of the experimental results showed that the frequency corresponds to the movement of the entire I-section relative to the reinforced concrete slab. Figure 16 presents a comparison of vibration forms generated with the RFE model for beam C1 with those obtained in the experiments.

Fig. 16

First distortional vibration mode for beam C1: a experiment; b RFE model

To determine the model parameters that would enable the best mapping of frequencies with those obtained experimentally, the index Z has been minimised. To solve the problem, an optimization procedure implemented in Optimization Toolbox package, which is part of MATLAB, was used.

7 Estimation results

The first estimation was conducted while accounting for the fit of natural vibration frequencies and modes. The estimation of parameters K_h, K_v, K_R,X, and E_c was conducted with identification algorithm I, given the pre-set weights ${w}_{f}=\mathrm{0,5}$ and ${w}_{\varphi }=\mathrm{0,5}$. The obtained parameter values are presented in Table 3. Five frequencies of flexural and torsional vibration modes, one frequency of distortional mode, plus one frequency of axial vibration were then determined for these values. A comparison of experimental and numerical frequency vibrations for all the composite beams was made, and the results are presented in Table 4. Index Δ calculated by formula (20) shows percentage differences for the numerical and experimental frequencies of natural vibrations.

Table 3 Estimated parameters K_h, K_v, K_R,X, and E_c

Table 4 Comparison of experimental ${f}_{i}^{exp}$ and numerical ${f}_{i}^{num}$ vibration frequencies for beams C1 and C3 for estimated parameter K_h, K_v, K_R,X, and E_c

Table 5 presents the values of indices S (23) and Z (24). The indices were broken down into their components: S_f,s, the sum of squares of relative deviations for frequencies of experimental and numerical torsional vibrations; S_f,g, the sum of squares of relative deviations for frequencies of experimental and numerical flexural vibrations; and S_f,o, the sum of squares of relative deviations for frequencies of experimental and numerical axial vibrations. The parameter reflecting the degree of fit for experimental and numerical modes of natural vibrations was determined only for torsional Z_f,s and flexural Z_f,g natural vibration modes.

Table 5 Indices S, Z, and J, for beams C1 and C3

A good fit of vibration frequencies was obtained for the tested beams. The highest value of index Δ (~ 3%) was obtained for axial vibration modes for beam C3, and for vibration frequency of the first torsional mode for beam C3. When comparing other experimental and calculated frequencies, index Δ was less than ~ 1%.

In the next step, a graphic comparison was made of vibration modes determined experimentally and those calculated with the RFE model with estimated parameters. All the graphs of the vibration modes were plotted to allow a direct comparison of vibration modes calculated with the RFE model with those obtained in dynamic tests. The measurement point mesh had 36 points (Fig. 12c). While solving the spatial RFE model, values were obtained as vectors of vibration modes for points located in the centres of gravity of RFEs of the reinforced concrete slab, and in the centres of gravity of RFEs of the steel section. For this reason, the mesh of measurement points did not overlap with the results obtained using RFE model. To enable direct comparison of calculated results and experimental vibration modes, results obtained from the RFE model were transformed to measurement points. Transformations were performed taking into account the distance from the point where accelerations were measured to the centre of gravity of a relevant RFE (in the X, Y, and Z directions) and rotation angles of a given element (in the RX, RY, and RZ directions). All computed eigenvectors were normalised in the same way as in the tests (the highest value of each vector is 1). All measurement points for the reinforced concrete slab and the steel section were marked in the graphs, and the results were scaled down to the geometry of the beam. To present results in a graphic form, a program was written in MATLAB.

The figures allow a comparison of experimental vibration forms of beam C1 (blue) and vibration forms calculated with the RFE model (red), with the estimated parameters presented in Table 3. The flexural vibration modes are shown in Fig. 17.

Fig. 17

Comparison of experimental and numerical modes of flexural vibrations, beam C1: a ${\varphi }_{1flex}^{exp}\text{/}{\varphi }_{1flex}^{num}$; b ${\varphi }_{2flex}^{exp}\text{/ }{\varphi }_{2flex}^{num}$; c ${\varphi }_{3flex}^{exp}\text{/ }{\varphi }_{3flex}^{num}$

A comparison of numerical and experimental torsional vibration modes for beam C1 is shown in Fig. 18.

Fig. 18

Comparison of experimental and numerical modes of torsional vibrations, beam C1: a ${\varphi }_{1tors}^{exp}\text{/}{\varphi }_{1tors}^{num}$; b ${\varphi }_{2tors}^{exp}\text{/ }{\varphi }_{2tors}^{num}$; and c ${\varphi }_{3tors}^{exp}\text{/ }{\varphi }_{3tors}^{num}$

Although some deviations can be observed, the analysis showed good fits for the experimental and numerical torsional and flexural vibration modes. Taking into account the possible lack of precision in the measurement of accelerations, the results can be said to be satisfactory. For comparison purposes, we analysed the fitting of the numerical and experimental fundamental distortional vibration mode (Fig. 19), whose frequency was taken into account in the estimation as the equality constraint (26). A good fit can be observed.

Fig. 19

Comparison of experimental ${\varphi }_{1dis}^{exp}$ and numerical ${\varphi }_{1dis}^{num}$ fundamental distortional vibration mode, beam C1

The parameter estimation was then conducted with the same algorithm, using different weights (${w}_{f}=0.7$ and ${w}_{\varphi }=0.3$). This second estimation was to obtain a more precise fitting of the natural vibration frequencies, with a less precise fit of vibration modes. From the obtained results, five frequencies of flexural and torsional vibrations and one frequency of axial and distortional vibrations were determined. A comparison of the experimental and calculated vibration frequencies for both the composite beams was performed, and is presented in Tables 6 and 7. The values of the estimated indices S, Z, and J are presented in Table 8.

Table 6 Estimated parameters K_h, K_v, K_R,X, and E_c

Table 7 Comparison of experimental ${f}_{i}^{exp}$ and numerical ${f}_{i}^{num}$ vibration frequencies for beams C1 and C3 for estimated parameters K_h, K_v, K_R,X, and E_c

Table 8 Indices S, Z, and J for beams C1 and C3

A good fit was observed for the natural vibration frequencies of both the composite beams. The greatest differences between the experimental and numerical vibration frequencies were observed for the torsional vibration modes for beam C1 f_5tors (~ 2%), and for flexural vibration modes for beam C1 f_5flex (~ 2%). Analysis of indices S, Z, and J showed that the best fit was obtained for beam C1, when comparing both components S and Z and the global index J (22).

The last estimation with algorithm I was conducted for weights enabling a better fit of MAC (${w}_{f}=0.3$ and ${w}_{\varphi }=0.7$). The results are presented in Tables 9, 10, and 11.

Table 9 Estimated parameters K_h, K_v, K_R,X, and E_c

Table 10 Comparison of experimental ${f}_{i}^{exp}$ and calculated ${f}_{i}^{num}$ vibration frequencies for beams C1 and C3 for estimated parameters K_h, K_v, K_R,X, and E_c

Table 11 Indices S, Z, and J for beams C1 and C3

For all three estimations conducted for beam C1, a comparison of goodness of fit was performed for the experimental and numerical vibration modes. The value of parameter Δ_φ was compared for torsional modes (line 1 of measurement points), and for flexural modes (line 2 of measurement points) (Fig. 20).

Fig. 20

Beam division into measurement lines

As can be observed (Figs. 21, 22), the estimation process had a minimal effect on the fit of the torsional vibration forms. A new criterion would have to be introduced to compare them and to fit them in a more precise manner.

Fig. 21

Comparison of fit for torsional vibration modes Δ_φ,tors for estimations 1, 2, and 3 – beam C1: a Δ_φ,1tors; b Δ_φ,2tors; and c Δ_φ,3tors

Fig. 22

Comparison of fit for flexural vibration modes Δ_φ,flex for estimations 1, 2, and 3 – beam C1: a Δ_φ,1flex; b Δ_φ,2flex; c Δ_φ,3flex; d Δ_φ,4flex; and e Δ_φ,5flex

In the analysis of goodness of fit for the flexural vibration forms, the smallest differences of parameter Δ_φ were obtained, as expected, for the 3rd estimation in which the weight coefficients were ${w}_{f}=0.3$ and ${w}_{\varphi }=0.7$, which made it possible to set a greater weight for index Z (24) responsible for the fit of natural vibration forms. Differences in the fitting are observed in the higher modes of flexural vibrations (from 3 to 5); while for the first, two only marginal differences were observed.

The values of parameters K_h, K_v, K_R,X, and E_c obtained in the three estimations are presented in Table 12. The percentage differences for the estimated parameters are presented in Table 13.

Table 12 Estimated parameters K_h, K_v, K_RX, and E_c for three estimations, for beams C1 and C3

Table 13 Estimated parameters K_h, K_v, and K_RX, and E_c for three estimations, for beams C1 and C3

Parameters K_R,X and E_c showed little change, regardless of the fitting weights used. The maximum difference between the obtained values of estimated parameter K_R,X was less than 0.5% for all the examined composite beams. The biggest difference for parameter E_c was less than 1.5%, observed for beam C3. More marked changes were observed for connection parameters K_h and K_v: a significant difference of approximately 20% of K_v for beam C1, and a difference of approximately 12% for parameter K_h for beam C3. This indicates that the choice of selecting a criterion and weights plays an important role in the process of identification. It also indicates the importance of accounting for vibration modes in estimation, as their fitting is critical for obtained values of parameters K_h and K_v.

8 Application of model parameter estimation method for damage detection–simulation

Diagnostics of the condition of a structure is one of the most important elements of engineering work. Modal analysis methods are commonly used to detect damage. The parameter estimation method originally developed can be effectively used to detect the scale of damage [28,29,30]. The question of damage detection in composite structures such as steel–concrete composite beams was the subject of the doctoral dissertation [31]. The dissertation analysed some selected methods of detecting and localising damage in steel–concrete composite beams. The analysed methods of damage detection used frequency changes of natural vibrations, changes of vibration modes, curvature of mode shapes, modal damping coefficient, and energy transfer ratio (ETR).

This section presents the use of the developed RFE model and parameter estimation methods for detecting the extent of damage. The analysis covered damage of steel studs connecting the reinforced concrete slab with the steel section. Estimation of damaged parameters was conducted using natural vibration frequencies and mode shapes, which is the reason identification algorithm I was used. Damage modelling was implemented through the modification of stiffness coefficients in SDEs connecting slab and the steel section.

Damage detection was divided into two stages. First, damage location was conducted by detecting changes in curvature mode shapes and residual stress [22, 32,33,34]. Second, estimation of K_v,DET, K_h,DET, and K_R,X,DET, parameters characterising the stiffness of the connection between the slab and the steel section, was performed. While simulating damage in the composite beam, a local weakening of the connection was introduced through either removing or reducing the connection stiffness. Damage was introduced in different locations along the length of the beam.

Damage simulation was conducted for composite beams C1 and C3. In the beams, steel studs were spaced every 200 mm and 100 mm, respectively. Damage implementation was begun by calculating the natural vibration frequencies and mode shapes for undamaged beams, for the parameters obtained in the estimation (Table 3). To simulate the process of detecting damage based on actual conditions and measurement points in experiments, the characteristics of natural vibration modes were not determined from RFE centres of gravity, but after transformation to the measurement points. The characteristics of natural vibration modes obtained in experiments were similarly determined (Fig. 12c). The model was then modified and a selected pair, or a number of pairs, of steel studs were damaged. Damage was introduced into the model through a percentage decrease of parameter values defining a single SDE, i.e. shear stiffness K_h, axial stiffness K_v, or rotational stiffness K_RX. For the damaged RFE model, the calculations were repeated and the frequencies and modes of the natural vibrations were determined. Therefore, two sets of results were produced, one for the undamaged and one for the damaged beam.

To estimate the connection parameters for the undamaged beam, whose values would define the percentage damage of the steel studs, it was necessary to localise the damaged positions. To this end, the mode shape curvature-based method and the residual stress method were used. The curvature of a segment of a vibration mode is the second derivative for the condition before and after damage, which was determined with the following Eq. (27) [7, 8, 35]:

$${\Delta }_{{\varphi }{^{\prime}}-\varphi }={k}{^{\prime}}-k,$$

$$k=\frac{{\varphi }_{i-1}-2{\varphi }_{i}+{\varphi }_{i+1}}{{h}^{2}},$$

$${k}{^{\prime}}=\frac{{\varphi }_{i-1}{^{\prime}}-2{\varphi }_{i}{^{\prime}}+{\varphi }_{i+1}{^{\prime}}}{{h}^{2}},$$

(27)

where, ${\Delta }_{{\varphi }{^{\prime}}-\varphi }$ is the mode curvature change, $k/{k}{^{\prime}}$ is the natural vibration mode curvature of undamaged/damaged structure, $h$ is the distance between measurement points, and, ${\varphi }_{i}/{\varphi }_{i}{^{\prime}}$ is the natural vibration modes at the i-th point of undamaged/damaged structure.

For undamaged structures, the value of changes in mode curvature ${\Delta }_{{\varphi }{^{\prime}}-\varphi }$ is zero. For damaged places, these values are greater than zero. Five curvatures were evaluated, for five modes of natural vibrations. The higher the mode, the easier it was to localise the damaged position. The method is reliable for large numbers of measurement points. With fewer points the damaged locations are more difficult to detect. A second method used for finding damage was measuring residual stress. The values of the residual force vector were determined with (28) [33, 36]:

$${\mathbf{E}}={\mathbf{K}}{{\varvec{\Phi}}}^{{{\prime}}}-\left({\mathbf{M}}{{\varvec{\Phi}}}^{{{\prime}}}\right){{\varvec{\Lambda}}}^{{{\prime}}},$$

(28)

where, $\mathbf{E}$ is the matrix of residual forces, $\mathbf{K}$, $\mathbf{M}$ is the stiffness and mass matrix of undamaged (so-called ‘healthy’), ${{\varvec{\Phi}}}^{{{\prime}}}$ is the matrix of natural vibration modes for damaged structure, and, ${{\varvec{\Lambda}}}^{{{\prime}}}$ is the diagonal matrix of natural vibration frequency for damaged structure.

For undamaged structures, the values of residual forces are zero, while those of damaged locations are greater than zero.

The MATLAB environment was used to develop a module with the implemented methods of mode shape curvature and residual forces, which could be used to find a damaged pair of studs. The module could identify damaged studs and provided data about graphically (Fig. 23).

Fig. 23

Scheme of composite beam, cross section with marked damaged pair of steel studs

Once a damaged place was detected, the extent of the damage was determined. The damaged model was used to determine the values of connection stiffness K_v, K_h, and K_R,X for localised damaged steel studs. These parameters were estimated using identification algorithm I. The final result was a value by which the stiffness of the given pair of steel studs had decreased.

The algorithm was used in a series of numerical experiments carried out for beams C1 and C3. Figures 24 and 25 show beams C1 and C3 with numbered pairs of steel studs.

Fig. 24

Scheme of beam C1 with marked pairs of steel studs: a spatial view; and b side view with marked damaged pairs of steel studs

Fig. 25

Scheme of beam C3 with marked pairs of steel studs: a spatial view; and b side view with marked damaged pairs of steel studs

Three types of damage were prepared for beams C1 and C3. They are presented in Tables 14 and 15, and shown in Figs. 24b and 25b with defined sizes and damage locations. The first damage, DET_1, was defined by a weakened connection between a stud and concrete, which was generated by reducing stiffness K_v, K_h, and K_R,X by 30%, and was placed at the beginning of the composite beam. DET_2, was defined as a 90% loss of contact between a stud and concrete, i.e. a decrease of stiffness K_v, K_h, and K_R,X by 90%, and was placed in the middle of the beam. DET_3 was defined as damage of two pairs of steel studs (one by 90% and the other by 30%) in the middle and either end of the beam (Tables 14 and 15). Index Δ_DET. is the percentage value of damage in the connection (decrease of values K_v, K_h, and K_R,X).

Table 14 Damage size and number of damaged pair of steel studs, beam C1

Table 15 Damage size and number of damaged pair of steel studs, beam C3

In the numerical simulations, calculations were performed for both the damaged and undamaged models. From these calculations, damage was localised and then estimations were performed for the stiffness parameters of the damaged connections K_v,DET, K_h,DET, and K_R,X,DET. Simulation results of all damage types for beam C1 are presented in Table 16, and those of C3 in Table 17. Index Δ_DET is the percentage value of damage in the connection resulting from the estimation of damaged parameters.

Table 16 Estimated parameters K_h,DET, K_v,DET, and K_R,X,DET for damage size and localisation of damaged pair of steel studs for damage types DET_1, DET_2, and DET_3, for beam C1

Table 17 Estimated parameters K_h,DET, K_v,DET, and K_R,X,DET for damage size and localisation of damaged pair of steel studs for damage types DET_1, DET_2, and DET_3, for beam C3

The resulting damage localisation was consistent throughout, and the obtained damage size data similar to that expected for beams C1 and C3. The developed method of model parameter estimation can be an effective tool used for damage detection. The next stage of ongoing studies will be to test the method on actual steel–concrete composite beams.

9 Conclusions

The proposed discrete model of steel–concrete composite beams developed with rigid finite element method enables analysis of different vibration modes, including flexural, longitudinal, torsional and distortional.

The developed spatial model of the composite beam, following estimation, was used to determine fundamental dynamic characteristics: frequencies of natural vibrations, natural vibration modes, and frequency response functions.

The developed identification algorithm I, based on a comparison between experimental and numerical frequencies and modes of natural vibrations, can be used to estimate the stiffness parameters of the model, including connection stiffness K_h, K_v, and K_R,X, and substitute dynamic longitudinal moduli of elasticity of concrete, E_c. The determined parameters can be used to develop a model that can satisfactorily map the actual behaviour of the steel–concrete composite beam. The calculated values of natural vibration frequencies are comparable to those obtained experimentally. A good fit of calculated and experimental modes of natural vibrations was obtained.

The authors plan to apply the developed models of composite beams to model more complex structures, such as a composite floors or a span of a composite beam bridge. The proposed identification algorithms can be used for actual composite structures. The authors’ analysis and conclusions can be useful for further studies on damage detection in composite structures.