Introduction

Kirigami is the art of cutting 2D templates and folding them into 3D structures. Nowadays, there is a growing interest on extending this ancient idea to design materials that fold spontaneously into targeted 3D structures. The driving mechanism depends on the lengthscale. At the macroscale, folding is driven by energy minimization (e.g., stress relaxation), and thus the folding pathway is deterministic1,2,3,4,5,6,7,8,9,10,11,12. By contrast, at the microscale, since folding occurs usually in suspension, the fluctuations in the fluid–structure interaction dominate and folding are stochastic13,14. This challenges the use of kirigami at the microscale as, for example, in encapsulation, drug delivery, and soft robotics15,16,17,18.

To design self-folding kirigami, one first needs to identify what are the 2D templates (nets) that fold into the desired structure. For shell-like structures of rigid panels connected by edges, these nets are obtained by edge unfolding, i.e., by cutting edges and opening the structure19. In principle, different nets can fold into the same 3D structure. However, recent experiments and numerical simulations show that the stochastic nature of folding might lead to misfolding and so, the probability for a given net to fold into the desired structure (yield) depends strongly on the topology of the net and experimental conditions13,14,20,21. Thus, the focus has been on identifying what are the optimal nets that maximize the yield13,21. But, what about the folding time? For practical applications, it is not only critical to reduce misfolding but also to guarantee that folding occurs in due time. Here, we address this question.

To focus on the folding time, we consider as a prototype the spontaneous folding of a pyramid with N lateral faces, where misfolding is not possible. We show that the time for self-folding has a non-monotonic dependence on the number of faces, with an optimal number of faces for fast folding. To explain the non-monotonic dependence, we describe the motion of faces as a set of Brownian processes. We show that the first binding event is a first-passage process in 2D with a characteristic time that decreases with the number of faces. All the other binding events are first-passage processes in 1D, and the time of the last one grows with the number of faces. We show that it is the balance between these two timescales that leads to a minimum in the total folding time for an optimal value of the number of faces.

Results

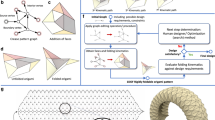
Let us consider a regular pyramid with N lateral faces (see Fig. 1). The 2D net is a N-pointed star, obtained by cutting the edges of the lateral faces and unfolding them. To simulate the folding dynamics, as explained in detail in the section “Methods” and summarized in Fig. 1, we performed particle-based simulations. At the microscale, the interactions are short ranged (contact like) and the binding between two faces is irreversible13. Thus, each face is described as a rigid body of three particles at the vertices. The attractive interaction along the edges and vertices is modeled by a strong inverted-Gaussian potential between particles. The stochastic trajectories of the faces under thermal fluctuations are obtained by solving the corresponding Langevin equations, where the noise term is parameterize by a rotational diffusion coefficient D0 of the lateral faces. To focus on folding time, we suppress misfolding by considering that the pyramid can only fold in one side, as in recent experiments22,23. In the simulations, we imposed such a constraint by pinning the base of the pyramid to a substrate (see section “Methods” for further details).

Fig. 1: Unfolding process and model.
figure 1

We consider pyramids (a) of one base and N lateral faces (N = 5 in the figure). The 2D template of microscopic panels (b) is obtained by cutting the edges between the lateral faces and unfolding the faces. To simulate the folding dynamics, we developed a coarse-grained numerical model where each face is described as a rigid body of three particles (c) at the vertices. The base is described by N particles at the vertices. The interaction between particles is considered pairwise and attractive. The base is pinned to a flat substrate and the lateral faces can only fold in one side.

Full size image

We performed independent simulations for different numbers of lateral faces N, starting from a flat (2D) configuration and running until the final pyramid is obtained. As shown in Fig. 2, we find that the total folding time T is a non-monotonic function of the number of faces N, with an optimal time for five faces. To characterize the dynamics, we define θi as the angle between the face i and the substrate (see scheme in Fig. 3a). Since the motion is constrained by the substrate, \({\theta }_{i}\in \left[0,\pi \right]\).

Fig. 2: Non-monotonic dependence of the folding time on the number of lateral faces.
figure 2

Folding time as a function of the number of lateral faces (N), defined as the total time necessary for all faces to fold into a pyramid. Time is in units of Brownian time, i.e., the average time for a noninteracting face to diffuse over an angular region of size π. Results are obtained numerically by averaging over 2 × 103 independent samples, starting from a flat template, and the error bars are given by the standard error.

Full size image
Fig. 3: Self-folding of a pyramid of N = 3 lateral faces.
figure 3

a Time dependence of the angle θi of each face i = A, B, C with the flat substrate (see scheme). Since the base of the pyramid is pinned and the faces can only move in one side, \({\theta }_{i}\in \left[0,\pi \right]\). Results are for one sample, starting from a flat template (θi(0) = 0). The statistics of θi is consistent with a Brownian process with reflective walls at θi = 0 and θi = π and folding occurs through a sequence of binding events between faces. For the first binding event, two faces need to be at θ* = 3π/4 ± Δ (region in blue) at the same time, where Δ ≈ π/180. In the example, this occurs for faces A and B at time \({t}_{{1}{{\rm{st}}}}\). b If we assume no interaction between A and B outside the blue region, the first binding event can be mapped into a 2D Brownian process, with coordinates θA and θB and a trap in a region where both θi = θ*. \({t}_{{1}{{\rm{st}}}}\) is then the first-passage time. The black line is the time dependence of the 2D Brownian process and the gray line its projection in the two-parameter (θA, θB) space. c After the first binding event, the third face C, performs a 1D Brownian motion until it hits θ*. In the example, this occurs at \({t}_{{2}{{\rm{nd}}}}\). Time is rescaled by Brownian time.

Full size image

As an example, we consider now the folding of a pyramid of three lateral faces (N = 3). The time dependence of the three angles is shown in Fig. 3a. Due to thermal fluctuation, each face jiggles around until the first two faces (A and B in the figure) meet at time \({t}_{{1}{{\rm{st}}}}\) and bind irreversibly, closing the edge between them. The third face (C) also binds to the first two at a later time \({t}_{{2}{{\rm{nd}}}}\). Thus, folding occurs through a sequence of irreversible binding events. Below, we discuss the first and subsequent binding events independently.

As shown in the Supplementary Fig. 1, the statistics of the three time series θi(t) in Fig. 3 is consistent with a 1D Brownian process with reflective boundaries at θi = 0 and θi = π. The short-ranged (attractive) interaction between faces is only effective in a small region of the angular space, θ* = 3π/4 ± Δ, with Δ ≈ π/180 as estimated from the properties of the potential (see Supplementary Note 1). For the first binding event to occur, the angle of two faces need to be at θ* at the same time and, once there, they get trapped. Thus, if we map the motion of each pair of faces j and k into a 2D Brownian process, with coordinates (θj, θk) and a trap at (θ*, θ*), the binding between j and k occurs when the corresponding 2D Brownian process hits the trap (see Fig. 3b). In the general case of N lateral faces a binding event can result either from an edge closing between two adjacent faces or binding between the vertices of two nonadjacent faces. Thus, there are N(N − 1)/2 possible pairs of faces that can bind and the time of the first binding event is the fastest of N(N − 1)/2 first-passage processes.

To estimate the average time TF of the first binding event for a pyramid of N lateral faces, we define g(t) as the first-passage time distribution of a 2D Brownian process. There are N(N − 1)/2 pairs of faces and so the same number of competing Brownian processes. The first binding event is the fastest of all possible ones and thus TF = min {t1, t2, t3 …,  tN(N−1)/2}, where ti are random values following the distribution g(t). If we neglect any correlations between the motion of the different faces, from the theory of order statistics24, we estimate that:

$${T}_{{F}}(N)=\frac{N(N-1)}{2}{\int_{0}^{\infty }}tg(t){\left[{\int_{t}^{\infty }}g(t^{\prime} )dt^{\prime} \right]}^{\frac{N(N-1)}{2}-1}dt,$$
(1)

where the term with the square brackets corresponds to the probability that, provided that a first-passage process occurs at time t, all the remaining N(N − 1)/2 − 1 occur at a later time. g(t) depends on the geometry and initial conditions25,26,27,28,29. For a set of N(N − 1)/2 Brownian processes26,30 starting at the origin (θi(0) = 0):

$${T}_{{F}}(N) \sim 1/{\mathrm{ln}}\,\left(\frac{N(N-1)}{2}\right).$$
(2)

So, the time of the first binding event should decrease with the number of possible pairs. Fig. 4a shows TF in units of Brownian time (see figure caption), for different numbers of lateral faces, obtained numerically by averaging over 2 × 103 samples. The solid line is given by \({T}_{{F}}={\tau }_{{F}}/{\mathrm{ln}}\,\left(N(N-1)/2\right)+{\tau }_{{{F}}_{0}}\), where τF = 1.57 ± 0.02 and \({\tau }_{{{F}}_{0}}=-0.097\pm 0.006\) are obtained by fitting the simulation data. Clearly, the decrease in TF with the number of faces is well described by Eq. (2).

Fig. 4: Dependence on the number of lateral faces.
figure 4

a Time of first binding event (TF) as a function of N(N − 1)/2, where N is the number of lateral faces, for D = D0. The first binding event occurs when two faces have θ = θ* = 3π/4 ± Δ, where Δ ≈ π/180 is the size of the interaction region in the angular space, estimated from the properties of the potential. TF decreases with N. The solid line is given by \({T}_{{F}}={\tau }_{{F}}/{\mathrm{ln}}\,(N(N-1)/2)+{\tau }_{{F}0}\), where τF = 1.57 ± 0.02 and \({\tau }_{{{F}}_{0}}=-0.097\pm 0.006\) are fitting parameters obtained by the least square fit of the simulation data. This expression corresponds to a first-passage time of a 2D Brownian process. b Last binding event time as a function of N − 2, for D = D0. After the first binding event, N − 2 faces remain that fold sequentially. TL is given by the slowest of (N − 2) 1D first-passage events. The solid line is given by \({T}_{{L}}={\tau }_{{L}}\mathop{\sum }\nolimits_{i = 1}^{N-2}\frac{1}{i}\), with τL = 0.474 in units of Brownian time. c Data collapse for the folding time, in units of Brownian time, rescaled by the square of the folding angle \({({\theta }^{* })}^{2}\), as a function of the number of faces N for different values of θ* = {3π/4, 2π/3, 5π/6} and D = {D0, D0/2, 2D0}. D0 is the angular diffusion coefficient of reference. Results are averages over 2 × 103 independent samples and the error bars are the standard error.

Full size image

The dynamics of the subsequent binding events is fundamentally different. While for the first binding event, two faces need to meet at a particular angular θ*, the remaining faces will bind one-by-one as soon as they reach θ*. The folding is complete when all faces reach this value. Thus, each of the subsequent (N − 2) binding events is a 1D first-passage process (see Fig. 3c). We define T as the total folding time and TL = T − TF as the time from the first to the last binding event. Each free face i binds when θi(TF + t) = θ* (with t ≥ 0) for the first time. To estimate TL, we assume that θi(TF) < θ* is for all i and that θi(TF + t) is well described by a 1D Brownian process, with one reflective boundary at θi = 0 and a trap at θ*. TL is then the slowest of the (N − 2) 1D first-passage processes. Thus:

$${T}_{{L}}(N)=(N-2){\int_{0}^{\infty }}tf(t){\left[1-{\int_{t}^{\infty }}f(t^{\prime} )dt^{\prime} \right]}^{(N-2)-1}dt,$$
(3)

where f(t) is the 1D first-passage time distribution and the term with square brackets is the probability that, provided that a first-passage process occurs at time t, all the remaining ones were faster. Assuming that θi(TF) is uniformly distributed in \(\left[0,{\theta }^{* }\right]\), the first-passage time distribution is \(f(t)\approx {e}^{-t/{\tau }_{L}}\), with \({\tau }_{L}=4{{\theta }^{* }}^{2}/{D}_{0}{\pi }^{2}\)31, where D0 is the diffusion coefficient of the Brownian process. This gives:

$${T}_{{L}}(N)={\tau }_{{L}}\mathop{\sum }\limits_{i = 1}^{N-2}\frac{1}{i},$$
(4)

and thus, \({T}_{{L}}(N)\approx {\tau }_{{L}}\left[{\mathrm{ln}}\,(N-2)+\gamma \right]\), where γ is the Euler–Mascheroni constant. Figure 4b depicts TL obtained numerically for different N. The numerical data are consistent with Eq. (4) (solid line).

The dependence on the number of lateral faces N of TF and TL is significantly different. While TF decreases with N, and TL grows. The total folding time T is the sum of the two. Thus, for low values of N, the total folding time is dominated by the time of the first binding event, whereas for large N is the last binding that sets the overall timescale. It is the interplay between these two timescales that explains the minimum observed in Fig. 2.

So far, we considered always the same closing angle θ* and diffusion coefficient D0. Since the motion of the faces is diffusive, we assume that all timescales scale with \(\tau ={{\theta }^{* }}^{2}/2{D}_{0}\), which is the average time for a noninteracting 1D Brownian process to diffuse in an angular region of size θ*. Figure 4c shows the folding time obtained numerically for different values of θ* = {3π/4, 2π/3, 5π/6} and D = {D0, D0/2, 2D0}. For large values of N, we observe a data collapse suggesting that the scaling assumption is valid in this limit. However, for small values of N we observe some deviations. For TL, the expected scaling with τ is only valid if θi(TF) < θ* for all i, which is a good approximation for large N. In this limit, the total folding time is dominated by TL. The solid line is the sum of the solid lines for TF and TL in Fig. 4a, b, respectively, and describes quantitatively the dependence on the number of lateral faces.

Discussion

Under thermal fluctuation, a N-pointed star template of rigid panels and flexible hinges folds into a 3D pyramid of N lateral faces. Folding occurs through a sequence of binding events between pair of faces, but the nature of the first and subsequent binding events is significantly different. For the first binding event, two jiggling faces need to meet at a particular angle, whereas for the subsequent binding events, only one face needs to reach that angle. We hypothesized that the first binding event can be mapped into a first-passage event of a 2D Brownian process27,28,32,33, obtaining an expression for the corresponding time. This expression predicts that the time for the first binding event decreases with N, what describes quantitatively the numerical data. By contrast, to estimate the time for the subsequent binding events, we mapped them into a set of first-passage events in 1D and derived the time for the slowest of them all. We predict that this time should rather grow logarithmically with N − 2, which is also observed numerically. Since the total folding time is the sum of the two times, a non-monotonic dependence on N is found.

Several strategies have been developed to regulate the efficiency and folding time of micrometer templates. For example, the folding of templates coated with cells into 3D cell-laden microstructures is regulated by the concentration and culturing time of cells22. For graphene-based hinges, folding can be tuned by temperature and pH, which enables an external control over the dynamics23. The results reported here show that further control is enabled if one changes the geometry of the template. This is an advantage since, in practice, it is easier to change the number of faces rather than the mechanics of the hinges or the driving forces.

Spontaneous folding at the microscale is an intricate process that might depend on the physical properties of the structure, fluid–structure interactions and thermostat temperature13,14,21. Our numerical simulations show that the motion of each face is well described by a Brownian process. By mapping folding into a set of competing Brownian processes and binding events, we predict accurately the relevant timescales. As in recent experiments22,23, we considered a regular pyramid, a structure where all panels are equivalent, to focus on the dependence on the number of faces. For non-regular pyramids the folding can still be described as a series of binding events of first-passage process in 2D and 1D. However, in general, the closing angles might be different and the time distribution for the first and last folding needs to account for such differences. Also, the faces might differ in shape and size. Such differences are straightforward to include, as they translate into different diffusion coefficients of the corresponding Brownian processes. For more elaborated templates, where complete folding requires a sequence of hierarchical binding events, we also need to consider the possible kinetic pathways of folding.

Methods

To simulate the dynamics of folding, as represented schematically in Fig. 1, we developed a coarse-grained model of a regular pyramid where each lateral (triangular) face is described as a rigid body of three particles located at the vertices. The base of the pyramid is also a rigid body of N particles. All particles have mass m.

The base of the pyramid is pinned to a substrate, i.e., the position of its N particles is constant, and the faces of the pyramid can only move in one side of the substrate. To resolve the trajectories of the faces, we integrate their Langevin equations of motion, using a velocity Verlet scheme implemented in the Large-scale Atomic/Molecular Massively Parallel Simulator34. Specifically, we integrate:

$$M\dot{{{\bf{v}}}_{{\bf{i}}}}(t)=-{\nabla }_{{{\bf{r}}}_{{\bf{i}}}}U-\frac{M}{{\tau }_{{t}}}{{\bf{v}}}_{{\bf{i}}}(t)+\sqrt{\frac{2M{k}_{{B}}T}{{\tau }_{{t}}}}{\xi }_{{t}}^{{\bf{i}}}(t)$$
(5)

for the translational degrees of freedom, and

$$I\dot{{\omega }_{{\bf{i}}}}(t)=-{\nabla }_{{\theta }_{{\bf{i}}}}U-\frac{I}{{\tau }_{{r}}}{\omega }_{{\bf{i}}}(t)+\sqrt{\frac{2I{k}_{{B}}T}{{\tau }_{{r}}}}{\xi }_{{r}}^{{\bf{i}}}(t)$$
(6)

for the rotational ones, where, vi and ωi are the translational and angular velocities of face i. M = 3m is the total mass of each face and I is the moment of inertia to rotate around the edge with the base. τt and τr are the translational and rotational damping times (we consider τr = τt). \({\xi }_{{t}}^{{\bf{i}}}(t)\) and \({\xi }_{{r}}^{{\bf{i}}}(t)\) are stochastic terms that fulfill the fluctuation-dissipation theorem, and U is the net potential from the interaction with all other faces (and base).

There are two relevant parameters for the dynamics: the rotational diffusion coefficient of the faces D0 = kBTτr/I and the closing angle of the pyramid θ* (see Fig. 3). To keep them constant for all N, we fixed the height L of the lateral faces and the mass of the vertices such that θ* and I is always the same (except for Fig. 4, where we change both the rotational diffusion coefficient and θ*).

For the particle–particle interaction (vertices), to describe the binding between faces, we consider an inverted-Gaussian potential given by:

$${U}_{{\rm{blue}}/{\rm{blue}}}({r}_{{b}})=-\epsilon \exp \left[-{\left({r}_{{b}}/\sigma \right)}^{2}\right],$$
(7)

where rb is the distance between vertices, ϵ = 20kBT is the interaction strength that sets the energy scale and σ the width of the Gaussian. The σ is set such that the strength of the interaction is kBT for rb = L/60, corresponding to an angle between faces of  ≈π/180. Without loss of generality, we set kBT = 1 in the simulations.

To constrain the motion of the faces to one side of the substrate, we consider a repulsive interaction between all particles and the substrate (located at a distance of L/10 below the base of the pyramid), described by the repulsive part of a Lennard–Jones potential, with a pre-factor of 4kBT, and that is 0 at a distance of L/50.