Finite mixtures of skew Laplace normal distributions with random skewness

Abstract

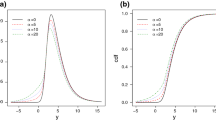
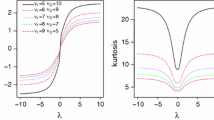
In this paper, the shape mixtures of the skew Laplace normal (SMSLN) distribution is introduced as a flexible extension of the skew Laplace normal distribution which is also a heavy-tailed distribution. The SMSLN distribution includes an extra shape parameter, which controls skewness and kurtosis. Some distributional properties of this distribution are derived. Besides, we propose finite mixtures of SMSLN distributions to model both skewness and heavy-tailedness in heterogeneous data sets. The maximum likelihood estimators for parameters of interests are obtained via the expectation–maximization algorithm. We also give a simulation study and examine a real data example for the numerical illustration of proposed estimators.

Appendices

Appendix A. Identifiability of the mixture model

We will give the following identifiability theorem for the general case of mixture modeling.

Theorem A1

If ${\mathcal{H}} = \left\{ {\mathop \sum \limits_{i = 1}^{g} w_{i} F_{i} \left( {y;{\varvec{\Theta}}} \right), w_{i} \ge 0,\mathop \sum \limits_{i = 1}^{g} w_{i} = 1} \right\}$ of all finite mixtures of the finite family ${\mathcal{F}} = \left\{ {F_{1} \left( y \right),F_{2} \left( y \right), \ldots ,F_{g} \left( y \right)} \right\}$ is identifiable, there is a $g$ real values $y_{1} ,y_{2} , \ldots ,y_{g}$ for the determinant of $F_{i} \left( {y_{j} } \right), 1 \le i,j \le g$. Let ${\mathcal{F}} = \left\{ F \right\}$ be a family of c.d.f’s with transformation $\psi \left( t \right)$ for $t \in S_{\psi }$ (the domain of definition of characteristic function) which the mapping $M:F \to \phi$ is linear. Assume that there is a total ordering ${ \preccurlyeq }$ of ${\mathcal{F}}$ that $F_{1} \prec F_{2}$ shows

• (i) $S_{{\psi_{1} }} \subseteq S_{{\psi_{2} }}$,

• (ii) for some $t \in \bar{S}_{{\psi_{1} }}$, $\mathop {\lim }\limits_{{t \to t_{1} }} \frac{{\psi_{2} \left( t \right)}}{{\psi_{2} \left( t \right)}} = 0$, where $t_{1}$ is independent of $\psi_{2}$.

Then the class ${\mathcal{H}^{\prime}}$ of all finite mixtures of ${\mathcal{F}}$ is identifiable.

Proof of the Theorem A1

We prove the Theorem A1 following the identifiability procedure given by Teicher (1961,1963) and Yakowitz and Spragins (1968). One can also see the papers by Kent (1983), Holzmann et al. (2004), and Holzmann et al. (2006) for further details about identifiability.□

Let ${\mathcal{F}} = \left\{ {F\left( {y;{\varvec{\Theta}}} \right),{\varvec{\Theta}} \in R^{m} } \right\}$ be a family of one-dimensional cumulative distribution functions (c.d.f.’s) that $F\left( {y;{\varvec{\Theta}}} \right)$ is measurable in $R^{1} \times R_{1}^{m}$ where $R_{1}^{m}$ is a Borel subset in Euclidian $m$-space $R^{m}$. The image under the mapping ${\tilde{\mathcal{F}}}$ can be represented by

$$ H\left( y \right) = \mathop \int \limits_{{R_{1}^{m} }} F\left( {y;{\varvec{\Theta}}} \right)dG\left( {\varvec{\Theta}} \right) $$

where $G$ is the $m$-dimensional c.d.f. and $H$ is a $G$-mixture of ${\mathcal{F}}$. Let ${\mathcal{H}}$ be the induced class of mixtures and ${\mathcal{G}}$ be the class of all $m$-dimensional c.d.f.’s $G$. Let ${\mathcal{H}}_{g}$ and ${\mathcal{H}^{\prime}}$, $g = 1,2, \ldots$ be the induced classes of finite mixtures.

Assume that there are two finite sets of elements of ${\mathcal{F}}$ with ${\mathcal{F}}_{1} = \left\{ {F_{i} ,1 \ge i \le g} \right\}$ and ${\mathcal{F}}_{2} = \left\{ {F_{i}^{*} ,1 \ge i \le g^{*} } \right\}$ which hold

$$ \sum\limits_{i = 1}^{g} {w_{i} F_{i} \left( {y;\mu_{i} ,\sigma_{i}^{2} ,\lambda_{i} ,\alpha_{i} } \right)} = \sum\limits_{j = 1}^{{g^{*} }} {w_{i}^{*} F_{i}^{*} \left( {y;\mu_{i}^{*} ,\sigma_{i}^{2*} ,\lambda_{i}^{*} ,\alpha_{i}^{*} } \right)} , $$

(40)

where $0 < w_{i} ,w_{i}^{*} \le 1$ and $\mathop \sum \nolimits_{i = 1}^{g} w_{i} = \mathop \sum \nolimits_{i = 1}^{{g^{*} }} w_{i}^{*} = 1$. It can be written that $F_{i} \prec F_{j} , F_{i}^{*} \prec F_{j}^{*}$ for $i < j$. Assume that $F_{1} \prec F_{1}^{*}$ if $F_{1} \ne F_{1}^{*}$. Next $F_{1} \prec F_{j}^{*} , 1 \le j \le g^{*}$ and after transforming (40) for $t \in T_{1} = S_{{\psi_{1} }} .\left[ {t:\psi_{1} \left( t \right) \ne 0} \right]$

$$ w1 + \mathop \sum \limits_{i = 2}^{g} w_{i} \frac{{\psi_{i} \left( t \right)}}{{\psi_{1} \left( t \right)}} \equiv_{t} \mathop \sum \limits_{j = 1}^{{g^{*} }} w_{i}^{*} \frac{{\psi_{i}^{*} \left( t \right)}}{{\psi_{1} \left( t \right)}}. $$

When $t \to t_{1}$ in $T_{1}$, $w_{1} = 0$, it conflicts with (40) that $w_{1} > 0$. Then, $F_{1} = F_{1}^{*}$ and for any $t \in T_{1}$

$$ \left( {w1 - w_{1}^{*} } \right) + \mathop \sum \limits_{i = 2}^{g} w_{i} \frac{{\psi_{i} \left( t \right)}}{{\psi_{1} \left( t \right)}} \equiv_{t} \mathop \sum \limits_{j = 2}^{{g^{*} }} w_{i}^{*} \frac{{\psi_{i}^{*} \left( t \right)}}{{\psi_{1} \left( t \right)}}. $$

After then, when $t \to t_{1}$ in $T_{1}$, $w_{1} = w_{1}^{*}$, thus,

$$ \sum\limits_{i = 2}^{g} {w_{i} F_{i} \left( {y;\mu_{i} ,\sigma_{i}^{2} ,\lambda_{i} ,\alpha_{i} } \right)} \equiv_{t} \sum\limits_{j = 2}^{{g^{*} }} {w_{i}^{*} F_{i}^{*} \left( {y;\mu_{i}^{*} ,\sigma_{i}^{2*} ,\lambda_{i}^{*} ,\alpha_{i}^{*} } \right)} . $$

Making this reputation for the finite number of times, we get that $F_{i} = F_{i}^{*}$ and $w_{i} = w_{i}^{*}$ for $i = 1,2, \ldots ,\hbox{min} \left( {g,g^{*} } \right)$. Also, if $g \ne g^{*}$, suppose that $g > g^{*}$ and $\mathop \sum \nolimits_{{i = g^{*} + 1}}^{g} w_{i} F_{i} \left( {y;\mu_{i} ,\sigma_{i}^{2} ,\lambda_{i} ,\alpha_{i} } \right) \equiv 0$ claims that $w_{i} = 0, g^{*} + 1 \le i \le g$ in contrast to (40). As a consequence, $g = g^{*} , w_{i} = w_{i}^{*}$ and $F_{i} = F_{i}^{*} , 1 \le i \le g$, shows that ${\mathcal{F}}_{1} = {\mathcal{F}}_{2}$ and they are identifiable on ${\mathcal{H}^{\prime}}$.

Appendix B. The steps of computing KS test statistic

• 1. Sort data in ascending order $y_{\left( 1 \right)} \le y_{\left( 2 \right)} \le \cdots \le y_{\left( n \right)}$.

• 2. Calculate the KS test statistic using the following formula:

$$ D = \mathop {\hbox{max} }\limits_{i = 1,2, \ldots ,n} \left\{ {\frac{i}{n} - \hat{F}\left( {y_{\left( i \right)} } \right),\hat{F}\left( {y_{\left( j \right)} } \right) - \frac{i - 1}{n}} \right\}, $$

where $\hat{F}\left( \cdot \right)$ is the fitted cdf of a specific distribution which should be continuous.

We note that we compute the cdf values of the mixture models given in Sect. 4.2 using the integral function in MATLAB R2017b software for calculating of the KS statistics.