Effective strain gradient continuum model of metamaterials and size effects analysis

Abstract

In this paper, a strain gradient continuum model for a metamaterial with a periodic lattice substructure is considered. A second gradient constitutive law is postulated at the macroscopic level. The effective classical and strain gradient stiffness tensors are obtained based on asymptotic homogenization techniques using the equivalence of energy at the macro- and microscales within a so-called representative volume element. Numerical studies by means of finite element analysis were performed to investigate the effects of changing volume ratio and characteristic length for a single unit cell of the metamaterial as well as changing properties of the underlying material. It is also shown that the size effects occurring in a cantilever beam made of a periodic metamaterial can be captured with appropriate accuracy by using the identified effective stiffness tensors.

1 Introduction

The modeling of solids and structures in the framework of classical Cauchy mechanics has been widely used in diverse fields. However, experimental evidence increasingly shows limitations of this approach to predict the behavior of some materials at small scales (micro- or nanometer scales), where the intrinsic microstructure of the materials becomes crucial [11, 26, 54, 61]. Heterogeneity inherited by microstructure leads to the so-called size effects, which cannot be captured by strain-based Cauchy mechanics. Particularly this is relevant to metamaterials whose effective properties are mainly determined by their microstructure [18, 37, 80, 85]. When metamaterials are tested, small samples may show different deformation behaviors than larger ones [86]. In order to evaluate metamaterials with appropriate accuracy, a qualitative but also quantitative understanding of size effects needs to be included either in a physically feasible way or, as an alternative method, by homogenization or identification of effective material properties. Indeed, size effects can be captured by using FEM and detailed modeling on a microstructural level with a relatively simple constitutive law [83, 84], which means that the size of a mesh should be much smaller than that of the microstructure. The FEM model will readily overpower most of the modern computers. Such analysis is still very time-consuming and unmanageable. Indeed, in engineering practice, it is convenient to replace the heterogeneous material by an equivalent homogeneous material [14, 47]. With the identified material parameters, engineers can efficiently design or optimize new structures or materials [24, 55,56,57, 71]. For this reason, different homogenization procedures have been proposed in the literature, including the well-known Voigt and Reuss bounds. For more examples, see [22, 23, 45, 47].

Often, the so-called representative volume element (RVE) [42, 46, 50, 74] is postulated. The topic of RVE definitions has been of interest in the scientific communities for over half a century. A recent review for this topic can be found in [19]. Such RVE-based methods divide the analysis into two scales: local and global scales. On the local scale, the microstructure is modeled in detail, and effective material properties are determined under boundary conditions. On the global scale, the material is treated as an equivalent homogeneous continuum with the aforementioned effective properties. There are a number of RVE-based methods, such as computational approaches [75], asymptotic homogenization methods [6, 8, 15, 20, 66], and variational-asymptotic methods [17, 88]. However, these methods depend on the ratio, $\epsilon$, of the unit size l to the size of the global region of interest L. Note that a unit cell can be different from an RVE. They are both constructed by considering an inclusion and the matrix of the material, but an RVE can be constituted by several unit cells. In general, the accuracy of RVE-based approaches increases as $\epsilon$ approaching zero. Nevertheless, for certain metamaterials, $\epsilon$ is fixed and sometimes significantly larger than zero. In this case, the size of the microstructure is comparable to the size of the whole structure, and the predicted effective properties will not be able to describe precisely the behavior of the material. In order to tackle these problems and capture these size-dependent phenomena, one possible way is to characterize and homogenize metamaterials in the framework of generalized continuum theories, also known as higher-order theories. Higher-order theories, including strain gradient theory, couple stress theory, micropolar theory, micromorphic theory, and so on, cover the microstructural information, and they are able to mimic the size effects. They have been studied by some researchers extensively, for example, see [5, 30, 35, 36, 38, 52, 59, 62, 76]. The main challenge for the higher-order continuum approach is to determine the corresponding additional constitutive parameters, which are difficult to measure experimentally. Many efforts have been made for the determination of metamaterial parameters [25, 40, 41, 60, 64, 67, 77] in the framework of generalized mechanics.

In [33, 34, 51], effective material parameters were derived in the framework of micropolar theory. In [58], an effective couple stress continuum was used for cellular solids. In a recent study [86], size effects occurring in lattice structures were studied and compared to micropolar elasticity. It is reported that the micropolar continuum model typically underpredicts the stiffness due to the size effects seen in the lattice model by an order of magnitude. In [49], the size-dependent bending, buckling, and vibration phenomena of 2D triangular lattices were investigated using simplified strain gradient theory. The effective elastic moduli, including classical moduli as well as additional moduli, were validated by matching the lattice response in benchmark problems. In [12, 13, 53, 65, 82], classical and higher-order elastic moduli were identified within the Toupin–Mindlin strain gradient theory due to its generality. In [53], the classical and higher-order elastic moduli were identified by means of the fast Fourier transform (FFT) method in the 2D case. In [13], FEM was used to identify these effective material parameters for materials of the so-called D4 as well as D6 symmetry. In [82], the effective material parameters were identified for square lattice structures. It is shown that the approach that was used in [13, 53, 82] guarantees a vanishing strain gradient stiffness tensor if the material is purely homogeneous, and it ensures that the resolved strain gradient parameters are not sensitive to choices of an RVE consisting in the repetition of smaller RVEs but depend upon the intrinsic size of the substructure. There are a few pieces of research in the literature validating the identified effective parameters, especially the higher-order moduli. For this reason, this work will focus on validations of effective materials parameters identified by a homogenization method proposed in [82]. Moreover, how the microstructures influence the effective material parameters is analyzed and discussed. It is also attempted in this work to answer the following question: Are the effective material parameters derived based on the homogenization method capable to capture size effects accurately? The paper is organized as follows: In Sect. 2, the homogenization method by means of asymptotic analysis by considering strain gradient effects is recalled. In Sect. 3, effective material parameters, including the classical as well as higher-order moduli, are obtained. The influences of the volume ratio between inclusions and matrices for a unit cell, of the properties of the solid material as well as of the unit cell sizes on the effective material parameters, are analyzed and discussed. In Sect. 4, three different types of computations, including direct FEM simulation of metamaterials with a very fine mesh, an equivalent Cauchy homogenized model, as well as an equivalent strain gradient homogenized model, are conducted and used to validate the identified effective parameters. size effects presented in cantilever beam bending for a metamaterial are also analyzed. Discussions in Sect. 5 and concluding remarks in Sect. 6 end this paper.

2 Asymptotic homogenization method by considering strain gradient effects

A periodic heterogeneous structure with a 2D domain $\varOmega$ is considered. Unlike the classical homogenization technique, where $\varOmega$ is constituted by an infinite number of RVEs, here $\varOmega$ is constructed with a finite number of RVEs $\varOmega _P$, namely:

$$\begin{aligned} \cup \varOmega _P = \varOmega , \quad \varOmega _P \cap \varOmega _Q = \emptyset , \quad P,Q = 1,2,3,\dots M, P \ne Q \end{aligned}$$

(1)

Assume that the equivalence of strain energy of an RVE at micro- $\varOmega ^\text {m}_P$ and macroscale $\varOmega ^\text {M}_P$ is possible by using different definitions of the microscale energy density $w^\text {m}$ and the macroscale energy density $w^\text {M}$:

$$\begin{aligned} \begin{aligned} \int _{\varOmega _P^\text {m}} { w^\text {m}} \, \mathrm {d} V^\text {m}&= \int _{\varOmega _P^\text {M}} { w^\text {M}} \, \mathrm {d} V^\text {M}, \\ \int _{\varOmega _P^\text {m}} \frac{1}{2} C^\text {m}_{ijkl} u^\text {m}_{i,j} u^\text {m}_{k,l} \, \mathrm {d} V^\text {m}&= \int _{\varOmega _P^\text {M}} \frac{1}{2} \left( C^\text {M}_{ijkl} u^\text {M}_{i,j} u_{k,l}^\text {M} + D_{ijklmn}^\text {M} u_{i,jk}^\text {M} u_{l,mn}^\text {M} \right) \, \mathrm {d} V^\text {M}, \end{aligned} \end{aligned}$$

(2)

where $C^\text {m}_{ijkl}$ is defined in each point of the heterogeneous continuum body $\varOmega _P^\text {m}$, and $C^\text {M}_{ijkl}$ and $D^\text {M}_{ijklmn}$ are the stiffness tensor and strain gradient stiffness tensor of the corresponding homogenized continuum $\varOmega _P^\text {M}$. It should be mentioned that Eq. (2) can be formulated in terms of the strain tensor and the strain gradient tensor as well. The present formulation is, however, equivalent to that in terms of strain tensors because of the symmetry properties of the stiffness tensors. For a discussion of the objectivity of the strain energy, we refer to [82].

The macro- and microscale energies for an RVE are derived by using the same quantity in order to find expressions for the $C^\text {M}_{ijkl}$ and $D^\text {M}_{ijklmn}$. According to [82], the macroscale strain energy for an RVE can be expressed as:

$$\begin{aligned} \begin{aligned}&\int _{\varOmega _P^\text {M}} \frac{1}{2} \left( C^\text {M}_{ijlm} u^\text {M}_{i,j} u^\text {M}_{l,m} + D^\text {M}_{ijklmn} u^\text {M}_{i,jk} u^\text {M}_{l,mn} \right) \, \mathrm {d} V^\text {M} \\&\quad = \frac{1}{2}V^\text {M} \Big ( C^\text {M}_{ijlm} \left\langle {u}_{i,j}^\text {M}\right\rangle \left\langle {u}_{l,m}^\text {M}\right\rangle + \left( C^\text {M}_{ijlm} \bar{I}_{kn} + D^\text {M}_{ijklmn} \right) \left\langle {u}_{i,jk}^\text {M}\right\rangle \left\langle {u}_{l,mn}^\text {M}\right\rangle \Big ) , \end{aligned} \end{aligned}$$

(3)

where

$$\begin{aligned} \begin{aligned} \bar{I}_{kn} = \frac{1}{V^\text {M}} \int _{\varOmega _P^\text {M}} \left( X_k-\overset{\text {c}}{X}_k\right) \left( X_n-\overset{\text {c}}{X}_n\right) \, \mathrm {d} V^\text {M} \ , \ \ \left\langle {u}_{i,j}^\text {M}\right\rangle = u^\text {M}_{i,j}\Big |_{\overset{\text {c}}{{\varvec{X}}}} \ , \ \ \left\langle {u}_{i,jk}^\text {M} \right\rangle = u^\text {M}_{i,jk} \Big |_{\overset{\text {c}}{{\varvec{X}}}}, \end{aligned} \end{aligned}$$

(4)

$\overset{\text {c}}{{\varvec{X}}}$ is the geometric center of the RVE. Therefore, the macroscale strain energy for an RVE is expressed in terms of the macroscopic gradient and the second gradient of displacement. If the microscale strain energy can be expressed by using the same quantities, the expressions for $C^\text {M}_{ijkl}$ and $D^\text {M}_{ijklmn}$ can be found. For this reason, the asymptotic homogenization method is employed at the microscale when deriving the microscale strain energy.

Following the asymptotic homogenization method in [82], the left-hand side of Eq. (2) is reformulated. The asymptotic homogenization method defines two levels of length scales. One is the macroscopic level $\varvec{X}$ to describe the global variation of a considered field, and the other one is the microscopic level $\varvec{y}$, which associates with the RVE and represents the local fluctuation of such a field. The relationship between $\varvec{X}$ and $\varvec{y}$ is the following:

$$\begin{aligned} y_j= \frac{1}{\epsilon }\left( X_j - \overset{\text {c}}{X}_j \right) , \end{aligned}$$

(5)

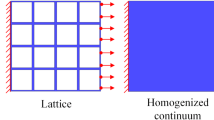
where $\epsilon$ is a scaling or homothetic ratio between the $\varvec{X}$ and $\varvec{y}$. Technically, $\epsilon$ can be set to be equal to l/L by magnifying the size of an RVE from l to L, as shown in Fig. 1. It should be noted that $\epsilon$ is regarded as zero in the classical homogenization technique since the macroscopic length L is infinite. However, in our case of finite macroscopic length L, $\epsilon$ has a finite value. We assume that field quantities, such as displacement, stress, and strain, vary as smoothly as required at the macroscopic level. At the microscopic level, the field quantities are assumed to be periodic, and their values fluctuate around the macroscopic values.

Fig. 1

A Cauchy heterogeneous metamaterial obtained by repeating unit cells periodically. The unit cell contains a square inclusion (white) within the matrix (blue). The unit cell is magnified $1/\epsilon$ times at local coordinate by using a homothetic ratio (color figure online)

Following [82], the displacement field of an RVE at macroscopic coordinate $\varvec{X}$ is expanded with respect to $\epsilon$ as a power series:

$$\begin{aligned} \varvec{u ^\text {m}}(\varvec{X}) = \overset{0}{\varvec{u}}( \varvec{X}, \varvec{y}) + \epsilon \overset{1}{\varvec{u}}(\varvec{X},\varvec{y}) + \epsilon ^2 \overset{2}{\varvec{u}}(\varvec{X}, \varvec{y}) + \dots , \end{aligned}$$

(6)

where $\overset{n}{\varvec{u}}( \varvec{X}, \varvec{y})$ (n = 0, 1, 2, ...) are assumed to be $\varvec{y}$-periodic. The first term $\overset{0}{\varvec{u}}( \varvec{X}, \varvec{y})$ depends only on $\varvec{X}$ [82], and thus, $\overset{0}{\varvec{u}}( \varvec{X})$ is assumed to be the macroscopic displacement field.

Within an RVE, the governing equation reads

$$\begin{aligned} \begin{aligned} \big ( C_{ijkl}^\text {m} u^\text {m}_{k,l} \big )_{,j} + f_{i} = 0 \quad \forall \varvec{X} \in \varOmega _P^\text {m}, \end{aligned} \end{aligned}$$

(7)

where $\varvec{f}$ is the body force field. By substituting Eq. (6) into Eq. (7) and after solving partial differential equations, Eq. (6) can be rewritten as

$$\begin{aligned} u^\text {m}_i(\varvec{X},\varvec{y}) = {u}_i^\text {M}(\varvec{X}) + \epsilon \varphi _{abi}(\varvec{y}) {u}_{a,b}^\text {M}(\varvec{X}) + \epsilon ^2 \psi _{abci}(\varvec{y}) {u}_{a,bc}^\text {M}(\varvec{X}) + \dots , \end{aligned}$$

(8)

where $\varphi _{abi}(\varvec{y})$ and $\psi _{abci}(\varvec{y})$ are both $\varvec{y}$-periodic. They are the solutions of the following two partial differential equations,

$$\begin{aligned}&\frac{\partial }{\partial y_j} \bigg ( C_{ijkl}^\text {m} \left( \frac{\partial \varphi _{abk}}{\partial y_l} + \delta _{ak} \delta _{bl} \right) \bigg ) = 0, \end{aligned}$$

(9)

$$\begin{aligned}&\frac{\partial }{\partial y_j} \bigg ( C_{ijkl}^\text {m} \left( \frac{\partial \psi _{abck}}{\partial y_l} + \varphi _{abk} \delta _{lc} \right) \bigg ) + C_{ickl}^\text {m} \left( \frac{\partial \varphi _{abk}}{\partial y_l} + \delta _{ka} \delta _{lb} \right) - {C}_{icab}^\text {M} = 0. \end{aligned}$$

(10)

The derivation of Eqs. (9) and (10) can be found in the appendix of [82]. By writing the gradient of the microscale displacement by neglecting terms higher than second gradients, we obtain

$$\begin{aligned} \begin{aligned} u^\text {m}_{i,j} = L_{abij}\left\langle {u}_{a,b}^\text {M} \right\rangle + \epsilon M_{abcij} \left\langle {u}_{a,bc}^\text {M} \right\rangle + \dots , \end{aligned} \end{aligned}$$

(11)

where

$$\begin{aligned} \begin{aligned} L_{abij}&= \delta _{ia} \delta _{jb} + \frac{\partial \varphi _{abi}}{\partial y_j}, \\ M_{abcij}&= y_{c} \left( \delta _{ia} \delta _{jb} + \frac{\partial \varphi _{abi}}{\partial y_j} \right) + \left( \varphi _{abi} \delta _{jc} + \frac{\partial \psi _{abci} }{\partial y_j} \right) . \end{aligned} \end{aligned}$$

(12)

By using the latter on the left-hand side of Eq. (2), the microscale energy becomes

$$\begin{aligned} \begin{aligned}\int _{\varOmega _P^\text{ m }} \frac{1}{2} C^\text{ m}_{ijkl} u^\text{ m}_{i,j} u^\text{ m}_{k,l} \, \mathrm {d} V ^\text{ m } = \frac{V^\text{ M }}{2}\Big ( \bar{C}_{abcd} \left\langle {u}_{a,b}^\text{ M }\right\rangle \left\langle {u}_{c,d}^\text{ M }\right\rangle + \bar{D}_{abcdef}\left\langle {u}_{a,bc}^\text{ M }\right\rangle \left\langle {u}_{d,ef}^\text{ M }\right\rangle + \bar{G}_{abcde}\left\langle {u}_{a,b}^\text{ M }\right\rangle \left\langle {u}_{c,de}^\text{ M }\right\rangle \Big )\end{aligned} \end{aligned}$$

(13)

with

$$\begin{aligned} \begin{aligned} \bar{C}_{abcd}&= \frac{1}{V^\text {M}} \int _{\varOmega _P^\text {m}} C_{ijkl}^\text {m} L_{abij} L_{cdkl} \, \mathrm {d} V^\text {m}, \\ \bar{D}_{abcdef}&= \frac{\epsilon ^2}{V^\text {M}} \int _{\varOmega _P^\text {m}} C_{ijkl}^\text {m} M_{abcij} M_{defkl} \, \mathrm {d} V^\text {m}, \\ \bar{G}_{abcde}&= \frac{2\epsilon }{V^\text {M}} \int _{\varOmega _P^\text {m}} C_{ijkl}^\text {m} L_{abij} M_{cdekl} \, \mathrm {d} V^\text {m}. \end{aligned} \end{aligned}$$

(14)

In the case of centrosymmetric materials, the rank 5 tensor vanishes, $\bar{\varvec{G}}=0$. By comparing with Eq. (3), the expressions for $C^\text {M}_{ijlm}$ and $D^\text {M}_{ijklmn}$ can be obtained as:

$$\begin{aligned} \begin{aligned} C^\text {M}_{ijlm}&= \bar{C}_{ijlm}, \\ C^\text {M}_{ijlm} \bar{I}_{kn} + D^\text {M}_{ijklmn}&= \bar{D}_{ijklmn}, \end{aligned} \end{aligned}$$

(15)

where

$$\begin{aligned} \begin{aligned} \bar{I}_{kn} = \frac{1}{V^\text {M}} \int _{\varOmega _P^\text {M}} \left( X_k-\overset{\text {c}}{X}_k\right) \left( X_n-\overset{\text {c}}{X}_n\right) \, \mathrm {d} V^\text {M} = \frac{\epsilon ^2}{V^\text {M}} \int _{\varOmega _P^\text {m}}y_k y_n \, \mathrm {d} V^\text {M}. \end{aligned} \end{aligned}$$

(16)

They can also be rewritten as:

$$\begin{aligned} \begin{aligned} C^\text {M}_{abcd}&= \frac{1}{V^\text {M}} \int _{\varOmega _P^\text {m}} C_{ijkl}^\text {m} L_{abij} L_{cdkl} \, \mathrm {d} V^\text {m}, \\ D^\text {M}_{abcdef}&= \frac{\epsilon ^2}{V^\text {M}} \left( \int _{\varOmega _P^\text {m}} C_{ijkl}^\text {m} M_{abcij} M_{defkl} \, \mathrm {d} V^\text {m} - C^\text {M}_{abef} \int _{\varOmega _P^\text {m}}y_c y_d \, \mathrm {d} V^\text {M} \right) . \end{aligned} \end{aligned}$$

(17)

3 Determination of effective material parameters

The set of factors influencing the effective properties contains the volume fraction of the matrix, the properties of the underlying material, and the size of unit cells. The way they affect the effective material properties is investigated quantitatively in this section. The computations for the identification process are performed by means of FEM using the FEniCS computing platform. For the implemented weak forms, we refer to [82]. A metamaterial constituted with square inclusions is studied. The constituents of the metamaterial (inclusions and matrix) are linear elastic isotropic materials characterized by two independent parameters (Young’s modulus and Poisson’s ratio). After homogenization, the continuum model is not isotropic at the macroscale of observation. Indeed, it is of D4-invariant symmetry [9, 10, 67]. The inclusions can be voids, with their material parameters being zero. Indeed, small values for these material parameters are used numerically. In this case, the metamaterial can also be regarded as a lattice structure. The effective moduli of the metamaterial are plotted as the functions of volume fraction of matrix, sizes of the unit cell as well as the properties of underlying material. The plots are shown in Figs. 2, 3 and 4, respectively. The Voigt notations used in this paper are shown in Tables 1 and 2. There are 3 independent parameters in the classical stiffness tensor, and there are 6 independent parameters in the strain gradient stiffness tensor as shown in what follows.

Table 1 Voigt notation used for 2D strain tensors

Table 2 Voigt notation used for 2D strain gradient tensors

$$\begin{aligned}&\left[ \begin{matrix} C_{1111}&{} \quad C_{1122} &{}\quad 0 \\ &{}\quad C_{1111} &{} \quad 0 \\ \mathrm{sym} &{} \quad &{} \quad C_{1212} \\ \end{matrix} \right] , \\&\left[ \begin{matrix} D_{111111}&{}\quad D_{111221} &{}\quad D_{111122} &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ &{} \quad D_{221221} &{}\quad D_{221122} &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ &{} \quad &{}\quad D_{122122} &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ &{} \quad &{} \quad &{}\quad D_{111111} &{}\quad D_{111221} &{}\quad D_{111122} \\ &{} \quad \mathrm{sym} &{} \quad &{} \quad &{}\quad D_{221221} &{}\quad D_{221122} \\ &{} \quad &{} \quad &{} \quad &{} \quad &{}\quad D_{122122} \\ \end{matrix} \right] . \end{aligned}$$

3.1 Influence of the volume fraction of matrix

A metamaterial whose microstructure is constructed with square voids inside a matrix, which is shaped like a lattice structure, is studied. The material parameters used for matrix are Young’s modulus $E = 100$ MPa and Poisson’s ratio $\nu = 0.3$. The material properties of the inclusions are all zero. The size of the unit cell l is set to 1 mm. The thickness of the cell wall t varies from 0.1 to 1.0 mm, leading to a change of the volume fraction $V_f$ of the matrix from 19 to 100% as indicated in Table 3. As shown in Fig. 2, with the increasing of the volume ratio of the matrix, the effective classical stiffness parameters increase accordingly. However, effective strain gradient parameters increase at first, and then, they decrease. When the volume ratio is 100%, the material is homogeneous, and the effective strain gradient parameters become zero. This is consistent with intuitive understandings.

Table 3 Varying the volume ratio of the matrix

Fig. 2

Effective material parameters versus volume ratio of matrix

3.2 Influence of the size of a unit cell

In this section, the size of the unit cell l varies in the set of values: 1 mm, 0.5 mm, and 0.2 mm. The thickness of the cell wall t is kept at 0.2 mm meaning the volume fraction of the matrix is fixed as 36% as indicated in Table 4. The material parameters used for the matrix entail Young’s modulus $E = 100$ MPa and Poisson’s ratio $\nu = 0.3$, while the inclusions are voids. The results are shown in Fig. 3. Corresponding to the variation of the size of the unit cell, it is found that the effective classical stiffness parameters are unchanged due to the fact that they have the same topology and volume fraction of matrix. However, the effective strain gradient stiffness parameters are sensitive to it. When decreasing the size of the unit cell, the effective stiffness parameters decrease as well. Indeed, when the size of the unit cell vanishes, the material tends to be homogeneous and in this case, the effective strain gradient stiffness parameters tend to be zero. Actually, the values of the effective strain gradient parameters are linearly dependent on $\epsilon ^2$. This can also be observed in Eq. (17).

Table 4 Varying the size of unit cell

Fig. 3

Effective material parameters versus size of a unit cell

3.3 Influence of the properties of base materials

In this section, Young’s modulus of the base material for inclusions is set to 0 MPa, 10 MPa, 30 MPa, 50 MPa, 70 MPa, 90 MPa. The Poisson’s ratio of the inclusions is the same for all cases studied here, $\nu = 0.3$. The properties of the base material for the matrix are kept at 100 MPa for Young’s modulus and Poisson’s ratio $\nu = 0.3$. The sizes of the unit cell l are all 1 mm. The thickness of the cell wall t is kept at 0.2 mm, which means the volume fraction of the matrix is fixed at 36% as indicated in Table 5. The results are shown in Fig. 4. It is indicated that with increasing Young’s modulus of the inclusions, the effective classical stiffness parameters monotonously increase. Although not every effective, the strain gradient parameter shows a monotonous trend, the dominant one, $D_{221221}$ (with the biggest absolute value), shows a monotonously decreasing trend. All the effective strain gradient parameters reach zero when the material is homogeneous. (Young’s modulus ratio between the matrix and inclusion is 1.)

Table 5 Varying the properties of base materials

Fig. 4

Effective material parameters versus properties of base materials

Fig. 5

Three types of conducted simulations and boundary conditions applied

Fig. 6

Cantilever beam: geometry and boundary conditions

4 Investigations of size effects by using the identified parameters

In order to investigate size effects and validate the identified parameters, comparisons are made employing FEM computations among a direct calculation of heterogeneous metamaterial, an equivalent Cauchy homogeneous continuum, as well as an equivalent strain gradient homogeneous continuum. Bending tests for a cantilever beam are modeled and studied for these three cases. The left edge of the beam is fixed in both x and y directions. Traction from 0 to 100 Pa (0.0001 MPa) is applied incrementally at the right edge of the beam along the vertical direction as shown in Fig. 5.

Table 6 Identified effective parameters $V_f = 19\%$

Fig. 7

Comparisons of lattice, Cauchy continuum, and strain gradient continuum for RVE with volume ratio 19%

Table 7 Identified effective parameters $V_f = 36\%$

Table 8 Identified effective parameters $V_f = 51\%$

Table 9 Identified effective parameters $V_f = 75\%$

Table 10 Identified effective parameters $V_f = 91\%$

Fig. 8

Comparisons of lattice, Cauchy continuum, and strain gradient continuum for RVE with volume ratio 36%

Fig. 9

Comparisons of lattice, Cauchy continuum, and strain gradient continuum for RVE with volume ratio 51%

Fig. 10

Comparisons of lattice, Cauchy continuum, and strain gradient continuum for RVE with volume ratio 75%

Fig. 11

Comparisons of lattice, Cauchy continuum, and strain gradient continuum for RVE with volume ratio 91%

Fig. 12

Comparisons of maximum deflection $\varvec{u}_y$ and strain energy versus volume fraction of matrix

Fig. 13

Cantilever beam: geometry and boundary conditions

A Lagrange element with quadratic shape function is used for the direct computation and in case of the equivalent Cauchy homogeneous continuum. It is known that for the numerical implementation of strain gradient elasticity, at least $C^1$ continuity is mandatory. In order to fulfill this requirement, isogeometric FEM is employed with non-uniform rational Bezier spline (NURBS)-based shape functions in the computations of the equivalent strain gradient homogeneous continuum case [21, 39, 43, 44, 48, 63, 69]. A derivation of the weak form of the strain gradient elasticity can be found in [1, 81]. The maximum deflection $\varvec{u}_y$ and deformation energies in the computations are calculated for comparison.

Simulations are carried out as follows:

• Five bending tests of cantilever beams constructed by RVEs for different volume fractions of the matrix, 19%, 36%, 51% , 75%, 91%.

• Three bending tests of cantilever beams constructed by RVEs with different unit cell sizes, 1 mm , 0.5 mm, 0.2 mm.

• Three bending tests of cantilever beams with different macrolengths (50 mm, 40 mm, 30 mm) but unchanged microstructures.

• Six bending tests of cantilever beams constructed by RVEs with different properties of base materials.

4.1 Different volume fractions of matrix

In this section, five bending tests of cantilever beams constructed by RVEs with volume fraction of matrix 19%, 36%, 51%, 75%, 91% are examined, as shown in Fig. 6. The macrolength L of beams is set to be 50 mm. The microlength l of the RVE is the same l = 1 mm in all five cases. The thickness t of the wall of the RVE is changing between 0.1 mm, 0.2 mm, 0.3 mm, 0.5 mm, 0.7 mm. These geometry parameters as well as the identified effective parameters can be found from Tables 6, 7, 8, 9, and 10. It can be observed from the figures (Figs. 7, 8, 9, 10, 11) that the results of homogenized strain gradient continua show a good quantitative match with direct computations of lattice structures both for the displacement field and for the strain energy. When the volume fraction of matrix $V_f$ becomes larger and larger, the discrepancy between the direct computations of lattice structures and homogenized Cauchy continuum becomes smaller and smaller. When the volume fraction of the matrix is equal to 91%, the results of the homogenized Cauchy continuum show a good agreement with direct computations, as depicted in Fig. 12.

Table 11 Identified effective parameters $l = 0.5$ mm

Table 12 Identified effective parameters $l = 0.2$ mm

Fig. 14

Comparisons of lattice, Cauchy continuum, and strain gradient continuum for unit cell with $l = 0.5$ mm

Fig. 15

Comparisons of lattice, Cauchy continuum, and strain gradient continuum for unit cell with $l = 0.2$ mm

Fig. 16

Comparisons of maximum deflection $\varvec{u}_y$ and strain energy with regard to microstructure size l

Fig. 17

Cantilever beams with the different macrolength L and the same microstructures

Fig. 18

Comparisons of lattice, Cauchy continuum, and strain gradient continuum for $L = 40$ mm

Fig. 19

Comparisons of lattice, Cauchy continuum, and strain gradient continuum for $L = 30$ mm

Fig. 20

Comparisons of maximum deflection $\varvec{u}_y$ and strain energy with regard to the macrolength L

Fig. 21

Cantilever beams constructed by RVEs with inclusions (red) and matrices (blue) (color figure online)

4.2 Different unit cell sizes

In this section, three bending tests of cantilever beams constructed by RVEs with different unit cell sizes 1 mm, 0.5 mm, 0.2 mm are compared, as shown in Fig. 13. The effective material parameters identified are shown in Tables 7, 11, and 12. We conclude that the homogenized strain gradient continua match well with the direct computations of lattice structures as indicated in Figs. 14, 15, and 16. With decreasing unit cell size, the results (strain energy and displacement field) of homogenized strain gradient continua are gradually converging to the results of the homogenized Cauchy continua, as shown in Fig. 16. The difference between the results (strain energy and displacement field) with a few unit cells and many unit cells must be attributed to a size-effect. This size-effect is largest when there are few unit cells. In other words, if the microstructure is comparable to macroscopic structures, size effects cannot be ignored.

4.3 Different macrolengths

In this section, three bending tests of cantilever beams with different macrolengths ($L = 50$ mm, 40 mm, 30 mm) but the same microstructure ($l = 1$ mm, $V_f= 36\%$, $t= 0.2$ mm) are compared, as shown in Fig. 17. The identified effective material parameters can be found in Table 7. As indicated in Figs. 8, 18, and 19, homogenized strain gradient continua results match well with direct computations of lattice structures. It should be remarked that (see Fig. 20) with increasing macrolength L of the beams, the differences between the Cauchy continua and the lattice structures increase. This occurs because if L increases, the beam will be softer, which leads to a larger deflection. This will conduct an increase in the bending energy resulting in the aforementioned large differences (Fig. 21).

4.4 Different material properties

Six bending tests of cantilever beams constructed by RVEs with different properties of underlying material are compared in this section. The Young’s modulus of the inclusions changes between 0, 10 MPa, 30 MPa, 50 MPa, 70 MPa, 90 MPa. The Young’s modulus of the matrix is kept at 100 MPa. The Poisson ratios for the inclusions and the matrix are equal to 0.3. The macrolengths L of the beams and the microlengths l of the microstructures are equal to 50 mm and 1 mm, respectively, in all cases. The other microstructure-related parameters, t, $V_f$, as well as the identified effective material parameters can be found in Tables 7, 13, 14, 15, 16, and 17.

The figures (Figs. 22, 23, 24, 25, 26) reveal that the results of homogenized strain gradient continua agree well with the results for heterogeneous continua. The differences between the homogenized Cauchy continuum and the heterogeneous continuum are due to size effects. It can also be observed from Fig. 27 that for an increasing ratio of Young’s modulus between the inclusions and the matrices ($E_\mathrm{inc}/E_\mathrm{mat}$), the size effects decay and the homogenized Cauchy continua show a satisfactory agreement with the heterogeneous continua.

Table 13 Identified effective parameters

Fig. 22

Comparisons of heterogeneous continuum, homogenized Cauchy continuum, and homogenized strain gradient continuum for $E_{\text {inc}} = 10$ MPa

Table 14 Identified effective parameters

Fig. 23

Comparisons of heterogeneous continuum, homogenized Cauchy continuum, and homogenized strain gradient continuum for $E_{\text {inc}} = 30$ MPa

5 Discussions

It should be noted that in this work, the periodicity of the microstructures and the linear elastic constituents of the metamaterial are required. The presented results show how the effective material properties change when varying the unit cell properties (volume fraction of matrix $V_f$, unit cell length l, and the material properties of base material $E_\mathrm{inc}$ and $E_\mathrm{mat}$). It was demonstrated that when the size of the microstructure of some metamaterial is comparable to the size of the whole structure, size effects become clearly visible. For instance, when $V_f$ decreases, the resistance to curvature of the microstructures tends to grow, but the normal and shear strains remain relatively constant, which leads to a size-effect. The homogenized strain gradient continua are able to model such size effects because the strain gradient energies cover the deformation energies resulting from local curvatures, which are not taken into account by homogenized Cauchy continua.

Table 15 Identified effective parameters

Fig. 24

Comparisons of heterogeneous continuum, homogenized Cauchy continuum, and homogenized strain gradient continuum for $E_{\text {inc}} = 50$ MPa

Table 16 Identified effective parameters

Fig. 25

Comparisons of heterogeneous continuum, homogenized Cauchy continuum, and homogenized strain gradient continuum for $E_{\text {inc}} = 70$ MPa

The size effects can also be examined by making use of the homogenization method for different metamaterials under different boundary conditions, for example, metamaterials of D4-invariant, D6-invariant, Z2-invariant, etc., as shown in [9] under stretching, shearing, transverse bending [86]. In a specific case, the pantographic metamaterial which has been largely studied by dell’Isola and his colleagues [7, 29, 31, 32, 68, 70, 72, 73, 78, 79] is a so-called higher gradient material [2,3,4, 16, 27, 28]. It is also possible to determine the effective material parameters of a pantographic metamaterial by using this method. Note that the investigated size effects result from the bending deformation of the cantilever beam. Nevertheless, it should be mentioned that the mechanism of size effects could also be the result of the so-called edge effects [58, 87], which lead to a softer response of structures. Therefore, in order to understand size effects, softening effects must be studied, and this will be left for the future.

Table 17 Identified effective parameters

Fig. 26

Comparisons of heterogeneous continuum, homogenized Cauchy continuum, and homogenized strain gradient continuum for $E_{\text {inc}} = 90$ MPa

Fig. 27

Comparisons of maximum deflection $\varvec{u}_y$ and strain energy with regard to the ratio of Young’s modulus of inclusion and matrix

As can be observed from previous sections, some negative values in the strain gradient stiffness tensor result. It is physically allowed as long as the strain gradient stiffness tensor is positive semi-definite. Indeed, an equivalence of strain energies for one RVE was used. At the microscale, the constituents of the RVE are linear elastic, which means that the strain energy (please see Eq. (2)) is always positive when specifying a specific Young’s modulus and Poisson’s ratio. Therefore, the corresponding strain energy for the RVE is always positive with the identified effective parameters at the macroscale. In the case of FEM, if the size of the FEM element is larger than or equal to that of RVE, an outcome of positive energy for the FEM computation is ensured. This was demonstrated also in [13, 53]. Fortunately, in the present work isogeometric analysis was utilized, and it is possible to specify a relatively big size of elements, and convergence of computations is assured by setting a higher polynomial degree of NURBS. Please note that choosing a bigger size of elements than RVE in FEM is a sufficient but not a necessary condition to ensure the positive-definite of the effective material parameters.

6 Conclusions

A homogenization method based on asymptotic analysis considering higher-order terms is utilized in this paper to identify the effective classical and strain gradient material parameters. A metamaterial of the so-called D4 invariant symmetry was investigated. The mathematical form of identified material parameters is in perfect agreement with the rigorous theoretical predictions of the results in [9]. The influences of the volume fraction of the matrix, the unit cell sizes, as well as the properties of the underlying material on the effective material properties, were investigated quantitatively. The size effects manifesting in a cantilever beam were investigated by using the identified effective material parameters. It is found that the homogenized Cauchy continua cannot capture the size effects, and the homogenized strain gradient continua match well with the size-dependent phenomena. This is due to the fact that the microstructural information is contained in the higher-order moduli. In addition, an investigation of critical buckling load, as well as eigenfrequencies based on the effective material parameters, is possible. An extension to the 3D case of this work is natural, which will be carried out in the future as well.