Hostname: page-component-8448b6f56d-wq2xx Total loading time: 0 Render date: 2024-04-25T05:19:01.368Z Has data issue: false hasContentIssue false
  • English
  • Français

Resilience of the rank of random matrices

Part of: Probability theory on algebraic and topological structures

Published online by Cambridge University Press:  28 August 2020

Asaf Ferber ,
Kyle Luh  and
Gweneth McKinley
Asaf Ferber
Affiliation:
Department of Mathematics, University of California, Irvine, CA92697, USA
Kyle Luh
Affiliation:
Department of Mathematics, University of Colorado Boulder, Campus Box 395, 2300 Colorado Avenue, Boulder, CO80309-0395, USA
Gweneth McKinley*
Affiliation:
Department of Mathematics, University of California, San Diego, 9500 Gilman Drive, La Jolla, CA92093-0112, USA
*
*Corresponding author. Email: gmckinley@ucsd.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

Let M be an n × m matrix of independent Rademacher (±1) random variables. It is well known that if 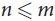$n \leq m$, then M is of full rank with high probability. We show that this property is resilient to adversarial changes to M. More precisely, if 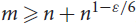$m \ge n + {n^{1 - \varepsilon /6}}$, then even after changing the sign of (1 – ε)m/2 entries, M is still of full rank with high probability. Note that this is asymptotically best possible as one can easily make any two rows proportional with at most m/2 changes. Moreover, this theorem gives an asymptotic solution to a slightly weakened version of a conjecture made by Van Vu in [17].

MSC classification

Primary: 60B20: Random matrices (probabilistic aspects; for algebraic aspects see )
Type
Paper
Information
Combinatorics, Probability and Computing , Volume 30 , Issue 2 , March 2021 , pp. 163 - 174
Check for updates
Copyright
© The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bourgain, J., Vu, V. H. and Wood, P. M. (2010) On the singularity probability of discrete random matrices. J. Funct. Anal. 258 559–603.CrossRefGoogle Scholar
Campos, M., Mattos, L., Morris, R. and Morrison, N. (2019) On the singularity of random symmetric matrices. arXiv:1904.11478Google Scholar
Ferber, A. and Jain, V. (2019) Singularity of random symmetric matrices–a combinatorial approach to improved bounds. Forum of Mathematics, Sigma 7 E22. doi: 10.1017/fms.2019.21 CrossRefGoogle Scholar
Ferber, A., Jain, V., Luh, K. and Samotij, W. (2019) On the counting problem in inverse Littlewood–Offord theory. arXiv:1904.10425Google Scholar
Halász, G. (1977) Estimates for the concentration function of combinatorial number theory and probability. Period. Math. Hungar. 8 197–211.CrossRefGoogle Scholar
Jain, V. (2019) The strong circular law: a combinatorial view. arXiv:1904.11108Google Scholar
Jain, V. (2019) Approximate Spielman–Teng theorems for the least singular value of random combinatorial matrices. To appear in Israel J. Math. arXiv:1904.10592Google Scholar
Kahn, J., Komlós, J. and Szemerédi, E. (1995) On the probability that a random ±1-matrix is singular. J. Amer. Math. Soc. 8 223–240.Google Scholar
Komlós, J. (1967) On the determinant of (0, 1) matrices. Studia Sci. Math. Hungar 2 7–21.Google Scholar
Luh, K., Meehan, S. and Nguyen, H. H. (2019) Random matrices over finite fields: methods and results. arXiv:1907.02575Google Scholar
Nguyen, H. H. (2013) On the singularity of random combinatorial matrices. SIAM J. Discrete Math. 27 447–458.CrossRefGoogle Scholar
Rudelson, M. and Vershynin, R. (2008) The Littlewood–Offord problem and invertibility of random matrices. Adv. Math. 218 600–633.CrossRefGoogle Scholar
Tao, T. and Vu, V. (2007) On the singularity probability of random Bernoulli matrices. J. Amer. Math. Soc. 20 603–628.CrossRefGoogle Scholar
Tao, T. and Vu, V. H. (2009) Inverse Littlewood–Offord theorems and the condition number of random discrete matrices. Ann. of Math. (2) 169 595–632.CrossRefGoogle Scholar
Tikhomirov, K. (2020) Singularity of random Bernoulli matrices. Annals of Mathematics 191, 593–634.CrossRefGoogle Scholar
Vershynin, R. (2014) Invertibility of symmetric random matrices. Random Struct. Algorithms 44 135–182.CrossRefGoogle Scholar
Vu, V. (2008) Random discrete matrices. In Horizons of Combinatorics, Vol. 17 of Bolyai Society Mathematical Studies, pp. 257–280. Springer.CrossRefGoogle Scholar