Consistent numerical implementation of hypoelastic constitutive models

Abstract

In hypoelastic constitutive models, an objective stress rate is related to the rate of deformation through an elasticity tensor. The Truesdell, Jaumann, and Green–Naghdi rates of the Cauchy and Kirchhoff stress tensors are examples of the objective stress rates. The finite element analysis software ABAQUS uses a co-rotational frame which is based on the Jaumann rate for solid elements and on the Green–Naghdi rate for shell and membrane elements. The user subroutine UMAT is the platform to implement a general constitutive model into ABAQUS, but, in order to update the Jacobian matrix DDSDDE in UMAT, the model must be expressed in terms of the Jaumann rate of the Kirchhoff stress tensor. This study aims to formulate and implement various hypoelastic constitutive models into the ABAQUS UMAT subroutine. The developed UMAT subroutine codes are validated using available solutions, and the consequence of using wrong Jacobian matrices is elucidated. The UMAT subroutine codes are provided in the “Electronic Supplementary Material” repository for the user’s consideration.

1 Introduction

Hypoelasticity is a rate form of elastic material model [1], in which an objective stress rate is linearly related to the rate of deformation by means of a fourth-order elasticity tensor which, in general, is not obtainable from a strain energy density. Originally, Dienes [2] showed that the zero-graded hypoelastic model, i.e. a hypoelastic model with constant isotropic elasticity tensor, exhibits oscillation in simple shear, if it is constructed based on the Jaumann rate of the Cauchy stress. However, zero-graded hypoelastic models which are based on the Truesdell or Green–Naghdi rates do not suffer this problem [3]. We remark that the definition of elements in ABAQUS is based on the Jaumann rate for solid elements [4] and on the Green–Naghdi rate for structural elements (shells, membranes, beams, trusses) [5, 6], as mentioned in the ABAQUS Theory Manual, Section 1.5.3 [7].

This study aims to formulate and implement various hypoelastic constitutive models into the ABAQUS UMAT (user material) subroutine. To attain this, it is essential to express the elasticity tensor of the hypoelastic model in terms of the elasticity tensor which relates the Jaumann rate of the Kirchhoff stress tensor to the rate of deformation. According to Pinsky et al. [8], such relations seemed difficult to be constructed for models associated with the Green–Naghdi stress rates; however, the kinematical relations provided in Mehrabadi and Nemat-Nasser [9] enable us to establish such connections.

The study starts with a review of some basic definitions, the concept of objective rate and the structure of hypoelastic constitutive models. Next, the relations between the elasticity tensors of various hypoelastic models and the elasticity tensor relating the Jaumann rate of the Kirchhoff stress to the rate of deformation are constructed. Next, the formulation behind such UMAT-subroutine variables as the consistent Jacobian (${\texttt {DDSDDE}}$), stress array (${\texttt {STRESS}}$), incremental strain array (${\texttt {DSTRAN}}$), and incremental rotation matrix (${\texttt {DROT}}$) is discussed. The understanding of the formulation is required to properly update the consistent Jacobian and the Cauchy stress in various hypoelastic constitutive models. Various simulations, including simple shear and uniaxial extension, are considered in ABAQUS, and the numerical solutions of the hypoelastic models are validated through the available solutions.

The models considered in this study are zero-graded models based on the Jaumann, Truesdell, and Green–Naghdi rates of the Cauchy and Kirchhoff stress tensors. However, development of UMAT subroutine codes for advanced hypoelastic constitutive equations follows the same steps. As an example of such advanced hypoelastic models, we refer the Reader to the hypoelasticity theory established by Freed [10], later refined in [11], for modelling the passive response of soft biological tissues.

2 Theoretical background

The notation follows essentially that traced by Truesdell and Noll [1] and Marsden and Hughes [12], but a simplified treatment in Cartesian coordinates is adopted throughout, following that by Bonet and Wood [13] or Bonet et al. [14], to which we refer the Reader for detailed definitions and proofs.

2.1 Basic definitions

The three-dimensional Euclidean space is denoted ${\mathcal {S}}$ and a material body is identified with a reference configuration ${\mathcal {B}}$, which is regarded as an open subset of ${\mathcal {S}}$ [12, 15].¹ The motion of the body ${\mathcal {B}}$ is described by the configuration map, which is defined, at each time t, by

$$\begin{aligned} \phi (\,\cdot ,t) : {\mathcal {B}} \rightarrow {\mathcal {S}} : X \mapsto x = \phi (X,t), \end{aligned}$$

(1)

where the material point X denotes the position of a particle in the reference configuration ${\mathcal {B}}$ and the spatial point $x = \phi (X,t)$ is the current placement of point X at time t. The placement or configuration of the body ${\mathcal {B}}$ at time t is denoted

$$\begin{aligned} {\mathcal {B}}_t \equiv \phi ({\mathcal {B}},t). \end{aligned}$$

(2)

The codomain restriction to ${\mathcal {B}}_t \equiv \phi ({\mathcal {B}},t)$ of the configuration map $\phi (\,\cdot ,t)$ is required to be invertible, continuous, and differentiable along with its inverse, i.e. a diffeomorphism.

The deformation gradient $\varvec{F}$ is a two-point tensor [12], mapping material vectors $\varvec{M}$ attached at point X into spatial vectors $\varvec{m}=\varvec{FM}$ attached at the spatial point x and is defined, in components, as

$$\begin{aligned} F_{iJ} = \frac{\partial \phi _i}{\partial X_J} \equiv \phi _{i,J}. \end{aligned}$$

(3)

The determinant $J = \det \varvec{F}$ of the deformation gradient $\varvec{F}$ describes the local change of volume and, due to the requirement of invertibility and regularity of $\phi$, it must be strictly positive. Cauchy’s polar decomposition theorem allows to express the deformation gradient $\varvec{F}$ as

$$\begin{aligned} \varvec{F} = \varvec{R} \, \varvec{U} = \varvec{V} \varvec{R}, \end{aligned}$$

(4)

where $\varvec{U}$ and $\varvec{V}$ are symmetric and positive definite tensors and $\varvec{R}$ is a proper orthogonal tensor. Moreover, the right stretch tensor $\varvec{U}$ is completely material, the left stretch tensor $\varvec{V}$ is completely spatial and the rotation tensor $\varvec{R}$ is, like $\varvec{F}$, a two-point tensor. The right and left Cauchy–Green deformation tensors are completely material and completely spatial, respectively, and are defined as

$$\begin{aligned} \varvec{C} = \varvec{F}^T \varvec{F} \equiv \varvec{U}^2, \qquad \varvec{b} = \varvec{F} \, \varvec{F}^T \equiv \varvec{V}^2. \end{aligned}$$

(5)

The Eulerian spatial velocity $\varvec{v}$ is defined as the vector field such that

$$\begin{aligned} \varvec{v}(x,t) = \varvec{v}(\phi (X,t),t) = {\dot{\phi }}(X,t), \end{aligned}$$

(6)

where ${\dot{\phi }}(X,t) \equiv (\partial _t \phi )(X,t)$ is the Lagrangian spatial velocity at $x = \phi (X,t)$. The gradient of the spatial velocity field $\varvec{v}$ with respect to the spatial coordinates $x_i$, i.e.²

$$\begin{aligned} \varvec{\ell } = \mathrm {grad}\,\varvec{v} \equiv {\scriptstyle {\nabla }}\varvec{v}, \end{aligned}$$

(7)

is called the velocity gradient and has components $\ell _{ij} = v_{i,j}$. The symmetric and skew-symmetric parts of the velocity gradient are the rate of deformation $\varvec{d}$ and the spin or vorticity tensor $\varvec{w}$, respectively:

$$\begin{aligned} \varvec{d}=\dfrac{1}{2}(\varvec{\ell }+\varvec{\ell }^T), \qquad \varvec{w}=\dfrac{1}{2}(\varvec{\ell }-\varvec{\ell }^T). \end{aligned}$$

(8)

The skew-symmetric tensor

$$\begin{aligned} \varvec{\Omega } = \dot{\varvec{R}} \, \varvec{R}^T, \end{aligned}$$

(9)

where $\varvec{R}$ is the two-point rotation tensor of the polar decomposition (4) of $\varvec{F}$, is called rigid spin [6]. Its skew-symmetry can be easily shown by taking the time derivative of $\varvec{R} \, \varvec{R}^T = \varvec{i}$, where $\varvec{i}$ is the spatial identity tensor. It can also be shown that the spin tensor $\varvec{w}$ and the rigid spin tensor $\varvec{\Omega }$ are related by (see, e.g. [13] or [14])

$$\begin{aligned} \varvec{w}=\varvec{\Omega }+\tfrac{1}{2}\,\varvec{R}\,\bigl (\dot{\varvec{U}}\,\varvec{U}^{-1}-\varvec{U}^{-1}\,\dot{\varvec{U}}\bigr )\varvec{R}^T. \end{aligned}$$

(10)

There are two cases for which $\varvec{w}$ and $\varvec{\Omega }$ coincide. The first case is when the motion is rigid and $\varvec{F} = \varvec{R}$, $\varvec{U} = \varvec{I}$, $\dot{\varvec{U}} = \varvec{0}$ and $\varvec{\ell } = \varvec{w}$ (or, equivalently, $\varvec{d} = {\mathbf {0}}$). The second case is when the (normalised) eigenvectors of $\varvec{U}$ remain constant during the motion, which implies that $\dot{\varvec{U}}$ has the same eigenvectors and thus commutes with $\varvec{U}$.

The fundamental measure of stress in continuum mechanics is the Cauchy stress $\varvec{\sigma }$, which linearly relates the unit normal vector $\varvec{n}$ at a point on the boundary $\partial {\mathcal {R}}_t$ of an arbitrary region ${\mathcal {R}}_t \equiv \phi ({\mathcal {R}},t)$, subset of the current configuration ${\mathcal {B}}_t \equiv \phi ({\mathcal {B}},t)$, to the corresponding surface traction vector $\varvec{t}_{\varvec{n}}$, i.e.

$$\begin{aligned} \varvec{t}_{\varvec{n}} = \varvec{\sigma } \, \varvec{n}. \end{aligned}$$

(11)

The Cauchy stress $\varvec{\sigma }$ is power-conjugated to the rate of deformation $\varvec{d}$ (or, equivalently, to the velocity gradient $\varvec{\ell }$), in the sense that the internal power (or deformation power) in an arbitrary region ${\mathcal {R}}_t$ is given by

$$\begin{aligned} {\mathcal {P}}_{\mathrm {int}} = \int \limits _{{\mathcal {R}}_t} \varvec{\sigma } : \varvec{d} \; \mathrm {d}\upsilon . \end{aligned}$$

(12)

Another measure of stress, often employed in numerical applications, is the Kirchhoff stress $\varvec{\tau }$, which is obtained by pulling the integral (12) on ${\mathcal {R}}_t$ back to the referential region ${\mathcal {R}}$, subset of ${\mathcal {B}}$ by means of the theorem of the change of variables, i.e.

$$\begin{aligned} {\mathcal {P}}_{\mathrm {int}} = \int \limits _{{\mathcal {R}}} J \, \varvec{\sigma } : \varvec{d} \; \mathrm {d}V = \int \limits _{{\mathcal {R}}} \varvec{\tau } : \varvec{d} \; \mathrm {d}V, \end{aligned}$$

(13)

from which we obtain the relation

$$\begin{aligned} \varvec{\tau } = J \, \varvec{\sigma }. \end{aligned}$$

(14)

2.2 Objective stress rates

The principle of material frame indifference states that the constitutive equations must be form-invariant under changes of the frame of reference, i.e. under arbitrary rototranslations [1, 16]. The regular substantial time derivative of a spatial measure of stress, such as the Cauchy stress, is not frame-indifferent, as we shall briefly show now. Let us denote the substantial time derivative by a superposed dot, i.e.

$$\begin{aligned} \dot{\varvec{\sigma }} \equiv \mathrm {D}_t \varvec{\sigma }, \qquad {\dot{\sigma }}_{ij} \equiv \mathrm {D}_t \sigma _{ij} = \sigma _{ij,k} \, v_k + \partial _t \sigma _{ij}. \end{aligned}$$

(15)

Under a spatial rotation $\varvec{Q}$, the stress transforms as

$$\begin{aligned} \tilde{\varvec{\sigma }} = \varvec{Q} \, \varvec{\sigma } \, \varvec{Q}^T. \end{aligned}$$

(16)

Therefore, the rate $\dot{\varvec{\sigma }}$ transforms as (see, e.g. [13, 14])

$$\begin{aligned} \dot{\tilde{\varvec{\sigma }}} = \dot{\varvec{Q}} \, \varvec{\sigma } \, \varvec{Q}^T + \varvec{Q} \, \dot{\varvec{\sigma }} \, \varvec{Q}^T + \varvec{Q} \, \varvec{\sigma } \, \dot{\varvec{Q}}{}^T, \end{aligned}$$

(17)

which does not preserve the form of the transformation (16). In contrast, it can be shown [13, 14] that the rate of deformation $\varvec{d}$ is frame-indifferent.

Objective stress rates have been introduced precisely to overcome the problem suffered by stress rates and are all essentially based on the use of Lie derivatives, as elegantly shown by Marsden and Hughes [12]: the Oldroyd rate is precisely a Lie derivative, the Jaumann rate is a linear combination of Lie derivatives, the Green–Naghdi rate is modelled after a linear combination of Lie derivatives, and finally, the Truesdell rate (of the Cauchy stress) is a Lie derivative involving the volume form (or volume element). In this work, we use the objective rates below, in the notation of Bonet and Wood [13].

Truesdell Rate of the Cauchy Stress:

$$\begin{aligned} \varvec{\sigma }^\circ = \dot{\varvec{\sigma }}-\varvec{\sigma } \, \varvec{\ell }^T-\varvec{\ell } \, \varvec{\sigma }+(\mathrm {tr}\,\varvec{d}) \, \varvec{\sigma }, \end{aligned}$$

(18)

Truesdell Rate of the Kirchhoff Stress (also called Oldroyd rate [17] and coincident with the Lie derivative of the Kirchhoff stress [13]):

$$\begin{aligned} \varvec{\tau }^\circ = \dot{\varvec{\tau }}-\varvec{\tau } \, \varvec{\ell }^T-\varvec{\ell } \, \varvec{\tau }, \end{aligned}$$

(19)

Jaumann Rate of the Cauchy Stress:

$$\begin{aligned} \varvec{\sigma }^\triangledown = \dot{\varvec{\sigma }}+\varvec{\sigma } \, \varvec{w}-\varvec{w} \, \varvec{\sigma }, \end{aligned}$$

(20)

Jaumann Rate of the Kirchhoff Stress:

$$\begin{aligned} \varvec{\tau }^\triangledown = \dot{\varvec{\tau }}+\varvec{\tau } \, \varvec{w}-\varvec{w} \, \varvec{\tau }, \end{aligned}$$

(21)

Green–Naghdi Rate of the Cauchy Stress:

$$\begin{aligned} \varvec{\sigma }^\vartriangle =\dot{\varvec{\sigma }}+\varvec{\sigma } \, \varvec{\Omega } - \varvec{\Omega }\, \varvec{\sigma }, \end{aligned}$$

(22)

Green–Naghdi Rate of the Kirchhoff Stress:

$$\begin{aligned} \varvec{\tau }^\vartriangle =\dot{\varvec{\tau }}+\varvec{\tau } \, \varvec{\Omega } - \varvec{\Omega }\, \varvec{\tau }. \end{aligned}$$

(23)

The proof of objectivity and non-objectivity of various kinematic and stress variables can be found in Sections 4.15 and 5.6 of Bonet and Wood [13] or Bonet et al. [14]. A more extensive discussion is provided in Chapter 1, Box 6.1 of the book by Marsden and Hughes [12], who also make the distinction between objectivity with respect to isometries (i.e. rototranslations), which coincides with frame indifference, and objectivity with respect to diffeomorphisms, which coincides with the condition of covariance.

2.3 Co-rotational frames

As discussed in Sect. 2.2, the definition of objective rates such as Truesdell, Jaumann, and Green–Naghdi is based on the notion of Lie derivative. Here, we show that, in an appropriate co-rotational frame, the components of the Jaumann and Green–Naghdi stress rates can be expressed as the time rate of the components of the stress (see also Section 1.5.3 of ABAQUS Theory Manual [7]).

A time-dependent basis $\{\varvec{e}_\alpha \}_{\alpha =1}^3$ is co-rotational with respect to the spin tensor $\varvec{w}$ if it transforms following Poisson’s Theorem³ locally, i.e. according to the value of the spin tensor $\varvec{w}$ at the point considered:

$$\begin{aligned} \dot{\varvec{e}}_{\alpha } = \varvec{w} \, \varvec{e}_\alpha = \varvec{e}_\alpha \, \varvec{w}^T = - \varvec{e}_\alpha \, \varvec{w}. \end{aligned}$$

(24)

Considering that $\varvec{w} = w_{\mu \nu } \, \varvec{e}_\mu \otimes \varvec{e}_\nu$ and using the properties of the tensor product, Eq. (24) reads

$$\begin{aligned} \dot{\varvec{e}}_{\alpha } = w_{\mu \nu } (\varvec{e}_\mu \otimes \varvec{e}_\nu ) \, \varvec{e}_\alpha = w_{\mu \alpha } \, \varvec{e}_\mu = - w_{\alpha \mu } \, \varvec{e}_\mu . \end{aligned}$$

(25)

In this $\varvec{w}$-co-rotational frame, the Cauchy stress $\varvec{\sigma }$ (exactly the same considerations can be made for the Kirchhoff stress $\varvec{\tau }$) reads

$$\begin{aligned} \varvec{\sigma }= \sigma _{\alpha \beta }\varvec{e}_\alpha \otimes \varvec{e}_\beta , \end{aligned}$$

(26)

and thus its substantial time derivative is

$$\begin{aligned} \dot{\varvec{\sigma }}\equiv & {} (\sigma _{\alpha \beta } \, \varvec{e}_\alpha \otimes \varvec{e}_\beta )\dot{} \nonumber \\= & {} {\dot{\sigma }}_{\alpha \beta } \, \varvec{e}_\alpha \otimes \varvec{e}_\beta + \sigma _{\alpha \beta } \, \dot{\varvec{e}}_\alpha \otimes \varvec{e}_\beta + \sigma _{\alpha \beta } \, \varvec{e}_\alpha \otimes \dot{\varvec{e}}_\beta \nonumber \\= & {} {\dot{\sigma }}_{\alpha \beta } \, \varvec{e}_\alpha \otimes \varvec{e}_\beta + \sigma _{\alpha \beta } \, (w_{\mu \alpha } \, \varvec{e}_\mu ) \otimes \varvec{e}_\beta + \sigma _{\alpha \beta } \, \varvec{e}_\alpha \otimes (- w_{\beta \nu } \, \varvec{e}_\nu ) \nonumber \\= & {} {\dot{\sigma }}_{\alpha \beta } \, \varvec{e}_\alpha \otimes \varvec{e}_\beta + w_{\mu \alpha } \, \sigma _{\alpha \beta }\, \varvec{e}_\mu \otimes \varvec{e}_\beta - \sigma _{\alpha \beta } \, w_{\beta \nu } \, \varvec{e}_\alpha \otimes \varvec{e}_\nu , \end{aligned}$$

(27)

where we used Eq. (25). Switching indices $\mu$ and $\alpha$ in the second term and $\nu$ and $\beta$ in the third term, we have

$$\begin{aligned} (\sigma _{\alpha \beta } \, \varvec{e}_\alpha \otimes \varvec{e}_\beta )\dot{} = {\dot{\sigma }}_{\alpha \beta } \, \varvec{e}_\alpha \otimes \varvec{e}_\beta + w_{\alpha \mu } \, \sigma _{\mu \beta }\, \varvec{e}_\alpha \otimes \varvec{e}_\beta - \sigma _{\alpha \nu } \, w_{\nu \beta } \, \varvec{e}_\alpha \otimes \varvec{e}_\beta , \end{aligned}$$

(28)

and, solving for ${\dot{\sigma }}_{\alpha \beta } \, \varvec{e}_\alpha \otimes \varvec{e}_\beta$, we obtain

$$\begin{aligned} {\dot{\sigma }}_{\alpha \beta } \, \varvec{e}_\alpha \otimes \varvec{e}_\beta = (\sigma _{\alpha \beta } \, \varvec{e}_\alpha \otimes \varvec{e}_\beta )\dot{} + \sigma _{\alpha \nu } \, w_{\nu \beta } \, \varvec{e}_\alpha \otimes \varvec{e}_\beta - w_{\alpha \mu } \, \sigma _{\mu \beta }\, \varvec{e}_\alpha \otimes \varvec{e}_\beta . \end{aligned}$$

(29)

On the right-hand side of Eq. (29), we recognise the Jaumann rate of the Cauchy stress, i.e.

$$\begin{aligned} \varvec{\sigma }^\triangledown&= (\varvec{\sigma }^\triangledown )_{\alpha \beta } \, \varvec{e}_\alpha \otimes \varvec{e}_\beta \nonumber \\&= (\sigma _{\alpha \beta } \, \varvec{e}_\alpha \otimes \varvec{e}_\beta )\dot{} + \sigma _{\alpha \nu } \, w_{\nu \beta } \, \varvec{e}_\alpha \otimes \varvec{e}_\beta - w_{\alpha \mu } \, \sigma _{\mu \beta }\, \varvec{e}_\alpha \otimes \varvec{e}_\beta . \end{aligned}$$

(30)

Therefore, comparing Eqs. (29) and (30), we finally obtain that, in this $\varvec{w}$-co-rotational basis, the components of the Jaumann rate are equal to the (substantial) time derivatives of the components of the stress, i.e.

$$\begin{aligned} (\varvec{\sigma }^\triangledown )_{\alpha \beta } = {\dot{\sigma }}_{\alpha \beta }. \end{aligned}$$

(31)

Analogously, if we define a basis $\{\varvec{e}_\alpha \}_{\alpha =1}^3$ that is co-rotational with respect to the rigid spin tensor $\varvec{\Omega }$, in the sense that

$$\begin{aligned} \dot{\varvec{e}}_{\alpha } = \varvec{\Omega } \, \varvec{e}_\alpha = \varvec{e}_\alpha \, \varvec{\Omega }^T = - \varvec{e}_\alpha \, \varvec{\Omega }, \end{aligned}$$

(32)

we can show that, in this $\varvec{\Omega }$-co-rotational basis, the components of the Green–Naghdi rate equal the (substantial) time derivatives of the components of the stress, i.e.

$$\begin{aligned} (\varvec{\sigma }^\vartriangle )_{\alpha \beta } = {\dot{\sigma }}_{\alpha \beta }. \end{aligned}$$

(33)

2.4 Linearisation of the deformation

Linearisation is essential in finite element formulations [13]. The linearisation of the deformation about a specific configuration map $\phi$ entails the evaluation of the deformation gradient $\varvec{F}$ and of all derived quantities, after a perturbation is applied to $\phi$. We call this perturbation an infinitesimal displacement,⁴ which we denote $\delta \varvec{{\mathfrak {u}}}$ when seen as a function of the material point X and $\delta \varvec{u}$ when seen as a function of the spatial point x, i.e.

$$\begin{aligned} (\delta \varvec{{\mathfrak {u}}})(X,t) = (\delta \varvec{u})(x,t). \end{aligned}$$

(34)

The perturbed configuration map is thus

$$\begin{aligned} \breve{\phi }(X,t) = \phi (X,t) + (\delta \varvec{{\mathfrak {u}}})(X,t). \end{aligned}$$

(35)

The deformation gradient of the perturbed configuration map $\breve{\phi }$ is given by (see Section 4.2 in the book by Marsden and Hughes [12])

$$\begin{aligned} \breve{\varvec{F}}(X,t) = \varvec{F}(X,t) + \nabla (\delta \varvec{{\mathfrak {u}}})(X,t), \end{aligned}$$

(36)

where $\varvec{F}$ is the deformation gradient of the unperturbed $\phi$ and we recall that the large nabla, $\nabla$, denotes the gradient performed with respect to the referential coordinates $X_I$. It is helpful to express (36) as a multiplicative decomposition [19]. Indeed, by definition of inverse, we have

$$\begin{aligned} \breve{\varvec{F}}(X,t) = \left[ \varvec{i} + \nabla (\delta \varvec{{\mathfrak {u}}})(X,t) \, \varvec{F}^{-1}(x,t) \right] \varvec{F}(X,t). \end{aligned}$$

(37)

Then, the transformation rule for the gradient states that

$$\begin{aligned} {\scriptstyle {\nabla }}(\delta \varvec{u})(x,t) = \nabla (\delta \varvec{{\mathfrak {u}}})(X,t) \, \varvec{F}^{-1}(x,t), \end{aligned}$$

(38)

where we recall that the small nabla, ${\scriptstyle {\nabla }}$, denotes the gradient with respect to the spatial coordinates $x_i$. Therefore, we can write (37) as

$$\begin{aligned} \breve{\varvec{F}}(X,t) = \left[ \varvec{i} + {\scriptstyle {\nabla }}(\delta \varvec{u})(x,t) \right] \varvec{F}(X,t), \end{aligned}$$

(39)

where

$$\begin{aligned} (\delta \varvec{F})(x,t) = \varvec{i} + {\scriptstyle {\nabla }}(\delta \varvec{u})(x,t), \end{aligned}$$

(40)

is the deformation gradient mapping from the configuration ${\mathcal {B}}_t = \phi ({\mathcal {B}},t)$ to the perturbed configuration $\breve{{\mathcal {B}}}_t = \breve{\phi }({\mathcal {B}},t)$. Finally, the multiplicative decomposition equivalent to (36) is given by (39) and (40) as

$$\begin{aligned} \breve{\varvec{F}}(X,t) = (\delta \varvec{F})(x,t) \; \varvec{F}(X,t). \end{aligned}$$

(41)

In the following, we shall need to perform the linearisation in time, i.e. considering the relative infinitesimal displacement between the configuration ${\mathcal {B}}_t = \phi ({\mathcal {B}},t)$ at time t and the configuration ${\mathcal {B}}_s = \phi ({\mathcal {B}},s)$ at time $s > t$. In this case, the perturbed configuration map $\breve{\phi }$ and the perturbed deformation gradient $\breve{\varvec{F}}$ are replaced by the configuration map $\phi (\,\cdot ,s)$ and deformation gradient $\varvec{F}(\,\cdot ,s)$ at time $s > t$. Thus, we have

$$\begin{aligned} \phi (X,s) = \phi (X,t) + (\delta \varvec{{\mathfrak {u}}})_s(X,t), \end{aligned}$$

(42)

and

$$\begin{aligned} \varvec{F}(X,s) = \varvec{F}(X,t) + \nabla (\delta \varvec{{\mathfrak {u}}})_s(X,t), \end{aligned}$$

(43)

where the subscript s emphasises that the relative displacement $(\delta \varvec{{\mathfrak {u}}})_s(X,t) = \phi (X,s) - \phi (X,t)$ points to $\phi (X,s)$. Passages analogous to those seen above yield

$$\begin{aligned} \varvec{F}(X,s) = (\delta \varvec{F})_s(x,t) \; \varvec{F}(X,t), \end{aligned}$$

(44)

where the relative deformation gradient $(\delta \varvec{F})_s(x,t)$ is given by

$$\begin{aligned} (\delta \varvec{F})_s(x,t) = \varvec{i} + {\scriptstyle {\nabla }}(\delta \varvec{u})_s(x,t), \end{aligned}$$

(45)

We note that this treatment is based on the concept of relative deformation, for which we refer the Reader to the treatise by Eringen [20].

2.5 Hypoelasticity

Hypoelasticity describes a class of elastic materials defined in rate-form. Truesdell and Noll [1] proved that the general forms of hypoelastic constitutive equation must necessarily be given by

$$\begin{aligned} \varvec{s}^\square = {\scriptstyle {\mathbb {C}}} : \varvec{d}, \end{aligned}$$

(46)

where $\varvec{s}^\square$ is an objective rate of a stress tensor $\varvec{s}$, which could be either the Cauchy stress $\varvec{\sigma }$ or the Kirchhoff stress $\varvec{\tau }$, $\varvec{d}$ is the rate of deformation and ${\scriptstyle {\mathbb {C}}}$ is the fourth-order elasticity tensor, which, in general, depends on the stress $\varvec{s}$, i.e. ${\scriptstyle {\mathbb {C}}} = \hat{{\scriptstyle {\mathbb {C}}}}(\varvec{s})$.

As mentioned in Sect. 1, in this study, the hypoelastic constitutive equations are assumed to be zero-graded, which means that the fourth-order elasticity tensor ${\scriptstyle {\mathbb {C}}}$ is isotropic and independent of the stress, i.e. can be expressed as

$$\begin{aligned} {\scriptstyle {\mathbb {C}}} \equiv {\scriptstyle {\mathbb {C}}}^{0} = \lambda \, \varvec{i} \otimes \varvec{i} + 2 \, \mu \, \varvec{i} \, \overline{{\underline{\otimes }}} \,\varvec{i}, \end{aligned}$$

(47)

where the superscript zero stands for zero-graded material, $\lambda$ and $\mu$ are Lamé’s constants, $\varvec{i}$ is the spatial identity tensor with components $\delta _{ij}$ (the Kronecker delta), and the special tensor product $\, \overline{{\underline{\otimes }}} \,$ is defined by Curnier et al. [21] and is such that the component representation of (47) is

$$\begin{aligned} {\scriptstyle {\mathrm {C}}}_{ijkl} \equiv {\scriptstyle {\mathrm {C}}}_{ijkl}^{0} = \lambda \, \delta _{ij} \delta _{kl} + 2 \, \mu \, \left[ \tfrac{1}{2} \left( \delta _{ik}\delta _{jl} + \delta _{il}\delta _{jk} \right) \right] . \end{aligned}$$

(48)

Given the Young’s modulus E and the Poisson’s ratio $\nu$, the Lamé’s constants can be calculated via the well-known relations

$$\begin{aligned} \lambda =\frac{E\nu }{(1+\nu )(1-2\nu )}, \qquad \mu =\frac{E}{2(1+\nu )}. \end{aligned}$$

(49)

3 Hypoelasticity in ABAQUS user subroutine UMAT

A clear understanding of variables provided by the UMAT subroutine is essential to properly implement constitutive models into ABAQUS. In this section, we shall discuss the essential theoretical and numerical aspects of the UMAT-subroutine variables. It should be noted that, also for the case of a hyperelastic material, which is described by a strain energy density, the Jacobian matrix of the UMAT subroutine DDSDDE should be updated based on a particular rate-form equation. In this sense, the treatment below holds for both hyperelastic and hypoelastic models.

3.1 UMAT-subroutine variable ${\texttt {DDSDDE}}$

Based on Section 1.1.44 of ABAQUS User Subroutines Reference Guide [7], in order to implement a hyperelastic material, for which the Cauchy stress tensor is explicitly expressed in terms of the deformation gradient and other kinematic variables, it is necessary to evaluate the consistent Jacobian matrix ${\texttt {DDSDDE}}$. This is defined as the matrix representing the fourth-order tensor ${\scriptstyle {\mathbb {D}}}$ featuring in the expression⁵

$$\begin{aligned} \dot{\varvec{\tau }} = J \, ({\scriptstyle {\mathbb {D}}} : \varvec{d} - \varvec{\sigma } \, \varvec{w} + \varvec{w} \, \varvec{\sigma }). \end{aligned}$$

(50)

Equation (50) can be promptly justified by using the definition (14) of Kirchhoff stress $\varvec{\tau }$ to eliminate the Cauchy stress $\varvec{\sigma }$ and the definition (21) of Jaumann rate $\varvec{\tau }^\triangledown$ of the Kirchhoff stress, i.e.

$$\begin{aligned} \varvec{\tau }^\triangledown = J \, {\scriptstyle {\mathbb {D}}} : \varvec{d}. \end{aligned}$$

(51)

If we define ${\scriptstyle {\mathbb {C}}}^{\varvec{\tau }^\triangledown }$ as the fourth-order tensor relating $\varvec{\tau }^\triangledown$ to $\varvec{d}$, i.e.

$$\begin{aligned} \varvec{\tau }^\triangledown = {\scriptstyle {\mathbb {C}}}^{\varvec{\tau }^\triangledown } : \varvec{d}, \end{aligned}$$

(52)

comparison of Eqs. (51) and (52) yields

$$\begin{aligned} {\scriptstyle {\mathbb {D}}} = J^{-1} \, {\scriptstyle {\mathbb {C}}}^{\varvec{\tau }^\triangledown }. \end{aligned}$$

(53)

A similar formulation is employed for the Jacobian matrix in hypoelastic materials, i.e. for rate-form constitutive models. As we shall show later in Sect. 4, the employment of the consistent Jacobian matrix ${\texttt {DDSDDE}}$ based on Eq. (53) results in convergence, while other Jacobian matrices may give rise to slow convergence [6, 22] or even divergence.

In order to implement a hypoelastic model into UMAT subroutine, it is essential to relate the elasticity tensor of the hypoelastic model to the fourth-order tensor ${\scriptstyle {\mathbb {D}}}$ of Eq. (53), represented by the consistent Jacobian matrix ${\texttt {DDSDDE}}$. Below, we report the tensor ${\scriptstyle {\mathbb {D}}}$ that must be used for each choice of hypoelastic formulation (proofs provided in “Appendix A”).

Truesdell Rate of the Cauchy Stress:

$$\begin{aligned} {\scriptstyle {\mathrm {D}}}_{ijkl}={\scriptstyle {\mathrm {C}}}_{ijkl}^{\varvec{\sigma }^\circ }+\sigma _{ik}\delta _{jl}+\sigma _{jl}\delta _{ik}, \end{aligned}$$

(54)

Truesdell Rate of the Kirchhoff Stress:

$$\begin{aligned} {\scriptstyle {\mathrm {D}}}_{ijkl}=J^{-1}{\scriptstyle {\mathrm {C}}}_{ijkl}^{\varvec{\tau }^\circ }+\sigma _{ik}\delta _{jl}+\sigma _{jl}\delta _{ik}, \end{aligned}$$

(55)

Jaumann Rate of the Cauchy Stress:

$$\begin{aligned} {\scriptstyle {\mathrm {D}}}_{ijkl}={\scriptstyle {\mathrm {C}}}_{ijkl}^{\varvec{\sigma }^\triangledown }+\sigma _{ij}\delta _{kl}, \end{aligned}$$

(56)

Jaumann Rate of the Kirchhoff Stress, i.e. the point of departure, Eq. (53):

$$\begin{aligned} {\scriptstyle {\mathrm {D}}}_{ijkl} = J^{-1} \, {\scriptstyle {\mathrm {C}}}_{ijkl}^{\varvec{\tau }^\triangledown }, \end{aligned}$$

(57)

Green–Naghdi Rate of the Cauchy Stress:

$$\begin{aligned} {\scriptstyle {\mathrm {D}}}_{ijkl} = {\scriptstyle {\mathrm {C}}}_{ijkl}^{\varvec{\tau }^\vartriangle }-\sigma _{im}{\scriptstyle {\mathrm {B}}}_{mjkl}+\sigma _{jm}{\scriptstyle {\mathrm {B}}}_{imkl}+\sigma _{ij}\delta _{kl}, \end{aligned}$$

(58)

Green–Naghdi Rate of the Kirchhoff Stress:

$$\begin{aligned} \begin{aligned} {\scriptstyle {\mathrm {D}}}_{ijkl} = J^{-1} \, {\scriptstyle {\mathrm {C}}}_{ijkl}^{\varvec{\tau }^\vartriangle }-\sigma _{im}{\scriptstyle {\mathrm {B}}}_{mjkl}+\sigma _{jm}{\scriptstyle {\mathrm {B}}}_{imkl}. \end{aligned} \end{aligned}$$

(59)

In the expressions above, we used

$$\begin{aligned} \begin{aligned} {\scriptstyle {\mathrm {B}}}_{ijkl}=\sum _{\alpha ,\beta =1}^{3}\frac{\lambda _\beta -\lambda _\alpha }{\lambda _\beta +\lambda _\alpha }({\varvec{b}_{\alpha }})_{ik}({\varvec{b}_{\beta }})_{jl}, \end{aligned} \end{aligned}$$

(60)

where $\lambda _\alpha$ are the principal stretches (eigenvalues of the left-stretch tensor $\varvec{V}$, so that $\lambda _\alpha ^2$ are the eigenvalues of the left Cauchy–Green deformation $\varvec{b}$), and

$$\begin{aligned} \varvec{b}_{\alpha }=\prod _{\beta =1,\beta \ne \alpha }^{3} \frac{\varvec{b}-\lambda _{\beta }^2\varvec{i}}{\lambda _{\alpha }^2-\lambda _{\beta }^2} \end{aligned}$$

(61)

are the eigenprojections of the left Cauchy–Green deformation $\varvec{b}$, with $\varvec{i}$ being the spatial second-order identity tensor, as seen earlier. The proof of Eqs. (54), (55), and (56) can also be found in Wooseok et al. [23] and the proof of Eqs. (58) and (59) is based on the relation.

$$\begin{aligned} \varvec{\Omega } = \varvec{w} + \sum _{\alpha ,\beta =1}^{3}\frac{\lambda _\beta -\lambda _\alpha }{\lambda _\beta +\lambda _\alpha } \, \varvec{b}_{\alpha } \varvec{d} \, \varvec{b}_{\beta }, \end{aligned}$$

(62)

the derivation of which can be found in Mehrabadi and Nemat-Nasser [9], and also Zhou and Tamma [24].

3.2 UMAT-subroutine variables DSTRAN and DROT

The UMAT-subroutine variables ${\texttt {DSTRAN}}$ and ${\texttt {DROT}}$ contain the components of the incremental strain and incremental rotation, respectively, between the configuration ${\mathcal {B}}_n = \phi ({\mathcal {B}},t_n)$ at time $t_n$ and the configuration ${\mathcal {B}}_{n+1} = \phi ({\mathcal {B}},t_{n+1})$ at time $t_{n+1}$.

The incremental deformation is evaluated following the procedure outlined in Sect. 2.4 and employs a midpoint formula [25] considering the configuration ${\mathcal {B}}_{n+1/2} = \phi ({\mathcal {B}},t_{n+1/2})$ at time

$$\begin{aligned} t_{n+1/2} = t_n + \tfrac{1}{2}(\delta t)_n = t_n + \tfrac{1}{2}(t_{n+1} - t_n), \end{aligned}$$

(63)

where $t_n$ is the time at the beginning of the increment and $(\delta t)_n = t_{n+1} - t_n$ is the increment from $t_n$ to $t_{n+1}$. Our goal here is to determine the relative displacement gradient, the midpoint displacement gradient, the midpoint velocity, and the midpoint velocity gradient. From the midpoint deformation rate, symmetric part of the midpoint velocity gradient, we shall derive the incremental strain ${\texttt {DSTRAN}}$.

The deformation gradient at time $t_{n+1}$ is obtained as a function of the relative deformation gradient and of the deformation gradient at time $t_n$, following Eq. (44), as

$$\begin{aligned} \varvec{F}(X,t_{n+1}) = (\delta \varvec{F})_{n+1}(x,t_n) \; \varvec{F}(X,t_n), \end{aligned}$$

(64)

with the relative deformation gradient as in Eq. (45), i.e.

$$\begin{aligned} \begin{aligned} (\delta \varvec{F})_{n+1}(x,t_n) = \varvec{i} + {\scriptstyle {\nabla }}(\delta \varvec{u})_{n+1}(x,t_n), \end{aligned} \end{aligned}$$

(65)

where we use the subscript $n+1$ in place of $t_{n+1}$ in $(\delta \varvec{F})_{n+1}(x,t_n)$ and $(\delta \varvec{u})_{n+1}(x,t_n)$.

Now, we approximate the displacement between $t_n$ and $t_{n+1/2}$ as half the displacement between $t_n$ and $t_{n+1}$:

$$\begin{aligned} (\delta \varvec{u})_{n+1/2}(x,t_n)= & {} \phi (X,t_{n+1/2}) - \phi (X,t_n) \nonumber \\\simeq & {} \tfrac{1}{2} \, (\delta \varvec{u})_{n+1}(x,t_n) = \tfrac{1}{2} \, \left[ \phi (X,t_{n+1}) - \phi (X,t_n) \right] . \end{aligned}$$

(66)

Using again Eq. (45) for the relative deformation gradient between $t_n$ to $t_{n+1/2}$ with the displacement (66), we have

$$\begin{aligned} \begin{aligned} (\delta \varvec{F})_{n+1/2}(x,t_n) = \varvec{i} + \tfrac{1}{2} \, {\scriptstyle {\nabla }}(\delta \varvec{u})_{n+1}(x,t_n), \end{aligned} \end{aligned}$$

(67)

which, together with Eq. (65), yields the alternative expression

$$\begin{aligned} (\delta \varvec{F})_{n+1/2}(x,t_n) = \tfrac{1}{2} \left[ \varvec{i} + (\delta \varvec{F})_{n+1}(x,t_n) \right] . \end{aligned}$$

(68)

Similarly, we approximate the displacement between $t_{n+1/2}$ and $t_{n+1}$ as

$$\begin{aligned} (\delta \varvec{u})_{n+1}(x',t_{n+1/2})&= \phi (X,t_{n+1}) - \phi (X,t_{n+1/2}) \nonumber \\&\simeq \tfrac{1}{2} \, (\delta \varvec{u})_{n+1}(x,t_n) = \tfrac{1}{2} \, \left[ \phi (X,t_{n+1}) - \phi (X,t_n) \right] , \end{aligned}$$

(69)

where $x' = \phi (X,t_{n+1/2})$ and it is understood that the displacement $\tfrac{1}{2}(\delta \varvec{u})_{n+1}(x,t_n)$ must be parallel-translated from $x = \phi (X,t_n)$ to $x' = \phi (X,t_{n+1/2})$. The corresponding incremental deformation gradient is

$$\begin{aligned} \begin{aligned} (\delta \varvec{F})_{n+1}(x',t_{n+1/2}) = \varvec{i} + \tfrac{1}{2} \, {\scriptstyle {\nabla }}' (\delta \varvec{u})_{n+1}(x,{t_{n}}). \end{aligned} \end{aligned}$$

(70)

where ${\scriptstyle {{\nabla }}'}$ denotes the gradient operator at $x' = \phi (X,t_{n+1/2})$, as opposed to the gradient operator ${\scriptstyle {{\nabla }}}$ at $x = \phi (X,t_n)$.

Using the incremental deformation gradients $(\delta \varvec{F})_{n+1}(x,t_n)$ and $(\delta \varvec{F})_{n+1}(x',t_{n+1/2})$, we can write the multiplicative decomposition

$$\begin{aligned} \varvec{F}(X,t_{n+1}) = (\delta \varvec{F})_{n+1}(x',t_{n+1/2}) \; (\delta \varvec{F})_{n+1/2}(x,t_n) \; \varvec{F}(X,t_n), \end{aligned}$$

(71)

which, comparing with Eq. (64) and using Eqs. (67) and (70), yields

$$\begin{aligned} (\delta \varvec{F})_{n+1}(x,t_n)= & {} (\delta \varvec{F})_{n+1}(x',t_{n+1/2}) \; (\delta \varvec{F})_{n+1/2}(x,t_n)\nonumber \\= & {} \left[ \varvec{i} + \tfrac{1}{2} \, {\scriptstyle {\nabla }}'(\delta \varvec{u})_{n+1}(x,t_n) \right] \left[ \varvec{i} + \tfrac{1}{2} \, {\scriptstyle {\nabla }}(\delta \varvec{u})_{n+1}(x,t_n) \right] . \end{aligned}$$

(72)

The midpoint displacement gradient ${\scriptstyle {\nabla }}'(\delta \varvec{u})_{n+1}(x,t_n)$ is evaluated from Eq. (72), considering Eq. (68), as

$$\begin{aligned} \begin{aligned} {\scriptstyle {\nabla }}'(\delta \varvec{u})_{n+1}(x,t_n) = 4 \, (\delta \varvec{F})_{n+1}(x,t_n) \left[ \varvec{i} + (\delta \varvec{F})_{n+1}(x,t_n) \right] ^{-1} - 2 \, \varvec{i}. \end{aligned} \end{aligned}$$

(73)

The velocity in the configuration ${\mathcal {B}}_{n+1/2}$ is approximated by the midpoint discrete derivative

$$\begin{aligned} \varvec{v}(x',t_{n+1/2}) = {\dot{\phi }}(X,t_{n+1/2}) \simeq \frac{\phi (X,t_{n+1}) - \phi (X,t_n)}{(\delta t)_n} = \frac{\delta \varvec{u}_{n+1}(x,t_n)}{(\delta t)_n}, \end{aligned}$$

(74)

where, again, the parallel translation from $x = \phi (X,t_n)$ to $x' = \phi (X,t_{n+1/2})$ is understood. Based on this approximation, the velocity gradient in the midpoint configuration ${\mathcal {B}}_{n+1/2}$ is given by

$$\begin{aligned} \varvec{\ell }(x',t_{n+1/2}) = {\scriptstyle {\nabla }}'\varvec{v}(x',t_{n+1/2}) \simeq \frac{1}{(\delta t)_n} \, {\scriptstyle {\nabla }}'(\delta \varvec{u})_{n+1}(x,t_n), \end{aligned}$$

(75)

with ${\scriptstyle {\nabla }}'(\delta \varvec{u})_{n+1}(x,t_n)$ given by Eq. (73). The corresponding deformation rate and spin are

(76a)

(76b)

The infinitesimal strain increment $\delta \varvec{\epsilon }_n$ is the tensor corresponding to the UMAT-subroutine variable ${\texttt {DSTRAN}}$ and is obtained from the midpoint deformation rate (76a) by multiplying by the time increment $(\delta t)_n$:

$$\begin{aligned} \delta \varvec{\epsilon }_n\equiv & {} \varvec{d}(x',t_{n+1/2}) \, (\delta t)_n \nonumber \\= & {} \tfrac{1}{2} \left[ {\scriptstyle {\nabla }}'(\delta \varvec{u})_{n+1}(x,t_n) + [{\scriptstyle {\nabla }}'(\delta \varvec{u})_{n+1}]^T(x,t_n) \right] . \end{aligned}$$

(77)

The midpoint spin (76b) is instead used to calculate the incremental rotation tensor $\varvec{Q}_n$ corresponding to the UMAT-subroutine variable ${\texttt {DROT}}$, according to the Hughes–Winget algorithm (see Hughes and Winget [26] and Section 14.10.6 of Neto et al. [25]), as

$$\begin{aligned} \varvec{Q}_n \equiv \left[ \varvec{i} - \tfrac{1}{2} (\delta t)_n \, {\varvec{w}(x',t_{n+1/2})} \right] ^{-1} \left[ \varvec{i} + \tfrac{1}{2} (\delta t)_n \, {\varvec{w}(x',t_{n+1/2})} \right] , \end{aligned}$$

(78)

the usage of which will be explained in the Sect. 3.3.

3.3 UMAT-subroutine variable STRESS

The stress array STRESS is the key UMAT-subroutine variable that provides the user with the components of the Cauchy stress tensor at the beginning of an increment. The user is, then, required to update the ${\texttt {STRESS}}$ array with the components of the Cauchy stress tensor at the end of the increment. In some cases, such as that of hyperelastic constitutive models, the user can easily utilise the deformation gradient at the end of the increment, i.e. UMAT-subroutine variable ${\texttt {DFGRD1}}$, to calculate the Cauchy stress components. However, for rate-dependent constitutive equations, updating the STRESS array requires careful consideration on part of the user.

ABAQUS uses the Hughes–Winget algorithm to integrate the rate-form constitutive equations and update the ${\texttt {STRESS}}$ array (see Section 3.2.2 of ABAQUS Theory Manual [7]). Based on the Hughes–Winget algorithm, the stress update reads [26]

$$\begin{aligned} \begin{aligned} \varvec{\sigma }_{n+1}=\varvec{Q}_n\,\varvec{\sigma }_n\,\varvec{Q}_n^T+{\scriptstyle {\mathbb {C}}}^{\varvec{\sigma }^\triangledown }_n:\delta \varvec{\epsilon }_n, \end{aligned} \end{aligned}$$

(79)

where $\varvec{\sigma }_n$ and $\varvec{\sigma }_{n+1}$ are the Cauchy stress tensor at time $t_n$ and $t_{n+1}$, respectively, $\varvec{Q}_n$ is the incremental rotation tensor and ${\scriptstyle {\mathbb {C}}}^{\varvec{\sigma }^\triangledown }_n$ is the elasticity tensor relating the Jaumann rate $\varvec{\sigma }^\triangledown$ of the Cauchy stress to the rate of deformation $\varvec{d}$ (see Eq. (A.14)). By defining

$$\begin{aligned} \tilde{\varvec{\sigma }}_n = \varvec{Q}_n\,\varvec{\sigma }_n\,\varvec{Q}_n^T, \end{aligned}$$

(80)

we can write Eq. (79) in the form

$$\begin{aligned} \begin{aligned} \varvec{\sigma }_{n+1} = \tilde{\varvec{\sigma }}_n+{\scriptstyle {\mathbb {C}}}^{\varvec{\sigma }^\triangledown }_n:\delta \varvec{\epsilon }_n. \end{aligned} \end{aligned}$$

(81)

The tensor $\tilde{\varvec{\sigma }}_n$ is the quantity corresponding to the UMAT-subroutine variable ${\texttt {STRESS}}$ (see Section 1.1.44 of the ABAQUS User Subroutines Reference Guide [7]). Based on Eq. (56), relating ${\scriptstyle {{\mathbb {C}}}}^{\varvec{\sigma }^\triangledown }$ to the consistent Jacobian ${\scriptstyle {{\mathbb {D}}}}$, we have

$$\begin{aligned} \begin{aligned} {\scriptstyle {\mathbb {C}}}^{\varvec{\sigma }^\triangledown }_n = {\scriptstyle {\mathbb {D}}}_n - \varvec{\sigma }_n \otimes \varvec{i}, \qquad ({\scriptstyle {\mathbb {C}}}^{\varvec{\sigma }^\triangledown }_n)_{ijkl} = ({\scriptstyle {\mathbb {D}}}_n)_{ijkl} - (\varvec{\sigma }_n)_{ij} \, \delta _{kl}, \end{aligned} \end{aligned}$$

(82)

where ${\scriptstyle {\mathbb {D}}}_n$ and $\varvec{\sigma }_n$ are the consistent Jacobian and the stress at the beginning of step n, respectively. Using Eq. (82), we can write (81) in terms of ${\scriptstyle {\mathbb {D}}}_n$ as

$$\begin{aligned} \begin{aligned} \varvec{\sigma }_{n+1} = \tilde{\varvec{\sigma }}_n + ({\scriptstyle {\mathbb {D}}}_n - \varvec{\sigma }_n \otimes \varvec{i}):\delta \varvec{\epsilon }_n. \end{aligned} \end{aligned}$$

(83)

The form of the consistent Jacobian ${\scriptstyle {\mathbb {D}}}_n$ depends on the selected hypoelastic model, see Eqs. (54)–(59).

4 Results and discussion

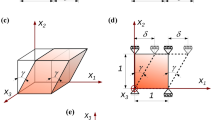
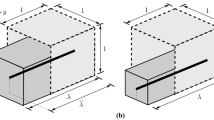
Four simulations are performed in ABAQUS to validate the update procedure of the Cauchy stress array ${\texttt {STRESS}}$ and the Jacobian matrix ${\texttt {DDSDDE}}$ for the hypoelastic constitutive equations. Each model consists of only one eight-node brick element ${\texttt {C3D8}}$ with unit dimensions $L=1$ (Fig. 1). The models are divided into displacement-based models and force-based models. The displacement-based models are used to check the correctness of the updated Cauchy stress tensor. In these models, the iterative procedure is not involved and, thus, the Jacobian matrix does not affect the material response. In contrast, in the force-based models, the implementation of the correct Jacobian matrix plays a crucial part in the convergence of the analysis. Employing the force-based models serves to validate the Jacobian matrices used in the hypoelastic constitutive equations and to show the consequences of using a Jacobian matrix that does not correspond to that required by the element type (for solid elements, that related to the Jaumann rate).

In ABAQUS, the ${\texttt {Static-General}}$ step employs the Newton-Raphson method for the iteration. For the force-based models, the incrementation type is set to automatic, and, for the displacement-based models, the fixed incrementation type is used. For automatic incrementation, the initial increment size is selected 100 times smaller than the maximum increment size and the minimum increment size is chosen 100 times smaller than the initial increment size.

Fig. 1

ABAQUS models for checking the correctness of the Cauchy stress array ${\texttt {STRESS}}$ and the Jacobian matrix ${\texttt {DDSDDE}}$

Fig. 2

Analytical solutions of the Cauchy stress tensor in a material body subjected to simple shear; zero-graded hypoelastic constitutive equations based on: the Jaumann rate of the Cauchy stress (CASE 1); the Truesdell rate of the Cauchy stress (CASE 2); and the Green–Naghdi rate of the Cauchy stress (CASE 3)

The hypoelastic constitutive equations used in these four models are based on: (i) the Jaumann rate of the Cauchy stress, (ii) the Jaumann rate of the Kirchhoff stress, (iii) the Truesdell rate of the Cauchy stress, (iv) the Truesdell rate of the Kirchhoff stress, (v) the Green–Naghdi rate of the Cauchy stress, and (vi) the Green–Naghdi rate of the Kirchhoff stress. The constitutive equations are all zero-graded. The Young’s modulus E and Poisson’s ratio $\nu$ are, respectively, set to 20 (with consistent units) and 0.2. We verified analytically that, for the cases studied, the material parameters E and $\nu$ appear linearly in the expressions of the Cauchy stress and, therefore, varying their magnitude does not introduce any further nonlinearity. Therefore, the conclusions drawn in this section are valid for arbitrary (and, naturally, physically admissible) values of the Young’s modulus E and the Poisson’s ratio $\nu$.

Fig. 3

The Cauchy stress components in the displacement-based model subjected to simple shear; zero-graded hypoelastic constitutive equations based on various rates (a–c); numerical solutions with fixed increment sizes of 0.1 (CASE 1), 0.01 (CASE 2), and 0.001 (CASE 3) in comparison with the analytical solutions (CASE 4)

In the first model (Fig. 1a), the nodes located on the bottom surface of the element are fixed in all directions, the nodes on the upper surface are fixed in $x_2$ and $x_3$ directions and a displacement equal to 5 is applied at the upper nodes in $x_1$ direction. This model is a displacement-based model subjected to simple shear. Using the zero-graded hypoelastic constitutive equations in this model, the numerical Cauchy stress tensors can be checked with the analytical counterparts provided in [2, 3] (see Fig. 2 for the analytical solutions of the zero-graded hypoelastic constitutive equations under simple shear).

In simple shear, the local volume does not change (i.e. $J=1$) and, thus, the Kirchhoff stress tensor coincides with the Cauchy stress tensor. Therefore, the hypoelastic constitutive equations based on the Kirchhoff stress tensor are equivalent to those based on the Cauchy stress tensor. Fig. 3 compares the analytical solutions (CASE 4) with the numerical ones, considering the fixed increment size as 0.1 (CASE 1), 0.01 (CASE 2), and 0.001 (CASE 3). For all hypoelastic constitutive equations, the numerical solutions corresponding to the increment size of 0.001 lie on the analytical solutions. For the hypoelastic models associated with the Jaumann and Green–Naghdi rates, the convergence occurs at the increment size of 0.01 (CASE 2).

In the second model (Fig. 1b), the nodes on the back surface are fixed in all directions; the nodes on the front surface are fixed in $x_2$ and $x_3$ directions and a displacement equal to 5 is applied in $x_1$ direction. This model is a displacement-based model subjected to uniaxial extension, which we use to double-check the update procedure of the Cauchy stress tensor for the zero-graded hypoelastic constitutive equations. In uniaxial extension, the eigenvectors of the right stretch tensor $\varvec{U}$ remain constant during the motion and thus the eigenvectors of $\dot{\varvec{U}}$ coincide with those of $\varvec{U}$. Consequently, $\varvec{U}$ and $\dot{\varvec{U}}$ commute and the spin tensor $\varvec{w}$ reduces to the rigid spin $\varvec{\Omega }$, as can be seen from Eq. (10). Accordingly, in uniaxial extension, the hypoelastic constitutive equations based on the Jaumann rates show the same mechanical behaviour as those based on the Green–Naghdi rates. Fig. 4 represents the numerical solutions considering the fixed increment size as: 0.1 (CASE 1), 0.01 (CASE 2), 0.001 (CASE 3), and 0.0001 (CASE 4). For all hypoelastic constitutive equations, the increment sizes of 0.01, 0.001, and 0.0001 result in the same responses.

In the third model (Fig. 1c), the bottom nodes are fixed in all directions; by defining a rigid body constraint, the upper nodes are rigidly constrained to a reference point located at the centre of the upper surface and a concentrated force in the $x_1$-direction is applied to the reference point. The reason behind the employment of the rigid constraint is that the application of equal concentrated forces at the upper nodes does not produce simple shear deformation. This is a force-based model, used to check the correctness of the Jacobian matrix for the zero-graded hypoelastic constitutive equations.

Fig. 4

The Cauchy stress components in the displacement-based model subjected to uniaxial extension deformation; zero-graded hypoelastic constitutive equations based on various rates (a–d); comparing numerical solutions with fixed increment sizes as: 0.1 (CASE 1), 0.01 (CASE 2), 0.001 (CASE 3), and 0.0001 (CASE 4)

Fig. 5

The Cauchy stress components in the force-based model subjected to simple shear; zero-graded hypoelastic constitutive equations based on various rates (a–c); numerical solutions using automatic incrementation with maximum increment sizes of 0.1 (CASE 1), 0.01 (CASE 2), and 0.001 (CASE 3) in comparison with analytical solutions (CASE 4)

Fig. 6

The Cauchy stress components in the force-based model subjected to uniaxial extension deformation; zero-graded hypoelastic constitutive equations based on various rates (a–d); using automatic incrementation with the maximum increment sizes of 0.1 (CASE 1), 0.01 (CASE 2), 0.001 (CASE 3), and 0.0001 (CASE 4)

Fig. 7

The Cauchy stress components in the force-based model subjected to uniaxial extension based on: the correct Jacobian ${\scriptstyle {\mathbb {D}}}_n$, based on the Jaumann rate of the Kirchhoff stress from Eq. (57) (CASE 1), and the incorrect version of the Jacobian, based on the Jaumann rate of the Cauchy stress ${\scriptstyle {\mathbb {C}}}^{\varvec{\sigma }^\triangledown }_n = {\scriptstyle {\mathbb {D}}}_n - \varvec{\sigma }_n \otimes \varvec{i}$ from Eq. (56) (CASE 2). The zero-graded hypoelastic constitutive equations based on various rates (a–d); using the automatic incrementation with the maximum increment size of 0.001. Note how the simulation based on the incorrect Jacobian ${\scriptstyle {\mathbb {C}}}^{\varvec{\sigma }^\triangledown }_n = {\scriptstyle {\mathbb {D}}}_n - \varvec{\sigma }_n \otimes \varvec{i}$ fails to converge (the red dot indicates where the simulation stops)

In this model, the applied force is in equilibrium with the shear Cauchy stress component, i.e. $\sigma _{12}$ (Fig. 1c). Noting that the iterative procedure, i.e. the Newton–Raphson method, is unable to pass the critical points (e.g. snap-through), for each hypoelastic constitutive equation, the value of the applied force must be selected based on the shear stress response in the displacement-based model under simple shear. Based on Fig. 3b c, for the hypoelastic constitutive equations associated with the Truesdell and Green–Naghdi rates, the shear stress is increasing in the course of the simple shear motion and its maximum value occurs at $u_1=5$. Nevertheless, for the hypoelastic constitutive equations associated with the Jaumann rates, the maximum shear stress occurs at a critical point located at $u_1=1.57$ (Fig. 3a). Employing the zero-graded hypoelastic constitutive equations and the corresponding applied force values into the model, in Fig. 5, a comparison is provided between the analytical solutions (CASE 4) and the numerical solutions using the automatic incrementation with maximum increment sizes as: 0.1 (CASE 1), 0.01 (CASE 2), and 0.001 (CASE 3). For all hypoelastic constitutive equations, the maximum increment size of 0.001 (CASE 3) provides numerical solutions which are located on the analytical solutions. For the hypoelastic constitutive equations based on the Jaumann and Green–Naghdi rates, even the numerical solutions associated with the maximum increment size of 0.1 lie on the analytical counterparts (Fig. 5a, b).

For the fourth model (Fig. 1d), the nodes in the back surface are fixed in all directions, the nodes in the front surface are restricted in $x_2$ and $x_3$ directions and, in the remaining degrees of freedom (DOFs), i.e. DOFs in $x_1$ direction at the nodes in the front, equal concentrated forces $f_1$ are applied. This model is a force-based model subjected to uniaxial extension, used to double-check the correctness of the Jacobian matrix for the zero-graded hypoelastic constitutive equations.

In this model, the sum of the concentrated forces, i.e. $4f_1$, is in equilibrium with the normal Cauchy stress component $\sigma _{11}$ (Fig. 1d). Thus, for each hypoelastic constitutive equation, the value of $f_1$ must be selected based on the response of the stress component $\sigma _{11}$ in the displacement-based model subjected to uniaxial extension (Fig. 4). As is clear from Fig. 4b, for the hypoelastic constitutive equations based on the Jaumann or Green–Naghdi rates of the Kirchhoff stress tensor, a critical point (snap-through) exists at $u_1=1.71$, whereas the stress component $\sigma _{11}$ is increasing during the uniaxial extension motion in other constitutive equations (Fig. 4a, c, d). In Fig. 6, employing the zero-graded hypoelastic constitutive equations alongside the proper values of $f_1$, the numerical solutions for the maximum increment sizes of 0.1 (CASE 1), 0.01 (CASE 2), 0.001 (CASE 3), and 0.0001 (CASE 4) are compared. It is clear from Fig. 6 that, for all of the hypoelastic constitutive equations, the numerical solutions corresponding to the maximum increment sizes of 0.01 to 0.0001, i.e. CASE 2 to CASE 4, are the same. For the hypoelastic constitutive equations associated with the Jaumann or Green–Naghdi rates, even the first case, i.e. the numerical solutions with the maximum increment size of 0.1 are the same as the rest of the numerical solutions.

The elasticity tensor ${\scriptstyle {\mathbb {C}}}^{\varvec{\sigma }^\triangledown }_n$ describes the relation between the Jaumann rate of the Cauchy stress and the rate of deformation (see Eq. (A.14)) and is related to the consistent Jacobian by ${\scriptstyle {\mathbb {C}}}^{\varvec{\sigma }^\triangledown }_n = {\scriptstyle {\mathbb {D}}}_n - \varvec{\sigma }_n \otimes \varvec{i}$, via Eq. (56). Since ${\scriptstyle {\mathbb {C}}}^{\varvec{\sigma }^\triangledown }_n$ is used in the Hughes–Winget algorithm [26] to update the stress (Eq. (79)), a possible coding error is to use ${\scriptstyle {\mathbb {C}}}^{\varvec{\sigma }^\triangledown }_n$ in place of the consistent Jacobian ${\scriptstyle {{{\mathbb {D}}}}}_n$ (Eq. (57)). Figure 7 compares the numerical solutions based on the correct Jacobian ${\scriptstyle {{{\mathbb {D}}}}}_n$ (CASE 1) and the incorrect Jacobian ${\scriptstyle {\mathbb {C}}}^{\varvec{\sigma }^\triangledown }_n = {\scriptstyle {\mathbb {D}}}_n - \varvec{\sigma }_n \otimes \varvec{i}$ (CASE 2) for the force-based model subjected to uniaxial extension.

Figure 7 shows how using the wrong Jacobian matrices results in non-convergence of the analyses at the early stages of the loading. Nevertheless, before the simulation fails to converge and stops (which is indicated by the red dots in the CASE 2 plots in Fig. 7), the Cauchy stress components are identical in both cases of the correct and incorrect Jacobian matrices. Therefore, the correctness of the Jacobian matrix is crucial for the convergence of the analyses, but has no effect on the correctness of the updated Cauchy stress tensor.

5 Summary

In this study, we implement various hypoelastic constitutive models into the finite element analysis software ABAQUS through the user subroutine UMAT. For the formulation of the consistent Jacobian, i.e. the matrix ${\texttt {DDSDDE}}$, ABAQUS uses the elasticity tensor relating the Jaumann rate of the Kirchhoff stress to the rate of deformation for solid elements and the elasticity tensor relating the Green–Naghdi rate of the Kirchhoff stress to the rate of deformation for shell elements. Therefore, it is essential to relate the elasticity tensor of various hypoelastic constitutive models to the elasticity tensor associated with the consistent Jacobian. In regard to the importance of the consistent Jacobian, it is shown that the usage of wrong Jacobian matrices would give rise to the non-convergence of the analyses in the early stages of loading. Additionally, in order to update the Cauchy stress in the various hypoelastic models presented, the comprehension of ABAQUS co-rotational framework and UMAT-subroutine variables such as ${\texttt {STRESS}}$, ${\texttt {DSTRAN}}$, and ${\texttt {DROT}}$ is essential, and this is why they were all described in detail. The correctness of the stress array ${\texttt {STRESS}}$ and Jacobian matrix ${\texttt {DDSDDE}}$ in the zero-graded hypoelastic constitutive equations is checked using displacement-based and force-based models subjected to simple shear and uniaxial extension. This work is aimed at providing a step-by-step guide to the implementation of hypoelastic materials in ABAQUS, but the procedures shown can be adapted to the modelling of hyperelastic materials as well.

Appendix A: Derivation of consistent Jacobians

For deriving the consistent Jacobian of a hypoelastic model in ABAQUS, the constitutive equation must be expressed in terms of the Jaumann rate of the Kirchhoff stress.

The constitutive equation of a hypoelastic model based on the Truesdell rate of the Cauchy stress is

$$\begin{aligned} \varvec{\sigma }^\circ =\dot{\varvec{\sigma }}-\varvec{\sigma }\,\varvec{\ell }^T-\varvec{\ell }\,\varvec{\sigma }+(\,\mathrm {tr}\,\varvec{d}\,)\,\varvec{\sigma }={\scriptstyle {\mathbb {C}}}^{\varvec{\sigma }^\circ }:\varvec{d}, \end{aligned}$$

(A.1)

in which the elasticity tensor ${\scriptstyle {\mathbb {C}}}^{\varvec{\sigma }^\circ }$ is given. Considering the expression of the time derivative of the volume ratio (a proof can be found, e.g. in Section 4.14 of [14]), i.e.

$$\begin{aligned} {\dot{J}} = J \, \mathrm {tr}\,\varvec{d}, \end{aligned}$$

(A.2)

multiplying Eq. (A.1) by J and employing Eqs. (8), (14) and (21) result in:

$$\begin{aligned} \varvec{\tau }^\triangledown =\dot{\varvec{\tau }}+\varvec{\tau }\,\varvec{w}-\varvec{w}\,\varvec{\tau }=J{\scriptstyle {\mathbb {C}}}^{\varvec{\sigma }^\circ }:\varvec{d}+J\varvec{\sigma }\,\varvec{d}+J\varvec{d}\,\varvec{\sigma }={\scriptstyle {\mathbb {C}}}^{\varvec{\tau }^\triangledown }:\varvec{d}. \end{aligned}$$

(A.3)

Now, representing the last equality in index notation, i.e.

$$\begin{aligned} J {\scriptstyle {\mathrm {C}}}_{ijkl}^{\varvec{\sigma }^\circ }d_{kl}+J\sigma _{im}d_{mj}+Jd_{im}\sigma _{mj}={\scriptstyle {\mathrm {C}}}_{ijkl}^{\varvec{\tau }^\triangledown }d_{kl}, \end{aligned}$$

(A.4)

rewriting $J\sigma _{im}d_{mj}$ as

$$\begin{aligned} J\sigma _{im}d_{mj}=J\sigma _{ik}\delta _{jl}d_{kl}, \end{aligned}$$

(A.5)

and $J d_{im}\sigma _{mj}$ as

$$\begin{aligned} J d_{im}\sigma _{mj}=J\sigma _{jl}\delta _{ik}d_{kl}, \end{aligned}$$

(A.6)

the following expression will be achieved:

$$\begin{aligned} (J {\scriptstyle {\mathrm {C}}}_{ijkl}^{\varvec{\sigma }^\circ }+J\sigma _{ik}\delta _{jl}+J\sigma _{jl}\delta _{ik})d_{kl}&={\scriptstyle {\mathrm {C}}}_{ijkl}^{\varvec{\tau }^\triangledown }d_{kl}. \end{aligned}$$

(A.7)

Now, based on Eq. (53), we can finally write

$$\begin{aligned} {\scriptstyle {\mathrm {C}}}_{ijkl}^{\varvec{\sigma }^\circ }+\sigma _{ik}\delta _{jl}+\sigma _{jl}\delta _{ik}={\scriptstyle {\mathrm {D}}}_{ijkl}, \end{aligned}$$

(A.8)

which coincides with Eq. (54).

For a hypoelastic model associated with the Truesdell rate of the Kirchhoff stress, the constitutive equation is

$$\begin{aligned} \varvec{\tau }^\circ ={\scriptstyle {\mathbb {C}}}^{\varvec{\tau }^\circ }:\varvec{d}. \end{aligned}$$

(A.9)

Considering Eqs. (14), (18), (19), and (A.2), we can easily obtain the expression

$$\begin{aligned} \varvec{\tau }^\circ =J\varvec{\sigma }^\circ . \end{aligned}$$

(A.10)

which, substituted into Eq. (A.9), yields

$$\begin{aligned} \varvec{\sigma }^\circ =J^{-1} {\scriptstyle {\mathbb {C}}}^{\varvec{\tau }^\circ }:\varvec{d}={\scriptstyle {\mathbb {C}}}^{\varvec{\sigma }^\circ }:\varvec{d}, \end{aligned}$$

(A.11)

and, therefore:

$$\begin{aligned} J^{-1}{\scriptstyle {\mathrm {C}}}_{ijkl}^{\varvec{\tau }^\circ }={\scriptstyle {\mathrm {C}}}_{ijkl}^{\varvec{\sigma }^\circ }. \end{aligned}$$

(A.12)

Now, employing the above relation into Eq. (A.8) leads to,

$$\begin{aligned} J^{-1}{\scriptstyle {\mathrm {C}}}_{ijkl}^{\varvec{\tau }^\circ }+\sigma _{ik}\delta _{jl}+\sigma _{jl}\delta _{ik}= {\scriptstyle {\mathrm {D}}}_{ijkl}, \end{aligned}$$

(A.13)

i.e. Eq. (55).

For a hypoelastic model based on the Jaumann rate of the Cauchy stress, the constitutive equation is

$$\begin{aligned} \varvec{\sigma }^\triangledown =\dot{\varvec{\sigma }}+\varvec{\sigma }\,\varvec{w}-\varvec{w}\,\varvec{\sigma }={\scriptstyle {\mathbb {C}}}^{\varvec{\sigma }^\triangledown }:\varvec{d}. \end{aligned}$$

(A.14)

Multiplying Eq. (A.14) by J, adding $(J\, \mathrm {tr}\,\varvec{d}\,)\,\varvec{\sigma }$ to both sides of the equation and employing Eqs. (14) and (21), we obtain

$$\begin{aligned} \varvec{\tau }^\triangledown =\dot{\varvec{\tau }}+\varvec{\tau }\,\varvec{w}-\varvec{w}\,\varvec{\tau }=J{\scriptstyle {\mathbb {C}}}^{\varvec{\sigma }^\triangledown }:\varvec{d}+(J\, \mathrm {tr}\,\varvec{d}\,)\,\varvec{\sigma }={\scriptstyle {\mathbb {C}}}^{\varvec{\tau }^\triangledown }:\varvec{d}. \end{aligned}$$

(A.15)

Now, expressing the last equality in index notation

$$\begin{aligned} J {\scriptstyle {\mathrm {C}}}_{ijkl}^{\varvec{\sigma }^\triangledown } d_{kl}+J\sigma _{ij}d_{mm}={\scriptstyle {\mathrm {C}}}_{ijkl}^{\varvec{\tau }^\triangledown }\,d_{kl}, \end{aligned}$$

(A.16)

rewriting the term $J\sigma _{ij}d_{mm}$ as

$$\begin{aligned} J\sigma _{ij}d_{mm}=J\sigma _{ij}\delta _{kl}d_{kl}, \end{aligned}$$

(A.17)

and eliminating $d_{kl}$ from both sides of (A.16), we obtain

$$\begin{aligned} J {\scriptstyle {\mathrm {C}}}_{ijkl}^{\varvec{\sigma }^\triangledown }+J \sigma _{ij}\delta _{kl}={\scriptstyle {\mathrm {C}}}_{ijkl}^{\varvec{\tau }^\triangledown }. \end{aligned}$$

(A.18)

Finally, considering Eq. (53), the elasticity tensor ${\scriptstyle {\mathbb {C}}}^{\varvec{\sigma }^\triangledown }$ of the hypoelastic model, which is known, could be related to the tensorial version of the consistent Jacobian, i.e.

$$\begin{aligned} {\scriptstyle {\mathrm {C}}}_{ijkl}^{\varvec{\sigma }^\triangledown }+\sigma _{ij}\delta _{kl}={\scriptstyle {\mathrm {D}}}_{ijkl}. \end{aligned}$$

(A.19)

which coincides with Eq. (56).

The constitutive equation of a hypoelastic model based on the Green–Naghdi rate of the Cauchy stress is

$$\begin{aligned} \varvec{\sigma }^\vartriangle =\dot{\varvec{\sigma }}+\varvec{\sigma } \, \varvec{\Omega } - \varvec{\Omega }\, \varvec{\sigma }={\scriptstyle {\mathbb {C}}}^{\varvec{\sigma }^\vartriangle }:\varvec{d}. \end{aligned}$$

(A.20)

Based on Eq. (62), we have

$$\begin{aligned}&\dot{\varvec{\sigma }} +\varvec{\sigma }\,\Biggl (\varvec{w}+\sum _{\alpha ,\beta =1}^{3} \frac{\lambda _\beta -\lambda _\alpha }{\lambda _\beta + \lambda _\alpha }{\varvec{b}_{\alpha }}\,\varvec{d}\,{\varvec{b}_{\beta }} \Biggr ) \nonumber \\ {}&\quad -\Biggl (\varvec{w}+\sum _{\alpha ,\beta =1}^{3}\frac{\lambda _\beta - \lambda _\alpha }{\lambda _\beta +\lambda _\alpha }{\varvec{b}_{\alpha }} \,\varvec{d}\,{\varvec{b}_{\beta }}\Biggr )\varvec{\sigma }={\scriptstyle {\mathbb {C}}}^{\varvec{\sigma }^\vartriangle }:\varvec{d}, \end{aligned}$$

(A.21)

from which, rearranging the terms,

$$\begin{aligned}&{\scriptstyle {\mathbb {C}}}^{\varvec{\sigma }^\vartriangle }:\varvec{d}-\varvec{\sigma }\,\Biggl (\sum _{\alpha ,\beta =1}^{3}\frac{\lambda _\beta -\lambda _\alpha }{\lambda _\beta +\lambda _\alpha }{\varvec{b}_{\alpha }}\,\varvec{d}\,{\varvec{b}_{\beta }}\Biggr )\nonumber \\ {}&\quad +\Biggl (\sum _{\alpha ,\beta =1}^{3}\frac{\lambda _\beta -\lambda _\alpha }{\lambda _\beta +\lambda _\alpha }{\varvec{b}_{\alpha }}\,\varvec{d}\,{\varvec{b}_{\beta }}\Biggr )\,\varvec{\sigma }=\dot{\varvec{\sigma }}+\varvec{\sigma } \, \varvec{w}-\varvec{w} \, \varvec{\sigma }. \end{aligned}$$

(A.22)

Now, using Eqs. (20) and (A.14) and index notation, we obtain

$$\begin{aligned}&{\scriptstyle {\mathrm {C}}}_{ijkl}^{\varvec{\sigma }^\vartriangle }d_{kl}-\sigma _{im} \Biggl (\sum _{\alpha ,\beta =1}^{3}\frac{\lambda _\beta -\lambda _\alpha }{\lambda _\beta +\lambda _\alpha }({\varvec{b}_{\alpha }})_{mk}d_{kl} ({\varvec{b}_{\beta }})_{lj}\Biggr )\nonumber \\ {}&\quad +\Biggl (\sum _{\alpha ,\beta =1}^{3}\frac{\lambda _\beta -\lambda _\alpha }{\lambda _\beta +\lambda _\alpha }({\varvec{b}_{\alpha }})_{ik}d_{kl} ({\varvec{b}_{\beta }})_{lm}\Biggr )\sigma _{mj}= {\scriptstyle {\mathrm {C}}}_{ijkl}^{\varvec{\sigma }^\triangledown }d_{kl}. \end{aligned}$$

(A.23)

Employing Eq. (60) and eliminating $d_{kl}$ from both sides, we get

$$\begin{aligned} {\scriptstyle {\mathrm {C}}}_{ijkl}^{\varvec{\sigma }^\vartriangle }-\sigma _{im}{{{\scriptstyle {\mathrm {B}}}}}_{mjkl}+\sigma _{jm}{{{\scriptstyle {\mathrm {B}}}}}_{imkl}={\scriptstyle {\mathrm {C}}}_{ijkl}^{\varvec{\sigma }^\triangledown }, \end{aligned}$$

(A.24)

and, finally, based on Eq. (A.19), we obtain Eq. (58)

$$\begin{aligned} {\scriptstyle {\mathrm {C}}}_{ijkl}^{\varvec{\sigma }^\vartriangle }-\sigma _{im}{{{\scriptstyle {\mathrm {B}}}}}_{mjkl}+\sigma _{jm}{{{\scriptstyle {\mathrm {B}}}}}_{imkl}+\sigma _{ij}\delta _{kl}={\scriptstyle {\mathrm {D}}}_{ijkl}. \end{aligned}$$

(A.25)

For a hypoelastic model based on the Green–Naghdi rate of the Kirchhoff stress, the constitutive equation is

$$\begin{aligned} \varvec{\tau }^\vartriangle =\dot{\varvec{\tau }}+\varvec{\tau } \, \varvec{\Omega } - \varvec{\Omega }\, \varvec{\tau }={\scriptstyle {\mathbb {C}}}^{\varvec{\sigma }^\vartriangle }:\varvec{d}. \end{aligned}$$

(A.26)

Using Eqs. (14), (21) and (A.2), we obtain

$$\begin{aligned} {\scriptstyle {\mathrm {C}}}_{ijkl}^{\varvec{\sigma }^\vartriangle }=J^{-1}{\scriptstyle {\mathrm {C}}}_{ijkl}^{\varvec{\tau }^\vartriangle }-\sigma _{ij}\delta _{kl}, \end{aligned}$$

(A.27)

substituting which into Eq. (A.25) yields Eq (59):

$$\begin{aligned} J^{-1}{\scriptstyle {\mathrm {C}}}_{ijkl}^{\varvec{\tau }^\vartriangle }-\sigma _{im}{\scriptstyle {\mathrm {B}}}_{mjkl}+\sigma _{mj}{\scriptstyle {\mathrm {B}}}_{imkl}={\scriptstyle {\mathrm {D}}}_{ijkl}. \end{aligned}$$

(A.28)