1 Introduction

SARS-CoV-2, causing pneumonia and even damaging other parts of the human body, has severely been pandemic in every corner globally. It once had terrible effects in China and has been stabilized in early March 2020. Later, Italy has received great concern due to its number of cumulative confirmed cases and high death ratio [1, 2]. Spain is an adjacent country of Italy; thus, the epidemic situation of COVID-19 in Spain has been dramatically affected, and it even has more cumulative confirmed cases than Italy, according to the report on May 5, 2020 [2]. The transmitting characteristics of COVID-19 and human’s curbing effort have been fighting each other, and the transmission and control as a whole is a dynamic system. Either studying the transmitting degree or investigating human quarantine will fail to find the system mechanism. The priority work is to find a correct dynamic model for COVID-19 in Spain, fitting the available data, and provide a control strategy concerning the spread of the virus. Then it might provide suggestions to suppress the spread-out of COVID-19 through studying the dynamic characteristics of such a dynamic model.

Backer et al. [3] provided a summary of the estimated incubation period for travelers infected with 2019 novel coronavirus in Wuhan for different parametric forms of the incubation period distribution. For the mean value of such an estimated incubation period, it gives 6.5 days for the Gamma distribution. Rong et al. [4] analyzed the possible impact of enhanced diagnosis efficiency and resource richness on the COVID-19 disease transmission, and the sensitivity analysis on model parameters was carried out. Based on the compartment model of SEIR (susceptible, exposed, infectious, recovered) type for clinical progression of COVID-19 developed in [4], Moore and Okyere [5] discussed how to control the transmission of COVID-19 disease. Anzai et al. [6] investigated the impact of reduced travel volume to and from China on the transmission dynamics of COVID-19 outside China, and a counterfactual model was employed to estimate the reduced volume of the exposed cases. Zhao and Chen [7] developed a SUQC (Susceptible, Un-quarantined infected, Quarantined infected, Confirmed infected) model for the epidemic dynamics and control of COVID-19, for which infection probability during the incubation period, the various isolation measures, and the delay of the main data source were taken into account. Roosa et al. [8] made 5, 10, 15 days forecasts for five consecutive days for cumulative cases of COVID-19 disease in China based on the Richards growth model and a sub-epidemic wave model. It was found that the proposed prediction method could be attributed to the smaller case counts and smaller initial prediction interval range seen in other provinces in China. The same research team [9] also provided the short term forecasts of cumulative reported cases of COVID-19 disease in Guangdong and Zhejiang, and previously validated phenomenological models were adopted. Fang et al. [10] applied the basic reproductive number to determine the potential of an epidemic, the extent of transmission in the absence of control measures, and the effect of control measures on disease spread. Then Chinazzi et al. [11] studied the effect of travel restrictions on the spread of the COVID-19 outbreak, and a global metapopulation disease transmission model was used to carry out the prediction and analysis. It was shown that the growth of COVID-19 could be effectively reduced with smaller relative transmissibility factor and higher travel reduction. Wu et al. [12] applied a susceptible-infected-recovered (SIR) model to simulate the COVID-19 epidemic in Wuhan, and the factor of age was considered to build such a dynamic model. Kucharski et al. [13] studied the transmission of COVID-19 in Wuhan with new internationally exported cases considered, and a stochastic transmission model combined with data was used. The aforementioned researches have provided various transmission-control models to study the spread of the COVID-19 disease. However, the focus of the development of COVID-19 disease nowadays moves from China to North America and European countries.

Additionally, asymptomatic carrier of COVID-19 may become a new threat [14], and cause the transmission rate from susceptible group to those exposed due to the delayed diagnosis. The average waiting time of the infectious for delayed diagnosis may also increase, since the asymptomatic carriers will not have any external symptoms such as abnormal temperature in the early period. Therefore, it is necessary to study the effect of the asymptomatic carrier on the spread of COVID-19 disease, especially for the current severe epidemic areas.

Taking easing measure and lift the lockdown, social distancing, quarantine, etc., for returning business, have been considered as one of the main reasons to cause such a second wave of COVID-19 in this paper. Such an assumption is validated and the corresponding comprehensive analysis has been carried out through the simulation studies.

In this paper, the COVID-19 disease transmission in Spain is modeled with an extended SEIR type dynamic model, for which the population is divided into susceptible, self-quarantine susceptible, exposed, infectious with timely diagnosis, infectious with delayed diagnosis, hospitalized, and recovered. The dynamic of the virus in the environment is coupled into the modeling. The parameters in the model are determined by correlating with the available data of daily confirmed cases, cumulative cases, and cumulative death in Spain. With the validated dynamic model, the effect of different transmission rates on daily confirmed cases is studied. The sensitiveness of daily confirmed cases influenced by the waiting time of infectious for both the timely and delayed diagnosis is analyzed. The main contributions in this paper are as follows: (1) the effect of the asymptomatic carrier of COVID-19 is studied; (2) double-peak dynamics (or called the second wave) for the daily confirmed cases in Spain would take place if the easing measures were taken. The findings in this paper are expected to provide suggestions for control the COVID-19 disease.

The paper is arranged as follows. In Sect. 2, the system parameters in the SEIR type dynamic model of COVID-19 are determined by fitting the reported data in Spain. In Sect. 3, the dynamic characteristics of new confirmed cases are studied by varying the parameters of transmission rates, and the influence of waiting time for diagnosis is also discussed. Section 4 predicts the double-peak dynamic behavior of COVID-19 by assuming the control measures become easing within a period. Finally, a brief discussion concludes the paper.

2 Model correlation

The data of confirmed COVID-19 cases and death due to such a disease in Spain was collected from the Coronavirus Resource Center of Johns Hopkins University [2]. The data of cumulative cases and death for COVID-19 in Spain from March 01 to April 30, 2020, is tabulated in Table 1. For sparing space, only the data for every 5 days is provided, and more details can be found in [2]. Since the number of cumulative death remains below ten before March 08, 2020, and the data set from March 07 to April 30, 2020, is used for correlation of the dynamic model.

Table 1 The confirmed cases and death in Spain from March 01 to April 30, 2020
Full size table

The SEIR type dynamic model for COVID-19 disease was given as in Eq. (1) [4].

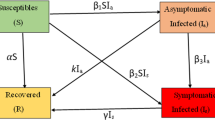
$$ \begin{aligned} \frac{{{\text{d}}S}}{{{\text{d}}t}} & = - (\beta_{e} E + \beta_{t} I_{1} + \beta_{d} I_{2} + \beta_{v} V)S - qS + q_{1} S_{q} \\ \frac{{{\text{d}}S_{q} }}{{{\text{d}}t}} & = qS - q_{1} S_{q} \\ \frac{{{\text{d}}E}}{{{\text{d}}t}} & = (\beta_{e} E + \beta_{t} I_{1} + \beta_{d} I_{2} + \beta_{v} V)S - \omega E \\ \frac{{{\text{d}}I_{1} }}{{{\text{d}}t}} & = \phi \omega E - \gamma_{1} I_{1} - \mu I_{1} \\ \frac{{{\text{d}}I_{2} }}{{{\text{d}}t}} & = \left( {1 - \phi } \right)\omega E - \gamma_{2} I_{2} - \mu I_{2} \\ \frac{{{\text{d}}H}}{{{\text{d}}t}} & = \gamma_{1} I_{1} + \gamma_{2} I_{2} - mH - \mu H \\ \frac{{{\text{d}}R}}{{{\text{d}}t}} & = mH \\ \frac{{{\text{d}}V}}{{{\text{d}}t}} & = f_{1} E + f_{2} I_{1} + f_{3} I_{2} - {\text{d}}_{v} V \\ \end{aligned} $$
(1)

Symbols “S”, “Sq” and “E” represent susceptible, self-quarantine susceptible, exposed, respectively. I1 and I2 are the number of infectious people with timely diagnosis and delayed diagnosis, respectively. Assume all of the confirmed cases can be admitted into hospitals, and the number of people in the hospital due to COVID-19 disease is H. R represents the recovered cases. V denotes the virus in the environment. In the beginning, the entire population in Spain is considered as susceptible. Thus the initial value of S in the model is about 46.7 million [15]. \( \beta_{e} \), \( \beta_{t} \), \( \beta_{d} \), \( \beta_{v} \) are the transmission rate from susceptible to exposed due to the current exposed, infectious with timely diagnosis, infectious with delayed diagnosis and virus in the environment, respectively. For individuals who take actions to isolate themselves at home, they transmitted from susceptible to self-quarantine susceptible with the rate q. As a reverse migrate, the self-quarantine susceptible can again become susceptible at the rate of q1. The incubation period is regarded as a factor to make exposed become infectious, and it equals to 1/ω. According to [3], \( \omega { = 1/6} . 5 \). Therefore, the model hides the time delay in the third sub-equations. The term \( - \omega E \) in the third equation plays the role of damping, which has the time delay of \( \tau { = 1/}\omega { = 6} . 5 \). ϕ denotes the proportion of the infectious individuals who can get timely diagnosis after 1/γ1 days, and the rest of the infectious can be diagnosed after 1/γ2 days. For the infectious and hospitalized individuals, the death rate due to the disease can be regarded as μ. The hospitalized individuals can also be recovered and cause reduction of the population of the hospitalized at the rate of m. The exposed and infectious can affect the population of the virus in the environment, for which the transmission rates are represented by fi, \( i = 1,2,3. \) The virus itself can get a reduction with rate of dv due to various reasons, such as weather and sterilization, etc.

To solve the equilibria \( (S,S_{q} ,E,I_{1} ,I_{2} ,H,V)* \) of the aforementioned dynamic model for COVID-19 disease in Eq. (1), let time derivative of the system states \( (S,S_{q} ,E,I_{1} ,I_{2} ,H,V) \) be zero. It gives

$$ \begin{aligned} qS - q_{1} S_{q} = 0 \hfill \\ E = I_{1} = I_{2} = H = V = 0 \hfill \\ \end{aligned} $$
(2)

Therefore, the equilibria for such a system can be given as \( (0,0,0,0,0,0,0) \) and \( (a,qa/q_{1} ,0,0,0,0,0) \) where a is an arbitrary value. The Jacobian matrix \( {\mathbf{J}}(S,S_{q} ,E,I_{1} ,I_{2} ,H,V) \) is

$$ {\mathbf{J}}(S,S_{q} ,E,I_{1} ,I_{2} ,H,V) = \left[ {\begin{array}{*{20}c} { - \beta_{e} E - \beta_{t} I_{1} - \beta_{d} I_{2} - \beta_{v} V - q} & {q_{1} } & { - \beta_{e} S} & { - \beta_{t} S} & { - \beta_{d} S} & 0 & { - \beta_{v} S} \\ q & { - q_{1} } & 0 & 0 & 0 & 0 & 0 \\ {\beta_{e} E + \beta_{t} I_{1} + \beta_{d} I_{2} + \beta_{v} V} & 0 & {\beta_{e} S - \omega } & {\beta_{t} S} & {\beta_{d} S} & 0 & {\beta_{v} S} \\ 0 & 0 & {\phi \omega } & { - \gamma_{1} - \mu } & 0 & 0 & 0 \\ 0 & 0 & {\left( {1 - \phi } \right)\omega } & 0 & { - \gamma_{2} - \mu } & 0 & 0 \\ 0 & 0 & 0 & {\gamma_{1} } & {\gamma_{2} } & { - m - \mu } & 0 \\ 0 & 0 & {f_{1} } & {f_{2} } & {f_{3} } & 0 & { - d_{v} } \\ \end{array} } \right] $$
(3)

Because the Jacobian matrix involves too many parameters, it is difficult to give an analytic for the polynomial to determine the stability. Once, the parameters are given, the eigenvalues of the Jacobian matrix \( {\mathbf{J}}(S,S_{q} ,E,I_{1} ,I_{2} ,H,V) \) can be computed at the equilibrium as in Eq. (4), and then the stability is determined locally.

$$ \left| {{\mathbf{J}}(S,S_{q} ,E,I_{1} ,I_{2} ,H,V) - \lambda {\mathbf{I}}_{7 \times 7} } \right| = 0 $$
(4)

The number of daily confirmed cases can be calculated as

$$ I = \gamma_{1} I_{1} + \gamma_{2} I_{2} $$
(5)

By integrating Eq. (5), the number of cumulative confirmed cases Ic is obtained as in Eq. (6).

$$ I_{c} = \int {Idt} $$
(6)

The number of cumulative death caused by COVID-19 disease Dc is computed as

$$ D_{c} = \int {\mu \left( {I_{1} + I_{2} + H} \right)dt} $$
(7)

Based on Ref. [4], the values of parameters are set as \( q = 1/10,q_{1} = 1/200000,f_{1} = 1440,f_{2} = 1008 \),\( f_{3} = 1728,d_{v} = 144,m = 1/14. \) We also estimate the initial population of the virus in the environment is 50, and the initial value of the self-quarantined susceptible is 159. According to Table 1, the initial value of the infectious with timely diagnosis I1 and delayed diagnosis I2 are 210 and 300, respectively. For such an SEIR type dynamic model for COVID-19 disease, the recovered individuals are not coupled with other states in the model, thus the 7th equation in Eq. (1) can be eliminated. Furthermore, the aforementioned ordinary differential equations in Eq. (1) can be simulated via an implicit middle-point algorithm, and the equation can be rewritten as

$$ \begin{aligned} S(t_{k + 1} ) & = S(t_{k} ) + (t_{k + 1} - t_{k} )\left[ { - \left( {\beta_{e} \frac{{E(t_{k} ) + E(t_{k + 1} )}}{2} + \beta_{t} \frac{{I_{1} (t_{k} ) + I_{1} (t_{k + 1} )}}{2}} \right.} \right. \\ & \quad + \beta_{d} \frac{{I_{2} (t_{k} ) + I_{2} (t_{k + 1} )}}{2}\left. { + \beta_{v} \frac{{V(t_{k} ) + V(t_{k + 1} )}}{2}} \right)\frac{{S(t_{k} ) + S(t_{k + 1} )}}{2} \\ & \quad \left. { - q\frac{{S(t_{k} ) + S(t_{k + 1} )}}{2} + q_{1} \frac{{S_{q} (t_{k} ) + S_{q} (t_{k + 1} )}}{2}} \right] \\ \end{aligned} $$
(8)
$$ S_{q} (t_{k + 1} ) = S_{q} (t_{k} ) + (t_{k + 1} - t_{k} )\left[ {q\frac{{S(t_{k} ) + S(t_{k + 1} )}}{2} - q_{1} \frac{{S_{q} (t_{k} ) + S_{q} (t_{k + 1} )}}{2}} \right] $$
(9)
$$ \begin{aligned} E(t_{k + 1} ) & = E(t_{k} ) + (t_{k + 1} - t_{k} )\left[ {\left( {\beta_{e} \frac{{E(t_{k} ) + E(t_{k + 1} )}}{2} + \beta_{t} \frac{{I_{1} (t_{k} ) + I_{1} (t_{k + 1} )}}{2}} \right.} \right. \\ & \quad + \beta_{d} \frac{{I_{2} (t_{k} ) + I_{2} (t_{k + 1} )}}{2}\left. { + \beta_{v} \frac{{V(t_{k} ) + V(t_{k + 1} )}}{2}} \right)\frac{{S(t_{k} ) + S(t_{k + 1} )}}{2}\left. { - \omega \frac{{E(t_{k} ) + E(t_{k + 1} )}}{2}} \right] \\ \end{aligned} $$
(10)
$$ I_{1} (t_{k + 1} ) = I_{1} (t_{k} ) + (t_{k + 1} - t_{k} )\left[ {\phi \omega \frac{{E(t_{k} ) + E(t_{k + 1} )}}{2} - \left( {\gamma_{1} + \mu } \right)\frac{{I_{1} (t_{k} ) + I_{1} (t_{k + 1} )}}{2}} \right] $$
(11)
$$ I_{2} (t_{k + 1} ) = I_{2} (t_{k} ) + (t_{k + 1} - t_{k} )\left[ {\left( {1 - \phi } \right)\omega \frac{{E(t_{k} ) + E(t_{k + 1} )}}{2} - \left( {\gamma_{2} + \mu } \right)\frac{{I_{2} (t_{k} ) + I_{2} (t_{k + 1} )}}{2}} \right] $$
(12)
$$ H(t_{k + 1} ) = H(t_{k} ) + (t_{k + 1} - t_{k} )\gamma_{1} \left[ {\frac{{I_{1} (t_{k} ) + I_{1} (t_{k + 1} )}}{2} + \gamma_{2} \frac{{I_{2} (t_{k} ) + I_{2} (t_{k + 1} )}}{2} - \left( {m + \mu } \right)\frac{{H(t_{k} ) + H(t_{k + 1} )}}{2}} \right] $$
(13)
$$ V(t_{k + 1} ) = V(t_{k} ) + (t_{k + 1} - t_{k} )\left[ {f_{1} \frac{{E(t_{k} ) + E(t_{k + 1} )}}{2} + f_{2} \frac{{I_{1} (t_{k} ) + I_{1} (t_{k + 1} )}}{2} + f_{3} \frac{{I_{2} (t_{k} ) + I_{2} (t_{k + 1} )}}{2} - d_{v} \frac{{V(t_{k} ) + V(t_{k + 1} )}}{2}} \right] $$
(14)

We also assume the initial value of the hospitalized is 10. The proportion of the timely diagnosis infectious is estimated as 40% at first. Then it is assumed to become larger due to the increase of the medical supply and government attention. A time-varying function \( \phi = 0.4 + 0.55t/(t + 3) \) is used to model the evolution of such a parameter. The waiting time of the infectious with timely diagnosis and delayed diagnosis is also assumed to drop as time increases. Herein, we use the exponential function to model these two parameters, i.e.,

$$ 1/\gamma_{1} = 2 + 0.9e^{ - 0.2t} \;{\text{and}}\;1/\gamma_{2} = 3 + 7e^{ - 0.2t} $$
(15)

Through manipulating the value of \( \beta_{e} \), \( \beta_{t} \), \( \beta_{d} \), \( \beta_{v} \), the objective function representing the average error norm of the infectious and death can be minimized to an optimum value. The formula for such an objective function is given in Eq. (16).

$$ \varepsilon (\beta_{e} ,\beta_{i1} ,\beta_{i2} ,\beta_{v} ,\mu ) = \frac{1}{n}\sum\limits_{i = 1}^{n} {\left( {\left\| {I(t_{i} ) - \tilde{I}_{n} (t_{i} )} \right\| + \left\| {D_{cn} (t_{i} ) - \tilde{D}_{cn} (t_{i} )} \right\|} \right)} $$
(16)

The parameters \( \tilde{I}(t_{i} ) \) and \( \tilde{D}_{c} (t_{i} ) \) represents the reported data of daily confirmed cases and death, as listed in Table 1. Through a large number of numerical simulation tests, a set of correlated results can be obtained as \( \beta_{e} = \beta_{t} = 10^{ - 8} \), \( \beta_{d} = 1.46 \times 10^{ - 7} \), \( \beta_{v} = 1.009 \times 10^{ - 7} \) and \( \mu = 0.01 \), as shown in Fig. 1. It can be seen that the model has a good correlation with the available data.

Fig. 1
figure 1

Correlated results with the reported data from March 08 to April 10, 2020: a daily confirmed cases, b cumulative confirmed cases, and c cumulative death

Full size image

To guarantee the disease-free equilibrium for the dynamic model of COVID-19 is locally asymptotically stable, the so-called basic reproduction number R0 is introduced, and it is calculated as

$$ R_{0} = S_{e} \left[ {\frac{{\beta_{e} }}{\omega } + \frac{{\beta_{t} \phi }}{{\gamma_{1} + \mu }} + \frac{{\beta_{d} \left( {1 - \phi } \right)}}{{\gamma_{2} + \mu }} + \frac{{\beta_{v} f_{1} }}{{d_{v} \omega }} + \frac{{\beta_{v} f_{2} \phi }}{{d_{v} \left( {\gamma_{1} + \mu } \right)}} + \frac{{\beta_{v} \left( {1 - \phi } \right)}}{{d_{v} \left( {\gamma_{2} + \mu } \right)}}} \right] $$
(17)

where Se is the number of the susceptible at such a disease-free equilibrium. The equilibrium is locally asymptotically stable if \( R_{0} < 1 \).

For the correlated dynamic model for COVID-19, the equilibrium \( (0, \)\( 0,0,0,0,0,0) \) has no biological significance. Thus it is not necessary to discuss the stability analysis for such an equilibrium.

For the equilibrium \( (a,20000a,0,0,0,0,0), \) it has \( S_{e} = a \). With the correlated system parameters, the basic reproduction number for such an equilibrium can be calculated to be \( R_{0} = 8.1554 \times 10^{ - 6} a \). Since the initial population for Spain is 16.7 million, the overall number of the susceptible and the self-quarantine susceptible has to be less than 16.7 million which gives \( a \le 46700000/20001 \). Thus, \( R_{0} \le 0.019 \) and it indicates that the equilibrium is locally asymptotically stable. Meanwhile, the Jacobian matrix is given in Eq. (18). For such a range of a, the eigenvalues almost stay at constant values, and have

$$ \lambda_{1} \approx - 144.0024,\lambda_{2} \approx - 10.0100,\lambda_{3} \approx - 2.9101,\lambda_{4} \approx - 0.1514,\lambda_{5} \approx - 0.1000,\lambda_{6} \approx - 0.0814,\lambda_{7} = 0. $$

It also shows that the equilibriums are all stable. For such a set of equilibriums, the infectious and the hospitalized are zero. Therefore, if the system converges to those equilibriums, it will always indicate the disease is under control, eventually with the current set of system parameters.

$$ {\mathbf{J}} = \left[ {\begin{array}{*{20}c} { - q} & {q_{1} } & { - \beta_{e} a} & { - \beta_{t} a} & { - \beta_{d} a} & 0 & { - \beta_{v} a} \\ q & { - q_{1} } & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & {\beta_{e} a - \omega } & {\beta_{t} a} & {\beta_{d} a} & 0 & {\beta_{v} a} \\ 0 & 0 & {\phi \omega } & { - \gamma_{1} - \mu } & 0 & 0 & 0 \\ 0 & 0 & {\left( {1 - \phi } \right)\omega } & 0 & { - \gamma_{2} - \mu } & 0 & 0 \\ 0 & 0 & 0 & {\gamma_{1} } & {\gamma_{2} } & { - m - \mu } & 0 \\ 0 & 0 & {f_{1} } & {f_{2} } & {f_{3} } & 0 & { - d_{v} } \\ \end{array} } \right] $$
(18)

3 Parameters study

3.1 Impact on daily confirmed cases for the transmission rates

If the susceptible do not take sufficient self-protection, the transmission rate from the susceptible to the exposed can get increased due to the social activities of exposed before being diagnosed. In Fig. 2, the influence on daily confirmed cases by varying the value of the parameter βe is presented. Four sets of results have been computed for \( \beta_{e} = 10^{ - 8} ,1.2 \times 10^{ - 8} ,1.4 \times 10^{ - 8} , \)\( 1.6 \times 10^{ - 8} . \) It can be found that the increase of βe can cause a prominent higher peak of the daily confirmed cases curve, and the date when such a peak occurs is slightly delayed. This result indicates the isolation for reducing the transmission rate is essential in reducing the daily cases.

Fig. 2
figure 2

Daily confirmed cases for different transmission rate from susceptible to exposed due to current exposed

Full size image

The effect of the asymptomatic carrier on the spread of COVID-19 disease can be studied by the parameter study of βt and βd. Because if the infectious being with no symptom cannot get isolated in time, it will cause a higher risk for the susceptible. The computation results for daily confirmed cases by varying βt and βd are illustrated in Fig. 3a and b. The peak of daily confirmed cases will be higher if the transmission rate βt or βd is greater. For transmission rate from the susceptible to the exposed due to the infectious with timely diagnosis, such a rate increases 60% from 10−8 to 1.6 × 10−8, and the peak of new confirmed cases only rises to a value close to 13,000, which is shown in Fig. 3a. However, if such a transmission rate due to the infectious with delayed diagnosis increases from \( 1.46 \times 10^{ - 7} \) to \( 2.1 \times 10^{ - 7} \) (43.84%), the peak of confirmed cases rises to about 25,200. It implies that it is necessary to take effective actions to have real-time RT-PCR (Reverse Transcription-Polymerase Chain Reaction) assays [16] on possible asymptomatic carriers in time to reduce the impact on the increase of daily confirmed cases.

Fig. 3
figure 3

Daily confirmed cases for different transmission rates from susceptible to exposed due to infectious: a infectious with timely diagnosis, b infectious with delayed diagnosis

Full size image

3.2 Impact on new confirmed cases for the waiting time of testing

In this section, the waiting time of infectious for the diagnosis is investigated. For the timely diagnosis situation, the waiting time for testing decreases to 2 days for all three simulation cases. The evolution of the waiting time of testing for all three simulation cases, each with 2 days difference at the beginning, is illustrated in Fig. 4a. Figure 4b shows that there is a small increase in peaks for daily confirmed cases for each case. The longer the waiting time at the beginning, the larger the daily confirmed case. Then, we make the waiting time of testing for delayed diagnosis drops to 3 days, and the initial waiting time is varying from 10 days to 20 days. It shows that the increase of initial waiting time for delayed diagnosis causes a much larger increase in the peaks of daily confirmed cases, as presented in Fig. 5b.

Fig. 4
figure 4

Daily confirmed cases for the different waiting time of infectious for timely diagnosis: a waiting time evolution, b new confirmed cases

Full size image
Fig. 5
figure 5

New confirmed cases for the different waiting time of infectious for delayed diagnosis: a waiting time evolution, b daily confirmed cases

Full size image

3.3 Double-peak caused by easing control measures

In this section, a concerning situation that whether a second wave of the outbreak would take place is considered. As the daily confirmed cases reduce to a relatively low level, the government would take the easing measure for lift tightened measures mandated before for the economy and essential people’s livelihood. Currently, in the U.S., more than 40 states have been open up, and many European countries also lift lockdown measures. Many epidemic experts and WHO warned this lift probably would pay a price that a second wave of the pandemic would come. The cost may much worse than that brought by lockdown in the economy because of the epidemic lengthening, and the death number would rise. Thus, the cost and risk need to be analyzed.

Remark 1

It is assumed that the transmission rate between the self-quarantine susceptible and the susceptible varies for different control measures. For the simulation in this section, we follow the rule as

  1. 1.

    Normal control measures: \( q = 0.1 \) and \( q_{1} = 1/200000. \)

  2. 2.

    Easing control measures: \( q = 1/200000 \) and \( q_{1} = 0.06,0.08,0.1,0.12. \)

From the reported data of the daily confirmed cases in Spain, the curve starts to rise again around April 16. We assume four sets of easing control measures mandate in the period from April 16 to April 26. As the second wave generates, the government returns to the normal control measures after April 26. The results of the daily confirmed cases are presented in Fig. 6 for four different q1. The numbers of daily confirmed cases climb to other peaks even if the easing control measures are taken only for 10 days. The transmission rate from the self-quarantine susceptible to the susceptible during the period with the easing control measures significantly affect the maximum number of the daily confirmed cases for the new peak. The maximum of the daily confirmed cases for the second peak for the four simulation cases are summarized in Table 2. Compared to Case 1 with Case 4, 10 days easing measure cause more than seven times higher in terms of daily confirmed cases. The increase of the transmission rate q1 also leads to a slight delay for the maximum date of the second peak. The ratio of the maximum daily confirmed cases for the second peak to that for the first peak is also tabulated in the table, showing that the second peak of the worst one is 4.5 times higher than the first peak.

Fig. 6
figure 6

The daily confirmed cases for easing control measures from April 16 to April 26

Full size image
Table 2 Risk in daily confirmed cases for the second peak due to the easing control measures in the period: April 16–26, q1 difference)
Full size table

It is also interesting to know what would happen if the starting date for easing control measures are different. From the results in the previous sections, it is known that it has less daily confirmed cases if the easing control measures are taken later after the first peak. Assume the third set of easing control measure is authorized, i.e., \( q = 1/200000 \) and \( q_{1} = 0.1. \) The starting dates of the easing control measures are assumed on April 16, 19, 21, 24, respectively, and they all last for 10 days. After that, they also return to normal control measures. The results in Fig. 7 shows that they all have the second peak for the daily confirmed cases for different starting dates of the easing control measures. The later the easing measure takes place, the lower the daily confirmed cases risk. Table 3 has summarized the information of daily confirmed cases for the second peak when the period of the easing control measures differs.

Fig. 7
figure 7

The daily confirmed cases for different starting date of the easing control measures

Full size image
Table 3 Influence of four different late easing measure on daily confirmed cases for the second peak where q1 = 0.1
Full size table

4 Conclusions

This paper well fitted a new comprehensive SEIR model using Spanish data of COVID-19, concerning the seven compartments including the susceptible, self-quarantine susceptible, exposed, infectious with timely diagnosis and delayed diagnosis, and hospitalized and environmental. The varying transmission rates showed the quarantine and isolation measures could cause the big difference of daily confirmed cases, and also indicated that the delayed diagnosis results huge impact increase of infected cases. Double-peaks are identified by easing control measures, showing the high risk that the second peak can be 4.5 times higher than the first peak in only 10 days of easing control. The later the easing measure takes place, the lower the daily confirmed cases risk. The resilience of transmission of COVID-19 in the analysis not only alarm the risk but also suggest that a balance of easing control measure between business and control is essential.