Understanding non-Fermi liquid behaviors1,2 due to a zero-temperature magnetic transition, a QCP, and the unconventional superconductivity that emerges around it is one of the central issues in condensed matter physics. These phenomena are widely seen in strongly correlated electron systems such as heavy fermion systems1, cuprates3, and iron pnictides4,5. In cuprates, iron pnictides, or other compounds containing 3d transition-metal elements6, the quantum phase transition is described by itinerant spin-density wave (SDW) theories, where the QCP is due to an instability of the underlying large Fermi surfaces7,8,9,10. Cerium(Ce)-based heavy fermion systems are understood based on the Kondo lattice model in which localized Ce 4f electron spins at high temperatures are screened below a characteristic temperature TK by the conduction electrons11. At high temperatures, the f electron spins are localized, and thus, the Fermi surface is small. With decreasing temperature, 4f electrons couple with the conduction electrons through Kondo hybridization, and the Fermi-surface volume gradually increases with decreasing temperature12,13. In addition to the Kondo effect, there also is a long-range Ruderman–Kittel–Kasuya–Yosida (RKKY) interaction that is the indirect exchange interaction among weakly screened, nearly localized 4f electrons. If the RKKY interaction overcomes the Kondo effect, f spins order antiferromagnetically below the Néel temperature TN. By tuning a nonthermal control parameter such as pressure and/or chemical substitution, TN can be suppressed completely to zero, and TK increases as the parameter increases11. A crossover from the small (localized) to the large (itinerant) Fermi surfaces will occur well below TK in the Kondo lattice14. Depending on the relative balance between Kondo hybridization and the RKKY interaction, magnetic order may be of the SDW-type or the RKKY-type antiferromagnetic (AF) order that is mediated by itinerant electrons of a small Fermi surface. Quantum criticality of the latter type of magnetic order is predicted theoretically to be qualitatively different from SDW criticality and involves a breakdown of Kondo screening and a transition from small-to-large Fermi surfaces at the QCP10,15,16. In practice, it can be difficult experimentally to distinguish unambiguously between these two scenarios, though distinctions have been inferred from combinations of thermodynamic, transport and inelastic neutron scattering measurements17. Unfortunately, it has not been possible to perform neutron scattering experiments under high pressure conditions, the “cleanest” tuning parameter that does not introduce additional disorder or break symmetry, to shed light on the nature of criticality in Kondo lattice systems. In contrast, pressure-dependent nuclear quadrupole resonance (NQR) measurements, which probe the dynamic spin susceptibility as well as the influence of Kondo hybridization, are straightforward, even at very low temperatures, and, as we show, can be used as differentiating probe of quantum criticality.

The AF superconductor CeRh0.5Ir0.5In518,19 is a good candidate to investigate this issue. CeRhIn5 has a small Fermi surface20, orders antiferromagnetically below TN = 3.8 K, and exhibits pressure-induced superconductivity above P = 1.6 GPa at the transition temperature Tc = 2.1 K21. Tc increases to 2.3 K at 2.35 GPa where, in the limit of zero temperature, there is a magnetic–nonmagnetic transition22,23 accompanied by a change from small-to-large Fermi surface20. The superconducting-gap symmetry is consistent with d-wave symmetry24,25. On the other hand, CeIrIn5 has a large Fermi surface26, and also shows d-wave superconductivity below Tc = 0.4 K27,28,29, which increases to 0.8 K at P = 2.1 GPa30. The alloyed compound CeRh0.5Ir0.5In5 orders antiferromagnetically below TN = 3.0 K at P = 031 and becomes superconducting below Tc = 0.9 K18,19,32. CeRh0.5Ir0.5In5 is closer to an AF QCP than CeRhIn5, suggesting that Ir substitution for Rh acts a positive chemical pressure. This suggestion can be understood by appreciating that underlying the evolution of ground states in the CeRh1−xIrxIn5 series is a systematic change in orbital anisotropy of the \({\Gamma }_{7}^{2}\) crystal-electric field ground state wave function that produces progressively stronger hybridization with increasing x33.

Here, we report the results of 115In-NQR measurements on CeRh0.5Ir0.5In5 under pressure, crystal structure analysis and a first-principle calculation of NQR frequency νQ (see “Methods” for details). From the temperature dependence of the nuclear spin-lattice relaxation rate (1/T1), we find that the AF QCP is at \({P}_{{\rm{c}}}^{{\rm{AF}}}=1.2\) GPa, where Tc(P) reaches its maximum. From the pressure dependence of νQ, we find a localized-to-itinerant transition at \({P}_{{\rm{c}}}^{* }\) = 0.8 GPa before the AF QCP appears. Superconductivity is not only optimized at the AF QCP but also is realized with a remarkable proliferation of residual gapless excitations. Our results suggest that the large Fermi surface and AF instabilities in the presence of “impurity” scattering trigger unconventional gapless superconductivity in CeRh0.5Ir0.5In5.

Results

The hyperfine coupling constant at the In(1) site

The hyperfine coupling between nuclear and electronic spins relates the measured 1/T1 to the underlying dynamical spin susceptibility as discussed in “Methods”. Figure 1 shows the pressure–temperature phase diagram of the CeRh1−xIrxIn5 system. If substituting Ir for Rh acts as a positive chemical pressure, we would expect the hyperfine coupling constant [115A(1)] at the In(1) site (Fig. 2a) of CeRh0.5Ir0.5In5 to be smaller than that of the host material CeRhIn5 because 115A(1) = 25 kOe \({\mu }_{{\rm{B}}}^{-1}\) in CeRhIn5 decreases with increasing pressure but becomes constant at 115A(1) ~7 kOe \({\mu }_{{\rm{B}}}^{-1}\) above P = 1 GPa. Such a pressure-dependent 115A(1) will affect the information inferred from 1/T134 and, therefore, it is important to determine 115A(1) for CeRh0.5Ir0.5In5 before proceeding to details of its T1 results under pressure. Figure 2b shows the frequency-swept 115In-nuclear magnetic resonance (NMR) spectra at a constant field. The spectrum is consistent with previously reported spectra of CeRhIn534. From these data, we establish the temperature dependence of the 115In(1)-NMR center line plotted in Fig. 2c. With these results, we calculate (Methods) the temperature dependence of the Knight shift 115K(1)c (%) and compare it to dc susceptibility χc (emu mol−1) in Fig. 2d. As clearly shown in the figure, the relation K(T) ∝ 115A(1)χ(T) holds above T = 30 K. A breakdown of this linear relationship at low temperature is common in heavy electron systems35, but a previous In-NMR study suggested that 115A(1) is temperature-independent in CeIrIn5 in such temperature regime36. In the inset of Fig. 2d, we plot 115K(1)c vs. χc and obtain the hyperfine coupling constant as 115A(1) = 7.64 kOe \({\mu }_{{\rm{B}}}^{-1}\). This closely corresponds to the value of 115A(1) in CeRhIn5 under a pressure of 1 GPa (Supplementary Note 1 and Supplementary Fig. 1), and thus, it substantiates the suggestion that Ir substitution with x = 0.5 (chemical pressure) is equivalent to the application of a physical pressure greater than P = 1 GPa to CeRhIn5. Therefore, we reasonably can ignore any significant pressure dependence of 115A(1) in inferring the pressure evolution of physical properties from 1/T1 in CeRh0.5Ir0.5In5.

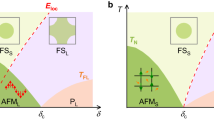
Fig. 1: Phase diagram of CeRh1−xIrxIn5.
figure 1

x and pressure dependence of the Neel temperature TN (open squares, triangles, and circles) and the superconducting transition temperature Tc (solid squares, triangles, circles, and diamonds) for CeRh1−xIrxIn5 (P = 0)19, CeRhIn521,22,23, and CeIrIn530 under pressure. AFM and SC indicate antiferromagnetic metal and superconductivity, respectively.

Full size image
Fig. 2: Hyperfine coupling constant.
figure 2

a Crystal structure of CeRh0.5Ir0.5In5. b Frequency-swept 115In-nuclear magnetic resonance (NMR) spectra of CeRh0.5Ir0.5In5. Solid [dotted] arrows indicate In(1)[In(2)] resonance peaks, respectively. c Temperature dependence of the 115In(1)-NMR center line. The curves are Gaussian fits. d Temperature dependence of the Knight shift 115K(1)c (open circles) and dc susceptibility χc (solid curve). The inset shows 115K(1)c vs. χc. The solid straight line is a fit to the data above T = 30 K, which yields the hyperfine coupling constant 115A(1) = 7.64 kOe \({\mu }_{{\rm{B}}}^{-1}\). Error bars are smaller than the size of the data points.

Full size image

Pressure dependence of TN and Tc

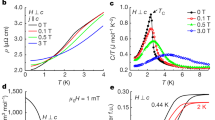
  Figure 3a and b shows the temperature dependence of 1/T1. The magnitude of 1/T1 for CeRh0.5Ir0.5In5 is much greater than that for the nonmagnetic reference material La(Rh,Ir)In537, due to f electron spin correlations, that are reflected in the dynamical susceptibility χ″ to which 1/T1 is proportional. At P = 0, 1/T1 exhibits a small peak at TN = 3.0 K and decreases below Tc = 0.9 K19. As shown in Fig. 3a and the inset, TN(P) can be identified up to P = 1.12 GPa but disappears above \({P}_{{\rm{c}}}^{{\rm{AF}}}=1.2\) GPa. A superconducting transition is observed at all pressures, as evidenced by an abrupt reduction of 1/T1 below T = Tc(P). Tc increases with increasing pressure and exhibits a maximum \({T}_{{\rm{c}}}^{\max }\) = 1.4 K around \({P}_{{\rm{c}}}^{{\rm{AF}}}=1.2\) GPa and then decreases with further increase of P; \({T}_{{\rm{c}}}^{\max }\) is 1.6 times higher than Tc = 0.9 K at P = 0.

Fig. 3: Antiferromagnetism and superconductivity under pressure.
figure 3

Temperature dependence of the In(1)-nuclear quadrupole resonance (NQR) nuclear spin-lattice relaxation rate 1/T1 (a) below and (b) above the antiferromagnetic (AF) quantum critical point \({P}_{{\rm{c}}}^{{\rm{AF}}}\). (Inset) Data for P = 1.12 and 1.24 GPa just around the Neel temperature TN and the superconducting transition temperature Tc. The dotted (solid) arrows indicate TN(Tc), while the dashed line for La(Ir,Rh)In5 indicates 1/T1T = constant. Data at P = 019 and for La(Ir,Rh)In5 are obtained from ref. 37. Error bars are smaller than the size of the data points.

Full size image

Pressure dependence of the Kondo hybridization

To probe the character of f electrons as a function of pressure, we use the In(1) 115In-NQR frequency νQ. In general, νQ is determined by the surrounding lattice and on-site electrons with the latter being dominant in strongly correlated electron systems38; in the current case the latter reflects f–c hybridization that generates an electric field gradient (EFG) at the In(1)-site, as was found in previous 115In-NQR and NMR studies on CeIn339 and CeRhIn534 under pressure. Figure 4a–c shows the pressure dependence of the In(1) NQR spectrum and νQ (see Supplementary Note 2 and Supplementary Fig. 2 for detail). In general, νQ is expected to increase smoothly with decreasing volume39; however, this is not the case here. At T = 4.2 K, νQ weakly increases up to P = 1.24 GPa but jumps at P* = 1.35 GPa above which the slope dνQ/dP increases by more than a factor of three. The same trend is found at lower temperatures where we see that P* decreases as T is reduced. We denote the midpoint of the νQ jump in the P–T plane as (P*, T*) = (1.35 GPa, 4.2 K), (1.13 GPa, 1.6 K), and (0.90 GPa, 0.3 K), respectively. The same result is also found in the In(2) site. Figure 4d, e shows the temperature dependence of the In(2) NQR spectrum and its peak position together with In(1) νQ at P = 1.12 GPa. As found in the In(1) site, the In(2) νQ increases below T* = 1.5 K. In a previous study on CeRhIn5, a similar change of EFG was found in the In(2) site at P* = 1.75 GPa, although detailed pressure dependence for the In(1) site with a high accuracy was not conducted34.

Fig. 4: Localized to itinerant transition.
figure 4

Pressure dependence of the In(1) 115In-nuclear quadrupole resonance (NQR) spectrum (±1/2 ↔ ±3/2 transition line) at T = 4.2 K (a) and 1.6 K (b). The curves are Gaussian fits. The dotted vertical lines indicate the peak positions at P = 0. c Pressure dependence of the NQR frequency (νQ) obtained at T = 0.3, 1.6, and 4.2 K. For clarity, the vertical axis for T = 1.6 and 4.2 K are offset by the amount shown in the parenthesis. Solid arrows indicate localized-to-itinerant transition pressure (P*) which is defined from the midpoint of νQ jump. Solid straight lines are fits to the data which yield the slope dνQ/dP = 0.008 (0.027) below (above) P*. Error bars represent the uncertainty in estimating νQ. d Temperature dependence of the In(2) 115In-NQR spectrum (±3/2 ↔ ±5/2 transition line) at P = 1.12 GPa. The curves are Gaussian fits. Vertical line indicates the peak position at T = 8 K. e Temperature dependence of the peak position of the In(2) spectrum (solid triangles) and In(1) νQ (open circles) at P = 1.12 GPa. Solid arrow indicates localized-to-itinerant transition temperature T* which is defined from the midpoint of νQ jump. The dashed line serves as visual guide. Error bars are smaller than the size of the data points except for those in (c).

Full size image

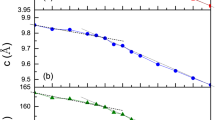
We consider the origin for the νQ jump. Figure 5a shows results of X-ray diffraction measurements that give the pressure dependence of a- and c-axis lengths; the lattice parameters decrease smoothly with increasing pressure to P = 4 GPa, without any signature of a structural transition. From these data, we calculate the EFG using the first-principles Hiroshima Linear-Augmented-Plane-Wave (HiLAPW) codes40. As expected, the calculated \({\nu }_{{\rm{Q}}}^{{\rm{HiLAPW}}}\) increases monotonically with applied pressure (Fig. 5b). This and the lack of any anomaly in 1/T1 at (P*, T*) rule out a change in lattice contribution to νQ as the origin of the νQ jump. Furthermore, Fig. 5b compares the pressure dependence of \({\nu }_{{\rm{Q}}}^{{\rm{HiLAPW}}}\) for CeRh(Ir)In5 and LaRh(Ir)In5. \({\nu }_{{\rm{Q}}}^{{\rm{HiLAPW}}}\) for CeRh(Ir)In5 is uniformly greater than that for LaRh(Ir)In5, because CeRh(Ir)In5 has the additional EFG from hybridized f electrons, unlike nonmagnetic LaRh(Ir)In5. This result is consistent with previous band calculations41,42.

Fig. 5: Lattice parameters and band calculation.
figure 5

a Pressure dependence of a- and c-axis lengths for CeRh0.5Ir0.5In5 at room temperature. b Pressure dependence of the nuclear quardrupole resonance frequency \({\nu }_{{\rm{Q}}}^{{\rm{HiLAPW}}}\) obtained from band calculations [Hiroshima Linear-Augmented-Plane-Wave (HiLAPW) code] for CeRh(Ir)In5 and LaRh(Ir)In5. LaRh(Ir)In5 corresponds to the 4f-localized model of CeRh(Ir)In5. Both are calculated with the same lattice constant. Error bars are smaller than the size of the data points.

Full size image

We conclude from these results that the jump in νQ(P) at (P*, T*) is due to a pronounced increase in Kondo hybridization at (P*, T*) and that the larger dνQ/dP above (P*, T*) reflects that increased hybridization. Because increased Kondo hybridization transfers f spectral weight from localized to itinerant degrees of freedom, and hence an increase in Fermi surface volume, the pronounced jump in νQ signals the experimental observation of a small (localized) to large (itinerant) Fermi surface. As the principal axis of the EFG at the In(2) site is perpendicular to that of the In(1) site, the νQ change at both sites suggests that the entire Fermi-surface volume changes at (P*, T*).

Determination of the AF QCP

The temperature dependence of T1 just above T ≥ Tc(P) can be described by the self-consistent renormalization (SCR) theory for spin fluctuations around an AF QCP43. A three-dimensional AF spin fluctuation model is applicable also to the low temperature thermopower S/T around the pressure-induced AF QCP of CeRh0.58Ir0.42In544. Near an AF QCP, the SCR model predicts \(1/{T}_{1}T\propto \sqrt{{\chi }_{{\bf{Q}}}(T)}=1/\sqrt{T+\theta }\)43, where χQ(T) is the Curie–Weiss staggered susceptibility and θ is a measure of the distance to the AF QCP. At the QCP, θ = 0 and χQ(T) diverges toward 0 K. 1/T1T can be represented by the sum of magnetic and small nonmagnetic contributions as 1/T1T = \(1/{({T}_{1}T)}_{{\rm{AF}}}+1/{({T}_{1}T)}_{{\rm{lattice}}}\). For the lattice term, we use the mean value of 1/T1T from reference materials LaRhIn5 and LaIrIn5 (Fig. 3b), which gives \(1/{({T}_{1}T)}_{{\rm{lattice}}}\) = 1.44 (s−1 K−1).

Figure 6a, b are plots of 1/T1T vs. T for the AF phase below P = 1.12 GPa and for the paramagnetic phase above P = 1.24 GPa, respectively. The solid curves in Fig. 6b are least-squares fits to 1/T1T = a/(T + θ)0.5 + 1.44 just above Tc(P), with a and θ as parameters. Approaching the AF QCP from P = 2.53 GPa, θ decreases with decreasing pressure, as can be seen in Fig. 6b. The pressure dependences of θ, TN, and Tc are plotted in Fig. 6c. From a linear fit of θ(P), the AF QCP (θ = 0 K) for CeRh0.5Ir0.5In5 is obtained at \({P}_{{\rm{c}}}^{{\rm{AF}}}\) = 1.2 GPa, where the highest Tc is realized. The present results clearly indicate that spin fluctuations play a significant role for superconductivity in CeRh0.5Ir0.5In5.

Fig. 6: Antiferromagnetic (AF) quantum critical point (\({P}_{{\rm{c}}}^{{\rm{AF}}}\)).
figure 6

Temperature dependence of the nuclear spin-lattice relaxation rate divided by temperature 1/T1T below (a) and above (b) \({P}_{{\rm{c}}}^{{\rm{AF}}}\) with the fitting curves (see text). The dotted (solid) arrows indicate the Neel temperature TN (the superconducting transition temperature Tc). c Summary of pressure dependence of the characteristic temperature θ (see text), TN, and Tc. The dotted straight line (filled diamonds) is a fit to the data which yields \({P}_{{\rm{c}}}^{{\rm{AF}}}\) (θ = 0) = 1.2 GPa. PM and AFM indicate paramagnetic and antiferromagnetic metal, respectively. SC indicates superconductivity. Error bars are smaller than the size of the data points.

Full size image

Unconventional superconductivity at \({P}_{{\rm{c}}}^{{\rm{AF}}}\)

As seen in Fig. 6a, b, there is a strong pressure dependence of the magnitude of 1/T1T at the lowest temperatures of these measurements. To place these results in perspective, we normalize 1/T1T by its value at Tc, 1/T1T(Tc), and plot the ratio in Figs. 7a, b as a function of reduced temperature T/Tc(P). Deep in the superconducting state, this ratio is clearly largest at P = 1.12 GPa near \({P}_{{\rm{c}}}^{{\rm{AF}}}\) and depends only weakly on temperature below Tc. This result contrasts with expectations for a fully gapped, e.g., s-wave, superconductor where 1/T1 should decrease exponentially to a very small value well below Tc and for a clean d-wave superconductor where 1/T1 decreases as T3. In CeRh0.5Ir0.5In5 at P = 1.12 GPa there must be a substantial fraction of low-lying excitations in the normal state that remains ungapped below Tc. Namely, \({[{T}_{1}T(T = 0.3\rm{K})]}^{-0.5}/{[{T}_{1}T({T}_{{\rm{c}}})]}^{-0.5}=N{({E}_{{\rm{F}}})}^{{\rm{residual}}}/N{({E}_{{\rm{F}}})}^{{\rm{normal}}}\) is the relative density of state (DOS) at T = 0.3 K, which is consistent with the fraction of ungapped quasiparticle DOS in the superconducting state.

Fig. 7: Low-lying excitations in the superconducting state.
figure 7

Temperature dependence of the nuclear spin-lattice relaxation rate divided by temperature 1/T1T below (a) and above (b) the antiferromagnetic (AF) quantum critical point (\({P}_{{\rm{c}}}^{{\rm{AF}}}\)). Data at P = 0 are obtained from the literature19. Horizontal and vertical axes are normalized by the superconducting transition temperature Tc(P) and 1/T1T[Tc(P)], respectively. Error bars are smaller than the size of the data points.

Full size image

To obtain the relative DOS, for simplicity we assume that T1 below Tc is predominantly determined by itinerant quasi particles. Previously, an analysis within the context of two-fluid phenomenological theory has deduced that the 4f local moments also contribute to relaxation45,46. Nonetheless, as shown in Supplementary Note 3 and Supplementary Figs. 3 and 4, such a model reproduces essentially the same result as we obtained here.

Phase diagram

  Figure 8a shows the pressure dependence of TN and T* inferred from In(1) NQR, together with Tc on the P–T plane. T* inferred from In(2) NQR at P = 1.12 GPa coincides with the result obtained from In(1). T* extrapolates to zero at \({P}_{{\rm{c}}}^{* }\) = 0.8 GPa, which is distinctly smaller than \({P}_{{\rm{c}}}^{{\rm{AF}}}\) = 1.2 GPa. In CeRhIn5 (x = 0), a similar result was suggested with \({P}_{{\rm{c}}}^{* }=1.75\) GPa34 and \({P}_{{\rm{c}}}^{{\rm{AF}}}=2.1\) GPa47. Comparison of these critical pressure values shows that Ir substitution with x = 0.5 (chemical pressure) is effectively equivalent to the application of a physical pressure of about P = 1 GPa to CeRhIn5. This conclusion is consistent with that drawn from our measurement of the hyperfine coupling presented earlier (Supplementary Note 1 and Supplementary Fig. 1). We emphasize again that, in the pressure regions we are interested for CeRhIn5 and CeRh0.5Ir0.5In5, 115A(1) is constant, and thus changes in physical properties are not related to a changing hyperfine coupling but to the quantum criticality.

Fig. 8: Phase diagram.
figure 8

a Pressure–temperature phase diagram for CeRh0.5Ir0.5In5 obtained at zero-magnetic field. The solid circles, squares, and stars indicate the Neel temperature TN, the superconducting transition temperature Tc, and the localized-to-itinerant transition temperature T*, respectively. The broken curve is a phase boundary separating small and large Fermi surfaces. b Pressure dependence of the relative density of states (DOS) on the T = 0.3 K plane. The dotted straight line indicates the antiferromagnetic (AF) quantum critical point (\({P}_{{\rm{c}}}^{{\rm{AF}}}=1.2\) GPa). The solid and dashed curves serve as visual guides. AFM and SC indicate antiferromagnetic metal and superconductivity, respectively. Error bars are smaller than the size of the data points.

Full size image

As shown in Fig. 8b, in CeRh0.5Ir0.5In5, remarkably, the fraction of ungapped excitations strongly depends on pressure, reaching a maximum at the AF QCP. In the coexistent state at P = 019, this fraction is 50%, but increases to 96% at \({P}_{{\rm{c}}}^{{\rm{AF}}}\) and then decreases to 55% with the increasing pressure at P = 2.53 GPa. The highest Tc around the AF QCP of CeRh0.5Ir0.5In5 is realized unexpectedly with the largest fraction of gapless excitations. The present observation is completely different from that for CeRhIn5 under pressure; in CeRhIn5, the relative fraction of gapless excitations (88%) in the coexistent state is rapidly suppressed to almost zero as it approaches the QCP47.

Discussion

From the phase diagram shown in Fig. 8, it is clear that the localized to itinerant transition (T*(P)) does not occur exactly at the AF QCP; in the limit of zero temperature, \({P}_{{\rm{c}}}^{* }\) precedes \({P}_{{\rm{c}}}^{{\rm{AF}}}\). One possibility would be that the Fermi-surface change across the T*(P) boundary marks a line of abrupt changes of the Ce valence that terminates near T = 0 in a critical end point. A model that considers this possibility, however, appears to exclude the T*(P) boundary from extending into the AF state48,49, contrary to our results. In contrast, a breakdown of the Kondo effect gives rise to a small-to large Fermi surface change across T*(P)50. This idea leads to a T = 0 phase diagram16,51 similar to the results of Fig. 8. Associated with the Kondo breakdown and development of a large Fermi surface, soft charge fluctuations can emerge without a change in formal valence of Ce ions52. Within experimental uncertainty of  ±1.5%, there is no detectable difference between CeRhIn5 and CeIrIn5 at 10 K in their spectroscopically determined Ce valence53, even though their Fermi volumes differ—a result that, together with the phase diagram of Fig. 8, supports a Kondo breakdown interpretation as do thermopower measurements on CeRh0.58Ir0.42In544. Notably, the T* boundary has no notable effect on the evolution of Tc(P). In passing, we mention a possibility of a more general case, a Lifshitz transition. Watanabe and Ogata54, and Kuramoto et al.55 pointed out that, even though the Kondo screening remains, a competition between the Kondo effect and the RKKY interaction can lead to a topological Fermi surface transition (Lifshitz transition) below the AF QCP54,55, which is also consistent with our observation.

The large 1/T1T below Tc at pressures near the AF QCP (Figs. 6 and 7) is quite remarkable, and its temperature independence implies a large DOS that remains ungapped in the superconducting state even though this is the pressure range where Tc is a maximum. Such an anomalously high value of ungapped DOS in the superconducting state has never been found in other QCP materials such as high Tc cuprates56 and the iron-pnictide superconductors5,57, even though magnetic fluctuations are also strong around their QCP. For the Ce115 family, no significant gapless excitations have been observed so far around a QCP58.

In general, gapless excitations are expected from impurity scattering in d-wave superconductors59,60,61,62. Though there are no intentionally added impurities in our crystal, the random replacement of 50 % Rh by Ir results in a broadening of the In(1) NQR line by a factor of  ~5 compared to CeIrIn519,27. Such randomness increases the resistivity at 4 K (just above TN) from ~4 μΩcm in CeRhIn5 to over 20 μΩcm in CeRh0.5Ir0.5In532. Quantum critical fluctuations can further enhance that scattering61 to make part of a multi-sheeted Fermi surface gapless63. Such scattering concomitantly leads to pair breaking, resulting in a large reduction of Tc59,60,61,62,63,64, which is inconsistent with our observations. The relative DOS at the pressure-induced QCP is almost zero in CeRhIn547 but is enhanced to 96% in CeRh0.5Ir0.5In5 at \({P}_{{\rm{c}}}^{{\rm{AF}}}\). If we assume that the symmetry of CeRh0.5Ir0.5In5 is also d-wave, Tc should be reduced to zero with such a significant residual DOS at EF65. In contrast to this expectation, the maximum Tc = 1.4 K for CeRh0.5Ir0.5In5 remains at 61% of Tc = 2.3 K for CeRhIn5 at their respective QCPs. Hence, the present results suggest that superconductivity near \({P}_{{\rm{c}}}^{{\rm{AF}}}\) in CeRh0.5Ir0.5In5 is more exotic than d-wave.

Model calculations of superconductivity in a two-dimensional Kondo lattice show that near an AF QCP d- and p-wave spin-singlet superconducting states are nearly degenerate, with an odd frequency p-wave spin-singlet state being favored when entering the large Fermi surfaces region to take advantage of the nesting condition with the vector Q = (π, π)66. A p-orbital wave function with spin-singlet pairing symmetry satisfies Fermi statistics in the odd-frequency channel67,68,69,70, and this odd-frequency pairing is more robust against nonmagnetic impurity scattering than even-frequency pairing71. Indeed, for a scattering strength that kills d-wave superconductivity completely, spin-singlet odd-frequency pairing will survive with a Tc that is approximately 60% of that in the absence of scattering71. Motivated by these theoretical results, we suggest that odd-frequency spin-singlet pairing is realized in CeRh0.5Ir0.5In5 in the vicinity of its critical pressures. Its robust Tc in the presence of substantial disorder scattering that gives rise to a large residual density of states at \({P}_{{\rm{c}}}^{{\rm{AF}}}\) where quantum critical fluctuations are strongest and the presence of a nearby change from small-to large Fermi surface at \({P}_{{\rm{c}}}^{* }\) are fully consistent with our proposal. We stress that the unique aspect of both strong fluctuations and large Fermi surface is not shared by the end members, CeIrIn5 or CeRhIn5. Knight shift and experiments that directly probe the gap symmetry will be useful to test this possibility.

In summary, we reported systematic 115In-NQR measurements on the heavy fermion AF superconductor CeRh0.5Ir0.5In5 under pressure and find that an AF QCP is located at \({P}_{{\rm{c}}}^{{\rm{AF}}}\) = 1.2 GPa, at which Tc(P) reaches its maximum. The pressure and temperature dependence of νQ reveal a pronounced increase in hybridization that signals a change from small-to large Fermi surface in the limit of zero temperature at \({P}_{{\rm{c}}}^{* }\) = 0.8 GPa which is notably lower than \({P}_{{\rm{c}}}^{{\rm{AF}}}\). Thus, our work sheds new light on the quantum phase transition in f-electron systems. There is a strong enhancement of the quasiparticle DOS in the superconducting state around \({P}_{{\rm{c}}}^{{\rm{AF}}}\) where the Fermi surface is large. The robustness of Tc under these conditions can be understood if the superconductivity is odd-frequency p-wave spin singlet. Traditionally, Hall coefficient and quantum oscillation experiments have been used to probe the Fermi surface change. Our work demonstrates that the NQR frequency can be used as a powerful tool to examine the change in Fermi surface volume for heavy electron systems. In particular, the NQR technique does not require single crystals and is not limited by sample quality or pressure, and thus will open a new venue to understand strongly correlated electron superconductivity.

Methods

Samples

Single crystals of CeRh0.5Ir0.5In5 were grown from an In flux as reported in a previous study18. All experiments were performed with the same batch of crystals used in the previous NQR study19. As documented in detail in ref. 19, there is no phase separation into Rh-rich and Ir-rich parts even in the coarsely crushed powder. In fact, no excess peaks in the NMR/NQR spectrum are found and the spectrum can be reproduced by a Gaussian function. Moreover, T1 is of single component, which also indicates that Ir is randomly distributed. For NMR Knight shift measurements, two single crystals, sized 2 mm—4 mm—0.5 mm and 2 mm—3 mm—0.4 mm, were used. For NQR measurements, the crystals were moderately crushed into grains to allow RF pulses to penetrate easily into the samples. Small and thin single-crystal platelets cleaved from an as-grown ingot were used for X-ray and dc-susceptibility measurements.

NQR measurement

For NQR, the nuclear spin Hamiltonian can be expressed as, \({{\mathcal{H}}}_{{\rm{Q}}}=(h{\nu }_{{\rm{Q}}}/6)[3{{I}_{z}}^{2}-I(I+1)+\eta ({{I}_{x}}^{2}-{{I}_{y}}^{2})]\), where h is Planck’s constant and I = 9/2 for the In nucleus is the nuclear spin; νQ and the asymmetry parameter η are defined as \({\nu }_{{\rm{Q}}}=\frac{3eQ{V}_{zz}}{2I(2I-1)h}\) and, \(\eta =\frac{{V}_{xx}-{V}_{yy}}{{V}_{zz}}\), respectively, and Q and Vαβ are the nuclear quadrupole moment and EFG tensor, respectively. In CeRh0.5Ir0.5In5, there are two inequivalent In sites, one in the CeIn [In(1)] layer and another in the (Rh,Ir)In4 [In(2)] layer (see Fig. 2a). The principle axis of the EFG at the In(1) [In(2)] site is parallel [perpendicular] to the c-axis. The 115In-NQR spectra for In(1) ± 1/2 ↔ ±3/2 transition line (Supplementary Note 2 and Supplementary Fig. 2),  ±7/2 ↔ ±9/2 transition line (Supplementary Fig. 5), the In(2)  ±3/2 ↔ ±5/2 transition line and T1 for the In(1) site (η = 0) (Supplementary Note 4 and Supplementary Figs. 6 and 7) were obtained as reported in an earlier study19,72. Here, T1 probes the dynamic spin susceptibility through the hyperfine coupling constant Aq as \(1/{T}_{1}\propto T{\sum }_{{\bf{q}}}{|{A}_{{\bf{q}}}|}^{2}{\chi }{^{\prime\prime} }({\bf{q}},{\omega }_{0})/{\omega }_{0}\), where ω0 is the NQR frequency73 and q is a wave vector for AF order and/or quantum critical fluctuation in CeRh0.5Ir0.5In5. Meanwhile, 1/T1 ∝ \(N{({E}_{{\rm{F}}})}^{2}\)kBT holds in a Pauli paramagnetic metal, i.e., in a heavy Fermi liquid state (Korringa law). Here, N(EF) is the density of states at EF.

A NiCrAl/BeCu piston-cylinder-type pressure-cell filled with Daphne (7474) oil was used. The Tc of Sn was measured to determine the pressure. Measurements below 1 K were performed using a 3He refrigerator.

X-ray measurement

A diamond anvil cell filled with a CeRh0.5Ir0.5In5 single crystal and Daphne oil were used for room temperature X-ray measurements under pressure; the pressure was determined by measuring the fluorescence of ruby. All measurements were made at zero-magnetic field.

EFG calculation

The EFG is calculated using the all electron full-potential linear augmented plane wave method implemented in the Hiroshima Linear-Augmented-Plane-Wave (HiLAPW) code with generalized gradient approximation including spin–orbit coupling40.

Hyperfine coupling constant

To estimate the hyperfine coupling constant for CeRh0.5Ir0.5In5, 115A(1), we measure the 115In(1)-NMR spectrum and dc susceptibility. For NMR, the nuclear spin Hamiltonian is expressed as \({\mathcal{H}}\) = −115γℏI ⋅ H\((1+K)+{{\mathcal{H}}}_{{\rm{Q}}}\), where the gyromagnetic ratio 115γ = 9.3295 MHz T−1, H is the external magnetic field, and K is the Knight shift. 115In-NMR spectra have nine transitions from Iz = (2m + 1)/2 to (2m − 1)/2 where m = −4, −3, −2, −1, 0, 1, 2, 3, 4 for In(1) and In(2) sites, respectively, with K, νQ, and η as parameters. At ambient pressure, νQ and η at the In(1) [In(2)] site are 6.35 MHz (17.37 MHz) and 0 (0.473), respectively19. The Knight shift for In(1), 115K(1)c(T), was calculated from the peak in the 115In(1)-NMR center line (m = 0) taken by sweeping the RF frequency at a fixed field H = 12.950 T and χc (emu mol−1) is obtained by dc susceptibility measurements at H = 3 T using a superconducting quantum interference device with the vibrating sample magnetometer. The magnetic field H is fixed perpendicular to the CeIn layer (c-axis).