Threshold $\pi ^-$ photoproduction on the neutron

Abstract

Recent data from the PIONS@MAX-lab Collaboration, measuring the total cross section of the incoherent pion photoproduction reaction, $\gamma d\rightarrow \pi ^- pp$, near threshold, have been used to extract the $E_{0+}$ multipole and total cross section of the reaction $\gamma n\rightarrow \pi ^-p$, also near threshold. These are the first measurements of the reaction $\gamma d\rightarrow \pi ^- pp$ in the threshold region. The value of $E_{0+}$ is extracted through a fit to the deuteron data in a photoproduction model accounting for final-state interactions. The model takes an S-wave approximation for the elementary reaction $\gamma n\rightarrow \pi ^-p$ with $\hbox {E}_{0+} =$ const in the threshold region. The fit over all the 6 deuteron data points gives the value $E_{0+} = -\,31.86\pm 0.8$ (in units $10^{-3}/m_\pi$). We explore the dependence of our results on the choice of data subsets included in the fit. The obtained values of $E_{0+}$, for different subsets, have overlapping errors and agree with previous determinations.

Appendix: the reaction amplitude

The invariant amplitude $M_{\gamma d}$ of the reaction $\gamma d\rightarrow \pi ^- pp$ can be written as

$$\begin{aligned} M_{\gamma d}= & {} c\varphi ^ + _1(L +i{\varvec{K}}\cdot {\varvec{\sigma }})\varphi ^c_2 , \nonumber \\ c= & {} 16\pi W\sqrt{m} \quad (W = m+ m_\pi ) , \nonumber \\ L= & {} L_a + L_b + L_c + L_d, \nonumber \\ L_a= & {} L^{(s)}_a + L^{(d)}_a , \nonumber \\ {\varvec{K}}= & {} {\varvec{K}}_a + {\varvec{K}}_b + {\varvec{K}}_c + {\varvec{K}}_d , \nonumber \\ {\varvec{K}}_a= & {} {\varvec{K}}^{(s)}_a + {\varvec{K}}^{(d)}_a . \end{aligned}$$

(A.1)

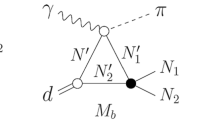
Here: $\varphi _{1,2}$ are the spinors of the final protons ($\varphi ^+\varphi \equiv 1$) and $\varphi ^c\equiv \sigma _2\varphi ^*$; the subscripts a, b, c, d (in $L_a$,.., ${\varvec{K}}_a$,..) correspond to the diagrams in Fig. 2; $L^{(s)}_a$ and ${\varvec{K}}^{(s)}_a$ ($L^{(d)}_a$ and ${\varvec{K}}^{(d)}_a$) are the IA amplitudes with S-wave (D-wave) part of the DWF. The amplitudes $L_a$,.. and ${\varvec{K}}_a$,.. are given below, where ${\varvec{e}}$ and ${\varvec{\epsilon }}$ are the photon and deuteron polarization three-vectors, respectively. Hereafter: ${\varvec{q}}$, ${\varvec{k}}$, ${\varvec{p}}_{1,2}$ stand for the three-momenta of the initial photon, final pion and final protons, respectively, in the laboratory frame.

(a) IA terms:

$$\begin{aligned} L^{(s)}_a= & {} x_aE_{0+}({\varvec{e}}\cdot {\varvec{\epsilon }}) ,\quad x_a = f_1 + f_2 , \nonumber \\ L^{(d)}_a= & {} -[g_1({\varvec{e}}\cdot {\varvec{n}}_1)({\varvec{e}}\cdot {\varvec{n}}_2) + \nonumber \\&+g_2({\varvec{e}}\cdot {\varvec{n}}_2)({\varvec{\epsilon }}\cdot {\varvec{n}}_1)]E_{0+} , \nonumber \\ {\varvec{K}}^{(s)}_a= & {} y_aE_{0+}[{\varvec{e}}\times {\varvec{\epsilon }}],\quad y_a = f_2 - f_1 , \nonumber \\ {\varvec{K}}^{(d)}_a= & {} (g_2({\varvec{\epsilon }}\cdot {\varvec{n}}_2)[{\varvec{n}}_2 \times \!{\varvec{e}}] - \nonumber \\&-g_1({\varvec{\epsilon }}\cdot {\varvec{n}}_1)[{\varvec{n}}_1 \times {\varvec{e}}])E_{0+} ; \nonumber \\ \displaystyle f_{1,2}= & {} \frac{u(p_{1,2})}{\sqrt{2}} + \frac{w(p_{1,2})}{2} , \nonumber \\ \displaystyle g_{1,2}= & {} \frac{3}{2}\,w(p_{1,2}) , \quad {\varvec{n}}_{1,2} = \frac{{\varvec{p}}_{1,2}}{p_{1,2}} . \end{aligned}$$

(A.2)

Here ${\varvec{n}}_{1,2}$ – the unit vectors; u(p) and w(p) are the S- and D-wave parts of the DWF. We use DWF [25], parametrized in the form

$$\begin{aligned} u(p) = \sum _j\frac{C_j}{p^2 + m^2_j} ,\quad w(p) = \sum _j\frac{D_j}{p^2 + m^2_j} \end{aligned}$$

(A.3)

with normalization $\int d{\varvec{p}}\,[u^2(p) + w^2(p)] = (2\pi )^3$ .

(b) $\underline{pp\text {-FSI terms}}$:

$$\begin{aligned} L_b= & {} x_b E_{0+}({\varvec{e}}\cdot {\varvec{\epsilon }}),\quad {\varvec{K}}_b = 0 , \nonumber \\ x_b= & {} 2 I_{pp}(p,\beta ,\Delta )f_{pp}(p) , \nonumber \\ \displaystyle I_{pp}(p,\beta ,\Delta )= & {} \int \frac{d{\varvec{x}}\,f(x,p)u(|{\varvec{x}}+ {\varvec{\Delta }}|)}{2\pi ^2\sqrt{2}\,(x^2 - p^2 -i0)} , \nonumber \\ \displaystyle f(x,p)= & {} \frac{p^2 + \beta ^2}{x^2 + \beta ^2} , \quad {\varvec{\Delta }}= \frac{1}{2}({\varvec{p}}_1 + {\varvec{p}}_2) . \end{aligned}$$

(A.4)

Here $f_{pp}(p)$ is the on-shell S-wave pp-scattering amplitude in the effective-range-approximation with Coulomb effects included [21]; ${\varvec{x}}$ is the relative three-momentum of the intermediate nucleons; f(x, p) is the form factor in the off-shell pp-scattering amplitude $f^{off}_{pp}(x,p) = f(x,p)f_{pp}(p)$ with parameter $\beta = 1.2\,$ fm, used earlier [20, 22]. The integral $I_{pp}(p,\beta ,\Delta )$ is written out in Eqs. (A.9) and (A.10).

(c) $\underline{\pi N\text {-FSI terms}}$:

$$\begin{aligned} L_c= & {} x_cE_{0+}a_{\pi ^- p}\,({\varvec{e}}\cdot {\varvec{\epsilon }}) , \quad x_c = I_1 + I_2; \nonumber \\ \displaystyle {\varvec{K}}_c= & {} y_cE_{0+}a_{\pi ^- p}\,[{\varvec{e}}\times {\varvec{\epsilon }}] , \quad y_c =I_1 - I_2; \nonumber \\ \displaystyle I_i= & {} I(k^2_i,\Delta _i) , \quad {\varvec{\Delta }}_i = \frac{m}{m + m_\pi }({\varvec{k}}+ {\varvec{p}}_i) . \end{aligned}$$

(A.5)

Here: $k_i$ are the relative momenta in the pion-proton pairs $\pi ^-p_i\, (i = 1,2)$; $a_{\pi ^- p}$ is the $\pi ^-p$-scattering amplitude in the scattering-length approximation (see the main text), $m_\pi$ and m are defined after Eq. (2) in the main text. The integral $I(k^2_{1,2}, \Delta _{1,2})$ is written out below in Eq. (A.9).

(d) 2-loop terms:

$$\begin{aligned} L_d= & {} x_d E_{0+}({\varvec{e}}\cdot {\varvec{\epsilon }}) ,\quad {\varvec{K}}_d = 0 , \nonumber \\ \displaystyle x_d= & {} 2K(p,b,\Delta )f_{pp}(p)a_{\pi ^- p} , \nonumber \\ \displaystyle K(p,b,\Delta )= & {} \frac{m + m_\pi }{m} \nonumber \\&\displaystyle \times \int \frac{d{\varvec{x}}d{\varvec{y}}\,u(|{\varvec{x}}+ {\varvec{y}}- \Delta |)f(x,p)}{4\pi ^4\sqrt{2}\,(x^2 - p^2 -i0)(y^2 - b^2 - i0)}, \nonumber \\ \displaystyle {\varvec{\Delta }}= & {} \frac{1}{2}({\varvec{q}}+ {\varvec{k}}) ,\quad b^2 = 2 m_\pi (\sqrt{s} - \sqrt{s_0})\ge 0 .\nonumber \\ \end{aligned}$$

(A.6)

Here $\sqrt{s_0} = 2m_p + m_\pi$; f(x, p) is given in Eq. (A.4); the denominator $(y^2 - b^2 - i0)$ of the pion propagator is obtained, neglecting the kinetic energies (static approximation) of the intermediate nucleons. The expression for $K(p,b,\Delta )$ is given in Eqs. (A.11) and (A.12).

1.1 The square of the amplitude

The square of the amplitude Eq. (A.1) for unpolarized nucleons is $|M_{\gamma d}|^2 = 2c^2\,(|L|^2 + |{\varvec{K}}|^2)$. Averaging it over the photon and deuteron polarization states, we write

$$\begin{aligned} \overline{|M_{\gamma d}|^2} = 2c^2\,(\overline{|L|^2} + \overline{|{\varvec{K}}|^2}) . \end{aligned}$$

(A.7)

Making use of Eqs. (A.2), (A.4), (A.5), and (A.6), we have

$$\begin{aligned} \displaystyle L= & {} A E_{0+}({\varvec{e}}\cdot {\varvec{\epsilon }}) + L^{(d)}_a , \quad A = x_a + x_b\!+\!x_c + x_d , \\ \displaystyle {\varvec{K}}\!= & {} B E_{0+}[{\varvec{e}}\!\times {\varvec{\epsilon }}] + {\varvec{K}}^{(d)}_a , \quad B = y_a + y_c . \end{aligned}$$

Then, we obtain

$$\begin{aligned} \displaystyle \overline{|L|^2}= & {} \frac{1}{3}\biggl [|A|^2 - (g_1 n^2_{1t} + g_2 n^2_{2t}) \mathrm{Re}[A] \nonumber \\&\displaystyle + \frac{1}{2}\,(g^2_1 n^2_{1t} + g^2_2 n^2_{2t}) \nonumber \\&\displaystyle + g_1g_2({\varvec{n}}_1\cdot {\varvec{n}}_2)({\varvec{n}}_{1t}\cdot {\varvec{n}}_{2t})\biggr ] (E_{0+})^2 , \nonumber \\ \displaystyle \overline{|{\varvec{K}}|^2}= & {} \frac{1}{3}\biggl [2|B|^2\displaystyle + [g_1(1 +n^2_{1z}) - g_2(1 + n^2_{2z})] \mathrm{Re}[B] \nonumber \\&\displaystyle + \frac{1}{2}\,[g^2_1(1 + n^2_{1z}) +g^2_2(1 + n^2_{2z})] \nonumber \\&\displaystyle - g_1g_2({\varvec{n}}_1\cdot {\varvec{n}}_2)[({\varvec{n}}_1\cdot {\varvec{n}}_2) + n_{1z}n_{2z}]\biggr ] (E_{0+})^2 . \end{aligned}$$

(A.8)

Here ${\varvec{n}}_{1t,2t}$ and $n_{1z,2z}$ are, respectively, the transverse parts and z-components of the unit vectors ${\varvec{n}}_{1,2}$, defined in Eq. (A.2), with z-axis along the photon three-momentum ${\varvec{q}}$ in the laboratory frame.

1.2 The integrals

The integral $I_{pp}(p,\beta ,\Delta )$ in Eq. (A.4) can be rewritten as

$$\begin{aligned} I_{pp}(p,\beta ,\Delta )= & {} I(p^2,\Delta ) - I(-\beta ^2,\Delta ) , \nonumber \\ \displaystyle I(a^2,\Delta )= & {} \int \frac{d{\varvec{x}}\,u(|{\varvec{x}}+ {\varvec{\Delta }}|)}{2\pi ^2\sqrt{2}\,(x^2 - a^2 -i0)} . \end{aligned}$$

(A.9)

For the DWF, given in the form Eq. (A.3), we obtain

$$\begin{aligned} \displaystyle I(a^2 > 0,\Delta )= & {} \sum _j\frac{C_j}{2\Delta \sqrt{2}} \biggl [\arctan \frac{|a| + \Delta }{m_j} \nonumber \\&\displaystyle - \arctan \frac{|a| - \Delta }{m_j} + \frac{i}{2}\ln \frac{m^2_j + (|a| + \Delta )^2}{m^2_j + (|a| - \Delta )^2} \biggr ] , \nonumber \\ \displaystyle I(a^2 < 0,\Delta )= & {} \sum _j\frac{C_j}{\Delta \sqrt{2}} \,\arctan \frac{\Delta }{m_j + |a|} . \end{aligned}$$

(A.10)

The integral $K(p,b,\Delta )$ in Eq. (A.6) can be written as

$$\begin{aligned} K(p,b,\Delta )= & {} K_0(p^2,b^2,\Delta ) - K_0(-\beta ^2,b^2,\Delta ) , \nonumber \\ \displaystyle K_0(a^2,b^2,\Delta )= & {} \frac{m + m_\pi }{m} \nonumber \\ \displaystyle&\times \int \frac{d{\varvec{x}}d{\varvec{y}}\,u(|{\varvec{x}}+ {\varvec{y}}- \Delta |)}{4\pi ^4\sqrt{2}\,(x^2 - a^2 - i0)(y^2 - b^2 -i0)} .\nonumber \\ \end{aligned}$$

(A.11)

For the DWF of the type Eq. (A.3), we obtain

$$\begin{aligned} \displaystyle K_0(a^2,b^2,\Delta )= & {} \sum _j\frac{C_j}{\Delta \sqrt{2}}\Bigl [U_j(a^2,b^2,\Delta ) \nonumber \\ \displaystyle&-U_j(a^2,b^2, - \Delta )\Bigr ] , \nonumber \\ \displaystyle U_j(a^2,b^2,\Delta )= & {} -x_jA_j - yL_j \nonumber \\ \displaystyle&+i(yA_j - x_jL_j) , \nonumber \\ \displaystyle L_j= & {} \frac{1}{2}\ln (x^2_j + y^2),~ A_j = \arctan \frac{y}{x_j} ; \nonumber \\ \displaystyle a^2 >0 :~ x_j= & {} m_j,~ y = |a| + \!|b| + \Delta ; \nonumber \\ \displaystyle a^2 <0 :~ x_j= & {} m_j + |a|,\quad y = |b| + \Delta . \end{aligned}$$

(A.12)