A goodness-of-fit test for regression models with spatially correlated errors

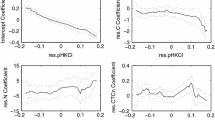
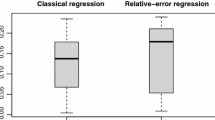
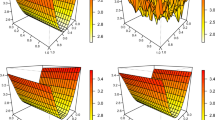
Abstract

The problem of assessing a parametric regression model in the presence of spatial correlation is addressed in this work. For that purpose, a goodness-of-fit test based on a $L_2$-distance comparing a parametric and nonparametric regression estimators is proposed. Asymptotic properties of the test statistic, both under the null hypothesis and under local alternatives, are derived. Additionally, a bootstrap procedure is designed to calibrate the test in practice. Finite sample performance of the test is analyzed through a simulation study, and its applicability is illustrated using a real data example.

Appendix: Proof of Theorem 1

The test statistic (6) can be written as

$$\begin{aligned} T_n= & {} n|\mathbf {H}|^{1/2}\int (\hat{m}^{LL}_{\mathbf {H}}(\mathbf {x})-\hat{m}^{LL}_{\mathbf {H},\hat{\varvec{\beta }}}(\mathbf {x}))^2w(\mathbf {x})\hbox {d}\mathbf {x}\\= & {} n|\mathbf {H}|^{1/2}\int \bigg [e_1'\left( \begin{array}{ll} \frac{1}{n}\sum _{i=1}^{n} K_{\mathbf {H}}(\mathbf {X}_i-\mathbf {x}) &{} \frac{1}{n}\sum _{i=1}^{n} K_{\mathbf {H}}(\mathbf {X}_i-\mathbf {x})(\mathbf {X}_i-\mathbf {x})' \\ \frac{1}{n}\sum _{i=1}^{n} K_{\mathbf {H}}(\mathbf {X}_i-\mathbf {x})(\mathbf {X}_i-\mathbf {x}) &{} \frac{1}{n}\sum _{i=1}^{n} K_{\mathbf {H}}(\mathbf {X}_i-\mathbf {x})(\mathbf {X}_i-\mathbf {x}) (\mathbf {X}_i-\mathbf {x}) ' \end{array} \right) ^{-1}\\&\cdot \left( \begin{array}{ll} \frac{1}{n}\sum _{i=1}^{n} K_{\mathbf {H}}(\mathbf {X}_i-\mathbf {x})(Z_i-m_{\hat{{\varvec{\beta }}}}(\mathbf {X}_i)) \\ \frac{1}{n}\sum _{i=1}^{n} K_{\mathbf {H}}(\mathbf {X}_i-\mathbf {x})(\mathbf {X}_i-\mathbf {x}) (Z_i-m_{\hat{{\varvec{\beta }}}}(\mathbf {X}_i)) \end{array} \right) \bigg ]^2w(\mathbf {x})\hbox {d}\mathbf {x}. \end{aligned}$$

Taking into account that, for every $\eta >0$, $\hat{f}_{\mathbf {H}}(\mathbf {x})=\frac{1}{n}\sum _{i=1}^{n} K_{\mathbf {H}}(\mathbf {X}_i-\mathbf {x})=f(\mathbf {x})+ O_p(n^{-2/(4+d)+\eta })$ uniformly in $\mathbf {x}$ (see Härdle and Mammen 1993), and according to Liu (2001), it follows that

$$\begin{aligned} T_n= & {} n|\mathbf {H}|^{1/2}\int \bigg [ \frac{1}{nf(\mathbf {x})}\sum _{i=1}^{n} K_{\mathbf {H}}(\mathbf {X}_i-\mathbf {x})(Z_i-m_{\hat{{\varvec{\beta }}}}(\mathbf {X}_i))\nonumber \\&-\nabla f(\mathbf {x}) \frac{1}{nf^{2}(\mathbf {x})}\sum _{i=1}^{n} K_{\mathbf {H}}(\mathbf {X}_i-\mathbf {x})(\mathbf {X}_i-\mathbf {x}) (Z_i-m_{\hat{{\varvec{\beta }}}}(\mathbf {X}_i))\bigg ]^2w(\mathbf {x})\hbox {d}\mathbf {x}\nonumber \\&\qquad +O_p(n^{-2/(4+d)+\eta })\nonumber \\= & {} T_{n1}+T_{n2}+2T_{n12}+O_p(n^{-2/(4+d)+\eta }), \end{aligned}$$

(11)

where $\nabla f(\mathbf {x})$ denotes the $d \times 1$ vector of first-order partial derivatives of f, and

$$\begin{aligned} T_{n1}= & {} n|\mathbf {H}|^{1/2}\int \bigg [ \frac{1}{nf(\mathbf {x})}\sum _{i=1}^{n} K_{\mathbf {H}}(\mathbf {X}_i-\mathbf {x})(Z_i-m_{\hat{{\varvec{\beta }}}}(\mathbf {X}_i))\bigg ]^2w(\mathbf {x})\hbox {d}\mathbf {x},\\ T_{n2}= & {} n|\mathbf {H}|^{1/2}\int \bigg [ \nabla f(\mathbf {x}) \frac{1}{nf^{2}(\mathbf {x})}\sum _{i=1}^{n} K_{\mathbf {H}}(\mathbf {X}_i-\mathbf {x})(\mathbf {X}_i-\mathbf {x}) (Z_i-m_{\hat{{\varvec{\beta }}}}(\mathbf {X}_i))\bigg ]^2w(\mathbf {x})\hbox {d}\mathbf {x}, \end{aligned}$$

denoting by $T_{n12}$ the integral of the cross product. Regarding $T_{n1}$, taking into account that the regression models considered are of the form $m(\mathbf {x}) =m_{{\varvec{\beta }}_0}(\mathbf {x}) + n^{-1/2}|\mathbf {H}|^{-1/4}g(\mathbf {x})$, one gets that

$$\begin{aligned} T_{n1}= & {} n|\mathbf {H}|^{1/2}\int \bigg [ \frac{1}{nf(\mathbf {x})}\sum _{i=1}^{n} K_{\mathbf {H}}(\mathbf {X}_i-\mathbf {x})(m_{{\varvec{\beta }}_0}(\mathbf {X}_i)+n^{-1/2}|\mathbf {H}|^{-1/4}g(\mathbf {X}_i)\\&+\,\varepsilon _i-m_{\hat{{\varvec{\beta }}}}(\mathbf {X}_i))\bigg ]^2w(\mathbf {x})\hbox {d}\mathbf {x}\\= & {} n|\mathbf {H}|^{1/2}\int \frac{1}{f^2(\mathbf {x})}(I_1(\mathbf {x})+I_2(\mathbf {x})+I_3(\mathbf {x}))^2w(\mathbf {x})\hbox {d}\mathbf {x}, \end{aligned}$$

where

$$\begin{aligned} I_1(\mathbf {x})= & {} \dfrac{1}{n}\sum _{i=1}^n K_{\mathbf {H}}\left( {\mathbf {X}_i-\mathbf {x}}\right) (m_{{\varvec{\beta }}_0}(\mathbf {X}_i)-m_{\hat{{\varvec{\beta }}}}(\mathbf {X}_i)),\\ I_2(\mathbf {x})= & {} \dfrac{1}{n}\sum _{i=1}^n K_{\mathbf {H}}\left( {\mathbf {X}_i-\mathbf {x}}\right) n^{-1/2}|\mathbf {H}|^{-1/4}g(\mathbf {X}_i),\\ I_3(\mathbf {x})= & {} \dfrac{1}{n}\sum _{i=1}^n K_{\mathbf {H}}\left( {\mathbf {X}_i-\mathbf {x}}\right) \varepsilon _i. \end{aligned}$$

Under assumptions (A1)–(A3) and (A7), and given that the difference $m_{\hat{{\varvec{\beta }}}}(\mathbf {x})-m_{{{\varvec{\beta }}}_0}(\mathbf {x})=O_p(n^{-1/2})$ uniformly in $\mathbf {x}$, it is obtained that

$$\begin{aligned}&n|\mathbf {H}|^{1/2}\int \frac{1}{f^2(\mathbf {x})}I_1^2(\mathbf {x})w(\mathbf {x})\hbox {d}\mathbf {x}=O_p(|\mathbf {H}|^{1/2}). \end{aligned}$$

(12)

As for the term $I_2(\mathbf {x})$, taking into account Lemma 1 (available in the Online Supplementary Material), by straightforward calculations it follows that

$$\begin{aligned}&n|\mathbf {H}|^{1/2}\int \frac{1}{f^2(\mathbf {x})}I_2^2(\mathbf {x})w(\mathbf {x})\hbox {d}\mathbf {x} \nonumber \\&\quad = \int (K_\mathbf {H}*g)^2(\mathbf {x})w(\mathbf {x})\hbox {d}\mathbf {x}\cdot \{1+o_p(1)\}. \end{aligned}$$

(13)

Note that the leading term of (13) is the term $b_{1\mathbf {H}}$ in Theorem 1. Finally, $I_3(\mathbf {x})$ (associated with the error component) can be decomposed as

$$\begin{aligned}&n|\mathbf {H}|^{1/2}\int \frac{1}{f^2(\mathbf {x})}I_3^2(\mathbf {x})w(\mathbf {x})\hbox {d}\mathbf {x}= n|\mathbf {H}|^{1/2}\int \frac{1}{f^2(\mathbf {x})n^2}\sum _{i=1}^n K^2_{\mathbf {H}}\left( {\mathbf {X}_i-\mathbf {x}}\right) \varepsilon ^2(\mathbf {X}_i)w(\mathbf {x})\hbox {d}\mathbf {x}\\&\qquad +n|\mathbf {H}|^{1/2}\int \frac{1}{f^2(\mathbf {x})n^2}\sum _{i\ne j} K_{\mathbf {H}}\left( {\mathbf {X}_i-\mathbf {x}}\right) K_{\mathbf {H}}\left( {\mathbf {X}_j-\mathbf {x}}\right) \varepsilon _i\varepsilon _jw(\mathbf {x})\hbox {d}\mathbf {x}\\&\quad =I_{31}+I_{32}. \end{aligned}$$

For the first term, one gets that

$$\begin{aligned} \mathbb {E}(I_{31})= & {} \mathbb {E}\bigg [\sigma ^2n|\mathbf {H}|^{1/2}\int \frac{1}{f^2(\mathbf {x})}\frac{1}{n^2}\sum _{i=1}^n K^2_{\mathbf {H}}\left( {\mathbf {X}_i-\mathbf {x}}\right) w(\mathbf {x})\hbox {d}\mathbf {x}\bigg ]\nonumber \\= & {} \sigma ^2 |\mathbf {H}|^{-1/2}{}K^{(2)}(\mathbf {0})\int \dfrac{w(\mathbf {x})}{f(\mathbf {x})}\hbox {d}\mathbf {x}\cdot \{1+o(1)\}. \end{aligned}$$

Similarly, it is obtained that $\text{ Var }(I_{31})=O_p(n^{-1}|\mathbf {H}|^{-1})$, and, therefore,

$$\begin{aligned} I_{31}=\sigma ^2 |\mathbf {H}|^{-1/2}{}K^{(2)}(\mathbf {0})\int \dfrac{w(\mathbf {x})}{f(\mathbf {x})}\hbox {d}\mathbf {x}\cdot \{1+o_p(1)\}. \end{aligned}$$

(14)

The leading term of (14) corresponds to the first term of $b_{0\mathbf {H}}$ in Theorem 1. For the term $I_{32}$, let

$$\begin{aligned} \kappa _{ij}= & {} n|\mathbf {H}|^{1/2}\int \frac{1}{f^2(\mathbf {x})}\dfrac{1}{n^2} K_{\mathbf {H}}\left( {\mathbf {X}_i-\mathbf {x}}\right) K_{\mathbf {H}}\left( {\mathbf {X}_j-\mathbf {x}}\right) \varepsilon _i\varepsilon _jw(\mathbf {x})\hbox {d}\mathbf {x}, \end{aligned}$$

thus,

$$\begin{aligned} I_{32}=\sum _{i\ne j}\kappa _{ij}, \end{aligned}$$

and this can be seen as a U-statistic with degenerate kernel. To obtain the asymptotic normality of $I_{32}$, considering assumption (A6), Theorem 2 given in Kim et al. (2013) will be applied. For this term, under assumptions (A4), (A7), (A8) and (A9), and according to Liu (2001), one gets that

$$\begin{aligned} \mathbb {E}(I_{32})= & {} \nonumber \dfrac{n-1}{n}|\mathbf {H}|^{-1/2}\sigma ^2\int \!\!\! \left( n|\mathbf {H}|\int \!\! \int \!\! K\left( \mathbf {p}\right) K\left( \mathbf {q}\right) \rho _n(\mathbf {H}(\mathbf {p}-\mathbf {q}))d\mathbf {p}d\mathbf {q}\right. \nonumber \\&+o(1)\bigg )w(\mathbf {x})\hbox {d}\mathbf {x}\nonumber \\= & {} |\mathbf {H}|^{-1/2}\sigma ^2K^{(2)}(0)\rho _{c}\int w(\mathbf {x})\hbox {d}\mathbf {x}\cdot \{1+o(1)\}, \end{aligned}$$

(15)

corresponding to the second term of $b_{0\mathbf {H}}$ in Theorem 1.

Similarly, it can be shown that the leading term of the variance of $I_{32}$ is given by:

$$\begin{aligned} V= & {} 2\sigma ^4 K^{(4)}(0)\bigg [\int \dfrac{w^2(\mathbf {x})}{f^2(\mathbf {x})}\hbox {d}\mathbf {x}+2\rho _{c}\int \dfrac{w^2(\mathbf {x})}{f(\mathbf {x})}\hbox {d}\mathbf {x}+4\rho ^2_{c}\int {w^2(\mathbf {x})}\hbox {d}\mathbf {x}\bigg ]. \end{aligned}$$

(16)

Therefore, using the central limit theorem for degenerate reduced U-statistics under $\alpha$-mixing conditions, given in Kim et al. (2013), it is obtained that the term $I_{32}$ converges, in distribution, to a normal distribution with mean the leading term of (15) and variance (16).

On the other hand, in virtue of the Cauchy–Schwarz inequality, the cross terms in $T_{n1}$ resulting from the products of $I_1(\mathbf {x})$, $I_2(\mathbf {x})$ and $I_3(\mathbf {x})$ are all of smaller order. Therefore, combining the results given in (12)–(14), and the asymptotic normality of $I_{32}$ [with bias the leading term of (15) and variance (16)], one gets

$$\begin{aligned} V^{-1/2}(T_{n1}-b_{0\mathbf {H}}-b_{1\mathbf {H}})\rightarrow _{\mathcal {L}} N(0,1) \text { as } n\rightarrow \infty , \end{aligned}$$

(17)

where

$$\begin{aligned} b_{0\mathbf {H}}= & {} |\mathbf {H}|^{-1/2}\sigma ^2K^{(2)}(\mathbf {0})\bigg [\int \dfrac{w(\mathbf {x})}{f(\mathbf {x})}\hbox {d}\mathbf {x}+\rho _{c}\int {w(\mathbf {x})}\hbox {d}\mathbf {x}\bigg ],\\ b_{1\mathbf {H}}= & {} \int ({K}_{\mathbf {H}}*g)^2(\mathbf {x})w(\mathbf {x})\hbox {d}\mathbf {x}, \end{aligned}$$

and

$$\begin{aligned} V=2\sigma ^4 K^{(4)}(0)\bigg [\int \dfrac{w^2(\mathbf {x})}{f^2(\mathbf {x})}\hbox {d}\mathbf {x}+2\rho _{c}\int \dfrac{w^2(\mathbf {x})}{f(\mathbf {x})}\hbox {d}\mathbf {x}+4\rho ^2_{c}\int {w^2(\mathbf {x})}\hbox {d}\mathbf {x}\bigg ]. \end{aligned}$$

The term $T_{n2}$ in $T_n$ is of smaller order than $T_{n1}$ (specifically, $T_{n2}=O_p(\text{ tr }(\mathbf {H}^2)T_{n1})$), and by the Cauchy–Schwarz inequality, the cross term $T_{n12}$ is of smaller order as well. Therefore, from (11), it follows that

$$\begin{aligned} T_n=T_{n1}+O_p(tr(\mathbf {H}^2))+O_p(n^{-2/(4+d)+\eta }). \end{aligned}$$

Taking into account (17), it follows that

$$\begin{aligned} V^{-1/2}(T_n-b_{0\mathbf {H}}-b_{1\mathbf {H}})\rightarrow _{\mathcal {L}} N(0,1) \text { as } n\rightarrow \infty . \end{aligned}$$

with $b_{0\mathbf {H}}$, $b_{1\mathbf {H}}$ and V given above.