Effective Resonant Model and Simulations in the Time-Domain of Wave Scattering from a Periodic Row of Highly-Contrasted Inclusions

Abstract

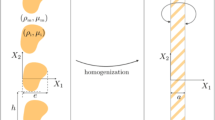
The time-domain propagation of scalar waves across a periodic row of inclusions is considered in 2D. As the typical wavelength within the background medium is assumed to be much larger than the spacing between inclusions and the row width, the physical configuration considered is in the low-frequency homogenization regime. Furthermore, a high contrast between one of the constitutive moduli of the inclusions and of the background medium is also assumed. So the wavelength within the inclusions is of the order of their typical size, which can further induce local resonances within the microstructure. In Pham et al. (J. Mech. Phys. Solids 106:80–94, 2017), two-scale homogenization techniques and matched-asymptotic expansions have been employed to derive, in the harmonic regime, effective jump conditions on an equivalent interface. This homogenized model is frequency-dependent due to the resonant behavior of the inclusions. In this context, the present article aims at investigating, directly in the time-domain, the scattering of waves by such a periodic row of resonant scatterers. Its effective behavior is first derived in the time-domain and some energy properties of the resulting homogenized model are analyzed. Time-domain numerical simulations are then performed to illustrate the main features of the effective interface model obtained and to assess its relevance in comparison with full-field simulations.

Appendices

Appendix A: Frequency-Domain Formulation

With the effective model (37) being derived in the time domain, this section focuses on assessing its equivalence with the frequency-domain formulation obtained in [20]. First, the frequency Fourier transform is defined:

$$ \mathscr{F}[f](\boldsymbol{X},\omega )=\hat{f}(\boldsymbol{X},\omega ) = \int _{ \mathbb{R}}f(\boldsymbol{X},t)e^{-i\omega t}\,\mathrm{d}t, $$

along with the convolution product:

$$ [f\ast g]({t})= \int _{\mathbb{R}}f(t-t')g(t)\,\mathrm{d}t'. $$

Due to the final effective jump condition (37), we seek closed-form identity for the field $W_{i}$ solution of (38). To do so, let us consider the time-domain Green’s function associated with the inclusion domain $\varOmega _{i}$ and a source point $\boldsymbol{y}_{0}$, i.e., the field $G:(\boldsymbol{y},t)\mapsto G(\boldsymbol{y},\boldsymbol{y}_{0}, t)$ that is the fundamental solution of the problem:

$$ \left \{ \begin{aligned} &\frac{\partial ^{2}G}{\partial t^{2}}(\boldsymbol{y},\boldsymbol{y}_{0}, t)- \frac{\mu _{i}}{\rho _{i}h^{2}}\Delta _{\boldsymbol{y}} G(\boldsymbol{y},\boldsymbol{y}_{0}, t) = \delta (\boldsymbol{y}-\boldsymbol{y}_{0})\delta (t) && (\boldsymbol{y}\in \varOmega _{i}), \\ &G(\boldsymbol{y},\boldsymbol{y}_{0}, t) = 0 && (\boldsymbol{y}\in \partial \varOmega _{i}), \\ & G(\boldsymbol{y},\boldsymbol{y}_{0},0) = \frac{\partial G}{\partial t}(\boldsymbol{y}, \boldsymbol{y}_{0},0) = 0 && (\boldsymbol{y}\in \varOmega _{i}). \end{aligned} \right . $$

The equations (38) at time $(t-t')$ are multiplied by $G$ taken at time $t'$ and integrated on $\varOmega _{i}\times [0,t]$, which leads to

$$ \int _{\varOmega _{i}}\left \{ \left [ \frac{\partial ^{2} W_{i}}{\partial t^{2}}*G\right ]\!(t)- \frac{\mu _{i}}{\rho _{i}h^{2}}\big[\Delta _{\boldsymbol{y}} W_{i}*G\big](t) \right \} \mathrm{d}\boldsymbol{y}=0. $$

Integrating by parts twice, the first term in time and the second term in space, respectively, and using the boundary conditions for $W_{i}$ and $G$ yields:

$$ W_{i}(\boldsymbol{y}_{0},X_{2},t) = -\frac{\mu _{i}}{\rho _{i}h^{2}}\left [ \left \langle V^{h} (\cdot ,X_{2},\cdot ) \right \rangle _{a}*\int _{ \partial \varOmega _{i}}\!\!\boldsymbol{\nabla }_{\!\boldsymbol{y}} G(\boldsymbol{y},\boldsymbol{y}_{0}, \cdot )\cdot \boldsymbol{n}\,\mathrm{d}\ell \right ]\!(t). $$

Going back to (37), we now get formally in the frequency domain:

$$\begin{aligned} &\mathscr{F}\left [\rho _{i}\int _{\varOmega _{i}} \frac{\partial W_{i}}{\partial t}\,\mathrm{d}\boldsymbol{y}\right ](\boldsymbol{X}, \omega ) \\ &\quad =\frac{\rho _{i}}{\rho _{m}}\left \langle \operatorname{div} \hat{\boldsymbol{\varSigma }}^{h}(\cdot ,X_{2},\omega ) \right \rangle _{a} \int _{\varOmega _{i}}\left \{ -\frac{\mu _{i}}{\rho _{i}h^{2}}\int _{ \partial \varOmega _{i}}\boldsymbol{\nabla }_{\boldsymbol{y}_{0}} \hat{G}(\boldsymbol{y}, \boldsymbol{y}_{0},\omega )\cdot \boldsymbol{n}\,\mathrm{d}\ell _{0}\right \} \mathrm{d}\boldsymbol{y}, \end{aligned}$$

(49)

where we have used the identity $i\omega \rho _{m}\hat{V}^{h}=\operatorname{div}\hat{\boldsymbol{\varSigma }}^{h}$ and the fact that $\hat{G}(\boldsymbol{y},\boldsymbol{y}_{0},\omega )=\hat{G}(\boldsymbol{y}_{0},\boldsymbol{y},\omega )$. We define the field $\hat{V}_{k_{m}}$ as

$$ \hat{V}_{k_{m}}(\boldsymbol{y},\omega )=-\frac{\mu _{i}}{\rho _{i}h^{2}}\int _{ \partial \varOmega _{i}}\!\!\boldsymbol{\nabla _{y_{0}}}\hat{G}(\boldsymbol{y},{\boldsymbol{y}}_{0}, \omega )\cdot \boldsymbol{n}\,\mathrm{d}\ell _{0}. $$

(50)

Owing to the following relation satisfied by $G$ in the frequency domain

$$ \Delta _{\boldsymbol{y}}\hat{G}(\boldsymbol{y},\boldsymbol{y}_{0}, \omega )+ \frac{\rho _{i}\mu _{m}}{\rho _{m}\mu _{0}}\hat{G}(\boldsymbol{y},\boldsymbol{y}_{0}, \omega )=-\frac{\rho _{i}h^{2}}{\mu _{i}}\delta (\boldsymbol{y}-\boldsymbol{y}_{0}), $$

then it turns out that $\hat{V}_{k_{m}}$ is the solution of the following problem:

$$ \left \{ \begin{aligned} &\Delta _{\boldsymbol{y}} \hat{V}_{k_{m}}(\boldsymbol{y},\omega )+{\kappa (k_{m})}^{2} \, \hat{V}_{k_{m}} (\boldsymbol{y},\omega )= 0 &&(\boldsymbol{y}\in \varOmega _{i}), \\ &\hat{V}_{k_{m}}(\boldsymbol{y},\omega )=1 && (\boldsymbol{y}\in \partial \varOmega _{i}), \end{aligned} \right . $$

(51)

where one has defined ${\kappa (k_{m})}=k_{m} h \sqrt{ \frac{\rho _{i}\mu _{m}}{\rho _{m}\mu _{i}}}$.

Therefore, provided that the Fourier transforms are well-defined, the time-domain model developed here is in agreement with the frequency-domain model of [20], see Equation (44) in the latter:

$$ \left \{ \begin{aligned} &\left [\!\![\hat{V}^{h} \right ]\!\!]_{a} =h \left \{ B \left \langle \frac{\partial \hat{V}^{h}}{\partial X_{1}} \right \rangle _{\!\!a}+ B_{2}\left \langle \frac{\partial \hat{V}^{h}}{\partial X_{2}} \right \rangle _{\!\!a} \right \} &&(X_{2}\in \mathbb{R}) \\ & \left [\!\![\hat{\varSigma }^{h}_{1} \right ]\!\!]_{a} = h \left \{ S\left \langle \frac{\partial \hat{\varSigma }^{h}_{1}}{\partial X_{1}} \right \rangle _{\!\!a}+C_{1}\left \langle \frac{\partial \hat{\varSigma }_{1}^{h}}{\partial X_{2}} \right \rangle _{ \!\!a}+C_{2}\left \langle \frac{\partial \hat{\varSigma }^{h}_{2}}{\partial X_{2}} \right \rangle _{\!\!a}+D(k_{m})\left \langle \operatorname{div} \hat{\boldsymbol{\varSigma }}^{h} \right \rangle _{a} \right \} &&(X_{2}\in \mathbb{R}), \end{aligned} \right . $$

(52)

where, due to (49) and (50), one has:

$$ D(k_{m})=\frac{\rho _{i}}{\rho _{m}}\int _{\varOmega _{i}}\hat{V}_{k_{m}}( \boldsymbol{y})\,\mathrm{d}\boldsymbol{y}. $$

(53)

Consequently, the agreement of the time-domain effective model with the frequency-dependent jump conditions is established. However, thanks to the time-domain formulation, we were able to perform an energy analysis and provide a sufficient condition for the effective model to be stable.

As shown in [20], the solution $\hat{V}_{k_{m}}$ to (51) can be found as an expansion onto the function basis of the eigensystem $(\lambda _{r},P_{r})_{r\geq 1}$ that is associated with the following self-adjoint eigenvalue problem within the inclusion:

$$ \left \{ \begin{aligned} &\Delta _{\boldsymbol{y}} P_{r}(\boldsymbol{y}) + \lambda _{r} P_{r}(\boldsymbol{y}) = 0 && \mbox{ in $\varOmega _{i}$,} \\ & P_{r}(\boldsymbol{y}) = 0 && \mbox{ on $\partial \varOmega _{i}$.} \end{aligned} \right . $$

(54)

In particular, let us define the resonant frequencies $\{ k_{r} \}_{r\geq 1}$ and the real-valued coefficients $\{\alpha _{r}\}_{r\geq 0}$ as follows

$$ \alpha _{0}=\int _{\varOmega _{i}}\mathrm{d}\boldsymbol{y} \qquad \alpha _{r} = \int _{\varOmega _{i}}P_{r}(\boldsymbol{y})\,\mathrm{d}\boldsymbol{y} \qquad \text{and} \qquad k_{r} = \frac{1}{h}\sqrt{ \frac{\rho _{m}\mu _{i}}{\rho _{i}\mu _{m}}\lambda _{r}}. $$

(55)

Then the term $D(k_{m})$ in (53) can be recast as the following infinite series:

$$ D(k_{m})=\frac{\rho _{i}}{\rho _{m}}\left \{ \alpha _{0}-\sum _{r\geq 1} \alpha _{r}^{2} \frac{k_{m}^{2}}{k_{m}^{2}-k_{r}^{2}}\right \} . $$

(56)

Note that, due to the expression of $\alpha _{r}$ in (55), the eigenmodes $P_{r}$ that have zero mean value do not contribute to the effective model obtained. Moreover, this expression of $D(k_{m})$ will be used later on in the numerical method chosen to handle this non-local in time jump conditions.

Appendix B: Positivity of the Parameter $B$

We seek a lower bound for the parameter $B$ that is defined by (36) and (22). It is useful for the energy analysis of Sect. 2.2, see Equation (44). To do so, we consider the variational formulation (45) that is satisfied by the field $\varPhi ^{(1)}$. Moreover, let us define the following quadratic functional:

$$ \mathscr {L}\big(\tilde{\varPhi }\big)= \int _{\varOmega \backslash \varOmega _{i}} \big[\frac{1}{2}\boldsymbol{\nabla }_{\!\boldsymbol{y}}\tilde{\varPhi }({\boldsymbol{y}})+\boldsymbol{e}_{1} \big]\cdot \boldsymbol{\nabla }_{\!\boldsymbol{y}}\tilde{\varPhi }({\boldsymbol{y}})\,\mathrm{d} \boldsymbol{y}-\lim _{y_{1}\to +\infty }\int _{-1/2}^{1/2}\big[\tilde{\varPhi }(y_{1},y_{2})- \tilde{\varPhi }(-y_{1},y_{2})\big]\mathrm{d}y_{2}. $$

Then, owing to (45), the field $\varPhi ^{(1)}$ minimizes ℒ on $\mathscr {H}^{\text{per}}_{0,1}(\varOmega \backslash \varOmega _{i})$ and one has

$$ \mathscr {L}\big(\varPhi ^{(1)}\big)=-\frac{B_{1}}{2}+\frac{1}{2}\int _{ \varOmega \backslash \varOmega _{i}}\boldsymbol{\nabla }_{\!\boldsymbol{y}}{\varPhi ^{(1)}} \cdot \boldsymbol{e}_{1}\,\mathrm{d}\boldsymbol{y}. $$

(57)

To have an explicit expression of the second term, we multiply the cell problem (21) by the function $y_{1}$ and we integrate in the bounded domain $\varOmega ^{b}\backslash \varOmega _{i}$, i.e.,

$$ \int _{\varOmega ^{b}\backslash \varOmega _{i}}\Delta _{\boldsymbol{y}} (\varPhi ^{(1)}+y_{1})y_{1} \,\mathrm{d}\boldsymbol{y}=0. $$

By integration by parts and due to the periodicity and boundary conditions for $\varPhi ^{(1)}$, this equation leads to

$$\begin{aligned} &\int _{-1/2}^{1/2}\big[\boldsymbol{\nabla }_{\!\boldsymbol{y}}\varPhi ^{(1)}(-y_{1}^{b},y_{2})+ \boldsymbol{\nabla }_{\!\boldsymbol{y}}\varPhi ^{(1)}(y_{1}^{b},y_{2}) \big]\cdot y_{1}^{b} \boldsymbol{e}_{1}\,\mathrm{d}y_{2}+ 2y_{1}^{b} \\ &\quad {}-\int _{\varOmega ^{b}\backslash \varOmega _{i}}\boldsymbol{\nabla }_{\!\boldsymbol{y}}\varPhi ^{(1)}\cdot \boldsymbol{e}_{1}\, \mathrm{d}\boldsymbol{y}-\int _{\varOmega ^{b}\backslash \varOmega _{i}}\mathrm{d} \boldsymbol{y}=0. \end{aligned}$$

Given that the last integral is equal to $(2y_{1}^{b}-e\varphi /h)$, then considering the previous identity in the limit $y_{1}^{b}\to +\infty$ entails

$$ \int _{\varOmega \backslash \varOmega _{i}}\boldsymbol{\nabla }_{\!\boldsymbol{y}}{\varPhi ^{(1)}} \cdot \boldsymbol{e}_{1}\,\mathrm{d}\boldsymbol{y}=\frac{e\varphi }{h}, $$

and thus, from (57), one gets

$$ \mathscr {L}\big(\varPhi ^{(1)}\big)=-\frac{B_{1}}{2}+\frac{e\varphi }{2h}. $$

As a consequence and due to the minimization principle for ℒ, one obtains the following lower bound for $B_{1}$:

$$ B_{1}\geq \frac{e\varphi }{h} - 2\mathscr {L}\big(\tilde{\varPhi }\big) \qquad \forall \tilde{\varPhi }\in \mathscr {H}^{\text{per}}_{0,1}(\varOmega \backslash \varOmega _{i}). $$

(58)

To have an explicit bound, we define $\tilde{\varPhi }\in \mathscr {H}^{\text{per}}_{0,1}(\varOmega \backslash \varOmega _{i})$ as the piecewise linear function:

$$ \tilde{\varPhi }(\boldsymbol{y}) = 2\tilde{\beta }h\frac{y_{1}}{e} \quad \text{if } 0 \leq |y_{1}| \leq \frac{e}{2h} \quad \text{and} \quad \tilde{\varPhi }(\boldsymbol{y}) =\tilde{\beta } \operatorname{sign}(y_{1}) \quad \text{if } |y_{1}| \geq \frac{e}{2h} $$

with $\tilde{\beta }$ a constant, from which one gets:

$$ \mathscr {L}\big(\tilde{\varPhi }\big)=2\frac{h}{e}(1-\varphi ){ \tilde{\beta }}^{2}-2\tilde{\beta }\varphi . $$

As a quadratic function of $\tilde{\beta }$, then $\mathscr {L}\big (\tilde{\varPhi }\big )$ reaches a minimum for $\tilde{\beta }=\frac{e\varphi }{2h(1-\varphi )}$, which inserted in (58) yields:

$$ B_{1}\geq \frac{e\varphi }{h} + \frac{e\varphi ^{2}}{h(1-\varphi )}. $$

To conclude, using (36), one finally obtains the following positive lower bound for $B$:

$$ B\geq \frac{a}{h}+\frac{e\varphi }{h}+ \frac{e\varphi ^{2}}{h(1-\varphi )}\geq 0. $$

Appendix C: Positivity of the Term $(S-C_{2})$

We seek a lower bound for the term $(S-C_{2})$ that is featured in (44) and is defined by (36) and (30). Let us introduce $\boldsymbol{\varPsi }^{(2)} = (\boldsymbol{\nabla }_{\!\boldsymbol{y}}{\varPhi }^{(2)}+\boldsymbol{e}_{2})$. Owing to the definition of the field ${\varPhi }^{(2)}$ as the solution to (21) and based on the definition of the functional space $\mathscr {H}^{\text{per}}_{0,2}(\varOmega \backslash \varOmega _{i})$ we consider in addition the following admissibility space:

$$\begin{aligned} &\mathscr {W}^{\text{per}}(\varOmega \backslash \varOmega _{i})=\Big\{ (\boldsymbol{f}- \boldsymbol{e}_{2})\in L^{2}_{\text{loc}}(\varOmega \backslash \varOmega _{i}) \text{ with } \boldsymbol{f}(y_{1},y_{2}+1)=\boldsymbol{f}(y_{1},y_{2}) \text{ for all } \boldsymbol{y}\in \varOmega \backslash \varOmega _{i} \\ &\quad \text{and such that }\operatorname{div}_{\boldsymbol{y}}\boldsymbol{f}=0 \text{ in } \varOmega \backslash \varOmega _{i},\ \boldsymbol{f}\cdot \boldsymbol{n}=0 \text{ on } \partial \varOmega _{i} \text{ and } \lim \limits _{y_{1}\to \pm \infty } \boldsymbol{f}=\boldsymbol{e}_{2}\Big\} , \end{aligned}$$

so that $\boldsymbol{\varPsi }^{(2)}\in \mathscr {W}^{\text{per}}(\varOmega \backslash \varOmega _{i})$. We also introduce for any $\tilde{\boldsymbol{\varPsi }}\in \mathscr {W}^{\text{per}}(\varOmega \backslash \varOmega _{i})$ the following functional:

$$ \mathscr {M}\big(\tilde{\boldsymbol{\varPsi }}\big) = \frac{1}{2}\int _{\varOmega \backslash \varOmega _{i}}\big|\tilde{\boldsymbol{\varPsi }}-\boldsymbol{e}_{2}\big|^{2}\, \mathrm{d}\boldsymbol{y}. $$

Upon noticing that for any admissible field $\tilde{\boldsymbol{\varPsi }}$ the derivative of ℳ in $\mathscr {W}^{\text{per}}(\varOmega \backslash \varOmega _{i})$ satisfies

$$ \mathscr {M}'\big[\boldsymbol{\varPsi }^{(2)}\big] \tilde{\boldsymbol{\varPsi }} = \int _{ \varOmega \backslash \varOmega _{i}} \boldsymbol{\nabla }_{\!\boldsymbol{y}}{\varPhi }^{(2)} \cdot \tilde{\boldsymbol{\varPsi }} \,\mathrm{d}\boldsymbol{y} = \int _{\partial (\varOmega \backslash \varOmega _{i})} {\varPhi }^{(2)}\tilde{\boldsymbol{\varPsi }}\cdot \boldsymbol{n} \, \mathrm{d}\boldsymbol{y} - \int _{\varOmega \backslash \varOmega _{i}} {\varPhi }^{(2)} \operatorname{div}_{\boldsymbol{y}}\tilde{\boldsymbol{\varPsi }} \,\mathrm{d}\boldsymbol{y} = 0, $$

then $\boldsymbol{\varPsi }^{(2)}$ minimizes the quadratic functional ℳ. Moreover, from the cell problem (21) one has

$$ \int _{\varOmega \backslash \varOmega _{i}}\Delta _{\boldsymbol{y}}(\varPhi ^{(2)}+y_{2}) \varPhi ^{(2)}\,\mathrm{d}\boldsymbol{y}=0. $$

By integration by parts and due to the periodicity and boundary conditions for $\varPhi ^{(2)}$ and its derivatives, this leads to

$$ C_{2}=\int _{\varOmega \backslash \varOmega _{i}}\big|\boldsymbol{\nabla }_{\!\boldsymbol{y}} \varPhi ^{(2)}\big|^{2}\,\mathrm{d}\boldsymbol{y}=2\mathscr {M}\big(\boldsymbol{\varPsi }^{(2)} \big). $$

As a consequence, we obtain that $C_{2}\leq 2\mathscr {M}\big (\tilde{\boldsymbol{\varPsi }}\big )$ for all $\tilde{\boldsymbol{\varPsi }}\in \mathscr {W}^{\text{per}}(\varOmega \backslash \varOmega _{i})$. Finally, we define $\tilde{\boldsymbol{\varPsi }}$ as

$$ \tilde{\boldsymbol{\varPsi }}(\boldsymbol{y}) = \boldsymbol{0} \quad \text{if } 0 \leq |y_{1}|< \frac{e}{2h} \quad \text{and} \quad \tilde{\boldsymbol{\varPsi }}(\boldsymbol{y}) = \boldsymbol{e}_{2} \quad \text{if } |y_{1}|\geq \frac{e}{2h} $$

from which one gets $\mathscr {M}(\tilde{\boldsymbol{\varPsi }}) = e(1-\varphi )/(2h)$. From the minimization principle, we finally obtain the following lower bound $(S-C_{2}) \geq (a-e)/h$, which proves that $(S-C_{2})\geq 0$ if $a\geq e$.