Skip to main content
SpringerLink
Log in

Sensitivity-based adaptive sequential sampling for metamodel uncertainty reduction in multilevel systems

  • Research Paper
  • Published:
Structural and Multidisciplinary Optimization Aims and scope Submit manuscript

Abstract

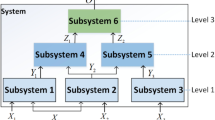
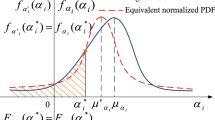
Decomposition-based technique is often used in the analysis and design of complex engineering systems for reducing the computational complexity by studying the subsystems decomposed from multilevel systems. Metamodels, as a replacement of original simulation models, can further alleviate the computational burden. However, discrepancy between the simulation models and metamodels, which is defined as metamodel uncertainty, may be introduced in the analysis process of multilevel systems owing to the lack of data. The metamodel uncertainties of sub-models will be further amplified because of the hierarchical uncertainty propagation and interaction between uncertainties, which will have a great impact on the system results. An adaptive sequential sampling strategy based on sensitivity is proposed in this paper so as to improve the prediction accuracy of system response. In this strategy, polynomial-chaos expansion is used to realize the forward propagation of metamodel uncertainty quantified by the Kriging model. The forward propagation is combined with optimization based on maximum variance criterion for searching the input locations that results in the largest variance of system response. Then, the indices of subsystems are obtained to make decisions about which subsystem needs extra samples by combining Karhunen-Loeve expansion and sensitivity analysis. The effectiveness of the proposed sequential sampling strategy method is verified by two mathematical examples and a multiscale composite material.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig.15
Fig. 16
Fig. 17
Fig. 18
Fig. 19
Fig. 20
Fig. 21

Similar content being viewed by others

References

  • Ademiloye AS, Zhang LW, Liew KM (2018) A multiscale framework for large deformation modeling of RBC membranes. Comput Methods Appl Mech Eng 329:144–167

    MathSciNet  MATH  Google Scholar 

  • Amaral S, Allaire D, Willcox K (2014) A decomposition-based approach to uncertainty analysis of feed-forward multicomponent systems. Int J Numer Methods Engng 100:982–1005

    MathSciNet  MATH  Google Scholar 

  • An D, Choi JH (2012) Efficient reliability analysis based on Bayesian framework under input variable and metamodel uncertainties. Struct Multidiscip Optim 46:533–547

    MathSciNet  MATH  Google Scholar 

  • Balokas G, Czichon S, Rolfes R (2018) Neural network assisted multiscale analysis for the elastic properties of 3D braided composites under uncertainty. Compos Struct 183:550–562

    Google Scholar 

  • Blatman G, Sudret B (2010) Efficient computation of global sensitivity indices using sparse polynomial chaos expansions. Reliab Eng Syst Saf 95(11):1216–1229

    Google Scholar 

  • Chakraborty S, Chowdhury R (2017a) Towards ‘h-p adaptive’ generalized ANOVA. Comput Methods Appl Mech Eng 320:558–581

    MathSciNet  MATH  Google Scholar 

  • Chakraborty S, Chowdhury R (2017b) Moment independent sensitivity analysis: H-PCFE-based approach. J Comput Civ Eng 31(1):06016001

    Google Scholar 

  • Chakraborty S, Chowdhury R (2017c) Hybrid framework for the estimation of rare failure event probability. J Eng Mech 143(5):04017010

    Google Scholar 

  • Chaudhuri A, Lam R, Willcox K (2018) Multifidelity uncertainty propagation via adaptive surrogated in coupled multidisciplinary systems. AIAA J 56(1):235–249

    Google Scholar 

  • Chen Z, Huang T, Shao Y, Li Y, Xu H, Avery K, Zeng D, Chen W, Su X (2019) Multiscale finite element modeling of sheet molding compound (SMC) composite structures based on stochastic mesostructure reconstruction. Compos Struct 188:25–38

    Google Scholar 

  • Choi CK, Yoo HH (2016) Stochastic inverse method to identify parameter random fields in a structure. Struct Multidiscip Optim 54:1557–1571

    MathSciNet  Google Scholar 

  • Dubreuil S, Bartoli N, Gogu C, Lefebvre T (2016) Propagation of modeling uncertainty by polynomial chaos expansion in multidisciplinary analysis. ASME J Mech Des 138:111411

    Google Scholar 

  • Dubreuil S, Bartoli N, Lefebvre T, Gogu C (2018) Efficient global multidisciplinary optimization based on surrogate models. Multidisciplinary analysis and optimization conference, Atlanta

  • Jiang Z, Chen W (2016) Multidisciplinary statistical sensitivity analysis considering both aleatory and epistemic uncertainties. AIAA J 54(4):1326–1338

    Google Scholar 

  • Jiang Z, Chen S, Apley DW, Chen W (2016) Reduction of epistemic model uncertainty in simulation-based multidisciplinary design. ASME J Mech Des 138:081403

    Google Scholar 

  • Li ZJ, Kokkolaras M, Papalambros P, Hu SJ (2008) Product and process tolerance allocation in multistation compliant assembly using analytical target cascading. ASME J Mech Des 130:091701

    Google Scholar 

  • Liang H, Zhu M, Wu Z (2014) Using cross-validation to design trend function in Kriging surrogate modeling. AIAA J 52(10):2313–2327

    Google Scholar 

  • Liu Y, Yin X, Arendt P, Chen W, Huang HZ (2010) A hierarchical statistical sensitivity analysis method for multilevel systems with shared variables. ASME J Mech Des 132:031006

    Google Scholar 

  • Liu J, Xu C, Han X, Jiang C, Liu GZ (2016a) Determination of the state parameters of explosive detonation products by computational inverse method. Inverse Probl Sci En 24(1):22–41

    Google Scholar 

  • Liu Y, Shi Y, Zhou Q, Xiu R (2016b) A sequential sampling strategy to improve the global fidelity of metamodels in multi-level system design. Struct Multidiscip Optim 53:1295–1313

    MathSciNet  Google Scholar 

  • Liu Z, Liu Z, Peng Y (2017) Dimension reduction of Karhunen-Loeve expansion for simulation of stochastic processes. J Sound Vib 408:168–189

    Google Scholar 

  • Liu H, Ong YS, Cai J (2018a) A survey of adaptive sampling for global metamodeling in support of simulation-based complex engineering design. Struct Multidiscip Optim 57:393–416

    Google Scholar 

  • Liu J, Meng X, Xu C, Zhang D, Jiang C (2018b) Forward and inverse structural uncertainty propagations under stochastic variables with arbitrary probability distributions. Comput Methods Appl Mech Eng 342:287–320

    MathSciNet  MATH  Google Scholar 

  • Liu J, Liu QM, Han X, Jiang C, Tao YR (2019) A new global sensitivity measure based on derivative-integral and variance decomposition and its application in structural crashworthiness. Struct Multidiscip Optim 60:2249–2264

    Google Scholar 

  • Martins JRRA, Lambe AB (2013) Multidisciplinary design optimization: a survey of architectures. AIAA J 51(9):2049–2075

    Google Scholar 

  • Mehrez L, Fish J, Aitharaju V, Rodgers WR (2017) A PCE-based multiscale framework for the characterization of uncertainties in complex systems. Comput Mech 61(1–2):219–236

    MathSciNet  MATH  Google Scholar 

  • Mohammadi A, Raisee M (2019) Stochastic field representation using bi-fidelity combination of proper orthogonal decomposition and Kriging. Comput Methods Appl Mech Eng 357:112589

    MathSciNet  MATH  Google Scholar 

  • Omairey SL, Dunning PD, Sriramula S (2019) Multiscale surrogate-based framework for reliability analysis of unidirectional FRP composites. Compos B-Eng 173:106925

    Google Scholar 

  • Palar PS, Zuhal LR, Shimoyama K, Tsuchiya T (2018) Global sensitivity analysis via multi-fidelity polynomial chaos expansion. Reliab Eng Syst Saf 170:175–190

    Google Scholar 

  • Pan H, Xi ZM, Yang RJ (2016) Model uncertainty approximation using a copula-based approach for reliability based design optimization. Struct Multidiscip Optim 54:1543–1556

    MathSciNet  Google Scholar 

  • Papadopoulos V, Soimiris G, Giovanis DG, Papadrakakis M (2018) A neural network-based surrogate model for carbon nanotubes with geometric nonlinearities. Comput Methods Appl Mech Eng 328:411–430

    MathSciNet  MATH  Google Scholar 

  • Pepper N, Montomoli F, Sharma S (2019) Multiscale uncertainty quantification with arbitrary polynomial. Comput Methods Appl Mech Eng 357:112571

    MathSciNet  MATH  Google Scholar 

  • Ramakrishnan K, Mastinu G (2019) Multidisciplinary design of electric vehicle based on hierarchical multi-objective optimization. ASME J Mech Des 141:091404

    Google Scholar 

  • Sankararaman S, McLemore K, Mahadevan S, Bradford SC, Peterson LD (2013) Test resource allocation in hierarchical systems using Bayesian networks. AIAA J 51(3):537–550

    Google Scholar 

  • Sanson F, Maitre OL, Congedo PM (2019) Systems of Gaussian process models for directed chains of solvers. Comput Methods Appl Mech Eng 352:32–55

    MathSciNet  MATH  Google Scholar 

  • Schobi R, Sudret B, Wiart J (2015) Polynomial-chaos-based Kriging. Int J Uncertain Quantif 5(2):171–193

    MathSciNet  Google Scholar 

  • Silva VAC, de Lima AMG, Bouhaddi N, Lacerda HB (2019) Uncertainty propagation and experimental verification of nonlinear viscoelastic sandwich beams. Mech Syst Signal Pr 132:654–669

    Google Scholar 

  • Sudret B (2008) Global sensitivity analysis using polynomial chaos expansions. Reliab Eng Syst Saf 93(7):964–979

    Google Scholar 

  • Tang KK, Congedo PM, Abgrall R (2015) Sensitivity analysis using anchored ANOVA expansion and high-order moments computation. Int J Numer Meth Engng 102:1554–1584

    MathSciNet  MATH  Google Scholar 

  • Tao T, Zhao G, Ren S (2020) An efficient kriging-based constrained optimization algorithm by global and local sampling in feasible region. ASME J Mech Des 142:051401

    Google Scholar 

  • Tao W, Zhu P, Xu C, Liu Z (2020a) Uncertainty quantification of mechanical properties for three-dimensional orthogonal woven composites. Part I: stochastic reinforcement geometry reconstruction. Compos Struct 235:111763

    Google Scholar 

  • Tao W, Zhu P, Xu C, Liu Z (2020b) Uncertainty quantification of mechanical properties for three-dimensional orthogonal woven composites. Part II: Multiscale simulation. Compos Struct 235:111764

    Google Scholar 

  • Viana FAC, Simpson TW, Balabanov V, Toropov V (2014) Metamodeling in multidisciplinary design optimization: how far have we really come? AIAA J 52(4):670–690

    Google Scholar 

  • Wang F, Li H (2018) The role of copulas in random fields: characterization and application. Struct Saf 75:75–88

    Google Scholar 

  • Wang FG, Xiong FF, Chen SS, Song JM (2019) Multi-fidelity uncertainty propagation using polynomial chaos and Gaussian process modeling. Struct Multidiscip Optim 60:1583–1604

    Google Scholar 

  • Xi Z (2019) Model-based reliability analysis with both model uncertainty and parameter uncertainty. ASME J Mech Des 141:051404

    Google Scholar 

  • Xu C, Liu Z, Tao W, Zhu P (2020) A vine copula-based hierarchical framework for multiscale uncertainty analysis. ASME J Mech Des 142:031101

    Google Scholar 

  • Yao W, Chen X, Luo W, Tooren MV, Guo J (2011) Review of uncertainty-based multidisciplinary design optimization methods for aerospace vehicles. Prog Aerosp Sci 47:450–479

    Google Scholar 

  • Yin X, Chen W (2008) A hierarchical statistical sensitivity analysis method for complex engineering systems design. ASME J Mech Des 130:071402

    Google Scholar 

  • Zhang S, Zhu P, Chen W, Arendt P (2013) Concurrent treatment of parametric uncertainty and metamodeling uncertainty in robust design. Struct Multidiscip Optim 47:63–76

    MathSciNet  MATH  Google Scholar 

  • Zhang Y, Kim NH, Haftka RT (2020) General-surrogate adaptive sampling using interquartile range for design space exploration. ASME J Mech Des 142:051402

    Google Scholar 

  • Zhao W, Tao T, Zio E (2013) Parameters tuning in support vector regression for reliability forecasting. Chem Eng Trans 33:523–528

    Google Scholar 

  • Zheng Z, Dai H (2017) Simulation of multi-dimensional random fields by Karhunen-Loeve expansion. Comput Methods Appl Mech Eng 324:221–247

    MathSciNet  MATH  Google Scholar 

  • Zhou Q, Wang Y, Choi SK et al (2018) A robust optimization approach based on multi-fidelity metamodel. Struct Multidiscip Optim 57:775–797

    Google Scholar 

  • Zhu C, Zhu P, Liu Z, Tao W, Chen W (2017) Hierarchical framework for quantifying multiscale structures of two-dimensional woven carbon fibre-reinforced composites considering geometric variability. J Ind Text 48(4):802–824

    Google Scholar 

Download references

Funding

This research is supported by the Key National Natural Science Foundation of China (Grant No. U1864211), National Natural Science Foundation of China (Grant No.11772191), and National Science Foundation for Young Scientists of China (Grant No.51705312).

Author information

Authors and Affiliations

  1. The State Key Laboratory of Mechanical System and Vibration, Shanghai Key Laboratory of Digital Manufacture for Thin-walled Structures, School of Mechanical Engineering, Shanghai Jiao Tong University, Shanghai, 200240, People’s Republic of China

    Can Xu, Ping Zhu & Mushi Li

  2. School of Design, Shanghai Jiao Tong University, Shanghai, 200240, People’s Republic of China

    Zhao Liu

Authors
  1. Can Xu
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Zhao Liu
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Ping Zhu
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Mushi Li
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding authors

Correspondence to Zhao Liu or Ping Zhu.

Ethics declarations

Conflict of interest

The authors declare that they have no conflict of interest.

Replication of results

The pseudocodes for the algorithms intended to facilitate the replication of results are provided in this section. The pseudocode of the M-MCS is presented below.

The pseudocode of PCE-quantification for multilevel metamodel uncertainty is presented below.

The pseudocode of the proposed adaptive sequential sampling strategy is presented below.

The toolbox SURROGATES is free software, which can be learned about through the website (http://sites.google.com/site/felipeacviana/surrogatestoolbox). The toolbox is employed to build the Kriging model using the following parameters: the correlation model is “corrgauss,” the regression model is “regpoly0,” the initial guess on “theta” is 0.5. The toolbox UQLab is completely free for academic users (https://www.uqlab.com). And the toolbox is used to construct the PCE models by the following parameters: the method is “LARS,” the hyperbolic norm is 1. The optimization is executed by MATLAB genetic algorithm tool with the following parameters: the “Generations” is 100, the “PopulationSize” is 100. The code for random filed representation is downloaded from the website (https://www.mathworks.com/matlabcentral/fileexchange/52372-random-field-representation-methods). Other related parameters for replicating this paper have been provided in Section 5.

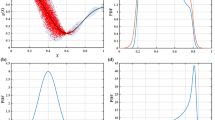
In order to further understand the proposed strategy and replicate the results presented in this paper, the MATLAB codes for examples 1~2 are provided as the supplementary material. Table 3 listed the basic information of the code files. The results of numerical examples can be obtained by running the main programs, and the following subprograms need to be called while running the main programs. It should be note that the results of each run will vary depending on the initial samples generated based on the LHS method. Therefore, the attachment also provides the data set that obtains the figures in this article.

Table 3 Basic information of the code files in the supplementary material
Full size table

Additional information

Responsible Editor: Shapour Azarm

Publisher’s note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Electronic supplementary material

ESM 1

(RAR 15.8 MB)

Appendix. Derivations of (9) and (10)

Appendix. Derivations of (9) and (10)

The metamodel uncertainty of the top-level sub-model in (7) is firstly considered; then, we have:

$$ {\displaystyle \begin{array}{l}{u}_{\mathrm{L}+\mathrm{U}}=E\left\{E\left[Z\left({u}_{\boldsymbol{Y}}\left(\boldsymbol{x}\right)+{\delta}_{\boldsymbol{Y}}\left(\boldsymbol{x}\right)\right)\left|{\delta}_Z\right.\right]\right\}\\ {}\kern3.5em =E\left\{{u}_Z\left({u}_{\boldsymbol{Y}}\left(\boldsymbol{x}\right)+{\delta}_{\boldsymbol{Y}}\left(\boldsymbol{x}\right)\right)\right\}\end{array}} $$
(34)

Considering the relationship between mean and variance which is shown:

$$ \mathrm{Var}(Z)=E\left({Z}^2\right)-E{(Z)}^2 $$
(35)

Equation (8) can be rewritten as:

$$ {\displaystyle \begin{array}{l}{\sigma}_{\mathrm{L}+\mathrm{U}}^2=\mathrm{Var}\left[Z\left({u}_{\boldsymbol{Y}}\left(\boldsymbol{x}\right)\right)\left|{\delta}_{\boldsymbol{Y}},{\delta}_Z\right.\right]\\ {}\kern4em =E\left[{Z}^2\left({u}_{\boldsymbol{Y}}\left(\boldsymbol{x}\right)\right)\left|{\delta}_{\boldsymbol{Y}},{\delta}_Z\right.\right]-E{\left[Z\left({u}_{\boldsymbol{Y}}\left(\boldsymbol{x}\right)\right)\left|{\delta}_{\boldsymbol{Y}},{\delta}_Z\right.\right]}^2\end{array}} $$
(36)

Similarly, the metamodel uncertainty of the top-level sub-model in (36) is firstly considered; then, we have:

$$ {\sigma}_{\mathrm{L}+\mathrm{U}}^2=E\left\{E\left[{Z}^2\left({u}_{\boldsymbol{Y}}\left(\boldsymbol{x}\right)+{\delta}_{\boldsymbol{Y}}\left(\boldsymbol{x}\right)\right)\left|{\delta}_Z\right.\right]\right\}-E{\left\{E\left[Z\left({u}_{\boldsymbol{Y}}\left(\boldsymbol{x}\right)+{\delta}_{\boldsymbol{Y}}\left(\boldsymbol{x}\right)\right)\left|{\delta}_Z\right.\right]\right\}}^2 $$
(37)

Use the relationship in (35) again. Equation (37) can be rewritten as:

$$ {\displaystyle \begin{array}{c}{\sigma}_{\mathrm{L}+\mathrm{U}}^2=E\left\{\mathrm{Var}\left[Z\left({u}_Y(x)+{\delta}_Y(x)\right)\left|{\delta}_Z\right.\right]+E{\left[Z\left({u}_Y(x)+{\delta}_Y(x)\right)\left|{\delta}_Z\right.\right]}^2\right\}\\ {}\kern3.63em -E{\left\{E\left[Z\left({u}_Y(x)+{\delta}_Y(x)\right)\left|{\delta}_Z\right.\right]\right\}}^2\\ {}\kern2.64em =E\left\{\mathrm{Var}\left[Z\left({u}_Y(x)+{\delta}_Y(x)\right)\left|{\delta}_Z\right.\right]\right\}+E\left\{E{\left[Z\left({u}_Y(x)+{\delta}_Y(x)\right)\left|{\delta}_Z\right.\right]}^2\right\}\\ {}\kern3.63em -E{\left\{E\left[Z\left({u}_Y(x)+{\delta}_Y(x)\right)\left|{\delta}_Z\right.\right]\right\}}^2\\ {}\kern2.64em =E\left\{{\sigma}_Z^2\left({u}_Y(x)+{\delta}_Y(x)\right)\right\}+E\left\{{u}_Z^2\left({u}_Y(x)+{\delta}_Y(x)\right)\right\}\\ {}\kern3.63em -E{\left\{{u}_Z\left({u}_Y(x)+{\delta}_Y(x)\right)\right\}}^2\\ {}\kern2.64em =E\left\{{\sigma}_Z^2\left({u}_Y(x)+{\delta}_Y(x)\right)\right\}+ Var\left\{{u}_Z\left({u}_Y(x)+{\delta}_Y(x)\right)\right\}\end{array}} $$
(38)

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Xu, C., Liu, Z., Zhu, P. et al. Sensitivity-based adaptive sequential sampling for metamodel uncertainty reduction in multilevel systems. Struct Multidisc Optim 62, 1473–1496 (2020). https://doi.org/10.1007/s00158-020-02673-6

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00158-020-02673-6

Keywords

Search

Navigation