Skip to main content
SpringerLink
Log in

Dynamic behavior of thermoelastic solid continua using mathematical model derived based on non-classical continuum mechanics with internal rotations

  • Recent advances in Computational Mechanics and Innovative Materials
  • Published:
Meccanica Aims and scope Submit manuscript

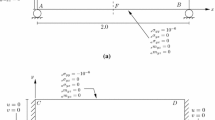
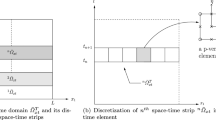
Abstract

This paper considers dynamic behavior of non-classical thermoelastic solid continua. The mathematical model consists of the conservation and balance laws of non-classical continuum mechanics that incorporates additional physics of internal rotations arising due to deformation gradient tensor. We consider plane stress behavior with small deformation, small strain physics only. Galerkin Method with Weak Form (GM/WF) in space is considered to construct a space–time decoupled finite element formulation giving rise to ordinary differential equations (ODEs) in time containing mass matrix, stiffness matrix due to classical as well as non-classical physics and acceleration and displacement associated with nodal degrees of freedom. This formulation is utilized to: (1) study natural undamped modes of vibration (2) study transient dynamic response by time integrating the ODEs in time (3) study the transient dynamic response by transforming the ODEs in time to modal basis using eigenvectors of the undamped natural modes. The ODEs in modal basis are used to construct transient dynamic response by time integrating them as well as by considering their analytical solutions. The solutions of the model problem obtained using the mathematical model based on non-classical continuum mechanics with internal rotations are presented and are compared with those obtained using the mathematical model based on classical continuum mechanics to demonstrate the influence of new physics due to internal rotations on the dynamic response of solid continua.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9

Similar content being viewed by others

References

  1. Eringen AC (1964) Mechanics of micromorphic materials. In: Gortler H (ed) Proceedings of the 11th international congress of applied mechanics, pp 131–138

  2. Eringen AC (1968) Mechanics of micromorphic continua. In: Kroner E (ed) Mechanics of generalized continua, pp 18–35

  3. Eringen AC (1968) Theory of micropolar elasticity. In: Liebowitz H (ed) Fracture

  4. Eringen AC (1970) Balance laws of micromorphic mechanics. Int J Eng Sci 8:819–828

    MATH  Google Scholar 

  5. Eringen AC (1990) Theory of thermo-microstretch fluids and bubbly liquids. Int J Eng Sci 28:133–143

    MathSciNet  MATH  Google Scholar 

  6. Eringen AC (1999) Theory of micropolar elasticity. Springer, New York

    MATH  Google Scholar 

  7. Eringen AC (1966) A unified theory of thermomechanical materials. Int J Eng Sci 4:179–202

    MathSciNet  MATH  Google Scholar 

  8. Eringen AC (1967) Linear theory of micropolar viscoelasticity. Int J Eng Sci 5:191–204

    MATH  Google Scholar 

  9. Eringen AC (1972) Theory of micromorphic materials with memory. Int J Eng Sci 10:623–641

    MATH  Google Scholar 

  10. Koiter W (1964) Couple stresses in the theory of elasticity, I and II. Nederl Akad Wetensch Proc Ser B 67:17–44

    MathSciNet  MATH  Google Scholar 

  11. Oevel W, Schröter J (1981) Balance equations for micromorphic materials. J Stat Phys 25:645–662

    MathSciNet  Google Scholar 

  12. Reddy JN (2007) Nonlocal theories for bending, buckling and vibration of beams. Int J Eng Sci 45:288–307

    MATH  Google Scholar 

  13. Reddy JN, Pang SD (2008) Nonlocal continuum theories of beams for the analysis of carbon nanotubes. J Appl Phys 103:023511

    Google Scholar 

  14. Reddy JN (2010) Nonlocal nonlinear formulations for bending of classical and shear deformation theories of beams and plates. Int J Eng Sci 48:1507–1518

    MathSciNet  MATH  Google Scholar 

  15. Lu P, Zhang PQ, Leo HP, Wang CM, Reddy JN (2007) Nonlocal elastic plate theories. Proc R Soc A 463:3225–3240

    MathSciNet  MATH  Google Scholar 

  16. Yang JFC, Lakes RS (1982) Experimental study of micropolar and couple stress elasticity in compact bone in bending. J Biomech 15:91–98

    Google Scholar 

  17. Lubarda VA, Markenscoff X (2000) Conservation integrals in couple stress elasticity. J Mech Phys Solids 48:553–564

    MathSciNet  MATH  Google Scholar 

  18. Ma HM, Gao XL, Reddy JN (2008) A microstructure-dependent Timoshenko beam model based on a modified couple stress theory. J Mech Phys Solids 56:3379–3391

    MathSciNet  MATH  Google Scholar 

  19. Ma HM, Gao XL, Reddy JN (2010) A nonclassical Reddy–Levinson beam model based on modified couple stress theory. J Multiscale Comput Eng 8:167–180

    Google Scholar 

  20. Reddy JN (2011) Microstructure dependent couple stress theories of functionally graded beams. J Mech Phys Solids 59:2382–2399

    MathSciNet  MATH  Google Scholar 

  21. Reddy JN, Arbind A (2012) Bending relationship between the modified couple stress-based functionally graded Timoshenko beams and homogeneous Bernoulli–Euler beams. Ann Solid Struct Mech 3:15–26

    Google Scholar 

  22. Srinivasa AR, Reddy JN (2013) A model for a constrained, finitely deforming elastic solid with rotation gradient dependent strain energy and its specialization to von Kármán plates and beams. J Mech Phys Solids 61:873–885

    MathSciNet  Google Scholar 

  23. Mora RJ, Waas AM (2007) Evaluation of the micropolar elasticity constants for honeycombs. Acta Mech 192:1–16

    MATH  Google Scholar 

  24. Onck PR (2002) Cosserat modeling of cellular solids. C R Mecanique 330:717–722

    MATH  Google Scholar 

  25. Segerstad PH, Toll S, Larsson R (2009) A micropolar theory for the finite elasticity of open-cell cellular solids. Proc R Soc A 465:843–865

    MathSciNet  MATH  Google Scholar 

  26. Grioli G (2003) Microstructures as a refinement of Cauchy theory. Problems of physical concreteness. Contin Mech Thermodyn 15:441–450

    MathSciNet  MATH  Google Scholar 

  27. Grekova EF, Maugin GA (2005) Modelling of complex elastic crystals by means of multi-spin micromorphic media. Int J Eng Sci 43:494–519

    MathSciNet  MATH  Google Scholar 

  28. Altenbach J, Altenbach H, Eremeyev VA (2010) On generalized Cosserat-type theories of plates and shells: a short review and bibliography. Arch Appl Mech 80:217–227

    MATH  Google Scholar 

  29. Lazar M, Maugin GA (2005) Nonsingular stress and strain fields of dislocations and disclinations in first strain gradient elasticity. Int J Eng Sci 43:1157–1184

    MathSciNet  MATH  Google Scholar 

  30. Lazar M, Maugin GA (2004) Defects in gradient micropolar elasticity—I: screw dislocation. J Mech Phys Solids 52:2263–2284

    MathSciNet  MATH  Google Scholar 

  31. Maugin GA (1978) A phenomenological theory of ferroliquids. Int J Eng Sci 16:1029–1044

    MathSciNet  MATH  Google Scholar 

  32. Maugin GA (1981) Wave motion in magnetizable deformable solids. Int J Eng Sci 19:321–388

    MathSciNet  MATH  Google Scholar 

  33. Maugin GA (1988) Wave motion in magnetizable deformable solids, philosophical transactions of the royal society of london. Ser A Math Phys Eng Sci 356:1367–1395

    Google Scholar 

  34. Cosserat E, Cosserat F (1909) Théorie des corps déformables

  35. Green AE (1965) Micro-materials and multipolar continuum mechanics. Int J Eng Sci 3:533–537

    MathSciNet  Google Scholar 

  36. Green AE, Rivlin RS (1967) The relation between director and multipolar theories in continuum mechanics. Zeitschrift fü, r angewandte Mathematik und Physik ZAMP 18:208–218

    MATH  Google Scholar 

  37. Green AE, Rivlin RS (1964) Multipolar continuum mechanics. Arch Ration Mech Anal 17:113–147

    MathSciNet  MATH  Google Scholar 

  38. Surana KS, Powell MJ, Reddy JN (2015) A more complete thermodynamic framework for solid continua. J Therm Eng 1:1–13

    Google Scholar 

  39. Surana KS, Powell MJ, Nunez D, Reddy JN (2015) A polar continuum theory for solid continua. Int J Eng Res Ind Appl 8:77–106

    Google Scholar 

  40. Surana KS, Powell MJ, Reddy JN (2015) Constitutive theories for internal polar thermoelastic solid continua. J Pure Appl Math Adv Appl 14:89–150

    Google Scholar 

  41. Surana KS, Joy AD, Reddy JN (2016) A non-classical internal polar continuum theory for finite deformation of solids using first Piola–Kirchhoff stress tensor. J Pure Appl Math Adv Appl 16:1–41

    Google Scholar 

  42. Surana KS, Joy AD, Reddy JN (2016) Non-classical internal polar continuum theory for finite deformation and finite strains in solids. Int J Pure Appl Math 4:59–97

    Google Scholar 

  43. Surana KS, Joy AD, Reddy JN (2017) Non-classical continuum theory for solids incorporating internal rotations and rotations of Cosserat theories. Continuum Mech Thermodyn 29:665–698

    MathSciNet  MATH  Google Scholar 

  44. Surana KS, Joy AD, Reddy JN (2017) Non-classical continuum theory for fluids incorporating internal and Cosserat rotation rates. Continuum Mech Thermodyn 29:1249–1289

    MathSciNet  MATH  Google Scholar 

  45. Surana KS, Shanbhag RR, Reddy JN (2017) Necessity of balance of moment of moments balance law in non-classical continuum theories for solid continua. Meccanica 53:2939–2972

    MATH  Google Scholar 

  46. Surana KS (2015) Advanced mechanics of continua. Taylor and Francis, Boca Raton

    MATH  Google Scholar 

  47. Eringen AC (1967) Mechanics of continua. Wiley, Hoboken

    MATH  Google Scholar 

  48. Prager W (1945) Strain hardening under combined stresses. J Appl Phys 16:837–840

    MathSciNet  Google Scholar 

  49. Reiner M (1945) A mathematical theory of dilatancy. Am J Math 67:350–362

    MathSciNet  MATH  Google Scholar 

  50. Todd JA (1948) Ternary quadratic types. Philos Trans R Soc Lond Ser A Math Phys Sci 241:399–456

    MathSciNet  MATH  Google Scholar 

  51. Rivlin RS, Ericksen JL (1955) Stress-deformation relations for isotropic materials. J Ration Mech Anal 4:323–425

    MathSciNet  MATH  Google Scholar 

  52. Rivlin RS (1955) Further remarks on the stress-deformation relations for isotropic materials. J Ration Mech Anal 4:681–702

    MathSciNet  MATH  Google Scholar 

  53. Wang CC (1969) On representations for isotropic functions, part I. Arch Ration Mech Anal 33:249

    Google Scholar 

  54. Wang CC (1969) On representations for isotropic functions, part II. Arch Ration Mech Anal 33:268

    Google Scholar 

  55. Wang CC (1970) A new representation theorem for isotropic functions, part I and part II. Arch Ration Mech Anal 36:166–223

    Google Scholar 

  56. Wang CC (1971) Corrigendum to my recent papers on “epresentations for isotropic functions”. Arch Ration Mech Anal 43:392–395

    Google Scholar 

  57. Smith GF (1970) On a fundamental error in two papers of C. C. Wang, on representations for isotropic functions, part I and part II. Arch Ration Mech Anal 36:161–165

    MATH  Google Scholar 

  58. Smith GF (1971) On isotropic functions of symmetric tensors, skew-symmetric tensors and vectors. Int J Eng Sci 9:899–916

    MathSciNet  MATH  Google Scholar 

  59. Spencer AJM, Rivlin RS (1959) The theory of matrix polynomials and its application to the mechanics of isotropic continua. Arch Ration Mech Anal 2:309–336

    MathSciNet  MATH  Google Scholar 

  60. Spencer AJM, Rivlin RS (1960) Further results in the theory of matrix polynomials. Arch Ration Mech Anal 4:214–230

    MathSciNet  MATH  Google Scholar 

  61. Spencer AJM (1971) Theory of invariants, Chapter 3. In: Eringen AC (ed) Treatise on continuum physics, I. Academic Press, New York

    Google Scholar 

  62. Boehler JP (1977) On irreducible representations for isotropic scalar functions. J App Math Mech/Zeitschrift für Angewandte Mathematik und Mechanik 57:323–327

    MathSciNet  MATH  Google Scholar 

  63. Zheng QS (1993) On the representations for isotropic vector-valued, symmetric tensor-valued and skew-symmetric tensor-valued functions. Int J Eng Sci 31:1013–1024

    MathSciNet  MATH  Google Scholar 

  64. Zheng QS (1993) On transversely isotropic, orthotropic and relatively isotropic functions of symmetric tensors, skew-symmetric tensors, and vectors. Int J Eng Sci 31:1399–1453

    MATH  Google Scholar 

  65. Surana KS, Reddy JN (2017) The finite element method for initial value problems. Taylor and Francis, Boca Raton

    MATH  Google Scholar 

  66. Surana KS, Reddy JN (2016) The finite element method for boundary value problems: mathematics and computations. Taylor and Francis, Boca Raton

    Google Scholar 

  67. Bathe KJ, Wilson EL (1976) Numerical methods in finite element analysis. Prentice Hall, Englewood Cliffs

    MATH  Google Scholar 

Download references

Acknowledgements

First author is grateful for his endowed professorships and the department of mechanical engineering of the University of Kansas for providing financial support to the second author. The computational facilities provided by the Computational Mechanics Laboratory of the mechanical engineering department are also acknowledged.

Author information

Authors and Affiliations

  1. Mechanical Engineering, University of Kansas, Lawrence, KS, USA

    K. S. Surana & C. H. Carranza

Authors
  1. K. S. Surana
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. C. H. Carranza
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to K. S. Surana.

Ethics declarations

Conflict of interest

The authors declare that they have no conflict of interest.

Additional information

In honor of Professor J. N. Reddy for his 75th Birthday.

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Surana, K.S., Carranza, C.H. Dynamic behavior of thermoelastic solid continua using mathematical model derived based on non-classical continuum mechanics with internal rotations. Meccanica 56, 1345–1375 (2021). https://doi.org/10.1007/s11012-020-01221-2

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11012-020-01221-2

Keywords

Search

Navigation