Introduction

Controlled wave amplification and attenuation are key features for numerous practical devices and systems in acoustics, electronics, and optics. Previously, gain and loss in such systems are in general treated as being independent of major inter-oscillator properties. Remarkable interplay between them has been found only in specific cases such as injection locking and synchronization phenomena1,2. However, recent development of the non-Hermitian wave dynamics suggests various novel effects produced by intentionally engaging gain and losses with inter-oscillator or inter-modal coupling properties. They are violation of the Friedel’s law of diffraction from stationary lattice structures3,4, unidirectional invisibility5,6, broadband optical nonreciprocity7, to mention a few. Remarkably, exotic non-Hermitian properties have been found even beyond the wave dynamics or classical physics domains as demonstrated in diffusive heat-transfer processes8 and single-photon systems consisting of a nitrogen vacancy in a diamond crystal9.

These intriguing effects essentially involve a non-Hermitian singularity referred to as an exceptional point (EP) that corresponds to a threshold of the spontaneous parity-time (PT) symmetry-breaking transition and creates extremely deformed vector spaces due to coalescence of multiple normal-mode solutions10. An EP involves a unique self-intersecting Riemann-surface geometry in the parametric eigenvalue spectrum11,12 that enables an exotic chiral effect under topological stimuli around an EP7,13,14,15,16,17,18,19,20,21,22,23,24,25. Following the initial theoretical proposal by Moiseyev et al.13,14, this chiral effect has been experimentally established in microwave transmission channels17, cryogenic optomechanical oscillators18, and silicon-photonic waveguide architectures very recently19. Therein, final states through the topological operations around an EP strongly suggest that it must involve the chiral mode-transfer effect originating from the time-asymmetric breakdown of the standard adiabaticity. Nevertheless, any direct observation of the effect in the courses of the operations has not been reported thus far. Considering the potential impact of the effect on the fundamental physics and device engineering, direct time-resolved observation of this exotic chiral effect should be an important step toward novel wave-controlling devices and systems pertaining to the far-reaching open-system properties and associated non-Hermitian dynamics.

Here, we provide an experimental analysis that reveals entire dynamics of the time-asymmetric non-Hermitian effect in the courses of the encircling-an-EP (EEP) operations. Using dynamically-tunable electrical-circuit oscillators, we create the Rieman-surface eigenvalue topology with an unprecedented accuracy and measure fully time-resolved complex amplitudes in real-time with the dynamic EEP operations. In contrast to the previous indirect observations due to final-state analyses, the measured dynamic state-evolution passages show how the unique non-Hermitian effects such as the adiabatic state flip, anti-adiabatic state jump, and subsequent time-asymmetric mode transfer properties occur in the passage of time. Therefore, our proposed approach provides a comprehensive experimental platform for fundamental study on exotic non-Hermitian dynamics.

Results

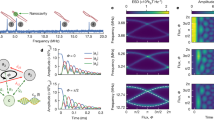
We use dynamically tunable binary electrical-circuit oscillators as shown in Fig. 1. The circuit configuration consists of two capacitively-coupled LRC oscillators. Similar electrical circuits have been used to explore intriguing non-Hermitian properties such as the PT-symmetric quantum brachistochrone problem26, enhanced remote sensor applications27,28, anomalous anti-PT-symmetric dynamics29, and robust wireless power-transfer devices30. In our configuration, distinguished features from the previously studied parity-time-symmetric oscillator circuits31 are negative-resistor units (partial circuitries with an operational amplifier AL1 or L2, resistors ρNR, and AR1 or R2) connected in serial with inductor λ1 or 2 and varactor-diode capacitors (dC and d2) included in the coupling mechanism at CC and the restoration force mechanism at C2 in Oscillator 2. The negative-resistor units eliminate parasitic resistance components in the inductors. The varactor-diode capacitors provide a control mechanism that dynamically tunes inter-oscillator coupling constant and free-running resonance frequency at Oscillator 2. Other variable components including resistors ρL1, ρL2, Δρ1, ρR1, ρR2, and a capacitor Δγ1 are manually tunable so that we precisely adjust an initial condition with a desired set of effective LRC-circuit constants {L1, R1, C1, L2, R2, C2}. Other details of the circuit configuration are provided in the figure legend for Fig. 1a.

Fig. 1: Binary non-Hermitian Hamiltonian simulator using tunable electrical oscillators.
figure 1

a A circuit diagram for binary electrical oscillators as a dynamic non-Hermitian Hamiltonian simulator. The circuit consists of two LRC oscillators coupled through an electrically-tunable capacitor unit CC including six varactor diodes (dC). In Oscillator n, an inductor unit Ln consists of a conventional coil inductor λn and a negative-resistance unit (an operational amplifier ALn and resistors ρNR and ρLn) compensating a parasitic resistance component in λn. A resistor unit Rn includes a manually-variable resistor Δρ1 (Oscillator 1 only) and another negative-resistance unit (an operational amplifier ARn and resistors ρNR and ρRn). A capacitor unit Cn contains a main capacitor γn and a manually-variable capacitor Δγ1 for Oscillator 1 or an electrically-tunable varactor-diode capacitor (four d2’s) for Oscillator 2. b Control configuration for dynamically encircling an exceptional point. An excitation signal current Iin from a function generator is injected to either one of the two oscillators depending on toggle-switch status. Voltage signals VC and VD from an analog-to-digital/digital-to-analog converter dynamically control inter-oscillator coupling constant at CC and frequency detuning at C2, respectively. The electrical responses V1 and V2 of the two oscillators are acquired with an oscilloscope. The excitation of the circuit and measurement start or stop with a trigger signal from the analog-to-digital/digital-to-analog converter. These controls are precisely managed with a desktop computer (Control desktop computer).

Full size image

Electrical response of this circuit configuration is described by the following binary Hamiltonian model

$$\frac{d}{{dt}}\left| v \right\rangle = - iH\left| v \right\rangle ,$$
(1)
$$H = \left[ {\begin{array}{*{20}{c}} {\omega _1 - \kappa + i\gamma } & \kappa \\ \kappa & {\omega _2 - \kappa } \end{array}} \right],$$
(2)

where |v〉 = [v1 v2]T is a state vector with vn being a voltage-amplitude phasor at Oscillator n, ωn = (LnCn)–1/2 is free-running resonance frequency, γ = (2Δρ1C1)–1 is decay rate, and κ = ω0CC(C1 + C2)–1 is a coupling constant with ω0 = 0.5(ω1 + ω2) being average free-running resonance frequency. Here, voltage signal Vn to be measured at Oscillator n is given by Vn = Re(vn). The diagonal elements in Eq. (2) consist of free-running resonance frequency ωn, decay rate γ, and frequency shift κ which is tunable by the varactor-diode capacitors connecting two LC oscillators. See Supplementary Note 1 for detailed mathematical treatment based on the Kirchhoff’s circuit laws. In Eq. (2), we note that coupling constant κ in the off-diagonal elements also appears in the diagonal elements in contrast to canonical coupled-oscillator models where diagonal and off-diagonal elements are independent on each other. This property originates from resonance-frequency shift induced by net alternating current passing through the coupling capacitor CC.

The Hamiltonian in Eq. (2) has a parity-time-symmetric EP at ω1 = ω2 and γ = 2κ. Therefore, an EEP operation requires simultaneous control of ωn and κ around the EP. In our circuit configuration in Fig. 1a, independent electrical tuning of the varactor-diode capacitors at CC and C2 immediately leads to simultaneous dynamic control of κ and ω2, respectively.

We realize the required control scenario with a computer-controlled system as illustrated in Fig. 1b. Therein, voltage signals VC and VD from a general purpose AD/DA converter are applied to the varactor-diode capacitors at CC and C2, respectively, and subsequently adjust κ and ω2, respectively. A function generator provides an excitation signal to either one of Oscillators 1 or 2 depending on the on/off relay and channel-selecting toggle switch status. An oscilloscope acquires excited signals V1 and V2 directly in real time. A desktop computer precisely synchronizes desired control and measurement sequences in communication with the general purpose AD/DA converter, function generator, and the oscilloscope.

In the first step of our experimental analyses, we measure eigenvalues and eigenstates of the system with the circuit constants L1 = L2 = 4.789 mH, R1 = 38 kΩ, R2 = 0, C1 = 10 nF, C2 = C1 + ΔC with ΔC varying from –100 pF to +100 pF, and CC changing from 90 pF to 350 pF. These constants are chosen so that the two oscillators resonate at frequencies around 20 kHz where the equipment that we use here operates in routinely stable and reliable conditions. See “Methods” section and Supplementary Note 2 for the eigenvalue-measurement procedures and underlying mathematical relations, respectively. Figure 2 shows wireframe surfaces for the measured real and imaginary eigenvalue spectra on a two-dimensional parametric plane represented by ΔC and CC. Therein, we label a set of eigenvalues for gain modes (or equivalently least-attenuating modes) as λG and that for loss modes as λL. They clearly show characteristic self-intersecting Riemann-surface geometry around an EP at (ΔC, CC) = (0 pF, 185 pF). Remarkably, the experimental and theoretical values agree within an error less than 5 Hz which is merely 0.02% of the minimal resonance frequency identified in this measurement. See Supplementary Fig. 2 for more details. Such high degree of accuracy enables precise further experimental analyses including dynamic EEP operations.

Fig. 2: Complex eigenvalue spectra and dynamic expectation-value passages for encircling-an-exceptional-point operations in experiment.
figure 2

Wireframe surfaces indicate measured real (a, c, e, g) and imaginary (b, d, f, h) eigenvalues on 2-dimentional (ΔC CC) plane, where ΔC is detuning capacitance and CC is coupling capacitance. Eigenvalue surfaces for the gain modes are in light-blue skin and labeled by λG while those for the loss modes are in light-red skin and labeled by λL. All real and imaginary eigenvalue surfaces in a–h are duplicated identical plots. Real (a, c, e, g) and imaginary (b, d, f, h) parts of expectation-value 〈H〉 passages are indicated by black arrow curves in every panel. Encircling-direction and initial-state conditions for each panel are (a, b) anticlockwise encircling from |ψ(0)〉 = |s〉, (c, d) clockwise encircling from | ψ(0)〉 = |s〉, (e, f) anticlockwise encircling from |ψ(0)〉 = |a〉, and (g, h) clockwise encircling from |ψ(0)〉 = |a〉. Yellow arrows in c–f indicate portions where anti-adiabatic state-jump events take place. Evolution-time constant T is fixed at 40 ms for all cases in this figure.

Full size image

We conduct EEP operations on a parametric loop defined by the relations

$${\mathrm{{\Delta} }}C = pA_{\mathrm{{\Delta} }}{\mathrm{sin}}(2\pi T^{-1}t),$$
(3)
$$\left. {C_{\mathrm{C}} = C_0 + A_{\mathrm{C}}{\mathrm{cos}}(2\pi T^{-1}t)} \right],$$
(4)

where p is an encircling-direction parity constant that takes +1 for anticlockwise (ACW) rotation or –1 for clockwise (CW) rotation, AΔ is an amplitude constant for the ΔC modulation, T denotes a time period for one complete EEP operation, C0 is an average-capacitance constant for CC, and AC are an amplitude constant for the CC modulation.

Dynamic EEP operations due to this scenario requires a well-prepared initial state |ψ(0)〉 that should be either one of the two eigenstates, i.e., symmetric-like (bonding) eigenstate |s〉 or anti-symmetric-like (anti-bonding) eigenstate |a〉 at our selected starting point (ΔC, CC) = (0 pF, 350 pF). This starting point is located in the unbroken PT-symmetric region (γ < 2κ) on the PT-symmetric line at the condition ω1 = ω2. For such initial condition, eigenstates |s〉 and |a〉 take identical dissipation rates, i.e., identical imaginary eigenvalues. Therefore, there is no preferred state if certain appropriate initial-state preparation procedures are not applied.

We obtain such an initial state by driving the oscillators with time-harmonic current-source signal Iin at a measured resonance-center frequency and a subsequent relaxation procedure that effectively eradicates parasitic modal-impurity noises from |ψ(0)〉. The relaxation procedure is performed by slightly detuning ΔC and CC towards gain-mode domain for the desired state and then returning to the starting point adiabatically. During this adiabatic process for the initial state preparation, parasitic modal-impurity component exponentially decays in the loss-mode domain while the desired mode component amplifies its amplitude in the gain-mode domain. For an optimally selected adiabatic detuning passage, we achieve desired initial-state with a purity exceeding 99%, as estimated from a real-time excitation-amplitude measurement. Once such a pure initial state is excited from this procedure, control signals VC and VD creating ΔC and CC profiles due to Eqs. (3) and (4) are then injected to perform a single complete round of a desired EEP operation. Meanwhile, excited voltage signals V1 and V2 are recorded in time domain as a complete evolution history of an associated dynamic state |ψ(t)〉. See “Methods” section for further details including associated circuit constants, dynamic control ranges of ΔC and CC.

The EEP operation in this way successfully produces the theoretically anticipated time-asymmetric mode-transfer effect as shown in Fig. 2 for a time-period constant T = 30 ms. Therein, we provide bi-orthogonal expectation value 〈H〉 = 〈ψ*(t)|H|ψ(t)〉 passages with respect to the measured eigenvalue surfaces. The bi-orthogonal expectation value in this way not only allows the simplest probabilistic description for non-Hermitian systems in our case but also can be directly obtained from dynamic-state |ψ(t)〉 measurement with no need of other independent measurements on eigenvalues and Hamiltonian parameters. See Supplementary Note 3 for detailed explanation. Note that Fig. 2a, b show ACW (p = +1) EEP case and Fig. 2c, d show CW (p = –1) case for an initial state |ψ(0)〉 = |s〉. The real and imaginary parts of 〈H〉 passages in the ACW case adiabatically evolve from the initial eigenvalue point for |s〉 to that for |a〉 while 〈H〉 passages in the CW case involve the anti-adiabatic state jump from the loss-mode (λL) surface to the gain-mode (λG) surface and the passages eventually end up in the eigenvalue point for |s〉.

Here, the essential physics is a fact that an EEP operation on a loss-mode surface inevitably undergoes an anti-adiabatic state jump toward a gain-mode surface while the time-reversed operation simply evolves along the adiabatic-state passage on a gain-mode surface. This property is clearly found in the other cases for |ψ(0)〉 = |a〉 as shown in Fig. 2e–h.

Discussion

Our electrical-circuit EEP simulator enables further experimental investigation on various parametric dependences of the time-asymmetric EEP operations. For a given EEP loop, a parameter of the most significant impact is the evolution-time constant T because it is a characteristic time scale of the EEP operation that is directly associated with the time-asymmetric mode-transfer efficiency18. In Fig. 3, we provide measured 〈H〉 passages for different T values in a range from 2 ms to 50 ms. It shows measured passages for all four possible cases from the two encircling-direction and two initial-state conditions. The adiabatic state flip takes place for the CCW case with initial state |s〉 (Fig. 3a) and CW case with initial state |a〉 (Fig. 3b). They experimentally demonstrate the time-asymmetric mode-transfer effect persisting over a broad T ranges. Importantly, Fig. 3c, d show significant details of the anti-adiabatic jump that has never been observed in experiments previously.

Fig. 3: Evolution passages of dynamic states in time domain.
figure 3

Complex expectation value 〈H〉 as a function of passage time t for different evolution-time constant T. Encircling-direction and initial-state conditions for each panel are (a) anticlockwise encircling from | ψ(0)〉 = |s〉, (b) clockwise encircling from |ψ(0)〉 = |a〉, (c) anticlockwise encircling from |ψ(0)〉 = |a〉, and (d) clockwise encircling from | ψ(0)〉 = |s〉. Colors of the expectation-value 〈H〉 passage curves indicate corresponding evolution-time constant T values in a 2-to-50-ms range as represented by the horizontal color-density bar above panel a. Gray curves in each panel indicate reference passages if a state follows the exact instantaneous eigenstates, i.e., adiabatic states, along the EEP loop. Light-gray arrow on the bottom of panel indicates the evolution-time direction.

Full size image

In the time-resolved passages during the anti-adiabatic state jump, we note two important observations. First, this state jump obviously becomes inevitable for larger T values as the binary Hamiltonian model predicts18. Therefore, we experimentally confirm that this effect is indeed anti-adiabatic in a sense that slower parametric change makes the abrupt non-adiabatic transition unavoidable.

Another important observation is that the passages during the jump seem remarkably chaotic for excessively large T values (T > 40 ms in our measurement). In our analyses, this property does not appear for ideal cases in theoretical study and becomes prominent whenever amplitude of the dynamic state |ψ(t)〉 is comparable to noise levels. Therefore, the chaotic behavior of the passages during the jump is attributed to amplified noises in the gain mode that dominate system’s response when the dynamic state before the jump stays at the loss mode for a significantly long time enough to attenuate its amplitude below a certain critical level. Developing practical device applications, this implies that care must be taken for device design in this aspect. The evolution-time constant T should be in a certain optimal range in order to avoid chaotic signal behaviors and to maintain certain encoded information carried by the dynamic states through the time-asymmetric EEP operations.

Further investigating the optimal range of the T values for a given EEP loop, we take a closer look at modal probability PG(t) = |〈ϕG*|ψ(t)〉|2 and PL(t) = |〈ϕL*|ψ(t)〉|2 curves in time domain, where |ϕG〉 and |ϕL〉 represent the gain and loss modes corresponding to the eigenvalues λG and λL, respectively. These curves are inferred from the measured complex amplitudes and are shown in Fig. 4. In Fig. 4a for the ACW EEP cases with initial-state condition |ψ(0)〉 = |s〉, the EEP operations do not involve the anti-adiabatic state jump and it results in PG(t) ≈ 1 and PL(t) ≈ 0 over the entire time domain from 0 to T. Significant deviation of PG(t) from 1 and PL(t) from 0 is found only for T < 5 ms. In this case, non-adiabatic coupling is strong due to fast parametric change beyond the standard adiabatic limit. Almost identical property is also found for CW EEP cases starting from |ψ(0)〉 = |s〉, as shown in Fig. 4b. Therefore, in order to induce efficient EEP operations for the adiabatic state flip, a necessary condition is to have a sufficiently large T so that |ψ(t)〉 undergoes time-varying system configuration well within the canonical adiabatic limit.

Fig. 4: Dependence of modal probability passage on evolution-time constant T.
figure 4

Modal probability PG (gain mode) and PL (loss mode) curves (solid and dashed curves, respectively) at different evolution-time constant T as a function of passage time t. Encircling-direction and initial-state conditions for each panel are (a) anticlockwise encircling from |ψ(0)〉 = |s〉, (b) clockwise encircling from |ψ(0)〉 = |a〉, (c) clockwise encircling from |ψ(0)〉 = |s〉, and (d) anticlockwise encircling from | ψ(0)〉 = a〉. Color scheme for curves for different T is identical to that in Fig. 3. The probability curves are inferred by bi-orthogonal inner product PG = |〈ϕG*|ψ〉|2 and PL = |〈ϕL*|ψ〉|2 with experimentally obtained dynamic state |ψ〉. |ϕG〉 and |ϕL〉 denote the gain and loss modes, respectively.

Full size image

For stable EEP operations involving the anti-adiabatic state jump, on the other hand, T does not have to be excessively large. Modal-probability curves involving the anti-adiabatic state jump are provided in Fig. 4c, d. In these cases, the curves start at PG(0) = 0 and PL(0) = 1, undergo abrupt transitions associated with the anti-adiabatic state jump near t ≈ 0.4 T, and finally relax at PG ≈ 1 and PL(t) ≈ 0 as the dynamic states settle down in the gain-mode (|ϕG〉) passage in each case. We notice that the curves toward t = T indicate that the dynamic states end up in a single-mode state |ψ(T)〉 ≈ |ϕG〉 for T > 20 ms and, thereby, excessively large T over 20 ms should not offer any remarkable advantage for the time-asymmetric EEP operations.

Moreover, dynamic responses of the system during the anti-adiabatic state jump become significantly instable due to noise-induced chaotic behaviors for excessively large T as signal strength of |ψ(t)〉 tends to enter the low signal regime where unpredictable noises present in general. Therefore, optimal dynamic-control speed conditions for given noise levels should be taken into account as a crucial design requirement for practical device applications.

In summary, we have developed a dynamic non-Hermitian simulator using tunable electrical-circuit oscillators. The proposed electrical-circuit simulator creates characteristic non-Hermitian spectral structures with unprecedented accuracy and enables fully time-resolved complex-amplitude measurements for unique non-Hermitian effects such as the adiabatic state flip, anti-adiabatic state jump, and time-asymmetric mode-transfer operation. Notably, arbitrary EEP loops and evolution-speed profiles are immediately realizable simply by injecting appropriately prepared control signals VC and VD in our proposed approach. As a reliable experimental test platform for emerging non-Hermitian physics and concomitant device applications, the tunable electrical-oscillator approach takes remarkable advantages in terms of simplicity in construction, flexibility in configuring desired non-Hermitian Hamiltonians, high control precision, and fully time-resolved measurement capability without any significant interruption of the excited state. Therefore, our proposed method is immediately applicable as a real-time simulator for dynamic non-Hermitian properties. Further development involving higher-order EPs or nonlinear components is greatly of interest for advanced experimental investigation on various non-Hermitian effects and their potential applications.

Methods

Eigenvalue-measurement procedures

In our eigenvalue-measurement method, we excite the circuit for given ΔC and CC with a time-harmonic current Iin at a frequency fn and an amplitude of 0.5 μA injected at Oscillator 1, wait for 100 ms until response of the circuit relaxes at a stationary state, take V2(t) at Oscillator 2 in time domain over 10 ms, identify oscillating amplitude a2(fn) from V2(t), and repeat this measurement cycle for a2(fn+1) at a next excitation frequency fn+1. Real and imaginary parts, i.e., Re(λ) and Im(λ), respectively, of the eigenvalue of H are identified by double-Lorentzian curve fitting of an acquired amplitude spectrum {a2(fn)} for resonance-peak center frequencies and linewidths, respectively.

Circuit constants for the EEP operation

In our dynamic EEP-operation experiment, fixed constants are AΔ = 80 pF, AC = 120 pF, and C0 = 230 pF, while p and T are taken as case-by-case variables in order to investigate corresponding changes in the dynamic state passages. Under this condition, corresponding EEP loop is an ellipse starting at (ΔC, CC) = (0 pF, 350 pF) and inscribing a rectangular area within –80 pF ≤ ΔC ≤ +80 pF and 110 pF  ≤  CC  ≤  350 pF ranges. In addition, we detune R2 off zero in a negative region of –200 kΩ < R2 < 0 (R2  ~ –115 kΩ in the EEP measurements) so that excited signals in the oscillators stay acceptably high with respect to a noise level ~ 2 mV in our laboratory environment and do not go beyond upper and lower amplifier thresholds at +10 V and –10 V, respectively. We note that R2 detuning in this way does not affect the established eigen-system structure since it changes the corresponding Hamiltonian in a specific way following H → H′ = H – igI, where g is an auxiliary gain coefficient and I is the identity operator. The amount of eigenvalue splitting and subsequent dynamic properties of the relative system responses are invariant for any change under this constraint. The only consequence of the R2 detuning is overall amplitude change in the excited signals while essential dynamics in relative signal amplitudes remain unspoiled in principle as far as the amplification and attenuation processes in the system operates in the linear regime.