Abstract
The difficulties of relativistic particle theories formulated by means of canonical quantization, such as those of Klein–Gordon and Dirac, ultimately led theoretical physicists to turn to quantum field theory to model elementary particle physics. In order to overcome these difficulties, the theories of the present approach are developed deductively from the physical principles that specify the system, without making use of canonical quantization. For a free particle these starting assumptions are invariance of the theory and covariance of position with respect to Poincaré transformations. In pursuing the approach, the effectiveness of group theoretical methods is exploited. The coherent development of our program has shown that robust classes of representations of the Poincaré group, discarded by the known particle theories, can in fact be taken as bases for perfectly consistent theories. For massive spin zero particles, six inequivalent theories have been determined, two of which do not correspond to any of the current ones; all of these theories overcome the difficulties of Klein–Gordon one. The present lack of the explicit transformation properties of position with respect to boosts prevents the complete determination of non zero spin particle theories. In the past a particular form of these transformation properties was adopted by Jordan and Mukunda. We check its consistency within the present approach and find that for spin \(\frac{1}{2}\) particles there is only one consistent theory, which is unitarily related to Dirac’s; yet, once again, it requires classes of irreducible representations previously discarded.
Similar content being viewed by others
1 Motivations and Overview
Canonical quantization was the primary method for formulating specific relativistic particle theories [1,2,3]; unlike the non-relativistic case, the results were affected by problems. The first problem was the order of the wave equation for a spin zero free particle, i.e. the Klein–Gordon equation, that turned out to be second order with respect to time, while according to the general laws of quantum theory it should have been first order. A related problem concerns the probability density \({\hat{\rho }}\) of the position of the particle, that the theory allowed to be negative [4]. The proposals [5] to solve this paradoxical situation, by a posteriori reinterpreting \({\hat{\rho }}\) in terms of charge density, violate the peculiar relativistic invariance required by the theory [6]. The difficulties of relativistic particle theory, effectively shown by Weinberg in full detail [7] also for Dirac equation [8,9,10], ultimately led theoretical physicists to turn to quantum field theory to model elementary particle physics.
The inability to solve these problems is bound up with the methodological features of canonical quantization. In order to formulate the quantum theory of a particle, canonical quantization prescribes to replacing the dynamical variables \(q_j\) and the conjugate momenta \(p_j\) of its classical theory with operators \(Q_j\) and \(P_j\), and to replacing the Poisson brackets \(\{\,,\,\}\) with operatorcommutators \(i[\,,\,]\) in the dynamical equations of the classical theory, to obtain the dynamical equations of the quantum theory of the particle. We see that the implementation of canonical quantization provides no deductive path that leads to results from physical principles. For this reason the real causes of problematic or inconsistent predictions cannot be singled out and thus resolved.
In order to overcome these inconsistencies, the present work does not apply canonical quantization; instead, the quantum theories of a particle are constructed according to a strictly deductive development starting from the symmetry and covariance principles that characterize the concept of free particle. This methodology avoids the shortcomings arising with canonical quantization, because the eventual occurrence of inconsistencies, whenever ascertained, would be the proof of the failure of the starting assumptions, which should be accordingly modified. This approach has turned out to be very effective in developing non-relativistic quantum theories of an interacting particle [11,12,13], by making use of group theoretical methods. Here we undertake the approach for the relativistic quantum theory of an isolated system and of a “massive” free particle in particular. From the results, we have found not only that
-
alternative theories of a free Klein–Gordon particle are completely derivable from the physical principles without the problems suffered by the earlier theory,
(a task not accomplished before) but even that
-
new species of particle theories, i.e. consistent theories that correspond to none of the known theories, can be coherently developed.
The principle we start from for an isolated physical system is relativistic invariance established by stating that the Poincaré group \({\mathcal {P}}\) is a group of symmetry transformations. After the needed mathematical prerequisites in Sect. 2, in Sect. 3 we show that this invariance principle implies the existence of a generalized projective representation \(g\rightarrow U_g\) of the Poincaré group that realizes the quantum transformations of observables according to \(A\rightarrow S_g[A]=U_gAU_g^{-1}\). Though this implication is widely exploited in the literature [14,15,16,17,18,19], it could in fact not be derived from the symmetry principle by making use of the standard quantum concept of transformation. We overcome this obstacle by introducing a more adequate concept of quantum transformation.
Then, the concept of free particle is introduced as an isolated system specified by the existence of a unique triple \({{\mathbf{Q}}}=(Q_1,Q_2,Q_3)\) of commuting quantum observables that represent the three coordinates of the position.Footnote 1 Accordingly, it is required that for each \(g\in {\mathcal {P}}\) the transformed position operator \(S_g[{{\mathbf{Q}}}]=U_g{{{{\mathbf{Q}}}}}U_g^{-1}\) and the untransformed \({{{\mathbf{Q}}}}\) must be related by the peculiar transformation properties of the coordinates of position with respect to g. For an elementary free particle the projective representation U such that \(S_g[{{\mathbf{Q}}}]=U_g{{{{\mathbf{Q}}}}}U_g^{-1}\) must be irreducible. Thus, a consistent theory of a free elementary particle is identifiable by checking which irreducible generalized projective representations of \({\mathcal {P}}\) admit a triple \({{{\mathbf{Q}}}}\) satisfying these transformation conditions.
The work of Sect. 3 shows that the identification of the irreducible generalized projective representations of \({\mathcal {P}}\) lays the groundwork for developing theories of elementary free particle. Several well known approaches based on relativistic invariance, from the fundamental works of Wigner [14], Wigner and Bargmann [15], to more recent contributions [7, 16,17,18], deal with this task. These approaches, however, discard robust classes of irreducible representations of \({\mathcal {P}}\). For instance, in [19] irreducible representations with anti-unitary space inversion operators are not taken into account. One reason put forward for this exclusion [7, 16, 27] is that anti-unitarity space inversion operators change the sign of the spectral values of the self-adjoint generator of time translations \(P_0\), that in these studies is identified with energy, and it is usually assumed that this change cannot happen (see [27, p. 135]). But we know that Dirac theory of spin-\(\frac{1}{2}\) particles does admit both signs for this spectrum; moreover, we shall show in Sect. 5 that perfectly consistent theories can be formulated with anti-unitary space inversion operators. In the present work no such a priori exclusion is assumed; any space inversion or time reversal operator is discarded only if it gives rise to inconsistencies.
The irreducible (positive “mass”) generalized projective representations of \({\mathcal {P}}\) without a priori preclusions are reported in Sect. 4.
The explicit determination of the theories of an elementary free particle is addressed in Sect. 5 by selecting which of the already identified irreducible representations of \({\mathcal {P}}\) admits a position operator \({{{\mathbf{Q}}}}\) with the required transformation properties. As a result, for each positive value of the mass parameter \(\mu \) six inequivalent theories for spin zero particles are fully determined. Two of these theories coincide with well known theories with positive or negative spectrum \(\sigma (P_0)\) of the Hamiltonian operator \(P_0\) and spin zero. Two further theories are characterized by symmetrical spectrum \(\sigma (P_0)\) of the Hamiltonian operator \(P_0\), hence recalling Klein–Gordon particles, albeit with fundamental differences with respect to the earlier theory; first of all, both theories are based on irreducible representations in the new classes with anti-unitary space inversion operator, and one has anti-unitary time reversal operator as well; moreover, being developed deductively, they avoid the problems of interpretative consistency associated with the Klein–Gordon theory. Two other theories are new species: they have no correspondence with currently known theories.
In the case of non zero spin particles, our selection of the representations that admit an observable position does not uniquely determine \({{{\mathbf{Q}}}}\). Section 6 explains how this indeterminacy is due to the present unavailability of a general form of the transformation properties of \({{{\mathbf{Q}}}}\) with respect to boosts. A particular form (JM) of these properties, expressed as commutation relations, was adopted by Jordan and Mukunda [18]. In Sect. 6 the selection is performed by making tentative use of (JM). For spin-\(\frac{1}{2}\) particles with symmetrical spectrum of the Hamiltonian operator \(P_0\), only one theory turns out to be consistent with (JM), which is unitarily related to Dirac theory. Moreover this theory requires an irreducible generalized projective representation of \({\mathcal {P}}\) in the new classes with anti-unitary space inversion operator.
Section 7 discusses the problem of identifying the real particles described by a given theory from those developed in the work.
In the final Sect. 8 future perspectives stemming from the present work are indicated.
2 Notation and Mathematical Prerequisites
First of all we introduce the notation for the mathematical structures of general interest in a quantum theory based on a Hilbert space \({\mathcal {H}}\).
-
The set \(\Omega ({{\mathcal {H}}})\) of all self-adjoint operators of \({\mathcal {H}}\); in a quantum theory these operators represent quantum observables.
-
The lattice \(\Pi ({{\mathcal {H}}})\) of all projections operators of \({\mathcal {H}}\); in a quantum theory they represent observables with outcome’ spectrum \(\{0,1\}\).
-
The set \(\Pi _1({{\mathcal {H}}})\) of all rank one orthogonal projections of \({\mathcal {H}}\).
-
The set \({{\mathcal {S}}}({{\mathcal {H}}})\) of all density operators of \({\mathcal {H}}\); in a quantum theory these operators represent quantum states.
-
The set \({{\mathcal {V}}}({{\mathcal {H}}})\) of all unitary or anti-unitary operators of the Hilbert space \({\mathcal {H}}\).
-
The set \({{\mathcal {U}}}({{\mathcal {H}}})\) of all unitary operators of \({\mathcal {H}}\); trivially, \({{\mathcal {U}}}({{\mathcal {H}}})\subseteq {{\mathcal {V}}}({{\mathcal {H}}})\) holds.
2.1 Representations of Groups; the Poincaré Group
The following definition introduces general notions concerning group representations.
Definition 2.1
Let G be a separable, locally compact group with identity element e. A correspondence \(U:G\rightarrow {{\mathcal {V}}}({{\mathcal {H}}})\), \(g\rightarrow U_g\), with \(U_e=\mathbb {1}\), is a generalized projective representation of G if the following conditions are satisfied.
-
(i)
A complex function \(\sigma :{G}\times {G}\rightarrow {\mathbb {C}}\), called multiplier, exists such that
\(U_{g_1g_2}=\sigma (g_1,g_2)U_{g_1}U_{g_2}\); the modulus \(\vert \sigma (g_1,g_2)\vert \) is always 1;
-
(ii)
for all \(\phi ,\psi \in {\mathcal {H}}\), the mapping \(g\rightarrow \langle U_g\phi \mid \psi \rangle \) is a Borel function in g.
Whenever \(U_g\) is unitary for all \(g\in G\), U is called projective representation, or \(\sigma \)-representation.
A generalized projective representation is said to be continuous if for any fixed \(\psi \in {\mathcal {H}}\) the mapping \(g\rightarrow U_g\psi \) from G to \({\mathcal {H}}\) is continuous with respect to g.
If \(U:G\rightarrow {{\mathcal {V}}}({{\mathcal {H}}})\) is a generalized projective representation and \(\theta (g)\in \mathbb {R}\) for all \(g\in G\), with \(e^{i\theta (e)}=\mathbb {1}\), then the generalized projective representation \({\tilde{U}}:G\rightarrow {{\mathcal {V}}}({{\mathcal {H}}})\), \(g\rightarrow {\tilde{U}}_g=e^{i\theta (g)}U_g\) is said to be equivalent to \(U:G\rightarrow {{\mathcal {V}}}({{\mathcal {H}}})\).
In [12] we have proved that the following statement holds.
Proposition 2.1
If G is a connected group, then every continuous generalized projective representation U of G is a projective representation, i.e. \(U_g\in {{\mathcal {U}}}({{\mathcal {H}}})\), for all \(g\in G\).
Given any vector \({\underline{x}}=(x_0,\mathbf{x})\in \mathbb {R}^4\), we call \(x_0\) the time component of \({\underline{x}}\) and \(\mathbf{x}=(x_1,x_2,x_3)\) the spatial component of \({\underline{x}}\). The proper orthochronous Poincaré group \({{\mathcal {P}}}_+^\uparrow \) is the separable locally compact group of all transformations of \(\mathbb {R}^4\) generated by the ten one-parameter sub-groups \({{\mathcal {T}}}_0\), \({{\mathcal {T}}}_j,{{\mathcal {R}}}_j\), \({{\mathcal {B}}}_j\), \(j=1,2,3\), of time translations, spatial translation, proper spatial rotations and Lorentz boosts, respectively, relative to the axes \(x_j\). Euclidean group \({\mathcal {E}}\) is the sub-group generated by all \({{\mathcal {T}}}_j\) and \({{\mathcal {R}}}_j\). The sub-group generated by all \({{\mathcal {R}}}_j\), \({{\mathcal {B}}}_j\) is the proper orthochronous Lorentz group \({{\mathcal {L}}}_+^\uparrow \) [17]. It does not include time reversal  and space inversion
and space inversion  . Time reversal
. Time reversal  transforms \({\underline{x}}=(x_0,\mathbf{x})\) into \((-x_0,\mathbf{x})\); space inversion
transforms \({\underline{x}}=(x_0,\mathbf{x})\) into \((-x_0,\mathbf{x})\); space inversion  transforms \({\underline{x}}=(x_0,\mathbf{x})\) into \((x_0,-\mathbf{x})\). The group generated by
transforms \({\underline{x}}=(x_0,\mathbf{x})\) into \((x_0,-\mathbf{x})\). The group generated by  is the separable and locally compact Poincaré group \({\mathcal {P}}\). By \({{\mathcal {L}}}_+\) we denote the subgroup generated by \({{\mathcal {L}}}_+^\uparrow \) and
is the separable and locally compact Poincaré group \({\mathcal {P}}\). By \({{\mathcal {L}}}_+\) we denote the subgroup generated by \({{\mathcal {L}}}_+^\uparrow \) and  , while \({{\mathcal {L}}}^\uparrow \) denotes the subgroup generated by \({{\mathcal {L}}}_+^\uparrow \) and
, while \({{\mathcal {L}}}^\uparrow \) denotes the subgroup generated by \({{\mathcal {L}}}_+^\uparrow \) and  ; analogously, \({{\mathcal {P}}}_+\) denotes the subgroup generated by \({{\mathcal {P}}}_+^\uparrow \) and
; analogously, \({{\mathcal {P}}}_+\) denotes the subgroup generated by \({{\mathcal {P}}}_+^\uparrow \) and  , while \({{\mathcal {P}}}^\uparrow \) is the subgroup generated by \({{\mathcal {P}}}_+^\uparrow \) and
, while \({{\mathcal {P}}}^\uparrow \) is the subgroup generated by \({{\mathcal {P}}}_+^\uparrow \) and  .
.
Since \({{\mathcal {P}}}_+^\uparrow \) is a connected group, according to Proposition 2.1 every continuous generalized projective representation of \({{\mathcal {P}}}_+^\uparrow \) is a projective representation.
All sub-groups \({{\mathcal {T}}}_0\), \({{\mathcal {T}}}_j,{{\mathcal {R}}}_j\), \({{\mathcal {B}}}_j\) of \({{\mathcal {P}}}_+^\uparrow \) are additive; in fact, \({{\mathcal {B}}}_j\) is not additive with respect to the parameter relative velocity u, but it is additive with respect to the parameter \(\varphi (u)=\frac{1}{2}\ln \frac{1+u}{1-u}\). For every continuous projective representation \({\tilde{U}}:{{\mathcal {P}}}_+^\uparrow \rightarrow {{\mathcal {U}}}({{\mathcal {H}}})\), according to Stone’s theorem [28], an equivalent continuous projective representation \(U:{{\mathcal {P}}}_+^\uparrow \rightarrow {{\mathcal {U}}}({{\mathcal {H}}})\) exists with ten self-adjoint generators \(P_0\), \(P_j\), \(J_j\), \(K_j\), \(j=1,2,3\), of the ten one-parameter unitary subgroups \(\{e^{iP_0t}\}\), \(\{e^{-i{P}_j a_j},\,a\in {\mathbb {R}}\}\), \(\{e^{-i{J}_j \theta _j},\,\theta _j\in {\mathbb {R}}\}\), \(\{e^{-i{K}_j \varphi (u_j)},\,u_j\in {\mathbb {R}}\}\) of \({{\mathcal {U}}}({{\mathcal {H}}})\) that represent the one-parameter sub-groups \({{\mathcal {T}}}_0\), \({{\mathcal {T}}}_j,{{\mathcal {R}}}_j\), \({{\mathcal {B}}}_j\) according to the projective representation U.
2.2 Commutation Relations in Representations of \({\mathcal {P}}\)
The structural properties of \({{\mathcal {P}}}_+^\uparrow \) as a Lie group imply that every continuous projective representation of \({{\mathcal {P}}}_+^\uparrow \) admits an equivalent projective representation whose generators satisfy the following commutation relations [19].
where \({{\hat{\epsilon }}}_{jkl}\) is the Levi-Civita symbol \({\epsilon }_{jkl}\) restricted by the condition \(j\ne l\ne k\).
Let \(U:{{\mathcal {P}}}\rightarrow {{\mathcal {V}}}({{\mathcal {H}}})\) be a generalized projective representation whose restriction to \({{\mathcal {P}}}_+^\uparrow \) is continuous, for which the commutation relations (1) hold. Each operator \(U_g\) can be unitary or anti-unitary, but according to Proposition 2.1\(U_g\) is unitary if \(g\in {{\mathcal {P}}}_+^\uparrow \). Since time reversal  and space inversion
and space inversion  are not connected with the identity transformation \(e\in {\mathcal {P}}\), the operators
are not connected with the identity transformation \(e\in {\mathcal {P}}\), the operators  and
and  that represent
that represent  and
and  are not necessarily unitary: each of them can be unitary or anti-unitary. By making use of the structural properties of the full Poincaré group \({\mathcal {P}}\) it can be shown [19] that the phase factor \(e^{i\theta (g)}\) can always be chosen so that, besides (1), the following statements also hold in the equivalent representation.
are not necessarily unitary: each of them can be unitary or anti-unitary. By making use of the structural properties of the full Poincaré group \({\mathcal {P}}\) it can be shown [19] that the phase factor \(e^{i\theta (g)}\) can always be chosen so that, besides (1), the following statements also hold in the equivalent representation.
If  is unitary, then the following relations hold.
is unitary, then the following relations hold.

In the case that  is anti-unitary, instead we have
is anti-unitary, instead we have

The following relations hold in the case that  is unitary.
is unitary.

Instead, for anti-unitary  we have
we have

The commutation condition to be satisfied by the pair  , independently of their unitary or anti-unitary character, is simply
, independently of their unitary or anti-unitary character, is simply

3 Single Particle Quantum Theories
In order to develop the specific quantum theories of a free particle, we interpret \({\mathcal {P}}\) as the group of changes of reference frame, according to special relativity. Hence, given a reference frame \(\Sigma \) in the class \({\mathcal {F}}\) of the (inertial) reference frames that move uniformly with respect to each other, for every \(g\in {{\mathcal {P}}}\) let \(\Sigma _g\) denote the reference frame related to \(\Sigma \) just by g, and let \(\textsf {g}:\mathbb {R}^4\rightarrow \mathbb {R}^4\) be the mapping such that if \({\underline{x}}=(t,x_1,x_2,x_3)\equiv (x_0,\mathbf{x})\) is the vector of the time-space coordinates of an event with respect to \(\Sigma \), then \(\textsf {g}({\underline{x}})\) is the vector of the time-space coordinates of that event with respect to \(\Sigma _g\).
Let us now consider an isolated physical system. The following statement establishes as a physical principle that \({\mathcal {P}}\) is a group of symmetry transformations.
- \({\mathcal {S}}\)ym:
-
The theory of an isolated system is invariant for changes of frames in \({\mathcal {F}}\).
We now introduce the concept of relative indistinguishability between measuring procedures of quantum observables, which allows to show that for each \(g\in {\mathcal {P}}\) a specific quantum transformation \(S_g:\Omega ({{\mathcal {H}}})\rightarrow \Omega ({{\mathcal {H}}})\), \(A\rightarrow S_g[A]\) of the quantum observables must exist, with peculiar properties (S.1)-(S.3).
Relative indistinguishability of measuring procedures. Given two reference frames \(\Sigma _1\) and \(\Sigma _2\) in \({\mathcal {F}}\), if a measuring procedure \({{\mathcal {M}}}_1\) is with respect to \(\Sigma _1\) identical to another measuring procedure \({{\mathcal {M}}}_2\) with respect to \(\Sigma _2\), we say that \({{\mathcal {M}}}_1\) and \({{\mathcal {M}}}_2\) are indistinguishable relative to \((\Sigma _1,\Sigma _2)\).
Given \(\Sigma _1\) and \(\Sigma _2\) in \({\mathcal {F}}\), for every measuring procedure \({{\mathcal {M}}}_1\) another measuring procedure \({{\mathcal {M}}}_2\) must exist such that \({{\mathcal {M}}}_1\) and \({{\mathcal {M}}}_2\) are indistinguishable relative to \((\Sigma _1,\Sigma _2)\), otherwise the invariance stated by \({\mathcal {S}}\)ym would not hold; this existence confers consistency to the following definition.
Definition 3.1
Quantum transformation.
Fixed any reference frame \(\Sigma \in {{\mathcal {F}}}\), for every \(g\in {{\mathcal {P}}}\) the mapping
such that the quantum observables A and \(S_g[A]\) respectively are measurable by two measuring procedures \({{\mathcal {M}}}_1\) and \({{\mathcal {M}}}_2\) indistinguishable relatively to \((\Sigma ,\Sigma _g)\), is called quantum transformation of g.
The following properties are compelled by the present specific concept of quantum transformation.
-
(S.1)
Every \(S_g:\Omega ({{\mathcal {H}}})\rightarrow \Omega ({{\mathcal {H}}})\) is bijective;
-
(S.2)
for every \(A\in \Omega ({{\mathcal {H}}})\) and every real function f such that \(f(A)\in \Omega ({{\mathcal {H}}})\),
the equality \(S_g[f(A)]=f(S_g[A])\) holds.
We show how this property is compelled by conceptual coherence. Let us consider two procedures \({{\mathcal {M}}}_1\) and \({{\mathcal {M}}}_2\) that measure A and \(S_g[A]\) respectively, \({{\mathcal {M}}}_1\) and \({{\mathcal {M}}}_2\) being indistinguishable relative to \(\Sigma \) and \(\Sigma _g\). General quantum theory [29] establishes that the quantum observable \(B=f(A)\) can be measured by performing the same measuring procedure \({{\mathcal {M}}}_1\) for measuring A and then transforming the obtained outcome a of A by the mathematical function f into the outcome \(b=f(a)\) of \(B=f(A)\); thus the same argument applies to \(S_g[A]\) and \(D=f(S_g[A])\). Therefore, the two procedures that measure the quantum observables f(A) and \(f(S_g[A])\) can be realized by transforming the outcomes yielded by the relatively indistinguishable \({{\mathcal {M}}}_1\) and \({{\mathcal {M}}}_2\) through the same function f; adding the application of the same mathematical function f to the outcomes of the procedures for \({{\mathcal {M}}}_1\) and \({{\mathcal {M}}}_2\) does not affect their relative indistinguishability. Thus \(S_g[f(A)]=f(S_g[A])\) follows.
-
(S.3)
\(S_{gh}[A]=S_g\left[ S_h[A]\right] \), for all \(g,h\in {\mathcal {P}}\) and every \(A\in \Omega [{{\mathcal {H}}})\).
Thus, from \(({\mathcal {S}}\)ym) the following further physical principle is implied.
- (\({{\mathcal {Q}}}{{\mathcal {T}}}\)):
-
A quantum transformation \(S_g:\Omega ({{\mathcal {H}}})\rightarrow \Omega ({{\mathcal {H}}})\) exists for every symmetry transformation \(g\in {\mathcal {P}}\), such that (S.1), (S.2) and (S.3) hold.
Properties (S.1) and (S.2) are sufficient [12] to prove that for each quantum transformation \(S_g\) a unitary or anti-unitary operator \({{\tilde{U}}}_{g}\) must exist such that
Remark 3.1
It is important not to confuse the present concept of quantum transformation with the “active” concept more often adopted. The transformation in this latter sense is obtained by “Moving everything by an element [\(g\in {\mathcal {P}}\)]” [30]. The active concept is not in fact adequate for our approach. Let us explain why. Let the apparatus \({\mathcal {M}}\) measuring A be at rest with respect to \(\Sigma \), but with an “internal” component endowed with a velocity \(\mathbf{v}\) with respect to \(\Sigma \), and let g be a boost. According to the active concept, the apparatus \({{\mathcal {M}}}'\) measuring \(S^{active}_g[A]\) is the apparatus \({\mathcal {M}}\) measuring A endowed with the velocity \(\mathbf{u}\) characterizing the boost g. Clearly apparatus \({{\mathcal {M}}}'\) is at rest with respect to \(\Sigma _g\), but the velocity of the moving component is not \(\mathbf{v}\) with respect to \(\Sigma '\), because of the relativistic composition law of velocities. Therefore, \({\mathcal {M}}\) and \({{\mathcal {M}}}'\) are not indistinguishable relative to \((\Sigma ,\Sigma ')\). Since such an indistinguishability is required in order to state that (S.2) holds, the present approach could not be developed with the active concept of transformation.
3.1 Theories of Isolated Systems
Given any real function \(\theta \) of g, the operators \({\tilde{U}}_g\) and \(e^{i\theta (g)}{\tilde{U}}_g\) yield the same quantum transformation as \({\tilde{U}}_g\), i.e. \({\tilde{U}}_gA {\tilde{U}}_g^{-1}= \left( e^{i\theta (g)}{\tilde{U}}_g\right) A\left( e^{i\theta (g)}{\tilde{U}}_g\right) ^{-1}\), and, hence, \(U_g =e^{i\theta (g)}{\tilde{U}}_g\) can replace \({\tilde{U}}_g\) in the specific quantum theory of the system. In particular, we can set \(U_e=\mathbb {1}\). Condition (S.3) implies that \(U_{g_1g_2}=\sigma (g_1,g_2)U_{g_1}U_{g_2}\) where \(\sigma (g_1,g_2)\) is a complex number of modulus 1. In general therefore the correspondence \(U:{{\mathcal {P}}}\rightarrow {{\mathcal {V}}}({{\mathcal {H}}})\) for which \(S_g[A]=U_gAU_g^{-1}\) is a generalized projective representation that satisfies (1)-(6). We assume that the correspondence \(g\rightarrow S_g\) restricted to \({{\mathcal {P}}}_+^\uparrow \) is continuous, according to the Bargmann topology [12]; this assumption can be justified by arguing that a small transformation \(g\in {{\mathcal {P}}}_+^\uparrow \) determines a small change from A to \(S_g[A]\). Now, it has been proved [12] that if the correspondence \(g\rightarrow S_g\) assigning each transformation \(g\in {{\mathcal {P}}}_+^\uparrow \) its quantum transformation \(S_g\) is continuous with respect to the Bargmann topology, then a choice of the free phase \(\theta (g)\) exists such that the restriction \(U:{{\mathcal {P}}}_+^\uparrow \rightarrow {{\mathcal {U}}}({{\mathcal {H}}})\) turns out to be continuous, and therefore a continuous projective representation, according to Proposition 2.1.
Thus, from the principles \({\mathcal {S}}\)ym and its“corollary” (\(\mathcal {QT}\)), we have shown that the Hilbert space of the quantum theory of an isolated system must necessarily be the Hilbert space of a generalized projective representation U of \({\mathcal {P}}\), that determines the quantum transformation of the observables as \(S_g[A]=U_gAU_g^{-1}\); moreover, under our continuity hypothesis for \(g\rightarrow S_g\), the restriction \(U\mid _{{{\mathcal {P}}}_+^\uparrow }\) is continuous.
Though this implication is widely shared [14,15,16,17,18,19], its proof in fact requires the present concept of quantum transformation, unike the one usually adopted, as explained in Remark 3.1.
3.2 Theories of a Localizable Free Particle
By localizable free particle, or free particle, we mean an isolated system whose specific quantum theory is endowed with a unique position observable, namely with a unique triple \((Q_1,Q_2,Q_3)\equiv {{\mathbf{Q}}}\) of self-adjoint operators, whose components \(Q_j\) are called coordinates of position, characterized by the following conditions.
- (Q.1):
-
\([Q_j,Q_k]=\mathbb {O}\), for all \(j,k=1,2,3\).
This condition establishes that a measurement of position yields all three values of the coordinates of the same specimen of the particle (see footnote 1, Sect. 1).
- (Q.2):
-
For every \(g\in {\mathcal {P}}\), the triple \((Q_1,Q_2,Q_3)\equiv {{\mathbf{Q}}}\) and the transformed position operators \(S_g[{{\mathbf{Q}}}]\) satisfy the specific relations implied by the transformation properties of position with respect to g.
Example 3.1
Let \({\mathcal {E}}\) be the Euclidean group, i.e. the group generated by spatial translations and rotations. Condition (Q.2) implies that for  the occurrence of \(\mathbf{x}=(x_1,x_2,x_3)\) as outcome of a measurement of the position at time \(t=0\) in a reference frame \(\Sigma \) is equivalent to the occurrence of \(\textsf {g}(\mathbf{x})\) as outcome of a measurement of the position at time \(t'=0\) in the reference frame \(\Sigma _g\). Therefore, by making use of spectral theory [31], from (Q.2) we derive
the occurrence of \(\mathbf{x}=(x_1,x_2,x_3)\) as outcome of a measurement of the position at time \(t=0\) in a reference frame \(\Sigma \) is equivalent to the occurrence of \(\textsf {g}(\mathbf{x})\) as outcome of a measurement of the position at time \(t'=0\) in the reference frame \(\Sigma _g\). Therefore, by making use of spectral theory [31], from (Q.2) we derive
- (Q.2.a):
-
 and
and  , i.e.
, i.e.  and
and  by (2)-(5),
by (2)-(5), - (Q.2.b):
-
\(S_g[{{\mathbf{Q}}}]=U_g{{\mathbf{Q}}}U_g^{-1}={\textsf {g}}({{\mathbf{Q}}})\) for every \(g\in {{\mathcal {E}}}\).
So, if g is a spatial translation, i.e. if \({\textsf {g}}(\mathbf{x})=\mathbf{x}-\mathbf{a}\), then the transformation property is \(S_g[{{\mathbf{Q}}}]\equiv U_g{{\mathbf{Q}}}U_g^{-1}={{\mathbf{Q}}}-\mathbf{a}\mathbb {1}\). It must be remarked that the extension of (Q.2.b) to boosts is yet to be found, as we shall explain in Sect. 6.
Condition (Q.2.b) implies relations that tie \({{{\mathbf{Q}}}}\) with the self-adjoint generators \(P_0\), \({{\mathbf{P}}}\), \({\mathbf{J}}\), \({\mathbf{K}}\). For instance, if g is a translation by a along \(x_1\), so that \(\textsf {g}(\mathbf{x})=(x_1-a,x_2,x_3)\) and \(U_g=e^{-iP_1a}\) hold, then (Q.2.b) yields the transformation properties
by expanding with respect to a, these properties can be expressed as the commutation relation \([Q_k,P_1]=i\delta _{1k}\); in general, the following canonical commutation rules hold.

Analogously, the transformation properties with respect to spatial rotations imply

Relations (9) are an equivalent form of transformation properties with respect to \({\mathcal {E}}\).
3.3 Theories of Elementary Free Particle
In the quantum theory of a localizable free particle, the system of operators \(\{U({{\mathcal {P}}}),{{\mathbf{Q}}}\}\) may or may not be reducible. Following a customary procedure, we introduce the following elementary particle concept.
Definition 3.2
A free particle is said to be elementary if the system of operators \(\{U({{\mathcal {P}}}), {{\mathbf{Q}}}\}\) is irreducible.
For elementary free particles, the generalized projective representation U that realizes the quantum transformations must be irreducible. Let us explain why. If U were reducible, then a unitary operator V would exist such that \([V,U_g]=\mathbb {O}\) for all \(g\in {\mathcal {P}}\), but \([V,Q_j]\ne \mathbb {O}\) for some j − if \([V,Q_k]=\mathbb {O}\) held for all k, then \(\{U({{\mathcal {P}}}),{{\mathbf{Q}}}\}\) would be reducible, and this is not possible for elementary particles. Hence, if we define \({\hat{Q}}_k=VQ_kV^{-1}\), then \(\hat{{\mathbf{Q}}}\ne {{\mathbf{Q}}}\), while \(VU_gV^{-1}=U_g\) for all \(g\in {\mathcal {P}}\). The mathematical relations between the operators \(\hat{{\mathbf{Q}}}=V{{\mathbf{Q}}}V^{-1}\) and each \(U_g=VU_gV^{-1}\) must be the same as the mathematical relations between \({\mathbf{Q}}\) and that \(U_g\), because \(\{U({{\mathcal {P}}}),{{\mathbf{Q}}}\}\) and \(\{U({{\mathcal {P}}}),\hat{{\mathbf{Q}}}\}\) are unitarily isomorphic. Then the triple \(\hat{{\mathbf{Q}}}\) satisfies (Q.2), because \({\mathbf{Q}}\) does, and therefore \(\hat{{\mathbf{Q}}}\) would be a position operator in all respects. Thus, for the same elementary particle two different position operators would exist, in contradiction with the required uniqueness.
Since in a theory of an elementary particle the generalized projective representation \(U:{{\mathcal {P}}}\rightarrow {{\mathcal {V}}}({{\mathcal {H}}})\) for which \(S_g[A]=U_gAU_g^{-1}\) must be irreducible, the possible theories can be concretely identified by selecting the irreducible generalized projective representations U of \({\mathcal {P}}\) that admit a triple \({\mathbf{Q}}\) satisfying (Q.1) and (Q.2). An irreducible representation can be excluded as basis of a particle theory only if it gives rise to inconsistency, not a priori. Therefore, the aimed identification requires selection on a as large as possible set of irreducible representations, including those discarded by the literature. In Sect. 4 we explicitly identify the irreducible generalized projective representations of \({\mathcal {P}}\) of positive “mass”; in Sects. 5 and 6 we perform the selection described above. The zero “mass” case will be dealt within a separate work.
4 Irreducible Representations of \({\mathcal {P}}\)
In this section we render explicit the form of the irreducible generalized projective representations of \({\mathcal {P}}\), without exclusions based on the unitary or anti-unitary character of operators  . A determination of these representations was worked out in [32], through a generalization of the imprimitivity theorem of Mackey [30]. Another approach was developed in [33, 34] by Cariñena and Santander, who also proposed a criterion to establish whether symmetry transformation can be represented by anti-unitary operators in a quantum theory [35]; unfortunately, such a criterion turned out to be ineffective in the relativistic case. In the present work we shall make use of the explicit form of the representations of \({\mathcal {P}}\) as determined in [36] and shown in this section, because this form is particularly suitable for our aims.
. A determination of these representations was worked out in [32], through a generalization of the imprimitivity theorem of Mackey [30]. Another approach was developed in [33, 34] by Cariñena and Santander, who also proposed a criterion to establish whether symmetry transformation can be represented by anti-unitary operators in a quantum theory [35]; unfortunately, such a criterion turned out to be ineffective in the relativistic case. In the present work we shall make use of the explicit form of the representations of \({\mathcal {P}}\) as determined in [36] and shown in this section, because this form is particularly suitable for our aims.
Let us denote the class of all such representations by \({{\mathcal {I}}}_{{\mathcal {P}}}\). Given any U in \({{\mathcal {I}}}_{{\mathcal {P}}}\), we define the projection operators \(E^{+}=\int _0^\infty dE_{p_0}\) and \(E^{-}=\int _{-\infty }^{0} dE_{p_0}=\mathbb {1}-E^+\), where \(p_0\rightarrow E_{p_0}\) is the resolution of the identity of the generator \(P_0\) (if the observable represented by \(P_0\) is called “energy”, then we can say that \(E^+\) and \(E^-\) project onto the positive energy and negative energy self-spaces of \({\mathcal {H}}\), respectively). So
where \({{\mathcal {I}}}_{{\mathcal {P}}}({\mathbf{u}})\) (resp.,\( {{\mathcal {I}}}_{{\mathcal {P}}}({\mathbf{d}})\) is formed by the representations in \({{\mathcal {I}}}_{{\mathcal {P}}}\) such that \(E^+=\mathbb {1}\) (resp,. \(E^-=\mathbb {1}\)), and \({{\mathcal {I}}}_{{\mathcal {P}}}({\mathbf{s}})\) is formed by the representations in \({{\mathcal {I}}}_{{\mathcal {P}}}\) such that \(E^+\), and hence \(E^-\), is different from \(\mathbb {O}\) and \(\mathbb {1}\).
Whenever \(U\in {{\mathcal {I}}}_{{\mathcal {P}}}(\mathbf{s})\), the restriction \(U\mid _{{{\mathcal {P}}}_+^\uparrow }\) always turns out to be reduced [36] by \(E^+\) into \(U^+:{{{\mathcal {P}}}_+^\uparrow }\rightarrow {{\mathcal {U}}}({{\mathcal {H}}})\), \(g\rightarrow U^+_g=E^+U_gE^+\) and by and \(E^-\) into \(U^-:{{{\mathcal {P}}}_+^\uparrow }\rightarrow {{\mathcal {U}}}({{\mathcal {H}}})\), \(g\rightarrow U^-_g=E^-U_gE^-\), so that \(U\mid _{{{\mathcal {P}}}_+^\uparrow }=U^+\oplus U^-\). In its turn, \(U^+\), could be reducible, though the unrestricted representation U of \({\mathcal {P}}\) is irreducible. This also holds if \(U\in {{\mathcal {I}}}_{{\mathcal {P}}}(\mathbf{u})\) or \(U\in {{\mathcal {I}}}_{{\mathcal {P}}}(\mathbf{d})\), for which we have \(U^+=U\mid _{{{\mathcal {P}}}_+^\uparrow }\) and \(U^-=U\mid _{{{\mathcal {P}}}_+^\uparrow }\) . Moreover, in the case \(U\in {{\mathcal {I}}}_{{\mathcal {P}}}(\mathbf{s})\) it can be shown that \(U^+\) is reducible if and only if \(U^-\) is reducible [36]. So
where \({{\mathcal {I}}}_{{\mathcal {P}}}(U^\pm \mathrm{irred.})\) is the class of the representations in \({{\mathcal {I}}}_{{\mathcal {P}}}\) for which each \(U^+\) or \(U^-\) is irreducible, and \({{\mathcal {I}}}_{{\mathcal {P}}}(U^\pm \mathrm{red.})\) is formed by the representations in \({{\mathcal {I}}}_{{\mathcal {P}}}\) for which \(U^+\) or \(U^-\) is reducible. The class \({{\mathcal {I}}}_{{\mathcal {P}}}(U^\pm \mathrm{irred.})\) can be brokendown into three non-overlapping subclasses:
where \({{\mathcal {I}}}_{{\mathcal {P}}}(U^+{\mathrm{irred.}}{\mathbf{u}})\) (resp., \({{\mathcal {I}}}_{{\mathcal {P}}}(U^+{\mathrm{irred.}}{\mathbf{d}})\)) is the subset of those representations in \({{\mathcal {I}}}_{{\mathcal {P}}}(\mathbf{u})\) (resp., \({{\mathcal {I}}}_{{\mathcal {P}}}(\mathbf{d})\)) such that \(U\mid _{{{\mathcal {P}}}_+^\uparrow }\) is irreducible, while \({{\mathcal {I}}}_{{\mathcal {P}}}(U^+{\mathrm{irred.}}{\mathbf{s}})\) is the subset of those representations in \({{\mathcal {I}}}_{{\mathcal {P}}}(\mathbf{s})\) such that \(U^+\) is irreducible.
Analogously, class \({{\mathcal {I}}}_{{\mathcal {P}}}(U^\pm \mathrm{red.})\) can be brokendown into three non-overlapping subclasses:
with obvious meaning of the notation.
The next subsections provide a complete specification of the three subclasses of \({{\mathcal {I}}}_{{\mathcal {P}}}(U^\pm \mathrm{irred.})\) and show that the subclasses of \({{\mathcal {I}}}_{{\mathcal {P}}}(U^\pm \mathrm{red.})\) are not empty.
4.1 Subclass \({{\mathcal {I}}}_{{\mathcal {P}}}(U^+\mathrm{irred.}{} \mathbf{u})\)
The representations in this subclass, as well as those in \({{\mathcal {I}}}_{{\mathcal {P}}}(U^-\mathrm{irred.}{} \mathbf{d})\), are well known [14]; each representation is characterized by a unique pair \((\mu ,s)\), where \(\mu \in \mathbb {R}_+\) is called mass parameter and \(s\in \frac{1}{2}\mathbb {N}\) is called spin. Fixed any pair \(\mu >0\) and \(s\in \frac{1}{2}\mathbb {N}\), modulo unitary isomorphism there is only one representation U characterized by \((\mu ,s)\); its Hilbert space is the space \(L_2(\mathbb {R}^3,\mathbb {C}^{2s+1},d\nu )\) of the functions \(\psi :\mathbb {R}^3\rightarrow \mathbb {C}^{2s+1}\), \({\mathbf{p}}\rightarrow \psi ({\mathbf{p}})\) square integrable with respect to the measure \(d\nu ({\mathbf{p}})=\frac{dp_1dp_2dp_3}{\sqrt{\mu ^2+{\mathbf{p}}^2}}\), in the sense that \(\int _{\mathbb {R}^3}\Vert \psi ({\mathbf{p}})\Vert _{_{\mathbb {C}^{2s+1}}}^2d\nu ({\mathbf{p}})<\infty \). The self-adjoint generators are identified by the following statements.
-
generators \(P_j\) are the multiplication operators defined by \((P_j\psi )({\mathbf{p}})=p_j\psi ({\mathbf{p}})\),
-
generator \(P_0\) is given by \((P_0\psi )({\mathbf{p}})=p_0\psi ({\mathbf{p}})\) where \(p_0=+\sqrt{\mu ^2+{\mathbf{p}}^2}\),
-
generators \(J_j\) are given by \(J_j=i\left( p_k\frac{\partial }{\partial p_l}-p_l\frac{\partial }{\partial p_k}\right) +S_k\), where (j, k, l) is any cyclic permutation of (1, 2, 3), and \(S_1,S_2,S_3\) are the self-adjoint generators of an irreducible projective representation \(L:SO(3)\rightarrow \mathbb {C}^{2s+1}\) such that \(S_1^2+S_2^2+S_3^2=s(s+1)\mathbb {1}\); hence, they can be fixed as the three spin operators of \(\mathbb {C}^{2s+1}\),
-
generators \(K_j\) are given by \(K_j=ip_0\frac{\partial }{\partial p_j}-\frac{(\mathbf{S}\wedge {\mathbf{p}})_j}{\mu +p_0}\).
The unitary space inversion operator and the anti-unitary time reversal operator are

-
\(\Upsilon \) is the unitary operator defined by \((\Upsilon \psi )({\mathbf{p}})=\psi (-{\mathbf{p}})\),
-
\(\tau \) is a unitary matrix of \(\mathbb {C}^{2s+1}\) such that \(\tau {{\overline{S}}_j}\tau ^{-1}= -{S_j}\), for all j; such a matrix always exists and it is unique up a complex factor of modulus 1; moreover, if \(s\in \mathbb {N}\) then \(\tau \) is symmetric and \(\tau {\overline{\tau }}=1\), while if \(s\in \left( \mathbb {N}+\frac{1}{2}\right) \) then \(\tau \) is anti-symmetric and \(\tau {\overline{\tau }}=-1\) [19];
-
\({\mathcal {K}}\) is the anti-unitary complex conjugation operator defined by \({{\mathcal {K}}}\psi ({\mathbf{p}})=\overline{\psi ({\mathbf{p}})}\).
These operators determine the projective representation.
The spectrum \(\sigma ({\underline{P}})\) of the four-operator \({\underline{P}}=(P_0,P_1,P_2,P_3)\) is the positive hyperboloid
4.2 Subclass \({{\mathcal {I}}}_{{\mathcal {P}}}(U^-\mathrm{irred.}{} \mathbf{d})\)
Each representation U in this subclass is characterized by a unique pair \((\mu ,s)\), where \(\mu >0\) and \(s\in \frac{1}{2}\mathbb {N}\). For every pair \(\mu >0\) and \(s\in \frac{1}{2}\mathbb {N}\), modulo unitary isomorphism there is only one representation U characterized by \((\mu , s)\); it differs from the representation of \({{\mathcal {I}}}_{{\mathcal {P}}}(U^+\mathrm{irred.}{} \mathbf{u})\) characterized by the same pair only for generators \(P_0\) and \(\mathbf{K}\), that are given by \((P_0\psi )({\mathbf{p}})=-p_0\psi ({\mathbf{p}})\) and \(K_j=-ip_0\frac{\partial }{\partial p_j}+\frac{(\mathbf{S}\wedge {\mathbf{p}})_j}{\mu +p_0}\).
The spectrum of \({\underline{P}}\) is the negative hyperboloid
4.3 Subclass \({{\mathcal {I}}}_{{\mathcal {P}}}(U^\pm {\mathrm{irred.}}{\mathbf{s}})\)
Each representation \(U\in {{\mathcal {I}}}_{{\mathcal {P}}}(U^\pm {\mathrm{irred.}}{\mathbf{s}})\) is characterized by a unique pair \((\mu ,s)\), \(\mu >0\), \(s\in \frac{1}{2}\mathbb {N}\). For every pair \(\mu >0\) and \(s\in \frac{1}{2}\mathbb {N}\) there are six inequivalent irreducible generalized projective representations \(U^{(l)}\), \(l=1,2,\dots ,6\) of \({\mathcal {P}}\); modulo unitary isomorphisms, the Hilbert space of each \(U^{(l)}\) is \(L_2(\mathbb {R}^3,\mathbb {C}^{2s+1},d\nu )\oplus L_2(\mathbb {R}^3,\mathbb {C}^{2s+1},d\nu )\). If each vector \(\psi \in {{\mathcal {H}}}\) is represented as a column vector \(\psi =\left[ \begin{array}{c}\psi ^+\\ \psi ^-\end{array}\right] \), with \(\psi ^\pm \in L_2(\mathbb {R}^3,\mathbb {C}^{2s+1},d\nu )\), then \(E^+=\left[ \begin{array}{cc}1&{}0\\ 0&{}0\end{array}\right] \), \(E^-=\left[ \begin{array}{cc}0&{}0\\ 0&{}1\end{array}\right] \), and the generators of \(U^{(l)}\mid _{{{\mathcal {P}}}_+^\uparrow }\) are represented in their canonical form
where \({\textsf {j}}_k=i\left( p_l\frac{\partial }{\partial p_j}-p_j\frac{\partial }{\partial p_l}\right) +S_k\) and \({\textsf {k}}_j=ip_0\frac{\partial }{\partial p_j}-\frac{(\mathbf{S}\wedge {{\mathbf{p}}})_j}{\mu +p_0}\). (The matrix entries “1” and “0” denote the identity and null operators of \(\mathbb {C}^{2s+1}\). This notation is adopted throughout the paper.)
The six representations \(U^{(l)}\), \(l=1,2,\dots ,6\) differ just for the different pairs of time reversal and space inversion operators, according to the following list.
-
\(U^{(1)}\) has unitary
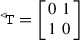 and unitary
and unitary  ;
; -
\(U^{(2)}\) has unitary
 and unitary
and unitary  ;
; -
\(U^{(3)}\) has unitary
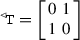 and anti-unitary
and anti-unitary  ;
; -
\(U^{(4)}\) has unitary
 and anti-unitary
and anti-unitary  ;
; -
\(U^{(5)}\) has anti-unitary
 and anti-unitary
and anti-unitary ;
; -
\(U^{(6)}\) has anti-unitary
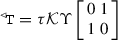 and anti-unitary
and anti-unitary .
.
The combination  unitary and
unitary and  anti-unitary is not in this subclass [36].
anti-unitary is not in this subclass [36].
The spectrum of \({\underline{P}}\) is the set theoretic union of the positive and negative hyperboloids: \(\sigma ({\underline{P}})=S_\mu ^+\cup S_\mu ^-\).
Representations \(U^{(1)},U^{(2)}\) are adopted in the literature as bases of particle theories. Instead, \(U^{(3)},U^{(4)},U^{(5)},U^{(6)}\) have never been considered, to the best of our knowledge.
4.4 The Class \({{\mathcal {I}}}_{{\mathcal {P}}}(U^\pm \mathrm{red.})\)
Once fixed \(\mu \) and s, Sects. 4.1–4.3 show that there are eight inequivalent irreducible generalized projective representations of \({\mathcal {P}}\) with \(U^+\) or \(U^-\) irreducible. The class of all such octets does not exhaust class \({{\mathcal {I}}}_{{\mathcal {P}}}\), because the class \({{\mathcal {I}}}_{{\mathcal {P}}}(U^\pm {\mathrm{red.}})\) is not empty. These representations, which have never been considered for particle theories, will give rise to new species of particle theories.
4.4.1 Subclasses \({{\mathcal {I}}}_{{\mathcal {P}}}(U^+{\mathrm{red.}}{} \mathbf{u})\), \({{\mathcal {I}}}_{{\mathcal {P}}}(U^-{\mathrm{red.}}{\mathbf{d}})\).
Fixed any pair \(\mu >0\), \(s\in \frac{1}{2}\mathbb {N}\), let us consider the Hilbert space \({{\mathcal {H}}}= L_2(\mathbb {R}^3,\mathbb {C}^{2s+1},d\nu ) \oplus L_2(\mathbb {R}^3,\mathbb {C}^{2s+1},d\nu )\); let every vector \(\psi =\psi _1+\psi _2\) in \({\mathcal {H}}\), with \(\psi _1,\psi _2\in L_2(\mathbb {R}^3,\mathbb {C}^{2s+1},d\nu )\) be represented as the column vector \(\psi \equiv \left[ \begin{array}{c}\psi _1\\ \psi _2\end{array}\right] \), so that every linear (resp., anti-linear) operator A of \({\mathcal {H}}\) can be represented by a matrix \(\left[ \begin{array}{cc}A_{11}&{} A_{12} \\ A_{21} &{} A_{22}\end{array}\right] \), where \(A_{mn}\) is a linear (resp., anti-linear) operator of \(L_2(\mathbb {R}^3,\mathbb {C}^{2s+1},d\nu )\), and
\(A\psi =\left[ \begin{array}{cc}A_{11} &{} A_{12} \\ A_{21} &{} A_{22}\end{array}\right] \left[ \begin{array}{c}\psi _1\\ \psi _2\end{array}\right] = \left[ \begin{array}{c} A_{11}\psi _1+A_{12}\psi _2 \\ A_{21}\psi _1+A_{22}\psi _2\end{array}\right] \). Let us define
where \({\textsf {j}}_k=i\left( p_l\frac{\partial }{\partial p_j}-p_j\frac{\partial }{\partial p_l}\right) +S_k\) and \({{\textsf {k}}}_j=ip_0\frac{\partial }{\partial p_j}-\frac{(\mathbf{S}\wedge {\mathbf{p}})_j}{\mu +p_0}\). Thus, a reducible projective representation \(U:{{\mathcal {P}}}_+^\uparrow \rightarrow L_2(\mathbb {R}^3,\mathbb {C}^{2s+1},d\nu )\oplus L_2(\mathbb {R}^3,\mathbb {C}^{2s+1},d\nu )\) satisfying (1) is determined. The operators

satisfy all conditions (2)–(6). By defining  and
and  , therefore, the projective representation U of \({{\mathcal {P}}}_+^\uparrow \) is extended to a generalized projective representation of \({\mathcal {P}}\). Moreover, if \(A=\left[ \begin{array}{cc}A_{11}&{} A_{12} \\ A_{21} &{} A_{22}\end{array}\right] \) is any self-adjoint operator of \({{\mathcal {H}}}=L_2(\mathbb {R}^3,\mathbb {C}^{2s+1},d\nu )\oplus L_2(\mathbb {R}^3,\mathbb {C}^{2s+1},d\nu )\), then the conditions
, therefore, the projective representation U of \({{\mathcal {P}}}_+^\uparrow \) is extended to a generalized projective representation of \({\mathcal {P}}\). Moreover, if \(A=\left[ \begin{array}{cc}A_{11}&{} A_{12} \\ A_{21} &{} A_{22}\end{array}\right] \) is any self-adjoint operator of \({{\mathcal {H}}}=L_2(\mathbb {R}^3,\mathbb {C}^{2s+1},d\nu )\oplus L_2(\mathbb {R}^3,\mathbb {C}^{2s+1},d\nu )\), then the conditions  imply \(A=\left[ \begin{array}{cc}a&{} 0 \\ 0 &{} a\end{array}\right] \equiv a\mathbb {1}\), and therefore the generalized projective representation U is irreducible.
imply \(A=\left[ \begin{array}{cc}a&{} 0 \\ 0 &{} a\end{array}\right] \equiv a\mathbb {1}\), and therefore the generalized projective representation U is irreducible.
The identification of a concrete irreducible representation of \({{\mathcal {I}}}_{{\mathcal {P}}}(U^-\mathrm{red.}\mathbf{d})\) is analogous.
4.4.2 Subclass \({{\mathcal {I}}}_{{\mathcal {P}}}(U^\pm \mathrm{red.}{} \mathbf{s})\).
Once again for these representations the combination  unitary and
unitary and  anti-unitary is forbidden [36]. We now give an irreducible representation U of \({\mathcal {P}}\) with \(\sigma ({\underline{P}})=S_\mu ^+\cup S_\mu ^-\), \(s=0\), and \(U^+\) reducible, where
anti-unitary is forbidden [36]. We now give an irreducible representation U of \({\mathcal {P}}\) with \(\sigma ({\underline{P}})=S_\mu ^+\cup S_\mu ^-\), \(s=0\), and \(U^+\) reducible, where  is unitary and
is unitary and  is anti-unitary.
is anti-unitary.
\({{\mathcal {H}}}=L_2(\mathbb {R}^3,d\nu )\oplus L_2(\mathbb {R}^3,d\nu )\oplus L_2(\mathbb {R}^3,d\nu )\oplus L_2(\mathbb {R}^3,d\nu )\) is the Hilbert space of the representation. Every vector \(\psi \in {{\mathcal {H}}}\) is represented as a column vector \(\psi =\left[ \begin{array}{c}\psi ^{(1)}_+\\ \psi ^{(1)}_-\\ \psi ^{(2)}_+\\ \psi ^{(2)}_-\end{array}\right] \), with \(\psi ^{(m)}_\pm \in L_2(\mathbb {R}^3,d\nu )\).
The projections \(E^+\), \(E^-\) and the self-adjoint generators relative to \({{\mathcal {P}}}_+^\uparrow \) satisfying (1) are
So, we have a reducible projective representation of \({{\mathcal {P}}}_+^\uparrow \). Now we extend it to an irreducible generalized representation of \({\mathcal {P}}\) by introducing a unitary  and an anti-unitary
and an anti-unitary  satisfying (2)-(6), as
satisfying (2)-(6), as  and
and  .
.
Indeed, let \(A=\left[ \begin{array}{cccc}A_{11}&{}A_{12}&{}A_{13}&{}A_{14}\\ A_{21}&{}A_{22}&{}A_{23}&{}A_{24}\\ A_{31}&{}A_{32}&{}A_{33}&{}A_{34}\\ A_{41}&{}A_{42}&{}A_{43}&{}A_{44} \end{array}\right] \) be any self-adjoint operator of \({\mathcal {H}}\); the conditions  are satisfied if and only if \(A=\left[ \begin{array}{cccc}a&{}0&{}0&{}0\\ 0&{}a&{}0&{}0\\ 0&{}0&{}a&{}0\\ 0&{}0&{}0&{}a \end{array}\right] \equiv a\mathbb {1}\) with \(a\in \mathbb {R}\). Thus the extended representation is irreducible.
are satisfied if and only if \(A=\left[ \begin{array}{cccc}a&{}0&{}0&{}0\\ 0&{}a&{}0&{}0\\ 0&{}0&{}a&{}0\\ 0&{}0&{}0&{}a \end{array}\right] \equiv a\mathbb {1}\) with \(a\in \mathbb {R}\). Thus the extended representation is irreducible.
5 Identifying Quantum Theories of an Elementary Free Particle
In line with our program, we now identify the quantum theories of an elementary free particle, by selecting those irreducible representations of \({\mathcal {P}}\) for which a triple \({{{\mathbf{Q}}}}\) exists such that (Q.1) and (Q.2) in Sect. 3 hold, in the more general domain of representations identified in Sect. 4. A representation can be excluded only if it is inconsistent with (Q.1) and (Q.2). Each theory so identified corresponds to a possible kind of particle; theories that are unitarily inequivalent correspond to a different kind of particle.
We will show that if the spin parameter s is zero, then there are precisely identified cases in which conditions (Q.1) and (Q.2.a,b) turn out to be sufficient to determine the position operator; this means that in these cases the lack of an explicit formulation, analogous to(Q.2.b), of the transformation properties with respect to boosts is not an insuperable barrier; in fact, the knowledge of the transformation properties missed by (Q.2a,b) is easily attained a posteriori as \(S_g[{{\mathbf{Q}}}]=e^{iK_j\varphi (u)}{{\mathbf{Q}}}e^{-iK_j\varphi (u)}\), since \({\mathbf{Q}}\) has been explicitly identified. For the irreducible generalized projective representations in \({{\mathcal {I}}}_{{\mathcal {P}}}(U^+\mathrm{irred.}{} \mathbf{u})\) and \({{\mathcal {I}}}_{{\mathcal {P}}}(U^-\mathrm{irred.}{} \mathbf{d})\) our results agree with those in the literature. For representations in \({{\mathcal {I}}}_{{\mathcal {P}}}(U^\pm \mathrm{irred.}{} \mathbf{s})\) the irreducible generalized projective representations for which the position operator is determined belong to the new class with anti-unitary  (Sects. 5.2, 5.3). In Sect. 5.4 we show that consistent particle theories can be based on representations in \({{\mathcal {I}}}_{{\mathcal {P}}}(U^-\mathrm{red.}{} \mathbf{u})\) or \({{\mathcal {I}}}_{{\mathcal {P}}}(U^-\mathrm{red.}{} \mathbf{d})\), though previously unconsidered.
(Sects. 5.2, 5.3). In Sect. 5.4 we show that consistent particle theories can be based on representations in \({{\mathcal {I}}}_{{\mathcal {P}}}(U^-\mathrm{red.}{} \mathbf{u})\) or \({{\mathcal {I}}}_{{\mathcal {P}}}(U^-\mathrm{red.}{} \mathbf{d})\), though previously unconsidered.
In the case \(s>0\) there are no free particle theories univocally determined by (Q.1), (Q.2.a) and (Q.2.b). In Sect. 6 we shall investigate these theories in relation with the work of Jordan and Mukunda who assumed a particular form of the lacking transformation property.
5.1 Elementary Particle Theories Based on \({{\mathcal {I}}}_{{\mathcal {P}}}(U^+{\mathrm{irred.}}{\mathbf{u}})\) or \({{\mathcal {I}}}_{{\mathcal {P}}}(U^-{\mathrm{irred.}}{\mathbf{d}})\)
In the Hilbert space \(L_2(\mathbb {R}^3,\mathbb {C}^{2s+1},d\nu )\) of an irreducible representation in \({{\mathcal {I}}}_{{\mathcal {P}}}(U^+{\mathrm{irred.}}{\mathbf{u}})\) with spin s, let us define the self-adjoint operators \(F_j=i\frac{\partial }{\partial p_j}-\frac{i}{2p_0^2}p_j\), known as Newton and Wigner operators [37]. From \([F_j,P_k]=i\delta _{jk}\) and (9i) we derive \(Q_j-F_j=d_j({\mathbf{P}})\), i.e. \(\left( (Q_j-F_j)\psi \right) ({\mathbf{p}})=d_j({\mathbf{p}})\psi ({\mathbf{p}})\), where \(d_j({\mathbf{p}})\in \Omega (\mathbb {C}^{2s+1})\) for all \({\mathbf{p}}\in \mathbb {R}^3\). On the other hand, \([J_j,F_k]=i{{\hat{\epsilon }}}_{jkl}F_l\) and (9ii) imply
In case \(s=0\), we have \(S_k=0\), \(\Omega (\mathbb {C}^{2s+1})=\Omega (\mathbb {C})\equiv \mathbb {R}\), and \(\tau =1\). Then (14) together with \([J_j,P_k]=i{{\hat{\epsilon }}}_{jkl}P_l\) implies \(d_j({\mathbf{P}})=h(\Vert {\mathbf{p}}\Vert )p_j\); by redefining \(h(\Vert {\mathbf{p}}\Vert )=f(p_0)\), with \(p_0=\sqrt{\mu ^2+{\mathbf{p}}^2}\), we have
Now,  holds and (Q.2.a) implies
holds and (Q.2.a) implies  , so that we obtain
, so that we obtain  ; from this equality, since
; from this equality, since  , by (20) we derive
, by (20) we derive
Since \(f(p_0)\in \mathbb {R}\), (21) implies \(f(p_0)=0\). Therefore, \({{\mathbf{Q}}}=\mathbf{F}\). The condition  , i.e.
, i.e.  , turns out to be automatically satisfied.
, turns out to be automatically satisfied.
Thus, if \(s=0\), there is a unique position operator \({\mathbf{Q}}=\mathbf{F}\) completely determined by (Q.1) and (Q.2.a),(Q.2.b). This result agrees with that of the well known derivations of the Newton and Wigner position operators [37, 38].
By means of a similar derivation, the same result \({{\mathbf{Q}}}=\mathbf{F}\) is obtained for representations in \({{\mathcal {I}}}_{{\mathcal {P}}}(U^-\mathrm{irred.}{} \mathbf{d})\)
5.2 Elementary Particle Theories Based on \({{\mathcal {I}}}_{{\mathcal {P}}}(U^\pm \mathrm{irred.}{} \mathbf{s})\)
The irreducible generalized projective representations in \({{\mathcal {I}}}_{{\mathcal {P}}}(U^\pm \mathrm{irred.}{} \mathbf{s})\) are explicitly identified in Sect. 4.3. To identify the triple \({\mathbf{Q}}\) representing the three coordinates of position we introduce the difference \(\mathbf{D}={{\mathbf{Q}}}-{\hat{\mathbf{F}}}\), where \({\hat{\mathbf{F}}}=\mathbf{F}\mathbb {1}\equiv \left[ \begin{array}{cc}\mathbf{F}&{}0\\ 0&{}\mathbf{F}\end{array}\right] \) is the Newton-Wigner operator in this representation.
Now, \([{\hat{F}}_j,P_k]=i\delta _{jk}\) and \([J_j,{\hat{F}}_k]=i\epsilon _{jkl}{\hat{F}}_k\) hold; on the other hand \([Q_j,P_k]=i\delta _{jk}\) and \([J_j,Q_k]=i\epsilon _{jkl}Q_k\) are conditions to be satisfied by \({\mathbf{Q}}\) according to (9); therefore, the relations \([D_j,P_k]=\mathbb {O}\) and \([J_j,D_k]=i\epsilon _{jkl}D_k\) must hold too. Thus we have
where each \(d^{(j)}_{mn}({\mathbf{p}})\) is \((2s+1)\times (2s+1)\) matrix such that \(\overline{{d^{(j)}_{mn}}({\mathbf{p}})}^t=d^{(j)}_{nm}({\mathbf{p}})\), the apex \(^t\) denoting matrix transposition.
For \(s=0\), similarly to Sects. 5.1, (18) and \([{\textsf {j}}_j,p_k]=i{\hat{\epsilon }}_{jkl}p_l\) imply \(d^{(j)}_{mn}({\mathbf{p}})=d_{mn}(p_0)p_j\), with \(d_{mn}(p_0)\in \mathbb {C}\). Hence
So, in order to identify \({\mathbf{Q}}\) we have to determine the functions \(d_{mn}\) of \(p_0\). The conditions  and
and  can help in solving the indeterminacy; however, according to Sect. 4.2, now the explicit form of
can help in solving the indeterminacy; however, according to Sect. 4.2, now the explicit form of  and
and  depends on their unitary or anti-unitary character; so we shall explore all possible combinations.
depends on their unitary or anti-unitary character; so we shall explore all possible combinations.
(UU) Let us begin with the case where both  and
and  are unitary, i.e. with \(U^{(1)}\) and \(U^{(2)}\), the only cases considered in the literature. We have
are unitary, i.e. with \(U^{(1)}\) and \(U^{(2)}\), the only cases considered in the literature. We have  , while
, while  in \(U^{(1)}\) and
in \(U^{(1)}\) and  in \(U^{(2)}\). By making use of the explicit form of
in \(U^{(2)}\). By making use of the explicit form of  we find that
we find that

(i) If  , then
, then  is satisfied whatsoever functions \(d_1(p_0)\), \(d_2(p_0)\) are used. Hence \({\mathbf{Q}}\) remains undetermined.
is satisfied whatsoever functions \(d_1(p_0)\), \(d_2(p_0)\) are used. Hence \({\mathbf{Q}}\) remains undetermined.
(ii) If  then
then  holds whenever \(d_2(p_0)=0\).
holds whenever \(d_2(p_0)=0\).
In the combination ( UU ) therefore, the position operator \({\mathbf{Q}}\) is still undetermined.
(UA) If  is unitary and
is unitary and  is anti-unitary, i.e. in cases \(U^{(3)},U^{(4)}\), we have
is anti-unitary, i.e. in cases \(U^{(3)},U^{(4)}\), we have  so that
so that  holds, while
holds, while  in \(U^{(3)}\) and
in \(U^{(3)}\) and  in \(U^{(4)}\).
in \(U^{(4)}\).
(i) If  , i.e. in \(U^{(4)}\), then
, i.e. in \(U^{(4)}\), then  is satisfied for \(d_1(p_0)=0\) and arbitrary \(d_2(p_0)\).
is satisfied for \(d_1(p_0)=0\) and arbitrary \(d_2(p_0)\).
Therefore \({\mathbf{Q}}\) is still undetermined.
(ii) In \(U^{(3)}\) we have  , so that
, so that  implies \(d_1(p_0)=d_2(p_0)=0\).
implies \(d_1(p_0)=d_2(p_0)=0\).
Therefore \({\mathbf{Q}}\) is uniquely determined, and \({{\mathbf{Q}}}={\hat{\mathbf{F}}}\).
(AA) In \(U^{(5)}\) and \(U^{(6)}\), being  anti-unitary,
anti-unitary,  must be anti-unitary too. We have
must be anti-unitary too. We have  , while
, while  in \(U^{(5)}\) and
in \(U^{(5)}\) and  in \(U^{(6)}\). With this explicit form of
in \(U^{(6)}\). With this explicit form of  we find that
we find that

(i) In \(U^{(6)}\), where  , it follows that
, it follows that  is always satisfied.
is always satisfied.
Therefore \({\mathbf{Q}}\) is still undetermined.
(ii) In \(U^{(5)}\), where  , we have that
, we have that  implies \(d(p_0)=0\), i.e. \(D_j=0\).
implies \(d(p_0)=0\), i.e. \(D_j=0\).
Therefore \({\mathbf{Q}}\) is uniquely determined and \({{\mathbf{Q}}}={\hat{\mathbf{F}}}\).
Thus, conditions (Q.1) and (Q.2.a), (Q.2.b) determine \({\mathbf{Q}}\) only in the cases (UA.ii) and (AA.ii), where  is anti-unitary. This anti-unitarity, however, is perfectly consistent within the respective theories.
is anti-unitary. This anti-unitarity, however, is perfectly consistent within the respective theories.
5.3 Klein–Gordon Particles
For every value of the mass parameter \(\mu >0\), four inequivalent single particle theories have been singled out in Sects. 5.1 and 5.2, according to methodological commitments that avoid the shortcomings of canonical quantization. In each of these the position operator is uniquely determined as the Newton-Wigner operator.
To complete the theories, the explicit form of the wave equations is needed. In all theories of the present approach time evolution from time 0 to time t is a translation of time, operated by the unitary operator
\(e^{iP_0t}\); therefore if the state vector is \(\psi \) at time 0, then it is \(\psi _t=e^{-iP_0t}\psi \) at time t, so that Schroedinger equation

immediately follows. The explicit wave equation is attained by replacing \(P_0\) with the the specific time translation operator, rendered explicit in each specific theory.
In order to explore how previous theories for spin 0 particles relate to the present ones, we re-formulate the latter in the following equivalent forms, obtained by means of unitary transformations operated by the unitary operator \(Z=Z_1Z_2\), where \(Z_2=\frac{1}{\sqrt{p_0}}\mathbb {1}\) and \(Z_1\) is the inverse of the Fourier-Plancherel operator.
- \({\mathcal {T}}\).1:
-
The theory in Sect. 5.1, based on an irreducible representation in \({{\mathcal {I}}}_{{\mathcal {P}}}(U^+\mathrm{irred.}{} \mathbf{u})\) with \(s=0\), can be reformulated in Hilbert space \({{\mathcal {H}}}=Z\left( L_2(\mathbb {R}^3,d\nu )\right) \equiv L_2(\mathbb {R}^3)\). Generators \(P_j\) are transformed into \({{\hat{P}}}_j=ZP_jZ^{-1}=-i\frac{\partial }{\partial x_j}\); analogously we find \({{\hat{P}}}_0=\sqrt{\mu ^2+{\nabla }^2}\), \({{\hat{J}}}_j=-i\left( x_k\frac{\partial }{\partial x_l}-x_l\frac{\partial }{\partial x_k}\right) \), \({{\hat{K}}}_j=\frac{1}{2}(x_j\sqrt{\mu ^2+{\nabla }^2}+\sqrt{\mu ^2+{\nabla }^2}x_j)\), while
 . In this representation the Newton-Wigner operators representing position become the multiplication operators \({{\hat{Q}}}_j\), defined by \({{\hat{Q}}}_j\psi (\mathbf{x})=x_j\psi (\mathbf{x})\). Accordingly, the wave equation is $$\begin{aligned} i\frac{\partial }{\partial t}\psi _t(\mathbf{x})=\sqrt{\mu ^2-\nabla ^2}\psi _t(\mathbf{x})\,. \end{aligned}$$(23)
. In this representation the Newton-Wigner operators representing position become the multiplication operators \({{\hat{Q}}}_j\), defined by \({{\hat{Q}}}_j\psi (\mathbf{x})=x_j\psi (\mathbf{x})\). Accordingly, the wave equation is $$\begin{aligned} i\frac{\partial }{\partial t}\psi _t(\mathbf{x})=\sqrt{\mu ^2-\nabla ^2}\psi _t(\mathbf{x})\,. \end{aligned}$$(23) - \({\mathcal {T}}\).2:
-
The new formulation of the theory based on an irreducible representation in \({{\mathcal {I}}}_{{\mathcal {P}}}(U^-\mathrm{irred.}{} \mathbf{d})\) with \(s=0\), as shown in Sect. 5.1, differs from \({\mathcal {T}}\).1 just for \({{\hat{P}}}_0=-\sqrt{\mu ^2+{\nabla }^2}\) and \({{\hat{K}}}_j=-\frac{1}{2}(x_j\sqrt{\mu ^2+{\nabla }^2}+\sqrt{\mu ^2+{\nabla }^2}x_j)\); hence, in the equivalent theory the wave equation is
$$\begin{aligned} i\frac{\partial }{\partial t}\psi _t(\mathbf{x})=-\sqrt{\mu ^2-\nabla ^2}\psi _t(\mathbf{x}). \end{aligned}$$(24) - \({\mathcal {T}}\).3:
-
The theory corresponding to (UA.ii) in Sect. 5.2, that is based on the irreducible representation \(U^{(3)}\) of Sect. 4.3 with \(\sigma ({\underline{P}})=S_\mu ^+\cup S_\mu ^-\) and \(s=0\), identified by
 and
and 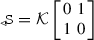 , can be reformulated in Hilbert space \({{\mathcal {H}}}=Z\left( L_2(\mathbb {R}^3,d\nu )\oplus L_2(\mathbb {R}^3,d\nu )\right) \equiv L_2(\mathbb {R}^3)\oplus L_2(\mathbb {R}^3)\); the new self-adjoint generators are \({{\hat{P}}}_j=\left[ \begin{array}{cc}-i\frac{\partial }{\partial x_j}&{}0\\ 0&{}-i\frac{\partial }{\partial x_j}\end{array}\right] \), \({{\hat{P}}}_0=\sqrt{\mu ^2-\nabla ^2}\left[ \begin{array}{cc}1&{}0\\ 0&{}-1\end{array}\right] \), \({{\hat{J}}}_j=-i\left( x_k\frac{\partial }{\partial x_l}-x_l\frac{\partial }{\partial x_k}\right) \left[ \begin{array}{cc}1&{}0\\ 0&{} 1\end{array}\right] \), \({{\hat{K}}}_j=\frac{1}{2}\left( x_j\sqrt{\mu ^2-\nabla ^2}+\sqrt{\mu ^2-\nabla ^2}x_j\right) \left[ \begin{array}{cc}1&{}0\\ 0&{}-1\end{array}\right] \), while
, can be reformulated in Hilbert space \({{\mathcal {H}}}=Z\left( L_2(\mathbb {R}^3,d\nu )\oplus L_2(\mathbb {R}^3,d\nu )\right) \equiv L_2(\mathbb {R}^3)\oplus L_2(\mathbb {R}^3)\); the new self-adjoint generators are \({{\hat{P}}}_j=\left[ \begin{array}{cc}-i\frac{\partial }{\partial x_j}&{}0\\ 0&{}-i\frac{\partial }{\partial x_j}\end{array}\right] \), \({{\hat{P}}}_0=\sqrt{\mu ^2-\nabla ^2}\left[ \begin{array}{cc}1&{}0\\ 0&{}-1\end{array}\right] \), \({{\hat{J}}}_j=-i\left( x_k\frac{\partial }{\partial x_l}-x_l\frac{\partial }{\partial x_k}\right) \left[ \begin{array}{cc}1&{}0\\ 0&{} 1\end{array}\right] \), \({{\hat{K}}}_j=\frac{1}{2}\left( x_j\sqrt{\mu ^2-\nabla ^2}+\sqrt{\mu ^2-\nabla ^2}x_j\right) \left[ \begin{array}{cc}1&{}0\\ 0&{}-1\end{array}\right] \), while  and
and  .
.The position operator is \({{\hat{Q}}}_j=\left[ \begin{array}{cc}x_j&{}0\\ 0&{}x_j\end{array}\right] \).
The wave equation is
$$\begin{aligned} i\frac{\partial }{\partial t}\left[ \begin{array}{c}\psi ^+_t(\mathbf{x})\\ \psi ^-_t(\mathbf{x})\end{array}\right] =\left[ \begin{array}{c}\sqrt{\mu ^2-\nabla ^2}\psi ^+_t(\mathbf{x})\\ -\sqrt{\mu ^2-\nabla ^2}\psi ^-_t(\mathbf{x})\end{array}\right] \,. \end{aligned}$$(25) - \({\mathcal {T}}\).4:
-
The theory corresponding to (AA.ii) in Sect. 5.2, based on the irreducible representation \(U^{(5)}\) with \(\sigma ({\underline{P}})=S_\mu ^+\cup S_\mu ^-\) and \(s=0\), identified by
 and
and 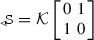 , differs from \({\mathcal {T}}\).3 only for
, differs from \({\mathcal {T}}\).3 only for  , that is now
, that is now  .
.
The early theory [1,2,3] for spin 0 particle establishes that the wave equation is the Klein–Gordon equation
that is second order with respect to time. This is the first evident difference vis-à-vis theories \({\mathcal {T}}\).1–\({\mathcal {T}}\).4, where all wave equations are first order. However, if in each theory \({\mathcal {T}}\).1–\({\mathcal {T}}\).4 the respective wave equation is solved by \(\psi _t\), then the derivative of the equation with respect to time yields \(-\frac{\partial ^2}{\partial t^2}\psi _t=iP_0\frac{\partial }{\partial t}\psi _t=P_0^2\psi _t\), since \(\frac{\partial }{\partial t}\) commutes with \(P_0\) in all cases, obtaining
Hence, Eq. (27) holds in all the theories \({\mathcal {T}}\).1–\({\mathcal {T}}\).4, which coincides with the Klein–Gordon equation, once parameter \(\mu \) with m is identified. This coincidence does not mean that the theories \({\mathcal {T}}\).1–\({\mathcal {T}}\).4 are equivalent to Klein–Gordon’s. The first difference is that in our approach there are four inequivalent theories for spin 0 and “mass” \(\mu \) particles. In \({\mathcal {T}}\).1 there are no wave functions corresponding to negative spectral values of \(P_0\). In \({\mathcal {T}}\).2 positive values are not permitted. Klein–Gordon’s theory does not have this differentiation; in particular, the space of the vector states is only one, namely the space generated by the solutions of (27).
Another obvious non-equivalence is the difference between the set of solutions of the respective wave equations: while all solutions of the wave equations of \({\mathcal {T}}\).1–\({\mathcal {T}}\).4 are solutions of Klein–Gordon’s equation, the converse is not true.
The third important difference concerns the physical interpretation and its consistency. By means of mathematical manipulation it can be deduced that for every solution \(\psi _t\) of the Klein–Gordon equation (26) the following equation holds.
since it has the form of a continuity equation for a quantity whose density is \({\hat{\rho }}(t,\mathbf{x})=\frac{i}{2m}\left( \overline{\psi _t}\frac{\partial }{\partial t}\psi _t-{\psi _t} \frac{\partial }{\partial t}\overline{\psi _t}\right) \) and whose current density is \(\hat{\mathbf{j}}(t,{\mathbf{x}})=\frac{i}{2m}\left( \psi _t\nabla \overline{\psi _t}-\overline{\psi _t}\nabla \psi _t\right) \), in the Klein–Gordon theory \({\hat{\rho }}\) was interpreted as the density probability of position, and \(\hat{\mathbf{j}}\) as the current density of the position probability. This interpretation is the source of serious problems for the Klein–Gordon theory. Dirac argued, indeed, that the presence of the time derivative of the wave function in \({\hat{\rho }}\) entails the possibility of negative values for this probability density [4, 7]. One way to overcome the difficulty was proposed by Feshbach and Villars [5]. They derive an equivalent form of the Klein–Gordon’s equation as a first order equation \(i\frac{\partial }{\partial t}\Psi _t=H\Psi _t\) for the state vector \(\Psi _t=\left[ \begin{array}{c}\phi _t\\ \chi _t\end{array}\right] \), where \(\phi _t=\frac{1}{\sqrt{2}}(\psi _t+\frac{1}{m}\frac{\partial }{\partial t}\psi _t)\), \(\chi _t=\frac{1}{\sqrt{2}}(\psi _t-\frac{1}{m}\frac{\partial }{\partial t}\psi _t)\), and \(H=(\sigma _3+\sigma _2)\frac{1}{2m}(\nabla +m\sigma _3)\); in this representation density takes the form \({\hat{\rho }}=\vert \phi _t\vert ^2-\vert \chi _t\vert ^2\), free from time derivatives of the new quantum state \(\Psi _t\). The proposal of Feshbach and Villars requires a drastic change in the interpretation of the Klein–Gordon equation: the quantum state is not \(\psi _t\), but \(\Psi _t\). However, the minus sign in \({\hat{\rho }}\) implies that the possibility of negative values is not solved. Feshbach and Villars intepreted \({\hat{\rho }}\) as density probability of charge. Nevertheless, acceptance of the Feshbach and Villars proposal requires another consistency test for \({\hat{\rho }}\), that is to say covariance with respect to boosts, which implies, according to Barut and Malin [6], that \({\hat{\rho }}\) must be the time component of a four-vector. Barut and Malin however proved that is not the case, so the proposal of Feshbach and Villars fails this consistency test.
In the theories \({\mathcal {T}}\).1–\({\mathcal {T}}\).4 position must be represented by the multiplication operator. The probability density of position therefore must necessarily be \(\rho (t,{\mathbf{x}})=\vert \psi _t(\mathbf{x})\vert ^2\) in \({\mathcal {T}}\).1, \({\mathcal {T}}\).2 and \(\rho (t,\mathbf{x})=\vert \psi _t^+(\mathbf{x})\vert ^2+\vert \psi _t^-(\mathbf{x})\vert ^2\) in \({\mathcal {T}}\).3, \({\mathcal {T}}\).4. Thus, the quantum state at a given time determines the non-negative probability density of position. There is no need of a posteriori reinterpretations. In the present approach the possibility of interpreting state vectors belonging to \(E^+{{\mathcal {H}}}\) (resp., state vectors in \(E^-{{\mathcal {H}}}\)) as positive charge states (resp., negative charge states) could eventually emerge in a future theory of an interacting particle derived from basic principles without using canonical quantization.
In \({\mathcal {T}}\).1–\({\mathcal {T}}\).4 the covariance properties with respect to boosts, \(K_j\) and \({\mathbf{Q}}\) being known explicitly , can be directly expressed by the relations \(S_g[{{\mathbf{Q}}}]=e^{iK_j\varphi (u)}{{\mathbf{Q}}}e^{-iK_j\varphi (u)}\) which are perfectly consistent with the whole theory.
With reference to the early difficulties of the relativistic quantum theory of a particle, Weinberg wrote [7, p. 3] “... it became generally clear that relativistic wave mechanics, in the sense of a relativistic quantum theory of a fixed number of particles, is an impossibility. Thus, despite its many successes, relativistic wave mechanics was ultimately to give way to quantum field theory”. The work of Sects. 5.1–5.3 has shown that coherent free elementary particle theories are possible. In so doing the theories for Klein Gordon free particles are settled.
5.4 New Species of Particle Theories
In this subsection we show how our approach also leads to particle theories that cannot be associated with known ones. The new species of particle theories to be identified are based on the irreducible representation of \({{\mathcal {I}}}_{{\mathcal {P}}}(U^+\mathrm{red.}\mathbf{u})\), with \(\sigma ({\underline{P}})=S_\mu ^+\) and \(s=0\), hence with \(U^+\) reducible.
Let us consider an irreducible representation in \({{\mathcal {I}}}_{{\mathcal {P}}}(U^+\mathrm{red.}{} \mathbf{u})\) with \(s=0\) of Sect. 4.4.1. The Hilbert space is \({{\mathcal {H}}}= L_2(\mathbb {R}^3,d\nu ) \oplus L_2(\mathbb {R}^3,d\nu )\), its generators are
with \({\textsf {j}}_k=i\left( p_l\frac{\partial }{\partial p_j}-p_j\frac{\partial }{\partial p_l}\right) \), \({{\textsf {k}}}_j=ip_0\frac{\partial }{\partial p_j}\), while  and
and  .
.
To identify the position operator \({\mathbf{Q}}\) we introduce the difference \(\mathbf{D}={{\mathbf{Q}}}-\tilde{\mathbf{F}}\), where \(\tilde{\mathbf{F}}=\mathbf{F}\mathbb {1}\equiv \left[ \begin{array}{cc}{} \mathbf{F}&{}0\\ 0&{}\mathbf{F}\end{array}\right] \) is the Newton-Wigner operator in this representation.
Now, \([{\tilde{F}}_j,P_k]=i\delta _{jk}\) and \([J_j,{\tilde{F}}_k]=i{\hat{\epsilon }}_{jkl}{\tilde{F}}_k\) hold; on the other hand, according to (9), \([Q_j,P_k]=i\delta _{jk}\) and \([J_j,Q_k]=i\epsilon _{jkl}Q_k\) hold too, so that the relations \([D_j,P_k]=\mathbb {O}\) and \([J_j,D_k]=i\epsilon _{jkl}D_k\) are implied. Thus we have \({{\mathbf{Q}}}=\tilde{\mathbf{F}}+\mathbf{D}\) where \(D_j= \left[ \begin{array}{cc}d^{(j)}_{11}({\mathbf{p}})&{}d^{(j)}_{12}({\mathbf{p}})\\ d^{(j)}_{21}({\mathbf{p}})&{}d^{(j)}_{22}({\mathbf{p}})\end{array}\right] \in \Omega (\mathbb {C}^2)\). Conditions \([J_j,D_k]=i\epsilon _{jkl}D_k\) entail \([{\textsf {j}}_j,d^{(k)}_{nm}({\mathbf{p}})]=i{\hat{\epsilon }}_{j,k,l}d^{(l)}_{nm}({\mathbf{p}})\) for all \({\mathbf{p}}\in \mathbb {R}^3\); together with \([{\textsf {j}}_j,p_k]=i{\hat{\epsilon }}_{j,k,l}P_l\) these relations imply \(d_{mn}^{(j)}({\mathbf{p}})=f_{mn}(p_0)p_j\). Now, since  holds, by making use of (Q.2.a) we obtain
holds, by making use of (Q.2.a) we obtain  , which entails
, which entails
Therefore \(D_j=\mathbb {O}\) and \({{\mathbf{Q}}}=\tilde{\mathbf{F}}\), so that also  turns out to be automatically satisfied since
turns out to be automatically satisfied since  . Thus, we have identified a new complete theory of an elementary spin 0 free particle. A similar derivation identifies a new complete theory based on \({{\mathcal {I}}}_{{\mathcal {P}}}(U^-\mathrm{red.}{\mathbf{d}})\); once again \({{\mathbf{Q}}}=\tilde{\mathbf{F}}\) is found. Which particles of nature are described by these theories, if they exist at all, is not a problem we are able to solve at present, as we argue in Sect. 7.
. Thus, we have identified a new complete theory of an elementary spin 0 free particle. A similar derivation identifies a new complete theory based on \({{\mathcal {I}}}_{{\mathcal {P}}}(U^-\mathrm{red.}{\mathbf{d}})\); once again \({{\mathbf{Q}}}=\tilde{\mathbf{F}}\) is found. Which particles of nature are described by these theories, if they exist at all, is not a problem we are able to solve at present, as we argue in Sect. 7.
It must be remarked that the present argument is not successful if applied to the new irreducible representation of class \({{\mathcal {I}}}_{{\mathcal {P}}}(U^\pm {\mathrm{red.}}{\mathbf{s}})\), in the sense that conditions (Q.1), (Q.2.a,b) do not uniquely determine \({\mathbf{Q}}\), so that a complete theory is not identified.
6 Transformation Properties Relative to Boosts
In general, apart from the cases identified in Sect. 5, conditions (Q.1) and (Q.2.a,b) do not univocally determine the position operator \({\mathbf{Q}}\), in particular when \(s>0\); for the case \(U\in {{\mathcal {I}}}_{{\mathcal {P}}}(U^+{\mathrm{irred.}}{} \mathbf{u})\) (Sect. 5.1) with \(s>0\) this non-uniqueness was also shown by Jordan, who in [38] writes “For nonzero spin there is more than one Hermitian operator [\({\mathbf{Q}}\)] that transforms as a position operator should for translations, rotations, and time reversal”. A cause of such indeterminacy is that conditions (Q.2.a,b) miss the explicit transformation properties of \({\mathbf{Q}}\) with respect to boosts; it is obvious that the implied further conditions could help to solve the indeterminacy of \({\mathbf{Q}}\).
In fact, for \(s>0\) the extension of (Q.2.b) to boosts is not an easy matter. To attain such an extension, given a boost g – for instance the boost characterized by a relative velocity \(\mathbf{u}=(u,0,0)\) – we have to consider the reference frame \(\Sigma \) and the frame \(\Sigma _g\) related to \(\Sigma \) just by g. Then the explicit relation between \(S_g[{{\mathbf{Q}}}]\) and \({\mathbf{Q}}\) is required to identify, given the position outcome \(\mathbf{x}\) at time \(t=0\) with respect to \(\Sigma \), the corresponding position outcome \(\mathbf{y}_\mathbf{x}\) with respect to \(\Sigma _g\), but at time \(t'=0\) with respect to \(\Sigma _g\), because of the condition of relative indistinguishability dictated by the concept of quantum transformation of Definition 3.1. Special relativity does not provide such a correspondence as a relation like (Q.2.b); in fact, if the outcome of position is \(\mathbf{x}=(x_1,x_2,x_3)\) at time \(t=0\) in \(\Sigma \), then according to Lorentz transformations we can state only that it corresponds to position \({\mathbf{y}}=\left( \frac{x_1}{\sqrt{1-u^2}},x_2,x_3\right) \) in \(\Sigma _g\), but at time \(t'=\frac{-ux_1}{\sqrt{1-u^2}}\), not at \(t'=0\)!
In standard presentations, based on canonical quantization, a necessary condition of covariance under boosts is taken to be the existence of a probability current density \(\hat{\mathbf{j}}(t,{\mathbf{x}})\) for every quantum state, which satisfies the continuity equation \(\frac{\partial }{\partial t}{\hat{\rho }}={{\varvec{\nabla }}}\cdot \hat{\mathbf{j}}\), where \({\hat{\rho }}(t,{\mathbf{x}})\) is the probability density of position, such that \(\hat{{\underline{j}}}=({\hat{\rho }},\hat{\mathbf{j}})\) transforms as a four-vector. In fact, in the present approach the existence of such a four-current density of probability does not have a formal proof; it could be assumed to hold by analogy with the electrical four-current density in non-quantum relativistic theory; but the proof in this last theory is based on the existence of a real motion of the charges characterized by a real velocity in every point \({\underline{x}}=(x_0,\mathbf{x})\); such a simultaneous existence is inconsistent in a quantum theory, and thus the concept is not viable if we are to maintain the methodology of the present work.
One way to obviate this problem could be to introduce a time-space position \({\underline{Q}}=(Q_0,{{\mathbf{Q}}})\), where the operator \(Q_0\) is just the time quantum observable, i.e. the time when the measurement of the spatial coordinates represented by \({\mathbf{Q}}\) occurs. Then, according to special relativity we could set \(S_g[Q_0]=\frac{Q_0-uQ_1}{\sqrt{1-u^2}}\), \(S_g[Q_1]=\frac{Q_1-uQ_0}{\sqrt{1-u^2}}\), \(S_g[Q_2]=Q_2\), \(S_g[Q_3]=Q_3\). But in a quantum theory of localizable particle such a time cannot be a quantum observable. Indeed, let us suppose that \(Q_0\) is a quantum observable representing this time, so that the four-operator \({\underline{Q}}=(Q_0,Q_1,Q_2,Q_3)\) represents the time-space coordinates of the particle. Accordingly, \([Q_\alpha ,Q_\beta ]=\mathbb {O}\), for all \(\alpha ,\beta \in \{0,1,2,3,\}\). Furthermore, since for every time-space translation \(g_\alpha \) such that \(U_{g_\alpha }=e^{-iP_\alpha a}\) we have \(S_{g_\alpha }[Q_\beta ]=e^{-iP_\alpha a}Q_\beta e^{iP_\alpha a}=Q_\beta -\delta _{\alpha \beta }a\), also \([Q_\alpha ,P_\beta ]=i\delta _{\alpha \beta }\) holds; in particular \([Q_0,P_0]=i\) and \([Q_0,P_j]=\mathbb {O}\) should hold for \(j=1,2,3\). In an irreducible representation of \({{\mathcal {I}}}_{{\mathcal {P}}}(U^+{\mathrm{irred.}}{\mathbf{u}})\), the condition \([Q_0,P_j]=\mathbb {O}\) implies \(\left( Q_0\psi \right) ({\mathbf{p}})=q_0({\mathbf{p}})\psi ({\mathbf{p}})\), where \(q_0({\mathbf{p}})\in \Omega (\mathbb {C}^{2s+1})\), for every \({\mathbf{p}}\in \mathbb {R}^3\). Thus \(P_0Q_0=p_0Q_0=Q_0p_0=Q_0P_0\), i.e. \([Q_0.P_0]=\mathbb {O}\) holds, in contradiction with \([Q_0,P_0]=i\).
The same contradiction also arises with a representation in \({{\mathcal {I}}}_{{\mathcal {P}}}(U^-\mathrm{irred.}{} \mathbf{d})\).
Finally, if we consider a representation in \({{\mathcal {I}}}_{{\mathcal {P}}}(U^\pm \mathrm{irred.}{} \mathbf{s})\), the same argument leads to \([Q_0,P_0]=\left[ \begin{array}{cc} 0&{}2q_{12}({\mathbf{p}})\\ 2q_{21}({\mathbf{p}})&{}0\end{array}\right] \), where each \(q_{mn}({\mathbf{p}})\) is a \((2s+1)\times (2s+1)\) matrix. Also in this case the hypothesis that \(Q_0\) is an observable contradicts \([Q_0,P_0]=i\).
This proof can be easily extended to the irreducible generalized projective representations of \({{\mathcal {I}}}_{{\mathcal {P}}}(U^\pm {\mathrm{red.}})\) identified in Sect. 4.4.
So, the hope of completing the development of the quantum theory of an elementary free particle remains tied to the possibility of attaining an explicit mathematical relation expressing the transformation properties of \({\mathbf{Q}}\) with respect to boosts, that is to say, to the possibility of finding the extension of the commutation rules (9) to \([K_j,Q_k]\). In theories \({\mathcal {T}}\).1–\({\mathcal {T}}\).4, where (Q.1) and (Q.2.a,b) are sufficient to determine \({\mathbf{Q}}\), the commutation relation \([K_j,Q_k]\) can be simply calculated, \(K_j\) and \({\mathbf{Q}}\) being known explicitly, and it turns out to be
Then the theory could be tentatively developed by assuming (JM) to hold in all theories. It is evident that this extension is supported only by heuristic arguments. In fact, in [39] (JM) was derived by making use of canonical quantization, a method extraneous to the present work; it also turns out to be the canonical quantization of the transformation property derived in [40]. However, the consistency of its implications can be explored. Jordan and Mukunda [18] checked the consistency of (JM) with the structural properties (1) of \({{\mathcal {P}}}_+^\uparrow \) and with the transformation properties (Q.2.b) of \({\mathbf{Q}}\) with respect to the Euclidean group \({\mathcal {E}}\). The results attained by Jordan and Mukunda are not homogeneous; an extract is given in Sect. 6.1. It is important to note, however, that in their work [18] the authors assume the transformation properties of \({\mathbf{Q}}\) with respect to the subgroup \({{\mathcal {P}}}_+^\uparrow \), ignoring the transformation properties  and
and  . On the other hand, in Sect. 5 it was shown that these conditions do have a decisive role in determining the position operator; therefore, the task of checking the consistency of (JM) with respect to time reversal and space inversion should be accomplished. We address this task in Sect. 6.2.
. On the other hand, in Sect. 5 it was shown that these conditions do have a decisive role in determining the position operator; therefore, the task of checking the consistency of (JM) with respect to time reversal and space inversion should be accomplished. We address this task in Sect. 6.2.
6.1 Jordan and Mukunda’s Results
For representations with \(\sigma ({\underline{P}})=S_\mu ^\pm \) and \(U^\pm \) irreducible, Jordan and Mukunda identified [18] which operators \({\mathbf{Q}}\) are consistent with (Q.2.b) and (JM); these representations correspond to those of Sects. 4.1 and 4.2. Jordan and Mukunda find that for \(s=0\) there is a unique position operator satisfying such a consistency: \({{\mathbf{Q}}}=\mathbf{F}\). This result agrees with that obtained in Sect. 5.1 where (JM) was not assumed and replaced by (Q.2.a). In general, for \(s\ge 0\) Jordan and Mukunda find that the solutions must have the form
According to [18], if \(s>0\) such a solution turns out to be non-commutative for any \(a\in \mathbb {R}\) , i.e. it does not satisfy (Q.1). Therefore, for \(s>0\) the transformation property (JM) is inconsistent with the notion of position expressed by (Q.1), (Q.2.a), (Q.2.b).
For representations with \(\sigma ({\underline{P}})=S_\mu ^+\cup S_\mu ^-\) and \(U^+\) irreducible, corresponding to those of the present Sect. 4.3, Jordan and Mukunda show that every solution for \({\mathbf{Q}}\), which satisfies (JM) and (Q.2.b), must have the form
where \(A=A({\mathbf{p}}^2)\), \(B=B({\mathbf{p}}^2)\) are real functions of \({\mathbf{p}}^2\), \(B'=\frac{d}{d({\mathbf{p}}^2)}B({\mathbf{p}}^2)\), \(\rho _1=\left[ \begin{array}{cc}0&{}1\\ 1&{}0\end{array}\right] \) and \(\rho _2=\left[ \begin{array}{cc}0&{}-i\\ i&{}0\end{array}\right] \).
We see that if \(s=0\) then \({\mathbf{Q}}\) depends on A and B; hence, the approach of Jordan and Mukunda is unable to univocally identify a theory for Klein–Gordon particles.
If \(s>0\) the operator \({\mathbf{Q}}\) in (30) is not uniquely determined, so generally it differs from \({\hat{\mathbf{F}}}\); but, in the case \(s=\frac{1}{2}\), if \(A=0\) and \(B\equiv \)constant, i.e. \(B'=0\), then by a suitable unitary transformation that leaves \({\mathbf{P}}\), \(P_0\), \(\mathbf{J}\), \(\mathbf{K}\) unaltered, (30) transforms into
Jordan and Mukunda show that in this particular case the theory is unitarily equivalent to the theory of Dirac for spin \(\frac{1}{2}\) particles.
6.2 Consistency of (JM) with 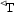 and
and 
In this section we check the consistency of the Jordan-Mukunda position operators with respect to time reversal and space inversion.
6.2.1 Consistency in the Case \({{\mathcal {I}}}_{{\mathcal {P}}}(U^+\mathrm{irred.}{} \mathbf{u})\) and \({{\mathcal {I}}}_{{\mathcal {P}}}(U^-\mathrm{irred.}{} \mathbf{d})\).
For representations in \({{\mathcal {I}}}_{{\mathcal {P}}}(U^+\mathrm{irred.}{} \mathbf{u})\) and \({{\mathcal {I}}}_{{\mathcal {P}}}(U^-\mathrm{irred.}{} \mathbf{d})\), provided that \(s=0\), there is no problem of consistency of the Jordan and Mukunda transformation property (JM) with (Q.1), (Q.2.a) and (Q.2.b). Indeed, the unique operator \({{\mathbf{Q}}}=\mathbf{F}\) determined in Sects. 5.1 and 5.2 by (Q.1), (Q.2.a) and (Q.2.b) coincides with the operator determined by Jordan and Mukunda, which satisfies (JM).
In the case \(s>0\), according to Sect. 4.1, the anti-unitary time reversal operator is  , and the space inversion operator is
, and the space inversion operator is  . By making use of these explicit operators and of (29), it turns out that the condition
. By making use of these explicit operators and of (29), it turns out that the condition  in (Q.2.a) implies \(a=0\). Hence
in (Q.2.a) implies \(a=0\). Hence
This operator satisfies  . However, according to Jordan and Mukunda, it is not commutative. Such non-commutativity has also been demonstrated elsewhere by alternative arguments [21, 25]. Thus, in this case there is no position operator that satisfies (Q.1), (Q.2.a) and (Q.2.b) consistent with the transformation property (JM).
. However, according to Jordan and Mukunda, it is not commutative. Such non-commutativity has also been demonstrated elsewhere by alternative arguments [21, 25]. Thus, in this case there is no position operator that satisfies (Q.1), (Q.2.a) and (Q.2.b) consistent with the transformation property (JM).
6.2.2 Consistency in the Case \({{\mathcal {I}}}_{{\mathcal {P}}}(U^\pm \mathrm{irred.}{} \mathbf{s})\).
From Sect. 4.3, all combinations  concerning their unitary or anti-unitary character are possible in \({{\mathcal {I}}}_{{\mathcal {P}}}(U^\pm \mathrm{irred.}{} \mathbf{s})\), except
concerning their unitary or anti-unitary character are possible in \({{\mathcal {I}}}_{{\mathcal {P}}}(U^\pm \mathrm{irred.}{} \mathbf{s})\), except  anti-unitary and
anti-unitary and  unitary.
unitary.
We have seen in Sect. 5.3 that for \(s=0\) there is a unique position operator \({{\mathbf{Q}}}={\hat{\mathbf{F}}}\) that is consistent with (Q.1), (Q.2.a) and (Q.2.b). This coincides with the operator (30) for \(A=B=\mathbb {O}\); according to Jordan and Mukunda it is also consistent with their transformation property (JM). Thus, in this particular case there is no consistency problem. According to Sect. 5.3, this solution is valid only if  is unitary and
is unitary and  is anti-unitary, namely
is anti-unitary, namely  and
and  , or if both
, or if both  are anti-unitary, namely
are anti-unitary, namely  and
and  . Thus, there is consistency with the new representations identified in Sect. 4.3.
. Thus, there is consistency with the new representations identified in Sect. 4.3.
Now we have to address the theories where \(s>0\). We begin by checking the cases where  is anti-unitary. From Sect. 4.3,
is anti-unitary. From Sect. 4.3,  ; by making use of (30) we find that
; by making use of (30) we find that  holds if and only if \(\sin B=0\) and \(B'\cos B=0\). Hence \({\mathbf{Q}}\) becomes
holds if and only if \(\sin B=0\) and \(B'\cos B=0\). Hence \({\mathbf{Q}}\) becomes
 being anti-unitary, also
being anti-unitary, also  must be anti-unitary, i.e.
must be anti-unitary, i.e.  or
or  . If
. If  , then
, then  would imply \(\frac{\partial }{\partial p_j}=0\), for all j. Therefore this possibility must be excluded. If
would imply \(\frac{\partial }{\partial p_j}=0\), for all j. Therefore this possibility must be excluded. If  , by making use of (33) we find that
, by making use of (33) we find that  holds if and only if \(\cos B=0\), which is impossible because \(\sin B=0\). Thus, for \(s>0\) there is no position operator \({\mathbf{Q}}\) that is consistent with (Q.1), (Q.2.a), (Q.2.b) and the transformation property (JM) in a theory where
holds if and only if \(\cos B=0\), which is impossible because \(\sin B=0\). Thus, for \(s>0\) there is no position operator \({\mathbf{Q}}\) that is consistent with (Q.1), (Q.2.a), (Q.2.b) and the transformation property (JM) in a theory where  is anti-unitary.
is anti-unitary.
Let us check the case where  is unitary, i.e.
is unitary, i.e.  . By making use of (30) we find that
. By making use of (30) we find that  holds if and only if \(\cos B=0\), so that \({\mathbf{Q}}\) becomes
holds if and only if \(\cos B=0\), so that \({\mathbf{Q}}\) becomes
If  is unitary, then
is unitary, then  or
or  . In the case
. In the case  implies \(\sin B=0\), which is impossible, because \(\cos B=0\). In the case
implies \(\sin B=0\), which is impossible, because \(\cos B=0\). In the case  , then
, then  implies \(\rho _1A(\sin B){\mathbf{P}}+\frac{{\mathbf{P}}\wedge \mathbf{S}}{p_0(p_0+\mu )}=0\), which is false. Thus, if both
implies \(\rho _1A(\sin B){\mathbf{P}}+\frac{{\mathbf{P}}\wedge \mathbf{S}}{p_0(p_0+\mu )}=0\), which is false. Thus, if both  and
and  are unitary, there is no position operator consistent with (Q.1), (Q.2.a), (Q.2.b) and (JM).
are unitary, there is no position operator consistent with (Q.1), (Q.2.a), (Q.2.b) and (JM).
The last possibility is the case where  is anti-unitary, i.e.
is anti-unitary, i.e.  or
or  . If
. If  then
then  cannot hold because it would imply \(\frac{\partial }{\partial p_j}=0\), for all j. If
cannot hold because it would imply \(\frac{\partial }{\partial p_j}=0\), for all j. If  , then by making use of (34) we find that
, then by making use of (34) we find that  holds if and only if \(A=0\). Now, \(\sin B=\pm 1\), since \(\cos B=0\), and (34) becomes
holds if and only if \(A=0\). Now, \(\sin B=\pm 1\), since \(\cos B=0\), and (34) becomes
Thus, the unique particle quantum theory based on representations in \({{\mathcal {I}}}_{{\mathcal {P}}}(U^\pm \mathrm{irred.}{} \mathbf{s})\) and \(s>0\), whose position operator is consistent with (Q.1), (Q.2.a), (Q.2.b) and (JM), has  unitary and anti-unitary
unitary and anti-unitary  , and the position operator is given by (35). By fixing \(\sin B=-1\), we have
, and the position operator is given by (35). By fixing \(\sin B=-1\), we have
We see that the position operator is different from the position operator of Dirac’s theory given by (36). However, by transforming every operator R into \(WRW^{-1}\), where \(W=e^{-i\frac{1}{2}\rho _3\frac{\pi }{2}}\), with \(\rho _3=\left[ \begin{array}{cc}1&{}0\\ 0&{}-1\end{array}\right] \), it turns out that all generators \(P_j\), \(P_0\), \(J_k\), \(K_j\) are left invariant, while \({\mathbf{Q}}\) of (41) is transformed into that of (31). Therefore, Dirac’s theory is the unique theory where (Q.1), (Q.2.a), (Q.2.b) and (JM) hold, but, once again, the new representations with  anti-unitary are necessary for the theory to be consistent.
anti-unitary are necessary for the theory to be consistent.
7 The Problem of Assigning a Theory to a Particle
Sections 5 and 6 identify possible theories of elementary free paricles. The actual existence in nature of the particle described by each theory is an issue that cannot be assessed within a purely theoretical investigation dealing with free particles. The reason is that real particles can be distinguished from each other by their different behaviour when they undergo a given interaction. So, a particle with a negative electrical charge can be distinguished from a particle with positive electrical charge because their paths have opposite curvatures interacting with a magnetic field in a cloud chamber. Yet to establish the relation between the side of the curvature and the sign of an observable charge of the particle, the theory of the interaction is needed.
This argument shows the fundamental importance of developing the relativistic quantum theory of an interacting particle, by complying with the methodology followed here. Interesting ideas about this have been traced by Lévy-Leblond in his attempt [40] based on transformation properties; they could be fruitful when applied to the present framework. An alternative could be to explore the possibility of extending the methods applied to develop the non-relativistic quantum theory of an interacting elementary particle [12, 13] to the relativistic case.
Such a theory being not available, we can tentatively identify the specific particle described by a given theory derived in the present work by exploiting its analogies with some theories of a specific particle present in the literature. For instance, the elementary particle theory based on representations \(U\in {{\mathcal {I}}}_{{\mathcal {P}}}(U^\pm \mathrm{irred.}{} \mathbf{s})\) of kind \(U^{(5)}\) with spin \(s=\frac{1}{2}\) identified in Sect. 6.2.2 turns out to be equivalent to Dirac’s theory under the assumption that \([K_j,Q_k]=\frac{1}{2}\left( Q_j[P_0,Q_k]+[P_0,Q_k]Q_j\right) \) holds. Now, Dirac presented his model as the theory of electrons and positrons [9]; therefore, the theory of the present work based on \(U^{(5)}\) with \(s=\frac{1}{2}\) can be considered as the theory of electrons and positrons to the same extent as Dirac. Needless to say, in so doing an anti-unitary space-inversion operator must be admitted, of course.
Analogously, the theories \({{\mathcal {T}}}.1\) and \({{\mathcal {T}}}.2\) in Sect. 5.3 can be considered as the theories of rest mass \(\mu \) spinless particles. According to this analogy-based method both theories \({{\mathcal {T}}}.3\) and \({{\mathcal {T}}}.4\) could be considered as the theories of the particles identified as Klein–Gordon particles in the literature.
The differences between the two inequivalent theories \({{\mathcal {T}}}.1\) and \({{\mathcal {T}}}.2\) can only be consistently interpreted once their different ways of interacting have been discovered. The same applies to \({{\mathcal {T}}}.3\) and \({{\mathcal {T}}}.4\).
It must be remarked that these corespondences cannot be considered as definitive. The reason is that, due to the profound difference of our methodology with repect to canonical quantization, the theories developed in the present work do not necessarily have to fit with the theories obtained by canonical quantization. So the identification of the specific particle decribed by a given theory from those here identified, whenever it exists, ultimately depends on the availability of a theory of the interacting particle.
This is especially true for the case of the new species of theory in Sect. 5.4 for which there is no exisiting theory with the same formalism. For this case, given the form of the generators \(P_0\), \(P_j\), \(J_j\), \(K_j\) and of the space inversion and time reversal operators shown in Sect. 5.4, we see that the observable represented by the operator \(N=\left[ \begin{array}{cc}1&{} 0 \\ 0 &{}-1\end{array}\right] \) turns out to be invariant under spatial translations, spatial rotations and boosts, while the two possible values of N, i.e. 1 and \(-1\), exchange with each other by space inversion and time reversal. So, a particle described by such a theory must be a spinless particle with rest mass \(\mu \), characterized by the existence of a two value observable satisfying these transformation properties.
8 Conclusions
In order to develop consistent relativistic quantum theories of a single free particle, we have pursued an approach based on group theoretical methods, that avoids the shortcomings inherent in canonical quantization. In so doing, from the principles of relativistic invariance and position covariance we have derived six complete inequivalent theories for spin 0 particles that are a coherent alternative to Klein–Gordon theory, two of which are a new species of particle theoriy.
For the case of non zero spin, our approach is still unable to determine complete theories, because of the present lack, in quantum theory, of explicit relations establishing the transformation properties of position with respect to boosts. Such transformation properties can be determined only in the complete theories for spin zero particles, where they can be calculated directly. They turn out to coincide with the transformation properties (JM) proposed by Jordan and Mukunda [18] also for the non zero spin case. Next we checked the consistency of the transformation property (JM) with the theories developed in our approach and found that Dirac’s theory is the unique theory for \(s=\frac{1}{2}\) and \(\sigma ({\underline{P}})=S_\mu ^+\cup S_\mu ^-\) such that (JM) are satisfied. On the other hand, (JM) is inconsistent with the existence of localizable particle with \(\sigma ({\underline{P}})=S_\mu ^+\) and \(s>0\). Hence there are arguments in favor but also against the general validity of (JM). Nevertheless, that said there is a way that would certainly solve the dilemma: to derive from the symmetry and covariance principles the explicit mathematical relation that expresses the transformation properties of position with respect to boosts, analogously to the method used to obtain (Q.2a) and (Q.2b). Let us denote these aimed mathematical relations by (KQ). Whenever such a deduction is successful, one of the following statements should hold.
-
Either
(KQ) are equivalent to (JM). In this case there would be precise consequences; for instance, one consequence would be that Poincaré invariance is incompatible with the existence of particles with \(\sigma ({\underline{P}})=S_\mu ^+\), or \(\sigma ({\underline{P}})=S_\mu ^-\), and \(s>0\). Another consequence would be that only Dirac theory is consistent with Poincaré invariance.
-
Or
(KQ) are not equivalent to (JM) in some theories. Let us suppose that equivalence fails for \(\sigma ({\underline{P}})=S_\mu ^+\cup S_\mu ^-\) and \(s=\frac{1}{2}\). In this case we should investigate which of the candidates for position operators identified by (22), (23) in Sect. 5.2 are consistent with (KQ). If exist, we would have determined an alternative theory to that of Dirac, based on physical principles without canonical quantization.
The arguments above highlight the importance of working for a determination of the relation (KQ), in order to advance the understanding of relativistic quantum particle theory.
Change history
24 November 2020
The following OA funding note is address above reference section: Open access funding provided by Università della Calabria within the CRUI-CARE Agreement.
Notes
The commutativity condition \([Q_j,Q_k]=\mathbb {O}\) establishes the possibility of performing a measurement that yields all three values of the position coordinates. The nonexistence of commutative position operators in certain circumstances [20] has led to search for more general concepts of position [21], such as non-commutative concepts [22,23,24,25], and for unsharp position (see [26] and references therein), circumstances. In the present work we are interested in the commutative concept of position only.
References
Klein, O.: Quantentheorie und Fnfdimensionale Relativittstheorie. Z. Physik 37, 895 (1926)
Fock, V.: Zur Schrdingerschen Wellenmechanik. Z. Physik 37, 242 (1926)
Gordon, W.: Der Comptoneffekt Nach der Schrdingerschen Theorie. Z. Physik 40, 117 (1926)
Gamow, G.: Thirty Years That Shook Physics. Doubleday and Co., Garden City, NY (1966)
Felshbach, H., Villars, F.: Elementary relativistic wave mechanics of spin 0 and spin 1/2 particles. Rev. Mod. Phys. 30, 24 (1958)
Barut, A.O., Malin, S.: Position operators and localizability of quantum systems described by finite- and infinite-dimensional wave equations. Rev. Mod. Phys. 40, 632 (1968)
Weinberg, S.: The Quantum Theory of Fields, vol. I. Cambridge University Press, Cambridge (1995)
Dirac, P.A.M.: The quantum theory of the electron. Proc. R. Soc. A117, 610 (1928)
Dirac, P.A.M.: A theory of electrons and protons. Proc. R. Soc. A126, 360 (1930)
Dirac, P.A.M.: Quantised singularities in the electromagnetic field. Proc. R. Soc. A133, 60 (1931)
Lévy-Leblond, J.M.: The pedagogical role and epistemological significance of group theory in quantum mechanics. Riv. Nuovo Cim. 4, 99 (1974)
Nisticò, G.: Group theoritical derivation of the minimum coupling principle. Proc. R. Soc. A473, 20160629 (2017)
Nisticò, G.: Group theoretical characterization of wave equations. Int. J. Theor. Phys. 56, 4047 (2017)
Wigner, E.: On unitary representations of the inhomogeneous Lorentz group. Ann. Math. 40, 149 (1939)
Bargmann, V., Wigner, E.P.: Group theoretical discussion of relativistic wave equations. Natl. Acad. Sci. 34, 211 (1948)
Costa, G., Fogli, G.: Lecture Notes in Physics, vol. 823. Springer, New York (2012)
Barut, A.O., Racza, R.: Theory of Group Repesentations and Applications. World Scientific, Singapore (1986)
Jordan, T.F., Mukunda, N.: Lorentz-covariant position operators for spinning particles. Phys. Rev. 132, 1842 (1963)
Foldy, L.L.: Synthesis of covariant particle equations. Phys. Rev. 102, 568 (1956)
Wightman, A.S.: On the localizability of quantum mechanical systems. Rev. Mod. Phys. 34, 845 (1962)
Kàlnay, A.J.: In: Bunge, M. (ed.) Problems in the Foundations of Physics. Springer, Berlin (1971)
Jadzyck, A.Z., Jancewicz, B.: Maximal localizability of photons. Bull. Acad. Sci. Polon. XXI, 477 (1972)
Bacry, H.: The Poincare group, the Dirac monopole and photon localisation. J. Phys. A 14, L73 (1981)
Bacry, H.: The Position operator revisited. Ann. Inst. H. Poincaré 49, 245 (1988)
Bacry, H.: Localizability and Space in Quantum Physics. Lecture Notes in Physics, vol. 308. Springer, Berlin (1988)
Schroeck, E.F.: Quantum Mechanics on Phase Space. Kluwer Academic Publishers, Dordrecht (1996)
Niederer, U.H., O’Raifeartaigh, L.: Realizations of the unitary representations of the inhomogeneous space-time groups. II. Covariant realizations of the Poincarè group. Fortschr. Phys. 22, 131 (1974)
Simon, B.: In: Lieb, E.H., Simon, B., Wightman, A.S. (ed.) Studies in Mathematical Physics: Essays in Honor of Valentine Bargmann, p. 327. Princeton University Press, Princeton (1976)
Von Neumann, J.: Mathematical Foundations of Quantum Mechanics. Princeton University Press, Princeton (1955)
Mackey, G.W.: Induced Representations of Group and Quantum Mechanics. Benjamin Inc., New York (1968)
Reed, M., Simon, B.: Methods of Modern Mathematical Physics. Academic Press, New York (1978)
Prthasarathy, K.R.: Projective unitary antiunitary representations of locally compact groups. Commun. Math. Phys. 15, 305 (1969)
Cariñena, J.F., Santander, M.: On the projective unitary representations of connected Lie groups. J. Math. Phys. 16, 1416 (1975)
Cariñena, J.F., Santander, M.: Projective covering group versus representation groups. J. Math. Phys. 21, 440 (1980)
Cariñena, J.F., Santander, M.: Antiunitary symmetry operators in quantum mechanics. Int. J. Theor. Phys. 20, 97 (1981)
Nisticò, G.: New representations of poincare group for consistent relativistic particle theories. J. Phys.: Conf. Ser. 1275, 012034 (2019). arXiv:1903.03066
Newton, T.D., Wigner, E.P.: Localized states for elementary systems. Rev. Mod. Phys. 21, 400 (1949)
Jordan, T.F.: Simple derivation of the Newton–Wigner position operator. J. Math. Phys. 21, 2028 (1980)
Currie, D.G., Jordan, T.F., Sudarshan, E.C.G.: Relativistic invariance and Hamiltonian theories of interacting particles. Rev. Mod. Phys. 35, 350 (1963)
Lévy-Leblond, J.M.: Minimal electromagnetic coupling as a consequence of Lorentz invariance. Ann. Phys. 57, 481 (1970)
Funding
Open access funding provided by Università della Calabria within the CRUI-CARE Agreement.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Nisticò, G. Group Theoretical Derivation of Consistent Free Particle Theories. Found Phys 50, 977–1007 (2020). https://doi.org/10.1007/s10701-020-00364-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10701-020-00364-2




 and
and  , i.e.
, i.e.  and
and  by (2)-(5),
by (2)-(5),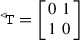 and unitary
and unitary  ;
; and unitary
and unitary  ;
;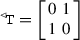 and anti-unitary
and anti-unitary  ;
; and anti-unitary
and anti-unitary  ;
; and anti-unitary
and anti-unitary ;
;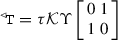 and anti-unitary
and anti-unitary .
. . In this representation the Newton-Wigner operators representing position become the multiplication operators
. In this representation the Newton-Wigner operators representing position become the multiplication operators  and
and 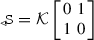 , can be reformulated in Hilbert space
, can be reformulated in Hilbert space  and
and  .
. and
and 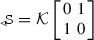 , differs from
, differs from  , that is now
, that is now  .
. and
and 