1 Introduction

Many epidemiological models consider that the population is compartmentalized into groups and the infectious individuals have the same probability of meeting any susceptible individual. Furthermore, it is assumed that there is homogeneity in both susceptibility and infectivity, and there is no differentiation related to age, behaviour, spatial position and/or stage of disease. (Anderson 1991; Kermack and McKendrick 1991; Capasso 1993; Soares 2010).

The assumptions above aim to simplify the understanding of an epidemic. Aron (1989) claims that simple models head to general conclusions of a qualitative analysis and more detailed models are effective for quantitative analysis. Moreover, according to Sattenspiel and Simon (1988) the heterogeneity in the population may interfere with the spread of diseases. Shaman et al. (2020) granted a model of the transmission dynamics of COVID-19 which takes into account the heterogeneity in infectivity, showing that the rapid spread of the virus can be elucidated by the contagion of infectious individuals who do not present severe symptoms. This work was of great relevance to combat COVID-19, also showing the importance of population heterogeneity in the dynamics of disease transmission.

According to Sattenspiel and Simon (1988) there are at least five sources of heterogeneity in the population that may interfere with the course of disease proliferation, which are variable susceptibility and infectivity, non-random encounters between individuals due to age, variation in contact numbers and variation in contact patterns between the subgroups. The studied and presented models in this article contemplate the population heterogeneity when there is variation in infectivity.

When there is an encounter between a susceptible individual and an infectious agent for the first time, the microorganism tries to overcome the initial defenses of the susceptible individual, which are formed by physical and chemical barriers, and in case of successful invasion the immune system is activated (Abbas et al. 2008).

The immune system is formed by natural and acquired immunity. Natural immunity initially responds to microorganisms attempting to prevent, control or eliminate host infection. On the other hand, acquired or adaptive immunity aims to activate defense mechanisms against the invading microorganism by adopting more effective strategies. Nonetheless, under a first infection acquired immunity is only activated after natural immunity fails to perform its function successfully (Abbas et al. 2008).

In this encounter between microorganism multiplication and immune system, there is a variation in the microorganism load in the organism and this variation generates different degrees of infectivity in the host. Therefore, the effectiveness of disease transmission, among other things, depends on the body’s microorganism load on the body (Santos et al. 2002). Summarizing, we can assume different infective capacity among the infectious individuals, during the infectious period.

These different degrees of infectivity are represented by dividing the infectious population into k subgroups, assuming that all infectious individuals will pass through these k phases of infectivity.

Leite et al. (2000) presented an epidemiological model of the type SEIRS with constant total population, which incorporating the heterogeneous infectivity that is related to the different phases through which an infected individual passes. Each phase differs by the infective capacity of individuals. Besides, it is shown a theorem relating the stability of the disease free equilibrium point to the independent term signal of the characteristic polynomial.

Our objective is to extend the result presented by Leite et al. (2000) to general epidemiological models that derive from the SEIRS type model and also to models that vary from the SEIR type model with vaccination. In addition, we want to relate the basic reproduction number, calculated by the methodology presented by van den Driessche and Watmough (2002), with our results and also analyze the stability of the population’s extinction equilibrium for these models.

This article is structured as follows. In Sect. 2 we present two models of the SEIRS type, a general one in which the input of the flow of the vital dynamics is given in a generic way and another which the input of the vital dynamics flow is given in a specific way, making the total population constant in time. A model of the SEIR type with vaccination is presented in Sect. 3. In both models the stability of the equilibrium points that correspond the disease free population and the population extinction are analyzed qualitatively and in the particular model of Sect. 2 we also analyze the equilibrium point represents the population in conviviality with the disease. In addition, the basic reproduction number is calculated for the models shown. Finally, in Sect. 4, we present our results and conclusions.

2 SEIRS model

In this section we present two epidemiological models of the type SEIRS, in both we consider the heterogeneous infectivity as proposed by Leite (1999).

The first is a general model in which the input flow of vital dynamics into the compartment of susceptible individuals is given by a generic function. From this structure, we analyzed two equilibrium points, which represents the disease free population and the population extinction. Moreover, we calculated the basic reproduction number and correlated this threshold with our result on the stability of the equilibrium point representing the disease free population.

The second model is a particular case for the function that models the input flow of vital dynamics making the total population constant in time. The aim of presenting this model is to try to infer some result about the stability of the endemic equilibrium point.

2.1 SEIRS general model

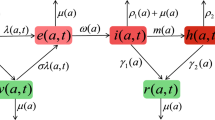
In the SEIRS type model, an individual who is susceptible (S(t)) to a successful encounter with an infectious individual (I(t)) passes into the exposed compartment (E(t)) . In this category, the individual is infected, but does not yet have the ability to transmit the disease. After the time of incubation of the invading pathogen passes, the individual is considered infectious, as soon as the infectious period ceases, it is removed to the compartment of the recovered (R(t)), in this category, the individual has temporary immunity to the disease, again being susceptible again.

For the formulation of the model was used the classical mass action law in homogeneously mixed individuals within a community, and we considered only direct horizontal transmission, in addition, we incorporate heterogeneous infectivity by dividing the infectious compartment into k stages, in which all susceptible contaminated individuals will pass, resulting in the following system of \(k+3\) differential equations

$$\begin{aligned} \left\{ \begin{array}{l} \displaystyle \dfrac{\mathrm{d}S}{\mathrm{d}t}= f(S,E,I_1,\ldots ,I_k,R) - \beta S \sum _{i=1}^k{\epsilon _i I_i}-\mu S+\delta R \\ \displaystyle \dfrac{\mathrm{d}E}{\mathrm{d}t} = \beta S \sum _{i=1}^k{\epsilon _i I_i} - (\sigma +\mu )E \\ \displaystyle \dfrac{\mathrm{d}I_1}{\mathrm{d}t}= \sigma E - (\gamma _1+\mu +\mu _1)I_1\\ \displaystyle \dfrac{\mathrm{d}I_i}{\mathrm{d}t}= \gamma _{i-1}I_{i-1} - (\gamma _i+\mu +\mu _i)I_i; \quad \text {for} \quad i=2,\ldots ,k \\ \displaystyle \dfrac{\mathrm{d}R}{\mathrm{d}t}=\gamma _k I_k - (\delta +\mu )R\\ S(0)=S_0, \quad E(0)=E_0, \quad I_j(0)=I_{j0} \quad j=1,\ldots ,k, \quad \text {and} \quad R(0)=R_0,\\ \end{array} \right. \end{aligned}$$
(1)

where \(f:\mathbb {R}^{k+3} \rightarrow \mathbb {R}\) and all its first order partial derivatives must be continuous. The function f represents the input flow of vital dynamics, which in turn depends on the total population (N) which can be variable in time, that is, f may depend on all compartments \(S,E,I_1,\ldots ,I_k\) e R, since, \(N(t)=S(t)+E(t)+I_1(t)+\cdots +I_k(t)+R(t)\). Moreover, since we are considering only horizontal transmission, the input flow of this dynamic influences only the class of susceptible individuals.

The rates \(\beta \), \(\sigma ^{-1}\), \(\mu \) e \(\delta \) are, respectively, contact rate, mean incubation period, natural mortality and loss of immunity.

The parameters \(\gamma _i^{-1}\), \(\epsilon _i\) and \(\mu _i\) are, respectively, the infectious period, the effectiveness of the transmission and the lethality of the disease in the i-th infectious stage.

Next, we will qualitatively analyze the stability of the equilibrium point representing the disease free population.

2.1.1 Disease free population

The stationary point representing the disease free population is given by \(P_0=(S^*,0,0,\ldots ,0,0)\), where \(S^*>0\) is a solution of equation \(f(S,0,\ldots ,0)-\mu S=0\).

The stability analysis of this point is performed through the Jacobian matrix of the system (1) which is given by:

$$\begin{aligned}&J_{m\times m}\nonumber \\&\quad = \left[ \begin{array}{c c c c c c c} \dfrac{\partial f}{\partial S}-\left( \beta \sum _{i=1}^k{\epsilon _i I_i}+\mu \right) &{} \dfrac{\partial f}{\partial E} &{} \dfrac{\partial f}{\partial I_1} - \beta \epsilon _1 S &{} \dfrac{\partial f}{\partial I_2}-\beta \epsilon _2 S &{} \cdots &{} \dfrac{\partial f}{\partial I_k}-\beta \epsilon _k S &{} \dfrac{\partial f}{\partial R}+ \delta \\ \beta \sum _{i=1}^k{\epsilon _i I_i} &{} -(\sigma +\mu ) &{} \beta \epsilon _1 S &{} \beta \epsilon _2 S &{} \cdots &{} \beta \epsilon _k S &{}0\\ 0 &{} \sigma &{} - (\gamma _1+\mu +\mu _1) &{} 0 &{} \cdots &{} 0 &{} 0\\ 0 &{} 0 &{} \gamma _1 &{} -(\gamma _2+\mu +\mu _2) &{} \cdots &{} 0 &{} 0\\ \vdots &{} \vdots &{} \vdots &{} \vdots &{} \ddots &{} \vdots &{} \vdots \\ 0 &{} 0 &{} 0 &{} 0 &{} \cdots &{}-(\gamma _k+\mu +\mu _k) &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} \cdots &{} \gamma _k &{} -(\mu +\delta ) \end{array}\right] \nonumber \\ \end{aligned}$$
(2)

where \(m=k+3\). This matrix evaluated at \(P_0\) is given below:

$$\begin{aligned} \left[ \begin{array}{c c c c c c c} \left. {\dfrac{\partial f}{\partial S}}\right| _{P_0}-\mu &{} \left. {\dfrac{\partial f}{\partial E}}\right| _{P_0} &{} \left. {\dfrac{\partial f}{\partial I_1}}\right| _{P_0} - \beta \epsilon _1 S^* &{} \left. {\dfrac{\partial f}{\partial I_2}}\right| _{P_0}-\beta \epsilon _2 S^* &{} \cdots &{} \left. {\dfrac{\partial f}{\partial I_k}}\right| _{P_0}-\beta \epsilon _k S^* &{} \left. {\dfrac{\partial f}{\partial R}}\right| _{P_0}+ \delta \\ 0 &{} -(\sigma +\mu ) &{} \beta \epsilon _1 S^* &{} \beta \epsilon _2 S^* &{} \cdots &{} \beta \epsilon _k S^* &{} 0\\ 0 &{} \sigma &{} - (\gamma _1+\mu +\mu _1) &{} 0 &{} \cdots &{} 0 &{} 0\\ 0 &{} 0 &{} \gamma _1 &{} -(\gamma _2+\mu +\mu _2) &{} \cdots &{} 0 &{} 0\\ \vdots &{} \vdots &{} \vdots &{} \vdots &{} \ddots &{} \vdots &{} \vdots \\ 0 &{} 0 &{} 0 &{} 0 &{} \cdots &{}-(\gamma _k+\mu +\mu _k) &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} \cdots &{} \gamma _k &{} -(\mu +\delta ) \end{array}\right] . \end{aligned}$$
(3)

The eigenvalues of the matrix given above are \(\lambda _1=\left. {\dfrac{\partial f}{\partial S}}\right| _{P_0}-\mu \) and \(\lambda _2=-(\mu +\delta )\) plus the eigenvalues of the matrix \(A \in \mathbb {R}^{n\times n}\), being \(n=k+1\)

$$\begin{aligned} A=\left[ \begin{array}{c c c c c c} -(\sigma +\mu ) &{} \beta \epsilon _1 S^* &{} \beta \epsilon _2 S^* &{} \cdots &{} \beta \epsilon _{k-1}S^* &{} \beta \epsilon _k S^*\\ \sigma &{} - (\gamma _1+\mu +\mu _1) &{} 0 &{} \cdots &{} 0 &{} 0 \\ 0 &{} \gamma _1 &{} -(\gamma _2+\mu +\mu _2) &{} \cdots &{} 0 &{} 0 \\ \vdots &{} \vdots &{} \vdots &{} \ddots &{} \vdots &{} \vdots \\ 0 &{} 0 &{} 0 &{} \cdots &{} -(\gamma _{k-1}+\mu +\mu _{k-1}) &{} 0 \\ 0 &{} 0 &{} 0 &{} \cdots &{} \gamma _{k-1} &{} -(\gamma _k+\mu +\mu _k) \\ \end{array}\right] . \end{aligned}$$
(4)

The characteristic polynomial of matrix A is given by \(P_A(\lambda )=det(\lambda I - A)=\lambda ^n+a_1\lambda ^{n-1}+\cdots +a_{n-1}\lambda +a_n\). For \(k=1\), \(k=2\) and \(k=3\) the polynomials are given, respectively, by

$$\begin{aligned} \displaystyle P_{A_{2}}(\lambda )= & {} (\lambda +\sigma +\mu ) (\lambda +\gamma _1+\mu +\mu _1)-\sigma \beta \epsilon _1 S^* \end{aligned}$$
(5)
$$\begin{aligned} \displaystyle P_{A_{3}}(\lambda )= & {} (\lambda +\sigma +\mu ) \prod _{j=1}^2{(\lambda +\gamma _j+\mu +\mu _j)}-\sigma \beta S^* \left[ \epsilon _1 (\lambda +\gamma _2+\mu +\mu _2) + \epsilon _2 \gamma _1\right] \nonumber \\\end{aligned}$$
(6)
$$\begin{aligned} \displaystyle P_{A_{k+1}}(\lambda )= & {} (\lambda +\sigma +\mu ) \prod _{j=1}^k{(\lambda +\gamma _j+\mu +\mu _j)}\nonumber \\&-\sigma \beta S^* \left[ \epsilon _1 \prod _{j=2}^k{(\lambda +\gamma _j+\mu +\mu _j)} \right. \nonumber \\&\left. + \sum _{i=2}^{k-1}{\epsilon _i} \prod _{j=i+1}^k{(\lambda +\gamma _j+\mu +\mu _j)} \prod _{m=1}^{i-1}{\gamma _m} + \epsilon _k \prod _{m=1}^{k-1}{\gamma _m}\right] . \end{aligned}$$
(7)

Thus, the independent terms of (5), (6) and (7) are given, respectively, by:

$$\begin{aligned} a_2= & {} (\sigma +\mu ) (\gamma _1+\mu +\mu _1)-\sigma \beta \epsilon _1 S^* \end{aligned}$$
(8)
$$\begin{aligned} a_3= & {} (\sigma +\mu ) \prod _{j=1}^2{(\gamma _j+\mu +\mu _j)}-\sigma \beta S^* \left[ \epsilon _1 (\gamma _2+\mu +\mu _2) + \epsilon _2 \gamma _1\right] \end{aligned}$$
(9)
$$\begin{aligned} \displaystyle a_n=a_{k+1}= & {} (\sigma +\mu ) \prod _{j=1}^k{(\gamma _j+\mu +\mu _j)}\nonumber \\&-\sigma \beta S^* \left[ \epsilon _1 \prod _{j=2}^k{(\gamma _j+\mu +\mu _j)} \right. \nonumber \\&\left. + \sum _{i=2}^{k-1}{\epsilon _i} \prod _{j=i+1}^k{(\gamma _j+\mu +\mu _j)} \prod _{m=1}^{i-1}{\gamma _m} + \epsilon _k \prod _{m=1}^{k-1}{\gamma _m}\right] . \end{aligned}$$
(10)

Qualitative stability analysis of equilibrium points can be performed by Routh-Hurwitz criteria, this technique analyzes the determinants of the Hurwitz matrices, as follows:

Theorem 1

(Routh-Hurwitz Criteria) Given the characteristic equation (5), define k matrices as follows:

$$\begin{aligned} H_1= & {} (a_1), H_2=\left( \begin{array}{cc}a_1 &{} 1 \\ a_3 &{} a_2 \end{array} \right) , H_3=\left( \begin{array}{ccc}a_1 &{} 1 &{} 0 \\ a_3 &{} a_2 &{} a_1\\ a_5 &{} a_4 &{} a_3\end{array} \right) ,\ldots \\ H_j= & {} \left( \begin{array}{cccccc}a_1 &{} 1 &{} 0 &{} 0 &{} \ldots &{} 0\\ a_3 &{} a_2 &{} a_1 &{} 1 &{} \ldots &{} 0\\ a_5 &{} a_4 &{} a_3 &{} a_2 &{} \ldots &{} 0\\ a_{2j-1} &{} a_{2j-2} &{} a_{2j-3} &{} a_{2j-4} &{} \ldots &{} a_j \end{array} \right) \ldots H_k=\left( \begin{array}{ccccc}a_1 &{} 1 &{} 0 &{} \ldots &{} 0\\ a_3 &{} a_2 &{} a_1 &{} \ldots &{} 0\\ \vdots &{} \vdots &{} \vdots &{} &{} \vdots \\ 0 &{} 0 &{} \ldots &{} &{} a_k \end{array} \right) \end{aligned}$$

where the (l, m) term in the matrix \(H_j\) is

$$\begin{aligned} \begin{array}{cl} a_{2l-m} &{} \text {for} \quad 0<2l-m<k,\\ 1 &{} \text {for} \quad 2l<m,\\ 0 &{} \text {for} \quad 2l<m \quad \text {or} \quad 2l>k+m.\\ \end{array} \end{aligned}$$

Then all eigenvalues have negative real parts, that is, the steady-state \(P_0\) is stable if and only if the determinants of all Hurwitz matrices are positive:

$$\begin{aligned} \det H_j >0 \quad j=1,2,\ldots ,k \end{aligned}$$

(Edelstein-Keshet (1988)).

Routh-Hurwitz criteria is precise but cumbersome method for determining stability of a large system. To facilitate the qualitative stability analysis of equilibrium points that represent the disease free population and the population extinction, we will present Theorem 2 and Theorem 3.

Following are some results that will be used in the demonstration of the Theorem 2, which analyzes the stability of the point \(P_0\).

Lemma 1

Consider the model described by (1) by the inclusion of one more infectious stage, that is, we are considering \(k+1\) infectious stages. Then the characteristic polynomial corresponding to the increased matrix \(\overline{A}\) size \(k+2\) may be written in recurring form:

$$\begin{aligned} \begin{array}{l} \displaystyle P_{\overline{A}}(\lambda )=(\lambda +\gamma _{k+1}+\mu +\mu _{k+1}) P_{A}(\lambda ) - \sigma \beta S^* \epsilon _{k+1} \prod _{m=1}^{k}{\gamma _m}\\ \end{array}, \end{aligned}$$
(11)

where \(\overline{A}= \left[ \begin{array}{cc} A &{} b\\ c^t &{} -(\gamma _{k+1}+\mu +\mu _{k+1}) \end{array} \right] \), \(b^t=\begin{array}{c c c c}(\beta \epsilon _{k+1} S^*&0&\ldots&0)\end{array}\) and \(c^t=\begin{array}{c c c c}(0&\ldots&0&\gamma _k) \end{array}\) being b and c column vectors of size \(k+1\), where A is given in (4).

Proof

In fact, through the characteristic polynomial given in (6) we get,

$$\begin{aligned}&\displaystyle P_{A_{3}}(\lambda )=\left[ (\lambda +\sigma +\mu ) (\lambda +\gamma _1+\mu +\mu _1)-\sigma \beta \epsilon _1 S^* \right] (\lambda +\gamma _2+\mu +\mu _2) - \sigma \beta S^* \epsilon _2 \gamma _1\\&\quad =(\lambda +\gamma _2+\mu +\mu _2) P_{A_{2}}(\lambda )-\sigma \beta S^* \epsilon _2 \gamma _1. \end{aligned}$$

The characteristic polynomial in (7) for \(k=3\) is given by:

$$\begin{aligned} \displaystyle P_{A_{4}}(\lambda )= & {} (\lambda +\sigma +\mu ) \prod _{j=1}^3{(\lambda +\gamma _j+\mu +\mu _j)}\nonumber \\&\quad -\,\sigma \beta S^* \left[ \epsilon _1 \prod _{j=2}^3{(\lambda +\gamma _j+\mu +\mu _j)} + \epsilon _2 (\lambda +\gamma _3+\mu +\mu _3) \gamma _1 + \epsilon _3 \prod _{m=1}^{2}{\gamma _m}\right] \\= & {} \left[ (\lambda +\sigma +\mu ) \prod _{j=1}^2{(\lambda +\gamma _j+\mu +\mu _j)} - \sigma \beta S^* (\epsilon _1 (\lambda +\gamma _2+\mu +\mu _2) + \epsilon _2 \gamma _1) \right] \\&\qquad (\lambda +\gamma _3+\mu +\mu _3) - \sigma \beta S^* \epsilon _3 \prod _{m=1}^{2}{\gamma _m}\\= & {} (\lambda +\gamma _3+\mu +\mu _3) P_{A_{3}} - \sigma \beta S^* \epsilon _3 \prod _{m=1}^{2}{\gamma _m}. \end{aligned}$$

Finally, the characteristic polynomial of the augmented matrix \(\overline{A}\) for \(k\ge 4\) can be obtained through the characteristic polynomial of the matrix A described in (7)

$$\begin{aligned} \displaystyle P_{\overline{A}}(\lambda )= & {} \displaystyle (\lambda +\sigma +\mu ) \prod _{j=1}^{k+1}{(\lambda +\gamma _j+\mu +\mu _j)}\nonumber \\&\quad -\,\sigma \beta S^* \left[ \epsilon _1 \prod _{j=2}^{k+1}{(\lambda +\gamma _j+\mu +\mu _j)} \right. \nonumber \\&\left. + \sum _{i=2}^{k}{\epsilon _i} \prod _{j=i+1}^{k+1}{(\lambda +\gamma _j+\mu +\mu _j)} \prod _{m=1}^{i-1}{\gamma _m} + \epsilon _{k+1} \prod _{m=1}^{k}{\gamma _m}\right] \nonumber \\= & {} \displaystyle (\lambda +\sigma +\mu ) \prod _{j=1}^{k}{(\lambda +\gamma _j+\mu +\mu _j)} (\lambda +\gamma _{k+1}+\mu +\mu _{k+1})\nonumber \\&\quad -\,\sigma \beta S^* \left[ \epsilon _1 \prod _{j=2}^{k}{(\lambda +\gamma _j+\mu +\mu _j)} (\lambda +\gamma _{k+1}+\mu +\mu _{k+1})\right. \nonumber \\&\quad \left. + \sum _{i=2}^{k-1}{\epsilon _i} \prod _{j=i+1}^{k}{(\lambda +\gamma _j+\mu +\mu _j)} (\lambda +\gamma _{k+1}+\mu +\mu _{k+1}) \prod _{m=1}^{i-1}{\gamma _m} \right. \nonumber \\&\left. + \epsilon _k (\lambda +\gamma _{k+1}+\mu +\mu _{k+1}) \prod _{m=1}^{k-1}{\gamma _m} + \epsilon _{k+1} \prod _{m=1}^{k}{\gamma _m} \right] \nonumber \\= & {} \displaystyle (\lambda +\gamma _{k+1}+\mu +\mu _{k+1}) \left[ (\lambda +\sigma +\mu ) \prod _{j=1}^{k}{(\lambda +\gamma _j+\mu +\mu _j)}\right. \nonumber \\&\quad -\,\sigma \beta S^* \left[ \epsilon _1 \prod _{j=2}^{k}{(\lambda +\gamma _j+\mu +\mu _j)} + \sum _{i=2}^{k-1}{\epsilon _i} \prod _{j=i+1}^{k}{(\lambda +\gamma _j+\mu +\mu _j)} \prod _{m=1}^{i-1}{\gamma _m} \right. \nonumber \\&\left. \left. + \epsilon _k \prod _{m=1}^{k-1}{\gamma _m}\right] \right] -\, \sigma \beta S^* \epsilon _{k+1} \prod _{m=1}^{k}{\gamma _m}\nonumber \\= & {} \displaystyle (\lambda +\gamma _{k+1}+\mu +\mu _{k+1}) P_{A}(\lambda ) - \sigma \beta S^* \epsilon _{k+1} \prod _{m=1}^{k}{\gamma _m}. \end{aligned}$$
(12)

\(\square \)

Corollary 1

The independent term of the characteristic polynomial of the augmented matrix \(\overline{A}\) can recursively given as

$$\begin{aligned} \displaystyle a_n^{k+1}=(\gamma _{k+1}+\mu +\mu _{k+1}) a_n^{k} -\sigma \beta S^* \epsilon _{k+1} \prod _{m=1}^{k}{\gamma _m} \end{aligned}$$
(13)

for all \(k \ge 1\), where \(a_n^{k}\) is the independent term of the characteristic polynomial of the matrix A.

Corollary 2

If the independent term \(a_n\) of the characteristic polynomial of matrix A given in(4) is positive, then all other coefficients of this polynomial are also positive.

Proof

We show by finite induction in the order of the matrix A.

For \(k=1\), we have

$$\begin{aligned} P_{A_{2}}(\lambda )=(\lambda +\sigma +\mu ) (\lambda +\gamma _1+\mu +\mu _1)-\sigma \beta \epsilon _1 S^*. \end{aligned}$$
(14)

Note that it is independent of the sign of the term \(a_2=(\sigma +\mu ) (\gamma _1+\mu +\mu _1)-\sigma \beta \epsilon _1 S^* \), we have \(a_1=\sigma +2\mu +\gamma _1+\mu _1 >0\).

Induction Hypothesis: If \(a_n^{k}>0\) then \(a_i^{k}>0 \quad \forall i=1,\ldots ,n-1\), where \(a_n^{k}\) is the independent term of the characteristic polynomial of the matrix A that has size \(k+1\).The characteristic polynomial corresponding to the matrix A can be given by:

$$\begin{aligned} \begin{array}{l} \displaystyle P_{A_{k+1}}(\lambda )=(\lambda +\gamma _{k+1}+\mu +\mu _{k+1}) P_{A_k}(\lambda ) - \sigma \beta S^* \epsilon _{k+1} \prod _{m=1}^{k}{\gamma _m}.\\ \end{array} \end{aligned}$$
(15)

Now, if \(a_n^{k+1}>0\), that is, if the term independent of the characteristic polynomial of the increased matrix \(\overline{A}\) size \(k+2\) is positive, then by Corollary 1 we have

$$\begin{aligned} \begin{array}{r c l c} \displaystyle (\gamma _{k+1}+\mu +\mu _{k+1}) a_n^{k} -\sigma \beta S^* \epsilon _{k+1} \prod _{m=1}^{k}{\gamma _m} &{}> &{} 0 &{} \Rightarrow \\ \displaystyle (\gamma _{k+1}+\mu +\mu _{k+1}) a_n^{k}> \sigma \beta S^* \epsilon _{k+1} \prod _{m=1}^{k}{\gamma _m} &{}>&{} 0 &{} \Rightarrow \\ \displaystyle a_n^{k} &{} > &{} 0. &{}\\ \end{array} \end{aligned}$$
(16)

In this way, if \(a_n^{k+1}>0\) then \(a_n^{k}>0\) and by the induction hypothesis we have \(a_i^{k}>0 \quad \forall i=1,...,n-1\).

Thus, due to the (15) we can guarantee that \(a_i^{k+1}>0 \quad \forall i=1,\ldots ,n-1\). \(\square \)

Corollary 3

If \(a_n>0\) then the characteristic polynomial of the matrix A, \(P_A(\lambda )\), is strictly increasing for all \(\lambda \ge 0\).

Proof

In fact, deriving \(P_A\) in relation to \(\lambda \) we get,

$$\begin{aligned} P'_A(\lambda )=n\lambda ^{n-1}+a_1(n-1)\lambda ^{n-2}+\cdots +a_{n-1}. \end{aligned}$$

Since \(a_n>0\), by Corollary 2 we have \(a_i>0 \quad \forall i=1,\ldots ,n-1\). This ensures that \(P'_A >0\) for all \(\lambda \ge 0\), implying that \(P_A(\lambda )\) is strictly increasing for all \(\lambda \ge 0\). \(\square \)

Lemma 2

(Martin 1978) Let \(A=(a_{ij}) \in \mathbb {R}^{n \times n}\) be a quasimonotone matrix, that is, \(a_{ij} \ge 0, i \ne j\) and let \(\sigma (A)\) be a set of eigenvalues of A. If \(\lambda ^*=max\{Re(\lambda ), \lambda \in \sigma (A)\}\), then \(\lambda ^* \in \sigma (A)\). In addition, there is a nonzero vector \(\xi \in \mathbb {R}_+^n\) such that \(A \xi =\lambda ^* \xi \).

The following theorem establishes necessary and sufficient conditions for asymptotic equilibrium stability representing the disease free population. This result, which we propose, generalizes the theorem presented in Leite et al. (2000).

Theorem 2

: The equilibrium point \(P_0\) of system (1) is locally asymptotically stable if \(\left. {\dfrac{\partial f}{\partial S}}\right| _{P_0}<\mu \) and the independent term \(a_n\) of characteristic polynomial of matrix A (4) is positive and is unstable if \(a_n\) is negative or \(\left. {\dfrac{\partial f}{\partial S}}\right| _{P_0} > \mu \).

Proof

Assume that \(\left. {\dfrac{\partial f}{\partial S}}\right| _{P_0} < \mu \) and \(a_n>0\), then we will demonstrate the eigenvalues of matrix evaluated at \(P_0\) given in (3) have strictly negative real part.

The eigenvalues of matrix given in (3) are \(\lambda _1=\left. {\dfrac{\partial f}{\partial S}}\right| _{P_0} -\mu \) and \(\lambda _2=-(\mu +\delta )\) plus the eigenvalues of the matrix A given in (4).

Since \(\left. {\dfrac{\partial f}{\partial S}}\right| _{P_0} < \mu \) and \(\mu +\delta > 0\), it follows that \(\lambda _1<0\) and \(\lambda _2<0\). Moreover, note that the matrix A is quasimonotone, then by Lemma 2, \(\lambda ^* \in \sigma (A)\) where \(\sigma (A)\) is the set of eigenvalues of A and \(\lambda ^*=max\{Re(\lambda ), \lambda \in \sigma (A)\}\).

Thus \(Re(\lambda )<\lambda ^*\) for all \(\lambda \in \sigma (A)\). Furthermore, as \(a_n>0\) then \(P_A(\lambda )\) is strictly increasing \(\forall \lambda \ge 0\) (by Lemma 3) and as \(P_A(0)=a_n\), it follows that \(P_A(0)>0\) and this implies that A does not have real non-negative eigenvalue and therefore \(\lambda ^*<0\).

Therefore, \(Re(\lambda )<0\) for all \(\lambda \in \sigma (A)\).

Now we will prove that if \(\lambda _1=\left. {\dfrac{\partial f}{\partial S}}\right| _{P_0} -\mu >0\) or \(a_n<0\) then \(P_0\) is unstable.

As \(\lambda _1=\left. {\dfrac{\partial f}{\partial S}}\right| _{P_0} -\mu >0\) is a eigenvalue of matrix given in (3) then \(P_0\) is unstable. Now suppose that \(a_n<0\), the independent term \(a_n\) is calculated as follow,

$$\begin{aligned} \displaystyle a_n=(-1)^n det(A)=(-1)^n \prod _{i=1}^m\lambda _i\prod _{i=1}^l\mu _i \end{aligned}$$

where \(\lambda _i\) and \(\mu _i\) are real and complex eigenvalues, respectively, of A where \(n=m+l\).

As the complex conjugates appear in pairs, then l is always an even number and \(\prod _{i=1}^l{\mu _i}>0\).

If n is an even number then m is necessarily an even number and \((-1)^n\) is positive. As \(a_n<0\) then \(\displaystyle \prod _{i=1}^m{\lambda _i}<0\), and this implies the existence of at least one positive real eigenvalue.

Now, if n is an odd number then m is necessarily an odd number and \((-1)^n\) is negative. As \(a_n<0\) then \(\displaystyle \prod _{i=1}^m{\lambda _i}>0\), and this guarantee the existence of at least one positive real eigenvalue.

Therefore, \(P_0\) is unstable in both cases. \(\square \)

Remark 1

By the second part of the proof of Theorem 2, we can conclude that any equilibrium point of any autonomous system is unstable, if the independent term of the characteristic polynomial of the Jacobian matrix evaluated at this point is negative.

Corollary 4

The stability of the point \(P_0\) of all classical epidemiological submodels that derive from the model (1) by removal of some compartment is locally asymptotically stable if \(\left. {\dfrac{\partial f}{\partial S}}\right| _{P_0}<\mu \) and the independent term \(a_n\) of the characteristic polynomial of matrix A(4), corresponding to the submodel, is positive and is unstable if \(a_n\) is negative or \(\left. {\dfrac{\partial f}{\partial S}}\right| _{P_0} > \mu \).

Proof

The submodels that derive from (1) are \(SEI_1 \ldots I_kR\), \(SEI_1 \ldots I_kS\), \(SEI_1 \ldots I_k\), \(SI_1 \ldots I_kRS\), \(SI_1 \ldots I_kR\), \(SI_1 \ldots I_kS\) and \(SI_1 \ldots I_k\).

(a) In the model \(SEI_1 \ldots I_kR\) there is no loss of immunity, that is, the individual recovered from the disease acquires permanent immunity to reinfection. The eigenvalues of the Jacobian matrix corresponding to this model evaluated at the trivial equilibrium point are the same as the model (1) except for eigenvalue \(\lambda _2\), that is \(\lambda _2=-\,\mu \).

(b) In the model \(SEI_1 \ldots I_kS\) the infectious individual does not acquire immunity to reinfection, they become immediately susceptible soon after the end of the infectious stage. Changes in the Jacobin matrix (2) for this model is the removal of the last column and the last line, because there is no compartment of the recovered and modification in the entry \(J_{1(k+2)}\), which do not compromise the matrix structure, nor the sign of the independent term \( a_n \) of the matrix A. The same justification applies to the \(SEI_1 \ldots I_k\) model .

(c) The latent period is not considered in the model \( SI_1 \ldots I_kRS \), in other words, in this model it is disregarded the period in which the pathogen is incubated in the body and infected individual cannot transmit the disease. The only eigenvalues changed are from the matrix A. But the matrix A for this model maintains the same structure as the old one. Therefore, it preserves all the results demonstrated here.

(d) For analogous justifications, the same goes for the models \(SI_1 \ldots I_kR\), \(SI_1 \ldots I_kS\) and \(SI_1 \ldots I_k\). \(\square \)

The Theorem 2 guarantees the asymptotic stability of the equilibrium point \(P_0\), even when the total population is not constant in time. In addition, the hypotheses presented are necessary and sufficient conditions that guarantee the asymptotic stability of the point \(P_0\) when we adjust the input flow of the vital dynamics according to the transmission dynamics of some specific disease. It is noteworthy that only the positivity of the independent term \( a_n \) of the characteristic polynomial of the matrix A given in (4), is not sufficient to ensure the stability of the disease free population equilibrium point.

The Corollary 4 guarantees the asymptotic stability of the point that represents the disease free population of any submodel that derives from the model (1). Even for classic models that do not contemplate heterogeneous infectivity.

In this way, we can conclude that the theorem presented by Leite et al. (2000) is a particular case of the Theorem 2.

2.1.2 Population extinction

The equilibrium point \(P_0\) which represents the disease free population is biologically reasonable when the first coordinate (\(S^*\)) is greater than zero, and this coordinate is obtained by the solution of equation \(f(S,0,\ldots ,0)-\mu S=0\). However, the null solution may be the only solution for this equation. Let’s look at an example.

Example 1

Taking \(f(S,E, I_1,\ldots ,I_k,R)=\alpha (S+E+I_1+ \cdots I_k+R)\) in (1) where \(\alpha \ne \mu \), we have that

\(f(S,0,0,\ldots ,0,0)-\mu S= 0 \Rightarrow (\alpha -\mu )S=0 \Rightarrow S=0.\)

The only solution to the equation \(f(S,0,0,\ldots ,0,0)-\mu S= 0\) is the null solution and the equilibrium point \((0,\ldots ,0)\) represents the extinction of population.

In this case, when \(S^*=0\) we obtain the equilibrium point that represents the population extinction, let us denote this point by \(P_{ext}\) and analyzing it qualitatively, we can verify by the matrices (2) e (4) that this point will be locally asymptotically stable if \(\left. {\dfrac{\partial f}{\partial S}}\right| _{P_{ext}}<\mu \).

By the arguments presented we have the following theorem:

Theorem 3

If the equilibrium point \(P_{ext}\) of system (1) exist, it will be locally asymptotically stable if \(\left. {\dfrac{\partial f}{\partial S}}\right| _{P_{ext}}<\mu \) and will be unstable if \(\left. {\dfrac{\partial f}{\partial S}}\right| _{P_{ext}}>\mu \)

The Theorem 3 presents a practical way to verify and the solution will converge to point \(P_{ext}\), that is, the condition \(\left. {\dfrac{\partial f}{\partial S}}\right| _{P_{ext}}<\mu \) lead a population to extinction.

2.1.3 The basic reproduction number

The basic reproduction number was computed using the methodology presented by van den Driessche and Watmough (2002), which is given by:

$$\begin{aligned} \displaystyle \mathcal {R}_0=\beta S^*\dfrac{\sigma }{\sigma +\mu }\sum _{l=1}^k{\epsilon _l\psi _{l-1}} \end{aligned}$$
(17)

where \( \displaystyle \psi _{l}=\left\{ \begin{array}{ccc} \dfrac{1}{\gamma _1+\mu +\mu _1} &{} \text {if} &{} l=0\\ \dfrac{\displaystyle \prod _{i=1}^l{\gamma _i}}{ \displaystyle \prod _{i=1}^{l+1}{\gamma _i+\mu +\mu _i}} &{}\text {if} &{}l=1,2,\ldots ,k-1. \end{array} \right. \)

Results presented by van den Driessche and Watmough (2002) insure that \(P_0\) is locally asymptotically stable if \(\left. \dfrac{\partial f}{\partial S}\right| _{P_0} <\mu \) and \(\mathcal {R}_0<1\).

The following theorem correlates the independent term \(a_n\) given in (5), (6) and (7) with the basic reproduction number \(\mathcal {R}_0\) given in (17).

Theorem 4

The independent term \(a_n\) given in (5), (6) and (7) is positive, if and only if \(\mathcal {R}_0<1\), where \(\mathcal {R}_0\) is given by (17).

Proof

For \(k=1\), the basic reproduction number is given by \(\mathcal {R}_0=\beta S^*\dfrac{\sigma }{\sigma +\mu }\dfrac{\epsilon _1}{\gamma _1+\mu +\mu _1}\) and \(n=2\) and it follows from (8) that

$$\begin{aligned} a_2= & {} (\sigma +\mu )(\gamma _1+\mu +\mu _1)-\sigma \beta \epsilon _1 S^* = (\sigma +\mu )(\gamma _1+\mu +\mu _1)\\&\times \left( 1-\dfrac{\sigma \beta \epsilon _1 S^*}{(\sigma +\mu )(\gamma _1+\mu +\mu _1)}\right) \\= & {} (\sigma +\mu )(\gamma _1+\mu +\mu _1)(1-R_0). \end{aligned}$$

Thus, \(a_2>0 \Leftrightarrow \mathcal {R}_0<1\).

For \(k=2\), \(\mathcal {R}_0=\beta S^*\dfrac{\sigma }{\sigma +\mu }\left[ \dfrac{\epsilon _1}{\gamma _1+\mu +\mu _1}+\dfrac{\epsilon _2 \gamma _1}{\prod _{j=1}^2{\gamma _j+\mu +\mu _j}}\right] \) and \(n=3\) and it follows from (9) that

$$\begin{aligned} a_3= & {} (\sigma +\mu )\prod _{j=1}^2{(\gamma _j+\mu +\mu _j)}-\sigma \beta S^*[\epsilon _1(\gamma _2+\mu +\mu _2)+\epsilon _2 \gamma _1]\\= & {} (\sigma +\mu )\prod _{j=1}^2{(\gamma _j+\mu +\mu _j)}\left( 1-\dfrac{\epsilon _1(\gamma _2+\mu +\mu _2)+\epsilon _2 \gamma _1}{(\sigma +\mu )\prod _{j=1}^2{(\gamma _j+\mu +\mu _j)}}\right) \\= & {} (\sigma +\mu )\prod _{j=1}^2{(\gamma _j+\mu +\mu _j)}(1-R_0). \end{aligned}$$

Therefore, \(a_3>0 \Leftrightarrow \mathcal {R}_0<1\).

Finally, for \(k \ge 3\), \(\mathcal {R}_0\) is given by

$$\begin{aligned} \mathcal {R}_0= & {} \beta S^*\dfrac{\sigma }{\sigma +\mu }\\&\times \left[ \dfrac{\epsilon _1 \prod _{j=2}^k{(\gamma _j+\mu +\mu _j)} + \sum _{i=2}^{k-1}{\epsilon _i} \prod _{j=i+1}^k{(\gamma _j+\mu +\mu _j)} \prod _{m=1}^{i-1}{\gamma _m} + \epsilon _k \prod _{m=1}^{k-1}{\gamma _m}}{\prod _{j=1}^k{(\gamma _j+\mu +\mu _j)}}\right] \end{aligned}$$

and \(n \ge 4\) and it follows from (10) that

$$\begin{aligned} a_n= & {} (\sigma +\mu ) \prod _{j=1}^k{(\gamma _j+\mu +\mu _j)}\\&-\,\sigma \beta S^* \left[ \epsilon _1 \prod _{j=2}^k{(\gamma _j+\mu +\mu _j)} + \sum _{i=2}^{k-1}{\epsilon _i} \prod _{j=i+1}^k{(\gamma _j+\mu +\mu _j)} \prod _{m=1}^{i-1}{\gamma _m} + \epsilon _k \prod _{m=1}^{k-1}{\gamma _m}\right] \\= & {} (\sigma +\mu ) \prod _{j=1}^k{(\gamma _j+\mu +\mu _j)}\\&\times \left[ 1-\dfrac{\sigma \beta S^* \left[ \epsilon _1 \prod _{j=2}^k{(\gamma _j+\mu +\mu _j)} + \sum _{i=2}^{k-1}{\epsilon _i} \prod _{j=i+1}^k{(\gamma _j+\mu +\mu _j)} \prod _{m=1}^{i-1}{\gamma _m} + \epsilon _k \prod _{m=1}^{k-1}{\gamma _m}\right] }{(\sigma +\mu ) \prod _{j=1}^k{(\gamma _j+\mu +\mu _j)}} \right] \\= & {} (\sigma +\mu ) \prod _{j=1}^k{(\gamma _j+\mu +\mu _j)}(1-\mathcal {R}_0). \end{aligned}$$

Accordingly, \(a_n>0 \Leftrightarrow \mathcal {R}_0<1\). \(\square \)

The Theorem 4 algebraically correlates the independent term \(a_n\) and \(\mathcal {R}_0\). In addition, it ensures that the independent term \(a_n\) of the characteristic polynomial of matrix A is greater than zero if, and only if, the basal reproduction number of the disease is less than one, in agreement with the presented results. Moreover, we can say that the instability of the disease free point indicates that the disease will invade the population.

2.2 SEIRS model with constant total population

In this subsection we present a particular model given in (1). We consider it a specific function to model the input flow of vital dynamics, for the purpose of making the constant total population. Moreover, we show some results on the stability of the equilibrium points that represent the disease free population and the disease at an endemic level in a community, the latter is called an endemic equilibrium point.

Our main interest is to investigate the stability of the endemic equilibrium point. For this, first, we must make explicit the input flow of vital dynamics and then calculate the endemic equilibrium point and analyze it qualitatively.

The algebraic choice to represent this flow was given so that the total population (N) is constant. Thus, the function that represents the input flow of the vital dynamics is given by \(f(S,E,I_1,\ldots ,I_k,R)=\mu N + \sum _{i=1}^k{\mu _iI_i}\) and the model is given by

$$\begin{aligned} \left\{ \begin{array}{l} \displaystyle \dfrac{dS}{dt}= \mu N + \sum _{i=1}^k{\mu _iI_i} - \beta S \sum _{i=1}^k{\epsilon _i I_i}-\mu S+\delta R \\ \displaystyle \dfrac{\mathrm{d}E}{\mathrm{d}t} = \beta S \sum _{i=1}^k{\epsilon _i I_i} - (\sigma +\mu )E \\ \displaystyle \dfrac{\mathrm{d}I_1}{\mathrm{d}t}= \sigma E - (\gamma _1+\mu +\mu _1)I_1\\ \displaystyle \dfrac{dI_i}{dt}= \gamma _{i-1}I_{i-1} - (\gamma _i+\mu +\mu _i)I_i; \quad \text {for} \quad i=2,\ldots ,k \\ \displaystyle \dfrac{\mathrm{d}R}{\mathrm{d}t}=\gamma _k I_k - (\delta +\mu )R\\ S(0)=S_0, \quad E(0)=E_0, \quad I_j(0)=I_{j0} \quad j=1,\ldots ,k, \quad R(0)=R_0.\\ \end{array} \right. \end{aligned}$$
(18)

Since the sum of the compartments is equal to the total population, that is, \(N(t)=S(t)+E(t)+\sum _{i=1}^k{I_i(t)}+R(t)\) and \(\dfrac{dN}{dt}=0\), it follows that the total population is constant at any instant.

The equilibrium points are given by \((\overline{S},0,\ldots ,0)\) and \((S^{*},E^*,\overline{I_1},I_2^{*},\ldots ,I_k^{*},R^*)\), where \(\overline{S}\) and \(\overline{I_1}\) are free and

$$\begin{aligned} \left\{ \begin{array}{l} \displaystyle S^*=\dfrac{N}{\mathcal {R}_0}\\ \displaystyle E^*= \dfrac{(\gamma _1+\mu +\mu _1)}{ \sigma } \overline{I_1} \\ \displaystyle I_j^*=\displaystyle \dfrac{\prod _{i=1}^{j-1}{\gamma _i}}{\prod _{i=2}^j{(\gamma _i+\mu +\mu _i)}} \overline{I_1} \quad \text {for} \quad j=2,\ldots ,k\\ \displaystyle R^*=\dfrac{\prod _{i=1}^{k}{\gamma _i}}{(\mu +\delta )\prod _{i=1}^k{(\gamma _i+\mu +\mu _i)}} \overline{I_1}.\\ \end{array} \right. \end{aligned}$$
(19)

Since the total population size is constant for any instant of time, then if the solution of the model approaches any of the two equilibrium points for large values of t, we have that the trajectory S approaches N or is approaching \(S^{*}=\dfrac{N}{\mathcal {R}_0}\) and the trajectory \(I_1\) approaches 0 or is approaching \(N-(S(t)+E(t)+\sum _{i=2}^k{I_i(t)}+R(t))\), respectively.

Considering the above, we will analyze only the equilibrium points \(P_0=(N,0,\ldots ,0)\) and \(P_e=(S^{*},E^*,I_1^{*},\ldots ,I_k^{*},R^*)\), where

$$\begin{aligned} \left\{ \begin{array}{l} \displaystyle S^*=\dfrac{N}{\mathcal {R}_0}\\ \displaystyle E^*=\dfrac{N }{\mathcal {R}_0}\dfrac{ (\mathcal {R}_0-1)}{M} \dfrac{(\gamma _1+\mu +\mu _1)}{ \sigma } \\ \displaystyle I_1^*=\dfrac{N }{\mathcal {R}_0}\dfrac{ (\mathcal {R}_0-1)}{M}\\ \displaystyle I_j^*=\dfrac{N}{\mathcal {R}_0}\dfrac{(\mathcal {R}_0-1)}{M}\displaystyle \dfrac{\prod _{i=1}^{j-1}{\gamma _i}}{\prod _{i=2}^j{(\gamma _i+\mu +\mu _i)}} \quad \text {for} \quad j=2,\ldots ,k\\ \displaystyle R^*=\dfrac{N}{\mathcal {R}_0}\dfrac{(\mathcal {R}_0-1)}{M}\dfrac{\prod _{i=1}^{k}{\gamma _i}}{(\mu +\delta )\prod _{i=1}^k{(\gamma _i+\mu +\mu _i)}}\\ \end{array} \right. \end{aligned}$$
(20)

and \(M=\displaystyle \left( 1+\dfrac{\gamma _1+\mu +\mu _1}{\sigma }+\displaystyle \sum _{j=1}^{k-1}{\dfrac{\prod _{i=1}^j{\gamma _i}}{\prod _{i=2}^{j+1}{(\gamma _i+\mu +\mu _i)}}} + \dfrac{\prod _{i=1}^k{\gamma _i}}{(\mu +\delta )\prod _{i=2}^k{(\gamma _i+\mu +\mu _i)}}\right) \).

Having determined the equilibrium points of our interest, we will make a qualitative analysis of these points. For the equilibrium point \(P_0\) we have checked the possibility of using the Theorem 2.

We have that \(f=\mu N + \sum _{i=1}^k{\mu _iI_i}\), then \(\left. {\dfrac{\partial f}{\partial S}}\right| _{P_0}=\mu \). Therefore, the first hypothesis of the Theorem 2 not satisfied. In addition, as \(\left. {\dfrac{\partial f}{\partial S}}\right| _{P_0}-\mu =0\) is the input of line 1 and column 1 of the matrix (3), it follows that the independent term of the characteristic polynomial associated with the matrix (3) is zero.

Given the impossibility of using the Theorem 2 to infer about the stability of the point \(P_0\), we will reduce the model given by (18) by

$$\begin{aligned} \left\{ \begin{array}{l} \displaystyle \dfrac{\mathrm{d}E}{\mathrm{d}t} = \beta \left( N-\left( E+\sum _{i=1}^k{I_i}+R\right) \right) \sum _{i=1}^k{\epsilon _i I_i} - (\sigma +\mu )E \\ \displaystyle \dfrac{\mathrm{d}I_1}{\mathrm{d}t}= \sigma E - (\gamma _1+\mu +\mu _1)I_1\\ \displaystyle \dfrac{\mathrm{d}\mathrm{d}I_i}{\mathrm{d}\mathrm{d}t}= \gamma _{i-1}I_{i-1} - (\gamma _i+\mu +\mu _i)I_i; \quad \text {for} \quad i=2,\ldots ,k \\ \displaystyle \dfrac{\mathrm{d}R}{\mathrm{d}t}=\gamma _k I_k - (\delta +\mu )R.\\ \end{array} \right. \end{aligned}$$
(21)

where \(S(t)=N-(E(t)+\sum _{i=1}^k{I_i(t)}+R(t))\). Thus, we have that the first line of the Jacobian matrix is given by the entries

$$\begin{aligned} \begin{array}{l} J_{11}=-\,\left( \beta \sum _{i=1}^k{\epsilon _i I_i}+\sigma +\mu \right) \\ J_{12}=- \,\beta \sum _{i=1}^k{\epsilon _i I_i}+\beta \epsilon _1 \left( N-\left( E+\sum _{i=1}^k{I_i}+R\right) \right) \\ J_{13}=- \,\beta \sum _{i=1}^k{\epsilon _i I_i}+\beta \epsilon _2 \left( N-\left( E+\sum _{i=1}^k{I_i}+R\right) \right) \\ J_{14}=-\, \beta \sum _{i=1}^k{\epsilon _i I_i}+\beta \epsilon _3 \left( N-\left( E+\sum _{i=1}^k{I_i}+R\right) \right) \\ \vdots \\ J_{1(k+1)}=- \,\beta \sum _{i=1}^k{\epsilon _i I_i}+\beta \epsilon _k \left( N-\left( E+\sum _{i=1}^k{I_i}+R\right) \right) \\ J_{1(k+2)}=-\,\beta \sum _{i=1}^k{\epsilon _i I_i}.\\ \end{array} \end{aligned}$$
(22)

In this way, we have that the Jacobian matrix of the model (21) evaluated at (0, 0, ..., 0) is given by:

$$\begin{aligned} \left[ \begin{array}{c c c c c c} -(\sigma +\mu ) &{} \beta \epsilon _1 N &{} \beta \epsilon _2 N &{} \cdots &{} \beta \epsilon _k N &{} 0\\ \sigma &{} - (\gamma _1+\mu +\mu _1) &{} 0 &{} \cdots &{} 0 &{} 0\\ 0 &{} \gamma _1 &{} -(\gamma _2+\mu +\mu _2) &{} \cdots &{} 0 &{} 0\\ \vdots &{} \vdots &{} \vdots &{} \ddots &{} \vdots &{} \vdots \\ 0 &{} 0 &{} 0 &{} \cdots &{}-(\gamma _k+\mu +\mu _k) &{} 0 \\ 0 &{} 0 &{} 0 &{} \cdots &{} \gamma _k &{} -(\mu +\delta ) \end{array}\right] . \end{aligned}$$
(23)

The eigenvalues of the matrix (23) above are \(-(\mu +\delta )\) plus the eigenvalues of the matrix

$$\begin{aligned} \left[ \begin{array}{c c c c c} -(\sigma +\mu ) &{} \beta \epsilon _1 N &{} \beta \epsilon _2 N &{} \cdots &{} \beta \epsilon _k N \\ \sigma &{} - (\gamma _1+\mu +\mu _1) &{} 0 &{} \cdots &{} 0 \\ 0 &{} \gamma _1 &{} -(\gamma _2+\mu +\mu _2) &{} \cdots &{} 0 \\ \vdots &{} \vdots &{} \vdots &{} \ddots &{} \vdots \\ 0 &{} 0 &{} 0 &{} \cdots &{}-(\gamma _k+\mu +\mu _k) \\ \end{array}\right] . \end{aligned}$$
(24)

The matrix (24) is equals the matrix A given in (4). Therefore, equilibrium point \(P_0\) is locally stable if and only if the independent term \(a_n\) of characteristic polynomial of matrix A given in (4) is positive.

Now we will check the local stability of the endemic equilibrium point \(P_e=(S^{*},E^*,I_1^{*},ldots,I_k^{*},R^*)\). The Jacobian matrix of the model (21) evaluated at point \((E^*,I_1^{*},\ldots ,I_k^{*},R^*)\) is given by

$$\begin{aligned} \left[ \begin{array}{c c c c c c} J_{11}(P_e) &{} J_{12}(P_e) &{} J_{13}(P_e) &{} \cdots &{} J_{1(k+1)}(P_e) &{} J_{1(k+2)}(P_e) \\ \sigma &{} -(\gamma _1+\mu +\mu _1) &{} 0 &{} \cdots &{} 0 &{} 0\\ 0 &{} \gamma _1 &{} -(\gamma _2+\mu +\mu _2) &{} \cdots &{} 0 &{} 0\\ \vdots &{} \vdots &{} \vdots &{} \ddots &{} \vdots &{} \vdots \\ 0 &{} 0 &{} 0 &{} \cdots &{}-(\gamma _k+\mu +\mu _k) &{} 0 \\ 0 &{} 0 &{} 0 &{} \cdots &{} \gamma _k &{} -(\mu +\delta ) \end{array}\right] , \end{aligned}$$
(25)

where

$$\begin{aligned} \begin{array}{l} J_{11}(P_e)=-\,\left( \dfrac{(\mathcal {R}_0-1)}{M}\dfrac{\sigma +\mu }{\sigma }(\gamma _1+\mu +\mu _1)+\sigma +\mu \right) \\ J_{12}(P_e)=-\, \dfrac{(\mathcal {R}_0-1)}{M}\dfrac{\sigma +\mu }{\sigma }(\gamma _1+\mu +\mu _1)+\beta \epsilon _1 \dfrac{N}{\mathcal {R}_0}\\ J_{13}(P_e)=- \,\dfrac{(\mathcal {R}_0-1)}{M}\dfrac{\sigma +\mu }{\sigma }(\gamma _1+\mu +\mu _1)+\beta \epsilon _2 \dfrac{N}{\mathcal {R}_0}\\ \vdots \\ J_{1(k+1)}(P_e)=-\, \dfrac{(\mathcal {R}_0-1)}{M}\dfrac{\sigma +\mu }{\sigma }(\gamma _1+\mu +\mu _1)+\beta \epsilon _k \dfrac{N}{\mathcal {R}_0}\\ J_{1(k+2)}(P_e)=-\,\left( \dfrac{(\mathcal {R}_0-1)}{M}\dfrac{\sigma +\mu }{\sigma }(\gamma _1+\mu +\mu _1)\right) .\\ \end{array} \end{aligned}$$
(26)

The expression of the independent term of characteristic polynomial of the matrix (25) is given by

$$\begin{aligned} a_n(P_e)=(\mathcal {R}_0-1)L \end{aligned}$$
(27)

where

$$\begin{aligned} L= & {} \dfrac{1}{M}\dfrac{(\sigma +\mu )}{\sigma }(\gamma _1+\mu +\mu _1) \left( (\mu +\delta ) \prod _{i=1}^k{(\gamma _i+\mu +\mu _i)} \right. \nonumber \\&\left. +\, \sigma (\mu +\delta )\left( \sum _{j=1}^{k-1}{\prod _{i=j+1}^k{(\gamma _i+\mu +\mu _i)}\prod _{i=0}^{j-1}{\gamma _i}}+\prod _{i=1}^{k-1}{\gamma _i}\right) +\sigma \prod _{i=1}^{k}{\gamma _i} \right) . \end{aligned}$$
(28)

Note that \(a_n(P_e)\) is positive if and only if \(\mathcal {R}_0\) is greater than one. So this is the necessary condition for the local stability of the endemic equilibrium point \(P_e\) and it is also the sufficient condition for instability of equilibrium point \(P_0\).

Therefore, the instability of the equilibrium \(P_0\) implies the necessary condition for the endemic equilibrium \(P_e\) be locally stable.

Note that the matrix (25) is not quasimonotone matrix. Therefore we cannot use the same methodology applied in the equilibrium stability study that represents the disease free population to infer about the stability of the endemic equilibrium point.

3 SEIR model with vaccination

In the section we present SEIR type model considering vaccination policies and heterogeneous infectivity, similarly exposed in the previous section.

In this model we consider that the susceptible individuals who are vaccinated are transferred to recovered compartment and the recovered individuals acquired immunity to reinfection.

The hypotheses for formulating this model are the same as those presented in the SEIRS general model in Sect. 2. In this way, the ODE system which describes mathematically a model is then the following,

$$\begin{aligned} \left\{ \begin{array}{l} \displaystyle \dfrac{\mathrm{d}S}{\mathrm{d}t}= f(S,E,I_1,\ldots ,I_k,R) - \beta S \sum _{i=1}^k{\epsilon _i I_i}-(\mu +\delta ) S \\ \displaystyle \dfrac{\mathrm{d}E}{\mathrm{d}t} = \beta S \sum _{i=1}^k{\epsilon _i I_i} - (\sigma +\mu )E \\ \displaystyle \dfrac{\mathrm{d}I_1}{\mathrm{d}t}= \sigma E - (\gamma _1+\mu +\mu _1)I_1\\ \displaystyle \dfrac{\mathrm{d}I_i}{\mathrm{d}t}= \gamma _{i-1}I_{i-1} - (\gamma _i+\mu +\mu _i)I_i; \quad \text {for} \quad i=2,\ldots ,k \\ \displaystyle \dfrac{\mathrm{d}R}{\mathrm{d}t}=\gamma _k I_k + \delta S - \mu R\\ S(0)=S_0, \quad E(0)=E_0, \quad I_j(0)=I_{j0} \quad j=1,\ldots ,k, \quad R(0)=R_0.\\ \end{array} \right. \end{aligned}$$
(29)

All parameters have the same representability of the SEIRS general model, except the parameter \(\delta \), which for this model represents the fraction immunized of the susceptible individuals.

As in model given in (1), in this model we also consider induced mortality and the vital dynamics given by a generic function.

3.1 Disease free population

The disease free population equilibrium point for this model is given by \(P_0=(S^*,0,0,0,\ldots 0,R^*)\), where \(S^* >0\) e \(R^* > 0\) are one of the solutions obtained from the system,

$$\begin{aligned} \left\{ \begin{array}{l} f(S,0,0,\ldots ,0,R) - (\mu + \delta ) S =0\\ \delta S - \mu R = 0.\\ \end{array} \right. \end{aligned}$$
(30)

The Jacobian matrix, of size \(m=k+3\), of the system (29) evaluated in the trivial point \(P_0=(S^*,0,0,0,\ldots 0,R^*)\) is given by:

$$\begin{aligned} J(P_0)=\left[ \begin{array}{c c c c c c c} \left. \dfrac{\partial f}{\partial S}\right| _{P_0}-(\mu +\delta ) &{} \left. \dfrac{\partial f}{\partial E} \right| _{P_0} &{} \left. \dfrac{\partial f}{\partial I_1}\right| _{P_0} - \beta \epsilon _1 S^* &{} \left. \dfrac{\partial f}{\partial I_2}\right| _{P_0}-\beta \epsilon _2 S^* &{} \cdots &{} \left. \dfrac{\partial f}{\partial I_k}\right| _{P_0}-\beta \epsilon _k S^* &{} \left. \dfrac{\partial f}{\partial R}\right| _{P_0} \\ 0 &{} -(\sigma +\mu ) &{} \beta \epsilon _1 S^* &{} \beta \epsilon _2 S^* &{} \cdots &{} \beta \epsilon _k S^* &{} 0\\ 0 &{} \sigma &{} - (\gamma _1+\mu +\mu _1) &{} 0 &{} \cdots &{} 0 &{} 0\\ 0 &{} 0 &{} \gamma _1 &{} -(\gamma _2+\mu +\mu _2) &{} \cdots &{} 0 &{} 0\\ \vdots &{} \vdots &{} \vdots &{} \vdots &{} \ddots &{} \vdots &{} \vdots \\ 0 &{} 0 &{} 0 &{} 0 &{} \cdots &{}-(\gamma _k+\mu +\mu _k) &{} 0 \\ \delta &{} 0 &{} 0 &{} 0 &{} \cdots &{} \gamma _k &{} -\mu \end{array}\right] . \end{aligned}$$
(31)

In this way, the characteristic polynomial of the Jacobian matrix evaluated at \(P_0\) is given by \(P(\lambda )=\left( \left( \lambda +\mu +\delta -\left. \dfrac{\partial f}{\partial S}\right| _{P_0}\right) (\lambda +\mu )-\delta \left. \dfrac{\partial f}{\partial R}\right| _{P_0} \right) \det (\lambda I - A)\) where the matrix A is given in (4).

Therefore, the eigenvalues of the matrix \(J(P_0)\) are the eigenvalues of the matrix A plus the eigenvalues given by:

$$\begin{aligned} \lambda _{1,2}=\dfrac{-\left( 2 \mu + \delta - \left. \dfrac{\partial f}{\partial S}\right| _{P_0}\right) \pm \left( \left( 2 \mu + \delta - \left. \dfrac{\partial f}{\partial S}\right| _{P_0} \right) ^2 - 4 \left( \mu \left( \mu +\delta -\left. \dfrac{\partial f}{\partial S}\right| _{P_0} \right) -\delta \left. \dfrac{\partial f}{\partial R}\right| _{P_0} \right) \right) ^{1/2}}{2}. \end{aligned}$$

The necessary and sufficient conditions to ensure that the real part of the eigenvalues \(\lambda _{1,2}\) are negative are

$$\begin{aligned} 2\mu + \delta - \left. \dfrac{\partial f}{\partial S}\right| _{P_0}>0 \end{aligned}$$
(32)

and

$$\begin{aligned} \mu \left( \mu + \delta - \left. \dfrac{\partial f}{\partial S}\right| _{P_0} \right) - \delta \left. \dfrac{\partial f}{\partial R}\right| _{P_0} >0. \end{aligned}$$
(33)

Note that the conditions \(\left. \dfrac{\partial f}{\partial S}\right| _{P_0} <0\) and \(\left. \dfrac{\partial f}{\partial R}\right| _{P_0}<0\) are sufficient to ensure that the real part of the eigenvalues \(\lambda _{1,2}\) are negative.

Therefore, if the conditions (32) and (33) are satisfied and, in addition, the term independent of the characteristic polynomial of the matrix A given in (4) is positive, then the point representing the disease free population of this model is locally asymptotically stable. In this way, we can state the following result:

Corollary 5

The equilibrium point \(P_0\) of system (29) is locally asymptotically stable if \(2\mu + \delta - \left. \dfrac{\partial f}{\partial S}\right| _{P_0}>0\), \(\mu \left( \mu + \delta - \left. \dfrac{\partial f}{\partial S}\right| _{P_0} \right) - \delta \left. \dfrac{\partial f}{\partial R}\right| _{P_0} >0\) and the independent term \(a_n\) of characteristic polynomial of matrix A (4) is positive. Moreover, \(P_0\) is unstable if \(2\mu + \delta - \left. \dfrac{\partial f}{\partial S}\right| _{P_0}<0\), \(\mu \left( \mu + \delta - \left. \dfrac{\partial f}{\partial S}\right| _{P_0} \right) - \delta \left. \dfrac{\partial f}{\partial R}\right| _{P_0}<0\) or \(a_n<0\).

We observed that the only submodel of (29) which contemplates heterogeneity is of the type \(SI_1 \ldots I_KR\) and since there are only changes in the size and some entries of A, the above result remains valid since the array does not lose the property of being quasimonotone matrix.

According to the observation given above, we can state the following result:

Corollary 6

The equilibrium point \(P_0\) of the submodel of (29) is locally asymptotically stable if \(2\mu + \delta - \left. \dfrac{\partial f}{\partial S}\right| _{P_0}>0\), \(\mu \left( \mu + \delta - \left. \dfrac{\partial f}{\partial S}\right| _{P_0} \right) - \delta \left. \dfrac{\partial f}{\partial R}\right| _{P_0} >0\) and the independent term \(a_n\) of characteristic polynomial of matrix A(4), corresponding to the submodel, is positive and is unstable if \(2\mu + \delta - \left. \dfrac{\partial f}{\partial S}\right| _{P_0}<0\), \(\mu \left( \mu + \delta - \left. \dfrac{\partial f}{\partial S}\right| _{P_0} \right) - \delta \left. \dfrac{\partial f}{\partial R}\right| _{P_0}<0\) or \(a_n<0\).

The Corollaries 5 and 6 guarantee that if there is a vaccination policies, the condition of the independent term \(a_n\) of characteristic polynomial of matrix A given in (4) is necessary, however, no sufficient to insures the asymptotic stability of the disease free population equilibrium point.

3.2 Population extinction

The equilibrium point \(P_0=(S^*,0,\ldots ,R^*)\) of the model (29), depends of expression of flow of vital dynamics (f). Once given the expression of f, we must find the coordinates \(S^*>0\) and \(R^*>0\) that satisfy (30). However, as mentioned in subsection 2.1.2, we cannot get such positive coordinates that are system solution (30), let’s look at the example below.

Example 2

Taking \(f(S,E,I_1,\ldots ,I_k,R)=\alpha (S+E+I_1+ \cdots I_k+R)\) in (29) where \(\alpha \ne \mu \), we have that

$$\begin{aligned} \left( \alpha \left( 1+\dfrac{\delta }{\mu }\right) - (\mu + \delta ) \right) S =0 \Rightarrow S=0 \Rightarrow R=0. \end{aligned}$$

Again, in this case we say that the stationary point represents the population extinction denoting it by \( P_{ext}\).

From matrix (31) we can verify that the point \(P_{ext}\) will be locally asymptotically stable if the conditions (32) and (33) are satisfied, and the derivatives of the cited conditions are evaluated at the point \(P_{ext}\). In this way, we can state the following result:

Theorem 5

If the equilibrium point \(P_{ext}\) of system (29) exists, it will be locally asymptotically stable if \(2\mu + \delta - \left. \dfrac{\partial f}{\partial S}\right| _{P_{ext}}>0\) e \(\mu \left( \mu + \delta - \left. \dfrac{\partial f}{\partial S}\right| _{P_{ext}} \right) - \delta \left. \dfrac{\partial f}{\partial R}\right| _{P_{ext}} >0\) and will be unstable if \(2\mu + \delta - \left. \dfrac{\partial f}{\partial S}\right| _{P_{ext}}<0\) or \(\mu \left( \mu + \delta - \left. \dfrac{\partial f}{\partial S}\right| _{P_{ext}} \right) - \delta \left. \dfrac{\partial f}{\partial R}\right| _{P_{ext}} <0\).

Analogous to the Theorem 3, the theorem 5 present a practical way of verifying whether the point \(P_{ext}\) is locally asymptotically stable for the model and submodel of (29).

The basic reproduction number of this model (29) is represented algebraically in the same way as given in (17). The only difference is that \(S^*\) of this model refers to the first coordinate of equilibrium point \(P_0\) of model (29) which is obtained by solving the system (30).

4 Results and conclusions

In this article we propose general compartmental epidemic models described by autonomous ordinary differential equations taking into account that heterogeneous infectivity and vital dynamics is given by a generic function.

For each model, we enunciate and demonstrate a result that analyzes the equilibrium point that represents the disease free population, through the methodology presented by Leite (1999). Briefly, the asymptotic local stability of the disease free equilibrium point is analyzed by the positivity of the term independent of the characteristic polynomial of the matrix A given in (4), plus some hypotheses depending on the model to be used.

The results we have obtained show that the positivity analysis of the term independent of the characteristic polynomial of matrix A, given in (4), is not enough to infer about the stability of the disease free equilibrium point when we change the model proposed by Leite et al. (2000). Therefore, changes in the (Leite et al. (2000)) generate additional hypotheses to guarantee the stability of the equilibrium that represents the disease free population.

The Theorem 2 and the Corollary 4 generalize the Theorem presented by Leite et al. (2000) and presented by Leite (1999). In addition, the Corollary 5 and 6 present the additional hypotheses which are necessary and sufficient conditions for the equilibrium stability that represents the disease free population when considering vaccination policies.

The choice of the function that represents the input flow of the vital dynamics can result in the existence of the equilibrium point that represents the population extinction (\(P_{ext}\)). If this point exists, we propose the Theorems 3 and 5, which analyze the stability of the equilibrium point \(P_{ext}\) of the models givens in (1) and (29).

We consider a particular model of the SEIRS model, which the total population is constant, and we can infer that the local stability of the disease free equilibrium ensures that endemic equilibrium is biologically unviable. Moreover, validation of the condition necessary for endemic equilibrium to be locally stable generates instability of disease free equilibrium point.

Finally, we calculated the basic reproduction number of the disease, and found an algebraic relationship between the term independent of the characteristic polynomial of the matrix A given in (4) and \(\mathcal {R}_0\) (Theorem 4). Thus, we correlate our results (Theorem 2 and Corollaries 4, 5 and 6), with the Theorem presenting van den Driessche and Watmough (2002).