1 Introduction

Berthing operation is one of the most burdensome tasks for crews among several ship operations [1]. Ship’s speed becomes low during berthing operation. The maneuverability of a ship at low speed deteriorates due to reduced rudder effectiveness and becomes more vulnerable to disturbances such as wind. Therefore, berthing operation requires advanced techniques for maneuvering a ship at low speed. On the other hand, in recent years, the domestic shipping industry in Japan has been facing a severe shortage of skilled ship officers and an aging population of seafarers [2]. Hence, it is necessary to support or automate operations that require advanced skills such as berthing operation.

Many studies on the automation of a berthing ship had proposed various approaches using different methods such as a proportional-derivative (PD) controller, neural network, optimal control theory, and evolution strategy. Ahmed et al. [3] proposed a controller that combines feed-forward neural networks and a PD heading controller. In this research, they created training data for an artificial neural network created by using nonlinear programming (NLP) for learning course changing control in the minimum time. They aimed to berth using a model ship of a VLCC tanker which its length is over 300 m in a full scale. In the paper, the accuracy of the final berthing position required to the controller was ± 1.5 L (> 450 m in a full scale). On the other hand, although they did not mention about the computation time in the paper, their method should be fast for the computation time, since it can have been controlled in real-time in the experiments using their model ship. Besides this research, Mizuno et al. [4] proposed the quasi real-time optimal control scheme for automatic berthing operation. This approach solves a minimum time approaching problem based on the formulation by Shoji and Ohtsu [5]. In the paper, the terminal conditions of the problem were set to ± 10 m for the ship position, ± 0.5 m/s for the surge velocity, and \(\pm \,10^{\circ }\) for the heading angle. This method can generate the approximate optimal solution in a few minutes using the multiple shooting algorithm [4]. They carried out experiments with the full-scale ship and obtained results satisfying the terminal conditions for all state valuables except for the heading angle. Maki et al. [6] utilize the covariance matrix adaptation evolution strategy (CMA-ES), which is an evolutionary algorithm to acquire optimal solutions for automatic berthing problems of a ship equipped one rudder and one propeller. The optimal solution obtained in the simulations had an accuracy of the order of \(10^{-4}\) for the L1 norm of the final state vector and the vector of the termination conditions. However, since it takes time to find an optimal solution, the CMA-ES solution can be used as an offline solution for the initial guess of an optimization problem for online control. From these studies, there is a trade-off between the accuracy and the real-time performance on berthing control. The nonlinearity of ship maneuvering motion makes the berthing problem complex.

From a practical standpoint, the automatic berthing algorithm must have sufficiently real-time performance, while maintaining the accuracy required for the berthing control. A simpler controller is required to increase real-time performance, which must have the performance to control a ship with sufficient precision. Here, we consider the problem of berthing control as a problem of autonomous navigation in the field of robotics. In the field of robotics, autonomous navigation usually deals with the following four items: localization, mapping, path planning, and path following. What is essential in this approach is that path planning and path following are separated. This approach simplifies the design of the system because it is possible to separate the design of the path planning and the design of the path following control in advance. A part of Ahmed’s approach [3] is close to this idea. They used the PD controller to follow a line path after changing course by neural networks. On the other hand, it is not always possible to approach the pier in a straight line in the actual berthing operation, so a lightweight algorithm that can follow a general curved path is needed. Besides, the controller should have the versatility to be applied to a typical ship with one rudder and one propeller.

For these purposes, we propose a novel system that applied a path following algorithm in this paper. We conducted field tests using our experimental ship to verify performance of the proposed algorithm. The proposed system performs in both calm wind conditions around 2 m/s and strong wind conditions around 6 m/s. We also describe a mathematical model of ship maneuvering motion at low speed, proposed automatic berthing algorithm. At last, we show results of field tests of automatic berthing control using our small experimental ship equipped with a high-precision positioning device using the Quasi-Zenith Satellite System (QZSS).

This paper is organized as follows: in the next section, we explain the specification of our experimental ship and the onboard control system, followed by a mathematical model of ship motion and model tuning based on full-scale experiment results. In Sect. 4, we describe the novel automatic berthing algorithm that is a combination of the path following algorithm and heading control. The path planning algorithm and the speed control scheme are also provided in this section. Results and evaluation of automatic berthing experiment to a floating pier using our experimental ship are shown in Sect. 5. Finally, we conclude the paper.

2 Subject ship and onboard control system

we utilized the experimental ship “Shinpo” managed by the National Maritime Research Institute shown in Fig. 1. This ship is equipped with one rudder and one propeller. Table 1 shows the principal particulars of Shinpo at the time of experiments. The areas \(A_F\) and \(A_A\) are the projected area of the ship above the waterline. Shinpo is equipped with a MAU-type propeller and a bow thruster.

An onboard control system was constructed to perform automatic berthing control. The architecture of the system is shown in Fig. 2. The control system consists of programmable logic controllers (PLCs), which is reliable and scalable, controls various actuators of the ship. The hydraulic steering system and the remote control system of the main engine can be monitored and operated by PLC, which can operate the rudder, governors (corresponding to engine telegraph command), the clutch, and the bow thruster used in berthing operations. The automatic berthing algorithm is implemented on a laptop computer, which can be connected to the PLC and actuators of the ship can be operated from the laptop computer. All measured sensor values are aggregated into the PLCs, then, recorded and displayed on the touch display connected to a PLC.

For berthing control, various sensors are installed on Shinpo. In the case of berthing operations for Shinpo, it is necessary to guide the ship so that the distance between the side of the ship and the pier is at most about 5 m in order for a deck crew to pass the mooring ropes to the pier stably. On the other hand, according to textbooks of ship handling (e.g. [7, 8]), when approaching the the pier at a low heading angle of 10\(^{\circ }\)–15\(^{\circ }\) against it, the ship should be stopped at a distance of 1.0 B–1.5 B before being moored when the influence of currents and a wind is sufficiently small [7]. Herein, since the ship has a \(L_{\text {oa}}\) of 16.5 m, when position control is applied to the midship position, even if the ship is ideally close to the pier at a low heading angle of exactly 10\(^\circ\) against the pier, the bow will be at most about 1.43 m close to the pier if we assume that the ship’s shape at the waterline is a rectangle of \(l_{\text {pp}} \times B\). Considering position control errors caused by disturbances, errors of sensors, high-precision control is required to maintain a safe distance from the pier to prevent contact between the pier and the bow. From these considerations, it is desirable to be able to obtain the ship’s position with an accuracy of less than a meter to perform berthing control in the experiments. Therefore, we have adopted the Centimeter Location Augmentation Service (CLAS) compatible receiver, the Chronosphere-L6, for the ship’s positioning. CLAS is the centimeter level augmentation information transmitted by QZSS. To increase the sensitivity of the receiver, the antenna is placed on the roof of the wheelhouse. The other sensors on the Shinpo are as follows. It is equipped with a GPS compass Furuno SC-50 to obtain the heading angle. The anemometer, which measures relative wind speed and direction, is also located above the wheelhouse. In addition, propeller revolution, engine speed, rudder angle, roll, pitch, etc. can also be measured.

Fig. 1
figure 1

Experimental ship “Shinpo”

Full size image
Table 1 Principal particulars of the experimental ship “Shinpo”
Full size table
Fig. 2
figure 2

Architecture of onboard control system

Full size image

3 System identification

The mathematical model of maneuvering motion of Shinpo was developed. This model utilized for the development and evaluation of the automatic berthing algorithm for Shinpo under various wind conditions. Unlike general maneuvering motions such as turning motion, a model that corresponds to changes in ship’s speed, including propeller reverse rotation, is required for berthing operation. In addition, as mentioned in the paragraph on ship-mounted sensors, high-precision motion control is required for berthing control, so the accuracy of motion prediction in simulation must be sufficiently high. We developed a dynamic model based on the Mathematical Modeling Group (MMG) model [9], which can predict the maneuvering motion of a ship with high accuracy. Hydrodynamic coefficients and other parameters of the model were determined based on the results of sea trials using Shinpo. In this section, we first describe the MMG-based motion equations of the maneuvering motion. Then, we give a brief description of the procedure to adjust parameters of the dynamic model and wind simulation. Note that waves and tidal currents are not treated this time, because the effects on ship hull due to these disturbances may be small enough around the pier.

3.1 Mathematical model of ship maneuvering motion

Fig. 3
figure 3

Coordinate systems of ship motion and wind

Full size image

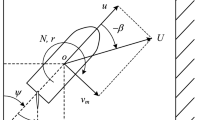
We use the mathematical model of maneuvering motion based on the MMG model to evaluate the response against the algorithm under disturbance, especially the effect of wind for ship motion at low speed. Figure 3 shows the coordinate systems used in this paper to describe motion equations. The notation for each symbol is in accordance with the paper [9]. The space-fixed coordinate system is denoted by \(o_0-x_0y_0z_0\) as shown in the Fig. 3. And \(o-xyz\) is the ship-fixed coordinate system, where o is taken on the midship of the ship. u, v and r are the surge velocity, the lateral velocity at center of midship, and the yaw rate, respectively. The heading angle is denoted by \(\psi\). The drift angle at midship position \(\beta\) is defined as \(\beta =\tan ^{-1}(-v/u)\), and the resultant velocity is represented as U, where the speed is \(U = \sqrt{u^2+v^2}\). The fundamental equations of ship maneuvering motion in 3-DOF is represented as Eq. (1).

$$\begin{aligned} \left. \begin{aligned} (m + m_x)\dot{u} - (m + m_y)vr - x_Gmr^2&= X \\ (m + m_y)\dot{v} + (m + m_x)ur + x_Gm\dot{r}&= Y \\ (I_{zG} + x_G^2m + J_z)\dot{r} + x_Gm(\dot{v}+ ur)&= N_m \end{aligned} \right\} \end{aligned}$$
(1)

Here, the added masses and the added moment of inertia of surge, sway and yaw motion are denoted by \(m_x\), \(m_y\) and \(I_z\), respectively. Added masses and the added moment of inertia are determined based on the multiple regression formulae of Motora’s chart [10,11,12].

Forces X, Y and moment \(N_m\) acting on a ship’s hull around the midship except added mass can be described separating into the following components from the viewpoint of the physical meaning according to the manners of the MMG standard method.

$$\begin{aligned} \left. \begin{aligned} X&= X_H + X_R + X_P + X_A \\ Y&= Y_H + Y_R + Y_P + Y_A \\ N&= N_H + N_R + N_P + N_A \\ \end{aligned} \right\} \end{aligned}$$
(2)

Here, subscript H, R, P and A means hull, rudder, propeller and air (wind), respectively. Force due to the bow thruster is omitted, because the bow thruster is never used in this paper.

For the calculation of the hydrodynamic force acting on the ship’s hull, we use the following model proposed by Yoshimura et al. [13] which is based on cross-flow drag theory. This model can express the hydrodynamic force in the transverse direction and the turning direction due to the large drift angle at low forward speed. This model requires a smaller number of coefficients compared with the standard MMG model such as [9].

$$\begin{aligned} \left. \begin{aligned} X_H =&\frac{1}{2}\rho Ld \Biggl[ \left\{ X^{\prime }_{0F} + (X_{0A}^{\prime } -X^{\prime }_{0F})\frac{|\beta |}{\pi }\right\} uU \\& + \left( m^{\prime }_y + X^{\prime }_{vr}\right) L \cdot vr \Biggl] \\ Y_H =&\frac{1}{2} \rho Ld \Biggl[ Y^{\prime }_vv|u| + Y^{\prime }_rL\cdot ur \\-&\frac{C_D}{L}\int ^{L/2}_{-L/2} |v+C_{rY}rx|(v+C_{rY}rx) \mathrm{{d}}x \Biggl] \\ N_H =&\frac{1}{2} \rho L^2d \Biggl[ N^{\prime }_vv|u| + N^{\prime }_rL \cdot |u|r \\-& \frac{C_D}{L^2}\int ^{-L/2}_{-L/2} \times |v+C_{rN}rx|(v+C_{rN}rx)x \mathrm{{d}}x \Biggl] \end{aligned} \right\} \end{aligned}$$
(3)

where \(X^{\prime }_{0F}\) and \(X^{\prime }_{0A}\) are resistance coefficients of ahead and astern, respectively. Here, \(X^{\prime }_{vr}\), \(Y^{\prime }_v\), \(Y^{\prime }_r\), \(N^{\prime }_v\) and \(N^{\prime }_r\) are hydrodynamic derivatives. \(C_D\) is the cross-flow drag coefficient, \(C_{rY}\) and \(C_{rN}\) are correction factor for lateral force and yaw moment, respectively. The resistance coefficient for ahead \(X^{\prime }_{0F}\) is determined based on the result of the speed trial test in full scale, where propeller rotation speed is 3.1 rps. The coefficient \(X^{\prime }_{0A}\) is determined from the database of the tank test results for the astern resistance test.

Hydrodynamic force due to rudder and propeller with forward and reverse rotation is expressed as the model by Kitagawa et al. [14, 15], which can deal with the generated unbalanced hydrodynamic force due to propeller reverse rotation.

$$\begin{aligned} \left. \begin{aligned} X_R&= -(1-t_R)F_N\sin \delta \\ Y_R&= -(1+a_H)F_N\cos \delta \\ N_R&= -(x_R+a_H x_H)F_N\cos \delta \end{aligned} \right\} \end{aligned}$$
(4)
$$\begin{aligned} \left. \begin{aligned} X_P&= (1-t_P)\rho n^2 D^4 \cdot K_T(J) \\ Y_P&= \left\{ \begin{aligned}&0, \text{ for } n \ge 0\\&\rho n^2 D^4 \cdot Y^{*}_P, \text{ for } n< 0 \end{aligned} \right. \\ N_P&= \left\{ \begin{aligned}&0, \text{ for } n \ge 0\\&\rho n^2 D^4 L (x^{\prime }_{PRR} Y^{*}_{P}), \text{ for } n < 0 \end{aligned} \right. \end{aligned} \right\} \end{aligned}$$
(5)

where \((1-t_R)\) is the steering resistance deduction factor, \(a_H\) is the rudder force increase factor, and \(x_H\) is the longitudinal coordinate of acting point of the additional lateral force. The thrust deduction factor \((1-t_P)\) is different depending on the sign of propeller revolution n. The propeller thrust open water characteristic \(K_T(J)\) for each quadrant shown in Fig. 4 are obtained from the estimation formula of MAU propellers for 1st quadrant and the database of B-series propellers for 2–4th quadrant. The propeller advanced ratio J is represented as

$$\begin{aligned} J = \frac{u(1-w_P)}{nD}, \end{aligned}$$
(6)

where D is the propeller diameter and n is the propeller revolution. The wake coefficient at propeller position is denoted by \(w_P\). Assuming that ship’s speed is controlled only by switching the clutch in the idle state of the main engine, the propeller revolution n corresponds to 3.1, 0, and − 3.1 rps for forward, neutral, and reverse of the clutch based on the actual ship measurement. In the simulations, the time delay of switching the clutch was ignored. When the clutch condition is neutral, the propeller revolution is 0, so the calculation of J is omitted. Then, the propeller thrust \(T = X_P/(1-t_P)\) is treated as 0, and the longitudinal inflow velocity to the rudder \(u_R = (1-w_R)u\) is computed based on the original definition of \(u_R\) [9, 16]. Thrust deduction factor \(t_P\) for \(n<0\) can be computed as follows:

$$\begin{aligned} 1-t_P = C_{tp1}\cdot J_P + C_{tp0}, \end{aligned}$$
(7)

where \(J_P {:}{=}\frac{u}{nP}\) is the so-called apparent advanced ratio used in Kitagawa’s model. \(C_{tp0}\) and \(C_{tp1}\) can be changed depending on \(J_P\) as shown in Table 3, whose values are identified by the database of captive model tests with propeller reverse rotation. The rudder normal force \(F_N\) is expressed as

$$\begin{aligned} F_N = \frac{1}{2}\rho A_R U_R^2 C_N(\alpha _R) \end{aligned}$$
(8)

Here, the resultant rudder velocity \(U_R\) and its effective inflow angle to rudder \(\alpha _R\) is expressed as follows:

$$\begin{aligned} \left. \begin{aligned} U_R&= \sqrt{u_R^2 + v_R^2} \\ \alpha _R&= \delta - \delta _0 - \tan ^{-1}\left( \frac{v_R}{u_R}\right) \\ \end{aligned} \right\} \end{aligned}$$
(9)

where \(\delta _0\) is a virtual zero rudder angle for the rudder normal force. The rudder normal force coefficient \(C_N\) is expressed as follows:

$$\begin{aligned} C_N(\alpha _{R}) = \left\{ \begin{aligned}&C_{N0} \sin \alpha _{R}, \text{ for } 0 \le |\alpha _{R}|< |\alpha _{Rstl}|\\&\text{ or } (\pi - |\alpha _{Rstl}|) \le |\alpha _{R}| \le \pi&\\&C_{N0} \sin (\mathrm{sgn}(\alpha _{R})\cdot \alpha _{Rstl}), \\&\text{ for } |\alpha _{Rstl}|< |\alpha _{R}| < (\pi - |\alpha _{Rstl}|)&\end{aligned} \right. \end{aligned}$$
(10)

where \(C_{N0}\) is the gradient coefficient of the rudder normal force, which is determined by using the Fujii’s formula [17]. The stall angle of the rudder is denoted by \(\alpha _{Rstl}\). Then, the inflow velocity to the rudder \(u_R\) is defined as follows:

$$\begin{aligned} u_R = \left\{ \begin{aligned}&u(1-w_R) \sqrt{ \eta \cos ^2\alpha _{S} \cdot \left\{ 1+k_x\frac{1-w_P}{1-w_R} \left( \sqrt{1+\frac{8K_T}{\pi J^2}}-1\right) \right\} ^2 +(1-\eta )}, \text{ for } n \ge 0 \\&\mathrm{sgn}(u_{RPRsq})\sqrt{(|u_{RPRsq}|)}, \text{ for } n < 0 \end{aligned} \right. \end{aligned}$$
(11)

where

$$\begin{aligned} \left. \begin{aligned} u_{RPRsq}&= \eta \cdot u_{PRR1}|u_{PRR1}| +(1-\eta )\cdot u_{PRR2}|u_{PRR2}|\\&+C_{PRR}\cdot u|u|\\ u_{PRR1}&= u(1-w_R) + \cos \alpha _{S} \cdot n D_P k_{xPR} \sqrt{\frac{8|K_{T}|}{\pi }}\\ u_{PRR2}&= u(1-w_R) \end{aligned} \right\} \end{aligned}$$
(12)

The wake coefficient at rudder position in maneuvering motion is denoted by \(w_R\). The term \(\cos (\alpha _S)\) is a correction factor that takes into account the direction of the velocity increases due to propeller. In Eq. (12), \(k_x\) is an experimental constant which is called the increment ratio of propeller slipstream. Additionally, \(\eta\) is the ratio of the effective area of the rudder for propeller slipstream to the whole rudder area. Here, the lateral inflow velocity \(v_R\) is expressed as

$$\begin{aligned} v_R = -\gamma _R(v+l_Rr), \end{aligned}$$
(13)

where \(\gamma _R\) and \(l_R\) are flow straightening coefficients.

3.2 Wind forces

As an external force acting on the hull, wind force is treated here. Longitudinal and lateral forces, and yaw moment acting on the hull due to wind are expressed as follows:

$$\begin{aligned} \left. \begin{aligned} X_A&= \frac{1}{2}\rho _A A_F U_A^2 C_{AX}(\psi _A)\\ Y_A&= \frac{1}{2}\rho _A A_L U_A^2 C_{AY}(\psi _A)\\ N_A&= \frac{1}{2}\rho _A A_L L_OA U_A^2 C_{AN}(\psi _A) \end{aligned} \right\} \end{aligned}$$
(14)

where relationship between a true wind and an apparent wind is shown as follows:

$$\begin{aligned} \begin{aligned} \varvec{U_A}&= [u_A, v_A]&= \begin{bmatrix} -U_W \cos \psi _W - u \cos \psi + v\sin \psi \\ -U_W \sin \psi _W - u \sin \psi - v\cos \psi \end{bmatrix}^{\mathrm {T}} \end{aligned} \end{aligned}$$
(15)

where \(U_W\) is the true wind speed, \(\psi _W\) is the true wind direction where \(0^{\circ }\) stands for a northerly wind, \(U_A\) is apparent wind speed and \(\psi _A\) is apparent wind direction where \(0^{\circ }\) stands for head wind. The direction of true wind is measured in degrees clockwise from due north and the heading of a ship. The direction of apparent wind is computed as \(\psi _A = \tan ^{-1}\left( v_A/u_A\right) -\psi _W\). The wind load coefficients \(C_{AX}\), \(C_{AY}\) and \(C_{AN}\) were determined using the method proposed by Kitamura et al. [18]. The curves of wind load coefficients are shown in Fig. 5. The wind conditions in simulation were generated in two settings: constant wind speed/direction and sampling using probability distributions. In the simulations using the probability distributions, the true wind speed was produced according to the Weibull distribution and the true wind direction according to the Gaussian distribution, as follows [19, 20].

$$\begin{aligned} f_{U_W}(U_W\mid \overline{U}_W, a, \lambda ) = \frac{a}{\lambda } \left( \frac{\overline{U}_W}{\lambda }\right) ^{a-1}e^{-(U_W/\lambda )^a} \end{aligned}$$
(16)
$$\begin{aligned} f_{\psi _W}(\psi _W\mid \overline{\psi }_W, \sigma ) = \frac{1}{\sqrt{2\pi \sigma ^2}} \exp \left( -\frac{(\psi _W-\overline{\psi }_W)}{2\sigma ^2}\right) \end{aligned}$$
(17)

Here, \(\overline{U}_W\) is the mean true wind speed and \(\overline{\psi }_W\) is the mean true wind direction. The shape parameter a in Eq. (16) was set to 2.0. The scale parameter \(\lambda\) is calculated as,

$$\begin{aligned} \lambda = \frac{2\overline{U}_W}{\sqrt{\pi }}. \end{aligned}$$

This formula is obtained from the formula of the expected value of the Weibull distribution where \(a=2.0\): \(\overline{U}_W {:}{=}\mathbb {E}[U_W] = \lambda \varGamma (3/2)\). Here, \(\varGamma (x)\) is the gamma function. The standard deviation \(\sigma\) is set to 30\(^{\circ }\) according to the measured wind direction in the test sea area.

Fig. 4
figure 4

Estimated \(K_{T}\)-J curves based on the estimate formula of MAU series propellers for the 1st quadrant and the database of B-series propellers for 2–4th quadrants

Full size image
Fig. 5
figure 5

Estimated wind load coefficients using method proposed by Kitamura et al. [18]

Full size image

3.3 Hydrodynamic coefficients and other parameters

The hydrodynamic coefficients and other parameters of the model were identified based on the measurements of sea trials. We carried out various tests such as turning tests with rudder angles of 20\(^{\circ }\) and 40\(^{\circ }\) for ahead and astern, and Zigzag tests of ± 10\(^{\circ }\) and ± 20\(^{\circ }\) only for ahead mainly with a propeller revolution of 3.1 rps in the idle state. Next, referring to various estimation formulae and databases [13, 14, 21, 22], initial parameters of the motion equations were set. However, since these estimated parameters are based on different ship types, the parameters were adjusted based on the measurement results of full-scale tests of Shinpo. Figure 2 shows adjusted parameters in this procedure and other parameters of the model used in this research is shown in Figs. 3 and 4. In this process, the unmeasured disturbance effects are taken into account by reproducing the steady state of the turning motion that includes fluctuation under the influence of disturbances such as tidal currents. Figure 6 shows the comparison between the measured values and the simulation results for change of the rudder angle and the propeller revolution. The turning motion in the steady state can be estimated sufficiently in the simulations. As for Zigzag tests, the simulation results are in good agreement with the measurements.

Figure 7 shows time series of turning test to compare between the measurement and simulations to see the performance of ahead at idle speed. For simulations in Fig. 7, the wind forces are calculated with assuming the mean true wind speed and direction of the measurement. Though there is a difference in trajectories, because the effect such as the current disturbance in full scale experiment which could not be measured was excluded in the simulation, the speed components u, v, r can reproduce the motion of the full-scale ship at low speed.

Table 2 Hydrodynamic force coefficients
Full size table
Table 3 Hydrodynamic coefficients and parameters for simulation
Full size table
Table 4 Coefficients to representing force due to and rudder
Full size table
Fig. 6
figure 6

Comparison on the full-scale ship experiment results and simulation results

Full size image
Fig. 7
figure 7

Comparison of turning test results at idle speed between the full-scale ship experiment and the simulation. (Rudder angle is + 45\(^{\circ }\). For full-scale ship experiment, the mean true wind speed is 2.08 m/s, the mean true wind direction is 348.4\(^{\circ }\))

Full size image

4 Automatic berthing algorithm

4.1 Overview of algorithm

The core algorithm of automatic berthing control consists of three parts path planning, path following and speed control. The path to berth is generated at the start of control sequences. There are several advantages of this approach. One is that the berthing path can be confirmed before the automatic control starts. The other is that it is clear whether the system is currently functioning properly or not, since deviations from the path are known during the automatic control. Furthermore, this approach divides the problem of the automatic berthing control into subproblems: the design of berthing path, the stability of heading control and the safe speed control.

Here, as shown in Fig. 8, the control modes are switched by dividing the berthing path indicated by a blue broken line into four control sequences. These switching positions are determined based on the procedure that a human operator is berthing a ship actually. In addition, to reduce the excessive load on the main engine, it was decided to decelerate in the neutral state without decelerating by the propeller reverse rotation except for the last stop mode. To allow the necessary distance for deceleration, the switching positions of the control modes are arranged at positions of 10, 70 and 100 m along the path from the berthing position. Obviously, when applied to other ships, the switch positions should be arranged according to a sufficient distance for deceleration.

Fig. 8
figure 8

Control sequences for automatic berthing control

Full size image

4.2 Path planning

The path planning algorithm is designed with reference to actual trajectories by a human operator. From the results of the previous studies and the actual operation examples of Shinpo [23], it can be seen that the trajectories of berthing is a smooth curve that extends in the direction of the heading from the initial position of the ship and connects to the berthing position at an angle parallel to the pier. Such shape can be represented by a cubic Bézier curve [24]. A Bézier curve of degree N is an N-th order curve defined by \(N+1\) control points \(B_0, \ldots B_{N}\) and expressed as follows with t as a parameter.

$$\begin{aligned} \hbox {B}\acute{\hbox {e}}\hbox {zier}(t;N) = \sum ^{N}_{i=0}{B_iJ_{N,t}(t)} \end{aligned}$$
(18)
$$\begin{aligned} J_{n,i}(t) = {{n}\atopwithdelims (){i}}t^i(1-t)^{n-i} \end{aligned}$$
(19)

where \(0<t<1\), and \(J_{n,i}(t)\) is the Bernstein basis polynomial of degree n.

A cubic Bézier curve can be expressed as a third-order polynomial of t. Figure 9 shows a schematic view of the berthing path by the Bézier curve with control points \(B_i\ (i=0,\ldots 3)\).

In Fig. 9, the control point \(B_0\) is placed at the initial position of a ship. \(B_1\) is a point that the angle of \(\overrightarrow{B_0B_1}\) is equivalent to the ship’s initial heading angle and its \(L_s=0.6 |y_{\text{berth}}|\). \(B_2\) is located at the point that \(L_e = 80\) m and parallel to the pier, and \(B_3\) is the target position of berthing. Here, the target position of berthing is set at \((x_{\text{berth}}\ [m],\ y_{\text{berth}}\ [m]) = (5,\ 0)\) considering the viewpoint of the safety of experiments as well as the distance that the mooring rope can be thrown from the ship to the pier. Since the length \(L_s\) changes according to the starting position, the ship can approach the pier at the almost same angle regardless of the position she starts the automatic berthing control from. The adjustment of the approach angle is mainly made by the length \(L_e\). In case of other ships, it is possible to change the approaching angle to the pier by changing \(L_e\).

Fig. 9
figure 9

Path planning using a cubic Bézier curve with control points

Full size image

4.3 Path following

In this study, the pure pursuit algorithm [25] is adopted as a path following control algorithm. The pure pursuit is a very simple algorithm that only performs simple geometric calculations to determine the direction of heading. This algorithm is practical and widely used because of its high robustness [26]. As shown in Fig. 10, the pure pursuit performs turning control so that the ship reaches target point on a predefined directional path a certain distance ahead. The distance from the closest point of ship’s GNSS position on the path to the target point is called the look ahead distance denoted by \(L_{T}\). Here, GNSS is an abbreviation for the Global Navigation Satellite System such as Global Positioning System (GPS) and Quasi-Zenith Satellite System (QZSS). Then, rudder angle is calculated based on the angle error \(\alpha _{T}\) using a PD heading controller. The command value of rudder is computed using \(\alpha _{T}\), with the maximum \(\pm 45^\circ\) as follows.

$$\begin{aligned} \delta ^{*} = {\text {clip}}(K_{P}[\alpha _{T}]_{-180^\circ ,180^\circ }-K_{D}r, -45^\circ , 45^\circ ) \end{aligned}$$
(20)

where \(K_{P}\) and \(K_{D}\) are the proportional and the derivative gain of the heading controller, respectively. \([x]_{-180^\circ ,180^\circ } = (x + 180^\circ\ \mathrm{mod}\ 360^\circ ) - 180^\circ\) represents the operation for keeping the angle x (deg) within the range of \(-180^\circ\) and 180\(^\circ\). The gain parameters \(K_{P}\) and \(K_{D}\) can be determined based on the settings of heading control system (HCS) installed on many ships. From the results of simulation and full-scale ship measurement, \(K_{P}=3.0\) and \(K_{D} = 1.0\) were set. For a reference, the HCS setting of \(K_{P}\) at navigation full ahead is about 2.0 for Shinpo. The pure pursuit realizes the function of the derivative control in the sense that it looks ahead the path and calculates the future course error. For this reason, in the gain design of the heading controller, it is recommended to set a larger value of \(K_{P}\) than usual HCS settings to increase the followability for the path, taking into account the followability for the section with the greatest curvature on the path. In this case, it is necessary to pay attention to the upper limit of \(K_{P}\) so that the heading control itself does not become unstable [27]. The look ahead distance \(L_{T}\) is set at 26.4 m, which is 1.6 times \(L_{\text {pp}}\), based on results of simulations and the full-scale ship experiments of following control of circular paths. The look ahead length \(L_{T}\) is basically fixed, but if the distance of the closest point on the path to the ship is greater than \(L_{T}\) due to disturbance, the closest point on the path is used as the target point. In addition to path planning, it is necessary to calculate the target point beyond the berthing position when the ship is close to the pier, so a straight path is extended from point \(B_3\) to be parallel to the pier.

Fig. 10
figure 10

Geometry of the pure pursuit algorithm

Full size image

4.4 Speed control

The ship’s speed is controlled by the operation of the clutch during the automatic berthing control. The control system of the experimental ship used in this study can operate the main engine telegraph and clutch to control the ship speed. On the other hand, in consideration of measures against mechanical loads to the main engine and safety in actual ship experiments, this time, it was decided to carry out the berthing control by fixing the main engine speed to the idling speed. Therefore, the speed can be controlled only by switching the clutch. The clutch can take three states of forward, neutral and reverse.

The ship’s speed was controlled by the clutch in the four control sections shown in Fig. 8 as follows:

  1. (1)

    In the path following mode, the clutch is set to forward.

  2. (2)

    In the neutral mode, the clutch is set to neutral and switched to forward when the surge velocity drops to \(u < 1.0\) m/s due to such as a strong headwind.

  3. (3)

    In the turning mode, the clutch is set to neutral, but the clutch is switched to forward when one of the following three conditions is met:

    1. (A)

      When \(\alpha _{T}<\) 0 deg and surge velocity \(u \le\) 1.0 m/s.

    2. (B)

      When the direct distance from the GNSS position to the berthing position is 50 m or more and \(|\alpha _{T}| >\) 5 deg.

    3. (C)

      When \(u<\) 0.3 m/s.

  4. (4)

    In the stop mode, the clutch is set to reverse step by step until the surge velocity u becomes 0.1 m/s or less. First, the clutch is switched to reverse when − 10.0 m \(< -x_{\text{berth}} < - 1.0\) m and \(u >\) 0.5 m/s. After that, the clutch can be set to reverse when u> 0.1 m/s. If \(u<\) 0 m/s at \(x_{\text{berth}}<\) 0.0 m before the berthing position, the clutch is set to forward. If these conditions are not met, the clutch is set to neutral.

Due to the restriction of the experimental sea area explained in Sect. 5, it is assumed to berth the ship at its starboard side. On the other hand, the direction of the inequality sign in (A) in (3) is reversed for berthing the ship port side. In case that the difference between \(\alpha _{T}\) becomes large but the ship speed is not sufficiently small, rapid turning by kick ahead maneuvering using propeller forward rotation will not be performed during the turning mode. As shown, the clutch will not be set to reverse for deceleration except in the stopping mode. This is to prevent the main engine from being overloaded by switching the clutch forward and reverse.

5 Experiments and evaluations

5.1 Environment and setting of full-scale ship experiments

The full-scale ship experiments were performed in the sea area at Innoshima Marina (Hiroshima, Japan) to validate the novel automatic berthing system. The implementation of the whole control program is written in Python. The real-time calculation of control inputs was performed using MacBook Pro [Core i7 (quad core, 2.8 GHz), RAM 16 GB]. The frequency of communication with the PLC system is set to 100 ms. This frequency determines the maximum frequency of the control loop. Figure 11 shows a map of the test sea area. There is a floating pier, and the ship will berth with the starboard side. As shown in Fig. 11, there is a shallow sea area near the floating pier in the test sea area, and it is necessary to draw a berthing path to avoid this.

Fig. 11
figure 11

Test field of automatic berthing experiments

Full size image

5.2 Results

For validation of the automatic berthing system, we present two results of automatic berthing control tests under calm wind and strong wind. First, Fig. 12 shows the experimental results of an automatic berthing control in calm wind. In Fig. 12, the actual trajectory with the ship’s position, the direction and velocity of true wind at intervals of 10 s on the left, and the states of the clutch corresponding to the trajectory are shown in color on the right. The measured values of this case are shown in Fig. 13. The distance in Fig. 13 represents the direct distance between the berthing position and the QZSS position of the ship. The deviation from the path decreases as the distance to the pier becomes small. On the other hand, it can be seen that the heading angle is adjusted by putting the clutch in the forward position intermittently during the turning mode. In this case, the speed controller keeps the surge velocity u to about 1.0 m/s, so that the ship can stop with enough time to slow down within the stopping mode. The stern is brought significantly close to the pier. There is almost no vibration in the heading angle due to the increased proportional gain in this situation. On the other hand, there are concerns about the load on the main engine due to the frequent clutch changes during the turning mode. Since performance of path following is satisfactory, the control law for clutch switching needs to be improved while balancing the path following performance. Figures 14 and 15 show the result of the automatic berthing control under a strong wind to observe tracking performance against wind disturbance. The mean of the true wind speed in this case was 5.42 m/s, and there were scenes it reaches 8.0 m/s. In this situation, the deviation from the path became larger than the previous result, but it did not increase until the berthing ends even after the neutral mode. The deviation of the path is compensated by increasing the rudder angle. However, the deviation from the path did not decrease until the end, and the ship made a sharp turn just before the berthing. Moreover, the heading angle has begun to oscillate, indicating the need to tune the gains of the PD heading controller in consideration of the balance between followability and course stability. The frequency of the clutch switch was reduced compared to the previous example, but we consider that this could be due to the crosswinds the ship received.

Fig. 12
figure 12

Trajectory of automatic berthing control using the pure pursuit in a calm wind

Full size image
Fig. 13
figure 13

Measured values of the automatic berthing control shown in Fig. 12

Full size image
Fig. 14
figure 14

Trajectory of automatic berthing control using the pure pursuit under strong wind disturbance

Full size image
Fig. 15
figure 15

Measured values of the automatic berthing control shown in Fig. 14

Full size image

5.3 Heading control on approaching pier

When the distance between the ship and the pier is small, approaching the pier with the ship’s bow facing the pier may give a sense of fear to operators. At the same time, this kind of approach increases the risk of the bow colliding with the pier. Thus, it is important to adequately control the change in the heading angle when approaching the pier for safety. The ship is equipped with a bow thruster, but we decided not to use the bow thruster in this study because we were concerned about the load on the bow thruster during continuous operation. And the yaw moment using the bow thruster is small when ship at forward speed. Thus, the heading angle during approach to the pier is adjusted by adding the correction angle \(\alpha _{\text {add}}\) to the \(\alpha _{T}\) when calculates the command rudder angle by the pure pursuit in the turning mode and the stopping mode as follows.

$$\begin{aligned} \delta ^{*} = clip(K_{P}[\alpha _{T}+\alpha _{\text {add}} ]_{-180^\circ ,180^\circ }-K_{D}r, -45^\circ , 45^\circ ) \end{aligned}$$
(21)

Figure 16 shows a geometric meaning of \(\alpha _{\text {add}}\) for heading control during approach to the pier. By adding \(\alpha _{\text {add}}\), the ship starts turning earlier than the original algorithm. The results of automatic berthing using Eq. (21) changing \(\alpha _{\text {add}}\) is shown in Fig. 17. By increasing \(\alpha _{\text {add}}\), \(\alpha _{T}\) is increased when the distance from the berthing position is small. In particular, when \(\alpha _{\text {add}}=-5^{\circ}\)s, \(\alpha _{T}\) is positive for most of the time during the approach to the pier. This means that the ship is approaching the pier facing parallel to or away from the pier. On the other hand, there is no significant difference in the terminal heading angle due to the change in \(\alpha _{\text {add}}\). Hence, this method is effective for controlling the heading angle when approaching the pier without changing the path.

Here, a correction angle \(\alpha _{\text {add}}\) is introduced to adjust the heading angle during approach to the pier. On the other hand, there is another way to redesign the path of the Bézier curve itself for the appropriate heading angle at the berthing position. The latter approach is simpler, however, the trajectory will not always follow the path in this case. Besides, there is almost no control margin at the extreme low speed state in the turning mode and later, and very complicated control is performed using the kick ahead and drifting to control the heading angle. Although it is possible to finally reach the berthing position by this approach, operator cannot judge whether the present state is normal or not during automatic berthing control. Hence, the method using the correction angle \(\alpha _{\text {add}}\) was adopted from the viewpoint of usability.

Fig. 16
figure 16

Geometric meaning of \(\alpha _{\text {add}}\) on approaching pier

Full size image
Fig. 17
figure 17

Comparison of timeseries of the heading angle and \(\alpha _{T}\) during automatic berthing control when changing \(\alpha _{\text {add}}\). Note that each value of \(\alpha _{T}\) in the figure does not include \(\alpha _{\text {add}}\).

Full size image

6 Conclusions

A new system of automatic berthing control using path following control has been developed. The performance of the system was verified using the experimental ship Shinpo with this system on board under various wind conditions.

To carry out full-scale ship experiment, we constructed the onboard control system centering on PLC which enables to control the ship by a laptop computer. In addition, we constructed the mathematical model of maneuvering motion at low speed with main engine idling based on the measurement result of full-scale ship experiments.

Proposed algorithm consists of path planning, path following and speed control. Path following algorithm is designed actual trajectories by a human operators and a path is expressed by a Bézier curve. Path following algorithm is pure pursuit. This approach is practical because of parameters of heading control can be determined based on the settings of HCS installed on a ship. Ship’s speed is controlled depending on the control modes.

In the verification of the automatic berthing system using the full-scale ship, the system has controlled the ship to follow the automatic generated Bézier path stably and brought the ship to berth successfully when the true wind speed was less than 3 m/s. Although the deviation from the path becomes larger than that at calm wind condition, berthing was finally made even at higher true wind speed.

The stability of the path following control by the pure pursuit is also shown in the scope of the experiments. However, it is not yet enough for the analysis required for the basic parameter design of the path following performance or for the applicability to other types of ship. In addition, a safe path planning method that considers the surrounding geometry and a condition of disturbance is required to improve our algorithm. These issues need to be solved in future research.