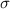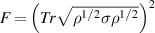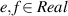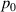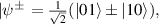Abstract
Remotely preparing quantum states, which possess some desired features, is an important task for future quantum network host providers. On the other hand, the non-degenerate discordant two-qubit states, the states with different left and right quantum discords, is necessary for the implementation of some quantum information and quantum computation processes. This paper presents a new preparation scheme of such states realized by the asymmetric quantum correlation teleportation (AQCT) protocol i.e. quantum correlation teleportation via two different quantum channels. In this way, some properties of AQCT protocol are studied to achieve the most appropriate and least expensive procedure of preparing the asymmetric discordant two-qubit quantum states.
Export citation and abstract BibTeX RIS
1. Introduction
The preparation of quantum correlated multipartite state is one of the fascinating tools in the field of quantum information and computation. Many kinds of quantum correlations such as entanglement [1], quantum discord (QD) [2], quantum consonance [3], are introduced in the literature. Entanglement has amazing properties and roles in quantum computing and information theories and can be used as a quantum resource for quantum communication. Maximally entangled states provide a perfect scheme to teleport unknown quantum states [4]. It is shown that the quality of quantum teleportation reduced if one uses non-maximally entangled states as a resource. However mixed quantum channels that can perform quantum teleportation with fidelity1 between input state and teleport (replica) states (F), greater than classical communication threshold (i.e. ), are worthwhile [5–7]. Here we use the concurrence as a measure of entanglement of two-qubit state
), are worthwhile [5–7]. Here we use the concurrence as a measure of entanglement of two-qubit state 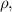 defined as
defined as 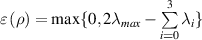 , where the
, where the 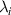 's are positive square roots of the eigenvalues of the non-Hermitian matrix
's are positive square roots of the eigenvalues of the non-Hermitian matrix 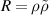 , and
, and  [8].
[8].
There are some quantum correlations beyond the concept of entanglement i.e. there are some quantum correlated states which are separable. One of these types of quantum correlations is named QD. QD is a measure of the quantum correlations introduced by Zurek et al [2] and Henderson [9]. QD is defined by the difference between total quantum mutual information and classical mutual information. QD is a measurement-based quantum correlation defined by applying the most disruptive measurement on one of the subsystems and calculating the difference of mutual information related to state and post-measurement state of the system. Searching for the most disruptive measurement should be done in the set of positive operator-valued measures. But Chen et al [10] show that for an important subset of the quantum state, called X-state (see equation (3)) projective measurement is adequate. QD is an asymmetric measure of the quantum correlation due to which subsystem is measured [11–13]. If the measurement is applied to the A (B) subsystem, we called it Left (Right) QD. To calculate right discord 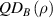 , the projective measurement
, the projective measurement 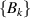 is applied on subsystem B. Post-measurement state associated by kth output is:
is applied on subsystem B. Post-measurement state associated by kth output is:
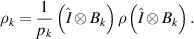
where 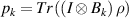 , is probability related to k-th output, and
, is probability related to k-th output, and 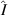 is the identity operator. The quantum conditional entropy with respect to the measurement
is the identity operator. The quantum conditional entropy with respect to the measurement 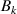 is written as:
is written as:
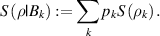
Here, 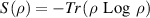 is von-Neumann entropy. The mutual information associated with the measurement
is von-Neumann entropy. The mutual information associated with the measurement 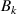 is defined as:
is defined as:
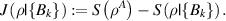
Classical correlation 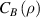 is the upper bound of
is the upper bound of 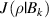 ,
,
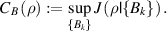
Quantum mutual information is defined as:
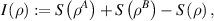
and QD is defined as the difference between 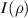 and
and 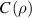 :
:
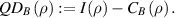
The left discord 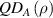 is obtained by swapping the role of A and B subsystems. There are important phenomena which use the asymmetric behavior of QD, such as explaining the quantum-to-classical transition in quantum Darwinism theory [14–16], determining the Markovianity and non-Markovianity of the dynamics of the system. So, preparing two-qubit states with different right and left QD (we call such states as non-degenerate discordant states) is a significant task. Our idea for preparing such non-degenerate bipartite discordant states is to teleport each party via different channels. This issue is referred to as the protocol of asymmetric quantum correlation teleportation (AQCT).
is obtained by swapping the role of A and B subsystems. There are important phenomena which use the asymmetric behavior of QD, such as explaining the quantum-to-classical transition in quantum Darwinism theory [14–16], determining the Markovianity and non-Markovianity of the dynamics of the system. So, preparing two-qubit states with different right and left QD (we call such states as non-degenerate discordant states) is a significant task. Our idea for preparing such non-degenerate bipartite discordant states is to teleport each party via different channels. This issue is referred to as the protocol of asymmetric quantum correlation teleportation (AQCT).
The organization of this paper is as follows. The standard teleportation protocol (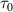 ) is reviewed in sec. II. The quantum correlation teleportation protocol (
) is reviewed in sec. II. The quantum correlation teleportation protocol (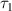 ) is represented from a new perspective in sec. III. Sec. IV devotes to remote state preparation of two-qubit non-degenerate discordant state by employing modified
) is represented from a new perspective in sec. III. Sec. IV devotes to remote state preparation of two-qubit non-degenerate discordant state by employing modified 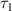 -protocol with two different quantum channels. The paper is concluded in Sec. V with a brief discussion.
-protocol with two different quantum channels. The paper is concluded in Sec. V with a brief discussion.
2. Quantum state teleportation: brief review
Suppose that Alice tends to send an unknown quantum state of a qubit to Bob [4] via a mixed quantum channel and classical communication. This channel may have emerged from a pure entangled state disrupted with the environmental noises. In the standard protocol of teleportation (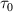 -protocol) Alice performs Bell state measurement (BSM) on unknown quantum state (input state) and her shared qubit which is entangled with Bob's qubit and sends the results of measurement to Bob via a classical communication. Then Bob performs his suitable local quantum operation related to information received from Alice. Ultimately, the input state,
-protocol) Alice performs Bell state measurement (BSM) on unknown quantum state (input state) and her shared qubit which is entangled with Bob's qubit and sends the results of measurement to Bob via a classical communication. Then Bob performs his suitable local quantum operation related to information received from Alice. Ultimately, the input state, 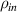 disappears from Alice's site and at that time an output (replica) state,
disappears from Alice's site and at that time an output (replica) state, 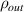 emerges in Bob's site. Bowen and Bose have shown that standard teleportation via an arbitrary mixed state channel,
emerges in Bob's site. Bowen and Bose have shown that standard teleportation via an arbitrary mixed state channel,  is equivalent to a general depolarizing channel with the probabilities given by the maximally entangled component of the resource [17]. Hence the replica state can be calculated as follow:
is equivalent to a general depolarizing channel with the probabilities given by the maximally entangled component of the resource [17]. Hence the replica state can be calculated as follow:
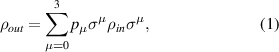
where 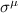 denotes Pauli matrices with
denotes Pauli matrices with 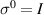 and
and 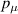 is the fraction of Bell states,
is the fraction of Bell states, 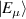 , finding in the teleportation channel i.e.
, finding in the teleportation channel i.e. 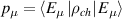 with the property
with the property 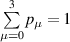 and the probability
and the probability 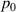 is chosen such that
is chosen such that 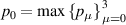 associated with the Bell state
associated with the Bell state 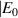 and other probabilities are related to the Bell states,
and other probabilities are related to the Bell states, 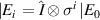 for
for 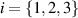 , respectively.
, respectively.
3. Quantum correlations teleportation: modification
Now assume that Alice has a two-qubit system and she wishes to send it to Bob. Bob needs these quantum correlated qubits for running some quantum information processing procedures. They can use 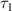 -protocol introduced by Kim and Lee [18]. In this protocol, each qubit is simply teleported via a separate quantum channel. The original version of
-protocol introduced by Kim and Lee [18]. In this protocol, each qubit is simply teleported via a separate quantum channel. The original version of 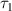 -protocol employs similar quantum states as quantum channels but in this paper, we consider more general cases in which each qubit teleports via different channels. Indeed this modified protocol is closer to reality because the errors or noises influenced on the channels are not necessarily the same. The whole process of quantum correlations teleportation can be considered as a generalized depolarizing map acting on input states [19, 20], hence we have:
-protocol employs similar quantum states as quantum channels but in this paper, we consider more general cases in which each qubit teleports via different channels. Indeed this modified protocol is closer to reality because the errors or noises influenced on the channels are not necessarily the same. The whole process of quantum correlations teleportation can be considered as a generalized depolarizing map acting on input states [19, 20], hence we have:
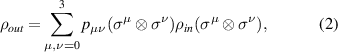
where 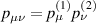 with
with 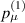 and
and 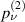 are the Bell fraction of
are the Bell fraction of 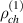 and
and 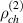 , respectively.
, respectively.
Suppose input two-qubit state is a general X-state i.e.
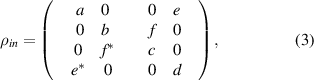
the replica state is obtained as:
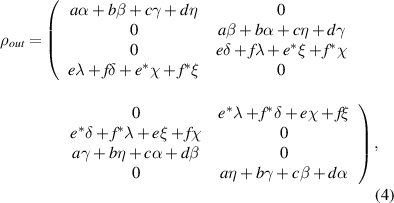
with
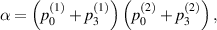
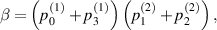
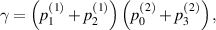
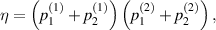
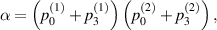
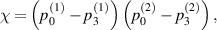
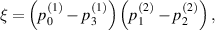
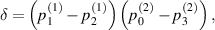
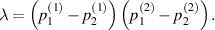
It is obvious that the  -protocol preserves the X-shape of the input state. For the special case of Bell-diagonal input states, the output state will be also Bell-diagonal state (BDS). More specifically, the
-protocol preserves the X-shape of the input state. For the special case of Bell-diagonal input states, the output state will be also Bell-diagonal state (BDS). More specifically, the  -protocol maps
-protocol maps 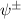 -BDS to
-BDS to 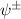 -BDS, and it maps
-BDS, and it maps 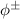 -BDS to
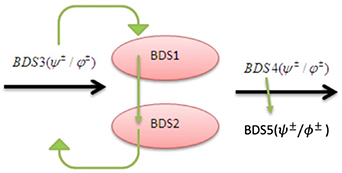
-BDS to 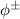 -BDS.2 There is an important symmetry if the resource states are also BDS: swapping the state of channels and input state does not change the amount of quantum correlation of replica state. The various situations are considered in figure 1.
-BDS.2 There is an important symmetry if the resource states are also BDS: swapping the state of channels and input state does not change the amount of quantum correlation of replica state. The various situations are considered in figure 1.
Figure 1. The scheme of teleportation via two different Bell-diagonal state channels (BDS). The output states, BDS4 and BDS5, have the same quantum correlation properties.
Download figure:
Standard image High-resolution imageThis fact helps us to choose the most appropriate and least expensive arrangement for the purpose of quantum correlation teleportation.
4. Remote state preparation of non-degenerate quantum discordant states
The classical-quantum (or quantum–classical) states are the most famous non-degenerate discordant states which maximum difference between right and left quantum discords. These states are separable and hence can be prepared by local operations and classical communication (LOCC) tasks. For example the classical-quantum state:
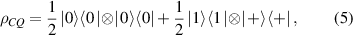
with 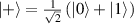 , can be prepared by applying a controlled-Hadamard (CH) gate on the initial state,
, can be prepared by applying a controlled-Hadamard (CH) gate on the initial state, 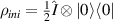 . Here
. Here  , is a
, is a 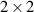 identity matrix. Note that the CH gate can be implemented by a LOCC task. However, this procedure does not work if we desire to prepare non-degenerate quantum discordant entangled states. In the following, we present a scheme that enables us to prepare non-degenerate quantum discordant states which possess some other quantum correlations beyond the quantum discord. For this purpose, we apply AQCT protocol on the general Schmidt form of two-qubit pure entangled state as input state:
identity matrix. Note that the CH gate can be implemented by a LOCC task. However, this procedure does not work if we desire to prepare non-degenerate quantum discordant entangled states. In the following, we present a scheme that enables us to prepare non-degenerate quantum discordant states which possess some other quantum correlations beyond the quantum discord. For this purpose, we apply AQCT protocol on the general Schmidt form of two-qubit pure entangled state as input state:
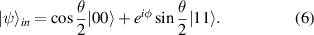
Obviously, the input state is a degenerate discordant state with 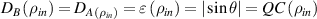 . Here
. Here  is an entanglement measure and
is an entanglement measure and 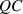 stands for any type of Quantum Correlation. The replica state is given by equation (4) with
stands for any type of Quantum Correlation. The replica state is given by equation (4) with 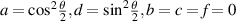 and
and 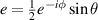 . The output fidelity is calculated easily as follows:
. The output fidelity is calculated easily as follows:
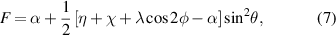
where  and
and 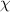 parameters determined by resource states. In the following we examine a simple but important example for the purpose of remote state preparation of non-degenerate discordant states.
parameters determined by resource states. In the following we examine a simple but important example for the purpose of remote state preparation of non-degenerate discordant states.
Considering two different Werner states, which are by their concurrences 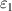 and
and 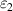 , respectively (
, respectively (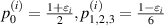 ), as resource states we obtain the replica state parameters as:
), as resource states we obtain the replica state parameters as:
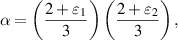
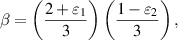

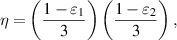
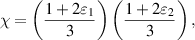
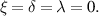
Hence fidelity of teleportation is given by:
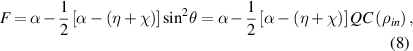
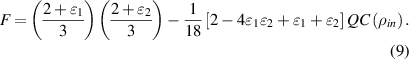
As we expected, the fidelity of teleportation decreases for the higher amount of quantum correlation of input state (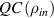 ). For the special case of identical quantum channels (i.e.
). For the special case of identical quantum channels (i.e. 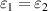 ), the results of Kim and Lee [18] for entanglement teleportation are achieved. It is shown that for general X-state
), the results of Kim and Lee [18] for entanglement teleportation are achieved. It is shown that for general X-state  , in computational basis, the formula of the left and the right quantum discords is the same, except that
, in computational basis, the formula of the left and the right quantum discords is the same, except that  is replaced by
is replaced by 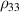 and vice versa [21]. Hence knowing the difference between these two components of
and vice versa [21]. Hence knowing the difference between these two components of 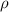 may illuminate the way of preparing the states with different right and left discords.
may illuminate the way of preparing the states with different right and left discords.

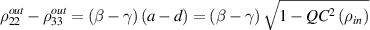

Unfortunately, the difference 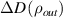 is not a linear function of
is not a linear function of 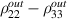 , due to entropic nature of quantum discord, but the above relation suggests that less quantum correlated input state and more different resource states may be a suitable choice. As a special case, suppose that one of the resource is noiseless maximally entangled state i.e.
, due to entropic nature of quantum discord, but the above relation suggests that less quantum correlated input state and more different resource states may be a suitable choice. As a special case, suppose that one of the resource is noiseless maximally entangled state i.e. 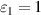 and
and 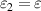 . In this case, the replica state is parametrized by:
. In this case, the replica state is parametrized by:

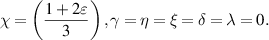
The formula of fidelity is simplified as:
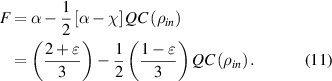
Hence, to achieve teleportation scheme superior to classical communication, i.e. 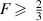 , one needs a Werner state with
, one needs a Werner state with 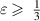 , as one of the resource states. The degeneracy of quantum discord of the input state is removed during the AQCT process due to the asymmetric property of the teleportation protocol (asymmetric-
, as one of the resource states. The degeneracy of quantum discord of the input state is removed during the AQCT process due to the asymmetric property of the teleportation protocol (asymmetric-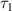 protocol). This fact is illustrated in figures 2 and 3. The results reveals that AQCT of a pure entangled input state through a noiseless, maximally entangled state, channel and a noisy channel described by a Werner state, can prepare the non-degenerate discordant state with large relative discord difference
protocol). This fact is illustrated in figures 2 and 3. The results reveals that AQCT of a pure entangled input state through a noiseless, maximally entangled state, channel and a noisy channel described by a Werner state, can prepare the non-degenerate discordant state with large relative discord difference 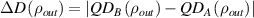 with respect to average discord,
with respect to average discord, 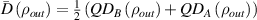 .
.
Figure 2. Left(dashed line) and right(solid line) quantum discord (a) and their relative difference with respect to average discord (b), of the replica state of asymmetric quantum correlation teleportation protocol for different input states, 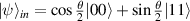 . One of the resource states is chosen as a maximally entangled state and the other is a Werner state with entanglement
. One of the resource states is chosen as a maximally entangled state and the other is a Werner state with entanglement 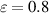 .
.
Download figure:
Standard image High-resolution imageFigure 3. Left(dashed line) and right(solid line) quantum discord (a) and their relative difference with respect to average discord (b), of the replica state of asymmetric quantum correlation teleportation protocol versus  for fixed input state,
for fixed input state, 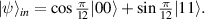 One of the resource states is chosen as maximally entangled state and the other is a Werner state with entanglement
One of the resource states is chosen as maximally entangled state and the other is a Werner state with entanglement  .
.
Download figure:
Standard image High-resolution imageFor small values of 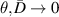 and hence the value of
and hence the value of 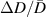 of replica state becomes very large. Discarding this illusive result of figure 2, we found the better result for about the value
of replica state becomes very large. Discarding this illusive result of figure 2, we found the better result for about the value 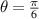 . Considering this fact in figure 3, we can prepare a non-degenerate state with left and right discords difference about 25% of their average discord at the end of the AQCT protocol.
. Considering this fact in figure 3, we can prepare a non-degenerate state with left and right discords difference about 25% of their average discord at the end of the AQCT protocol.
5. Conclusion
The teleportation scheme with two different channels is investigated and is used to remote state preparing of some non-degenerate discordant states. In this way, we first introduce an AQCT protocol and calculate its output (replica) state through arbitrary resource states and the fidelity of teleportation for a general X-shaped input state. The resources are determined by their Bell-fractions. Furthermore, AQCT protocol has an important and noticeable cyclic property: for the Bell-diagonal input and resource states, the switching of them will not affect the final result of the quantum correlations and the physical properties of the replica state. Due to the asymmetric nature of the AQCT protocol, we expect that the degeneracy of left and right quantum discords of the input state is removed during the teleportation process. We examine this fact by implementing AQCT protocol via a maximally entangled resource and a Werner state as the other resource. This enables us to prepare non-degenerate discordant states with left and right disco rds difference about 25% of their average discord. We hope that the results can be useful and significant in the field of quantum information and computation.