Abstract
The measurement precision for two incompatible observables in a typical quantum system can be improved by the aid of one particle as a quantum memory. In this work, we study the entropic uncertainty relation in the presence of quantum memory (EUR-QM) and dense coding capacity (DCC) for arbitrary two-qubit X-states, and then we obtain an explicit relationship between the lower bound of the uncertainty and DCC. As an example, we examine the thermal EUR-QM as well as DCC in two kinds of two-qubit spin squeezing models (one-axis twisting model and two-axis counter-twisting model) under an external magnetic field. In the following, we relate EUR-QM to DCC and show analytically that there is an anti-correlated relation between them, and especially in the ground state. Our results show that for both the models, the entropic uncertainty and its bound can be decreased by reinforcing the spin squeezing parameters or decreasing the temperature of the system. Notably, we reveal that the valid dense coding cannot carry out in the one-axis twisting model, nevertheless, if we properly choose the Hamiltonian parameters, the two-axis counter-twisting model not only carries out the valid dense coding but also the optimal dense coding surely can be achieved. Thereby, our observations might offer new insights into quantum measurement precision and the optimal dense coding for the regimes of various solid-state systems.
Export citation and abstract BibTeX RIS
1. Introduction
Historically, the uncertainty principle which was introduced originally by Heisenberg [1] is an inherent feature of quantum mechanics limiting our capability to predict the measurement outcomes of two incompatible observables concurrently. Afterward, Robertson [2] and then Schrödinger [3] presented an inequality (so-called Robertson-Schrödinger uncertainty relation) for two arbitrary incompatible observables U and V as the following simple form
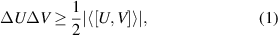
where 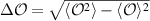 with
with  is the standard deviation,
is the standard deviation, 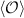 denotes the expectation value of operator
denotes the expectation value of operator  and [U, V] = UV − VU stands for the commutator. Unfortunately, the uncertainty relation (1) has a significant shortcoming, since the lower bound of this uncertainty relation depends on the state of the system, which leads to a trivial bound if the expectation value of the commutator on the state is zero, i.e.
and [U, V] = UV − VU stands for the commutator. Unfortunately, the uncertainty relation (1) has a significant shortcoming, since the lower bound of this uncertainty relation depends on the state of the system, which leads to a trivial bound if the expectation value of the commutator on the state is zero, i.e. ![$|\langle [U, V]\rangle|$](https://content.cld.iop.org/journals/1612-202X/17/9/095205/revision1/lplaba2f0ieqn5.gif) = 0. To overcome this deficiency, Deutsch [4] suggested a novel expression including the Shannon entropy (so-called entropic uncertainty relation) instead of the standard deviation as
= 0. To overcome this deficiency, Deutsch [4] suggested a novel expression including the Shannon entropy (so-called entropic uncertainty relation) instead of the standard deviation as
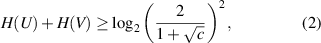
where 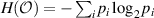 is the Shannon entropy, pi represents the probability of obtaining ith outcome, and
is the Shannon entropy, pi represents the probability of obtaining ith outcome, and 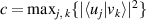 where
where  and
and 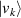 are the eigenvectors of the Hermitian observables U and V, respectively. A few years later, Kraus proposed a clear formula [5], and later it was exactly demonstrated by Maassen and Uffink [6], whose form can be formulated as
are the eigenvectors of the Hermitian observables U and V, respectively. A few years later, Kraus proposed a clear formula [5], and later it was exactly demonstrated by Maassen and Uffink [6], whose form can be formulated as
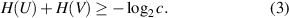
Furthermore, Maccone and Pati [7] obtained the stronger uncertainty relations (so-called Maccone–Pati uncertainty relations) related to the sum of the variances, that its lower bound is non-trivial for two incompatible observables. The most initial works on uncertainty relations formulated as the sum of variances include (e.g. see [8]). Next, Wang et al [9] demonstrated these optimal outcomes for a fully optical setup.
Newly, an entropic uncertainty relation in the presence of quantum memory (EUR-QM) has been proposed [10–13] which has more efficiency than equation (3) (see [12] and [13] for detailed reviews on EUR-QM). To study EUR-QM, let us represent it from the viewpoint of uncertainty game between two legitimate players (so-called Alice and Bob). First, Bob prepares a correlated two-qubit quantum state ϱAB and transmits qubit A to Alice, with considering qubit B as a quantum memory during the game. Next, she measures one of the two incompatible observables U or V and sends to Bob her measurement outcomes. Bob can minimize the uncertainty from Alice's measurement outcomes. When two qubits A and B are fully entangled, Bob can precisely predict Alice's measurement results as stated in EPR paper. However, if there is no entanglement between them, the relation can be simplified to Deutsch's outcome [4]. Mathematically, this mysterious game is expressed as follows
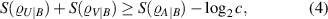
in which ![$S(\varrho) = -\mathrm{{Tr}}[\varrho \log_{2} \varrho]$](https://content.cld.iop.org/journals/1612-202X/17/9/095205/revision1/lplaba2f0ieqn10.gif) is the von Neumann entropy,
is the von Neumann entropy, 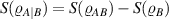 is the conditional von Neumann entropy with
is the conditional von Neumann entropy with  which is the reduced density matrix of quantum memory, and
which is the reduced density matrix of quantum memory, and 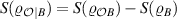 gives the conditional von Neumann entropy of the post-measurement state. After measuring qubit A by operator U or V, the post-measurement states are
gives the conditional von Neumann entropy of the post-measurement state. After measuring qubit A by operator U or V, the post-measurement states are
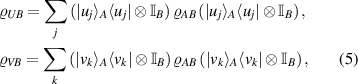
where  is the identity matrix.
is the identity matrix.
As usual, we consider U = σz and V = σx where σz and σx are the Pauli matrices, and so we obtain c = 1/2. Herein, we use notations UL (so-called uncertainty) and UR (so-called uncertainty lower bound) for the left-hand side (LHS) and the right-hand side (RHS) of inequality (4) respectively.
So far, many efforts have been made to improve EUR-QM [14–23], since it has various applications in quantum information processing, e.g. quantum cryptography [24], quantum metrology [25, 26], quantum key distribution [27, 28], entanglement witness [29, 30], and so on.
In recent years, many investigations have risen regarding quantum correlations and EUR-QM, and the relation between them in various quantum systems has been studied by [31–66]. Therefore, we are insisting that there is some intrinsic relationship between the uncertainty and quantum correlations. For example, Hu and Fan [32] determined a tight upper bound for quantum discord using EUR-QM, as well as the other works in this field [33, 34]. Impressively, Wang et al [35–56] investigated solid-state systems such as Heisenberg models and open quantum systems [57], and they also examined the relationship between quantum correlations and uncertainty. Recently, they experimentally investigated the linear-entropy-based uncertainty relations in all-optical systems [58] and they certificated the steering criterion based on a general entropic uncertainty relation [59]. They also experimentally explored the entropic uncertainty relations and coherence uncertainty relations [60]. Furthermore, Pourkarimi [61, 62] and Huang [63] investigated EUR-QM in the spin chain models with Dzyaloshinskii–Moriya interaction. Fang et al [64] studied the dynamic behavior of EUR-QM and quantum coherence in the structured reservoir, and they have shown that the EUR-QM is smallest in the disappearing limit of noise regardless of the forms of the initial state, while the quantum coherence keeps the maximum value. More recently, we investigated thermal quantum correlations and EUR-QM under two kinds of spin squeezing models and got a simple relationship between the quantum discord and entropic uncertainty [65]. Next, we examined EUR-QM, quantum discord, and fidelity of teleportation under decohering environments and found an explicit relationship between them [66].
The dense coding protocol initially proposed by Bennett and Wiesner [67], where the sender can send two bits of classical information to the receiver by transmitting a single-qubit, if they share a two-qubit maximally entangled state. After that, several works on dense coding have been presented theoretically and experimentally [68–80]. The dense coding capacity (DCC) is a vital parameter to measure the quality of the chosen quantum channel, i.e. when the sender (Bob) transmits a single-qubit to the receiver (Alice), how much classical information might be transmitted. The amount of information that can be moved is known to be limited by the Holevo quantity [81]. Since the Holevo quantity is asymptotically obtainable [82], we put forward DCC as

where 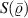 is the von Neumann entropy of the signal ensemble average state
is the von Neumann entropy of the signal ensemble average state 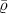 and S(ϱ) is the von Neumann entropy of original state ϱ shared between Alice and Bob. The average quantum state of the signal ensemble for two-qubit can be expressed as
and S(ϱ) is the von Neumann entropy of original state ϱ shared between Alice and Bob. The average quantum state of the signal ensemble for two-qubit can be expressed as
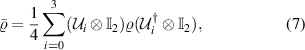
where the set of the mutually orthogonal unitary transformations are  ,
, 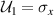 ,
, 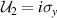 , and
, and 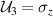 . What physically happens is that Bob performs the set of mutually orthogonal unitary transformations on his quantum system to put the initially shared entangled state ϱ in
. What physically happens is that Bob performs the set of mutually orthogonal unitary transformations on his quantum system to put the initially shared entangled state ϱ in 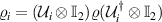 , and sends off his quantum system to Alice, then Alice makes appropriate measurements on the quantum system ϱi to extract the signal. Note that when χ > 1, we have the valid dense coding, and for the optimal dense coding, χ must be the maximum (
, and sends off his quantum system to Alice, then Alice makes appropriate measurements on the quantum system ϱi to extract the signal. Note that when χ > 1, we have the valid dense coding, and for the optimal dense coding, χ must be the maximum (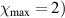 .
.
As discussed above, lots of investigations have been devoted to reviewing the entropic uncertainty relations and quantum correlations. Still, no one has examined EUR-QM and DCC together in any study of quantum systems. That is why we are motivated to study EUR-QM and DCC in arbitrary two-qubit X-states to be looking for a connection between them. Hence, the framework of this work is structured as follows. In the next section, we obtain the uncertainty and its bound as well as DCC for arbitrary two-qubit X-states. In section 3, we consider a typical solid-state system (known as two-qubit spin squeezing model) as an example and then we try to analyze the relationship between EUR-QM and DCC analytically and numerically in section 4. Finally, we close the paper with a brief conclusion in section 5.
2. EUR-QM and DCC in two-qubit X-states
Suppose that the density matrix of arbitrary two-qubit X-states based on the standard basis of 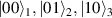 and
and 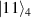 is as follows
is as follows

where the unit trace (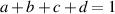 ) and positivity conditions (
) and positivity conditions (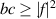 and
and 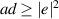 ) are fulfilled.
) are fulfilled.
For this density matrix (8), from (5), the post-measurement states are
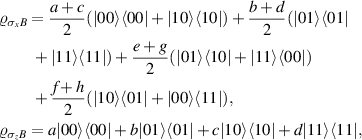
therefore, the eigenvalues of 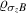 are as {a, b, c, d} and the eigenvalues of
are as {a, b, c, d} and the eigenvalues of 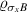 are as
are as 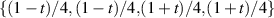 in which
in which ![$t = \sqrt{[1-2(b+d)]^{2}+4|e+g|^{2}}$](https://content.cld.iop.org/journals/1612-202X/17/9/095205/revision1/lplaba2f0ieqn31.gif) . Besides, the von Neumann entropy of reduced density matrix is given by
. Besides, the von Neumann entropy of reduced density matrix is given by 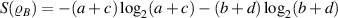 . Then, the von Neumann entropies of the post-measurement states read
. Then, the von Neumann entropies of the post-measurement states read

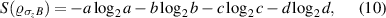
so we get the uncertainty (LHS) as
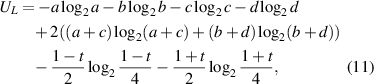
and for the lower bound of uncertainty (RHS) we find
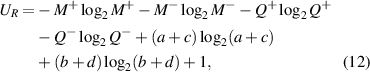
where 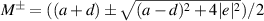 and
and 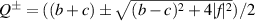 . On the other hand, the average quantum state of the signal ensemble for two-qubit ϱAB can be expressed as
. On the other hand, the average quantum state of the signal ensemble for two-qubit ϱAB can be expressed as

hence, the analytic expression of DCC (6) can be obtained as
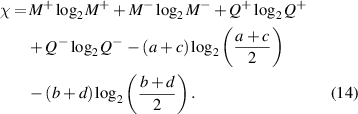
Significantly, we obtain a simple relationship between the lower bound of uncertainty and DCC after algebraic computations as

3. The example: Two-qubit spin squeezing model
Due to their suitable scalability and integrability, solid-state systems attract much attention nowadays [83–95]. In this section, we consider a typical solid-state system with the Hamiltonian H for the two-qubit spin squeezing model under the external magnetic field B as (ћ = 1) [83, 84]

where µ(≥ 0) and ς(≥ 0) are the strength of the spin squeezing interaction in x and y directions respectively, γ(≥ 0) describes the strength of the spin squeezing interaction in the x − y plan, and B(≥ 0) explains the strength of the external magnetic field in z-direction. Herein, 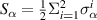 is the collective spin operators, and
is the collective spin operators, and 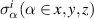 is the Pauli matrix of the ith spin.
is the Pauli matrix of the ith spin.
Case 1. If ς = γ = 0, the Hamiltonian is reduced to the one-axis twisting model (OATM) with a transverse field

Case 2. If ς = µ = 0, the Hamiltonian is reduced to the two-axis counter-twisting model (TACM) with a transverse field
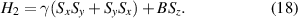
The density operator when the typical two-qubit system is in a thermal equilibrium at temperature T can be described as
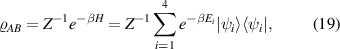
where ![$Z = \mathrm{{Tr}}[\exp( -\beta H)]$](https://content.cld.iop.org/journals/1612-202X/17/9/095205/revision1/lplaba2f0ieqn37.gif) is the partition function of the system, β = 1/κBT for which κB denotes the Boltzmann constant (considered as κB = 1 for simplicity), and Ei and
is the partition function of the system, β = 1/κBT for which κB denotes the Boltzmann constant (considered as κB = 1 for simplicity), and Ei and  are respectively eigenvalues and eigenvectors of the Hamiltonian.
are respectively eigenvalues and eigenvectors of the Hamiltonian.
4. EUR-QM and DCC for two cases of the Hamiltonian
4.1. EUR-QM and DCC in OATM
From equation (17), the eigenvalues and the corresponding eigenvectors of the Hamiltonian for case 1 are obtained as
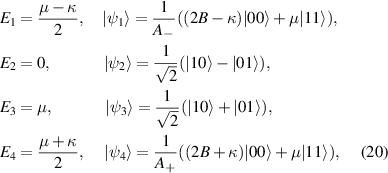
where 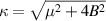 and
and 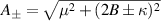 . Thus, by using equation (19) one obtains the density matrix of the bipartite system ϱAB as
. Thus, by using equation (19) one obtains the density matrix of the bipartite system ϱAB as
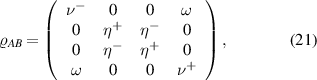
where

It is straightforward to obtain analytical expressions of UL, UR, and DCC by substituting (21) into (11), (12), and (14) respectively. So we obtain the uncertainty and its lower bound as what follows
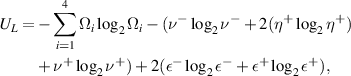
and
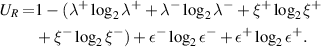
Also for DCC we get
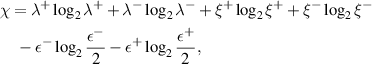
where  ,
, 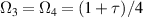 ,
, 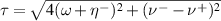 ,
, 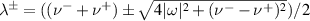 ,
, 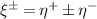 , and
, and 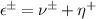 .
.
In the ground state 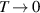 , by analyzing the eigensystem (20), we know that
, by analyzing the eigensystem (20), we know that 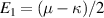 has minimal energy, and
has minimal energy, and 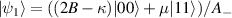 is the corresponding eigenstate. Therefore, we obtain the simplified expressions of UL, UR, and DCC in the ground state as
is the corresponding eigenstate. Therefore, we obtain the simplified expressions of UL, UR, and DCC in the ground state as
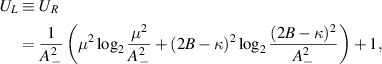
and

As a result, 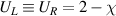 which implies a fully anti-correlated relationship between EUR-QM and DCC.
which implies a fully anti-correlated relationship between EUR-QM and DCC.
4.2. EUR-QM and DCC in TACM
As described by the Hamiltonian (18), the eigenvalues and the corresponding eigenstates for case 2 are achieved as
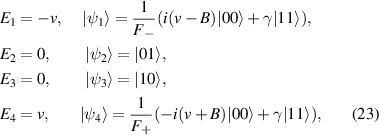
where 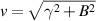 and
and 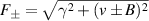 . By substituting (23) into (19), one can obtain the density operator as follows
. By substituting (23) into (19), one can obtain the density operator as follows
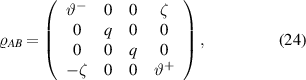
where
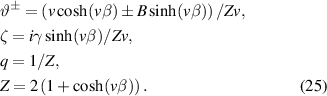
Having known the density matrix (24) and by using the definition of EUR-QM and DCC, we obtain the analytical expressions of UL, UR, and DCC in TACM. First, we obtain the uncertainty (11) as

then, for the lower bound of uncertainty (12) we get
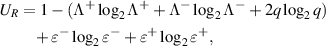
on the other hand, we find DCC (14) as

where  ,
, 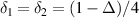 ,
, 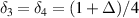 ,
, 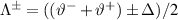 , and
, and 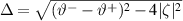 .
.
As explained in the previous section, we find the simplified expressions of UL, UR, and DCC in the ground state as
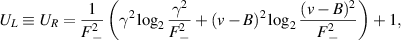
and
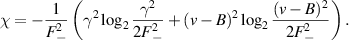
Consequently, 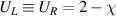 implies that the uncertainty and its bound have a fully anti-correlated relationship with DCC in the ground state.
implies that the uncertainty and its bound have a fully anti-correlated relationship with DCC in the ground state.
4.3. The comparison of EUR-QM and DCC for two cases
Now, let us analyze and compare the thermal EUR-QM and DCC in two cases as functions of temperature (T), spin squeezing parameters (µ and γ), and the external magnetic field (B).
The thermal evolution of the uncertainty and DCC has been displayed in figures 1 and 2 for OATM and TACM respectively with different values of the strength of the magnetic field and spin squeezing. As shown in figure 1(a), DCC collapses with increasing temperature when the strength of the magnetic field, B, and spin squeezing, µ, are weak. Conversely, the uncertainty and its bound rise from more than 0.5 to get their maximal value. Based on this figure and the other figures in this work, one observes that there is a fully anti-correlated relationship between DCC and the lower bound of the uncertainty as expected from (15). DCC remains unchanged at the beginning for low temperatures and then suddenly falls to disappear asymptotically as displayed in figure 1(a). However, as seen from figures 1(b) and (c), it is clear that the threshold value of the critical temperature Tc is enhanced by increasing µ and B. We note that Tc is the critical point for which EUR-QM and DCC suddenly change and they remain unchanged for 0 < T < Tc.
Figure 1. EQMUR- and DCC for OATM in terms of T. Graph (a): µ = B = 0.2, graph (b): µ = B = 0.5, and graph (c): µ = B = 0.9.
Download figure:
Standard image High-resolution imageFigure 2. EUR-QM and DCC for TACM in terms of T. Graph (a): γ = B = 0.2, graph (b): γ = B = 0.5, and graph (c): γ = B = 0.9.
Download figure:
Standard image High-resolution imageThis scenario happens similarly for TACM except for the beginning points of DCC and EUR-QM which are upper and lower than ones in OATM for the same values of the magnetic field and spin squeezing parameters. Notably, in this case, UL, UR, and DCC most remain unchanged for higher temperatures than the previous case, i.e. the threshold value of Tc is enhanced by increasing γ and B.
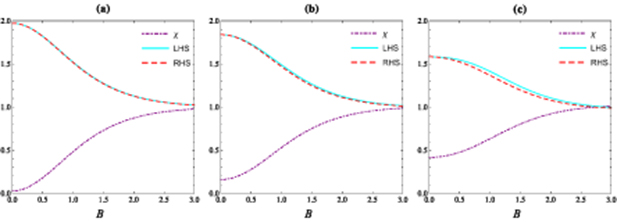
Figures 3 and 4 reveal the uncertainty and its bound, as well as DCC as functions of B for specific value of T = 0.5 and different values of µ and γ for OATM and TACM, respectively. In both the cases, DCC increases and the uncertainty decreases with increasing the strength of the external magnetic field. As mentioned before, χ must be greater than 1 to get a valid dense coding. Hence, this condition cannot be fulfilled in OATM case even for strong values of B and µ. However, the valid value can be achieved in TACM case when  and the strong value of B as shown in figure 4(c). In this case, the uncertainty becomes lesser than 1 and it gets the lower bound, UL ≡ UR.
and the strong value of B as shown in figure 4(c). In this case, the uncertainty becomes lesser than 1 and it gets the lower bound, UL ≡ UR.
Figure 3. EUR-QM and DCC for OATM in terms of B. Graph (a): µ = 0.2, graph (b): µ = 0.5, and graph (c): µ = 0.9. For all plotted T = 0.5.
Download figure:
Standard image High-resolution imageFigure 4. EUR-QM and DCC for TACM in terms of B. Graph (a): γ = 0.2, graph (b): γ = 0.5, and graph (c): γ = 0.9. For all plotted T = 0.5.
Download figure:
Standard image High-resolution imageFigures 5 and 6 are devoted to studying the effect of µ and γ on the uncertainty of incompatible observables and DCC. From these figures, it is clear that µ and γ play a constructive role to increase DCC and decrease the amount of EUR-QM. Obviously, the strength of spin squeezing can lead to growing χ and reduce the uncertainty in two cases, which is more desirable in quantum information processing. Again, OATM shows its inability to obtain valid dense coding. Nevertheless, the strength of spin squeezing in TACM can cause the uncertainty and its bound to vanish, but DCC to get its maximal value, which is called optimal dense coding.
Figure 5. EUR-QM and DCC for OATM in terms of µ. Graph (a): B = 0.2, graph (b): B = 0.5, and graph (c): B = 0.9. For all plotted T = 0.5.
Download figure:
Standard image High-resolution imageFigure 6. EUR-QM and DCC for TACM in terms of γ. Graph (a): B = 0.2, graph (b): B = 0.5, and graph (c): B = 0.9. For all plotted T = 0.5.
Download figure:
Standard image High-resolution image5. Conclusion
In summary, we have presented the analytical expressions for the uncertainty and its lower bound and also DCC for an arbitrary two-qubit X-state. Interestingly, we have obtained a simple relationship between the lower bound of the uncertainty and DCC as UR = 2 − χ, which is true for all two-qubit X-state density matrices. To be specific, we have examined the thermal EUR-QM and DCC in two kinds of two-qubit spin squeezing models under an external magnetic field. Generally, the results reveal that EUR-QM and DCC have different behaviors, that means the uncertainty and its bound decrease when DCC increases and vice versa. In the ground state, we have provided the analytical expressions of EUR-QM and DCC for two cases which lead to a simple relation between them. This relation reveals a fully anti-correlated relationship between EUR-QM and dense coding. In both the cases, the uncertainties achieve the lower bounds in the limit of zero temperature. Remarkably, our analysis shows that the valid dense coding cannot be fulfilled in OATM case. However, if one properly chooses the parameters γ and B, TACM case not only carries out the valid dense coding but also the optimal dense coding easily can be achieved. Hopefully, we believe that our examinations may present a non-trivial insight into thermal dense coding and entropic uncertainty in spin squeezing systems, and be helpful to understand about quantum measurement precision in quantum information theory, especially solid-state systems.