New insight into air flow distribution in alveoli based on air- and saline-filled lungs

Abstract

Understanding flow distributions in human lungs has attracted significant attention since the last few decades. However, there are still large discrepancies between different studies in the distribution of air flow into alveoli at different generations of bifurcation. In this study, a new method has been developed to calculate expansion ratio of alveoli and ratio of alveolar to ductal flow rate at different generations for air- and saline-filled lungs. The effects of alveolar number, breathing period, lung tidal volume, and surface tension are examined. It is found that the expansion ratio of alveoli varies significantly at different generations in the saline-filled lungs. For the air-filled lung, the expansion ratio of individual alveolus remains constant for different generations. The current study provides new data on the flow rate ratios which is critical for understanding flow distributions and flow behaviors in alveoli. Surface tension in alveoli and alveolar number has obvious effects on the value of flow ratio. The current study sheds new light into the flow behavior in lungs and lays the foundation for detailed study on flow and particle transport characteristics in human lungs.

Appendices

Appendix 1 Volume of intersection between a cylinder and a sphere

Monte Carlo method

We create a cube whose center locates in the coordinate origin in the cartesian coordinate system. There is an inscribed sphere inside the cube and this spherical diameter is same with alveolar diameter. To derive the intersection volume V_a∩D, we randomly generate a large number of coordinate points that are only inside the cube first. Then V_a∩D can be calculated by counting the percentage of points which locate in the intersection body. To simplify the process, V_a∩D is only calculated once at the FRC condition. The domain of the intersection volume can be expressed by the equations below:

$$\begin{gathered} {\text{alveoli}}: \, x^{2} + y^{2} + z^{2} - \mathop R\nolimits_{\text{a}}^{2} < 0, \hfill \\ {\text{ducts}}: \, \left[ {x - \left( {R_{\text{d}} + h + t} \right)} \right]^{2} + y^{2} - \mathop R\nolimits_{\text{d}}^{2} < 0, \hfill \\ \end{gathered}$$

(13)

where R_a is the alveolar radius; R_d is the ductal radius; t is the thickness of the ductal wall; h is the distance between the spherical center and the outer surface of the alveolar duct along the line connecting spherical center and ductal center. If there are totally X and X_in coordinate points inside the cube and the intersection volume respectively, then the volume V_a∩D is given by

$$V_{{{\text{a}} \cap {\text{D}}}} = \frac{{X_{{{\text{in}}}} }}{X} \cdot \left( {2R_{\text{a}} } \right)^{3} .$$

(14)

Double integral method

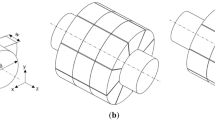
As shown in Fig. 

Fig. 7

Schematic diagram. a A section along the axis of the duct through the center of the spherical alveolus. b Cross section of the duct through the center of the spherical alveolus. c Section of an inscribed sphere inside a cube. V_a∩D is the intersection volume between the alveolar duct and the alveolus at a typical generation under the FRC condition; R_a is the alveolar radius; R_d is the ductal radius; t is the thickness of the ductal wall; h is the distance between the spherical center and the outer surface of the alveolar duct along the line connecting spherical center and ductal center

7b, the alveolus and duct in the cartesian coordinate system are defined by

$$\begin{gathered} {\text{alveolus}}: \, x^{2} + y^{2} + z^{2} = \mathop R\nolimits_{\text{a}}^{2} , \hfill \\ {\text{duct}}: \, \left( {x - m} \right)^{2} + y^{2} = \mathop R\nolimits_{\text{d}}^{2} , \hfill \\ \end{gathered}$$

(15)

where m = R_d + h + t. The intersection points in yz plane between alveolus and duct is

$$\begin{gathered} y_{1} = y_{2} = \frac{{\mathop R\nolimits_{\text{a}}^{2} + m^{2} - R_{\text{d}}^{2} }}{2m}, \hfill \\ z_{1} = - \sqrt {\mathop R\nolimits_{\text{a}}^{2} - \left( {\frac{{\mathop R\nolimits_{\text{a}}^{2} + m^{2} - \mathop R\nolimits_{\text{d}}^{2} }}{2m}} \right)^{2} } , \hfill \\ z_{2} = \sqrt {\mathop R\nolimits_{\text{a}}^{2} - \left( {\frac{{\mathop R\nolimits_{\text{a}}^{2} + m^{2} - \mathop R\nolimits_{\text{d}}^{2} }}{2m}} \right)^{2} } . \hfill \\ \end{gathered}$$

(16)

The intersection volume is derived by double integral as

$$\begin{gathered} V_{{{\text{a}} \cap {\text{D}}}} = 2 \cdot \iint {\sqrt {R_{\text{a}}^{2} - y^{2} - z^{2} } dydz}, \hfill \\ \, = 2 \cdot \int_{{z_{1} }}^{{z_{2} }} {\left( {\int_{{m - \sqrt {R_{\text{d}}^{2} - z^{2} } }}^{{\sqrt {R_{\text{a}}^{2} - z^{2} } }} {\sqrt {R_{\text{a}}^{2} - y^{2} - z^{2} } } dy} \right)} dz, \hfill \\ \, = 2 \cdot \int_{{z_{1} }}^{{z_{2} }} {f(z)} dz, \hfill \\ \end{gathered}$$

(17)

where f(z) is derived by integration by part,

$$\begin{gathered} f(z) = \frac{\pi }{2} \cdot \frac{{\mathop R\nolimits_{\text{a}}^{2} - z^{2} }}{2} - \frac{1}{2} \cdot \left( {m - \sqrt {\mathop R\nolimits_{\text{d}}^{2} - z^{2} } } \right) \cdot \sqrt {\mathop R\nolimits_{\text{a}}^{2} - \mathop R\nolimits_{\text{d}}^{2} - m^{2} + 2m \cdot \sqrt {\mathop R\nolimits_{\text{d}}^{2} - z^{2} } } \hfill \\ \, - \frac{{\mathop R\nolimits_{\text{a}}^{2} - z^{2} }}{2}\arcsin \left( {\frac{{m - \sqrt {\mathop R\nolimits_{\text{d}}^{2} - z^{2} } }}{{\sqrt {\mathop R\nolimits_{\text{a}}^{2} - z^{2} } }}} \right). \hfill \\ \end{gathered}$$

(18)

Then a numerical integration, named composite Simpson’s rule, is applied to approximate integral for f(z),

$$V_{{{\text{a}} \cap {\text{D}}}} = 2 \cdot \int_{{z_{1} }}^{{z_{2} }} {f(z)dz} = \frac{2h}{3}\left( {f(z_{1} ) + f(z_{2} ) + 4\sum\limits_{j = 1}^{n/2} {f\left( {z_{2j - 1} } \right) + 2\sum\limits_{j = 1}^{n/2 - 1} {f\left( {z_{2j} } \right)} } } \right),$$

(19)

where n is an even number of subintervals between z₁ and z₂; h = (z₂ − z₁)/n is the spacing of one subinterval.