Skip to main content
SpringerLink
Log in

General Modular Quantum Dilogarithm and Beta Integrals

  • Published:
Proceedings of the Steklov Institute of Mathematics Aims and scope Submit manuscript

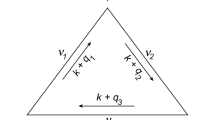
Abstract

We consider a univariate beta integral composed of general modular quantum dilogarithm functions and prove its exact evaluation formula. It represents the partition function of a particular 3d supersymmetric field theory on the general squashed lens space. Its possible applications to 2d conformal field theory are briefly discussed as well.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. S. Alexandrov and B. Pioline, “Theta series, wall-crossing and quantum dilogarithm identities,” Lett. Math. Phys. 106 (8), 1037–1066 (2016).

    MathSciNet  MATH  Google Scholar 

  2. J. E. Andersen and R. Kashaev, “Complex quantum Chern-Simons,” arXiv: 1409.1208 [math.QA].

  3. G. E. Andrews, R. Askey, and R. Roy, Special Functions (Cambridge Univ. Press, Cambridge, 1999), Encycl. Math. Appl. 71.

    MATH  Google Scholar 

  4. V. V. Bazhanov, V. V. Mangazeev, and S. M. Sergeev, “Faddeev-Volkov solution of the Yang-Baxter equation and discrete conformal symmetry,” Nucl. Phys. B 784 (3), 234–258 (2007).

    MathSciNet  MATH  Google Scholar 

  5. V. V. Bazhanov, V. V. Mangazeev, and S. M. Sergeev, “Exact solution of the Faddeev-Volkov model,” Phys. Lett. A 372 (10), 1547–1550 (2008).

    MathSciNet  MATH  Google Scholar 

  6. M. A. Bershtein, V. A. Fateev, and A. V. Litvinov, “Parafermionic polynomials, Selberg integrals and three-point correlation function in parafermionic Liouville field theory,” Nucl. Phys. B 847, 413–459 (2011).

    MathSciNet  MATH  Google Scholar 

  7. N. N. Bogolyubov and D. V. Shirkov, Introduction to the Theory of Quantized Fields, 3rd ed. (Nauka, Moscow, 1976; J. Wiley & Sons, New York, 1980); 4th ed. (Nauka, Moscow, 1984).

    MATH  Google Scholar 

  8. G. Bonelli, K. Maruyoshi, A. Tanzini, and F. Yagi, “N = 2 gauge theories on toric singularities, blow-up formulae and W-algebrae,” J. High Energy Phys. 2013 (01), 014 (2013).

    MathSciNet  MATH  Google Scholar 

  9. F. J. van de Bult, E. M. Rains, and J. V. Stokman, “Properties of generalized univariate hypergeometric functions,” Commun. Math. Phys. 275 (1), 37–95 (2007).

    MathSciNet  MATH  Google Scholar 

  10. A. G. Bytsko and J. Teschner, “Quantization of models with non-compact quantum group symmetry: Modular XXZ magnet and lattice sinh-Gordon model,” J. Phys. A: Math. Gen. 39 (41), 12927–12981 (2006).

    MathSciNet  MATH  Google Scholar 

  11. D. Chicherin and S. Derkachov, “The R-operator for a modular double,” J. Phys. A: Math. Theor. 47 (11), 115203 (2014).

    MathSciNet  MATH  Google Scholar 

  12. D. Chicherin and V. P. Spiridonov, “The hyperbolic modular double and the Yang-Baxter equation,” in Representation Theory, Special Functions and Painvlevé Equations — RIMS 2015 (Math. Soc. Japan, Tokyo, 2018), Adv. Stud. Pure Math. 76, pp. 95–123.

    MATH  Google Scholar 

  13. T. Dimofte, “Complex Chern-Simons theory at level k via the 3d-3d correspondence,” Commun. Math. Phys. 339 (2), 619–662 (2015).

    MathSciNet  MATH  Google Scholar 

  14. T. Dimofte, D. Gaiotto, and S. Gukov, “Gauge theories labelled by three-manifolds,” Commun. Math. Phys. 325 (2), 367–419 (2014).

    MathSciNet  MATH  Google Scholar 

  15. F. A. Dolan and H. Osborn, “Applications of the superconformal index for protected operators and q-hypergeometric identities to N = 1 dual theories,” Nucl. Phys. B 818 (3), 137–178 (2009).

    MathSciNet  MATH  Google Scholar 

  16. F. A. H. Dolan, V. P. Spiridonov, and G. S. Vartanov, “From 4d superconformal indices to 3d partition functions,” Phys. Lett. B 704 (3), 234–241 (2011).

    MathSciNet  Google Scholar 

  17. M. Eichler and D. Zagier, The Theory of Jacobi Forms (Birkhäuser, Boston, 1985), Prog. Math. 55.

    MATH  Google Scholar 

  18. L. Faddeev, “Currentlike variables in massive and massless integrable models,” in Quantum Groups and Their Applications in Physics (IOS Press, Amsterdam, 1996), Proc. Int. Sch. Phys. “Enrico Fermi” 127, pp. 117–135.

    MATH  Google Scholar 

  19. L. D. Faddeev, “Discrete Heisenberg-Weyl group and modular group,” Lett. Math. Phys. 34 (3), 249–254 (1995).

    MathSciNet  MATH  Google Scholar 

  20. V. Fateev, A. Zamolodchikov, and Al. Zamolodchikov, “Boundary Liouville field theory. I: Boundary state and boundary two-point function,” arXiv: hep-th/0001012.

  21. I. Gahramanov and A. P. Kels, “The star-triangle relation, lens partition function, and hypergeometric sum/integrals,” J. High Energy Phys. 2017 (02), 040 (2017).

    MathSciNet  MATH  Google Scholar 

  22. L. Griguolo, D. Seminara, R. J. Szabo, and A. Tanzini, “Black holes, instanton counting on toric singularities and q-deformed two-dimensional Yang-Mills theory,” Nucl. Phys. B 772 (1-2), 1–24 (2007).

    MathSciNet  MATH  Google Scholar 

  23. N. Hama, K. Hosomichi, and S. Lee, “SUSY gauge theories on squashed three-spheres,” J. High Energy Phys. 2011 (05), 014 (2011).

    MathSciNet  MATH  Google Scholar 

  24. S. K. Hansen and T. Takata, “Reshetikhin-Turaev invariants of Seifert 3-manifolds for classical simple Lie algebras,” J. Knot Theory Ramifications 13 (5), 617–668 (2004).

    MathSciNet  MATH  Google Scholar 

  25. Y. Imamura, H. Matsuno, and D. Yokoyama, “Factorization of the S3/ℤn partition function,” Phys. Rev. D 89 (8), 085003 (2014).

    Google Scholar 

  26. Y. Imamura and D. Yokoyama, “S3/ℤn partition function and dualities,” J. High Energy Phys. 2012 (11), 122 (2012).

    MATH  Google Scholar 

  27. A. Kapustin, B. Willett, and I. Yaakov, “Exact results for Wilson loops in superconformal Chern-Simons theories with matter,” J. High Energy Phys. 2010 (03), 089 (2010).

    MathSciNet  MATH  Google Scholar 

  28. R. Kashaev, “The quantum dilogarithm and Dehn twists in quantum Teichmüller theory,” in Integrable Structures of Exactly Solvable Two-Dimensional Models of Quantum Field Theory, Ed. by S. Pakuliak and G. von Gehlen (Kluwer, Dordrecht, 2001), NATO Sci. Ser. II: Math. Phys. Chem. 35, pp. 211–221.

    MATH  Google Scholar 

  29. R. M. Kashaev, “Beta pentagon relations,” Theor. Math. Phys. 181 (1), 1194–1205 (2014) [transl. from Teor. Mat. Fiz. 181 (1), 73–85 (2014)].

    MathSciNet  MATH  Google Scholar 

  30. R. Kashaev, “The Yang-Baxter relation and gauge invariance,” J. Phys. A: Math. Theor. 49 (16), 164001 (2016).

    MathSciNet  MATH  Google Scholar 

  31. R. Kashaev, F. Luo, and G. Vartanov, “A TQFT of Turaev-Viro type on shaped triangulations,” Ann. Henri Poincaré 17 (5), 1109–1143 (2016).

    MathSciNet  MATH  Google Scholar 

  32. S. Kharchev, D. Lebedev, and M. Semenov-Tian-Shansky, “Unitary representations of \({U_q}(\mathfrak{sl}(2,\mathbb{R}))\), the modular double and the multiparticle q-deformed Toda chains,” Commun. Math. Phys. 225 (3), 573–609 (2002).

    MATH  Google Scholar 

  33. F. Nieri and S. Pasquetti, “Factorisation and holomorphic blocks in 4d,” J. High Energy Phys. 2015 (11), 155 (2015).

    MathSciNet  MATH  Google Scholar 

  34. “NIST digital library of mathematical functions,” http://dlmf.nist.gov/.

  35. V. Pestun et al., “Localization techniques in quantum field theories,” J. Phys. A: Math. Theor. 50 (44), 440301 (2017).

    MathSciNet  MATH  Google Scholar 

  36. H. Rademacher, Topics in Analytic Number Theory (Springer, Berlin, 1973).

    MATH  Google Scholar 

  37. H. Rademacher and E. Grosswald, Dedekind Sums (Math. Assoc. Am., Washington, D.C., 1972).

    MATH  Google Scholar 

  38. S. N. M. Ruijsenaars, “A generalized hypergeometric function satisfying four analytic difference equations of Askey-Wilson type,” Commun. Math. Phys. 206 (3), 639–690 (1999).

    MathSciNet  MATH  Google Scholar 

  39. G. Sarkissian and V. P. Spiridonov, “From rarefied elliptic beta integral to parafermionic star-triangle relation,” J. High Energy Phys. 2018 (10), 097 (2018).

    MATH  Google Scholar 

  40. G. A. Sarkissian and V. P. Spiridonov, “Modular group and hyperbolic beta integral,” Russ. Math. Surv. 75 (3) (2020) [transl. from Usp. Mat. Nauk 75 (3), 187–188 (2020)].

  41. A. A. Slavnov and L. D. Faddeev, Introduction to Quantum Theory of Gauge Fields (Nauka, Moscow, 1978). Engl. transl.: L. D. Faddeev and A. A. Slavnov, Gauge Fields: Introduction to Quantum Theory (Addison-Wesley, Redwood City, CA, 1991), Front. Phys. 83.

    Google Scholar 

  42. V. P. Spiridonov, “On the elliptic beta function,” Russ. Math. Surv. 56 (1), 185–186 (2001) [transl. from Usp. Mat. Nauk 56 (1), 181–182 (2001)].

    MathSciNet  MATH  Google Scholar 

  43. V. P. Spiridonov, “Short proofs of the elliptic beta integrals,” Ramanujan J. 13, 265–283 (2007).

    MathSciNet  MATH  Google Scholar 

  44. V. P. Spiridonov, “Essays on the theory of elliptic hypergeometric functions,” Russ. Math. Surv. 63 (3), 405–472 (2008) [transl. from Usp. Mat. Nauk 63 (3), 3–72 (2008)].

    MathSciNet  MATH  Google Scholar 

  45. V. P. Spiridonov, “Elliptic beta integrals and solvable models of statistical mechanics,” in Algebraic Aspects of Darboux Transformations, Quantum Integrable Systems and Supersymmetric Quantum Mechanics (Am. Math. Soc., Providence, RI, 2012), Contemp. Math. 563, pp. 181–211.

    Google Scholar 

  46. V. P. Spiridonov, “Rarefied elliptic hypergeometric functions,” Adv. Math. 331, 830–873 (2018).

    MathSciNet  MATH  Google Scholar 

  47. V. P. Spiridonov and G. S. Vartanov, “Elliptic hypergeometry of supersymmetric dualities,” Commun. Math. Phys. 304 (3), 797–874 (2011); arXiv: 0910.5944 [hep-th].

    MathSciNet  MATH  Google Scholar 

  48. J. V. Stokman, “Hyperbolic beta integrals,” Adv. Math. 190 (1), 119–160 (2004).

    MathSciNet  MATH  Google Scholar 

  49. A. Yu. Volkov and L. D. Faddeev, “Yang-baxterization of the quantum dilogarithm,” J. Math. Sci. 88 (2), 202–207 (1998) [transl. from Zap. Nauchn. Semin. POMI 224, 146–154 (1995)].

    MathSciNet  MATH  Google Scholar 

  50. Wikipedia contributors, “Lens space,” Wikipedia, The Free Encyclopedia (2019), https://en.wikipedia.org/w/index.php?title=Lens_space&oldid=922730842.

Download references

Acknowledgments

The authors are indebted to A. B. Kalmynin and R. M. Kashaev for a discussion of the obtained results.

Funding

This work is supported in part by the HSE Laboratory for Mirror Symmetry and Automorphic Forms (Russian Federation Government grant, contract no. 14.641.31.0001).

Author information

Authors and Affiliations

  1. Bogoliubov Laboratory of Theoretical Physics, Joint Institute for Nuclear Research, ul. Joliot-Curie 6, Dubna, Moscow oblast, 141980, Russia

    Gor A. Sarkissian & Vyacheslav P. Spiridonov

  2. Faculty of Physics, Yerevan State University, Alex Manoogian 1, 0025, Yerevan, Armenia

    Gor A. Sarkissian

  3. National Research University Higher School of Economics, ul. Myasnitskaya 20, Moscow, 101000, Russia

    Vyacheslav P. Spiridonov

Authors
  1. Gor A. Sarkissian
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Vyacheslav P. Spiridonov
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding authors

Correspondence to Gor A. Sarkissian or Vyacheslav P. Spiridonov.

Additional information

To A. A. Slavnov on the occasion of his 80th birthdayfs

This article was submitted by the authors simultaneously in Russian and English

Published in Russian in Trudy Matematicheskogo Instituta imeni V.A. Steklova, 2020, Vol. 309, pp. 269–289.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Sarkissian, G.A., Spiridonov, V.P. General Modular Quantum Dilogarithm and Beta Integrals. Proc. Steklov Inst. Math. 309, 251–270 (2020). https://doi.org/10.1134/S0081543820030190

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1134/S0081543820030190

Search

Navigation