Abstract
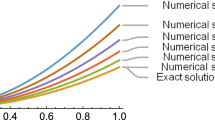
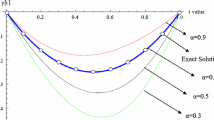
This research propounds a fractional-order Legendre functions operational matrix of fractional integration in order to solve the fractional delay differential equations. The fractional derivative is regarded in the Caputo sense. The suggested method is implemented to reduce the problem to the solution of a system of algebraic equations. Using the presented method, some examples are solved and numerical stability of the proposed method is examined. Compared to other published methods, the presented technique proved to be more accurate.










Similar content being viewed by others
References
Abbasbandy S, Kazem S, Alhuthali M, Alsulami H (2015) Application of the operational matrix of fractional-order Legendre functions for solving the time-fractional convection-diffusion equation. Appl Math Comput 266:31–40
Balachandran K, Kiruthika S, Trujillo JJ (2013) Existence of solutions of nonlinear fractional pantograph equations. Acta Math Sci 33B(3):712–720
Benson DAA, Meerschaert MM, Revielle J (2013) Fractional calculus in hydrologic modeling: a numerical perspective. Adv Water Resour 51:479–497
Bohannan GW (2008) Analog fractional order controller in temperature and motor control applications. J Vib Control 14:1487–1498
Brunner H, Huang Q, Xies H (2011) Discontinuous Galerkin methods for delay differential equations of pantograph type. SIAM J Numer Anal 48:1944–1967
Fakharzadeh Jahromi AR, Baneshi Z (2017) A numerical method for solving fractional optimal control problems. Iran J Sci Technol Trans Sci 41:439–443
Heris MS, Javidi M (2017a) On fbdf5 method for delay differential equations of fractional order with periodic and anti-periodic conditions. Mediterr J Math 14(3):1–19
Heris MS, Javidi M (2017b) On fractional backward differential formulas for fractional delay differential equations with periodic and anti-periodic conditions. Appl Numer Math 118(Supplement C):203–220
Hooshmandasl MR, Heydari MH, Cattani C (2016) Numerical solution of fractional sub-diffusion and time-fractional diffusion-wave equations via fractional-order Legendre functions. Nonlinear Dyn 88:131–268
Hussien HS (2019) Efficient collocation operational matrix method for delay differential equations of fractional order. Iran J Sci Technol Trans Sci 43(4):1841–1850
Kazem S, Abbasbandy S, Kumar S (2013) fractional-order Legendre functions for solving fractional-order differential equations. Appl Math Model 37:5498–5510
Khader MM, Hendy AS (2012) The approximate and exact solutions of the fractional-order delay differential equations using Legendre seudospectral method. Int J Pure Appl Math 74(3):287–297
Knipl DH, Rst G, Wu J (2013) Epidemic spread and variation of peak times in connected regions due to travel-related infections dynamics of an antigravity-type delay differential model. SIAM J Appl Dyn Syst 12(4):1722–1762
Kreyszig E (1978) Introductory functional analysis with applications. Wiley, New York
Magin RL (2004) Fractional calculus in bioengineering. Crit Rev Biomed Eng 32:1–104
Magin RL (2010) Fractional calculus models of complex dynamics in biological tissues. Comput Math Appl 59:1586–1593
Magin R, Ortigueira MD, Podlubny I, Trujillo J (2011) On the fractional signals and systems. Signal Process 91(3):350–371
Maleki M, Davari A (2019) Fractional retarded differential equations and their numerical solution via a multistepcollocation method. Appl Numer Math 143:203–222
Moghaddam BP, Mostaghim ZS (2013) A numerical method based on finite difference for solving fractional delay differential equations. J Taibah Univ Sci 7:120–127
Morgado ML, Ford NJ, Lima PM (2013) Analysis and numerical methods for fractional differential equations with delay. J Comput Appl Math 252:159–168
Muroya Y, Ishiwata E, Brunner H (2003) On the attainable order of collocation methods for pantograph integro-differential equations. J Comput Appl Math 152:347–366
Podlubny I (1999) Fractional differential equations. Academic Press, New York
Rahimkhani P, Ordokhani Y (2017) Numerical studies for fractional pantograph differential equations based on piecewise fractional order Taylor function approximations. Iran J Sci Technol Trans A Sci. https://doi.org/10.1007/s40995-017-0373-z
Rahimkhani P, Ordokhani Y, Babolian E (2017) A new operational matrix based on Bernoulli wavelets for solving fractional delay differential equations. Numer Algorithms 74(1):223–245
Rossikhin YA, Shitikova MV (1997) Applications of fractional calculus to dynamic problems of linear and nonlinear hereditary mechanics of solids. Appl Mech Rev 50(1):15–67
Saeed U, ur Rehman M (2014) Hermite wavelet method for fractional delay differential equations. J Differ Equ 2014:1–8
Saeed U, ur Rehman M, Iqbal MA (2015) Modied Chebyshev wavelet methods for fractional delay-type equations. Appl Math Comput 264:431–442
Torelli L (1989) Stability of numerical methods for delay differential equations. J Comput Appl Math 25:15–26
Tyagi S, Abbas S, Pinto M, Sepulveda D (2016) Approximation of solutions of fractional-order delayed cellular neural network on [0, 1]. Mediterr J Math 14(1):1–25
Wang Z (2013) A numerical method for delayed fractional-order differential equations. J Appl Math 5:1–7
Xu MQ, Lin YZ (2016) Simplified reproducing kernel method for fractional differential equations with delay. Appl Math Lett 52:156–161
Yang Y, Huang Y (2013) Spectral-collocation methods for fractional pantograph delay-integrodifferential equations. Adv Math Phys 2013:1–14
Acknowledgements
The authors are very grateful to the reviewers for carefully reading this article and for their comments and suggestions that have improved this article.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Mesgari, S., Barikbin, Z. Fractional-Order Legendre Functions for Solving Fractional Delay Differential Equations. Iran J Sci Technol Trans Sci 44, 1673–1683 (2020). https://doi.org/10.1007/s40995-020-00954-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40995-020-00954-9