1 Introduction

Interstitial Free steel (IF) steel is often termed as a clean steel that refers to very low to negligible level of interstitial solute atoms that may be present in the steel and hence the Fe lattice is practically free of strains caused by the interstitials, thus resulting in high formability and high strain rate sensitivity. Microalloying elements Nb and Ti added to the steel combine with C and N atoms and hence, make the steel essentially free of interstitials. Recently, IF steels are being intended for applications in various structural parts viz., cross members, B-pillars, longitudinal beams etc. [1, 2], besides regular applications in automobile industry. These steels are normally characterized with low yield strength and hence high formability and deep drawability. Thus, new scientific approaches should be explored to optimize the processing parameters in order to achieve optimized properties in IF steels with high strength and toughness without compromising on formability. Recently, analysis of flow stress versus strain curves describing the hot/warm working characteristics of metals and alloys has received great attraction and several works have since been executed to characterize the flow behavior using physical simulations as well as mathematical modeling, cf. [3,4,5,6]. However, the constitutive models reported by Fang et al. [3]; Phaniraj et al. [4] and Wei et al. [6] are considered unsuitable as they did not consider the effect of applied strain on the flow stress modeling. Basically, their models predict that either the flow stress does not change with strain under a steady-state situation or it is considered as the peak stress. Hence, these constitutive models are considered inappropriate when the material exhibits dynamic recovery (DRV), dynamic recrystallization (DRX) or work hardening (WH) during deformation.

Thus, in recent years, many researchers have performed simulation/modeling of thermomechanically controlled processing (TMCP) by considering the effects of DRX, DRV, WH, phase transformation, strain localization, etc. in order to provide a realistic prediction of flow stress behavior during deformation. Wietbrock et al. [7] and Wan et al. [8] investigated the hot working behavior of an austenitic steel and a TiAl-based alloy, respectively, considering WH and softening behavior due to DRX through rigid-viscoplastic finite element simulation (FES) and reported that the predicted grain size through FES analysis correlated well with the experimentally obtained results. A similar study has also been conducted by Baron et al. [9] on martensitic steels by using a modified constitutive model to predict the average grain size during DRX through the FES and presented a good correlation with the experimentally derived data. Furthermore, Li et al. [10] simulated the DRX behavior of a microalloyed steel through 3D-FES using an elastic–plastic model and showed that the predicted data correlated well with the experimentally obtained grain size. Zhou et al. [11] have recently suggested a criterion for hot deformation simulation considering the role of the grain size and its orientation during DRX through a visco-plastic model with a deformation energy-based DRX criterion and the predicted textures correlated well with experimentally obtained results. Furthermore, Mourad et al. [12] conducted a hot working simulation on polycrystalline metallic materials through introducing a criterion of strain localization and shear band formation during deformation. Their results indicate that the DRX process can provide the required extra softening besides thermal softening. Takaki et al. [13] proposed a relation between the initial microstructure and mechanical behavior of the materials through a multi-phase field, FES-DRX model considering the DRX kinetics. Using this model, they could estimate the macroscopic mechanical behavior during hot-working and the predictions matched well the experimentally obtained results. Furthermore, Shang et al. [14] suggested that DRX could influence void evolution during hot working processes and they proposed a DRX-based GTN-Thomason ductile fracture damage model to avoid the occurrence of ductile fracture.

However, the execution of all these kinds of constitutive models may not be suitable for describing the actual thermomechanically controlled deformation processes under transient conditions, as the constitutive equations were formulated based on the integration over constant temperatures and strain rates. Thus, various researchers were motivated to develop constitutive equations considering both the kinetic as well as thermostatistical approaches. For example, Puchi-Cabrera et al. [15] performed a hot working simulation study on a C–Mn steel using Sellars-Tegart-Garofalo model and derived an innovative constitutive equation in differential form. These approaches were found to be beneficial to represent the evolution of flow stress under variable temperature and strain rate conditions. To investigate the effect of strain rate and temperature on the mechanical response of the material, Egner and Egner [16] expressed a constitutive model of thermo-viscoplastic coupling on tempered martensitic steel subjected to cyclic thermomechanical loading. They reported that the coupling between dissipative phenomena and temperature in the constitutive model had a substantial effect on the response of mechanical properties. Zaera et al. [17] carried out modeling of the strain induced martensitic transformation in a dual phase steel considering the influence of adiabatic temperature rise at high strain rate deformation. They suggested that the thermal effect should be considered during the modeling in order to estimate the strain induced martensitic transformation at high strain rates. Papatriantafillou et al. [18] proposed a methodology of numerical integration through finite element method that described the mechanical behavior of TRIP steels precisely. Hao et al. [19] proposed a hierarchical constitutive model and successfully established a relationship of overall mechanical properties in modern ultrahigh-strength steel design. Incorporating the phase transformation laws, Neumann et al. [20] proposed a Hashin–Shtrikman type thermomechanical model for steel and reported that the model presented a good correlation with experimental results. The modified version of the Khan-Huang-Liang constitutive model [21] predicted the stress–strain behavior of various alloys more precisely under variable strain rates and temperatures.

Most of the simulation studies of hot-working processes discussed above are based on mesh-based FEM simulation technique. Although, the technique is a very effective tool to investigate the hot working behavior of materials, these formulations have certain limitations as reported by Liu and Gu [22], e.g. (i) construction of mesh while using any FEM code is very tedious and complex, since proper connectivity may not be easy to achieve (ii) the predicted stress values by mesh-based model are often discontinuous and may be less accurate frequently, and many more. To overcome these complexities and difficulties, new efforts are required to develop different methods. Hence, in the present study, a simplistic approach comprising constitutive modeling of Ti + Nb stabilized IF steel has been adopted contemplating the effect of strain using both Hollomon as well as Modified Hollomon equations [23, 24]. The effect of strain has been introduced in the model considering various material constants (i.e. Q, n, α1, β, n′ and A) as the polynomial functions of strain [25] and established as simple constitutive equations, separately for α and γ phase regions. Recently, constitutive relationships of some carbon and alloy steels have been widely studied [23, 24]. However, reports and research results about the constitutive relationship of Ti + Nb stabilized IF steel are rare. Hence, the main purpose of present study is to investigate the hot deformation behavior of Ti + Nb stabilized IF steel over a wide range of temperatures and strain rates, and to employ a modified hyperbolic sine constitutive equation to describe the corresponding flow behavior of the IF steel in different phase fields separately (α and γ phase regions) by considering the combined effects of strain, strain rate and temperature. Meanwhile, the reliability of the constitutive equations for different phases developed in the present study, have also been validated through determining the values of correlation coefficients (Rcc) and average absolute relative errors (AARE).

2 Experimental Details

2.1 Materials

The material used in the current study is a Ti + Nb stabilized interstitial free steel from production provided by TATA Steel Ltd., Jamshedpur, India. Elemental analysis (wt%) was carried out through optical emission spectroscopy (Spectrolab, Germany) and the result is summarized in Table 1.

Table 1 Elemental details (wt%) of the IF steel
Full size table

2.2 Determination of Phase Transformation Temperatures

The phase transformation temperatures i.e. upper (Ar3) and lower (Ar1) critical transformation temperatures were estimated from the dilatometer measurements in a Gleeble 3800 thermomechanical simulator. The sample (φ10 × 80 mm) was first heated up to 1200 °C at a heating rate of 5 °C s-1 and then soaked at 1200 °C for 2 min. The specimen was then cooled slowly to room temperature at a cooling rate of 1 °C s-1 to avoid diffusionless transformation. The temperature was measured by a K-type thermocouple, which was spot welded at the middle of the test sample, and a LVDT (linear variable displacement transducer) type dilatometer was used to record the dilatation change of the sample as a function of the temperature. Furthermore, Ar3/Ar1 temperatures were also assessed from a continuous cooling compression (CCC) curve obtained through a test performed in the Gleeble. Similarly, as in dilatation test a compression specimen (φ10 × 15 mm) was first reheated to the austenitization temperature (1200 °C) at 5 °C s−1, held for 2 min followed by cooling at 1 °C s−1 to 1000 °C. The specimen was then allowed to cool at 0.7 °C s-1 from 1000 to 500 °C while undergoing continuous deformation at a constant true strain rate of 10−3 s−1 to 0.7 strain.

2.3 Hot Compression Test

Hot compression tests were conducted using specimens of the dimensions φ10x15 mm, with the test chamber in the Gleeble evacuated to a vacuum of the order of 1 Pa. The sample temperature was monitored during the test using a K-type thermocouple spot welded in the middle of the specimen as per the prescribed technique. A graphite foil along with a nickel-based conducting lubricant was used between the anvil and the sample to reduce friction and possible temperature gradient. Initially, all the samples were reheated to 1200 °C at 5 °C s-1 and soaked for 2 min, followed by cooling at 1 °C s−1 to the deformation temperature. Compression tests were carried out in the temperature range of 1100–650 °C in steps of 50 °C. At each processing temperature, the samples were deformed to about 50% reduction (equivalent to a true strain of ~ 0.7) at constant true strain rates of 10−3, 10−2, 10−1, 1 and 10 s−1. Following the compression testing, the samples were quenched in water to freeze the structures in order to prevent any subsequent static/meta-dynamic recrystallization (SRX/MDRX) or grain growth phenomena. Flow stress data obtained from the flow curves were corrected for the adiabatic temperature rise by using the linear interpolation of log σ versus 1000/T plot, where σ is the true stress and T is the temperature in Kelvin. Besides the graphite foil and nickel-based conducting lubricant, to further reduce the friction between the specimen and the anvil, a tantalum foil of 0.05 mm thickness has been inserted between the anvils and graphite foil as per the guideline provided by National Physical Laboratory, UK [26]. These guidelines are applicable to deformation strain rates in the range 10−4 to 102 s−1, relevant to industrial forging and rolling processes [26]. An important aspect of these guidelines is the use of shape measurements on the deformed test pieces to confirm the validity of the test data. For example, if the barreling during compression is greater than a specified amount, the flow stress data will be significantly in error. The barreling coefficient (B) can be defined as follows [26].

$${\text{Barreling}}\;{\text{coefficient}}\left( {\text{B}} \right) = {\raise0.7ex\hbox{${h_{f} \times (d_{f} )^{2} }$} \!\mathord{\left/ {\vphantom {{h_{f} \times (d_{f} )^{2} } {h_{o} \times (d_{0} )^{2} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${h_{o} \times (d_{0} )^{2} }$}}$$

If B is greater than 1.10, then the test will be considered as invalid. In the present case, the total amount of true strain applied was 0.69 only and corresponding value of B calculated was estimated as ~ 0.6 or lower for the compression tests. So, the influence of friction should be minimal in this case. Also, the study was aimed at modelling the nominal strain in accord with the guidelines stated above and any study on lubrication effect was beyond the scope of this work. Hence, we have not considered the influence of friction during flow stress calculation.

2.4 Microstructural Investigation

Microstructural investigation of deformed specimens was carried out through light optical microscopy, electron backscattered diffraction (EBSD), transmission electron microscopy (TEM). For light optical microscopy the deformed specimens were polished using different emery papers/cloth and subsequently etched by 2% Nital solution. For EBSD analysis the specimens were further electropolished for 50 s using an electrolyte of 20% perchloric acid + 80% methanol at − 20 °C and 21 V. EBSD detector was attached with SEM (ZEISS, 51-ADD0048). TEM study was performed using an electron microscope (FEI Technai 20 G2S-Twin), operated at 200 kV. The specimens were first thinned down to a thickness of 0.08μm by mechanical polishing. 3 mm dia discs punched from the mechanically thinned samples were subjected to twin-jet electro-polishing at a potential of 40 V DC by using a solution of 10% perchloric acid and 90% methanol cooled to −20 °C.

3 Results and Discussion

3.1 Phase Transformation Characterization

The dilation versus temperature curve acquired from the dilatometry test and the stress (compressive) versus temperature curve generated from the CCC test for the IF steel are shown in Fig. 2a, b, respectively. The phase transformation temperatures Ar3 and Ar1 correspond to the 1st and 2nd inflexion points in the dilatation and the CCC curves as marked by arrows in Fig. 1a, b, respectively. Using the dilatometer measurements, the Ar3 and Ar1 temperatures are estimated to be 880 and 820 °C, respectively (Fig. 2a), whereas the corresponding values estimated from the CCC curve are ~ 905 and 855 °C, respectively. Hence, it is apparent that the continuous cooling of deformed sample marginally raises the critical temperatures (Ar3, Ar1), presumably due to the fact that the plastic deformation during cooling marginally increases the Gibbs free energy of austenite phase (γ) and/or owing to the refinement of austenite grains via dynamic recrystallization (DRX) [27]. Moreover, the existence of high dislocation density raises the heterogeneous nucleation sites for α ferrite grains, besides accelerating the carbon diffusion, which thereby changes the kinetics of phase transformation [28].

Fig. 1
figure 1

Axisymmetric compression geometries

Full size image
Fig. 2
figure 2

a Dilatometry and b continuous cooling compression (CCC) curves of the IF steel. The Inflexion points as marked by arrows indicate the Ar3 and Ar1 temperatures

Full size image

Additionally, very small inflexions can be seen in the dilatometry and CCC-curves at the temperature just above Ar3 temperature. Those very small inflexions may be associated with the temperature gradient along the length of the sample.

3.2 Analysis of Flow Stress–Strain Behavior

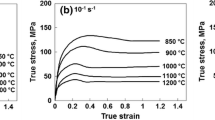
The compressive stress versus strain curves of the IF steel at different strain rates (10−3, 10−2, 10−1, 1 and 10 s−1) and temperatures (650–1100 °C) are shown in Fig. 3a–e, respectively. As expected, the flow stress values gradually decreased for a given constant true strain rate as the deformation temperature was raised. The compression flow stress curves can be categorized into two distinct types, i.e. with or without the presence of steady state flow. It can be noticed from Fig. 3a–d that the flow stress curves generated at the combination of higher temperatures and lower strain rates (e.g. 900–1100 °C at 10−3 s−1, 950–1100 °C at 10−2 s−1,1050–1100 °C at 10−1 s−1 and 1050–1100 °C at 1 s−1) exhibited initially a broad peak over a certain amount of strain. Thereafter, the flow stress dropped on further straining before reaching a steady-state behavior at higher strains. From Fig. 3a–d, it can also be observed that the peaks on the flow curves are shifted to higher strains with the increase in strain rate. A flow curve exhibiting a broad peak behavior generally suggests that DRX is the governing microstructural mechanism [29, 30], whereas a flow stress curve without any peak strain behavior indicates DRV [29, 30]. Therefore, DRX and DRV are the dominant mechanisms operating during the hot working process. It can be observed from Fig. 3b–d that the flow curves of the IF steel exhibit a steady state behavior without any peak strain behavior in the temperature range 650–750 °C (i.e. in the ferritic region) and at intermediate strain rates of 10−2 to 1 s−1, suggesting a balance between strain hardening and dynamic recovery during continuous straining. A slight strain hardening (Fig. 2b–d) is observed within the temperature range of 900–950 °C at the intermediate strain rate of 10−2 s−1 to 1 s−1. Moreover, at higher strain rates (e.g.10 s−1), the flow stress of the steel increases continuously over the entire deformation strain without exhibiting a steady state plateau signifying the occurrence of continuous strain hardening at the highest strain rate used in these experiments (10 s−1). Generally, DRV is known to be the only restoration process for warm deformation of the α-phase at low to high strain rates and the DRX normally does not take place in this range due to its high stacking fault energy thus facilitating fast recovery of dislocations [31, 32]. Hence, the stored energy essential for the facilitation of DRX is not attained during warm deformation of α-phase [31, 32].

Fig. 3
figure 3

Flow stress curves of IF steel in the temperature range of 650–1100 °C at a particular strain rate of a 10−3 s−1, b 10−2 s−1, c 10−1s−1, d 1 s−1 and e 10 s−1

Full size image

It could also be observed from Fig. 3a–c that the flow stress curves for ferrite in the high temperature range of 850–800 °C and at low strain rates of 10−3–10−1 s−1 exhibit a stress drop after peak formation, a behavior typically observed for austenite during hot deformation at lower strain rates. It is also to be noted that the rate of flow softening mechanism is greater at lower stain rate (10−3 s−1) and it decreases appreciably at comparatively higher stain rate (10−1 s−1). This behavior is attributed to the dynamic recrystallization of ferrite during deformation at extremely lower strain rate at relatively higher ferritic temperature [31, 32].

Deformation process generally involves both the dislocation nucleation (strain hardening) as well as annihilation (dynamic softening). These two conflicting activities may occur concurrently during deformation process and directly affect the resultant dislocation density which is signified by the flow stress curves. The homogenization annealing (at 1200 °C for 2 min) of the steel prior to the deformation process, develops a uniform structure having a low dislocation density. Therefore, during deformation, a large dislocation density is accumulated, rising rapidly initially as the deformation progresses, facilitating strain hardening. This is contested by annihilation of dislocations and hence, there is an appearance of peak in the stress versus strain curve. As the dynamic restoration process is well-adjusted by strain hardening, the flow stress decreases and grasps a steady state during further straining. On the other hand, DRX encountered during deformation process when the true strain overcomes the critical strain required for DRX. Prior to the stress value reaching the peak stress, the work hardening in respect of dislocation density enhancement occurs simultaneously. Hence, the flow stress rises up to a peak value, following which the rising rate gradually drops as the dynamic softening rate becomes greater than the work hardening rate. There is a significant effect of temperature on the appearance of the peak stress. It can be seen that the critical strain for the peak stress gradually increases with increasing strain rate and/or decreasing temperature. Moreover, at higher temperatures and lower strain rates, both the ferrite and austenite phases exhibit relatively low critical strains to achieve a steady state stress. This suggests that the rate of dislocation generation is balanced by the dynamic restoration process [33].

It can be noted (Fig. 3e) that when the applied strain rate is extremely high (10 s−1), the flow stress curves exhibit unusual behavior resembling unstable flow due to the fact that the transducer takes up the vibrations of the testing system during high strain rate testing and includes it in the actual measured signal. [34]. A similar stress–strain behavior has also been reported for the hot deformation working of low carbon bainitic steel by Yang et al. [35].

Generally, it is believed that flow softening of metallic materials suggests either dynamic recrystallization or flow instability. Likewise, a steady state stress–strain behavior can also be indicative of superplastic deformation [36]. Therefore, it will not be correct to jump at any conclusion based solely on the shape of the stress–strain curve and it must be supported by further analysis. The Z parameter, also known as the temperature compensated strain rate with significant influence on the flow behavior, can be presented to explain the deformation behavior of the IF steel. Z parameter can be stated as expressed in Eq. (1) [37]:

$$Z = \dot{\varepsilon }\exp \left( {\frac{Q}{RT}} \right)$$
(1)

where Q is the activation energy (kJ/mol) for deformation, T is the absolute temperature (K) and R is the universal gas constant (8.314 J/mol K−1). Hence, it can be stated that the dynamic recrystallization and recovery processes often take place under low Z condition (i.e. at low strain rate and high temperature), and when the Z is high, mainly the strain hardening governs the hot working process. Under low Z condition, the movement of dislocation becomes easier which enables DRX and/or DRV thereby decreasing the density of dislocations. Furthermore, the strain hardening is well-adjusted by the strain softening [33] and the flow curve exhibits a steady-state plateau. On the other hand, for the high Z condition, due to the low rate of the movement of dislocations and short test times imposed, the possibility of annihilation of dislocations is significantly reduced, thereby weakening the effect of dynamic softening processes, i.e. DRV or DRX. Also, at higher strain rates, the rate of dislocation multiplication is greater thus leading to dislocation strengthening effect with the flow stress gradually going up with increasing strain [33].

Furthermore, Fig. 4a shows the change in flow stress with deformation temperatures at different strain rates. It is clear from Fig. 4a that there is an existence of dual phase region in the temperature range 855–900 °C, even after high strain rate deformation (10 s−1). Furthermore, it was observed that at a given strain rate, the flow stress decreases gradually with increasing temperature (both for the austenite and ferrite). On the other hand, Fig. 4b shows the variation of flow stress with strain rate at fixed temperature for IF steel at true strain of 0.6. It was seen that for a fixed temperature, the flow stress rises in both the phase regions with the increase in strain rate. It can also be seen from Fig. 4a that at a small range of temperatures (800–850 °C), the flow stress of ferrite is lower than that of the austenite phase. Thus, less force is required for deformation of ferrite, e.g. during thermomechanical rolling.

Fig. 4
figure 4

a Flow stress versus deformation temperatures at different strain rates and b flow stress versus logarithm of strain rate at a particular temperature for the IF steel at a true strain of 0.6

Full size image

3.3 Microstructural Characterization

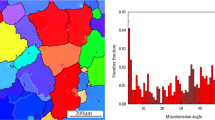
The optical microscopy (Fig. 5a, d) and EBSD analysis (Fig. 5b, c, e, f) have been performed to rationalize the occurrence of DRX in ferrite and austenite phase regimes. Figure 5a–c depict the optical micrograph, EBSD inverse pole figure and grain boundary map, respectively, of the specimen deformed at 850 °C/10−2s−1. Similarly, Fig. 5d–f display the optical micrograph, EBSD inverse pole figure and grain boundary map, respectively, of the specimen deformed at 1050 °C/10−2s−1. It can be observed clearly from Fig. 5a, b, d, e that the equiaxed DRX grains are homogeneously distributed throughout the structure and the corresponding grain boundary maps (Fig. 5c, f, respectively) reveal the presence of high fractions of subgrain boundaries (substructures) along with high angle boundaries. This confirms that the peak stress behaviors occurring in both the ferritic and austenitic phase fields correspond to the DRX phenomena.

Fig. 5
figure 5

a–c Light optical microstructure, EBSD inverse pole figure and grain boundary map of IF steel sample deformed at 850 °C/10−2 s−1, d–f Light optical microstructure, EBSD inverse pole figure and grain boundary map of IF steel specimen deformed at 1050 °C/10−2 s−1

Full size image

3.4 Constitutive Modeling of Flow Stress of Ti + Nb Stabilized IF Steel

Constitutive equations have been developed to predict the flow stress behavior during isothermal hot compression testing and finally a relationship has been established between total strain, strain rate, temperature and flow stress of the IF steel. The detailed analysis is presented in following sections.

3.4.1 Kinetic Analysis

The correlation between the flow stress (σ), strain rate (\(\dot{\varepsilon }\)) and temperature (T) (generally at high temperature) could be represented through an Arrhenius type equation [35, 38]. The effect of strain rate and temperature on hot working behavior could be denoted by Zener–Hollomon Parameter (Z) in an exponent type equation [35, 38]:

$$Z_{p} = A_{p} \sigma_{p}^{{n^{{{\prime \prime }}} }} = \dot{\varepsilon }\exp \left( {\frac{{Q_{p} }}{RT}} \right)$$
(2)
$$Z_{E} = A_{E} \exp \left( {\beta \sigma_{E} } \right) = \dot{\varepsilon }\exp \left( {\frac{{Q_{E} }}{RT}} \right)$$
(3)
$$Z = A\sinh \left( {\alpha_{1} \sigma } \right)^{n} = \dot{\varepsilon }\exp \left( {\frac{Q}{RT}} \right)$$
(4)

here R is the universal gas constant (8.314 J mole−1 K−1), T is the absolute temperature, Q is the activation energy for hot deformation (kJ mole−1) and A, n, \(n^{{{\prime \prime }}}\), β and \(\alpha_{1}\)(= β/n′) are material constants and subscripts P and E denote power and exponential laws, respectively. From the above equations, strain rate can be expressed as:

$$\dot{\varepsilon } = A_{p} \sigma_{p}^{{n^{{{\prime \prime }}} }} \exp \left( { - \frac{{Q_{p} }}{RT}} \right)$$
(5)
$$\dot{\varepsilon } = A_{E} \exp \left( {\beta \sigma_{E} } \right)\exp \left( { - \frac{{Q_{E} }}{RT}} \right)$$
(6)
$$\dot{\varepsilon } = A\sinh \left( {\alpha_{1} \sigma } \right)^{n} \exp \left( { - \frac{Q}{RT}} \right).$$
(7)

Generally, the power law equation (Eq. 2) is used for low stresses (α1σ < 0.8), which breaks down at high stresses. On the other hand, the exponential law equation (Eq. 3) is applicable for high stresses (α1σ > 1.2), which breaks down at high T and below l s−1. Therefore, for a wide range of stress levels (including the low and high stress levels), a universal constitutive equation (Eq. 4) is used, as proposed by Sellars et al. [35, 38]. Equations 5 and 6 are used to estimate the values of \(n^{{{\prime \prime }}}\) and β, and then α1 is calculated from these two parameters as \(\alpha_{1}\) = β/n′. By taking the logarithm on both sides of the Eqs. 5 and 6, the following Eqs. (Equations 8 and 9) can be obtained.

$$\ln \dot{\varepsilon } = \ln A_{p} + n^{{{\prime \prime }}} \ln \sigma_{p} - \frac{{Q_{p} }}{RT}$$
(8)
$$\ln \dot{\varepsilon } = \ln A_{E} + \beta \sigma_{E} - \frac{{Q_{E} }}{RT}$$
(9)

The values of β and \(n^{{{\prime \prime }}}\) are estimated by computing the slope of ln \(\dot{\varepsilon }\) versus lnσ and ln \(\dot{\varepsilon }\) versus σ, respectively, as per the Eqs. 8 and 9. Representation of such values is displayed in Fig. 6a–d based on the flow stress data at a true strain of 0.6. Accordingly, \(n^{{{\prime \prime }}}\) and β were estimated to be 6.129 and 0.0542, respectively, in γ region and 9.96 and 0.0592, respectively, in α region. Thus, the value of α1 is estimated to be 0.0088 and 0.0059 in γ and α regions, respectively. Finally, the logarithmic values of both sides of Eq. 7 are used to obtain n and Q as follows.

$$\frac{1}{n} = \left[ {\frac{{\partial \ln \left[ {\sinh \left( {\alpha_{1} \sigma } \right)} \right]}}{{\partial \ln \dot{\varepsilon }}}} \right]_{T}$$
(10)
$$Q = Rn\left[ {\frac{{\partial \ln \left[ {\sinh \left( {\alpha_{1} \sigma } \right)} \right]}}{{\partial \left( {{1 \mathord{\left/ {\vphantom {1 T}} \right. \kern-0pt} T}} \right)}}} \right]_{{\dot{\varepsilon }}}$$
(11)
Fig. 6
figure 6

(a and b) Plots of ln (\(\dot{\varepsilon }\)) versus lnσ and (c and d) ln strain rate versus σ for obtaining n″ and β in α and γ phases, respectively

Full size image

The plots of ln (\(\dot{\varepsilon }\)) versus ln [sinh (\(\alpha_{1}\) σ)] and ln [sinh (\(\alpha_{1}\) σ)] versus 1000/T are shown, respectively, in Fig. 7a–b, c–d. The average values of the slopes from Fig. 7a–b, c–d were used to derive n and Q, respectively, both for α and γ phases.

Fig. 7
figure 7

(a and b) Plots of ln (strain rate) versus ln [sinh (α1σ)] for obtaining n and (c and d) ln [sinh (α1σ)] versus 1000/T for obtaining Q, respectively in α and γ phases

Full size image

3.4.2 Activation Energy (Q) and Stress Exponent (n) Values in α and γ Phase Regions

It is the most common fact that the resistance of hot deformation of any material can be directly depicted through the activation energy (Q) required for deformation. As mentioned above, it is possible to estimate the activation energy of deformation, Q for the present material from Fig. 5c, d. It can be noted that Q value of the IF steel decreases from 324 to 285 kJ/mol in ferritic phase region (α) and 365 to 342 kJ/mol in austenite phase region (γ) with a rise in the true strain from 0.05 to 0.6, which differs greatly from the self-diffusion Q of α (239 kJ/mol) and γ (270 kJ/mol) [37], especially at the small strains. Wang et al. [37] stated that the deviation of Q from the self-diffusion activation energy can be explained in terms of the change of Young’s modulus with temperature. Phaniraj et al. [4] suggested that the higher hot working Q values as compared to the self-diffusion Q (i.e. atomic mechanism) can be attributed to the degree of pre-heats in the initial samples and strain rates during testing. Furthermore, the microalloying elements also play important roles in raising the Q, caused by the solute drag effect of Nb and Ti in IF steel as well as the solid solution strengthening [39, 40]. Fan et al. [41] studied the hot deformation behavior of pure iron having relatively similar composition but without Ti and Nb additions and the activation energy of hot deformation was estimated as ~ 310 kJ/mol at 0.6 true strain. This value is ~ 10% lower than the corresponding value of 342 kJ/mol estimated for the present Ti + Nb stabilized IF steel. Depending on the deformation temperature, Nb/Ti can be present either in solution or may have formed some precipitates (NbC/TiC), too [39, 40]. The progress of recrystallization during deformation, therefore, can be retarded due to Zener pinning effect of the NbC/TiC precipitates [39, 40]. Therefore, the present work exhibits a relatively higher Q of the Ti + Nb stabilized IF steel. Moreover, in the present study, the result indicates a reducing effect of the Q value with rising strain (up to 0.6), which specifies a gradually diminished hot working resistance. At the early stage of hot working, a few numbers of slip systems are favorably oriented for slip. With rising strain, the grains are progressively rotated. Thus, extra slip systems are activated resulting in a decreasing Q [35, 39].

Average stress exponent (n) values obtained from the modeled equations for α and γ phase regions are 6.7 and 5.5, respectively. The obtained n value suggests that the mechanism of hot deformation of the steel is precisely dominated by dislocation glide controlled by dislocation climb [35, 39]. The interactions between the dislocations and TiC precipitates in IF steel following deformation at a moderate strain rate of 1 s−1 at 800, 850, 950 and 1000 °C were further investigated through transmission electron microscopy (TEM). From Fig. 8a–d, dislocation bypassing of the TiC precipitates by glide/climb can clearly be observed. The Energy dispersive spectroscopy analysis on TEM foils combined with the selected area diffraction pattern (SADP) further confirms the presence of TiC precipitates. Hence, TEM analysis endorses the view that the plastic deformation is controlled by the motion of dislocations through bypassing of the precipitates via glide/climb mechanism, further corroborating the stress exponent (n) values. These fine TiC precipiates can serve as effective barriers to the dislocation motion and increase the resistance to deformation. Furthermore, as compared to high temperature mechanisms, low temp deformation generates relatively higher amounts of dislocations along with fine dynamic precipitates and their interactions with dislocations lead to an enhanced n value. This corroborates the higher n value of α phase (6.7) in comparison to that of the γ phase regions (5.5). Hence, TEM analysis endorses the view that plastic deformation is controlled by the motion of dislocations through bypassing of the precipitates by glide/climb mechanism, further corroborating the stress exponent (n) values.

Fig. 8
figure 8

a–d Interactions between dislocations and TiC precipitates in IF steel after deformation at a moderate strain rate (1 s−1) at 800, 850, 950 and 1000 °C, respectively

Full size image

3.4.3 Constitutive Equation for Flow Stress

Now, the Zener–Hollomon parameter, Z can be obtained by putting the values of Q, R, and \(\dot{\varepsilon }\) into Eq. 1. Combining the Eqs. 1 and 7 and taking the logarithm of both sides of the new equation, the Eq. 12 can be stated as follows.

$$\ln Z = \ln A + n\ln \left[ {\sinh \left( {\alpha_{1} \sigma } \right)} \right]$$
(12)

For the IF steel, the value of A is estimated to be about 5.6 × 1012 for α phase and the corresponding value for γ phase is 4.26 × 1012, according to the intercepts of the fitted lines from the Fig. 9a, b, respectively.

Fig. 9
figure 9

(a and b) Plots of ln Z versus ln [sinh (α1σ)] for calculation of the value of A in α a and γ b phases, respectively

Full size image

Finally, the Arrhenius type equations representing the constitutive modeling of the IF steel at a true strain of 0.6 for both α and γ phases can be expressed as follows.

$$\dot{\varepsilon } = 5.6 \times 10^{12} \left[ {\sinh \left( {0.0088\sigma_{0.6} } \right)} \right]^{5.8} \exp \left( { - \frac{284950}{RT}} \right)$$
(13)
$$\dot{\varepsilon } = 4.26 \times 10^{12} \left[ {\sinh \left( {0.0059\sigma_{0.6} } \right)} \right]^{4.6} \exp \left( { - \frac{341779}{RT}} \right)$$
(14)

All the above-mentioned equations and the constitutive equations do not contemplate the influence of applied strain on the flow stress. Basically, this model predicts that either the flow stress does not change with strain under a steady-state condition or it happens to be the peak stress [30, 38]. However, the flow stress of the investigated steel differs continuously with rising strain and/or at higher strain rate deformation, and the peak stress behavior is observed only for low strain rate deformation. Also, many authors have suggested that the strain has a prominent effect on the flow stress (among other parameters) of the material [6]. Hence, the effect of applied strain on the hot deformation flow stress should be taken into consideration in order to derive a complete constitutive equation to be able to predict the flow stress correctly.

In the present study, the effect of strain in the constitutive equation modeling is included by considering the various material constants (i.e.\(\alpha_{1}\), n, Q and A) as polynomial functions of strain. The material constants were calculated at different strains in the range of 0.05 to 0.6 at an interval of 0.05, as shown in Fig. 10a–h both for α (Fig. 10a, c, e, g) and γ (Fig. 10b, d, f, h) phase regimes. The behaviors of the material constants with strain were fitted to fifth order polynomial equations to accommodate the effect of strain on the flow stress precisely. The fifth order polynomials fitted to different materials constants are reproduced below with the suffixes denoting the phase type.

$$\ln \;{\text{A}}_{\alpha } = - 2100.5\varepsilon^{5} + 3617.6\varepsilon^{4} - 2296.2\varepsilon^{3} + 663.2\varepsilon^{2} - 91.547\varepsilon + 39.769$$
(15)
$$\ln \;{\text{A}}_{\gamma } = - 21673\varepsilon^{5} + 40219\varepsilon^{4} - 28142\varepsilon^{3} + 9100.2\varepsilon^{2} - 1336.4\varepsilon + 91.185$$
(16)
$$\alpha_{1\alpha } = - 6.5636\varepsilon^{5} + 11.542\varepsilon^{4} - 7.526\varepsilon^{3} - 2.2119\varepsilon^{2} + 0.2855\varepsilon + 0.0254 \,$$
(17)
$$\alpha_{1\gamma } = - 0.0756\varepsilon^{5} - 0.1211\varepsilon^{4} + 0.0602\varepsilon^{3} - 0.001\varepsilon^{2} - 0.0064\varepsilon + 0.0051$$
(18)
$$n_{\alpha } = - 1094.9\varepsilon^{5} + 1902.8\varepsilon^{4} - 1246.6\varepsilon^{3} + 389.16\varepsilon^{2} - 64.318\varepsilon + 11.098$$
(19)
$$n_{\gamma } \, = - 762.94\varepsilon^{5} + 1398\varepsilon^{4} - 965.13\varepsilon^{3} + 310.88\varepsilon^{2} - 47.651\varepsilon + 7.2008$$
(20)
$$Q_{\alpha } = - 28859\varepsilon^{5} + 48065\varepsilon^{4} - 29647\varepsilon^{3} + 8409.5\varepsilon^{2} - 1165.6\varepsilon + 421.07$$
(21)
$$Q_{\gamma } = - 232125\varepsilon^{5} + 429391\varepsilon^{4} - 299591\varepsilon^{3} + 96645\varepsilon^{2} - 14180\varepsilon + 1008.7$$
(22)
Fig. 10
figure 10

a–h The values of ln A, α1, n and Q obtained at different true strain levels and the fitted curves using fifth order polynomials for both α (a, c, e and g) and γ (b, d, f and h) phase regimes

Full size image

Once the material constants were described by the polynomial fit equations for any amount of strain (here up to 0.6), the flow stress can be estimated fairly accurately as a function of experimental parameters (temperature, strain rate and strain) and tallied with the experimental data. The constitutive equation that relates the flow stress and Zener–Hollomon parameter (Z) can be equated as follows (Eq. 23):

$$\sigma = \frac{1}{{\sigma_{1} }}\ln \left\{ {\left( {\frac{Z}{A}} \right)^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 n}}\right.\kern-0pt} \!\lower0.7ex\hbox{$n$}}}} + \left[ {\left( {\frac{Z}{A}} \right)^{{{\raise0.7ex\hbox{$2$} \!\mathord{\left/ {\vphantom {2 n}}\right.\kern-0pt} \!\lower0.7ex\hbox{$n$}}}} + 1} \right]^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}}} } \right\}$$
(23)

where the material parameters Q, A, \(\alpha_{1}\) and n have been described through polynomial fits (Eqs. 15–22) as a function of strain for both α and γ phase regimes, as described above and \(Z = \dot{\varepsilon }\exp \left( {\frac{Q}{RT}} \right)\).

3.4.4 Authentication of the Constitutive Equations

Considering the influence of strain, new constitutive equations were developed as discussed above, and the predicted flow stress as per the new modeled equations is verified with the experimental results as shown in Fig. 11a–j encompassing both α (Fig. 11a–e) and γ (Fig. 11f–j) phase regimes. It can be seen that the experimental data correlates well with the predicated flow stress, both in α and γ phase regions. However, there is a slight deviation in the predicted data observed mainly in the α-phase region (Fig. 11d, e), where the developed constitutive equation consistently predicts somewhat higher flow stress as compared to the experimental flow behavior. On the other hand, in γ-phase region, prediction of the flow stress is only underestimated when the deformation was done at high temperatures (1050–1100 °C) and at very low strain rate (0.001 s−1). This may be due to the DRX followed by grain growth occurring at this condition of deformation.

Fig. 11
figure 11

Comparisons between experimental and predicted flow stresses from the constitutive equations (considering compensation of strain) at temperatures a 650 °C, b 700 °C, c 750 °C, d 800 °C, e 850 °C, f 900 °C, g 950 °C, h 1000 °C, i 1050 °C and j 1100 °C

Full size image

The liability of the constitutive equation is also being quantified by employing the standard statistical parameters, such as average absolute relative error (AARE) and correlation coefficient (Rcc). These may be presented as [42, 43]:

$$R_{CC} = \frac{{\sum {_{i = 1}^{N} } \left( {E_{i} - \bar{E}} \right)\left( {P_{i} - \bar{P}} \right)}}{{\sqrt {\sum {_{i = 1}^{N} } \left( {E_{i} - \bar{E}} \right)^{2} \sum {_{i = 1}^{N} } \left( {P_{i} - \bar{P}} \right)^{2} } }}$$
(24)
$$AARE = \frac{1}{N}\sum\limits_{i = 1}^{N} {\left| {\frac{{E_{i} - P_{i} }}{{E_{i} }}} \right|} \times 100$$
(25)

where E is the experimentally obtained and P is the expected value obtained through the constitutive equation. The mean values of E and P are \(\bar{E}\) and \(\bar{P}\), respectively. The number of data employed in the investigation is denoted as N. The commonly used statistical parameter, which provides information about linear relationship between the observed and predicted values of flow stress, is the correlation coefficient (Rcc). Rcc is commonly seen as a number between 0 and 1. Rcc close to 1, signifies that a regression line matches with the plotted data well, while an Rcc near to 0 signifies a regression line does not fit the data well. Moreover, the high fraction of Rcc may not always signify good performance of an equation/model. Because, high value of Rcc may always have the tendency to be biased towards higher or lower values of data points [42, 43]. Therefore, ARRE analysis has been carried out in order to measure the predictability of the model equation. The ARRE is calculated through a term by term judgment of the relative error to attain unbiased statistics for substantiating the implementation of the developed model. Therefore, it is an unbiased statistical parameter. The values of Rcc and ARRE are estimated to be 0.982/7% and 0.936/11%, respectively, for γ and α phase deformation. As the value of Rcc is very close to 1 (as seen from Fig. 12a, b) and error % is also very low, the proposed constitutive equation can provide precise estimation of the flow stress in both the α and γ phase deformation of the IF steel.

Fig. 12
figure 12

a, b Correlation between predicted and experimental flow stresses at temperatures 650–1100 °C and strain rates (10−3–101) in γ and α phases, respectively

Full size image

4 Conclusions

In the current investigation, the hot/warm deformation tests were performed on an IF steel within the temperature range of 650–1100 °C and at different strain rates in the range 10−3 to 10 s−1. On the basis of the data obtained from flow stress curves, strain compensated constitutive analysis was carried out in order to be able to accurately predict the flow stress of the material in the hot/warm working regime. The main findings of the present investigation are demonstrated as follows:

  1. a.

    Obviously, the flow stress behavior is considerably influenced by strain rate and temperature. The flow stress increases with higher Z (high strain rate and low temperature) values and vice versa. The flow curves at lower strain rates (10−3 to 10−1s−1) exhibited peak stress behavior followed by attaining a steady state regime. At moderate strain rate (1 s−1), the flow curve showed a steady state behavior without revealing any peak, whereas continuous strain hardening behavior of the material could be observed at still higher strain rate (10 s−1). During the deformation of the IF steel at strain rates in the range of 10−2–10−1s−1, the flow curves indicate that the DRX occurred in both the phase regimes, i.e. in α phase field from 850 to 800 °C and in γ phase region from 1000 to 1050 °C.

  2. b.

    The apparent Q for warm/hot deformation of the IF steel is found to decrease continuously from 324 to 285 kJ/mol in the ferritic phase region (α) and 365 to 342 kJ/mol in the austenite phase region (γ) with the increase of true strain from 0.05 to 0.6. The activation energies of deformation differ greatly from the corresponding self-diffusion activation energies of α (239 kJ/mol) and γ (270 kJ/mol). This is due to the work hardening effect dominated in the early stage of deformation of the IF steel and the DRX/DRV dominating the deformation with increase in the amount of strain. Furthermore, the average value of stress exponent (n) is calculated to be 6.7 and 5.5 for α and γ phase regions, respectively. It indicates that the hot/warm deformation is controlled by the mechanisms of dislocation glide and dislocation climb. TEM analysis also confirms that the plastic deformation is controlled by dislocations motion through bypassing of the precipitates by glide/climb mechanisms.

  3. c.

    Two separate constitutive equations (as shown below) have been developed for two separate phase regimes (i.e. α and γ) of the IF steel for hot deformation at a true strain of 0.6.

    $$\dot{\varepsilon } = 5.6 \times 10^{12} \left[ {\sinh \left( {0.0088\sigma_{0.6} } \right)} \right]^{5.8} \exp \left( { - \frac{284950}{RT}} \right)$$
    $$\dot{\varepsilon } = 4.26 \times 10^{12} \left[ {\sinh \left( {0.0059\sigma_{0.6} } \right)} \right]^{4.6} \exp \left( { - \frac{341779}{RT}} \right)$$
  4. d.

    To develop a modified strain-compensated constitutive equation, the effect of strain is incorporated by estimating the material constants A, n, α and activation energy, Q both for α and γ phases. Fifth order polynomial equations (Eqs. 15–22) fitted to the material constants (A, n, α and Q) have been found to represent the effect of strain on the flow stress with fairly good accuracy. The modified constitutive model equation that correlates the flow stress and Zener–Hollomon parameter is represented as:

    $$\sigma = \frac{1}{{\sigma_{1} }}\ln \left\{ {\left( {\frac{Z}{A}} \right)^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 n}}\right.\kern-0pt} \!\lower0.7ex\hbox{$n$}}}} + \left[ {\left( {\frac{Z}{A}} \right)^{{{\raise0.7ex\hbox{$2$} \!\mathord{\left/ {\vphantom {2 n}}\right.\kern-0pt} \!\lower0.7ex\hbox{$n$}}}} + 1} \right]^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}}} } \right\}$$

    where each of the materials constants, viz., Q, A,\(\alpha_{1}\) and n is a function of strain as described above and \(Z = \dot{\varepsilon }\exp \left( {\frac{Q}{RT}} \right)\). The modified constitutive equation is found to predict the flow stress precisely with the experimentally obtained data both in γ and α phase regions showing an excellent fitting with high correlation coefficient, Rcc (0.982 and 0.936, respectively) and extremely low value of AREE (7% and and 11%, respectively).