Introduction

It is well known that the growth of dendritic crystals takes place in many areas of modern science ranging from materials physics, geophysics and atmosphere physics to the chemical industry, biophysics and life science1,2,3,4,5,–6. As this takes place, the growth mechanisms of dendrites, their shape and interaction determine the characteristics of the internal microstructure of the crystallized substance7,8,–9. These mechanisms, in turn, depend on heat and mass transfer processes complicated by hydrodynamic and convective fluid flows, the presence of dissolved impurities and various crystal growth symmetries. To determine the stable dendritic growth mode, as well as to establish the boundaries of morphologic transitions of the internal structure in solidified materials, it is necessary to independently determine the growth rate V of the dendrite tip and its diameter \(\rho \) depending on the melt undercooling \(\Delta T\). This problem can be solved using the microscopic solvability theory together with the sharp interface model, which lead to two transcendental equations for V and \(\rho \) as functions of \(\Delta T\) and other physical parameters of dendritic growth. Such a theoretical approach has been recently tested against experimental data and computations in a series of works10,11,12,–13 in the absence of a forced convection. The present study compares the theory of stable dendritic growth in the presence of a forced convection with computer simulations by the enthalpy method.

Our article is organized as follows. Section 2 summarizes the main outcomes following from the solvability theory and the sharp interface model keeping in mind the fourfold crystalline symmetry and a forced convective flow. Here, we present the thermally controlled model of anisotropic dendritic growth as well as its final analytical solution, which consists of two transcendental equations for V and \(\rho \). Section 3 is concerned with the background of the enthalpy method and our main results following from simulations of dendritic growth. The main outcomes of our analysis and future directions are discussed in Sect. 4.

Sharp Interface Model and the Solvability Theory

Governing Equations

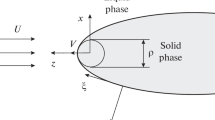
Consider the steady-state growth of a two-dimensional thermal dendritic crystal along the spatial axis z in the presence of a forced convective flow coming from the opposite direction14 (Fig. 1).

Fig. 1
figure 1

A scheme of growing dendritic crystal in a convective flow.

Full size image

The heat balance condition at the dendritic interface can be written as

$$\begin{aligned} T_{Q}\left( \mathbf{v}\cdot \mathbf{n} \right) = D_{T}\left( \mathbf{\nabla }T_\mathrm{s} - {\nabla }T_\mathrm{l} \right) \cdot \mathbf{n}, \end{aligned}$$
(1)

where \(T_{Q}\) is the hypercooling, \(\mathbf{v }\cdot \mathbf{n }\) is the growth velocity, \(D_{T}\) is the thermal diffusivity, \(T_\mathrm{s}\) and \(T_\mathrm{l}\) are the temperatures in solid and liquid phases, respectively.

The heat transport equations in the liquid and solid phases take the form

$$\begin{aligned} \frac{\partial T_\mathrm{l}}{\partial t} +\left( \mathbf{w}\cdot {\nabla } \right) T_\mathrm{l} = D_{T}\nabla ^2 T_\mathrm{l},\quad \frac{\partial T_\mathrm{s}}{\partial t} = D_{T}\nabla ^2 T_\mathrm{s}, \end{aligned}$$
(2)

where \(\mathbf{w}\) is the fluid velocity, t is the time variable, and \(\nabla \) is the differential nabla operator. Note that we consider the case of equal thermal diffusivities in both the phases, because this hypothesis does not change the selection criterion (it can change the selection constant only).

To describe the hydrodynamic flows, we use the linearized Oseen model for a viscous flow15,16,–17

$$\begin{aligned} U\frac{\partial \mathbf{w}}{\partial z}=-\frac{1}{\rho _\mathrm{l}}\nabla p + \nu \nabla ^2 \mathbf{w},\quad \nabla \cdot \mathbf{w}=0. \end{aligned}$$
(3)

Here, U is the fluid velocity far from the dendritic surface (see Fig. 1), p is the pressure, \(\rho _\mathrm{l}\) is the density of liquid, and \(\nu \) is the kinematic viscosity.

The Gibbs-Thomson equation at the solid-liquid boundary holds

$$\begin{aligned} T_{\mathrm{{int}}}=T_\mathrm{l}=T_\mathrm{s}=T_\mathrm{m} - T_{Q}d(\theta ,\phi )\mathcal {K} - {\tilde{\beta }}(\theta ,\phi )v_n , \end{aligned}$$
(4)

where \(T_{\mathrm{{int}}}\) is the phase transition temperature at the dendrite interface, \(T_\mathrm{m}\) is the melting temperature for the pure system, and \(\mathcal {K}\) is the interface curvature, \(d(\theta ,\phi )\), and \({\tilde{\beta }}(\theta ,\phi )\) are the capillary length and the function of anisotropic kinetics with the spherical angles \(\theta \) and \(\phi \), which define the orientation of the normal to the dendrite interface and its growth direction.

In the case of cubic symmetry, \(d(\theta , \phi )\) and \({\tilde{\beta }}(\theta ,\phi )\) are described by

$$\begin{aligned} d(\theta , \phi )&= d_0 \left\{ 1 - \alpha _d \left[ \cos ^4\theta + \sin ^4\theta \left( 1 - 2 \sin ^2\phi \cos ^2\phi \right) \right] \right\} , \end{aligned}$$
(5)
$$\begin{aligned} {\tilde{\beta }}(\theta , \phi )&= \beta _0 \left\{ 1 - \alpha _\beta \left[ \cos ^4\theta + \sin ^4\theta \left( 1 - 2 \sin ^2\phi \cos ^2\phi \right) \right] \right\} , \end{aligned}$$
(6)

where \(d_0\) is the capillary constant, \(\alpha _d\ll 1\) stands for the stiffness, which depends on a small anisotropy parameter \(\varepsilon _c\) of surface energy, \(\beta _0\) is the kinetic constant, and \(\alpha _\beta \ll 1\) is the kinetic anisotropy parameter.

Considering the case of needle-like crystal in the form of a paraboloid of revolution, Eq. 5 can be reduced by averaging over \(\phi \)18 and written out for the case of n-fold symmetry:

$$\begin{aligned} d(\theta )&= d_0\left\{ 1-\alpha _d \cos \left[ n\left( \theta - \theta _d \right) \right] \right\} , \end{aligned}$$
(7)
$$\begin{aligned} {\tilde{\beta }}(\theta )&= \beta _0 T_{Q} \left\{ 1-\alpha _\beta \cos \left[ n\left( \theta - \theta _\beta \right) \right] \right\} , \end{aligned}$$
(8)

where \(\theta _d\) and \(\theta _\beta \) designate the angles between the directions of growth and minimal functions \(d(\theta )\) and \({\tilde{\beta }}(\theta )\).

The convective heat transfer problem (1)–(8) written out for the case of n-fold symmetry of crystal growth enables us to find the generalized solvability criterion including convection and the effects of kinetics.

Analytical Solution

In the first instance, we define the corresponding parabolic coordinates \(\xi \) and \(\eta \) connected with the Cartesian ones, x and z, by means of the familiar expressions

$$\begin{aligned} x=\rho \sqrt{\xi \eta }, \quad z=\frac{\rho }{2}\left( \eta -\xi \right) , \end{aligned}$$
(9)

where \(\rho /2\) represents the dendritic tip radius. The equation \(\eta =1\) corresponds to the solid/liquid surface of the dendrite.

The Oseen hydrodynamic Eq. 3 supplemented by the corresponding no-slip boundary conditions for the fluid velocity components \(u_\eta \) and \(u_\xi \) in a parabolic reference frame take the form17,19

$$\begin{aligned} u_\eta = -\frac{f(\eta )}{2\sqrt{\xi +\eta }},\quad u_\xi = \frac{\sqrt{\xi \eta }}{\sqrt{\xi +\eta }}\frac{{\hbox {d}}f(\eta )}{\hbox {d}\eta } , \end{aligned}$$
(10)

where

$$\begin{aligned} f(\eta )&= 2(U+V)\sqrt{\eta } -2Ug(\eta ),\nonumber \\ g(\eta )&= \sqrt{\eta }\frac{\mathrm{erfc} \sqrt{\eta {\mathfrak {R}}/2}}{\mathrm{erfc }\sqrt{{\mathfrak {R}}/2}} + \frac{\sqrt{2/(\pi {\mathfrak {R}})}}{\mathrm{erfc} \sqrt{{\mathfrak {R}}/2}} \left[ \exp \left( -\frac{{\mathfrak {R}}}{2} \right) -\exp \left( -\frac{\eta {\mathfrak {R}}}{2} \right) \right] \end{aligned}$$
(11)

with the Reynolds number \({{\mathfrak {R}}}=\rho U /\nu \).

Now rewriting the heat transfer Eq. 2 as well as the boundary condition (1) in parabolic coordinates, and then integrating them, we find the temperature distribution in the two-dimensional geometry as

$$\begin{aligned} T_\mathrm{l}(\eta ) = T_i +\left( T_\infty -T_i \right) \frac{I_{T}(\eta )}{I_{T}(\infty )},\quad \end{aligned}$$
(12)

where

$$\begin{aligned} I_{T}(\eta )&= \int _{1}^{\eta } \exp \left[ P_{f}\int _{1}^{\eta '}\frac{g\left( \eta ''\right) }{\sqrt{\eta ''}}d\eta ''- P_{0}\eta '\right] \frac{d\eta '}{\sqrt{\eta '}},\\ T_i&= T_\infty +T_{Q}P_g\exp (P_0) I_{T} (\infty ),\quad P_0 = P_g +P_f. \end{aligned}$$

\(T_\infty \) is the temperature in the liquid phase far from the dendrite surface, and \(P_g=\rho V/(2D_{T})\) and \(P_f=\rho U/(2D_{T})\) stand for the growth and flow Péclet numbers.

Solvability Condition

Pelcé, Bouissou and Bensimon3,19,20 showed that the solvability condition, which gives a unique combination between \(\rho \) and V, describes a stable dendritic growth mode as

$$\begin{aligned} \int \limits _{-\infty }^{\infty } G\left[ X_0(l) \right] Y_\mathrm{m}(l) \hbox {d}l =0,\quad Y_\mathrm{m}(l) = \exp \left[ i\int \limits _0^l k_\mathrm{m} (l_1)\hbox {d}l_1 \right] , \end{aligned}$$
(13)

where G is the curvature operator, \(k_\mathrm{m}(l)\) designates the marginal wavenumber mode, i represents the imaginary unit, and \(X_0(l)\) is a continuum of solutions from which the dependence \(k_\mathrm{m}(l)\) can be derived.

Furthermore, to obtain the marginal wavenumbers \(k_\mathrm{m}\) entering in the solvability integral (13), the linear stability analysis should be carried out (see, among others,14). It leads to the marginal mode of the wavenumber \(k_\mathrm{m}\) (see, for details,19,21), which is determined by the following cubic equation

$$\begin{aligned} \begin{aligned} k_\mathrm{m}^3&= \frac{V\exp (i\theta )}{2d(\theta )D_{T}}k_\mathrm{m} + \frac{iaU\sin \theta \cos \theta }{8\rho D_{T}}k_\mathrm{m} \\&\quad -\frac{iV\sin \theta }{2D_{T}}k_\mathrm{m}^2 +\frac{V^2\cos \theta \exp (i\theta )}{4d(\theta )D_{T}^2} +\frac{iV{{{\tilde{\beta }}}(\theta )}\sin \theta }{d(\theta )T_{Q}}k_\mathrm{m}^2. \end{aligned} \end{aligned}$$
(14)

An analytical solution of the cubic equation (14) has been found using Cardano’s formula (\(d_0\ne 0\)) for the fourfold symmetry of dendritic growth as22

$$\begin{aligned} k_{m}=k_{mBP} + \frac{V\exp \left( -i\theta \right) }{4D_{T}} + \frac{iV{{{\tilde{\beta }}}(\theta )}\sin \theta }{2d(\theta )T_{Q}}, \end{aligned}$$
(15)

where

$$\begin{aligned} k_{mBP}=-\sqrt{\frac{V\exp \left( i\theta \right) }{2d(\theta )D_{T}}}\sqrt{1+\frac{iaUd(\theta )}{8\rho V}\sin (2\theta )\exp \left( -i\theta \right) }. \end{aligned}$$

Solvability Criterion for the Thermally Controlled Growth

Let us consider the purely thermal mode of dendritic solidification when \(\alpha _d\ll 1\), \(\alpha _\beta \ll 1\), \(\theta _d =0\) and \(\theta _\beta \ne 0\). Substituting the analytical solution for the fourfold symmetry of the dendritic growth wavenumber (15) into the solvability integral (13), we arrive at

$$\begin{aligned} \begin{aligned} \displaystyle \int \limits _{-\infty }^{\infty }\hbox {d}\eta G\left[ X_0(\eta ) \right] \exp \left\{ -i\int \limits _0^\eta \left[ \frac{P_g(1-i\eta _1)}{2}+\frac{i\rho V\beta _0\eta _1 }{2d_0} \right. \right. \\ \displaystyle \left. \left. - \sqrt{\frac{\left( 1+i\eta _1\right) \left( 1+\eta _1^2\right) ^{\lambda _n}+i\alpha \eta _1 B_n(\eta _1)}{\sigma ^* B_n(\eta _1)}}\right] \hbox {d}\eta _1 \right\} =0, \end{aligned} \end{aligned}$$
(16)

where

$$\begin{aligned} l_1&= -\frac{\rho }{2}\left[ \frac{\tan \theta }{\cos \theta }+\ln \left( \frac{1}{\cos \theta }+\tan \theta \right) \right] ,\quad \eta = \tan \theta ,\quad \\ \alpha&= \frac{aUd_0}{4\rho V},\quad \lambda _n = \frac{n+1}{2},\quad \sigma ^* = \frac{2d_0D_{T}}{\rho ^2V} ,\\ B_n(\eta )&= \left( 1+\eta ^2 \right) ^{n/2} -\alpha _d \sum \limits _{k=0}^n \left( {\begin{array}{c}n\\ k\end{array}}\right) \eta ^{n-k}\cos \frac{(n-k)\pi }{2}. \end{aligned}$$

The wave-number in the kinetically limited regime can be obtained under the assumption that \(\theta _\beta =0\) and \(\theta _d \ne 0\):14

$$\begin{aligned}&\displaystyle \int \limits _{-\infty }^{\infty }\hbox {d}\eta G\left[ X_0(\eta ) \right] \exp \left\{ -i\int \limits _0^\eta \left[ P_g + \frac{i\rho \left( 1+i\eta _1\right) \left( 1+\eta _1^2\right) ^{\lambda _n}}{2D_{T}\beta _0\eta _1 B_n^\prime (\eta _1)}\right] \hbox {d}\eta _1\right\} =0,\nonumber \\&\quad B_n^\prime (\eta ) = \left( 1+\eta ^2 \right) ^{n/2} -\alpha _\beta \sum \limits _{k=0}^n \left( {\begin{array}{c}n\\ k\end{array}}\right) \eta ^{n-k}\cos \frac{(n-k)\pi }{2}. \end{aligned}$$
(17)

We calculate the solvability integral (16) in two stages as detailed in22. At the first stage, we neglect the kinetic contribution (proportional to \(\beta _0\) in (16)) and pay our attention to the case known as “thermally controlled” crystal growth. Setting \(\beta _0 =0\), we come to the selection criterion (see also19,21,23)

$$\begin{aligned} \sigma ^*=\frac{2d_0D_{T}}{\rho ^2V}=\frac{\sigma _{0}\alpha _d^{7/n}A_n^{7/n}}{\left( 1+a_{1}\alpha _d^{2/n}A_n^{2/n}P_g \right) ^2 \left( 1+b\tau _n^{\upsilon _n}\right) }, \end{aligned}$$
(18)

where

$$\begin{aligned} \tau _n = \alpha \alpha _d^{-3/n}A_n^{-3/n},\quad \upsilon _n = \frac{n+7}{2(n+3)},\quad \end{aligned}$$
$$\begin{aligned} A_n=2^{-3n/4}\sum \limits _{k=0}^n \left( {\begin{array}{c}n\\ k\end{array}}\right) i^{n-k}\cos \frac{(n-k)\pi }{2} , \end{aligned}$$

and \(\sigma _{0}\) and b are the constants.

The second stage to evaluate the integral expression (16) is to analyze the dendrite growth mode controlled by the kinetic contribution (proportional to \(\beta _0\)). By doing that, we neglect the summand proportional to the growth Péclet number in (16) and arrive at (by analogy with22)

$$\begin{aligned} \sigma ^*=\frac{\sigma _{0}\alpha _d^{7/n}A_n^{7/n}}{\left[ 1+a_{1}^\prime \alpha _d^{2/n}P_gD_{T}\beta _0A_n^{2/n}/d_0 \right] ^2 \left( 1+b\tau _n^{\upsilon _n}\right) }, \end{aligned}$$
(19)

where \(a_{1}^\prime \) represents a new constant.

Sewing together the obtained limiting criteria (18) and (19), we come to the generalized criterion of the form

$$\begin{aligned} \sigma ^*= {\frac{2d_0D_{T}}{\rho ^2V}=} \frac{\sigma _{0}\alpha _d^{7/n}A_n^{7/n}}{\left[ 1+a_{1}\alpha _d^{2/n}A_n^{2/n}P_g \left( 1+\delta _0 D_{T}\beta _0/d_0\right) \right] ^2 \left( 1+b\tau _n^{\upsilon _n}\right) }, \end{aligned}$$
(20)

where \(a_{1}^\prime = a_{1}\delta _0\) and \(\delta _0\) represents a fitting constant. Note that the selection constants \(\sigma _{0}\) and b for each n might be found experimentally or from the phase-field modeling.

Undercooling Balance

The second relation for V and \(\rho \) is called the undercooling balance. This second relation and selection criterion (20) allow us to obtain a pair of most important parameters of primary solidification, V and \(\rho \), at a unique undercooling \(\Delta T\). The total undercooling balance connects the melting temperature \(T_\mathrm{m}\) of a one-component liquid and the far-field temperature \(T_{\infty }\) as \(\Delta T = T_\mathrm{m} - T_{\infty }\) and introduces the first model equation, which consists of several contributions:

$$\begin{aligned} \Delta T = \Delta T_{T} + \Delta T_{R} + \Delta T_{K}, \end{aligned}$$
(21)

where \(\Delta T_{T}\) represents the thermal contribution, \(\Delta T_{R} = 2d_{0} T_{Q} /R\) is the undercooling due to the Gibbs-Thomson effect, and \(\Delta T_{K} =V/\mu _{k}\) is the kinetic undercooling (where \(\mu _k\) stands for the kinetic coefficient).

The thermal contribution \(\Delta T_{T}\) can be written out using the Ivantsov function \(\mathrm {Iv}_{T}\), which describes the temperature field around the growing steady-state dendrite of a parabolic form:

$$\begin{aligned} \Delta T_{T} =T_{Q} \mathrm {Iv}_{T}(P_{g},P_{f}), \end{aligned}$$
(22)

where the Ivantsov function

$$\begin{aligned} \mathrm {Iv}_{T}(P_{g},P_{f}) = P_{g}\exp (P_0)I_{T}(\infty ),\quad P_0=P_{g}+P_f \end{aligned}$$
(23)

depends on the growth \(P_g={\rho V}/({2 D_{T}})\) and flow \(P_g={\rho U}/({2 D_{T}})\) Péclet numbers.

Expression (21) represents a function of two variables, velocity V and diameter \(\rho \), through the functions \(\Delta T_{T}\), \(\Delta T_R\) and \(\Delta T_K\) for a given full undercooling \(\Delta T\). To obtain V and \(\rho \) simultaneously, we use the second equation in the form of stability criterion (20). These two equations allow us to obtain V and \(\rho \) for a given \(\Delta T\).

Methodology

In this work, an enthalpy-based method that captures solidification is coupled to a lattice Boltzmann method (LBM) that resolves fluid flow. The methods are linked by the convective thermal transport equation and solid fraction, although in other work they can also be linked by body forces.24 The enthalpy-based method is based on the work of Voller,25 and before that Tacke,26,27 and it is written using a finite difference scheme. The LBM uses a discretized form of the Boltzmann equation. This section outlines the two methods and then describes the problem setup and typical solution procedure for generating steady-state solutions for dendrite tip velocity and tip radius for a given bulk undercooling and mean flow.

Enthalpy Method

Convective transport of enthalpy is governed by

$$\begin{aligned} \frac{\partial H}{\partial t} = \nabla ^2(KT)-\mathbf{u} (\nabla H), \end{aligned}$$
(24)

where t is time, K is the thermal conductivity, which is assumed to be the same for both liquid and solid phases, u is velocity, and H is enthalpy, which is a function of the heat capacity \(c_p\), temperature T and the latent L. The volumetric enthalpy is defined as a sum of sensible and latent heats

$$\begin{aligned} H = c_p T + f_{\text {liq}}L, \end{aligned}$$
(25)

where \(f_{\text {liq}}\) is the liquid fraction phase variable and is 0 for fully solid and 1 for fully liquid. At the solid-liquid interface, the Gibbs-Thompson condition gives the temperature for a pure material neglecting any kinetic effects as

$$\begin{aligned} T^i = T_f - \frac{\varGamma \left( \theta \right) T_f}{L} \kappa , \end{aligned}$$
(26)

where \(T_f\) is the fusion temperature for a surface energy anisotropy, \(\gamma \), of the form \(\gamma =d_0 (1+\epsilon _4 \cos 4\theta )\), the surface stiffness \(\varGamma (\theta )\) given by

$$\begin{aligned} \varGamma \left( \theta \right) = \gamma + \frac{\partial ^2 \gamma }{\partial \theta ^2} = d_0 \left( 1 - \epsilon _4 \cos 4 \theta \right) . \end{aligned}$$
(27)

and \(\kappa \) is the interface curvature that can be captured from the liquid fraction gradients as

$$\begin{aligned} \kappa = \nabla \cdot \frac{ \nabla f_{\text {liq}}}{ \left| \nabla f_{\text {liq}} \right| } = (f_{y}^2f_{xx}-2f_xf_yf_{xy}+{f_x}^2f_{yy})\cdot \left( f_x^2+f_y^2\right) ^{-\frac{3}{2}}. \end{aligned}$$
(28)

Here, \(f_x\) and \(f_{xx}\) represent the first and the second derivatives of \(f_{\text {liq}}\) with respect to the coordinate x. The interface orientation \(\theta \), which is the angle between the interface normal and the x-axis, is given by

$$\begin{aligned} \theta = \arctan \frac{f_x}{f_y}. \end{aligned}$$
(29)

Lattice Boltzmann Method

The momentum transport for an incompressible flow is given by the Navier-Stokes equations (NSEs) as

$$\begin{aligned} \nabla \cdot \mathbf{u} = 0, \end{aligned}$$
(30)
$$\begin{aligned} \frac{\partial \mathbf{u} }{\partial t} + \mathbf{u} \cdot \nabla \mathbf{u} = - \frac{1}{\rho _\mathrm{l}} \nabla p + \nu \nabla ^2 \mathbf{u} , \end{aligned}$$
(31)

where \(\rho _\mathrm{l}\) is density, p is pressure, and \(\nu \) is the kinematic viscosity. To avoid non-linearity in the convective term and to improve convergence of the problem, the lattice Boltzmann method is employed. It describes the evolution of a particle distribution function (PDF), \(f_i\), and it has been shown to recover the NSEs in the low Mach number limit via the Chapman and Enskog multi-scale analysis. The implementation is 3D, using a D3Q19 lattice, which in this two-dimensional analysis reduces to the equivalent D2Q9 lattice. The lattice Boltzmann equation generally can be written as

$$\begin{aligned} f_i (\mathbf {x} + \mathbf{c} _i \Delta t,t +\Delta t) - f_i(\mathbf {x},t) = -\frac{1}{\tau } \left( f_i(\mathbf {x},t) - {f_i}^{eq}(\mathbf {x},t) \right) , \end{aligned}$$
(32)

where the left-hand side represents the streaming process and the right-hand side describes collisions. Here, \(\mathbf {x}\) is the lattice node coordinate, \(\mathbf{c} _i\) are the discretized lattice velocities, \(\Delta t\) is the LBM time step, \(\tau \) is a non-dimensional relaxation parameter, and \({f_i}^{eq}\) is the equilibrium PDF given by

$$\begin{aligned} {f_i}^{eq} = \rho ^{*} w_i \left( 1+\frac{3 \mathbf {c}_i \cdot \mathbf {u}^{*}}{c^2} + \frac{(3 \mathbf {c}_i \cdot \mathbf {u}^{*})^2}{2c^4} - \frac{3 {\mathbf {u}^{*}}^2}{2c^2}\right) , \end{aligned}$$
(33)

where the asterisks (\(*\)) mark the non-dimensional lattice Boltzmann variables, \(w_i\) is the lattice weight coefficient, and \(c=\Delta x/\Delta t\) is the lattice speed. The lattice spacing, \(\Delta x\), time stepping, \(\Delta t\) and equilibrium density, \(\rho ^{*}\), are all defined as unity. Fluid properties such as density and fluid velocities can be calculated from the PDF by taking the velocity moments as

$$\begin{aligned} \rho ^{*} = \sum \limits _{i} f_i, \quad \rho ^{*} \mathbf {u}^{*} = \sum \limits _{i} f_i \mathbf {c}_i. \end{aligned}$$
(34)

Other physical quantities like the fluid density and viscosity can be calculated from the following expressions:

$$\begin{aligned} p^{*} = \frac{\rho ^{*}}{3}, \quad \nu ^{*} = \frac{1}{3}\left( \tau - \frac{1}{2}\right) . \end{aligned}$$
(35)

For stability purposes, the two-relaxation-time collision scheme28 is used in the model. The moment-based boundary method29,30 describes the flat domain boundaries while the bounce-back scheme describes the advancing solid front of the growing crystal.

Problem Setup and Solution Procedure

The main advantage of the enthalpy method is that it is derived without explicitly using the atomic scale interface thickness, in contrast to traditional phase-field methods. A single-cell-thick interface is still required to track phase change; however, this method can be used at both the macro- and micro-scales. In the context of this work, the method can encompass a wide range of undercoolings. However, the drawback is that the method suffers from two errors that are a consequence of using a single cell to represent the interface and related to the cell size and the problem considered. If the cell size is too large, then the error analogous to using too coarse of a mesh becomes significant; however, if the cell size is too small, the so-called narrow band error feature appears. The latter has a significant effect on calculating interfacial features, namely curvature, where with refinement the local features become either flat or a corner representing either a zero or a very large curvature, respectively. Consequently, this causes the formation of an unrealistic faceted-like structure. To address this problem, the authors developed an adaptive cell size method for the enthalpy method, where the tip radius was defined by a fixed number of cells. However, as the tip radius is unknown, so too is the cell size, and it becomes a solved variable. For brevity, the full method is not repeated here, but in summary, through an iterative approach, a steady-state solution for a given undercooling was found when the cell size, tip radius (hence curvature) and tip velocity all became constant in time. The same approach is used here, but with the addition of forced convection. Aside from resolving the fluid flow, no significant changes are necessary for this adaptive cell size method. There are three key solvers that are weakly coupled with each solved sequentially. A single time step consists of first resolving the thermal transport (24), which determines the local free energy for solidification, which is resolved by the enthalpy equation with input from the Gibbs-Thompson condition (26), and finally fluid flow is calculated. The fluid velocity then feeds into the transport equation. Therefore, while fluid flow has a significant effect on solidification, it does not directly feed into the calculation of tip velocity, curvature or the update of the cell size.

The numerical model represents a square domain of \(1200 \times 1200\) cells with a dendrite tip growing from the origin along the positive x-axis. Due to the symmetry of the problem along the x-axis, only half of the problem is solved with the negative y boundary acting as a symmetry plane. The far field boundary conditions (positive x and positive y boundaries) are set to the bulk undercooling and mean fluid flow values. The negative x boundary acts as a zero Neumann condition. To prevent the dendrite tip from growing too close and being influenced by the far field boundaries, a moving mesh technique is used that keeps the dendrite in the same relative position within the domain. Both the numerical model and analytic solution use the same physical parameters given in Table I.

Table I Physical and numerical parameters used in the present analytical calculations and numerical simulations for the pure nickel
Full size table

Results and Conclusions

An example of a steady-state solution for 1.08 m/s incident flow is given in Fig. 2, showing the dendrite tip morphology and the x and y components of the velocity profile (u and v in Fig. 2a and b respectively). As the dendrite is solid, fluid flow must go around, and this leads to a stagnation point at the very tip with higher velocities inside the thermal boundary layer. However, as the relative velocity at the interface is zero, a viscous boundary layer forms between the interface and the higher velocity region.

Fig. 2
figure 2

Incident fluid flow velocity of 1.08 m/s onto the dendrite tip for \(\Delta T = 106\) K. a Absolute of x-component of velocity. b y-component of velocity.

Full size image

Figure 3 shows a comparison of the thermal field for \(\Delta T = 106\) K with an incident flow of 0 m/s, 1.08 m/s and 8.66 m/s. In the presence of an incident fluid flow, advective thermal transport causes the isotherms to bunch up, leading to an increase in thermal gradient in the liquid. This in turn allows for a higher diffusion rate of temperature back into the liquid and therefore an increase in free energy. In all cases with increasing flow velocity, there is an increase in tip velocity and consequently a reduction in tip radius; the latter leads to an increase in tip undercooling, highlighted by Fig. 3d, e and f. In Figs. 2 and 3, the axes are in terms of cell numbers, where the adaptive cell size method10 has the tip radius defined as eight cells, and therefore with increasing velocity the steady-state cell size decreases. Figures 2 and 3 are also focused on the lower left corner of the computational domain encompassing the first 360 cells in x and y. The full domain is much larger so that the far field boundaries do not have any direct influence on the tip dynamics.

Fig. 3
figure 3

Thermal field for \(\Delta T = 106\) K with incident flow velocity of a, d 0 m/s, b, e 1.08 m/s and c, f 8.66 m/s. d–f Reduced temperature scaled to highlight tip undercooling. The circle in d corresponds to the defined tip radius for all cases.

Full size image

The stability criterion (20) and undercooling balance condition (21) represent a set of two nonlinear equations. Solving these two simulatneous equations gives the tip velocity V and tip diameter \(\rho \) as functions of the melt undercooling \(\Delta T\). The solution of these is compared with the enthalpy method in Fig. 4 for pure nickel at different flow velocities U. The results show a good agreement between the theoretical and numerical models over a broad range of fluid velocities for fixed values of selection constants \(\sigma _0\) and b listed in Table I.

Fig. 4
figure 4

a Dendrite tip velocity and b tip radius for pure nickel versus the melt undercooling for different flow velocities U. Physical parameters are listed in Table I.

Full size image

Analyzing a series of curves shown in Fig. 4, we conclude that the dendrite tip radius \(\rho /2\) decreases and the tip velocity V increases with increasing the fluid velocity U at a fixed value of undercooling \(\Delta T\). This means that the dendritic crystals become narrower and grow faster as a forced flow of melt rises.

This article tests the convective theory of stable dendritic growth with computer simulation data for pure (impurity-free) melts. The results highlight that the enthalpy-based method, along with an adaptive cell size approach, is capable of accurately predicting the behavior of dendritic growth in the presence of forced convection. In practice, fluid flow is generally present in terrestial experiments. Consequently, further understanding its effect is necessary to bridge knowledge between solidification under terrestrial and microgravity conditions.

The next step is to test the theory for binary systems with the modified stability criterion and undercooling balance written out with allowance for impurity effects (see, for details, the theory developed in Refs. 14,22,23,32 for a binary melt). Furthermore, the effects of non-equilibrium crystallization occurring at high growth rates should be tested against experimental data according to the theory developed in Ref. 33. Finally, a full three-dimensional approach will allow for direct comparison of the numerical model, analytic theory and experimental evidence.