A geometric Gauss–Newton method for least squares inverse eigenvalue problems

Abstract

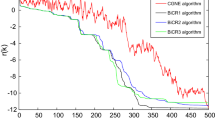
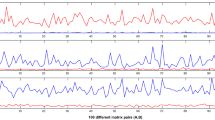
This paper is concerned with the least squares inverse eigenvalue problem of reconstructing a linear parameterized real symmetric matrix from the prescribed partial eigenvalues in the sense of least squares, which was originally proposed by Chen and Chu (SIAM J Numer Anal 33:2417–2430, 1996). We provide a geometric Gauss–Newton method for solving the least squares inverse eigenvalue problem. The global and local convergence analysis of the proposed method is established under some assumptions. Also, a preconditioned conjugate gradient method with an efficient preconditioner is proposed for solving the geometric Gauss–Newton equation. Finally, some numerical tests, including an application in the inverse Sturm–Liouville problem, are reported to illustrate the efficiency of the proposed method.

Appendix A

In this appendix, we deduce (2.4) and (2.6). To derive the Riemannian differential of $H:\mathscr {Z}\rightarrow \mathbb {SR}^{n\times n}$ defined by (2.2), we consider the following extended mapping

$$\begin{aligned} \widetilde{H} : \mathbb {R}^{l} \times \mathbb {R}^{n\times n} \times \mathscr {D}(n-m) \rightarrow \mathbb {SR}^{n\times n}, \end{aligned}$$

(A.1)

which is defined by

$$\begin{aligned} \widetilde{H} (\mathbf {c},Q,\varLambda ):= A(\mathbf {c}) - Q\overline{\varLambda }Q^T, \end{aligned}$$

for all $(\mathbf {c}, Q, \varLambda )\in \mathbb {R}^{l} \times \mathbb {R}^{n\times n} \times \mathscr {D}(n-m)$, where $\overline{\varLambda }$ is defined as in (2.1). Thus the map H is the restriction of $\widetilde{H}$ from the Euclidean space $\mathbb {R}^{l} \times \mathbb {R}^{n\times n} \times \mathscr {D}(n-m)$ to the Riemannian product manifold $\mathscr {Z}$, i.e., $H =\widetilde{H}|_{\mathscr {Z}}$.

Similar to [2, (3.17)], for any $(\varDelta \mathbf {c},\varDelta Q, \varDelta \varLambda ) \in T_{(\mathbf {c},Q,\varLambda )}\mathscr {Z}$, one has

$$\begin{aligned} \mathrm {D}H(\mathbf {c},Q,\varLambda )[ (\varDelta \mathbf {c}, \varDelta Q, \varDelta \varLambda ) ] =\mathrm {D}\widetilde{H}(\mathbf {c},Q,\varLambda )[ (\varDelta \mathbf {c}, \varDelta Q, \varDelta \varLambda ) ]. \end{aligned}$$

(A.2)

For a tangent vector $(\varDelta \mathbf {c},\varDelta Q, \varDelta \varLambda ) \in T_{(\mathbf {c},Q,\varLambda )}\mathscr {Z}$, the matrix $\varDelta QQ^T$ is skew-symmetric [2, (3.26)], i.e.,

$$\begin{aligned} (\varDelta QQ^T)^T = -\varDelta QQ^T. \end{aligned}$$

(A.3)

By the definition of P in (2.5) we have

$$\begin{aligned} \mathrm{blkdiag} (\mathbf{0}_m ,\varDelta \varLambda ) = P \varDelta \varLambda P^T. \end{aligned}$$

(A.4)

Using (2.1), (2.5), (A.1), (A.3), and (A.4) we have

$$\begin{aligned}&\widetilde{H}(\mathbf {c}+t\varDelta \mathbf {c},Q +t\varDelta Q, \varLambda + t\varDelta \varLambda ) \\&\quad = A(\mathbf {c}+t\varDelta \mathbf {c}) -(Q+t\varDelta Q)\,\mathrm{blkdiag}\big (\varLambda ^*_m,\; \varLambda +t\varDelta \varLambda \big )(Q+t\varDelta Q)^T \\&\quad = A(\mathbf {c}+t\varDelta \mathbf {c}) -(Q+t\varDelta Q)\overline{\varLambda }(Q+t\varDelta Q)^T\\&\qquad -\,(Q+t\varDelta Q)\,\mathrm{blkdiag}\big (\mathbf{0}_m ,\;t\varDelta \varLambda \big )(Q+t\varDelta Q)^T \\&\quad = \widetilde{H}(\mathbf {c},Q,\varLambda ) + t(A(\varDelta \mathbf {c})-A_0) + t[ Q\overline{\varLambda } Q^T , \varDelta QQ^T ]\\&\qquad -\,t(QP)\varDelta \varLambda (QP)^T + O(t^2), \end{aligned}$$

where $t\in {\mathbb {R}}$. Based on Proposition 2.5 in [16] and the above equality, we have

$$\begin{aligned}&\mathrm {D}\widetilde{H}(\mathbf {c},Q,\varLambda ) [(\varDelta \mathbf {c}, \varDelta Q, \varDelta \varLambda )] \\&\quad =\displaystyle \lim \limits _{t\rightarrow 0} \frac{\widetilde{H}(\mathbf {c}+t\varDelta \mathbf {c},Q +t\varDelta Q, \varLambda + t\varDelta \varLambda ) -\widetilde{H}(\mathbf {c},Q, \varLambda )}{t}\\&\quad =(A(\varDelta \mathbf {c})-A_0) + [ Q\overline{\varLambda } Q^T ,\varDelta QQ^T ] -(QP)\varDelta \varLambda (QP)^T. \end{aligned}$$

This, together with (A.2), yields

$$\begin{aligned}&\mathrm {D}H(\mathbf {c},Q,\varLambda ) [(\varDelta \mathbf {c}, \varDelta Q, \varDelta \varLambda )]\nonumber \\&\quad =(A(\varDelta \mathbf {c})-A_0) + [ Q\overline{\varLambda } Q^T ,\varDelta QQ^T ] -(QP)\varDelta \varLambda (QP)^T, \end{aligned}$$

(A.5)

for all $(\mathbf {c}, Q, \varLambda )\in \mathscr {Z}$ and $(\varDelta \mathbf {c},\varDelta Q, \varDelta \varLambda ) \in T_{(\mathbf {c},Q,\varLambda )}\mathscr {Z}$, and thus (2.4) holds.

Let $(\mathbf {c}, Q, \varLambda )\in \mathscr {Z}$. For the Riemannian differential $\mathrm {D}H(\mathbf {c},Q,\varLambda )$ and its adjoint $(\mathrm {D}H(\mathbf {c},Q,\varLambda ))^*$ with respect to the Riemannian metric g, one has [2, p. 185],

$$\begin{aligned}&\mathrm{tr}\big (\varDelta Z^T \mathrm {D}H(\mathbf {c},Q,\varLambda )[(\varDelta \mathbf {c}, \varDelta Q, \varDelta \varLambda )] \big )\nonumber \\&\quad = g_{(\mathbf {c},Q,\varLambda )} \big ((\mathrm {D}H(\mathbf {c},Q,\varLambda ))^*[ \varDelta Z], (\varDelta \mathbf {c}, \varDelta Q, \varDelta \varLambda ) \big ), \end{aligned}$$

(A.6)

for any $(\varDelta \mathbf {c},\varDelta Q, \varDelta \varLambda ) \in T_{(\mathbf {c},Q,\varLambda )}\mathscr {Z}$ and $\varDelta Z \in T_{H(\mathbf {c},Q,\varLambda )}\mathbb {SR}^{n\times n}$. Using (3.36) in [2], the definition of the linear operator $\mathbf {v}$ in (2.7), (A.5), and (A.6) we have

$$\begin{aligned}&\mathrm{tr}\big ( \varDelta Z\;\mathrm {D}H(\mathbf {c},Q,\varLambda )[(\varDelta \mathbf {c}, \varDelta Q, \varDelta \varLambda )] \big ) \\&\quad =\mathrm{tr}\big ( \varDelta Z(A(\varDelta \mathbf {c})-A_0) \big ) -\mathrm{tr}\big ( \varDelta Z Q\overline{\varLambda } (\varDelta Q)^T\big )\\&\qquad -\,\mathrm{tr}\big (\varDelta Z (\varDelta Q)\overline{\varLambda } Q^T\big ) -\mathrm{tr}\big (\varDelta Z (QP)\varDelta \varLambda (QP)^T \big ) \\&\quad = \mathrm{tr}\big ( \varDelta Z \sum \limits _{i=1}^{m} (\varDelta \mathbf {c})_iA_i \big ) -2\mathrm{tr}\big ( (\varDelta Z Q\overline{\varLambda })^T\varDelta Q \big ) - \mathrm{tr}\big ( (QP)^T\varDelta Z (QP) \varDelta \varLambda \big ) \\&\quad = \sum \limits _{i=1}^{m} (\varDelta \mathrm {c})_i \mathrm{tr}(A_i^T\varDelta Z) -2\mathrm{tr}\big ( \big (Q\,\mathrm{skew}(Q^T\varDelta Z Q\overline{\varLambda })\big )^T\varDelta Q \big )\\&\qquad -\, \mathrm{tr}\big ( (QP)^T\varDelta Z (QP) \varDelta \varLambda \big ) \\&\quad = \big (\mathbf {v}(\varDelta Z)\big )^T\varDelta \mathbf {c} + \mathrm{tr}\big ( ([ Q\overline{\varLambda } Q^T , \varDelta Z ]Q)^T \varDelta Q \big ) -\mathrm{tr}\big (\mathrm{Diag}\big ((QP)^T\varDelta Z (QP)\big ) \varDelta \varLambda \big ) \\&\quad =g_{(\mathbf {c},Q,\varLambda )} \big (\mathbf {v} (\varDelta Z), [ Q\overline{\varLambda } Q^T ,\varDelta Z ]Q, -\mathrm{Diag}\big ((QP)^T\varDelta Z (QP)\big ), (\varDelta \mathbf {c}, \varDelta Q, \varDelta \varLambda )\big ) \\&\quad =g_{(\mathbf {c},Q,\varLambda )} \big ((\mathrm {D}H(\mathbf {c}, Q,\varLambda ))^*[ \varDelta Z], (\varDelta \mathbf {c}, \varDelta Q, \varDelta \varLambda ) \big ), \end{aligned}$$

where $\mathrm{skew}(A):=\frac{1}{2}(A-A^T)$. Thus,

$$\begin{aligned} (\mathrm {D}H(\mathbf {c},Q,\varLambda ))^* [ \varDelta Z] =\big (\mathbf {v}(\varDelta Z), [ Q\overline{\varLambda } Q^T , \varDelta Z ]Q, -\mathrm{Diag}\big ((QP)^T\varDelta Z (QP)\big )\big ) \end{aligned}$$

for all $\varDelta Z \in T_{H(\mathbf {c},Q,\varLambda )}\mathbb {SR}^{n\times n}$. This proves (2.6).