Analysis of discontinuous reception (DRX) on energy efficiency and transmission delay with bursty packet data traffic

Abstract

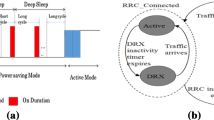
Discontinuous reception (DRX) is a way for user equipment (UE) to save energy. DRX forces a UE to turn off its transceivers for a DRX cycle when it does not have a packet to receive from a base station, called an eNB. However, if a packet arrives at an eNB when the UE is performing a DRX cycle, the transmission of the packet is delayed until the UE finishes the DRX cycle. Therefore, as the length of the DRX cycle increases, not only the amount of UE energy saved by the DRX but also the transmission delay of a packet increase. Different applications have different traffic arrival patterns and require different optimal balances between energy efficiency and transmission delay. Thus, understanding the tradeoff between these two performance metrics is important for achieving the optimal use of DRX in a wide range of use cases. In this paper, we mathematically analyze DRX to understand this tradeoff. We note that previous studies were limited in that their analysis models only partially reflect the DRX operation, and they make assumptions to simplify the analysis, which creates a gap between the analysis results and the actual performance of the DRX. To fill this gap, in this paper, we present an analysis model that fully reflects the DRX operation. To quantify the energy efficiency of the DRX, we also propose a new metric called a real power-saving (RPS) factor by considering all the states and state transitions in the DRX specification. In addition, we improve the accuracy of the analysis result for the average packet transmission delay by removing unrealistic assumptions. Through extensive simulation studies, we validate our analysis results. We also show that compared with the other analysis results, our analysis model improves the accuracy of the performance metrics.

Appendix

1.1 A.1 Proof of lemma 1

If we denote by φ_i(i ≥ 0) the probability that the inactivity timer restarts i times until it exceeds C_T or a new packet arrives, the average duration of an active state (in one RC) is obtained as

$$ E[T_{a}] = E[\tilde{t}_{B}] + \sum\limits_{i=0}^{\infty}i\varphi_{i}(E[\hat{t}_{I}]+E[t_{B}])+C_{T}, $$

(27)

Since the inactivity timer restarts if a packet arrives before it becomes greater than C_T, the probability that a packet arrives within C_T after an inactivity timer starts becomes 1 − Pr{ν(C_T) = 0}. Therefore, φ_i is given as

$$ \begin{array}{@{}rcl@{}} \varphi_{i} & = & (1-Pr\{\nu(C_{T})=0\})^{i} \times Pr\{\nu(C_{T})=0\} \\ &=& (1-p_{B}e^{-\lambda_{ipc}C_{T}}-p_{C}e^{-\lambda_{is}C_{T}})^{i} \\ && \times (p_{B}e^{-\lambda_{ipc}C_{T}}+p_{C}e^{-\lambda_{is}C_{T}}). \end{array} $$

(28)

Combining Eq. 28 with 27, we obtain

$$ \begin{array}{@{}rcl@{}} E[T_{a}] &=& E[\tilde{t}_{B}]+(E[\hat{t}_{I}]+E[t_{B}])\cdot (\frac{1}{Pr\{\nu(C_{T})=0\}}-1)+C_{T}. \end{array} $$

(29)

The first inactivity period ($\hat {t}_{I}$) ends when a packet arrives within C_T. Since both t_is and t_ipc follow an exponential distribution, we can obtain the probability density function (pdf) of $\hat {t}_{I}$ as

$$ f_{\hat{t}_{I}}(t) = \left\{ \begin{array}{ll} \frac{p_{B}\lambda_{ipc}e^{-\lambda_{ipc}t}+p_{C}\lambda_{is}e^{-\lambda_{is}t}}{1-Pr\{\nu(C_{T})=0\}}, & 0 \leq t \leq C_{T}\\ 0. & C_{T}<t \end{array} \right. $$

(30)

Therefore, we can derive

$$ \begin{array}{@{}rcl@{}} E[\hat{t}_{I}]&=&{\int}_{0}^{\infty} t f_{\hat{t}_{I}}(t) \mathrm{d} t \\ &=& \frac{1}{1-Pr\{\nu(C_{T})=0\}}\times {\int}_{0}^{C_{T}} (p_{B}\lambda_{ipc}te^{-\lambda_{ipc}t}+p_{C}\lambda_{is}te^{-\lambda_{is}t}) \mathrm{d} t \\ &=&\frac{ p_{B}[1-(C_{T}\lambda_{ipc}+1)e^{-C_{T}\lambda_{ipc}}]}{\lambda_{ipc}(1-Pr\{\nu(C_{T})=0\})} +\frac{ p_{C}[1-(C_{T}\lambda_{is}+1)e^{-C_{T}\lambda_{is}}] }{\lambda_{is}(1-Pr\{\nu(C_{T})=0\})}. \end{array} $$

(31)

Since an activity period is identical to the duration of a packet call delivery, t_B consists of N_p packet service times. From Wald’s theorem [30], we have

$$ E[t_{B}]=E[N_{p}]E[t_{x}]=\frac{\mu_{p}}{\lambda_{x}}. $$

(32)

Since $\tilde {t}_{B}$ is the first activity period in an RC, it is followed by one of the DRX states. Thus, $\tilde {t}_{B}$ also contains N_p packet service times. Thus, we can also obtain

$$ E[\tilde{t}_{B}]=E[N_{p}]E[t_{x}]=\frac{\mu_{p}}{\lambda_{x}}. $$

(33)

Combining Eqs. 3 and 31–33 into Eq. 29, we can obtain

$$ \begin{array}{@{}rcl@{}} E[T_{a}]&=&\frac{(\mu_{pc}-1)[1-(\lambda_{ipc}C_{T}+1)e^{-\lambda_{ipc}C_{T}}]}{\lambda_{ipc}[e^{-\lambda_{ipc}C_{T}}(\mu_{pc}-1)+e^{-\lambda_{is}C_{T}}]} \\ && +\frac{1-(\lambda_{is}C_{T}+1)e^{-\lambda_{is}C_{T}}}{\lambda_{is}[e^{-\lambda_{ipc}C_{T}}(\mu_{pc}-1)+e^{-\lambda_{is}C_{T}}]} \\ && +\frac{\mu_{pc}{\mu^{2}_{p}}}{\lambda_{x}[e^{-\lambda_{ipc}C_{T}}(\mu_{pc}-1)+e^{-\lambda_{is}C_{T}}]}+C_{T}. \end{array} $$

(34)

1.2 A.2 Proof of lemma 2

Since t_Λ follows the truncated exponential distribution, f_Λ(t) is given as

$$ f_{\Lambda}(t) = \left\{ \begin{array}{ll} (\frac{1}{1-e^{-\lambda_{ipc}C_{S}}})\lambda_{ipc}e^{-\lambda_{ipc}t}, & 0 \leq t \leq C_{S}\\ 0. & otherwise \end{array} \right. $$

(35)

Since 𝜃_k is the probability that subcase k occurs for a given t_Λ, it can be obtained as follows. It is clear that

$$ \theta_{1}=\frac{1}{\mu_{p}}. $$

(36)

We denote by T_D the time interval between the first packet arrival time of a packet call and the last packet arrival time of the packet call. Then, we can obtain $\theta _{2}=(1-\frac {1}{\mu _{p}})Pr[T_{D}>C_{S}-t_{\Lambda }].$ According to [12], T_D follows the Erlang-N_p distribution with rate λ_ip; then, 𝜃₂ can be derived as

$$ \theta_{2}=(1-\frac{1}{\mu_{p}})e^{-\frac{\lambda_{ip}}{\mu_{p}}(C_{S}-t_{\Lambda})}. $$

(37)

From Eqs. 36 and 37, we can obtain

$$ \theta_{3}=1-\theta_{1}-\theta_{2}=(1-\frac{1}{\mu_{p}})\left[1-e^{-\frac{\lambda_{ip}}{\mu_{p}}(C_{S}-t_{\Lambda})}\right]. $$

(38)

In subcase 1, only one packet arrived at t_Λ when a UE was in a short DRX state. Therefore, in this case (i.e., subcase 1, k = 1), we obtain

$$ \begin{array}{@{}rcl@{}} E[N^{\prime}_{1,1|k=1}]=1, E[N^{\prime\prime}_{1,1|k=1}]=0, \\ E[W^{\prime}_{1,1|k=1}]=C_{S}-t_{\Lambda}, \ E[W^{\prime\prime}_{1,1|k=1}]=0. \end{array} $$

(39)

For subcase 2, we follow similar procedures taken in [12] and obtain

$$ \begin{array}{@{}rcl@{}} E[N^{\prime}_{1,1|k=2}]&=&1+\lambda_{ip}(1-\frac{1}{\mu_{p}})(C_{S}-t_{\Lambda}), \\ E[N^{\prime\prime}_{1,1|k=2}]&=&\mu_{p}, \\ E[W^{\prime}_{1,1|k=2}]&=&(C_{S}-t_{\Lambda})+\frac{1}{2}(E[N^{\prime}_{1,1|k=2}]-1)(C_{S}-t_{\Lambda}) \\ && +(\frac{1}{2\lambda_{x}})(E[N^{\prime2}_{1,1|k=2}]-E[N^{\prime}_{1,1|k=2}]),\\ E[W^{\prime\prime}_{1,1|k=2}]&=&(\frac{1}{\lambda_{x}})E[N^{\prime\prime}_{1,1|k=2}]E[N^{\prime}_{1,1|k=2}]-(\frac{1}{\lambda_{ip}})E[N^{\prime\prime}_{1,1|k=2}]\\ &&+\frac{1}{2}(\frac{1}{\lambda_{x}}-\frac{1}{\lambda_{ip}})(E[N^{{{\prime\prime}}2}_{1,1|k=2}]-E[N^{\prime\prime}_{1,1|k=2}]), \end{array} $$

(40)

where $E[N^{\prime 2}_{1,1|k=2}]$ and $E[N^{{\prime \prime }2}_{1,1|k=2}]$ are given as follows:

$$ \begin{array}{@{}rcl@{}} E[N^{\prime2}_{1,1|k=2}]&=&\lambda_{ip}(1-\frac{1}{\mu_{p}})(C_{S}-t_{\Lambda})+(E[N^{\prime}_{1,1|k=2}])^{2}, \\ E[N^{{\prime\prime}2}_{1,1|k=2}]&=&2{\mu_{p}^{2}}-\mu_{p}. \end{array} $$

In subcase 3, all the packets of a packet call arrive when a UE is in the short DRX state. Therefore, we obtain

$$ E[N^{\prime\prime}_{1,1|k=3}]=0, E[W^{\prime\prime}_{1,1|k=3}]=0. $$

(41)

Given t_Λ, according to the decomposition property of Poisson processes [31], (t_Υ − t_Λ) follows the exponential distribution with rate $\frac {\lambda _{ip}}{\mu _{p}}$. Therefore, we can obtain the conditional probability density function of t_Υ as

$$ f_{\Upsilon|{\Lambda}}(t_{\Upsilon}|t_{\Lambda})=\left[\frac{1}{1-e^{-\frac{\lambda_{ip}}{\mu_{p}}(C_{S}-t_{\Lambda})}}\right](\frac{\lambda_{ip}}{\mu_{p}})e^{-\frac{\lambda_{ip}}{\mu_{p}}(t_{\Upsilon}-t_{\Lambda})}, $$

(42)

where t_Λ ≤ t_Υ ≤ C_S. According to Eq. 42, we derive E[t_Υ|t_Λ] and $E[t^{2}_{\Upsilon }|t_{\Lambda }]$ as

$$ \begin{array}{@{}rcl@{}} E[t_{\Upsilon}|t_{\Lambda}]&=&t_{\Lambda}+\left[ \frac{1}{1-e^{-\frac{\lambda_{ip}}{\mu_{p}}(C_{S}-t_{\Lambda})}}\right] \left[\frac{\mu_{p}}{\lambda_{ip}}-(C_{S}-t_{\Lambda}+\frac{\mu_{p}}{\lambda_{ip}})e^{-\frac{\lambda_{ip}}{\mu_{p}}(C_{S}-t_{\Lambda})} \right], \\ E[t^{2}_{\Upsilon}|t_{\Lambda}]&=&t^{2}_{\Lambda}+ \left[ \frac{1}{1-e^{-\frac{\lambda_{ip}}{\mu_{p}}(C_{S}-t_{\Lambda})}}\right]\left\{2t_{\Lambda}(\frac{\mu_{p}}{\lambda_{ip}})\right.+2(\frac{\mu_{p}}{\lambda_{ip}})^{2}-[2t_{\Lambda}(C_{S}-t_{\Lambda} \\ &&+\frac{\mu_{p}}{\lambda_{ip}}) +2(\frac{\mu_{p}}{\lambda_{ip}})^{2}+2(\frac{\mu_{p}}{\lambda_{ip}})(C_{S}-t_{\Lambda})+\left. \left.(C_{S}-t_{\Lambda})^{2} \right]e^{-\frac{\lambda_{ip}}{\mu_{p}}(C_{S}-t_{\Lambda})}\right\}.\\ \end{array} $$

(43)

Following a similar procedure to obtain $E[N^{\prime }_{1,1|2}]$, we obtain

$$ E[N^{\prime}_{1,1|k=3}]=2+\lambda_{ip}(1-\frac{1}{\mu_{p}})(E[t_{\Upsilon}|t_{\Lambda}]-t_{\Lambda}). $$

(44)

According to the decomposition property of the Poisson processes [31], for a given t_Υ, the number of packet arrivals in this period follows a shifted Poisson distribution. However, if t_Υ is a random variable, then the number of packet arrivals in this period is not merely a shifted Poisson distribution. Therefore, in contrast to [12], we do not make any assumptions to obtain the variance of $N^{\prime }_{1,1|k=3}$. Then, we can derive $E[N^{\prime 2}_{1,1|k=3}]$ as follows.

$$ \begin{array}{@{}rcl@{}} E[N^{\prime2}_{1,1|k=3}] & = & Var[N^{\prime}_{1,1|k=3}]+(E[N^{\prime}_{1,1|k=3}])^{2} \\ & = & Var[N^{\prime}_{1,1|k=3}-2]+(E[N^{\prime}_{1,1|k=3}])^{2} \\ &=& \sum\limits_{t_{\Upsilon}=t_{\Lambda}}^{C_{S}}\sum\limits_{k=0}^{\infty}k^{2}f_{\Upsilon|{\Lambda}}(t_{\Upsilon})\frac{[\lambda_{ip}(1-\frac{1}{\mu_{p}})(t_{\Upsilon}-t_{\Lambda})]^{k} }{k!} \\ &&\cdot e^{-\lambda_{ip}(1-\frac{1}{\mu_{p}})(t_{\Upsilon}-t_{\Lambda})}+4E[N^{\prime}_{1,3|k=3}]-4 \\ &=& [\lambda_{ip}(1-\frac{1}{\mu_{p}})]^{2}E[t_{\Upsilon}^{2}|t_{\Lambda}]+\{5\lambda_{ip}(1-\frac{1}{\mu_{p}}) \\ &&-2[\lambda_{ip}(1-\frac{1}{\mu_{p}})]^{2}t_{\Lambda}\}E[t_{\Upsilon}|t_{\Lambda}] \\ &&+[\lambda_{ip}(1-\frac{1}{\mu_{p}})]^{2}t_{\Lambda}^{2}-5\lambda_{ip}(1-\frac{1}{\mu_{p}})t_{\Lambda}+4. \end{array} $$

(45)

Therefore, we can obtain the average waiting time of $N^{\prime }_{1,1|k=3}$ as

$$ \begin{array}{@{}rcl@{}} E[W^{\prime}_{1,1|k=3}]&=&E[N^{\prime}_{1,1|k=3}]\left[C_{S}-\frac{1}{2}(E[t_{\Upsilon}|t_{\Lambda}]+t_{\Lambda})\right] +E\left[{\sum}_{k=1}^{N^{\prime}_{1,1|k=3}}(k-1)\frac{1}{\lambda_{x}} \right] \\ &=&E[N^{\prime}_{1,1|k=3}]\left[C_{S}-\frac{1}{2}(E[t_{\Upsilon}|t_{\Lambda}]+t_{\Lambda})\right] +(\frac{1}{2\lambda_{x}})(E[N^{\prime2}_{1,1|k=3}]-E[N^{\prime}_{1,1|k=3}]).\\ \end{array} $$

(46)

Combining Eqs. 35–41, 44–46, we obtain

$$ \begin{array}{@{}rcl@{}} E[N_{1,1}]&=&{\int}_{t=0}^{C_{S}}\left\{\sum\limits_{k=1}^{3}\theta_{k}(E[N^{\prime}_{1,1|k}]+E[N^{\prime\prime}_{1,1|k}])\right\}f_{\Lambda}(t)\mathrm{d} t, \\ E[W_{1,1}]&=&{\int}_{t=0}^{C_{S}} \left\{\sum\limits_{k=1}^{3} \theta_{k} (E[W^{\prime}_{1,1|k}]+E[W^{\prime\prime}_{1,1|k}])\right\}f_{\Lambda}(t) \mathrm{d} t. \end{array} $$

(47)