Classification of trapezoidal bipolar neutrosophic number, de-bipolarization technique and its execution in cloud service-based MCGDM problem

Abstract

Neutrosophic set can deal with the uncertainties related to the information of any decision making problem in real life scenarios, where fuzzy set may fail to handle those uncertainties properly. In this study, we present the perception of trapezoidal bipolar neutrosophic numbers and its classification in different frame. We introduce the idea of disjunctive structures of trapezoidal bipolar neutrosophic numbers namely type-1 trapezoidal bipolar neutrosophic number, type-2 trapezoidal bipolar neutrosophic numbers, and type-3 trapezoidal bipolar neutrosophic number based on the perception of dependency among membership functions in neutrosophic set. In any neutrosophic decision-making problem, the decision maker uses the comparison of neutrosophic numbers to choose among alternatives solutions. Here, we introduce a ranking method, i.e., De-bipolarization scheme for trapezoidal bipolar neutrosophic number (TrBNN) using removal area technique. We also describe the utility of trapezoidal bipolar neutrosophic number and its appliance in a multi criteria group decision making problem (MCGDM) for distinct users in trapezoidal bipolar arena which is more ethical, precise and reliable in neutrosophic field.

Introduction

The theory of impreciseness was first portrayed by Professor L. A. Zadeh in 1965. Demonstration of membership function and its logical significance was described briefly in [1]. In this contemporary era, the theory of ambiguity theater a fundamental position in different domain of research field like mathematical modeling, social science, networking, decision making problem, medical diagnoses problems etc. Furthermore, researchers from disjunctive arena invented trapezoidal [2], pentagonal [3], hexagonal [4] fuzzy numbers and their different applications in various fields. Later, in 1986, Atanassov [5] represents a legerdemain idea namely intuitionistic fuzzy set (IFS), where both membership and non-membership functions are well thought-out together in a graphical frame. After that, Liu and Yuan [6] introduced triangular IFS and Ye [7] invented trapezoidal IFS which are the congenial combination of triangular, trapezoidal FS and IFS, respectively. Later, in 1998, Smarandache [8] ignited a legerdemain conception of neutrosophic set (NS) which actually deals with three different categories of membership functions namely (i) truth, (ii) false and (iii) hesitation membership function. Invention of NS plays an important impact in science and engineering research domain. In this current epoch, it is generally used in decision making (D.M) problem and mathematical modeling. As researches goes on, researchers developed single valued NS [9], triangular NS [10], trapezoidal NS [11] and recently, Chakraborty [12] constructed the theory of pentagonal neutrosophic set. Basset et al. [13] developed the perception of type 2 neutrosophic numbers, Peng et al. [14] ignited power aggregation operator-based MCGDM, Maity et al. [15] focused on backlogging EOQ model in dense environment, Garg [16] analyzed L.P.P-based D.M problem, Wang et al. [17] established linguistic MCGDM problem in cloud model, Jiang [18] introduced learning model using defuzzification skill, Nabeeh et al. [19] formulated neutrosophic AHP model based on IoT, Biswas et al. [20] proposed TOPSIS skill MCGDM problem, Yu-Han et al. [21] proposed MCGDM problem using VIKOR method, Stanujkic et al. [22] represents MULTIMOORA technique MCDM problem, Haque et al. [23] structured generalized spherical number, Chakraborty [24] evolved neutron-logic oriented EOQ model, the authors [25, 26] developed cylindrical neutrosophic number etc.

Recently, conception of bipolarity [27, 28, 29] has been introduced in research domain to grab human mind’s dilemma based on positive and negative part by Bosc and Pivert [30]. Demonstration of positive and negative membership functions has been developed in this bipolarity concept. Furthermore, Lee [31, 32] extensive the thought of bipolar fuzzy set and Kang and Kang [33] applied this conception into group theory algebra, semi group and other group-related fields. After that, Deli [25] manifested the conception of decision making problem in bipolar environment. Broumi [26] introduced bipolar graph concept and further Ali [34] developed the idea of complex neutrosophic set in uncertainty domain. Later, Molodtsov [31] manifested soft bipolar set and Aslam [32] applied it in D.M problem. After that, Uluçay [35] and Wang [36] developed similarity measure in bipolar set and operators in bipolar domain, respectively. In recent times, Chakraborty et al. [37] ignited the idea of bipolar number in triangular form and its classification in different aspects and Hashim [38] introduced hope function related to bipolar domain. Furthermore, Lee [39] developed operations on bipolar set, Jana [40] established dombi aggregation operation on bipolar arena and Broumi et al. [41] formulated bipolar neutrosophic shortest path problem. Cloud computing (CC) is a computational system model which assigned different computing assets to the users. The main goal of computation of a cloud service-based model is to construct the important scope for cloud service user by accessing the minimum infrastructure and software applications from any instance. So, CC gives a new kind of details and services that increase the new vision of IT services. The recent development of the CC and at the same time the growth of the smart mobile components help us to imagine mobile cloud computing. Recently, cloud service-based problem plays a crucial impact on uncertainty research domain. Fei Tao et al. [42] developed cloud manufacturing service problem, Shuai et al. [43] germinated cloud-based MCDM problem using trust evaluation, Rehman et al. [44] proposed cloud selection-based MCDM skill, Garg [45] established ranking of cloud services under uncertainty, Yang et al. [46] ignited service assortment skill for cross cloud services, Jaiganesh et al. [47] proposed load optimization in CC, Wei et al. [48] manifested gray analysis C.C using MADM problem, Ashtiani et al. [49] developed TOPSIS-based C.C problem, Chen et al. [50] build up MCDM problem in CC services and VIKOR skill under impreciseness, Su et al. [51] framed VIKOR method in CC services etc. There exists [52–56] lots of work in this domain.

In this article, we demonstrate different form of trapezoidal bipolar neutrosophic number and its classification. We also manifested the conception of both linear and non-linear single valued trapezoidal bipolar neutrosophic number and its disjunctive categories according to the dependency and independency of membership functions. Additionally, a new de-bipolarized technique is developed here using the conception of removal area method of linear trapezoidal bipolar neutrosophic number. Utilizing this novel technique anyone can find out the crispified value of a trapezoidal neutrosophic number. Finally, we consider a cloud service-based MCGDM problem as an application of the work under trapezoidal bipolar neutrosophic environment in which we applied the developed results of de-bipolarization skill. Here, our main goal is to catch the best alternative cloud service provider among finite number of service providers. Lastly, a sensitivity analysis has been performed on weights of the attribute function that clearly shows us disjunctive ranking cases of the proposed problem. This novel thought will help the researchers to identify classification of trapezoidal bipolar model, de-bipolarization skill, MCGDM problem and sensitivity analysis in future research work.

Motivation

The conception of bipolar number has been widely applied in various scientific mathematical modeling nowadays. Recently, some important questions has been arises in researchers mind that if someone want to construct linear and non-linear trapezoidal bipolar neutrosophic number then what will the mathematical form of the membership functions? What will be the graphical representation and significance of both linear and non-linear trapezoidal bipolar neutrosophic number? Also, how can we classify class—1, 2, 3 of linear trapezoidal bipolar neutrosophic number and its disjunctive forms in case of dependency and independency of the membership functions? Instead of these question further, there is a burning question arises in human thinking that how could we relate this number with the crisp number that is, what will be the technique of crispification in bipolar-neutrosophic logic? In this feature, we shall try to create the article but again we faced some logical question like what will be the application arena of this proposed number and can we utilize this number in cloud service-based decision making theory? Also, if the attribute values are changed in a certain limit what will be the effect in case of ranking? To find out the answers of these raised questions we started our work to establish this article in trapezoidal bipolar-neutrosophic domain.

Novelties of the work

Various research idea had been previously published in neutrosophic ground specifically in bipolar domain. Different types of formulations, application and simulations are developed by researchers in this field. Moreover, some important results and analysis are still unrevealed. We shall try to solve these unknown points describes below:

• (i) Formulation of linear TrBNN.

• (ii) Classification of the proposed number (Category 1, 2, 3) according to dependency and independency of the membership functions.

• (iii) Geometrical importance and significance of linear TrBNN.

• (iv) Structure of generalized linear form of TrBNN.

• (v) Establishment of non- linear trapezoidal bipolar neutrosophic number.

• (vi) Geometrical representation of Non- linear form of the proposed number.

• (vii) Computation of de-bipolarization technique for TrBNN, i.e., the crispification skill.

• (viii) Construction of cloud service provider-related hypothetical MCGDM problem in bipolar-neutro arena and finally it’s ranking in a logical way.

• (ix) Sensitivity analysis of the proposed MCGDM method for different attribute weights.

• (x) Formulation of Sensitivity chart and Comparison of proposed work with the other published work.

Verbal phrase-related neutrosophic idea

In our daily life, some researchers often focused on the point that how anyone can establish a logical relationship between neutrosophic conception and the real life problem with the help of verbal phrase concept? In this phenomenon, we shall try to construct an idea such that this raised question can be revealed so easily.

Example 1.1 Suppose we need to construct a committee from the group members maintain the democratic way in an important meeting. Thus, this will be a problem of vote casting. Member have different sentiments, feelings, hope, ethics, dream etc. Thus in vagueness aspect we can select different kind of vagueness parameters like fuzzy, intuitionistic, neutrosophic numbers etc. Here, we construct verbal phrases in various environment for this given problem (Table 1).

Table 1 Verbal phrases for different uncertain number

Mathematical preliminaries

Definition 2.1 Fuzzy set: [1] A set ${\tilde{S}}$, defined as ${\tilde{S}} =\left\{\left(A,{\varphi}_{ {{\tilde{S}}}}\left({A}\right)\right):{A}\in {S},{\varphi }_{ {{\tilde{S}}} }\left({A}\right)\in [{0,1}]\right\}$ and usually denoted by the pair as $\left({A},{{\varphi }}_{\tilde{S}}\left({A}\right)\right)$, $A$ $\in S$ and ${{\varphi }}_{\tilde{S}}\left({A}\right)\in [{0,1}]$, then ${\tilde{S}}$ is said to be a fuzzy set.

Definition 2.2 Neutrosophic set: [5] A set ${\tilde{T}}$ is identified as a neutrosophic set if ${\tilde{T}}=\left\{\langle p;\left[{\tau }_{{\tilde{T}}}\left(p\right),{\psi }_{{\tilde{T}}}\left(p\right),{{\varphi }}_{{\tilde{T}}}\left(p\right)\right]\rangle \vdots x\in P, P=\text{universal}\,\text{set}\right\}$, where ${\tau }_{{\tilde{T}}}\left(p\right):P\to \left[{0,1}\right]$ signifies the scale of confidence, $\psi_{{\widetilde{{{\text{neuBiT}}}}}} \left( p \right):P \to \left[ {0,1} \right]$ signifies the scale of hesitation and ${\varphi }_{{\tilde{T}}}\left(p\right):P\to [{0,1}]$ signifies the scale of falseness. Where, ${\tau }_{{\tilde{T}}}\left(p\right), {\psi }_{{\tilde{T}}}\left(p\right)\,\text{and}\,{ \varphi }_{{\tilde{T}}}\left(p\right)$ satisfies the relation:

$$-0\le {\tau }_{{\tilde{T}}}\left(p\right)+{\psi }_{{\tilde{T}}}\left(p\right)+{\varphi }_{{\tilde{T}}}\left(p\right)\le 3+.$$

Definition 2.3 Single typed neutrosophic number: $\left({\tilde{N}}\right)$ is called STNN, if it can be written as ${\tilde{N}}=\langle \left[\left({a}^{1},{b}^{1},{c}^{1},{d}^{1}\right);\mu \right],\left[\left({a}^{2},{b}^{2},{c}^{2},{d}^{2}\right);\rho \right],\left[\left({a}^{3},{b}^{3},{c}^{3},{d}^{3}\right);\sigma \right]\rangle$ where $\mu ,\rho ,\sigma \in \left[\mathrm{0,1}\right]$, where $\left({\uptau }_{\tilde{N}}\right):{\mathbb{R}}\to \left[0,\mu \right]$, $\left({\psi }_{{\tilde{N}}}\right):{\mathbb{R}}\to [\rho ,1]$ and $\left({\varphi }_{{\tilde{N}}}\right):{\mathbb{R}}\to \left[\sigma ,1\right]$ is given as:

$${\tau }_{{\tilde{N}}}\left(p\right)=\left\{\begin{array}{l}{\tau }_{\tilde{{N}_{l}}}\left(p\right)\,\,\,\quad \mathrm{w}\mathrm{h}\mathrm{e}\mathrm{n} \\ \mu\, \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\quad\mathrm{w}\mathrm{h}\mathrm{e}\mathrm{n}\\ \begin{array}{l}{\tau }_{\tilde{{N}_{u}}}\left(p\right) \,\quad\mathrm{w}\mathrm{h}\mathrm{e}\mathrm{n} \\ 0 \end{array}\end{array}\begin{array}{l}{a}^{1}\le p\le {b}^{1}\\ {b}^{1}\le p\le {c}^{1}\\ \begin{array}{ll}{c}^{1}\le p\le {d}^{1}\\\quad \mathrm{o}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{w}\mathrm{i}\mathrm{s}\mathrm{e}\end{array}\end{array}\right.,$$

$${\psi }_{{\tilde{N}}}\left(x\right)=\left\{\begin{array}{l}{\psi }_{\tilde{{N}_{l}}}\left(p\right) \,\,\,\quad\mathrm{w}\mathrm{h}\mathrm{e}\mathrm{n} \\ \rho\, \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\quad\mathrm{w}\mathrm{h}\mathrm{e}\mathrm{n}\\ \begin{array}{l}{\psi }_{\tilde{{N}_{u}}}\left(p\right)\,\quad\mathrm{w}\mathrm{h}\mathrm{e}\mathrm{n}\\ 1 \end{array}\end{array}\begin{array}{l}{a}^{2}\le p\le {b}^{2}\\ {b}^{2}\le p\le {c}^{2}\\ \begin{array}{l}{c}^{2}\le p\le {d}^{2}\\ \mathrm{o}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{w}\mathrm{i}\mathrm{s}\mathrm{e}\end{array}\end{array}\right.,$$

and

$${\varphi }_{{\tilde{N}}}\left(p\right)=\left\{\begin{array}{l}{\varphi }_{\tilde{{N}_{l}}}\left(p\right)\,\,\,\,\,\quad \mathrm{w}\mathrm{h}\mathrm{e}\mathrm{n} \\ \gamma\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\quad\mathrm{w}\mathrm{h}\mathrm{e}\mathrm{n}\\ \begin{array}{l}{\varphi }_{\tilde{{N}_{u}}}\left(p\right) \,\,\,\quad\mathrm{w}\mathrm{h}\mathrm{e}\mathrm{n} \\ 1 \end{array}\end{array}\begin{array}{l}{a}^{3}\le p\le {b}^{3}\\ {b}^{3}\le p\le {c}^{3}\\ \begin{array}{l}{c}^{3}\le p\le {d}^{3}\\ \mathrm{o}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{w}\mathrm{i}\mathrm{s}\mathrm{e}\end{array}\end{array}\right..$$

Definition 2.4 Bipolar neutrosophic set: A set ${\tilde{{T}_{Bi}}}$ is identified as BNS if, ${\tilde{{T}_{Bi}}}=\left\{\langle p;\left[{{\tau }_{{\tilde{{T}_{Bi}}}}}^{+}\left(p\right),{{\psi }_{{\tilde{{T}_{Bi}}}}}^{+}\left(p\right),{{ \varphi }_{{\tilde{{T}_{Bi}}}}}^{+}\left(p\right),{{\tau }_{\tilde{Bi}}}^{-}\left(p\right),{{\psi }_{{\tilde{{T}_{Bi}}}}}^{-}\left(p\right),{{ \varphi }_{{\tilde{{T}_{Bi}}}}}^{-}\left(p\right)\right]\rangle \vdots p\in P\right\}$, where ${{\tau }_{{\tilde{{T}_{Bi}}}}}^{+}\left(p\right):P\to \left[\mathrm{0,1}\right], {{\tau }_{{\tilde{{T}_{Bi}}}}}^{-}\left(p\right):P\to \left[-\mathrm{1,0}\right],$ signifies the scale of confidence, ${{\psi }_{{\tilde{{T}_{Bi}}}}}^{+}\left(p\right):P\to \left[\mathrm{0,1}\right],{{\psi }_{{\tilde{{T}_{Bi}}}}}^{-}\left(p\right):P\to \left[-\mathrm{1,0}\right]$ signifies the scale of hesitation and ${{\varphi }_{{\tilde{{T}_{Bi}}}}}^{+}\left(p\right):P\to \left[\mathrm{0,1}\right],{{ \varphi }_{{\tilde{{T}_{Bi}}}}}^{-}\left(p\right):P\to \left[-\mathrm{1,0}\right]$ signifies the scale of falseness.

Single type linear trapezoidal bipolar neutrosophic number

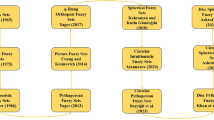
This block diagram shows various types of uncertain parameters and their classifications (Fig. 1).

Fig. 1

Schematic map for special types of single type linear trapezoidal bipolar neutrosophic number

Trapezoidal single typed bipolar neutrosophic number of category 1: the portion of the validity, indecision and negation are independent

A single typed TrBNN of Category 1 is described as:

$${{\tilde{S}}}_{\mathrm{B}\mathrm{i}\mathrm{T}\mathrm{r}}=({e}_{1},{e}_{2},{e}_{3};{f}_{1},{f}_{2},{f}_{3};{g}_{1},{g}_{2},{g}_{3}).$$

Whose validity, indecision and negation membership function portions are scaled as:

$$ T^{ + } _{{\tilde{S}_{{\text{BiTr}}} }} \left( x \right) = \left\{ \begin{gathered} \frac{{x - e_{1} }}{{e_{2} - e_{1} }}\quad {\text{when}}\;~e_{1} \le x < e_{2} \hfill \\ 1\quad \quad \quad \;{\text{when}}\;e_{2} \le x \le e_{3} \hfill \\ \frac{{e_{4} - x}}{{e_{4} - e_{3} }}\quad {\text{when}}\;e_{3} < x \le e_{4} \hfill \\ 0\quad \quad \quad \;{\text{otherwise}} \hfill \\ \end{gathered} \right.,\;T^{ - } _{{\tilde{S}_{{\text{BiTr}}} }} \left( x \right) = \left\{ \begin{gathered} \frac{{e_{2} - x}}{{e_{2} - e_{1} }}\quad {\text{when}}\;~e_{1} \le x < e_{2} \hfill \\ - 1\quad \quad \;\;{\text{when}}\;e_{2} \le x \le e_{3} \hfill \\ \frac{{x - e_{4} }}{{e_{4} - e_{3} }}\quad {\text{when}}\;e_{3} < x \le e_{4} \hfill \\ 0\quad \quad \quad \;{\text{otherwise}} \hfill \\ \end{gathered} \right., $$

and

$$ I^{ + } _{{\tilde{S}_{{\text{BiTr}}} }} \left( x \right) = \left\{ \begin{gathered} \frac{{f_{2} - x}}{{f_{2} - f_{1} }}\quad {\text{when}}\;~f_{1} \le x < f_{2} \hfill \\ 0\quad \quad \quad \;{\text{when}}\;f_{2} \le x \le f_{3} \hfill \\ \frac{{x - f_{4} }}{{f_{4} - f_{3} }}\quad {\text{when}}\;f_{3} < x \le f_{4} \hfill \\ 1\quad \quad \quad \;\;{\text{otherwise}} \hfill \\ \end{gathered} \right.,\;I^{ - } _{{\tilde{S}_{{\text{BiTr}}} }} \left( x \right) = \left\{ \begin{gathered} \frac{{x - f_{2} }}{{f_{2} - f_{1} }}\quad {\text{when}}\;~f_{1} \le x < f_{2} \hfill \\ 0\quad \quad \;\;\;\;\;{\text{when}}\;f_{2} \le x \le f_{3} \hfill \\ \frac{{f_{4} - x}}{{f_{4} - f_{3} }}\quad {\text{when}}\;f_{3} < x \le f_{4} \hfill \\ - 1\quad \quad \;\;\;{\text{otherwise}} \hfill \\ \end{gathered} \right., $$

and

$$ F^{ + } _{{\tilde{S}_{{\text{BiTr}}} }} \left( x \right) = \left\{ \begin{gathered} \frac{{g_{2} - x}}{{g_{2} - g_{1} }}\quad {\text{when}}\;~g_{1} \le x < g_{2} \hfill \\ 0\quad \quad \quad \;\;{\text{when}}\;g_{2} \le x \le g_{3} \hfill \\ \frac{{x - g_{4} }}{{g_{4} - g_{3} }}\quad {\text{when}}\;g_{3} < x \le g_{4} \hfill \\ 1\quad \quad \quad \;\;{\text{otherwise}} \hfill \\ \end{gathered} \right.,\;F^{ - } _{{\tilde{S}_{{\text{BiTr}}} }} \left( x \right) = \left\{ \begin{gathered} \frac{{x - g_{2} }}{{g_{2} - g_{1} }}\quad {\text{when}}\;~g_{1} \le x < g_{2} \hfill \\ 0\quad \quad \;\;\;\;\;{\text{when}}\;g_{2} \le x \le g_{3} \hfill \\ \frac{{g_{4} - x}}{{g_{4} - g_{3} }}\quad {\text{when}}\;g_{3} < x \le g_{4} \hfill \\ - 1\quad \quad \;\;\;{\text{otherwise}} \hfill \\ \end{gathered} \right., $$

where $-3\le {T}_{{\tilde{S}_{{{\text{BiTr}}}}}}\left(x\right)+{I}_{{\tilde{S}_{{{\text{BiTr}}}}}}\left(x\right)+{F}_{{\tilde{S}_{{{\text{BiTr}}}}}}\left(x\right)\le 3+$ and $x\in {{\tilde{S}}}_{{\tilde{S}_{{{\text{BiTr}}}}}}$.

Note: Here, ${{T}^{+}}_{{\tilde{S}_{{{\text{BiTr}}}}}}$ and ${{T}^{-}}_{{\tilde{S}_{{{\text{BiTr}}}}}}$ represents the positive part and negative part of validity membership function ${T}_{{\tilde{S}_{{{\text{BiTr}}}}}}$, respectively, ${{I}^{+}}_{{\tilde{S}_{{{\text{BiTr}}}}}}$ and ${{I}^{-}}_{{\tilde{S}_{{{\text{BiTr}}}}}}$ represents the positive part and negative part of indecision membership function ${I}_{{\tilde{S}_{{{\text{BiTr}}}}}}$, respectively, and ${{F}^{+}}_{{\tilde{S}_{{{\text{BiTr}}}}}}$ and ${{F}^{-}}_{{\tilde{S}_{{{\text{BiTr}}}}}}$ represents the positive part and negative part of negation membership function ${F}_{{\tilde{S}_{{{\text{BiTr}}}}}}$, respectively, of trapezoidal single typed bipolar neutrosophic number of Category 1.

Parametric form of the number

The parametric form or $(\alpha ,\beta ,\gamma )$—cut form of the developed category-1 number is describes as follows:

$${( {\tilde{ S}}_{\text{BiTr}})}_{\alpha ,\beta ,\gamma }=\left[{{T}^{+}}_{{\text{BiTr}}1}\left(\alpha \right),\,\,{{T}^{+}}_{{\text{BiTr}}2}\left(\alpha \right);\,\,{{I}^{+}}_{{\text{BiTr}}1}\left(\beta \right),\,\,{{I}^{+}}_{{\text{BiTr}}2}\left(\beta \right);\,\,{{F}^{+}}_{{\text{BiTr}}1}\left(\gamma \right),\,\,{{F}^{-}}_{{\text{BiTr}}2}(\gamma )\right],$$

where ${{T}^{+}}_{{\text{BiTr}}1}\left(\alpha \right)={e}_{1}+\alpha \left({e}_{2}-{e}_{1}\right), {{ T}^{+}}_{{\text{BiTr}}2}\left(\alpha \right)={e}_{4}-\alpha ({e}_{4}-{e}_{3}),$

${{T}^{-}}_{{\text{BiTr}}1}\left(\alpha \right)={e}_{2}-\alpha \left({e}_{2}-{e}_{1}\right),{{T}^{-}}_{{\text{BiTr}}2}\left(\alpha \right)={e}_{4}+\alpha ({e}_{4}-{e}_{3}),$

${{I}^{+}}_{{\text{BiTr}}1}\left(\beta \right)={f}_{2}-\beta ({f}_{2}-{f}_{1}),$, ${{I}^{+}}_{{\text{BiTr}}2}\left(\beta \right)={f}_{3}+\beta ({f}_{4}-{f}_{3}),$

${{I}^{-}}_{{\text{BiTr}}1}\left(\beta \right)={f}_{2}+\beta ({f}_{2}-{f}_{1}),$, ${{I}^{-}}_{{\text{BiTr}}2}\left(\beta \right)={f}_{3}-\beta ({f}_{4}-{f}_{3}),$

${{F}^{+}}_{{\text{BiTr}}1}\left(\gamma \right)={g}_{2}-\gamma ({g}_{2}-{g}_{1}),$ ${{F}^{+}}_{{\text{BiTr}}2}\left(\gamma \right)={g}_{3}+\gamma ({g}_{4}-{g}_{3}),$

${{F}^{-}}_{{\text{BiTr}}1}\left(\gamma \right)={g}_{2}+\gamma \left({g}_{2}-{g}_{1}\right),{{F}^{-}}_{{\text{BiTr}}2}\left(\gamma \right)={g}_{3}-\gamma ({g}_{4}-{g}_{3}).$

Here, $-1\le \alpha \le 1$, $-1\le \beta \le 1$, $-1\le \gamma \le 1$ and $-3\le \alpha +\beta +\gamma \le 3$.

Note: Here, ${{T}^{+}}_{\text{BiTr}}\left(\alpha \right),{{T}^{-}}_{\text{BiTr}}\left(\alpha \right);{{I}^{+}}_{\text{BiTr}}\left(\beta \right),{{I}^{-}}_{\text{BiTr}}\left(\beta \right);{{F}^{+}}_{\text{BiTr}}\left(\gamma \right),{{F}^{-}}_{\text{BiTr}}(\gamma )$ denotes the $(\alpha ,\beta ,\gamma )$—cut form of positive and negative validity, indecision and negation membership function of trapezoidal single typed bipolar neutrosophic number of Category 1.

Trapezoidal single typed bipolar neutrosophic number of category 2: the portion of indecision and negation are dependent

A single typed TrBNN of Category 2 is described as ${{\tilde{S}}}_{\text{BiTr}}=({e}_{1},\,\,{e}_{2},\,\,{e}_{3};\,\,{f}_{1},\,\,{f}_{2},\,\,{f}_{3};\,\,{s}_{\text{BN}},\,\,{t}_{\text{BN}})$ whose validity, indecision and negation membership function is scaled as:

$$ T^{ + } _{{\tilde{S}_{{\text{BiTr}}} }} \left( x \right) = \left\{ \begin{gathered} \frac{{x - e_{1} }}{{e_{2} - e_{1} }}\quad {\text{when}}\;~e_{1} \le x < e_{2} \hfill \\ 1\quad \quad \quad \;{\text{when}}\;e_{2} \le x \le e_{3} \hfill \\ \frac{{e_{4} - x}}{{e_{4} - e_{3} }}\quad {\text{when}}\;e_{3} < x \le e_{4} \hfill \\ 0\quad \quad \quad \;{\text{otherwise}} \hfill \\ \end{gathered} \right.,\;T^{ - } _{{\tilde{S}_{{\text{BiTr}}} }} \left( x \right) = \left\{ \begin{gathered} \frac{{e_{2} - x}}{{e_{2} - e_{1} }}\quad {\text{when}}\;~e_{1} \le x < e_{2} \hfill \\ - 1\quad \quad \;\;{\text{when}}\;x = e_{2} \le x \le e_{3} \hfill \\ \frac{{x - e_{4} }}{{e_{4} - e_{3} }}\quad {\text{when}}\;e_{3} < x \le e_{4} \hfill \\ 0\quad \quad \quad \;{\text{otherwise}} \hfill \\ \end{gathered} \right., $$

and

$$ I^{ + } _{{\tilde{S}_{{{\text{BiTr}}}} }} \left( x \right) = \left\{ \begin{gathered} \frac{{f_{2} - x + s_{{BN}} \left( {x - f_{1} } \right)}}{{f_{2} - f_{1} }}\quad {\text{when}}\;~f_{1} \le x < f_{2} \hfill \\ s_{{{\text{BN}}}} \quad \quad \quad \quad \quad \quad \quad\;\;\; {\text{when}}\;f_{2} \le x \le f_{3} \hfill \\ \frac{{x - f_{3} + s_{{{\text{BN}}}} \left( {f_{4} - x} \right)}}{{f_{4} - f_{3} }}\quad {\text{when}}\;f_{3} < x \le f_{4} \hfill \\ 1\quad \quad \quad \;\quad \quad \quad \quad \quad \;\;{\text{otherwise}} \hfill \\ \end{gathered} \right.,\;I^{ - } _{{\tilde{S}_{{{\text{BiTr}}}} }} \left( x \right) = \left\{ \begin{gathered} \frac{{x - f_{1} + s_{{{\text{BN}}}} \left( {f_{2} - x} \right)}}{{j_{2} - j_{1} }}\quad {\text{when}}\;~f_{1} \le x < f_{2} \hfill \\ s_{{{\text{BN}}}} \quad \quad \;\;\;\;\;\quad \quad \quad \quad \;{\text{when}}\;f_{2} \le x \le f_{3} \hfill \\ \frac{{f_{4} - x + s_{{{\text{BN}}}} \left( {x - f_{3} } \right)}}{{f_{4} - f_{3} }}\quad {\text{when}}\;f_{3} < x \le f_{4} \hfill \\ - 1\quad \quad \;\;\quad \quad \quad \quad \quad \;\;{\text{otherwise}} \hfill \\ \end{gathered} \right., $$

and

$$ F^{ + } _{{\tilde{S}_{{{\text{BiTr}}}} }} \left( x \right) = \left\{ \begin{gathered} \frac{{f_{2} - x + t_{{BN}} \left( {x - f_{1} } \right)}}{{f_{2} - f_{1} }}\quad {\text{when}}\;~f_{1} \le x < f_{2} \hfill \\ t_{{{\text{BN}}}} \quad \quad \quad \quad \quad \quad \quad \;\;\;{\text{when}}\;f_{2} \le x \le f_{3} \hfill \\ \frac{{x - f_{3} + t_{{{\text{BN}}}} \left( {f_{4} - x} \right)}}{{f_{4} - f_{3} }}\quad {\text{when}}\;f_{3} < x \le f_{4} \hfill \\ 1\quad \quad \quad \;\quad \quad \quad \quad \quad \;{\text{otherwise}} \hfill \\ \end{gathered} \right.,\;F^{ - } _{{\tilde{S}_{{{\text{BiTr}}}} }} \left( x \right) = \left\{ \begin{gathered} \frac{{x - f_{1} + t_{{{\text{BN}}}} \left( {f_{2} - x} \right)}}{{f_{2} - f_{1} }}\quad {\text{when}}\;~f_{1} \le x < f_{2} \hfill \\ t_{{{\text{BN}}}} \quad \quad \;\;\;\;\;\quad \quad \quad \quad \;{\text{when}}\;f_{2} \le x \le f_{3} \hfill \\ \frac{{f_{4} - x + t_{{{\text{BN}}}} \left( {x - f_{3} } \right)}}{{f_{4} - f_{3} }}\quad {\text{when}}\;f_{3} < x \le f_{4} \hfill \\ - 1\quad \quad \;\;\quad \quad \quad \quad \quad \;{\text{otherwise}} \hfill \\ \end{gathered} \right., $$

where $-2\le {T}_{{\tilde{S}_{{{\text{BiTr}}}}}}\left(x\right)+{I}_{{\tilde{S}_{{{\text{BiTr}}}}}}\left(x\right)+{F}_{{\tilde{S}_{{{\text{BiTr}}}}}}\left(x\right)\le 2$ and $x\in {{\tilde{S}}}_{{\tilde{S}_{{{\text{BiTr}}}}}}$.

Note: Here, ${{T}^{+}}_{{\tilde{S}_{{{\text{BiTr}}}}}}$ and ${{T}^{-}}_{{\tilde{S}_{{{\text{BiTr}}}}}}$ represents the positive part and negative part of validity membership function ${T}_{{\tilde{S}_{{{\text{BiTr}}}}}}$, respectively, ${{I}^{+}}_{{\tilde{S}_{{{\text{BiTr}}}}}}$ and ${{I}^{-}}_{{\tilde{S}_{{{\text{BiTr}}}}}}$ represents the positive part and negative part of indecision membership function ${I}_{{\tilde{S}_{{{\text{BiTr}}}}}}$, respectively, and ${{F}^{+}}_{{\tilde{S}_{{{\text{BiTr}}}}}}$ and ${{F}^{-}}_{{\tilde{S}_{{{\text{BiTr}}}}}}$ represents the positive part and negative part of negation membership function ${F}_{{\tilde{S}_{{{\text{BiTr}}}}}}$, respectively, of trapezoidal single typed bipolar neutrosophic number of Category 2. Also, here ${I}_{{\tilde{S}_{{{\text{BiTr}}}}}}$ and ${F}_{{\tilde{S}_{{{\text{BiTr}}}}}}$ are dependent to each other.

Parametric form of the number

The parametric form or the $(\alpha ,\beta ,\gamma )$—cut form of the developed category-2 number is describes as follows:

$${\left({{\tilde{S}}}_{\text{BiTr}}\right)}_{\alpha ,\beta ,\gamma }=\left[{T}_{\text{BiTr}1}\left(\alpha \right),\,\,{T}_{\text{BiTr}2}\left(\alpha \right);\,\,{I}_{\text{BiTr}1}\left(\beta \right),\,\,{I}_{\text{BiTr}2}\left(\beta \right);\,\,{F}_{\text{BiTr}1}\left(\gamma \right),\,\,{F}_{\text{BiTr}2}(\gamma )\right],$$

where ${{T}^{+}}_{\text{BiTr}1}\left(\alpha \right)={e}_{1}+\alpha \left({e}_{2}-{e}_{1}\right),\,\,{{T}^{+}}_{\text{BiTr}2}\left(\alpha \right)={e}_{4}-\alpha ({e}_{4}-{e}_{3}),$

$${{T}^{-}}_{\text{BiTr}1}\left(\alpha \right)={e}_{2}-\alpha \left({e}_{2}-{e}_{1}\right),\,\,{{T}^{-}}_{\text{BiTr}2}\left(\alpha \right)={e}_{4}+\alpha ({e}_{4}-{e}_{3}),$$

$${{I}^{+}}_{\text{BiTr}1}\left(\beta \right)=\frac{{{f}_{2}-s}_{\text{BN}}{f}_{1}-\beta ({f}_{2}-{f}_{1})}{1-{u}_{\text{BN}}},\,\,{{I}^{+}}_{\text{BiTr}2}\left(\beta \right)=\frac{{f}_{3}-{s}_{\text{BN}}{f}_{4}+\beta ({f}_{4}-{f}_{3})}{1-{u}_{\text{BN}}},$$

$${{I}^{-}}_{\text{BiTr}1}\left(\beta \right)=\frac{{{f}_{1}-s}_{\text{BN}}{f}_{2}+\beta ({f}_{2}-{f}_{1})}{1-{u}_{\text{BN}}},\,\,{{I}^{-}}_{\text{BiTr}2}\left(\beta \right)=\frac{{f}_{4}-{s}_{\text{BN}}{f}_{3}-\beta ({f}_{4}-{f}_{3})}{1-{u}_{\text{BN}}},$$

$${{F}^{+}}_{\text{BiTr}1}\left(\gamma \right)=\frac{{f}_{2}-{t}_{\text{BN}}{f}_{1}-\gamma ({f}_{2}-{f}_{1})}{1-{y}_{\text{BN}}},\,\,{{F}^{+}}_{\text{BiTr}2}\left(\gamma \right)=\frac{{f}_{3}-{t}_{\text{BN}}{f}_{4}+\gamma ({f}_{4}-{f}_{3})}{1-{y}_{\text{BN}}},$$

$${{F}^{-}}_{\text{BiTr}1}\left(\gamma \right)=\frac{{f}_{1}-{t}_{\text{BN}}{f}_{2}+\gamma ({f}_{2}-{f}_{1})}{1-{y}_{\text{BN}}},\,\,{{F}^{-}}_{\text{BiTr}2}\left(\gamma \right)=\frac{{f}_{4}-{t}_{\text{BN}}{f}_{3}-\gamma ({f}_{4}-{f}_{3})}{1-{y}_{\text{BN}}},$$

Here, $-1\le \alpha \le 1$, ${s}_{\text{BN}}\le \beta \le 1$, ${t}_{\text{BN}}\le \gamma \le 1$ and $-1\le \beta +\gamma \le 1$ and $-1\le \alpha +\beta +\gamma \le 2$.

Note: Here, ${{T}^{+}}_{\text{BiTr}}\left(\alpha \right),\,\,{{T}^{-}}_{\text{BiTr}}\left(\alpha \right);\,\,{{I}^{+}}_{\text{BiTr}}\left(\beta \right),\,\,{{I}^{-}}_{\text{BiTr}}\left(\beta \right);{{F}^{+}}_{\text{BiTr}}\left(\gamma \right),\,\,{{F}^{-}}_{\text{BiTr}}(\gamma )$ denotes the $\alpha ,\beta ,\gamma$—cut form of positive and negative validity, indecision and negation membership function of trapezoidal single typed bipolar neutrosophic number of Category 2.

Trapezoidal single typed bipolar neutrosophic number of category 3: the portion of the validity, indecision and negation are dependent

A single typed TrBNN of Category 3 is described as ${{\tilde{S}}}_{\text{BiTr}}=({e}_{1},\,\,{e}_{2},\,\,{e}_{3};\,\,{q}_{\text{BN}},\,\,{s}_{\text{BN}},\,\,{t}_{\text{BN}})$ whose validity, indecision and negation membership function is scaled as:

$$ T^{ + } _{{\tilde{S}_{{\text{BiTr}}} }} \left( x \right) = \left\{ \begin{gathered} q_{{{\text{BN}}}} \frac{{x - e_{1} }}{{e_{2} - e_{1} }}\quad {\text{when}}\;~e_{1} \le x < e_{2} \hfill \\ q_{{{\text{BN}}}} \quad \quad \quad \;\;\,\,{\text{when}}\;e_{2} \le x \le e_{3} \hfill \\ q_{{{\text{BN}}}} \frac{{e_{4} - x}}{{e_{4} - e_{3} }}\quad {\text{when}}\;e_{3} < x \le e_{4} \hfill \\ 0\quad \quad \quad \;\;\quad \;\,{\text{otherwise}} \hfill \\ \end{gathered} \right.,\;T^{ - } _{{\tilde{S}_{{\text{BiTr}}} }} \left( x \right) = \left\{ \begin{gathered} q_{{{\text{BN}}}} \frac{{e_{2} - x}}{{e_{2} - e_{1} }}\quad {\text{when}}\;~e_{1} \le x < e_{2} \hfill \\ q_{{{\text{BN}}}} \quad \quad \;\;\;\;\;\;\,{\text{when}}\;e_{2} \le x \le e_{3} \hfill \\ q_{{{\text{BN}}}} \frac{{x - e_{4} }}{{e_{4} - e_{3} }}\quad {\text{when}}\;e_{3} < x \le e_{4} \hfill \\ 0\quad \quad \;\;\quad \quad \;\,{\text{otherwise}} \hfill \\ \end{gathered} \right., $$

and

$$ I^{ + } _{{\tilde{S}_{{{\text{BiTr}}}} }} \left( x \right) = \left\{ \begin{gathered} \frac{{e_{2} - x + s_{{BN}} \left( {x - e_{1} } \right)}}{{e_{2} - e_{1} }}\quad {\text{when}}\;~e_{1} \le x < e_{2} \hfill \\ s_{{{\text{BN}}}} \quad \quad \quad \quad \quad \quad \quad \;\;\;{\text{when}}\;e_{2} \le x \le e_{3} \hfill \\ \frac{{x - e_{3} + s_{{{\text{BN}}}} \left( {e_{4} - x} \right)}}{{e_{4} - e_{3} }}\quad {\text{when}}\;e_{3} < x \le e_{4} \hfill \\ 1\quad \quad \quad \;\quad \quad \quad \quad \quad \;{\text{otherwise}} \hfill \\ \end{gathered} \right.,\;I^{ - } _{{\tilde{S}_{{{\text{BiTr}}}} }} \left( x \right) = \left\{ \begin{gathered} \frac{{x - e_{1} + s_{{{\text{BN}}}} \left( {e_{2} - x} \right)}}{{e_{2} - e_{1} }}\quad {\text{when}}\;~e_{1} \le x < e_{2} \hfill \\ s_{{{\text{BN}}}} \quad \quad \;\;\;\;\;\quad \quad \quad \quad \;{\text{when}}\;e_{2} \le x \le e_{3} \hfill \\ \frac{{e_{4} - x + s_{{{\text{BN}}}} \left( {x - e_{3} } \right)}}{{e_{4} - e_{3} }}\quad {\text{when}}\;e_{3} < x \le e_{4} \hfill \\ - 1\quad \quad \;\;\quad \quad \quad \quad \quad \;{\text{otherwise}} \hfill \\ \end{gathered} \right., $$

and

$$ F^{ + } _{{\tilde{S}_{{{\text{BiTr}}}} }} \left( x \right) = \left\{ \begin{gathered} \frac{{e_{2} - x + t_{{BN}} \left( {x - e_{1} } \right)}}{{e_{2} - e_{1} }}\quad {\text{when}}\;~e_{1} \le x < e_{2} \hfill \\ t_{{{\text{BN}}}} \quad \quad \quad \quad \quad \quad \quad \;\;\;{\text{when}}\;e_{2} \le x \le e_{3} \hfill \\ \frac{{x - e_{3} + t_{{{\text{BN}}}} \left( {e_{4} - x} \right)}}{{e_{4} - e_{3} }}\quad {\text{when}}\;e_{3} < x \le e_{4} \hfill \\ 1\quad \quad \quad \;\quad \quad \quad \quad \quad \;{\text{otherwise}} \hfill \\ \end{gathered} \right.,\;F^{ - } _{{\tilde{S}_{{{\text{BiTr}}}} }} \left( x \right) = \left\{ \begin{gathered} \frac{{x - e_{1} + t_{{{\text{BN}}}} \left( {e_{2} - x} \right)}}{{e_{2} - e_{1} }}\quad {\text{when}}\;~e_{1} \le x < e_{2} \hfill \\ t_{{{\text{BN}}}} \quad \quad \;\;\;\;\;\quad \quad \quad \quad \;{\text{when}}\;e_{2} \le x \le e_{3} \hfill \\ \frac{{e_{4} - x + t_{{{\text{BN}}}} \left( {x - e_{3} } \right)}}{{e_{4} - e_{3} }}\quad {\text{when}}\;e_{3} < x \le e_{4} \hfill \\ - 1\quad \quad \;\;\quad \quad \quad \quad \quad \;{\text{otherwise}} \hfill \\ \end{gathered} \right., $$

where $-1\le {T}_{{\tilde{S}_{{{\text{BiTr}}}}}}\left(x\right)+{I}_{{\tilde{S}_{{{\text{BiTr}}}}}}\left(x\right)+{F}_{{\tilde{S}_{{{\text{BiTr}}}}}}\left(x\right)\le 1$, $x\in {{\tilde{S}}}_{\text{BiTr}}$.

Note: Here, ${{T}^{+}}_{{\tilde{S}_{{{\text{BiTr}}}}}}$ and ${{T}^{-}}_{{\tilde{S}_{{{\text{BiTr}}}}}}$ represents the positive part and negative part of validity membership function ${T}_{{\tilde{S}_{{{\text{BiTr}}}}}}$, respectively, ${{I}^{+}}_{{\tilde{S}_{{{\text{BiTr}}}}}}$ and ${{I}^{-}}_{{\tilde{S}_{{{\text{BiTr}}}}}}$ represents the positive part and negative part of indecision membership function ${I}_{{\tilde{S}_{{{\text{BiTr}}}}}}$, respectively, and ${{F}^{+}}_{{\tilde{S}_{{{\text{BiTr}}}}}}$ and ${{F}^{-}}_{{\tilde{S}_{{{\text{BiTr}}}}}}$ represents the positive part and negative part of negation membership function ${F}_{{\tilde{S}_{{{\text{BiTr}}}}}}$, respectively, of trapezoidal single typed bipolar neutrosophic number of Category 3. Also, here ${T}_{{\tilde{S}_{{{\text{BiTr}}}}}},$ ${I}_{{\tilde{S}_{{{\text{BiTr}}}}}}$ and ${F}_{{\tilde{S}_{{{\text{BiTr}}}}}}$ are dependent to each other.

Parametric form of the number

The parametric form or the $(\alpha ,\beta ,\gamma )$—cut form of the developed category-3 number is describes as follows:

$${\left({{\tilde{S}}}_{\text{BiTr}}\right)}_{\alpha ,\beta ,\gamma }=\left[{T}_{\text{BiTr}1}\left(\alpha \right),\,\,{T}_{\text{BiTr}2}\left(\alpha \right);\,\,{I}_{\text{BiTr}1}\left(\beta \right),\,\,{I}_{\text{BiTr}2}\left(\beta \right);\,\,{F}_{\text{BiTr}1}\left(\gamma \right),\,\,{F}_{\text{BiTr}2}(\gamma )\right],$$

where ${{T}^{+}}_{\text{BiTr}1}\left(\alpha \right)={e}_{1}+\frac{\alpha }{{q}_{\text{BN}}}\left({e}_{2}-{e}_{1}\right),{{T}^{+}}_{\text{BiTr}2}\left(\alpha \right)={e}_{4}-\frac{\alpha }{{q}_{\text{BN}}}({e}_{4}-{e}_{3}),$

$${{T}^{-}}_{\text{BiTr}1}\left(\alpha \right)={e}_{2}-\frac{\alpha }{{q}_{\text{BN}}}\left({e}_{2}-{e}_{1}\right),{{T}^{-}}_{\text{BiTr}2}\left(\alpha \right)={e}_{4}+\frac{\alpha }{{q}_{\text{BN}}}({e}_{4}-{e}_{3}),$$

$${{I}^{+}}_{\text{BiTr}1}\left(\beta \right)=\frac{{{e}_{2}-s}_{\text{BN}}{e}_{1}-\beta ({e}_{2}-{e}_{1})}{1-{s}_{\text{BN}}},{{I}^{+}}_{\text{BiTr}2}\left(\beta \right)=\frac{{e}_{3}-{s}_{\text{BN}}{e}_{4}+\beta ({e}_{4}-{e}_{3})}{1-{s}_{\text{BN}}},$$

$${{I}^{-}}_{\text{BiTr}1}\left(\beta \right)=\frac{{{e}_{1}-s}_{\text{BN}}{e}_{2}+\beta ({e}_{2}-{e}_{1})}{1-{s}_{\text{BN}}},{{I}^{-}}_{\text{BiTr}2}\left(\beta \right)=\frac{{e}_{4}-{s}_{\text{BN}}{e}_{3}-\beta ({e}_{4}-{e}_{3})}{1-{s}_{\text{BN}}},$$

$${{F}^{+}}_{\text{BiTr}1}\left(\gamma \right)=\frac{{e}_{2}-{t}_{\text{BN}}{e}_{1}-\gamma ({e}_{2}-{e}_{1})}{1-{t}_{\text{BN}}},{{F}^{+}}_{\text{BiTr}2}\left(\gamma \right)=\frac{{e}_{3}-{t}_{\text{BN}}{e}_{4}+\gamma ({e}_{4}-{e}_{3})}{1-{t}_{\text{BN}}},$$

$${{F}^{-}}_{\text{BiTr}1}\left(\gamma \right)=\frac{{e}_{1}-{t}_{\text{BN}}{e}_{2}+\gamma ({e}_{2}-{e}_{1})}{1-{t}_{\text{BN}}},{{F}^{-}}_{\text{BiTr}2}\left(\gamma \right)=\frac{{e}_{3}-{t}_{\text{BN}}{e}_{3}-\gamma ({e}_{4}-{e}_{3})}{1-{t}_{\text{BN}}},$$

Here, $-1\le \alpha \le {q}_{\text{BN}}$, ${s}_{\text{BN}}\le \beta \le 1$, ${t}_{\text{BN}}\le \gamma \le 1$ and $-1\le \alpha +\beta +\gamma \le 1.$

Note: Here, ${{T}^{+}}_{\text{BiTr}}\left(\alpha \right),\,\,{{T}^{-}}_{\text{BiTr}}\left(\alpha \right);\,\,{{I}^{+}}_{\text{BiTr}}\left(\beta \right),\,\,{{I}^{-}}_{\text{BiTr}}\left(\beta \right);\,\,{{F}^{+}}_{\text{BiTr}}\left(\gamma \right),\,\,{{F}^{-}}_{\text{BiTr}}(\gamma )$ denotes the $\alpha ,\beta ,\gamma$—cut form of positive and negative validity, indecision and negation membership function of trapezoidal single typed bipolar neutrosophic number of Category 3.

Single typed non-linear trapezoidal bipolar neutrosophic number

Single typed non-linear trapezoidal bipolar neutrosophic number

A single typed non linear TrBNN is precise as ${{\tilde{S}}}_{\text{BiTr}}=\left({e}_{1},\,\,{e}_{2},\,\,{e}_{3};\,\,{f}_{1},\,\,{f}_{2},\,\,{f}_{3};\,\,{g}_{1},\,\,{g}_{2},\,\,{g}_{3}\right|{p}_{1},\,\,{p}_{2};\,\,{q}_{1},\,\,{q}_{2};\,\,{r}_{1},\,\,{r}_{2})$ whose validity, indecision and negation membership function is scaled as:

$$T^{ + } _{{\tilde{S}_{{\text{BiTr}}} }} \left( x \right) = \left\{ \begin{gathered} \left( {\frac{{x - e_{1} }}{{e_{2} - e_{1} }}} \right)^{{p_{1} }} \quad {\text{when}}\;~e_{1} \le x < e_{2} \hfill \\ 1\quad \quad \quad \;\;\,\,\quad \,{\text{when}}\;e_{2} \le x \le e_{3} \hfill \\ \left( {\frac{{e_{4} - x}}{{e_{4} - e_{3} }}} \right)^{{p_{2} }} \quad {\text{when}}\;e_{3} < x \le e_{4} \hfill \\ 0\quad \quad \quad \;\;\quad \;\;{\text{otherwise}} \hfill \\ \end{gathered} \right.,\;T^{ - } _{{\tilde{S}_{{\text{BiTr}}} }} \left( x \right) = \left\{ \begin{gathered} \left( {\frac{{e_{2} - x}}{{e_{2} - e_{1} }}} \right)^{{p_{1} }} \quad {\text{when}}\;~e_{1} \le x < e_{2} \hfill \\ - 1\quad \quad \;\;\;\;\;\;\;\;\,{\text{when}}\;e_{2} \le x \le e_{3} \hfill \\ \left( {\frac{{x - e_{4} }}{{e_{4} - e_{3} }}} \right)^{{p_{2} }} \quad {\text{when}}\;e_{3} < x \le e_{4} \hfill \\ 0\quad \quad \;\;\quad \quad \;\;{\text{otherwise}} \hfill \\ \end{gathered} \right., $$

and

$$ I^{ + } _{{\tilde{S}_{{{\text{BiTr}}}} }} \left( x \right) = \left\{ \begin{gathered} \left( {\frac{{x - f_{1} }}{{f_{2} - f_{1} }}} \right)^{{q_{1} }} \quad {\text{when}}\;~f_{1} \le x < f_{2} \hfill \\ 0\quad \quad \quad \;\;\,\quad \,{\text{when}}\;f_{2} \le x \le f_{3} \hfill \\ \left( {\frac{{x - f_{4} }}{{f_{4} - f_{3} }}} \right)^{{q_{2} }} \quad {\text{when}}\;f_{3} < x \le f_{4} \hfill \\ 1\quad \quad \quad \;\;\quad \;\;{\text{otherwise}} \hfill \\ \end{gathered} \right.,\;I^{ - } _{{\tilde{S}_{{{\text{BiTr}}}} }} \left( x \right) = \left\{ \begin{gathered} \left( {\frac{{x - f_{2} }}{{f_{2} - f_{1} }}} \right)^{{q_{1} }} \quad {\text{when}}\;~f_{1} \le x < f_{2} \hfill \\ 0\quad \quad \;\;\;\;\;\;\;\;\;\,\;{\text{when}}\;f_{2} \le x \le f_{3} \hfill \\ \left( {\frac{{f_{3} - x}}{{f_{4} - f_{3} }}} \right)^{{q_{2} }} \quad {\text{when}}\;f_{3} < x \le f_{4} \hfill \\ - 1\quad \quad \;\;\quad \quad {\text{otherwise}} \hfill \\ \end{gathered} \right., $$

and

$$ F^{ + } _{{\tilde{S}_{{{\text{BiTr}}}} }} \left( x \right) = \left\{ \begin{gathered} \left( {\frac{{x - g_{1} }}{{g_{2} - g_{1} }}} \right)^{{r_{1} }} \quad {\text{when}}\;~g_{1} \le x < g_{2} \hfill \\ 0\quad \quad \quad \;\;\,\quad \,{\text{when}}\;g_{2} \le x \le g_{3} \hfill \\ \left( {\frac{{x - g_{4} }}{{g_{4} - g_{3} }}} \right)^{{r_{2} }} \quad {\text{when}}\;g_{3} < x \le g_{4} \hfill \\ 1\quad \quad \quad \;\;\quad \;\,\;{\text{otherwise}} \hfill \\ \end{gathered} \right.,\;F^{ - } _{{\tilde{S}_{{{\text{BiTr}}}} }} \left( x \right) = \left\{ \begin{gathered} \left( {\frac{{x - g_{2} }}{{g_{2} - g_{1} }}} \right)^{{r_{1} }} \quad {\text{when}}\;~g_{1} \le x < g_{2} \hfill \\ 0\quad \quad \;\;\;\;\;\;\;\;\;\,\;{\text{when}}\;g_{2} \le x \le g_{3} \hfill \\ \left( {\frac{{x - g_{4} }}{{g_{4} - g_{3} }}} \right)^{{r_{2} }} \quad {\text{when}}\;g_{3} < x \le g_{4} \hfill \\ - 1\quad \quad \;\;\quad \quad {\text{otherwise}} \hfill \\ \end{gathered} \right., $$

where ${{T}^{+}}_{{\tilde{S}_{{{\text{BiTr}}}}}} \left(x\right):X\in \left[\mathrm{0,1}\right], {{T}^{-}}_{{\tilde{S}_{{{\text{BiTr}}}}}} \left(x\right):X\in \left[-\mathrm{1,0}\right],{{I}^{+}}_{{\tilde{S}_{{{\text{BiTr}}}}}} \left(x\right):X\in \left[\mathrm{0,1}\right],$

$${{I}^{-}}_{{\tilde{S}_{{{\text{BiTr}}}}}} \left(x\right):X\in \left[-\mathrm{1,0}\right], {{F}^{+}}_{{\tilde{S}_{{{\text{BiTr}}}}}} \left(x\right):X\in \left[\mathrm{0,1}\right],{{F}^{-}}_{{\tilde{S}_{{{\text{BiTr}}}}}} \left(x\right):X\in \left[-\mathrm{1,0}\right].$$

Note: Here, ${{T}^{+}}_{{\tilde{S}_{{{\text{BiTr}}}}}}$ and ${{T}^{-}}_{{\tilde{S}_{{{\text{BiTr}}}}}}$ represents the positive part and negative part of validity membership function ${T}_{{\tilde{S}_{{{\text{BiTr}}}}}}$, respectively, ${{I}^{+}}_{{\tilde{S}_{{{\text{BiTr}}}}}}$ and ${{I}^{-}}_{{\tilde{S}_{{{\text{BiTr}}}}}}$ represents the positive part and negative part of indecision membership function ${I}_{{\tilde{S}_{{{\text{BiTr}}}}}}$, respectively, and ${{F}^{+}}_{{\tilde{S}_{{{\text{BiTr}}}}}}$ and ${{F}^{-}}_{{\tilde{S}_{{{\text{BiTr}}}}}}$ represents the positive part and negative part of negation membership function ${F}_{{\tilde{S}_{{{\text{BiTr}}}}}}$, respectively, of single typed non-linear trapezoidal bipolar neutrosophic number (Fig. 2).

Fig. 2

Non-linear trapezoidal bipolar neutrosophic number

Single typed generalized trapezoidal bipolar neutrosophic number

A single typed generalized TrBNN is precise as ${{\tilde{S}}}_{\text{BiTr}}=({e}_{1},\,\,{e}_{2},\,\,{e}_{3};\,\,{f}_{1},\,\,{f}_{2},\,\,{f}_{3};\,\,{g}_{1},\,\,{g}_{2},\,\,{g}_{3}|\omega ;\,\,\rho ;)$ whose validity, indecision and negation membership function is scaled as:

$$ T^{ + } _{{\tilde{S}_{{{\text{BiTr}}}} }} \left( x \right) = \left\{ \begin{gathered} \omega \frac{{x - e_{1} }}{{e_{2} - e_{1} }}\quad {\text{when}}\;~e_{1} \le x < e_{2} \hfill \\ \omega \quad \quad \quad \;\;\,{\text{when}}\;e_{2} \le x \le e_{3} \hfill \\ \omega \frac{{e_{4} - x}}{{e_{4} - e_{3} }}\quad {\text{when}}\;e_{3} < x \le e_{4} \hfill \\ 0\quad \quad \quad \;\;\;\;{\text{otherwise}} \hfill \\ \end{gathered} \right.,\;T^{ - } _{{\tilde{S}_{{{\text{BiTr}}}} }} \left( x \right) = \left\{ \begin{gathered} \omega \frac{{e_{2} - x}}{{e_{2} - e_{1} }}\quad {\text{when}}\;~e_{1} \le x < e_{2} \hfill \\ - \omega \quad \quad \;\;\;\;{\text{when}}\;e_{2} \le x \le e_{3} \hfill \\ \omega \frac{{x - e_{4} }}{{e_{4} - e_{3} }}\quad {\text{when}}\;e_{3} < x \le e_{4} \hfill \\ 0\quad \quad \;\;\quad \;\;{\text{otherwise}} \hfill \\ \end{gathered} \right., $$

and

$$ I^{ + } _{{\tilde{S}_{{{\text{BiTr}}}} }} \left( x \right) = \left\{ \begin{gathered} \rho \frac{{x - f_{1} }}{{f_{2} - f_{1} }}\quad {\text{when}}\;~f_{1} \le x < f_{2} \hfill \\ 0\quad \quad \quad \;\;\,{\text{when}}\;f_{2} \le x \le f_{3} \hfill \\ \rho \frac{{x - f_{4} }}{{f_{4} - f_{3} }}\quad {\text{when}}\;f_{3} < x \le f_{4} \hfill \\ \rho \quad \quad \quad \;\;\;{\text{otherwise}} \hfill \\ \end{gathered} \right.,\;I^{ - } _{{\tilde{S}_{{{\text{BiTr}}}} }} \left( x \right) = \left\{ \begin{gathered} \rho \frac{{f_{2} - x}}{{f_{2} - f_{1} }}\quad {\text{when}}\;~f_{1} \le x < f_{2} \hfill \\ 0\quad \quad \;\;\;\;\;\;{\text{when}}\;f_{2} \le x \le f_{3} \hfill \\ \rho \frac{{f_{4} - x}}{{f_{4} - f_{3} }}\quad {\text{when}}\;f_{3} < x \le f_{4} \hfill \\ - \rho \quad \quad \;\quad {\text{otherwise}} \hfill \\ \end{gathered} \right., $$

and

$$F^{ + } _{{\tilde{S}_{{{\text{BiTr}}}} }} \left( x \right) = \left\{ \begin{gathered} \lambda \frac{{x - g_{1} }}{{g_{2} - g_{1} }}\quad {\text{when}}\;~g_{1} \le x < g_{2} \hfill \\ 0\quad \quad \quad \;\;\,\;{\text{when}}\;g_{2} \le x \le g_{3} \hfill \\ \lambda \frac{{x - g_{4} }}{{g_{4} - g_{3} }}\quad {\text{when}}\;g_{3} < x \le g_{4} \hfill \\ \lambda \quad \quad \quad \;\;\;\;{\text{otherwise}} \hfill \\ \end{gathered} \right.,\;F^{ - } _{{\tilde{S}_{{{\text{BiTr}}}} }} \left( x \right) = \left\{ \begin{gathered} \lambda \frac{{f_{2} - x}}{{f_{2} - f_{1} }}\quad {\text{when}}\;~f_{1} \le x < f_{2} \hfill \\ 0\quad \quad \;\;\;\;\;\;\;{\text{when}}\;f_{2} \le x \le f_{3} \hfill \\ \lambda \frac{{f_{4} - x}}{{f_{4} - f_{3} }}\quad {\text{when}}\;f_{3} < x \le f_{4} \hfill \\ - \lambda \quad \quad \;\quad {\text{otherwise}} \hfill \\ \end{gathered} \right., $$

where ${{T}^{+}}_{{\tilde{S}_{{{\text{BiTr}}}}}} \left(x\right):X\in \left[\mathrm{0,1}\right], {{T}^{-}}_{{\tilde{S}_{{{\text{BiTr}}}}}} \left(x\right):X\in \left[-\mathrm{1,0}\right],{{I}^{+}}_{{\tilde{S}_{{{\text{BiTr}}}}}} \left(x\right):X\in \left[\mathrm{0,1}\right],{{I}^{-}}_{{\tilde{S}_{{{\text{BiTr}}}}}} \left(x\right):X\in \left[-\mathrm{1,0}\right],{{F}^{+}}_{{\tilde{S}_{{{\text{BiTr}}}}}} \left(x\right):X\in \left[\mathrm{0,1}\right],{{F}^{-}}_{{\tilde{S}_{{{\text{BiTr}}}}}} \left(x\right):X\in \left[-\mathrm{1,0}\right].$

Note: Here, ${{T}^{+}}_{{\tilde{S}_{{{\text{BiTr}}}}}}$ and ${{T}^{-}}_{{\tilde{S}_{{{\text{BiTr}}}}}}$ represents the positive part and negative part of validity membership function ${T}_{{\tilde{S}_{{{\text{BiTr}}}}}}$, respectively, ${{I}^{+}}_{{\tilde{S}_{{{\text{BiTr}}}}}}$ and ${{I}^{-}}_{{\tilde{S}_{{{\text{BiTr}}}}}}$ represents the positive part and negative part of indecision membership function ${I}_{{\tilde{S}_{{{\text{BiTr}}}}}}$, respectively, and ${{F}^{+}}_{{\tilde{S}_{{{\text{BiTr}}}}}}$ and ${{F}^{-}}_{{\tilde{S}_{{{\text{BiTr}}}}}}$ represents the positive part and negative part of negation membership function ${F}_{{\tilde{S}_{{{\text{BiTr}}}}}}$, respectively, of single typed non-linear trapezoidal bipolar neutrosophic number.

Single typed generalized non linear trapezoidal bipolar neutrosophic number

A single typed non linear generalized TrBNN with nine components is precise as ${{\tilde{A}}}_{\mathrm{B}\mathrm{i}\mathrm{N}\mathrm{e}\mathrm{u}}=({e}_{1},\,\,{e}_{2},\,\,{e}_{3};\,\,{f}_{1},\,\,{f}_{2},\,\,{f}_{3};\,\,{g}_{1},\,\,{g}_{2},\,\,{g}_{3}|{p}_{1},\,\,{p}_{2};\,\,{q}_{1},\,\,{q}_{2};\,\,{r}_{1},\,\,{r}_{2}:\omega ;\,\,\rho ;)$ whose validity, indecision and negation membership function is scaled as:

$$ T^{ + } _{{\tilde{S}_{{{\text{BiTr}}}} }} \left( x \right) = \left\{ \begin{gathered} \omega \left( {\frac{{x - e_{1} }}{{e_{2} - e_{1} }}} \right)^{{p_{1} }} \quad {\text{when}}\;~e_{1} \le x < e_{2} \hfill \\ \omega \quad \quad \quad \quad \quad \;\,\,{\text{when}}\;e_{2} \le x \le e_{3} \hfill \\ \omega \left( {\frac{{e_{4} - x}}{{e_{4} - e_{3} }}} \right)^{{p_{2} }} \quad {\text{when}}\;e_{3} < x \le e_{4} \hfill \\ 0\quad \quad \quad \quad \quad \quad {\text{otherwise}} \hfill \\ \end{gathered} \right.,\;T^{ - } _{{\tilde{S}_{{{\text{BiTr}}}} }} \left( x \right) = \left\{ \begin{gathered} \omega \left( {\frac{{x - e_{1} }}{{e_{2} - e_{1} }}} \right)^{{p_{1} }} \quad {\text{when}}\;~e_{1} \le x < e_{2} \hfill \\ \omega \quad \quad \;\;\quad \quad \quad {\text{when}}\;e_{2} \le x \le e_{3} \hfill \\ \omega \left( {\frac{{e_{4} - x}}{{e_{4} - e_{3} }}} \right)^{{p_{2} }} \quad {\text{when}}\;e_{3} < x \le e_{4} \hfill \\ 0\quad \quad \;\;\quad \quad \quad \;{\text{otherwise}} \hfill \\ \end{gathered} \right., $$

and

$$ I^{ + } _{{\tilde{S}_{{{\text{BiTr}}}} }} \left( x \right) = \left\{ \begin{gathered} \rho \left( {\frac{{x - f_{1} }}{{f_{2} - f_{1} }}} \right)^{{q_{1} }} \quad {\text{when}}\;~f_{1} \le x < f_{2} \hfill \\ 0\quad \quad \quad \quad \quad \;\; {\text{when}}\;f_{2} \le x \le f_{3} \hfill \\ \rho \left( {\frac{{x - f_{4} }}{{f_{4} - f_{3} }}} \right)^{{q_{2} }} \quad {\text{when}}\;f_{3} < x \le f_{4} \hfill \\ \rho \quad \quad \quad \quad \quad \;\;\;{\text{otherwise}} \hfill \\ \end{gathered} \right.,\;I^{ - } _{{\tilde{S}_{{{\text{BiTr}}}} }} \left( x \right) = \left\{ \begin{gathered} \rho \left( {\frac{{f_{2} - x}}{{f_{2} - f_{1} }}} \right)^{{q_{1} }} \quad {\text{when}}\;~f_{1} \le x < f_{2} \hfill \\ 0\quad \quad \;\;\;\;\;\;\;\;\quad \;{\text{when}}\;f_{2} \le x \le f_{3} \hfill \\ \rho \left( {\frac{{f_{4} - x}}{{f_{4} - f_{3} }}} \right)^{{q_{2} }} \quad {\text{when}}\;f_{3} < x \le f_{4} \hfill \\ \rho \quad \quad \quad \quad \quad \;\;{\text{otherwise}} \hfill \\ \end{gathered} \right., $$

and

$$F^{ + } _{{\tilde{S}_{{{\text{BiTr}}}} }} \left( x \right) = \left\{ \begin{gathered} \lambda \left( {\frac{{x - g_{1} }}{{g_{2} - g_{1} }}} \right)^{{r_{1} }} \quad {\text{when}}\;~g_{1} \le x < g_{2} \hfill \\ 0\quad \quad \quad \;\;\,\quad \,\;\;\;{\text{when}}\;g_{2} \le x \le g_{3} \hfill \\ \lambda \left( {\frac{{x - g_{4} }}{{g_{4} - g_{3} }}} \right)^{{r_{2} }} \quad {\text{when}}\;g_{3} < x \le g_{4} \hfill \\ \lambda \quad \quad \quad \;\;\quad \;\,\;\;\;{\text{otherwise}} \hfill \\ \end{gathered} \right.,\;F^{ - } _{{\tilde{S}_{{{\text{BiTr}}}} }} \left( x \right) = \left\{ \begin{gathered} \lambda \left( {\frac{{g_{2} - x}}{{g_{2} - g_{1} }}} \right)^{{r_{1} }} \quad {\text{when}}\;~g_{1} \le x < g_{2} \hfill \\ 0\quad \quad \;\;\;\;\;\;\;\;\;\,\;\;\;\;{\text{when}}\;g_{2} \le x \le g_{3} \hfill \\ \lambda \left( {\frac{{g_{4} - x}}{{g_{4} - g_{3} }}} \right)^{{r_{2} }} \quad {\text{when}}\;g_{3} < x \le g_{4} \hfill \\ - \lambda \quad \quad \;\;\quad \quad \;\,{\text{otherwise}} \hfill \\ \end{gathered} \right., $$

where ${{T}^{+}}_{{\tilde{S}_{{{\text{BiTr}}}}}} \left(x\right):X\in \left[\mathrm{0,1}\right], {{T}^{-}}_{{\tilde{S}_{{{\text{BiTr}}}}}} \left(x\right):X\in \left[-\mathrm{1,0}\right],{{I}^{+}}_{{\tilde{S}_{{{\text{BiTr}}}}}} \left(x\right):X\in \left[\mathrm{0,1}\right],{{I}^{-}}_{{\tilde{S}_{{{\text{BiTr}}}}}} \left(x\right):X\in \left[-\mathrm{1,0}\right]$

${{F}^{+}}_{{\tilde{S}_{{{\text{BiTr}}}}}} \left(x\right):X\in \left[\mathrm{0,1}\right],{{F}^{-}}_{{\tilde{S}_{{{\text{BiTr}}}}}} \left(x\right):X\in \left[-\mathrm{1,0}\right].$

Note: Here, ${{T}^{+}}_{{\tilde{S}_{{{\text{BiTr}}}}}}$ and ${{T}^{-}}_{{\tilde{S}_{{{\text{BiTr}}}}}}$ represents the positive part and negative part of validity membership function ${T}_{{\tilde{S}_{{{\text{BiTr}}}}}}$, respectively, ${{I}^{+}}_{{\tilde{S}_{{{\text{BiTr}}}}}}$ and ${{I}^{-}}_{{\tilde{S}_{{{\text{BiTr}}}}}}$ represents the positive part and negative part of indecision membership function ${I}_{{\tilde{S}_{{{\text{BiTr}}}}}}$, respectively, and ${{F}^{+}}_{{\tilde{S}_{{{\text{BiTr}}}}}}$ and ${{F}^{-}}_{{\tilde{S}_{{{\text{BiTr}}}}}}$ represents the positive part and negative part of negation membership function ${F}_{{\tilde{S}_{{{\text{BiTr}}}}}}$, respectively, of single typed generalized non linear trapezoidal bipolar neutrosophic number.

De-bipolarization technique of linear TrBNN

It is a technique in which we can generate a certain fixed crisp value corresponding to a TrBNN in a logical way utilizing a suitable skill. All around the whole world researchers from every states have been interested about the fact that what will be the equivalent crisp value coupled with TrBNN? Gradually, researchers thought various processes which are very much useful for crispification of a fuzzy number.

In case of our trapezoidal bipolar neutrosophic condition researchers have keen interest to recognize the appropriate and rational process of converting a TrBNN into a crisp number. Three several membership functions are present in case of TrBNN. At last we mentioned “Removal area method” which converts a TrBNN into a crisp number.

De-bipolarization utilizing removal area skill

Suppose, we take a linear TrBNN as follows:

$${{\tilde{S}}}_{\mathrm{B}\mathrm{i}\mathrm{T}\mathrm{r}}=(a,\,b,\,c,\,d;\,e,\,f,\,g,\,h;\,i,\,j,\,k,\,l).$$

The graphical representation of a TrBNN is (Fig. 3).

Fig. 3

Linear trapezoidal bipolar neutrosophic number

Let us consider a real number $s\in R$ and a fuzzy number ${\tilde{P}}$ for black line mentioned trapezium, the left part area of ${\tilde{P}}$ w.r.t $s$ is ${S}_{l}\left({\tilde{P}},s\right)$ is described as the region covered by $s$ and the left part of the TrBNN number ${\tilde{P}}.$ Now, the right side area of ${\tilde{P}}$ w.r.t $s$ is ${S}_{r}\left({\tilde{P}},s\right),$ again we consider a real number $s\in R$ along with a TrBNN ${\tilde{Q}}$ for the left top most red colored trapezium and the left portion area of ${\tilde{Q}}$ wr.t $s$ is ${S}_{l}\left({\tilde{Q}},s\right)$ is pointed as the section covered by $s$ and the left section of the TrBNN ${\tilde{Q}}.$ Again, the right side area of ${\tilde{Q}}$ wr.t $s$ is ${S}_{r}\left({\tilde{Q}},s\right)$. Now, TrBNN of ${\tilde{R}}$ for the right most blue colored trapezium, then left portion removal of ${\tilde{R}}$ w.r.t $s$ is ${S}_{l}\left({\tilde{R}},s\right)$ is pointed out as the region covered by $s$ and the left side of the fuzzy number ${\tilde{R}}.$ similarly, the right portion removal of $R$ w.r.t $s$ is ${S}_{r}\left({\tilde{R}},s\right).$

Mean is described as:

$$S\left({\tilde{P}},s\right)=\frac{{S}_{l}\left({\tilde{P}},s\right)+{S}_{r}\left({\tilde{P}},s\right)}{2},$$

$$S\left({\tilde{Q}},s\right)=\frac{{S}_{l}\left({\tilde{Q}},s\right)+{S}_{r}\left({\tilde{Q}},s\right)}{2},$$

$$S\left({\tilde{R}},s\right)=\frac{{S}_{l}\left({\tilde{R}},s\right)+{S}_{r}\left({\tilde{R}},s\right)}{2}.$$

Hence, the de-bipolarization value of a linear TrBNN as,

$$S ({{\tilde{D}}}_{\text{TrBipo}},l)=\frac{S\left({\tilde{P}},s\right)+S\left({\tilde{Q}},s\right)+S\left({\tilde{R}},s\right)}{3},$$

For $s=0, S\left({\tilde{P}},0\right)=\frac{{S}_{l}\left({\tilde{P}},0\right)+{S}_{r}\left({\tilde{P}},0\right)}{2}$,  $S\left({\tilde{Q}},0\right)=\frac{{S}_{l}\left({\tilde{Q}},0\right)+{S}_{r}\left({\tilde{Q}},0\right)}{2}$,  $S\left({\tilde{R}},0\right)=\frac{{S}_{l}\left({\tilde{R}},0\right)+{S}_{r}\left({\tilde{R}},0\right)}{2}$.

Then, $S\left({{\tilde{D}}}_{TrBipo},0\right)=\frac{S\left({\tilde{P}},0\right)+S\left({\tilde{Q}},0\right)+S\left({\tilde{R}},0\right)}{3}$.

We take ${\tilde{A}}=\left(a,b,c,d\right), {\tilde{B}}=\left(e,f,g,h\right), \stackrel{\sim }{C}=\left(i,j,k,l\right)$.

Then,

${S}_{l}\left({\tilde{Q}},0\right)=$ Area of Fig. 4  = $\frac{\left(e+f\right)}{2}. 2=(e+f)$

Fig. 4

Step 1

${S}_{r}\left({\tilde{Q}},0\right)=$ Area of Fig. 5  = $\frac{\left(g+h\right)}{2}. 2=(g+h)$

Fig. 5

Step 2

${S}_{l}\left({\tilde{R}},0\right)=$ Area of Fig. 6  = $\frac{\left(i+j\right)}{2}.2=(i+j)$

Fig. 6

Step 3

${S}_{r}\left({\tilde{R}},0\right)=$ Area of Fig. 7  = $\frac{\left(k+l\right)}{2}.2=(k+l)$

Fig. 7

Step 4

${S}_{l}\left({\tilde{P}},0\right)=$ Area of Fig. 8  = $\frac{\left(a+b\right)}{2}.2=(a+b)$

Fig. 8

Step 5

${S}_{r}\left({\tilde{P}},0\right)=$ Area of Fig. 9  = $\frac{\left(c+d\right)}{2}.2=(c+d)$

Fig. 9

Step 6

Hence, $\left({\tilde{P}},0\right)=\frac{\left(a+b+c+d\right)}{2}, S\left({\tilde{Q}},0\right)=\frac{\left(e+f+g+h\right)}{2}$ , $S\left({\tilde{R}},0\right)=\frac{\left(i+j+k+l\right)}{2}$

So, $S\left({{\tilde{D}}}_{\mathrm{T}\mathrm{r}\mathrm{B}\mathrm{i}\mathrm{p}\mathrm{o}},0\right)=\frac{\left(a+b+c+d+e+f+g+h+i+j+k+l\right)}{6}$

Cloud Service base multi-criteria group decision making problem in bipolar trapezoidal neutrosophic environment

MCGDM skill is one of the reliable, logistical and mostly used topics in this current era. Different kind of alternatives and finite number of attributes having distinct weights are associated with a decision making problem. The problem is to find out the best alternatives among all of them maintaining the alternative vs. attribute core relationship. Comparison analysis can be done in case ordering the alternatives and that will give us more realistic and prominent results. Recently, lots of researchers are invented different techniques to solve the problem but we applied this cloud service-based MCGDM problem in TrBNN environment. Finally, we compare our result with the established methods and make a ranking order using our developed de-bipolarized value. Cloud computing is a service providing accessible object of computer system reservoir, basically data accumulation and capability of computing, without vibrant controlling by the accessorise. This terminology is most frequently used to elucidate data hubs obtainable to numerous users over the internet. Nowaday’s large clouds occasionally are used to allocate functions over several stations from central servers. Moreover, if the connection accessed by the user is reasonably close, it can be delegated as an edge server. Clouds can be confined to a single agency, or be accessible from multiple agencies. Cloud computing depends on distribution of supply to acquire consistency and economics of scale. Reformers of public and hybrid clouds observe that cloud computing permit companies to neglect or diminish IT infrastructure expenditure. Profounder also demand that cloud computing enables enterprises to secure their applications and move with a brisk pace, with refined manageability and meagre maintenance system, and that it provides IT experts to more swiftly synchronize resources to meet oscillating and random demands.

In this section, we consider a multi criteria decision making problem based on cloud services in which we need to select the best cloud service according to different opinions from the engineers. The developed algorithm is described briefly as follows:

Design of the MCGDM problem

Let $C=\{ {C}_{1},{C}_{2},{C}_{3}\dots \dots \dots ..{C}_{m}\}$ be the set of different alternative and $R=\{ {R}_{1},{R}_{2},{R}_{3}\dots \dots \dots ..{R}_{n}\}$ be the set of disjunctive attributes. Also, $\omega =\{ {\omega }_{1},{\omega }_{2},{\omega }_{3}\dots \dots \dots ..{\omega }_{n}\}$ are the weights co-related with set $R$ in which all $\omega \ge$ 0 and $\sum_{i=1}^{n}{\omega }_{i}=1$. Additionally, $D=\{ {D}_{1},{D}_{2},{D}_{3}\dots \dots \dots ..{D}_{K}\}$ be the set of decision maker co-related with set $C$ whose weights are pointed as $\Delta =\left\{{\Delta }_{1},{\Delta }_{2},{\Delta }_{3}\dots \dots \dots ..{\Delta }_{k}\right\}$, ${\Delta }_{i}\ge$ 0 and $\sum_{i=1}^{k}{\Delta }_{i}=1$. According to the knowledge, philosophical view and opinion of the decision maker the set $\Delta$ will be created.

Algorithm of the proposed MCGDM problem

Step 1: Formulation of decision matrices (D.M)

Here, all the D.M’s are formulated maintaining the connection in between alternatives and attributes according to the choice of the decision makers. Also, the entire member’s ${y}_{ij}$ of each matrix are TrBNN. Thus, the computed matrix is described as:

$${X}^{K}=\left(\begin{array}{cccccc}.& {R}_{1}& {R}_{2}& {R}_{3}& .& \begin{array}{ccc}.& .& { R}_{n}\end{array}\\ {C}_{1}& {y}_{11}^{k}& {y}_{12}^{k}& {y}_{13}^{k}& .& .\begin{array}{ccc}.& .& {y}_{1n}^{k}\end{array}\\ {C}_{2}& {y}_{21}^{k}& {y}_{22}^{k}& {y}_{23}^{k}& .& \begin{array}{ccc}.& .& {y}_{2n}^{k}\end{array}\\ \begin{array}{c}{C}_{3}\\ .\\ {C}_{m}\end{array}& \begin{array}{c}.\\ .\\ \begin{array}{c}.\\ {y}_{m1}^{k}\end{array}\end{array}& \begin{array}{c}.\\ .\\ {y}_{m2}^{k}\end{array}& \begin{array}{c}.\\ .\\ {y}_{m3}^{k}\end{array}& \begin{array}{c}.\\ .\\ .\end{array}& \begin{array}{c}\begin{array}{ccc}.& .& .\end{array}\\ \begin{array}{ccc}.& .& .\end{array}\\ \begin{array}{ccc}.& .& {y}_{mn}^{k}\end{array}\end{array}\end{array}\right).$$

(1)

Step 2: Formulation of normalised single D.M

To make a single group D.M namely X, we incorporated this logical procedure ${y}_{ij}^{^{\prime}}=\{\sum_{i=1}^{k}{\omega }_{i}{X}^{i}\}$ for every D.M of ${X}^{i}.$ Thus, the concluding matrix becomes:

$$X=\left(\begin{array}{cccccc}.& {R}_{1}& {R}_{2}& {R}_{3}& .& \begin{array}{ccc}.& .& { R}_{n}\end{array}\\ {C}_{1}& {y}_{11}^{^{\prime}}& {y}_{12}^{^{\prime}}& {y}_{13}^{^{\prime}}& .& .\begin{array}{ccc}.& .& {y}_{1n}^{^{\prime}}\end{array}\\ {C}_{2}& {y}_{21}^{^{\prime}}& {y}_{22}^{^{\prime}}& {y}_{23}^{^{\prime}}& .& \begin{array}{ccc}.& .& {y}_{2n}^{^{\prime}}\end{array}\\ \begin{array}{c}{C}_{3}\\ .\\ {C}_{m}\end{array}& \begin{array}{c}.\\ .\\ \begin{array}{c}.\\ {y}_{m1}^{^{\prime}}\end{array}\end{array}& \begin{array}{c}.\\ .\\ {y}_{m2}^{^{\prime}}\end{array}& \begin{array}{c}.\\ .\\ {y}_{m3}^{^{\prime}}\end{array}& \begin{array}{c}.\\ .\\ .\end{array}& \begin{array}{c}\begin{array}{ccc}.& .& .\end{array}\\ \begin{array}{ccc}.& .& .\end{array}\\ \begin{array}{ccc}.& .& {y}_{mn}^{^{\prime}}\end{array}\end{array}\end{array}\right).$$

(2)

Step 3: Formulation of priority matrix

To make single D.M we incorporated the logical computation ${y}_{ij}^{\prime\prime}=\left\{ \sum_{i=1}^{n}{\Delta }_{i}{y}_{ci }^{^{\prime}}, c=\mathrm{1,2}\dots .m\right\}$ for every column entity and finally, we find the D.M as,

$$X=\left(\begin{array}{c}\begin{array}{cc}.& {R}_{1}\end{array}\\ \begin{array}{cc}{C}_{1}& {y}_{11}^{{\prime\prime}}\end{array}\\ \begin{array}{c}\begin{array}{cc}{C}_{2}& {y}_{21}^{{\prime\prime}}\end{array}\\ \begin{array}{cc}. & .\end{array}\\ \begin{array}{cc}\begin{array}{c}.\\ { C}_{m}\end{array}& \begin{array}{c}.\\ {y}_{m1}^{{\prime\prime}}\end{array}\end{array}\end{array}\end{array}\right).$$

(3)

Step 4: Ranking

Now, by considering the de-bipolarization skill for crispification of the matrix Eq. (3), we can calculate the best alternative of the corresponding problem. The best alternative result will be the maximum value and the minimum value will be the lowest one.

Flowchart for the associated MCGDM problem

(After sensitivity circle another circle should be added as final decision) (Fig. 10).

Fig. 10

Flowchart for the associated problem

Illustrative example

Here, we construct a cloud service-based problem in which there are three different cloud services are available. Among those cloud services facility we want to select the best cloud service in a logical way. Normally, cloud services are fully depends on the attributes accountability, reliability, service and security of the system. Keeping these points in mind different computer science engineers provides some opinions and according to their suggestions we construct the distinct decision matrices in bipolar trapezoidal environment shows below:

$${C}_{1}=\mathrm{C}\mathrm{l}\mathrm{o}\mathrm{u}\mathrm{d}\, \mathrm{S}\mathrm{e}\mathrm{r}\mathrm{v}\mathrm{i}\mathrm{c}\mathrm{e} \,1,$$

$${C}_{2}=\mathrm{C}\mathrm{l}\mathrm{o}\mathrm{u}\mathrm{d}\, \mathrm{S}\mathrm{e}\mathrm{r}\mathrm{v}\mathrm{i}\mathrm{c}\mathrm{e}\, 2,$$

$${C}_{3}=\mathrm{C}\mathrm{l}\mathrm{o}\mathrm{u}\mathrm{d}\, \mathrm{S}\mathrm{e}\mathrm{r}\mathrm{v}\mathrm{i}\mathrm{c}\mathrm{e}\, 3$$

are the alternatives and

$${R}_{1}= \mathrm{A}\mathrm{c}\mathrm{c}\mathrm{o}\mathrm{u}\mathrm{n}\mathrm{t}\mathrm{a}\mathrm{b}\mathrm{i}\mathrm{l}\mathrm{i}\mathrm{t}\mathrm{y},$$

$${R}_{2}=\mathrm{R}\mathrm{e}\mathrm{l}\mathrm{i}\mathrm{a}\mathrm{b}\mathrm{i}\mathrm{l}\mathrm{t}\mathrm{y},$$

$${R}_{3}=\mathrm{S}\mathrm{e}\mathrm{r}\mathrm{v}\mathrm{i}\mathrm{c}\mathrm{e}\, \mathrm{a}\mathrm{n}\mathrm{d}\, \mathrm{S}\mathrm{e}\mathrm{c}\mathrm{u}\mathrm{r}\mathrm{i}\mathrm{t}\mathrm{y}$$

are the attributes.

Let us select four distinct decision makers from our environment,

$${D}_{1}=\mathrm{Y}\mathrm{o}\mathrm{u}\mathrm{t}\mathrm{h}\, \mathrm{E}\mathrm{n}\mathrm{g}\mathrm{i}\mathrm{n}\mathrm{e}\mathrm{e}\mathrm{r},$$

$${D}_{2}=\mathrm{L}\mathrm{i}\mathrm{t}\mathrm{t}\mathrm{l}\mathrm{e}\, \mathrm{E}\mathrm{x}\mathrm{p}\mathrm{e}\mathrm{r}\mathrm{i}\mathrm{e}\mathrm{n}\mathrm{c}\mathrm{e}\mathrm{d}\, \mathrm{E}\mathrm{n}\mathrm{g}\mathrm{i}\mathrm{n}\mathrm{e}\mathrm{e}\mathrm{r},$$

$${D}_{3}=\mathrm{H}\mathrm{i}\mathrm{g}\mathrm{h}\mathrm{l}\mathrm{y}\, \mathrm{E}\mathrm{x}\mathrm{p}\mathrm{e}\mathrm{r}\mathrm{i}\mathrm{e}\mathrm{n}\mathrm{c}\mathrm{e}\mathrm{d} \,\mathrm{E}\mathrm{n}\mathrm{g}\mathrm{i}\mathrm{n}\mathrm{e}\mathrm{e}\mathrm{r}$$

of computer science background having weight distribution $D=\{ 0.30, 0.33, 0.37 \}$ and the weight vector related to the attribute function $\Delta =\left\{\mathrm{0.35,\,\,0.33,\,\,0.32}\right\}.$ A verbal matrix is formulated by the engineers to support the decision maker classifying the D.M. Attribute vs. verbal phrase matrix is given below in the Tables 2 and 3.

Table 2 List of verbal phrase

Table 3 Verbal matrix

Step 1: According to the D.M’s opinion the decision matrices are shown like this:

$${D}^{1}=\left(\begin{array}{cccc}.& {R}_{1}& {R}_{2}& {R}_{3}\\ {C}_{1}& <\mathrm{1,\,2},\,\mathrm{3,\,4};\,\mathrm{0.5,\,1.2,\,2.5,\,3};\,\mathrm{1.3,\,2.3,\,3.5,\,4.5}>& <\mathrm{1,\,4},\,\mathrm{6,\,9};\,\mathrm{0.5,\,3},\,\mathrm{6,\,8};\,\mathrm{3.5,\,6},\mathrm{7.5,\,10}>& <\mathrm{1,\,5},\,\mathrm{7,\,9};\,\mathrm{0.6,\,2},\,\mathrm{4,\,6};\,\mathrm{2,\,4.5,\,6.5,\,9.5}>\\ {C}_{2}& <\mathrm{0.7,\,2},\mathrm{3,\,4};\,\mathrm{0.5,\,1},\,\mathrm{2.5,\,3};\,\mathrm{1.5,\,3},\,\mathrm{4.5,\,5.5}>& <\mathrm{2,\,4},\,\mathrm{6,\,8};\,\mathrm{1.5,\,2.3,\,3.5,\,5};\,\mathrm{3,\,5},\,\mathrm{7,\,9}>& <\mathrm{1.5,\,2.5,\,3.5,\,4.5};\,\mathrm{1,\,2},\,\mathrm{3,\,4};\,\mathrm{2,\,3},\,\mathrm{4,\,6}>\\ {C}_{3}& <\mathrm{1,\,4},\,\mathrm{7,\,9};\,\mathrm{1,\,2},\,\mathrm{3,\,5};\,\mathrm{3,\,5},\,\mathrm{7,\,9}>& <\mathrm{1.5,\,2.5,\,3.5,\,4.5};\,\mathrm{1,\,2},\,\mathrm{3,\,4};\,\mathrm{2,\,3},\,\mathrm{4,\,6}>& <\mathrm{1,\,2},\,\mathrm{4,\,6};\,0.5,\,\mathrm{1,\,2},\,\mathrm{3,\,4};\,\mathrm{3,\,4},\,\mathrm{5,\,7}>\end{array}\right),$$

$$\mathrm{Y}\mathrm{o}\mathrm{u}\mathrm{t}\mathrm{h}\, \mathrm{E}\mathrm{n}\mathrm{g}\mathrm{i}\mathrm{n}\mathrm{e}\mathrm{e}{\mathrm{r}}^{\prime}\mathrm{s}\, \mathrm{o}\mathrm{p}\mathrm{i}\mathrm{n}\mathrm{i}\mathrm{o}\mathrm{n}.$$

$${D}^{2}=\left(\begin{array}{cccc}.& {R}_{1}& {R}_{2}& {R}_{3}\\ {C}_{1}& <\mathrm{1,\,3},\,\mathrm{5,\,7};\,\mathrm{0.5,\,1.5,\,2.5,\,3.5};\,\mathrm{2,\,4},\,\mathrm{6,\,8}>& <\mathrm{2,\,4},\,\mathrm{5,\,6};\,\mathrm{1.5,\,2.5,\,3.5,\,5.5};\,\mathrm{4,\,5},\,\mathrm{7,\,8}>& <\mathrm{1,\,2},\,\mathrm{3,\,4};\,\mathrm{0.5,\,1},\,\mathrm{2.5,\,3};\,\mathrm{0.8,\,1.5,\,2.5,\,5}>\\ {C}_{2}& <\mathrm{2.5,\,4.5,\,6.5,\,8.5};\,\mathrm{1,\,3},\,\mathrm{5,\,7};\,\mathrm{5,\,6},\,\mathrm{7,\,9}>& <\mathrm{1.5,\,2.5,\,3.5,\,5};\,\mathrm{1,\,2},\,\mathrm{3,\,5};\,\mathrm{2.5,\,3.5,\,6},\,7>& <\mathrm{1,\,4},\,\mathrm{7,\,9};\,\mathrm{0.5,\,2},\,\mathrm{3,\,5};\,\mathrm{3.9,\,5.5,\,7.5,\,9}>\\ {C}_{3}& <\mathrm{1.5,\,2},\,\mathrm{3,\,4.5};\,\mathrm{1,\,2},\,\mathrm{3,\,4};\,\mathrm{2.5,\,3},\,\mathrm{5,\,7}>& <\mathrm{1,\,4},\,\mathrm{7,\,9};\,\mathrm{0.5,\,1.5,\,3},\,5;\,\mathrm{3.5,\,5.5,\,7.5,\,9.5}>& <\mathrm{1,\,5},\,\mathrm{9,\,13};\,\mathrm{0.6,\,2},\,\mathrm{6,\,8};\,\mathrm{2,\,6},\,\mathrm{9.5,\,11}>\end{array}\right),$$

$$\mathrm{L}\mathrm{i}\mathrm{t}\mathrm{t}\mathrm{l}\mathrm{e}\, \mathrm{E}\mathrm{x}\mathrm{p}\mathrm{e}\mathrm{r}\mathrm{i}\mathrm{e}\mathrm{n}\mathrm{c}\mathrm{e}\mathrm{d}\, \mathrm{E}\mathrm{n}\mathrm{g}\mathrm{i}\mathrm{n}\mathrm{e}\mathrm{e}{\mathrm{r}}^{\prime}\mathrm{s} \,\mathrm{O}\mathrm{p}\mathrm{i}\mathrm{n}\mathrm{i}\mathrm{o}\mathrm{n}.$$

$${D}^{3}=\left(\begin{array}{cccc}.& {R}_{1}& {R}_{2}& {R}_{3}\\ {C}_{1}& <\mathrm{2,\,4},\,\mathrm{6,\,8};\mathrm{1.5,\,3.5,\,5.5,\,7.5};\,\mathrm{4,\,6},\,\mathrm{8,\,10}>& <\mathrm{1.5,\,3.5,\,5},\,7;\,\mathrm{1,\,3},\,\mathrm{5,\,6};\,\mathrm{2.5,\,4},\,\mathrm{6,\,8}>& <\mathrm{1,\,2},\,\mathrm{3,\,4};\,\mathrm{0.5,\,1},\,\mathrm{2,\,3.5};\,\mathrm{1.2,\,3},\,\mathrm{4,\,5.5}>\\ {C}_{2}& <\mathrm{1,\,2},\,\mathrm{3,\,4};\,\mathrm{0.5,\,1.5,\,2.5,\,3.5};\,\mathrm{1.3,\,2.3,\,3.3,\,5}>& <\mathrm{1,\,3},\,\mathrm{5,\,7};\,\mathrm{1.5,\,3},\,\mathrm{5,\,8};\,\mathrm{3.5,\,5},\,\mathrm{7,\,8.5}>& <\mathrm{1,\,4},\,\mathrm{7,\,9};\,\mathrm{0.4,\,2},\,\mathrm{4,\,6};\,\mathrm{2,\,5},\,\mathrm{7.5,\,9.5}>\\ {C}_{3}& <\mathrm{0.5,\,1},\,\mathrm{2,\,3.5};\,\mathrm{0.3,\,1},\,\mathrm{1.5,\,2.5};\,\mathrm{1.5,\,3},\,\mathrm{4,\,5}>& <\mathrm{0.3,\,2},\,\mathrm{4.3,\,6};\,\mathrm{1,\,2},\,\mathrm{3,\,4};\,\mathrm{1.2,\,3.4,\,5},\,7>& <\mathrm{1,\,3},\,\mathrm{5,\,7};\,\mathrm{0.6,\,2.6,\,3.6,\,6};\,\mathrm{2.5,\,5},\,\mathrm{6,\,8}>\end{array}\right),$$

$$\mathrm{H}\mathrm{i}\mathrm{g}\mathrm{h}\mathrm{l}\mathrm{y}\, \mathrm{E}\mathrm{x}\mathrm{p}\mathrm{e}\mathrm{r}\mathrm{i}\mathrm{e}\mathrm{n}\mathrm{c}\mathrm{e}\mathrm{d}\, \mathrm{E}\mathrm{n}\mathrm{g}\mathrm{i}\mathrm{n}\mathrm{e}\mathrm{e}{\mathrm{r}}^{\prime}\mathrm{s} \,\mathrm{O}\mathrm{p}\mathrm{i}\mathrm{n}\mathrm{i}\mathrm{o}\mathrm{n}.$$

Step 2: Formulation of weighted decision matrix

$$M=\left(\begin{array}{cccc}.& {R}_{1}& {R}_{2}& {R}_{3}\\ {C}_{1}& <\mathrm{1.37,\,3.07,\,4.77,\,6.47};\,\mathrm{0.87,\,2.15,\,3.61,\,4.83};\,\mathrm{2.53,\,4.23,\,5.99,\,7.69}>& <\mathrm{1.52,\,3.81,\,5.30,\,7.27};\,\mathrm{1.01,\,2.83,\,4.80,\,6.43};\,\mathrm{3.29,\,4.93,\,6.78,\,8.60}>& <\mathrm{1.00,\,2.90},\, \mathrm{4.20,\,5.50};\,0.53,\, 1.30,\, 2.76,\, 4.08;\,\mathrm{1.30,\,2.95,\,4.25,\,6.53}>\\ {C}_{2}& <1.[34],\, \mathrm{2.82,\,4.15,\,5.48};\,\mathrm{0.66,\,1.84,\,3.32,\,4.50};\,\mathrm{2.58,\,3.73,\,4.88,\,6.47}>& <\mathrm{1.46,\,3.13,\,4.80,\,6.64};\,1.33,\, \mathrm{2.46,\,3.89,\,6.11};\,\mathrm{3.02,\,4.50,\,6.67,\,8.15}>& <\mathrm{1.15,\,3.55,\,5.95,\,7.65};\,\mathrm{0.61,\,2.00,\,3.37,\,5.07};\,\mathrm{2.62,\,4.56,\,6.45,\,8.28}>\\ {C}_{3}& <\mathrm{0.98,\,2.23,\,3.83,\,5.48};\,\mathrm{0.74,\,1.63,\,2.44,\,3.74};\,\mathrm{2.28,\,3.60,\,5.23,\,6.86}>& <\mathrm{0.89,\,2.81,\,4.95,\,6.54};\,\mathrm{0.83,\,1.83,\,3.00,\,4.33};\,2.19,\, \mathrm{3.97,\,5.52},\, 7.52 >& <\mathrm{1.00,\,3.36,\,6.02,\,8.68};\,\mathrm{0.57,\,1.92,\,4.21,\,6.06};\,\mathrm{2.48,\,5.03,\,6.85,\,8.69}>\end{array}\right).$$

Step 3: Formulation of priority matrix

$$M=\left(\begin{array}{c}<\mathrm{1.25,\,2.72},\, 4.26,\, 5.82;\, \mathrm{0.76,\,1.88},\, 3.14 ,\,4.37;\,\mathrm{2.46,\,3.86,\,5.38,\,7.02} >\\ < \mathrm{1.29,\,3.26,\,5.02,\,6.82};\,\mathrm{1.06,\,2.39,\,3.92,\,5.65};\,\mathrm{2.85,\,4.48,\,6.34,\,8.10}>\\ <\mathrm{1.04,\,3.26,\,5.35,\,7.22};\,\mathrm{0.57,\,1.73,\,3.42,\,5.04};\,\mathrm{2.11,\,4.15,\,5.81,\,7.80}>\end{array}\right).$$

Step 4: Ranking

Now, the de-bipolarization technique for the crispification of TrBNN has been performed here to get the final ideal D.M as,

$$M=\left(\begin{array}{c}<7.15>\\ <8.53>\\ <7.91>\end{array}\right).$$

Thus, the computed ranking order is $7.15<7.91<8.53$. So, ordering of the cloud service is pointed out as ${C}_{2}>{C}_{3}>{C}_{1}$.

Sensitivity analysis (SA)

In general, sensitivity analysis of a MCGDM problem shows ranking order of the alternatives in different situations. A sensitivity analysis is performed to recognize how weights of the attribute of every criterion changing the computed matrix and their ordering. The fundamental idea of SA is to swap weights of the attributes keeping the others term are fixed. The lower table is the assessment table which illustrate the SA results in distinct cases (Figs. 11, 12).

Fig. 11

Sensitivity analysis table on attribute function

Fig. 12

Best alternative cloud service table

Attribute weight	Final decision matrix	Ordering
< ($\mathrm{0.35,\,0.33,\,0.32})$>	$\left(\begin{array}{c}<7.15>\\ <8.53>\\ <7.91>\end{array}\right)$	${C}_{2}>{C}_{3}>{C}_{1}$
< ($\mathrm{0.33,\,0.33,\,0.34})$>	$\left(\begin{array}{c}<7.12>\\ <8.49>\\ <7.97>\end{array}\right)$	${C}_{2}>{C}_{3}>{C}_{1}$
< ($\mathrm{0.4,\,0.33,\,0.27})$>	$\left(\begin{array}{c}<7.22>\\ <8.64>\\ <7.77>\end{array}\right)$	${C}_{2}>{C}_{3}>{C}_{1}$
< ($\mathrm{0.3,\,0.4,\,0.3})$>	$\left(\begin{array}{c}<7.12>\\ <8.53>\\ <8.02>\end{array}\right)$	${C}_{2}>{C}_{3}>{C}_{1}$
< ($\mathrm{0.3,\,0.3,\,0.4})$>	$\left(\begin{array}{c}<7.07>\\ <8.[34]>\\ <8.08>\end{array}\right)$	${C}_{2}>{C}_{3}>{C}_{1}$
< ($\mathrm{0.35,\,0.3,\,0.35})$>	$\left(\begin{array}{c}<7.14>\\ <8.50>\\ <7.94>\end{array}\right)$	${C}_{2}>{C}_{3}>{C}_{1}$
$<\left(\mathrm{0.33,\,0.35,\,0.32}\right)>$	$\left(\begin{array}{c}<7.14>\\ <8.53>\\ <7.97>\end{array}\right)$	${C}_{2}>{C}_{3}>{C}_{1}$
$<\left(\mathrm{0.25,\,0.4,\,0.35}\right)>$	$\left(\begin{array}{c}<7.05>\\ <8.43>\\ <8.12>\end{array}\right)$	${C}_{2}>{C}_{3}>{C}_{1}$
$<\left(\mathrm{0.35,\,0.25,\,0.4}\right)>$	$\left(\begin{array}{c}<7.12>\\ <8.44>\\ <7.97>\end{array}\right)$	${C}_{2}>{C}_{3}>{C}_{1}$
$<\left(\mathrm{0.3,\,0.35,\,0.35}\right)>$	$\left(\begin{array}{c}<7.10>\\ <8.46>\\ <8.06>\end{array}\right)$	${C}_{2}>{C}_{3}>{C}_{1}$
$<\left(\mathrm{0.35,\,0.35,\,0.3}\right)>$	$\left(\begin{array}{c}<7.17>\\ <8.57>\\ <7.91>\end{array}\right)$	${C}_{2}>{C}_{3}>{C}_{1}$

Remarks: From the above sensitivity analysis table, it can be observed that for different values of attribute functions, ultimately ${C}_{2}$ becomes the best cloud service provider in all cases although rest of the others changed their positions according to different conditions. The above two graphs are represents the sensitivity analysis results in dissimilar cases.

Comparison table

In this section, we compared this proposed work with the established works proposed by the researchers [32, 36, 41, 42, 46, 60] to find the best cloud service among those three and it is noticed that in each cases ${C}_{2}$ becomes the best cloud service provider. The comparison table is shown as below:

Established methods	Ranking
Deli [36]	${C}_{2}>{C}_{3}>{C}_{1}$
Aslam [32]	${C}_{2}>{C}_{3}>{C}_{1}$
Ulucay [41]	${C}_{2}>{C}_{3}>{C}_{1}$
Wang [42]	${C}_{2}>{C}_{3}>{C}_{1}$
Jana [46]	${C}_{2}>{C}_{1}>{C}_{3}$
Garg [60]	${C}_{2}>{C}_{1}>{C}_{3}$
Our proposed method	${C}_{2}>{C}_{3}>{C}_{1}$

Conclusion and future research scope

In this current epoch, the theory of bipolarity and its extension are widely applied in the field of mathematical modeling and engineering oriented technical problems. In this article, the conception of trapezoidal bipolar neutrosophic set is pragmatic, fascinating and has an important practical application in present-day research domain. Moreover, we formulated the concept of both linear and non-linear TrBNN along with generalized TrBNN and its graphical significance in neutrosophic arena. The construction of disjunctive categories of TrBNN according to membership component’s dependency and non-dependency plays a fundamental impact in real life. Furthermore, establishment of de-bipolarization skill utilizing removal area technique gave an additional weight in Crispification method. Also, we consider a cloud computing-based MCGDM problem associated with different decision makers from disjunctive domain in TrBNN environment. To resolve this MCGDM problem we utilized different operators of TrBNN and applied the established de-bipolarization skill for ordering of the alternatives. Additionally, a sensitivity analysis is performed in MCGDM problem considering different kinds of weight in place of attribute functions. Lastly, we performed a comparison analysis with several established methods and generate the comparison table which indicates the different ranking order in distinct cases.

In future, researchers can apply this valuable conception of TrBNN in disjunctive fields like pattern recognition problem, image-processing, big-data analysis, circuit theory problem, medical diagnoses problem and other mathematical modeling etc. Also, the crispification value can be applied in various realistic problems. Additionally, several new mathematical models can be formulated using the help of TrBNN classification and its non-linear cases. This remarkable concept will help researchers to counter a plethora of realistic problems in TrBNN arena.