1 Introduction

The present-day, thin-walled structures are frequently made of composite materials. The main reason is that they are becoming progressively stronger, lighter or less expensive, compared to traditional materials such as steel or aluminium. Hence, a composite material made of a polymer matrix reinforced with fibres (FRP) may be applied in the branches of civil engineering, ship structures, transportation industry and more.

The fibres are usually glass, carbon, aramid or basalt, and other fibre materials, e.g. paper, wood or asbestos are also applied. The polymer matrix is usually epoxy, vinyl ester or polyester thermosetting plastic. The orientation of reinforcing fibres affects strength and resistance to deformation of the polymer (the properties of composites). Unidirectional, bidirectional or random categories of composites, with respect to fibre alignment, are possible. Unidirectional composites show the greatest strength of all composites, while load is aligned with the fibres; in other directions, their strength decreases considerably depending on the matrix material. In the case of bidirectional composites, ultimate strength is lower than in the case of unidirectional composites, but if occurs in two directions; thus, the properties are more uniform in all loading directions. In the case of the random distribution of fibres, the parameters depend on fibre arrangement; in this case, material has usually the lowest strength. The strength of the material does not only depend on the orientation of the fibres but also on density of fibres in the matrix.

Therefore, it is worth to consider the influence of variation of fibre density on the variation of selected static or geometric parameters, e.g. the critical force, the frequency of free vibrations and others. Such a research problem generally comes down to determining derivative (variation) of quantities structural behaviour due to design parameters. Two approaches can be naturally distinguished: the first, variational, considering a structure as a continuous medium, and the second, discrete, dealing with sensitivity of a discretized structure. The first approach is applied in the paper. A comprehensive discussion and review of sensitivity analysis and optimization methods can be found in the publications [1,2,3, 9,10,11, 14, 18].

Fig. 1
figure 1

Geometry of the I-beam and state of displacement

Full size image

The application of unidirectional fibre-reinforced laminate structures in engineering increases due to their mechanical and economic advantages [4, 5, 12, 20]. In structural design, the constraints related to frequencies of free vibrations can be taken into account. If the constraints on frequency are not fulfilled, re-analysis is necessary to redirect the value in the admissible region. Here, dynamic re-analysis of structures with updated design variables may be replaced by sensitivity analysis of frequencies. Moreover, the results of sensitivity analysis lead to the advantageous region the design variable change, determining its necessary variations. The paper deals with the first-order sensitivity analysis of free torsional vibration frequencies of thin-walled beams of bisymmetric cross section made of unidirectional fibre-reinforced laminate subjected to axial end loads. The design variables undergoing variations are cross-sectional dimensions, (excluding cross-sectional height) and the properties of a laminate material. The beam behaviour is described according to the classical thin-walled members of non-deformable cross section [21]. Homogenization modelling of a laminate material [19] is based on the theory of mixtures cells. The first variation of free torsional vibration frequencies with respect to variations of the design variation is derived by means of variational calculus [6, 7, 13]. A numerical example of the paper deals with a simply supported I-beam. Here, fibre volume fraction is assumed the design variable under investigation. Sensitivity analysis of accuracy is discussed and compared with re-analysis results of the beam with updated parameters. The paper continues the prior research included in the paper [15].

2 First variation of free torsional vibration

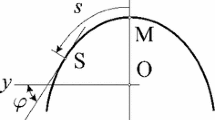
Consider free torsional vibrations of an axially loaded thin-walled I-beam of bisymmetric cross section made of unidirectional fibre-reinforced laminate presented in Fig. 1. It is well known that the flexural and torsional vibrations for these kinds of cross sections are independent [21]. The torsional vibrations are described according to the classical theory of thin-walled beams of non-deformable cross section [21]. The analysis is focused on the single natural frequencies. The Cartesian coordinate system shown in Fig. 1 defines the z-axis representing the beam longitudinal axis and x- and y-axes representing cross-sectional symmetry axes.

The model of laminate material behaviour after homogenization procedure based on the theory of mixtures cells is represented by the following relations:

$$\begin{aligned}&m=m_\mathrm{m}(1-f)+m_\mathrm{f} f\nonumber \\&E_\mathrm{l}=E_\mathrm{m}(1-f)+E_\mathrm{f} f \nonumber \\&E_\mathrm{t}=E_\mathrm{m}\frac{E_\mathrm{m}(1-\sqrt{f})+E_\mathrm{f} \sqrt{f}}{E_\mathrm{m}[1-\sqrt{f}(1-\sqrt{f})]+E_\mathrm{f} \sqrt{f}(1-\sqrt{f})} \nonumber \\&G=G_\mathrm{m}\frac{G_\mathrm{m}\sqrt{f}(1-\sqrt{f})+G_\mathrm{f}[1-\sqrt{f}(1-\sqrt{f})]}{G_\mathrm{m} \sqrt{f}+G_\mathrm{f}(1-\sqrt{f})}\nonumber \\&v=v_\mathrm{m}(1-\sqrt{f})+v_\mathrm{f} \sqrt{f}, \end{aligned}$$
(1)

where \(E_\mathrm{l}\) , \(E_\mathrm{t}\)—Young’s moduli in longitudinal and transverse directions, \(E_\mathrm{m}\), \(E_\mathrm{f}\)—Young’s moduli of matrix and fibres, G—homogenized shear modulus, v—Poisson’s ratio in longitudinal direction, \(v_\mathrm{m}\), \(v_\mathrm{f}\)—Poisson’s ratios of matrix and fibres, and f—fibre volume fraction, m—homogenized mass density, \(m_\mathrm{m}\), \(m_\mathrm{f}\)—mass density of matrix and fibre.

In the plane stress case, the modified elastic modulus \(D_\mathrm{l}\) in longitudinal direction is assumed in the form [19]

$$\begin{aligned} D_\mathrm{l}=\frac{E_\mathrm{l}}{1-\frac{E_\mathrm{t}}{E_\mathrm{l}}v^2}. \end{aligned}$$
(2)

The total potential energy of the beam length L subjected to the axial end loads P covers the warping stress energy (first term), the free torsion energy (second term) and the potential energy of the end axial loads (last term) [17]:

$$\begin{aligned} V=\frac{1}{2}\int _0^L\Big (D_\mathrm{l} J_{\omega }\theta ''^2+GJ_d\theta '^2-P r_0^2 \theta '^2\Big )\mathrm{d}z, \end{aligned}$$
(3)

where \(\theta \)—rotation of a cross section, \(J_{\omega }\)—warping moment of inertia of a cross section, \(J_d\)—free torsion moment of inertia, \(r_0^2=J_0/A\)—square of radius of gyration, \(J_0\)—radial moment of inertia, A—cross section area, (...)\('\)=d(...)/dz and (...)\(''\)—first and second derivatives with respect to axial coordinate z.

Kinetic energy T of a homogeneous beam of mass density m is

$$\begin{aligned} T=\frac{1}{2}m \int _0^L \Big (J_0 {\dot{\theta }}^2+J_{\omega }{\dot{\theta }}'^2 \Big )\mathrm{d}z. \end{aligned}$$
(4)

Here, the upper dot represents time derivative. (For more details, see [17, 22] and [16].)

The harmonic torsional vibration of the beam can be written as

$$\begin{aligned} \theta (z,t)=\phi (z)\sin \theta t, \end{aligned}$$
(5)

where \(\phi (z)\)—mode of torsional vibration, and \(\theta \)—frequency of free torsional vibration.

The sum of potential and kinetic energy parts for a conservative system is constant; thus, applying Eq. (5) in (4) and (3) it is easy to prove that the maximum values of both energy components should be equal:

$$\begin{aligned} V_\mathrm{{max}}=T_\mathrm{{max}}, \end{aligned}$$
(6)

where \(V_\mathrm{{max}}\)—maximum total potential energy and \(T_\mathrm{{max}}\)—maximum kinetic energy corresponding to the vibration mode. The equivalence relation of these energies expressed in the vibration mode \(\phi (z)\) may be written as

$$\begin{aligned} \int _0^L\Big [D_\mathrm{l} J_{\omega }\phi ''^2+GJ_d\phi '^2-Pr_0^2\phi '^2-\omega ^2m\Big (J_0\phi ^2+J_{\omega }\phi '^2 \Big )\Big ]\mathrm{d}z=0. \end{aligned}$$
(7)

The Euler necessary condition for stationary total energy represented by the left-hand side of Eq. (7) leads to the differential equation:

$$\begin{aligned} \big (D_\mathrm{l} J_{\omega } \phi ''\big ){''}+\Big [\Big (Pr_0^2-GJ_d+\omega ^2m J_{\omega } \Big ) \phi ' \Big ]'-\omega ^2m J_0 \phi =0 \end{aligned}$$
(8)

together with boundary conditions at the both beam ends

$$\begin{aligned}&\Big \{\big (D_\mathrm{l} J_{\omega } \phi ''\big )'+\Big (Pr_0^2-GJ_d+\omega ^2m J_{\omega } \Big ) \phi ' \Big \}\delta \phi \Big |_0^L=0\nonumber \\ \text {or}\nonumber \\&\big (D_\mathrm{l} J_{\omega } \phi ''\big )\delta \phi '\Big |_0^L=0. \end{aligned}$$
(9)

The solution of Eq. (8) leads to free torsional vibration frequencies and eigenmodes.

It should be noted that the differential equation (8) is valid for a beam of bisymmetric variable cross section excluding its height.

Let us consider a perturbation \(\mathrm{d}s\) of an arbitrary design variable s. The dimensions of the cross section and the material properties are assumed design variables. In order to derive the first variation of the square of the natural frequency with respect to the variation \(\mathrm{d}s\), the first variation of the functional (7) is computed

$$\begin{aligned}&\int _0^L\Big \{\big (D_\mathrm {l} J_{\omega } \big ),_s \phi ''^2+\Big [\big (GJ_d\big ),_s-\big (Pr_0^2\big ),_s-\big (\omega ^2mJ_{\omega }\big ),_s \Big ]\phi '^2+\ldots \nonumber \\&\quad -\big (\omega ^2mJ_0\big ),_s\phi ^2 \Big \}\delta s \mathrm {d}z+\ldots \nonumber \\&\quad -2\int _0^L\Big [D_\mathrm {l}J_{\omega }\phi ''\delta \phi '',_s+\big (GJ_d-Pr_0^2-\omega ^2mJ_{\omega } \big )\phi '\delta \phi ',_s+\ldots \nonumber \\&\quad -\omega ^2mJ_0\phi \phi ,_s \Big ]\mathrm {d}s \mathrm {d}z, \end{aligned}$$
(10)

where \((\ldots ),_s\)—first partial derivative of \((\ldots )\) with respect to the design variable s. The latter integral in Eq. (10) expresses the virtual work of the internal forces on arbitrary virtual displacements, due to the virtual work theorem it equals zero. The last two terms in the first integral can be rewritten as

$$\begin{aligned} (\omega ^2mJ_{\omega }),_s\delta s= & {} mJ_{\omega }(\omega ^2),_s\delta s+\omega ^2(mJ_{\omega }),_s\delta s =\ldots \nonumber \\= & {} mJ_{\omega }\delta (\omega ^2)+\omega ^2(mJ_{\omega }),_s\delta s \nonumber \\ (\omega ^2mJ_{0}),_s\delta s= & {} {} mJ_{0}(\omega ^2),_s\delta s+\omega ^2(mJ_{0}),_s\delta s =\ldots \nonumber \\= & {} mJ_{0}\delta (\omega ^2)+\omega ^2(mJ_{0}),_s\delta s. \end{aligned}$$
(11)

Substituting Eq. (11) into the integral (10), the variation of the square frequency reads

$$\begin{aligned} \delta \big (\omega ^2\big )=\frac{\int _0^L\left\{ \begin{array}{ll} (D_\mathrm{l} J_{\omega }),_s\phi ''^2+\ldots \\ +\Big [(GJ_d),_s-(Pr_0^2),_s-\omega ^2(m J_{\omega }),_s \Big ]\phi '^2+\ldots \\ -\omega ^2(mJ_0),_s\phi ^2 \end{array}\right\} \delta s \mathrm{d}z}{\int _0^Lm\big (J_0\phi ^2+J_{\omega }\phi '^2\big )\mathrm{d}z} \end{aligned}$$
(12)

or

$$\begin{aligned} \delta (\omega ^2)=\int _0^L F(z)\delta s(z)\mathrm{d}z. \end{aligned}$$
(13)

The integrated function F(z) represents variation of square frequency of torsional vibrations due to a variation of the design variable \(\delta s(z)\) in the cross section z. Distribution of the function F(z) can be stated analytically or numerically by means of the finite element method.

Table 1 Material properties for matrix, fibres and composite for \(f=5\), 50 and 95%
Full size table
Table 2 Geometrical characteristics of the I-section (\(L=3\) m, \(b=0.1\) m, \(h=0.2\) m, \(t_0=0.003\) m) (Fig. 1)
Full size table

3 Numerical examples

Consider a simply supported thin-walled I-beam of constant cross section made of unidirectional fibre-reinforced laminate, shown in Fig. 1. Material and geometric parameters of the cross section are shown in Tables 1 and 2. The squares of free torsional vibration frequencies result from the differential equation (13), substituting the vibration mode fulfilling simply supported system boundary conditions:

$$\begin{aligned}&\phi _n(z)=B\sin \Big (\frac{n \pi }{L}z \Big ) \end{aligned}$$
(14)
$$\begin{aligned}&\omega ^2=\frac{D_\mathrm{l} J_{\omega }\Big (\frac{n \pi }{L}\Big )^2+GJ_d-Pr_0^2}{m\Big [ J_{\omega }+J_0\Big (\frac{L}{n \pi } \Big )^2\Big ]}. \end{aligned}$$
(15)

The fibre volume fraction arbitrary variable along the column axis is assumed to be the parameter undergoing variation \(s=f\). Thus, the sensitivity function of the square free torsional vibration frequency arrives at

$$\begin{aligned} F_{\omega ^2,f}=\frac{\Big [D_{l,f}J_{\omega }\phi ''^2+\big (G_{,f}J_d-\omega ^2m_{,f}J_{\omega }\big )\phi '^2-\omega ^2m_{,f}J_0\phi ^2 \Big ]}{\int _0^L m\big ( J_0\phi ^2+J_{\omega }\phi '^2\big )\mathrm{d}z}. \end{aligned}$$
(16)
Table 3 Square free torsional vibration frequency \(\omega ^2\) for \(n=1\) and \(f=5\), 50, 95% (\(L=3\) m, \(b=0.1\) m, \(h=0.2\) m, \(t_0=0.003\) m) (Fig. 1)
Full size table
Fig. 2
figure 2

Geometry of a 3D FEM model (boundary conditions, load) and its investigated torsional vibration mode

Full size image
Fig. 3
figure 3

Sensitivity functions of square free torsional vibration frequency related to the fibre volume fraction parameter f (from 5 to 95%) along the I-beam axis, the axial end loads \(P=-50, 0, 50\, \hbox {kN}\), the number of half-waves a\(n=1\) and b\(n=2\)

Full size image
Fig. 4
figure 4

Sensitivity functions of square free torsional vibration frequency related to the axial ends load P, the fibre volume fraction parameters a\(f=5\)%, b 50% and c 95% along the I-beam axis, number of the half-waves \(n=1\)

Full size image
Fig. 5
figure 5

Sensitivity functions of square free torsional vibration frequency related to the axial ends load P, the fibre volume fraction parameters \(f=5, 50\) and 95% along the I-beam axis, number of the half-waves \(n=1\) in section \(\gamma -\gamma \) (Fig. 4)

Full size image
Fig. 6
figure 6

Sensitivity functions of square free torsional vibration frequency relative to \(\omega _0^2\) (at \(P=0\), \(f=50\%\): \(\omega _0^2=78,936.5\) (rad/s)\(^2\), see Table 3) (15) with regard to axial ends load P, the fibre volume fraction parameters a\(f=5\%\), b\(f=50\%\), c\(f=95\%\) along the I-beam axis number of half-waves \(n=\)1

Full size image

The analytical solutions are compared with the FEM numerical results. Numerical analysis is conducted by means of ABAQUS software [8]. The idea of the FEM models is presented in Fig. 2. The I-beams are modelled by shell elements—S4R (\(0.01\times 0.01~\hbox {m}^2\)), i.e. 40 elements along an entire cross section. The total number of elements in all models is equal to 12,000. The material is modelled by a lamina-type procedure available in ABAQUS [8]. Numerical analysis is performed in two steps. In the first step static, general analysis is carried out; the next, second step covers frequency analysis. In both steps, nonlinear effect of large deformations and displacements is taken into account. The values of material parameters are shown in Table 1. The I-beams are regarded as members without load or under axial compression or tension load P due to different load values: \(P=-5 \,\hbox {kN}\) (tension) or 5 kN (compression), in the case of the analytical solution ranging from \(-50\) to 50 kN.

Fig. 7
figure 7

First-order sensitivity analysis solution compared with the FEM numerical result of square free torsional vibration frequencies, relative to \(\omega _0^2\) (at \(P=0\), \(f=50\%\): \(\omega _0^2\)=78,936.5 (rad/s)\(^2\), see Table 3) (15) of an I-beam a under axial compressive load \(P=5\,\hbox {kN}\)b without any axial load, c under tensile load \(P=-5\,\hbox {kN}\), with regard to fibre volume fraction parameters, the number of half-waves \(n=1\)

Full size image

The results of analytical and numerical analyses are shown in Table 3 and in Figs. 3, 4, 5, 6 and 7. Table 3 compares two solutions of square free vibration frequency, i.e. the analytical solution (15) proposed in the paper with the FEM solution for three different axial loads. Figures 3, 4 and 5 show sensitivity functions of square free vibration frequency (16) with regard to fibre volume fraction parameter f along the I-beam axis in the case of axial tensile and compressive end loads and without a load, considering two different numbers of half-waves \(n=1\) and 2. Furthermore, Fig. 6 shows relative values of sensitivity functions of square free torsional vibration frequency, related to the axial end load P regarding different fibre volume fraction parameters a) \(f=5\%\), b) \(f=50\%\), c) \(f=95\%\) along the I-beam axis due to a number of half-waves \(n=1\). Figure 7 show the main solutions, i.e. first-order sensitivity analysis compared with the FEM based due to a relative values of square free torsional vibration frequency function of the I-beam under axial loads depending on the fibre volume fraction parameters, regarding number of the half-waves \(n=1\).

The numerical analysis carried out indicates high convergence of the results of analytical and numerical approaches. The differences between solutions remain at an average level of 10%.

Furthermore, it should be indicated that:

  • the square free torsional vibration frequency increases with the fibre volume rise in a composite material; it decreases while the fibre volume fraction in the material is reduced (see Table 3),

  • the difference between analytical and numerical solutions is directly proportional to the homogeneity extent of the composite material, i.e. in the case of a highly homogeneous material the differences are smaller; oppositely, while material is more heterogeneous the differences are greater (Table 3),

  • the influence of compressive or tensile forces on the square free torsional vibration frequency is negligible, as shown in the results presented in Figs. 3 and 7,

  • the numerical analysis indicates that square free torsional vibration frequency with regard to fibre volume is weakly nonlinear; thus, the first-order sensitivity analysis (linear solution) is a suitable approximation (with an accuracy of 10–15%) of the solution, ranging from 20 to 80% of the fibre volume fraction (Fig. 7).

4 Conclusions

The paper deals with the first-order sensitivity analysis of the square free torsional vibration with regard to the fibre volume. Analytical solution of the problem is investigated and compared with the FEM solution. The first-order sensitivity analysis proves a sufficient approximation of the numerical FEM solution. The proposed analytical solution based on classical theory of thin-walled beams of non-deformable cross sections, taking into account the warping effect, showed its validity in the analysis of such a kind of structures. The differences between compared solutions, the FEM solution and a linear approach to the sensitivity analysis are acceptable from an engineering point of view, remaining at an average level of 10%. Finally, it should be emphasized that the proposed simplified solution based on the sensitivity analysis seems a useful tool in the optimal design or the analysis of beams with variable cross sections and mechanical properties of the beam material.