Skip to main content
SpringerLink
Log in

A semi-implicit finite difference scheme for the multi-term time-fractional Burgers-type equations

  • Original Research
  • Published:
Journal of Applied Mathematics and Computing Aims and scope Submit manuscript

Abstract

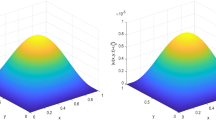
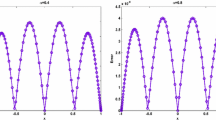
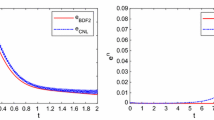
The main purpose of this paper is to construct a semi-implicit difference scheme for the multi-term time-fractional Burgers-type equations. Firstly, the L2-discretization formula is applied to the discretization of the multi-term Caputo fractional derivatives. Secondly, the second-order spatial derivative is approximated by using the second-order central difference quotient approximation and the nonlinear convection term \(uu_x\) is discretized via the semi-implicit method. Then, a fully discrete finite difference scheme is established. The unconditional stability and convergence in maximum-norm are derived by the discrete energy method and the mathematical induction. Numerical experiments are performed to validate the theoretical analysis.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2

Similar content being viewed by others

References

  1. Ai, Y., Wu, H.: A second-order difference scheme for Burgers’ equation with nonlinear force. Mathematica Applicata 23, 116–124 (2010)

    MathSciNet  MATH  Google Scholar 

  2. Chen, H., Xu, D.: A second-order fully discrete difference scheme for a nonlinear partial integro-differential equation (in Chinese). J. Sys. Sci. Math. Sci. 28, 51–70 (2008)

    MATH  Google Scholar 

  3. Dehghan, M., Manafian, J., Saadatmandi, A.: Solving nonlinear fractional partial differential equations using the homotopy analysis method. Numer. Meth. Part Differ. Equ. 26, 448–479 (2010)

    Article  MathSciNet  Google Scholar 

  4. Djordjevica, V.D., Atanackovic, T.M.: Similarity solutions to nonlinear heat conduction and Burgers/Korteweg-deVries fractional equations. J. Comput. Appl. Math. 222, 701–714 (2008)

    Article  MathSciNet  Google Scholar 

  5. Esen, A., Tasbozan, O.: Numerical solution of time fractional Burgers equation. Acta Univ. Sapientiae Mathematica 7, 167–185 (2015)

    Article  MathSciNet  Google Scholar 

  6. Esen, A., Tasbozan, O.: Numerical solution of time fractional Burgers equation by cubic B-spline finite elements. Mediterr. J. Math. 13, 1325–1337 (2016)

    Article  MathSciNet  Google Scholar 

  7. Garra, R.: Fractional-calculus model for temperature and pressure waves in fluid-saturated porous rocks. Phys. Rev. E 84, 036605 (2011)

    Article  Google Scholar 

  8. Hassani, H., Naraghirad, E.: A new computational method based on optimization scheme for solving variable-order time fractional Burgers’ equation. Math. Comput. Simul. 162, 1–17 (2019)

    Article  MathSciNet  Google Scholar 

  9. Inc, M.: The approximate and exact solutions of the space- and time- fractional Burgers equation with initial conditions by variational iteration method. J. Math. Anal. Appl. 345, 476–484 (2008)

    Article  MathSciNet  Google Scholar 

  10. Jiang, H., Liu, F., Turner, I., Burrage, K.: Analytical solutions for the multi-term time-fractional diffusion-wave/diffusion equations in a finite domain. Comput. Math. Appl. 64, 3377–3388 (2012)

    Article  MathSciNet  Google Scholar 

  11. Jin, B., Lazarov, R., Liu, Y., Zhou, Z.: The Galerkin finite element method for a multi-term time-fractional diffusion equation. J. Comput. Phys. 281, 825–843 (2015)

    Article  MathSciNet  Google Scholar 

  12. Keller, J.J.: Propagation of simple nonlinear waves in gas-filled tubes with friction. Z. Angew. Math. Phys. 32, 170–181 (1981)

    Article  Google Scholar 

  13. Koksal, M.E., Senol, M., Unver, A.K.: Numerical simulation of power transmission lines. Chin. J. Phys. 59, 507–524 (2019)

    Article  MathSciNet  Google Scholar 

  14. Koksal, M.E.: Time and frequency responses of non-integer order RLC circuits. AIMS Math. 4, 61–75 (2019)

    Article  MathSciNet  Google Scholar 

  15. Koksal, M.E.: Stability analysis of fractional differential equations with unknown parameters. Nonlinear Anal. Model Control 24, 224–240 (2019)

    Article  MathSciNet  Google Scholar 

  16. Li, C., Zhao, Z., Chen, Y.: Numerical approximation of nonlinear fractional differential equations with subdiffusion and superdiffusion. Comput. Math. Appl. 62, 855–875 (2011)

    Article  MathSciNet  Google Scholar 

  17. Li, D., Zhang, J.: Efficient implementation to numerically solve the nonlinear time fractional parabolic problems on unbounded spatial domain. J. Comput. Phys. 322, 415–428 (2016)

    Article  MathSciNet  Google Scholar 

  18. Li, D., Zhang, C., Ran, M.: A linear finite difference scheme for generalized time fractional Burgers equation. Appl. Math. Model. 40, 6069–6081 (2016)

    Article  MathSciNet  Google Scholar 

  19. Li, D., Wu, C., Zhang, Z.: Linearized Galerkin FEMs for nonlinear time fractional parabolic problems with non-smooth solutions in time direction. J. Sci. Comput. 80, 403–419 (2019)

    Article  MathSciNet  Google Scholar 

  20. Li, L., Li, D.: Exact solutions and numerical study of time fractional Burgers’ equations. Appl. Math. Lett. 100, 106011 (2020)

    Article  MathSciNet  Google Scholar 

  21. Liu, C.: The fictitious time integration method to solve the space- and time-fractional Burgers equations. Comput. Mater. Contin. 15, 221–240 (2010)

    Google Scholar 

  22. Liu, F., Yang, C., Burrage, K.: Numerical method and analytical technique of the modified anomalous sub-diffusion equation with a nonlinear source term. J. Comput. Appl. Math. 231, 160–176 (2009)

    Article  MathSciNet  Google Scholar 

  23. López-Marcos, J.C.: A difference scheme for a nonlinear partial integro-differential equation. SIAM J. Numer. Anal. 27, 20–31 (1990)

    Article  MathSciNet  Google Scholar 

  24. Momani, S.: Non-perturbative analytical solutions of the space- and time-fractional Burgers equations. Chaos Solutions Fractals 28, 930–937 (2006)

    Article  MathSciNet  Google Scholar 

  25. Oldham, K.B., Spanier, J.: The Fractional Calculus. Academic Press, New York (1999)

    MATH  Google Scholar 

  26. Podlubny, I.: Fractional Differential Equations. Academic Press, San Diego (1999)

    MATH  Google Scholar 

  27. Qiu, W., Chen, H., Zheng, X.: An implicit difference scheme and algorithm implementation for the one-dimensional time-fractional Burgers equations. Math. Comput. Simul. 166, 298–314 (2019)

    Article  MathSciNet  Google Scholar 

  28. Qiu, W., Xu, D., Guo, J., Zhou, J.: A time two-grid algorithm based on finite difference method for the two-dimensional nonlinear time-fractional mobile/immobile transport model. Numer. Algorithms (2019). https://doi.org/10.1007/s11075-019-00801-y

    Article  MATH  Google Scholar 

  29. Sloan, I.H., Thomée, V.: Time discretization of an integro-differential equation of parabolic type. SIAM J. Numer. Anal. 23, 1052–1061 (1986)

    Article  MathSciNet  Google Scholar 

  30. Song, L., Zhang, H.: Application of homotopy analysis method to fractional Kdv–Burgers–Kuramoto equation. Phys. Lett. A. 367, 88–94 (2007)

    Article  MathSciNet  Google Scholar 

  31. Sugimoto, N.: Burgers equation with a fractional derivative; hereditary effects on non-linear acoustic waves. J. Fluid Mech. 225, 631–653 (1991)

    Article  MathSciNet  Google Scholar 

  32. Sun, Z.: Numerical Methods for Partial Differential Equations (in Chinese). Science Press, Beijing (2005)

    Google Scholar 

  33. Sun, Z., Wu, X.: A fully discrete difference scheme for a diffusion-wave system. Appl. Numer. Math. 56, 193–209 (2006)

    Article  MathSciNet  Google Scholar 

  34. Sun, H., Sun, Z.: On two linearized difference schemes for Burgers’ equation. Int. J. Comput. Math. 92, 1160–1179 (2015)

    Article  MathSciNet  Google Scholar 

  35. Tang, T.: A finite difference scheme for partial integro-differential equations with a weakly singular kernel. Appl. Numer. Math. 11, 309–319 (1993)

    Article  MathSciNet  Google Scholar 

  36. Vong, S., Lyu, P.: Unconditional convergence in maximum-norm of a second-order linearized scheme for a time-fractional Burgers-type equation. J. Sci. Comput. 76, 1252–1273 (2018)

    Article  MathSciNet  Google Scholar 

  37. Wang, Q.: Numerical solutions for fractional Kdv-Burgers equation by Adomian decomposition method. Appl. Math. Comput. 182, 1048–1055 (2006)

    MathSciNet  MATH  Google Scholar 

  38. Xu, D., Qiu, W., Guo, J.: A compact finite difference scheme for the fourth-order time-fractional integro-differential equation with a weakly singular kernel. Numer. Meth. Part Differ. Equ. 36, 439–458 (2020)

    Article  MathSciNet  Google Scholar 

  39. Yildirim, A., Mohyud-Din, S.T.: Analytical approach to space- and time-fractional Burgers equations. Chin. Phys. Lett. 27, 090501 (2010)

    Article  Google Scholar 

  40. Yokus, A., Kaya, D.: Numerical and exact solutions for time fractional Burgers’ equation. J. Nonlinear Sci. Appl. 10, 3419–3428 (2017)

    Article  MathSciNet  Google Scholar 

  41. Zhang, Y., Sun, Z., Wu, H.: Error estimates of Crank–Nicolson-type difference schemes for the subdiffusion equation. SIAM J. Numer. Anal. 49, 2302–2322 (2011)

    Article  MathSciNet  Google Scholar 

  42. Zheng, X., Qiu, W., Chen, H.: Three semi-implicit compact finite difference schemes for the nonlinear partial integro-differential equation arising from viscoelasticity. Int. J. Model. Simul. (2020). https://doi.org/10.1080/02286203.2020.1720566

    Article  Google Scholar 

Download references

Acknowledgements

The author is very grateful for the reviewers’ valuable comments and suggestions. This article is supported by the Construct Program of the Key Discipline in Hunan Province, Performance Computing and Stochastic Information Processing (Ministry of Education of China).

Author information

Authors and Affiliations

  1. Key Laboratory of Computing and Stochastic Mathematics (Ministry of Education), School of Mathematics and Statistics, Hunan Normal University, Changsha, 410081, Hunan, China

    Wen Zhang

Authors
  1. Wen Zhang
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Wen Zhang.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Zhang, W. A semi-implicit finite difference scheme for the multi-term time-fractional Burgers-type equations. J. Appl. Math. Comput. 65, 813–830 (2021). https://doi.org/10.1007/s12190-020-01416-6

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s12190-020-01416-6

Keywords

AMS Subject Classification (2020)

Search

Navigation