Explicit estimates versus numerical bounds for the electrical conductivity of dispersions with dissimilar particle shape and distribution

Abstract

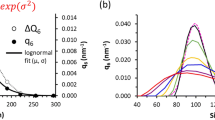
An effective-medium theory for the electrical conductivity of Ohmic dispersions taking explicit account of particle shape and spatial distribution independently is available from the work of Ponte Castañeda and Willis [J Mech Phys Solids 43:1919–1951, 1996]. When both shape and distribution take particular “ellipsoidal” forms, the theory provides analytically explicit estimates. The purpose of the present work is to evaluate the predictive capabilities of these estimates when dispersions exhibit dissimilar particle shape and distribution. To this end, comparisons are made with numerical bounds for coated ellipsoid assemblages computed via the finite element method. It is found that estimates and bounds exhibit good agreement for the entire range of volume fractions, aspect ratios, and conductivity contrasts considered, including those limiting values corresponding to an isotropic distribution of circular cracks. The fact that the explicit estimates lie systematically within the numerical bounds hints at their possible realizability beyond the class of isotropic dispersions.

Appendix: The tensor \(\mathbf{P}\) for an isotropic tensor \({\varvec{\sigma }}^{(1)}\) and an axisymmetric tensor \(\mathbf{Z}\)

Let ${\varvec{\sigma }}^{(1)} = \sigma ^{(1)} \mathbf{I}$ and $\mathbf{Z}= a_\parallel \mathbf{e} \otimes \mathbf{e} + a_\perp (\mathbf{I}- \mathbf{e} \otimes \mathbf{e})$, where $\mathbf{I}$ is the identity tensor and $\mathbf{e}$ is the unit vector indicating the direction of axial symmetry of $\mathbf{Z}$. In view of the isotropy of ${\varvec{\sigma }}^{(1)}$, the corresponding tensor $\mathbf{P}$, as given by (2), inherits the axial symmetry of $\mathbf{Z}$. Thus, we can write $\sigma ^{(1)}\mathbf{P}= P_\parallel \mathbf{e} \otimes \mathbf{e} + P_\perp (\mathbf{I}- \mathbf{e} \otimes \mathbf{e})$, where

$$\begin{aligned} P_\parallel&= \mathbf{e} \cdot \mathbf{P}\mathbf{e} = \frac{\det \mathbf{Z}}{4\pi } \int _{|{\varvec{\xi }}|=1} (\mathbf{e} \cdot {\varvec{\xi }})^2 |\mathbf{Z}{\varvec{\xi }}|^{-3} \mathrm{d}{\varvec{\xi }}=\frac{a_\parallel a_\perp ^2}{4\pi } \int _{|{\varvec{\xi }}|=1} \frac{(\mathbf{e} \cdot {\varvec{\xi }})^2}{[a_\parallel ^2 (\mathbf{e} \cdot {\varvec{\xi }})^2 + a_\perp ^2 (1-(\mathbf{e} \cdot {\varvec{\xi }})^2)]^{3/2}} \mathrm{d}{\varvec{\xi }}\nonumber \\&= \frac{w}{2} \int _0^\pi \frac{\cos ^2\varphi }{[\sin ^2\varphi +w^2\cos ^2\varphi ]^{3/2}} \sin \varphi \ \mathrm{d}\varphi \end{aligned}$$

(9)

$$\begin{aligned} P_\parallel + 2 P_\perp&= \mathrm{tr}\mathbf{P}= \frac{\det \mathbf{Z}}{4\pi } \int _{|{\varvec{\xi }}|=1} |\mathbf{Z}{\varvec{\xi }}|^{-3} \mathrm{d}{\varvec{\xi }}= 1. \end{aligned}$$

(10)

Expressions (4) follow from these.