Predicting site-specific storm wave run-up

Abstract

Storm wave run-up causes beach erosion, wave overtopping, and street flooding. Extreme runup estimates may be improved, relative to predictions from general empirical formulae with default parameter values, by using historical storm waves and eroded profiles in numerical runup simulations. A climatology of storm wave run-up at Imperial Beach, California is developed using the numerical model SWASH, and over a decade of hindcast spectral waves and observed depth profiles. For use in a local flood warning system, the relationship between incident wave energy spectra E(f) and SWASH-modeled shoreline water levels is approximated with the numerically simple integrated power law approximation (IPA). Broad and multi-peaked E(f) are accommodated by characterizing wave forcing with frequency-weighted integrals of E(f). This integral approach improves runup estimates compared to the more commonly used bulk parameterization using deep water wave height $H_0$ and deep water wavelength $L_0$ Hunt (Trans Am Soc Civ Eng 126(4):542–570, 1961) and Stockdon et al. (Coast Eng 53(7):573–588, 2006. https://doi.org/10.1016/j.coastaleng.2005.12.005). Scaling of energy and frequency contributions in IPA, determined by searching parameter space for the best fit to SWASH, show an $H_0L_0$ scaling is near optimal. IPA performance is tested with LiDAR observations of storm run-up, which reached 2.5 m above the offshore water level, overtopped backshore riprap, and eroded the foreshore beach slope. Driven with estimates from a regional wave model and observed $\beta _f$, the IPA reproduced observed run-up with $<30\%$ error. However, errors in model physics, depth profile, and incoming wave predictions partially cancelled. IPA (or alternative empirical forms) can be calibrated (using SWASH or similar) for sites where historical waves and eroded bathymetry are available.

1 Introduction

As sea level rises, high shoreline water levels will increase in frequency and severity. Total shoreline water level (TWL) contains components with wide ranges of time and space scales, including sea-level rise, climatic and seasonal cycles, tides, oceanic eddies, storm surge, and local waves (e.g., Idier et al. 2019; Woodworth et al. 2019). When several components co-occur, high TWL threatens coastal infrastructure. In northern hemisphere mid-latitudes, continental west coast TWL hazards largely come from high waves combined with high tides, rather than from tropical and extratropical storm surges important on east coasts (Rueda et al. 2017). On US West Coast beaches, wave run-up and setup are estimated to contribute more than 50% to extreme TWL (Serafin et al. 2017). In consideration of the significant impact and associated uncertainties, the wave component of TWL has been identified by the California Climate Change Assessment (Kalansky et al. 2018) as research needed for coastal management and adaptation.

The most southern city in California, Imperial Beach (IB), is historically impacted by flooding driven by coincident high waves and tides. IB lies at the tip of a once natural sand spit formed by sediment from the nearby Tijuana River (Flick 1993). To counter wave-related erosion and flooding, approximately  344,000 m$^3$ of offshore sand was added to the city’s shoreline in Fall 2012 (SANDAG 2011; Ludka et al. 2018). Despite this adaptation strategy, IB continues to experience erosion and street flooding during high waves and tides. Gallien (2016) observed and modeled a 2014 flooding event from a winter storm with moderate waves and long period swell, and found large errors in the flooding extent predicted by traditional empirical models.

We develop an IB storm wave run-up (the wave-driven component of TWL) climatology by forcing the numerical model SWASH with waves from a 17-year offshore wave hindcast, on a typical winter depth profile based on 10 years of bathymetry observations. SWASH has been extensively tested in the laboratory and field on gentle and steep slopes (e.g., Nicolae Lerma et al. 2017; Smit et al. 2014; Suzuki et al. 2017; Fiedler et al. 2018, and others). Lacking site-specific observations of storm wave run-up, we create a model runup data set to calibrate an integrated power law approximation (IPA), relating frequency-weighted integrals of the incident sea-swell spectrum to bulk runup statistics. IPA is an emulator, a numerically simple empirical model of a more complex (here SWASH) model (e.g., Reichert et al. 2011). Uncertainty in offshore boundary conditions and depth h(x) translate into IPA uncertainty. IPA can be used for runup forecasts at sites where a spectral storm wave climatology and typical eroded bathymetry are available.

Runup parameterizations are reviewed and the IPA developed in Sect. 2. The wave and bathymetry climatology, and storm wave selection, are discussed in Sect. 3. The SWASH model configuration and the key role of boundary conditions are described in Sect. 4. IPA results are discussed in Sect. 5, and compared with few hours of observed storm run-up in Sect. 6. Model uncertainty and approaches to error reduction are discussed in Sect. 7.

2 Wave runup models

2.1 Review

Runup models range from highly complex (Smoothed-Particle Hydrodynamics and Volume of Fluid solvers) to empirical equations based on bulk wave parameters. Highly accurate dynamical models solve the Reynolds-averaged Navier–Stokes (RANS) equations, with some approximations for breaking (e.g., Lara et al. 2011; Torres-Freyermuth et al. 2010). Laboratory experiments in wave flumes with known boundary conditions have demonstrated the accuracy of these advanced models, but at high computational cost, for example requiring 30 h to compute 300 s of a numerical simulation (Lara et al. 2011). Phase-resolving models solving the nonlinear shallow water (NLSW) equations include nonlinear random wave physics and are numerically faster but less exact. Despite limitations, phase resolving models have been shown to accurately simulate wave shoaling, breaking, and run-up in both the field and laboratory (e.g., Rijnsdorp et al. 2015; Pomeroy et al. 2012; Suzuki et al. 2017, and others). Although numerical models for run-up have been validated in controlled laboratory and field settings, they require information often poorly known in practical applications. For example, specification of shoreward propagating infragravity waves at the model offshore boundary, and the beach profile both above and below the water line. Empirical models, on the other end of the accuracy and ease-of-use scale, can estimate run-up using only bulk properties of incident sea and swell (wave height and period), with surfzone bathymetry h(x) characterized by at most a single foreshore or surfzone slope (e.g., Hunt 1961; Battjes 1974; Holman 1986; Stockdon et al. 2006; Gomes da Silva et al. 2020, and others). Wave effects at the shoreline are usually separated into wave setup ($\eta$, a super-elevation of the mean shoreline water level), and swash (S, the oscillatory up- and down-rush of waves). Swash is often further decomposed into two frequency bands: sea-swell (SS, 4-20 s) and infragravity (IG, 20-250 s). Assuming Gaussian distributed run-up, $\eta$, $S_{IG}$, and $S_{SS}$ are combined to estimate a wave-induced total water $R_{2\%,G}$ (the level exceeded by 2% of wave up-rushes),

$$\begin{aligned} R_{2\%,G} = \eta + S/2,~~~~ \text {where} ~~~~ S = \frac{1}{2} (S_{SS}^2 + S_{IG}^2)^{1/2} \end{aligned}$$

(1)

Total water level (TWL) superposes wave effects on SWL, the still water level without waves. In field studies, SWL is often taken as the water level observed seaward of the surfzone, so that SWL includes both tides and other processes (e.g., subtidal shelf waves) effecting coastal water levels,

$$\begin{aligned} TWL = R_{2\%,G} + SWL. \end{aligned}$$

(2)

Using video observations on 11 beaches, Stockdon et al. (2006) (hereafter S06) calibrated empirical relationships for wave runup components that depend on $\sqrt{H_0L_0}$ and $\beta _f$, where $H_0$ and $L_0= (g/2\pi ) f_p^{-2}$ are the deepwater significant wave height and wave length, respectively, g is gravity, $f_p$ is the peak frequency, and $\beta _f$ is the foreshore beach slope:

$$\begin{aligned} S_{SS}= & {} \alpha _1\beta _f (gH_0)^{1/2}f_p^{-1},\quad \eta = \alpha _2\beta _f(gH_0)^{1/2}f_p^{-1},\quad \text {and}\nonumber \\ S_{IG}= & {} \alpha _3(gH_0)^{1/2}f_p^{-1}, \end{aligned}$$

(3)

where $\alpha _1$ , $\alpha _2$, $\alpha _3$ are best-fit dimensionless constants. All 3 terms depend on $f_p^{-1}H_0^{1/2} \sim (H_0L_0)^{1/2}$, and $S_{SS}$ and $\eta$ are proportional to $\beta _f$. Substitution in (Eq. 1) with $\alpha _i$ from S06 yields

$$\begin{aligned} R_{2\%} = 1.1\left( 0.35\beta _f(H_0L_0)^{1/2} + \frac{[H_0L_0(0.563\beta _f^2+0.004)]^{1/2}}{2}\right) . \end{aligned}$$

(4)

where the factor of 1.1 corrects for non-Gaussian runup statistics. In the present work, in both observations and models, $R_{2\%,G}$ is based on swash spectra (Eq. 1) without a correction factor, and is considered a metric of extreme run-up. Individual wave run-ups, defined for example with zero upcrossings, are not considered. Equation 4 is widely used, including in the US Federal Emergency Management Authority’s flood mapping guidance (Federal Emergency Management Agency (FEMA) 2015).

Empirical formulae for run-up and setup are abundant, with many alternate forms proposed prior to and since S06. In their “non-exhaustive” list, Dodet et al. (2019) provide 10 empirical equations for setup and 17 for $R_{2\%}$. O’Grady et al. (2019) regressed 15 different empirical setup equations with observations. Gomes da Silva et al. (2020) also provide a comprehensive review of various runup and setup formulae. A commonality is the use of $S_{SS} \approx \beta _f\sqrt{H_0L_0}$ (Hunt 1961) to characterize the SS runup response to incident wave forcing (e.g., Eq. 4). There is less agreement on the functional form for $S_{IG}$ and $\eta$. Best-fit parameter values for a given model vary between beaches, and no single parameterization is uniformly superior on all beaches.

In Eq. 3, the E(f) peak frequency $f_p$ is used to estimate $L_o$, and bimodal $E_{ss}$ yield unrealistic (unstable) results when $f_p$ varies in time between the sea and swell peak. Definitions of “sea-swell frequency” based on integrals of E(f) are stable, with different definitions weighting E(f) differently via a ratio of spectral moments (e.g., O’Reilly et al. 2016; Poate et al. 2016, and others). However, $H_{0}$ is still based on combined sea and swell energy. In Sect. 2.2 below, the (generalized) spectral equivalent of $H_0L_0$ is effectively integrated over sea-swell frequencies.

Simple empirical models are necessarily scattered about observations owing to the extreme simplification of incident waves and beach parameters (e.g., Stockdon et al. 2006; Dodet et al. 2019). For example, setup $\eta$ depends on h(x) across the surfzone, and not only on $\beta _f$ (e.g., Longuet-Higgins and Stewart 1962; Stephens et al. 2011). Additionally, only bulk $H_0$ and f (peak, mean, or otherwise) appear in empirical $S_{IG}$, but $S_{IG}$ depends on incident wave frequency-directional spectra (e.g., Guza and Feddersen 2012; Ruju et al. 2019, and others). Despite these shortcomings, empirical equations have predictive skill, especially if $\alpha$ has been calibrated at the prediction beach. In this case, $\alpha _i$ is essentially tuned to the site h(x) and wave characteristics (e.g., frequency and directional spread).

2.2 Frequency-integrated power-law approximation (IPA)

A generic empirical power law form for the energy of the wave-driven components of TWL at the shoreline is

$$\begin{aligned} \,[E_{IG,SS,\eta }]_{shoreline} = \left[ \alpha \beta ^l E_{SS}^m f_{SS}^n\right] _{deep}, \end{aligned}$$

(5)

Equation 5 includes many existing empirical runup formulas as special cases. For example, with the commonly used $S_{IG} = \alpha \sqrt{H_0L_0}$ (Eq. 3), the corresponding shoreline $E_{IG} \approx S_{IG}^{2} \approx H_0L_0$ and $l=0, m=0.5, n=-2$ (Eq. 6). In S06, $S_{SS}$ depends linearly on $\beta _f$, so shoreline $E_{SS}$ has $l=2, m=0.5, n=-2$. With setup proportional to $H_0$, independent of f and $\beta$ (e.g., Guza and Thornton 1982; Ruggiero et al. 2001), $l=0, m=1/2,n=0$. Runup energy $E_{IG}$ proportional to offshore energy flux $EC_g$ (Inch et al. 2017) corresponds to $m=1,n=-1$. Ji et al. (2018) parameterized setup with $l=0.54$, $m=0.31$, and $n=-0.74$. Very low-frequency IG energy ($0.0005<f < 0.003$ Hz) observed in a harbor was best fit with $m=0.9$, and $n=-3$ near the harbor mouth (Cuomo and Guza 2017). Note for run-up $E_{IG}$ and $E_{SS}$, $\alpha$ is dimensionless only when $m=1$ and $n=0$. For setup, $\alpha$ is dimensionless when $m=1/2$ and $n=0$. The different dynamics and length scales of $S_{SS}$, $S_{IG}$, and $\eta$ can result in different (l,m,n) for each component.

Here, Eq. 5 is used in an integrated power law approximation (hereafter IPA), where

$$\begin{aligned} \left[ \int _{\eta ,IG,SS} E(f)df\right] _{shoreline} = \left[ \alpha \beta ^l\int _{SS} E^m(f) f^n df\right] _{deep}. \end{aligned}$$

(6)

Best-fit values of $\alpha , m$ and n are determined separately for each component ($\eta$, IG, and SS, Sect. 5). Values of l are either 2 or 0, following (Stockdon et al. 2006). The integral on the left side of Eq. 6 corresponds to the SWASH-modeled runup spectrum at the 10-cm water depth threshold and the right hand side uses offshore sea-swell from a regional wave model. Skill $R^2 = 1$-NMSE, where

$$\begin{aligned} NMSE = \frac{\sum _{i=1}^n (p-o)^2}{\sum _{i=1}^n (o-{\overline{o}})^2}, \end{aligned}$$

(7)

with o the observations and p the prediction.

3 Historical waves and bathymetry at Imperial Beach

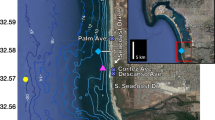
The study transect, oriented approximately East-West directly offshore of Cortez Ave (Fig. 1), is included in an ongoing long-term monthly monitoring program by Scripps Institution of Oceanography (SIO) (Ludka et al. 2019). Wave predictions for IB are available through the Coastal Data Information Program (CDIP) MOnitoring and Prediction (MOP) System (O’Reilly et al. 2016). From these data bases, we extract idealizations used in SWASH.

Fig. 1

a Location map, with MOP D0045 line (red) extending $\sim$1.2 km offshore. b overwashing of riprap (rock structures fronting condos) during the high water level on January 18, 2019. D0045 is shown in red. The image is mirrored for consistency with other subplots, such that true south appears north. Photograph: Rob Grenzeback. c Depth versus cross-shore distance on D0045; representative eroded profile (purple), typical lidar profile (red), historical eroded profiles (light gray). Dotted lines indicate tide levels and extrapolation above the rip rap ($x>45$ m ). An ADV (“PUV”) was located at $x \sim -300$ m. d Lidar-derived subaerial bed level versus cross-shore location for different times on January 18, 2019. The curve colors correspond to vertical shading in the inset. (Inset) La Jolla pier end water level (left axis, red) and foreshore slopes (blue dots, right axis) versus time

3.1 Idealized bathymetry

The Cortez Ave cross-shore transect (MOP line D0045) has been surveyed 95 times between 2008 and 2016. Observations were interpolated and smoothed (mapped) as described in Ludka et al. (2019). A typical eroded profile is defined as the average of the mapped eroded profiles (n = 26), which have a horizontal mean sea level (MSL) shoreline position landward of the mean MSL shoreline position ($x=0$ m) by 10m or more. Eroded profiles occurred before the 2012 nourishment, and a few years after nourishment. Run-up on recently nourished profiles is not considered here.

For use in the SWASH model, the average eroded profile (Fig. 1c) was extended to $h=-15$ m with constant slope ($\beta = 0.01$), and smoothed with a 50-m Gaussian filter from $x=-450$ m to −20 m, where the mean sampling is relatively coarse, and with 20-m smoothing elsewhere. The riprap above $\sim$4 m is not included in the model h(x). Instead, the beach slope at elevations greater than 4 m is extended above 4 m (thick dashed lines in Fig. 1). In doing so, the riprap is assumed to be an extension of the sandy beach; porosity, infiltration, and overtopping are not considered. Two concave up foreshore profiles are used; (1) an averaged eroded profile (average $\beta _f$=0.08), and (2) a steeper (average $\beta _f$=0.12), lidar-derived profile from a January 2019 storm. The profiles are identical from $x=-50$ m seaward (Fig. 1c).

3.2 Idealized storm waves

Spectral wave hindcasts ($f=0.04$ to 0.25 Hz) are obtained from the MOPS model (O’Reilly et al. 2016). MOPS, a linear wave propagation model, uses the CDIP buoy network to produce hourly hindcasts of coastal waves. Tides are not included. We used hourly 1D (frequency) wave spectra from January 1, 2000 to Dec 31 2017, 157,800 total hours. In Southern California, MOPS wave hindcasts are on the 10-m depth contour seaward of the typical surfzone (MOPS does not include wave breaking). MOPS simulates spatially variable island shadowing, sheltering by changing shoreline orientation, and the local effects of shallow shoals and reefs. Ideally, the linear MOPS is used for non-breaking waves over possibly 2D bathymetry seaward of the surfzone, and SWASH 1D is applied to 1D, nonlinear surfzone and run-up. For this application to the most energetic few percent of waves (Fig. 2), MOPS is used to initialize SWASH 1D in 15m depth (see Sect. 4.2). The effect of 2D bathymetry shallower than 15 m is not included. Deep water wave height $H_0$ is obtained by reverse shoaling the E(f) spectrum at 10m water depth. Deep water wavelength is $L_0=g f_c^{-2}/2\pi$, where $f_c$ is the centroid (mean) frequency,

$$\begin{aligned} f_c = \frac{\int E(f)fdf}{\int E(f)df}. \end{aligned}$$

(8)

Fig. 2

Hindcast (17 years) wave statistics in 10-m depth at Imperial Beach MOP line D0045. a counts of frequency spread (over all $\sqrt{H_0L_0}$) versus frequency spread, b mean frequency (see color bar) versus $\sqrt{H_0L_0}$ and frequency spread, c counts of $\sqrt{H_0L_0}$ (over all spreads) versus $\sqrt{H_0L_0}$, d mean frequency (see color bar) versus significant ${H_0}$ (back-refracted to deepwater) and frequency spread, e counts (over all spreads) versus $\sqrt{H_0L_0}$. The January 2019 waves (Fig. 1), star in b and d, was relatively energetic, low frequency with moderate spread. Red lines in b–e indicate the threshold used for modeled storm events ($\sqrt{H_0L_0}>25$ m, $H_0>2$ m)

Frequency spread $f_{sp}$ is used as a metric of E(f) narrow bandedness,

$$\begin{aligned} f_{sp} = \left( \frac{\int (f-f_c)^2E(f) df }{\int E(f) df}\right) ^{1/2}. \end{aligned}$$

(9)

For large offshore $\sqrt{H_0L_0}$ or $H_0$ (Fig. 2), the spread $f_{sp}$ is usually relatively small. SWASH is used to simulate run-up for the low $f_p$ (Fig. 2a) and small $f_{sp}$ typical of the largest IB winter storms. During the 17-year hindcast, less than 1% ($\sim 1427$ h) of the total have $\sqrt{H_0L_0} > 25$ m, and $\sim 2.5\%$ have $H_0 > 2$  m.

A total of 439 storm cases were selected, 295 with high $\sqrt{H_0L_0}>25$ m and an additional 144 with high $H>2$ m (and $\sqrt{H_0L_0}<25$  m). For each $\sqrt{H_0L_0}>25$ m data bin, the centroid frequencies were randomly sampled to obtain up to 20 unique values spanning the minimum to maximum observed $f_c$. The high $H_s>$ 2 m cases were binned in 0.5 m wide bins, and unique peak frequencies selected randomly from each bin, excluding the already selected cases with $\sqrt{H_0L_0}>$25 m.

4 SWASH model

4.1 Model configuration

SWASH is run in 2D mode with a narrow, 2-m alongshore mesh, effectively emulating a 1D profile but with more detail resolved by the variable grid spacing available in 2D mode. The grid spacing decreased from 2 m offshore to 25 cm in the swash zone. As a compromise between computational efficiency and model accuracy, the model uses 2 vertical layers (e.g., Suzuki et al. 2017; Fiedler et al. 2018).

The water level is constant at mean high water (MHW, 1.34 m NAVD88). Tidal effects are not included. To avoid repeating a random wave sequence in the 60-min simulation, the coarse E(f) SS spectrum from MOP (variable df= 0.005-0.05 hz) was interpolated to finer frequency resolution $df = 0.00028$ hz, (1/df = 60 min). Background viscosity of $0.1e^{-4}$ m$^2$/s improved numerical stability. Bottom friction was parameterized using the Manning–Strickler formulation, with the default Manning roughness coefficient of 0.019 s m$^{-1/3}$, a value that worked well at a nearby Southern California beach (Fiedler et al. 2018). Breaking parameters were $\alpha = 0.6,\, \beta = 0.3$ and $\mu = 0.25$ (Smit et al. 2014). A first-order upwind scheme is used for vertical advective terms, with high-order interpolation for second-order accuracy in the horizontal advective terms using the MUSCL limiter. The ILU preconditioner with the Keller Box scheme was used to capture more accurately the physics of large waves. All model runs were 60  min with 10 additional minutes of spin up.

Runup statistics were obtained from the cross-shore and vertical location of the runup edge, defined using 1-h records and a 10-cm threshold depth. Varying the threshold has small effect on SS and IG swash, but increased threshold reduces setup (Appendix 1). Vertical runup spectra were computed with 10-min Hanning windows with 50% overlap, typically translating into roughly 10% statistical chatter in run-up $H_{IG}$ (Elgar 1987; Fiedler et al. 2018). This statistical noise is small relative to boundary condition and other uncertainties.

4.2 Offshore boundary condition

SWASH requires specification at the offshore boundary of shoreward propagating sea-swell and IG waves. The nonlinearity of long surface gravity waves in shallow water is characterized with the Ursell number $Ur= (a/h)/(kh^2)$, with a, k,  and h the wave amplitude, wavenumber, and water depth, respectively (Ursell 1952). In 10-m water depth, the average Ursell number of the considered storm waves is 0.53. The applicability range of the underlying theory that $Ur<<1$ was sometimes substantially exceeded, leading to unrealistically large 1D-bound waves for SWASH initialization. Initializing in 15-m water depth reduced the average to $Ur=0.23$. We use the 1D MOP energy spectrum with random SS phases. Offshore $E_{IG}$ was either set to zero, or to a second-order, 1D boundwave (Hasselmann et al. 1963). These boundary conditions can be inaccurate in the field, but more accurate information for IG waves is generally lacking (Fiedler et al. 2019).

In detailed laboratory and field studies, shoreward propagating sea-swell and IG waves at the offshore model boundary observations are known, and used to initialize SWASH (e.g., Rijnsdorp et al. 2015). Weakly nonlinear wavemaker theory has been used to generate the theoretical 1D-bound IG wave given by Stokes-like perturbation theory (Hasselmann 1962). However, in the field, infragravity waves seaward of the surfzone are a mix of free and forced directionally spread (2D) waves (Okihiro and Guza 1995), complicating specification of IG boundary conditions. A co-located pressure-current meter at the offshore boundary provides an approximate 1D boundary condition initialization that includes phase-coupled and free infragravity waves (Fiedler et al. 2019). However, in the present application, incident sea-swell spectra are provided by the MOPS regional wave propagation model. MOPS does not include IG waves, and IG waves are not measured accurately by local wave buoys.

Lacking the IG components of the incident wave spectrum at the offshore boundary (15-m depth), two contrasting BC are implemented here; a theoretical 1D boundwave ($E_{IG}=$ Bound), and zero incident IG energy $E_{IG}=0$. Fiedler et al. (2019) showed that, with energetic sea-swell, 1D bound theory over-estimated the observed $E_{IG}$ at the 11-m depth boundary by as much as a factor of 4, while $E_{IG}=0$ (of course) underestimated the BC observations. Given proper initial conditions, the phase-resolving model is able to accurately capture the transfers of energy throughout the surfzone between sea-swell and infragravity waves. The over- and underestimations at the offshore BC converged to a common $E_{IG}$ in the model inner surfzone, and run-up was not very sensitive to the offshore IG BC. At IB, variations in run-up predicted using these two different BC are therefore considered part of prediction uncertainty.

5 Results

The 439 large H and $\sqrt{H_0L_0}$ storm wave cases are run on the two different profiles with two different IG-component boundary conditions for a total of 1756 SWASH model runs. Each incident wave case and $\beta _f$ yields different SWASH results for $E_{IG}=0$ and $E_{IG}=$Bound, indicating sensitivity to the unknown offshore BC.

5.1 Components: IG, SS, and $\eta$

Contours of IPA skill in (m,n) space for shoreline $\eta$, $E_{ss}$ and $E_{IG}$ (Fig. 3) show that with offshore bathymetry and tide level held constant, a range of (m, n) values have high skill (e.g., dark red in Fig. 3). Note that the skill numbers shown here encompass all boundary conditions and slopes. An example that further explores slope dependence for IG swash is shown in Fig. 4, and slope and boundary condition input in Fig. 5a–c. Optimal (m, n) values do not vary wildly between shoreline $\eta$, $E_{IG}$ and $E_{SS}$, i.e., the red zones are similarly located in (m,n) space. The optimal (m,n) values (A in Fig. 3a–c) correspond to

$$\begin{aligned} \int _{IG} E(f)_rdf= & {} 0.15 \int _{SS} E(f)^{0.9} f^{-0.65} df, \end{aligned}$$

(10)

$$\begin{aligned} \int _{SS} E(f)_rdf= & {} 0.99 ~\beta _f^{2} \int _{SS} E(f)^{0.45} f^{-1.85} df, \end{aligned}$$

(11)

$$\begin{aligned} \eta= & {} 0.21 \int _{SS} E(f)^{0.45} f^{-1} df, \end{aligned}$$

(12)

for IG, SS and $\eta$, respectively, where $E(f)_r$ refers to the “runup” energy. The $\alpha$ in (Eq. 5) are dimensional. The left-hand side units are m$^2$ in Eqs. 10 and 11, and m in Eq. 12. The units of $\alpha$ result in the same units for the right-hand side. Deviation in SWASH, via slope dependence or boundary input, degrades the skill of the IPA.

Fig. 3

Skill $R^2$ (see color bar) of power law fit to SWASH-modeled IB storm runup climatology (colors) versus the exponents (m,n) in the integral form ($\int E_{\eta ,IG,SS} \sim \alpha \int E_{SS}^m f_{SS}^ndf$, Eq 6). Skills are for a setup, b $E_{SS}$ and c $E_{IG}$. The spectral water level input is applied at the offshore boundary in 15 m depth with two different IG boundary conditions, $E_{IG}$; specifying $E_{IG}$ as an added boundwave or as $E_{IG} = 0$. In addition, two different foreshore slopes are used, for a total of n=1756 runs. Letters on each panel indicate particular model fits (see text): A optimal, (B) $\sqrt{H_0L_0}$, (C) harbor seiche, and (D) energy flux

Fig. 4

$S_{IG}/2$ from SWASH versus integral parameterization for a best fit (A, see Fig. 3), b $H_0L_0$-like (B), c a harbor entrance Cuomo and Guza (2017) (C), and d energy flux-like (D). Foreshore slopes (Fig. 1) are $\beta _f$ = 0.08 (purple) and 0.12 (red). Star indicates the first record of the January 2019 storm, using MOPS $E_{IG}= 0$ input

Fig. 5

Empirical models (Eq. 12) versus the SWASH modeled extreme run-up ($R_{2\%,G}$) using (left column) the $E_{IG}= 0$ boundary condition and (middle column) the Boundwave boundary condition, and (right column) combined conditions, colored by foreshore slope ($\beta _f$ either 0.08, purple or 0.12, red). The 1:1 line (black) is bounded in light gray by ± rmse, binned in 20-cm increments. The left and middle columns are fit to their respective data sets, using the IPA parameterization, derived by fitting to each boundary condition separately. $E_{IG}=0$ at the offshore BC shows more scatter than the boundwave. These BC are lower and plausible upper bounds on the incident IG energy; dotted lines indicate a 20% error threshold in the parameterization. Also shown are the tuned S06 (Table 1, middle row) and the $H_0L_0$-like IPA fit (bottom row). Star indicates the first record of the January 2019 storm

The optimal fit for (m,n) maximizes model skill for each runup component (parameterization A (Fig. 3). Parameterization D ($m=1, n=-1$), a proportionality with SS incident energy flux (Inch et al. 2017), works well for IG, but poorly for $\eta$ and SS. Perhaps coincidentally, the harbor seiche parameterization C ($m=0.45,\, n=-1.5$) (Cuomo and Guza 2017) performs well for all components. Performance similar to optimal is provided by the integral equivalent of $\sqrt{H_0L_0}$ (Parameterization B), where $m=0.5, n=-2$ for $E_{IG}$ and $E_{SS}$ (equivalent to Eqs. 10 and 11, and $m=0.25, n=-1$ for $\eta$:

$$\begin{aligned} \int _{IG} E(f)_r\,df= & {} 0.010 \int _{SS} E(f)^{0.5} f^{-2} df, \end{aligned}$$

(13)

$$\begin{aligned} \int _{SS} E(f)_r\,df= & {} 0.60 \beta _f^{2} \int _{SS} E(f)^{0.5} f^{-2} df, \end{aligned}$$

(14)

$$\begin{aligned} \eta= & {} 0.27 \int _{SS} E(f)^{0.25} f^{-1} df. \end{aligned}$$

(15)

From Eqs. 13,14, the $\sqrt{H_0L_0}$-scaled IPA equivalent yields $E_{SS}$/$E_{IG} = 60 \beta ^{2}$, independent of $H_0L_0$. Stockdon et al. (2006) (Eq. 3), based on bulk parameters, also predicts a ratio that depends on only $\beta$, but with a different constant ($E_{SS}$/$E_{IG} \approx 140 \beta ^{2}$ using default parameter values). The $\alpha$ values in Eqs. 13–15 are specific to the low-frequency swell and beach profiles characteristic of Imperial Beach winter storms. When $\alpha$ values in S06 (Eq. 3) are optimized, the fit improves above the skill using default S06 values, but is still lower than with integral forms (Table 1, discussed below). Using tuned parameter values, $E_{SS}$/$E_{IG} = 65 \beta ^{2}$.

Miche (1951), Carrier and Greenspan (1958), Hunt (1961), Stockdon et al. (2006) and many others have shown that SS swash generally depends on beach slope (the exception is on low slope dissipative beaches, where SS is small). Here, held at constant tide stage, $\beta _f$, defined as $\pm 2\sigma$ around the mean wave setup, varies by less than 5% about the mean values (0.12 and 0.08) owing to the variable cross-shore swash extent. Including the $\beta _f$ term in the SS parameterization (Eq. 11) yields $R^2=0.57$, whereas assuming no $\beta _f$ dependence yields $R^2=0.20$. During a January 2019 storm (Sect. 6), the lidar-observed $\beta _f$ varied between 0.14 to 0.10 over a single high tide, and the observed run-up $S_{SS}/2$ decreased approximately proportionally from about 1.6 to 1.0m, further supporting the $\beta _f$ term in (Eq. 11) .

Wave setup, a super-elevation of the mean water level, is supported by the cross-shore decrease in the wave radiation stress associated with wave breaking (Longuet-Higgins and Stewart 1962, and many others). Shoreline setup depends on surfzone bathymetry, including sand bars and terraces (e.g., Raubenheimer 2001; Stephens et al. 2011). Here, $\eta$ was approximated with the same bulk parameters $H_0,L_0,\beta _f$ as SS and IG. The best-fit integral form ($R^2= 0.85$, not shown), unlike S06, does not depend on foreshore beach slope. Including a beach slope term reduced the skill from 0.85 to 0.54 because the model setup is determined by h(x) across the entire surfzone, and is little altered by these spatially limited changes in $\beta _f$ (Fig. 1). The dependence of $\eta$ on a typical eroded h(x) is included implicitly in (Eq. 12).

5.2 Total run-up $R_{2\%,G}$

The best-fit IPA $\alpha , n, m$ for all components of total run-up yields $R^2$=0.83 and rmse=0.20 m (Fig. 5c, Table 1). The $H_0L_0$ IPA only modestly alters skill (0.70) and rmse (0.26m) from optimal (Fig. 5i), reinforcing previous findings that $H_0L_0$ parameterizations work reasonably well for swash. The separation of total run-up by slope reveals a slight divergence of fits, especially for the calibrated S06 model. This can be attributed to the poor fits for setup on the two different slopes (Fig. 6c). Calibrating the S06 model improves, but cannot resolve, the error stemming from the $\beta _f$ term in setup. Uncalibrated S06 has the largest errors for the steeper slope (dark blues, Fig. 6). Tuning S06 to the Cortez location reduces the $R_{2\%}$ rmse to 0.44m , but does not altogether remove the stratification of setup and SS-swash components by bathymetry. Note that $\beta _f=0.14$ is steeper than used to calibrate S06. In addition to the slope errors, the two different boundary conditions yield slightly different fits, which when combined can be attributed to errors in unknown IG forcing offshore. Using both boundary conditions yields a roughly 20% prediction error in total runup level (black dotted lines, Fig. 5).

Fig. 6

S06 model (Eq. 4), including $\beta _f$ terms) versus SWASH simulations of the IB runup climatology for a $S_{SS}/2$, b $S_{IG}/2$, c $\eta$, and d $R_{2\%,G}$ = $\eta + S/2$. Stockdon constants are default (dark) and tuned (light), as shown in legend. Red and purple colors indicate the steep and shallow slopes ($\beta _f \sim 0.12$ or $\beta _f \sim 0.08$, respectively). Note that RMSE is based on S/2, and vertical scale on $R_{2\%,G}$ (d) differs from the individual components (a–c). Tuning (lighter colors) reduces S06 model error using default parameter values (darker colors). In c, the vertical stratification of $\eta$ errors by $\beta _f$ (compare red and purple) is consistent with errors in the S06 $\beta _f$ dependence (Eq. 3), motivating the present use of Eq. 12, that lacks a $\beta _f$ term

Table 1 Goodness of fit statistics fitting the various parameterizations to the SWASH modeled run-up for incident swash ($S_{SS}$), IG swash ($S_{IG}$), setup ($\eta$), and extreme run-up $R_{2\%,G}$

6 Application to a January 2019 storm event

Run-up was measured with lidar line scans at Cortez Ave (Fig. 1b), during the peak and ebb of a spring high tide on January 18, 2019 from 12:55 to 17:30 UTM (Fig. 7). Observations were split into nine 28-min long records. Lidar returns were gridded by median value into 10-cm horizontal bins, following Brodie et al. (2012). The estimated runup lines were extracted at the 10-cm depth threshold. Noise from breaking wave foam and splashing were smoothed with a Savitzky-Golay filter. When waves occasionally overtopped the rip-rap, a continuous smooth runup (and rundown) line was extrapolated using an objective map with Gaussian covariance.

Fig. 7

MOPS-model ($h=15$ m) incident (spectrally reverse shoaled to deepwater) SS wave properties versus time for the January 19 event a (left) wave height and (right) mean frequency $f_c$, open circles; peak frequency $f_p$, closed circles; b $H_0L_0^{1/2}$; c (left) still water level SWL and (right) foreshore beach slope $\beta _f$. Yellow dashed line indicates constant $\beta _f= 0.1$. d Hunt-like runup parameter with variable and constant $\beta _f$ (black and yellow, respectively)

The swash zone beach profile for each 28-min record was defined by the minimum vertical elevation in each horizontal bin. Cross-shore locations with vertical variance greater than 1 cm of the roughly 100 s moving minimum value were classified as water and removed from the profile. The foreshore beach slope $\beta _f$ decreased from 0.14 to 0.10 over the 5-h record (Fig. 8d), where $\beta _f$ is determined with bathymetry around $\eta \, \pm \, 2\sigma$, with $\sigma ^2$ the runup variance (Stockdon et al. 2006).

Fig. 8

Observed (o) and parameterized (lines) water level components (28-min records) versus time for 5 h: a sea-swell swash SS/2, b IG swash IG/2, c setup $\eta$ and d wave-driven $R_{2\%,G}$, and e TWL= $R_{2\%,G}$ + SWL. Lidar-observed and constant $\beta _f=0.1$ are dotted and solid, respectively. Best-fit IPA model (see Table 1) with MOP input (variable $\beta _f$, dotted black; and constant $\beta _f=0.1$, yellow), tuned S06 parameterization with MOPS input with variable $\beta _f$ (dotted light blue) and $\beta _f=0.1$ (green). The vertical bars on observations correspond to 95% statistical confidence

Hourly MOP waves (D0046) were used to estimate E(f), $H_0$, $L_0$, and $\beta _f (H_0L_0)^{1/2}$ for each 28-min lidar record (Fig. 8). These steep slopes yield an Iribarren number $\xi _0 = \beta _f(H_0/L_0)^{-0.5} \sim$ 1.5, corresponding to plunging breakers, not the spilling waves present further offshore, where $\beta$ is much lower (e.g., 0.01). Using E(f) in IPA (Eqs. 10–12) yields estimates of $S_{ss}/2$ and $\eta$ that both typically differ by $<0.2$ m from observations (Fig. 7a, c). Although $S_{IG}$ is over-estimated by as much as a factor of 2 (Fig. 7b), $S_{IG}<S_{SS}$ and $S_{ss}$ is predicted relatively accurately.

Thus, relatively large errors in $S_{IG}$ do not necessarily translate into large $R_{2\%,G}$ errors. Furthermore, errors of opposite sign in $\eta$ and $S_{IG}$ partially cancel, and total wave-induced water level $R_{2\%,G}$ is predicted with rms error = 0.25 m, about 10% (Fig.  7d). For this event, calibrated S06 (‘S06t’) and IPA yield very similar results. S06t uses $\alpha$ best-fit values (Eq. 3), given in Table 1. With constant $\beta _f$ =0.1, rather than the observed variable $\beta _f$, the observed variation in $S_{ss}$ is not simulated (dashed curve in Fig. 7). The falling tide (SWL in Fig. 8c) and decreasing $\beta _f$ (and hence decreasing $S_{SS}$, Fig. 7a) both contribute to the decrease in $R_{2\%,G}$ after high tide, Fig. 7e).

7 Discussion

During the event for which onsite observations were available, IPA over-prediction of $S_{IG}$ (Fig. 7b) is eliminated by using incident (IG and SS) waves observed in 7 m depth, rather than estimated with the MOP model and $E_{IG} =0$ or 1D bound, as above. However, uncertainty in subaqueous h(x) continues to limit SWASH accuracy, and errors in $R_{2\%,G}$ are similar using the observed PUV to drive SWASH, and the MOPS-driven IPA emulator.

Lidar profiles (Fig. 9) were merged with the offshore portion of the representative eroded profile (Fig. 1) to obtain h(x) to 8 m depth (6 m, navd88, Fig. 9), where SWASH is initialized. Three plausible offshore profiles were tested, based on historical surveys, with each 28-min model run using the time-varying lidar-derived foreshore (Fig. 9). Profile 2 is monotonic, with a constant depth terrace-like feature from $x=0$ to $x=-100$ m. Profile 3 represents extreme erosion for this site, and is from an El Niño year with a well-developed offshore bar. Profile 1 has a much smaller bar, located closer to shore.

Fig. 9

Three depth profiles (thick curves) used for SWASH modeling of the January event. Profile 3 has a large offshore bar characteristic of a strongly erosive winter, whereas Profiles 1 and 2 represent more moderate winters. All profiles use the time varying lidar-observed profiles observed in the swash zone (dashed box at $x,y>0$ m, detailed in Fig. 1d). Swash is initialized in either 6m (PUV) or 15m depth (Fig. 1c). Dotted horizontal lines denote the observed highest and lowest mean offshore water levels (e.g., SWL)

In situ PUV (between 7 and 8 m depth) show $H_s$ = 2.0–2.6 m with peak frequency varying from 0.055 to 0.062 Hz. MOP hindcasts in 15 m depth predict $H_s$ = 3.01–3.74 m with constant $f_p=0.06$ Hz (starred locations in Figs. 2, 8a). The PUV was likely sometimes in the surfzone, perhaps contributing to the reduced $H_s$ compared with MOPS. Differences may also be the result of poor MOPS model skill for this particular event.

Modeled and observed bulk run-up agreed well when PUV input is used with Profiles 2 and 3 (Fig. 10, red and yellow lines), rmse = 18.3 cm). However, the shallow bar in Profile 1 (blue line in Fig. 9) resulted in large underprediction of sea-swell swash and setup (blue lines in Fig. 10), perhaps because the bar sheltered the shoreline. Similar to previous studies (e.g., Raubenheimer 2001), setup and SS swash can be sensitive to inner surfzone bathymetry. Suppressing lidar-observed changes in swash bathymetry using the lidar first record (Fig. 8a) with Profile 2 (Fig. 8b) introduces error in IG swash and setup that propagate into $R_{2\%,G}$ (not shown), increasing the rmse from 18.3 to 41 cm.

Fig. 10

Observed runup components (28-min records) versus time for 5 h: a sea-swell swash SS/2, b IG swash IG/2, c setup $\eta$ and d total run-up $R_{2\%,G}$, and e SWL and foreshore beach slope $\beta _f$. Shown are lidar observations (black circles), SWASH model with PUV input (Profiles 1, blue; 2, red; and 3, yellow), and the new IPA parameterization with MOPS input (dashed black line). Numerical models (colored lines) use the time-varying lidar-observed foreshore beach slope (e, solid magenta), whereas the IPA uses a constant slope of 0.1 (dotted magenta line)

Using the lidar-observed $\beta _f$, the integrated power law approach for $R_{2\%,G}$ performs well on the January 2019 storm event (Fig. 7), with rmse = 18.3 cm (Sk = 0.55). The site-specific tuned S06 model yields similar rmse = 19.6 cm (Sk = 0.49). Note that $\beta _f=0.14$ used in IPA is steeper than the slopes (0.08 and 0.12) used for model calibration. The sizeable bias in IG swash for both empirical models could result from using a representative (rather than observed) offshore h(x) bathymetry in IPA calibration, and from MOPS model overestimation of SS waves at the offshore boundary.

Using the observed $\beta _f$, uncalibrated S06 (Eq. 4) over-predicts wave run-up with approximate bias of $\sim 1.4$ m (not shown), primarily from setup error. The resulting skill is negative, with rmse=1.16 m. Although the choice of runup depth threshold alters estimates of the observed runup parameters, this overestimate is larger than can be explained by decreasing the threshold depth from 10 to 3 cm (Appendix 2).

8 Conclusion

Improved prediction of shoreline erosion, wave overtopping, and oceanfront flooding will improve the efficiency of both emergency response and long-term planning. On the US West coast, tides and waves are the largest contributors to elevated nearshore water levels. Sea-level rise is a confounding future factor. Tidal amplitudes and phases are well-known, and seasonal and local deviations (e.g., “tidal residuals”) are routinely available. In comparison, wave-driven contributions to total water level are difficult to predict in both magnitude and timing (Kalansky et al. 2018). The MOPS-based training data set for IPA (Fig. 2) is intended only to mimic the range of historically plausible events, not to simulate accurately any individual event. An offshore water level of MHHW is assumed, and tides are not considered further. In practical application, tides are necessarily included in $R_{2\%,G}$. The accuracy of $R_{2\%,G}$ predictions (IPA or otherwise) therefore depends on both storm wave timing and spectral characteristics. Storm impacts can vary dramatically depending on the tide stage (e.g., spring versus neap and high versus low). The present discussion (Figs. 3, 4, 5, 6) considers model scatter caused by uncertainty in the IG boundary conditions and h(x). Uncertainty in SS predictions is not included. More complete error bars, including errors in MOP estimates, will be included in the future.

Setup depends on h(x) across the surfzone (Bowen et al. 1968; Longuet-Higgins and Stewart 1962; Raubenheimer 2001). Simulations of setup using an accurate h(x) will outperform parametric models using only beach face $\beta _f$. Swash also depends on surfzone h(x), especially inner surf zone sandbars that shelter the beach face (Fig. 9). With a wide range of historical h(x) IB storm profiles (Fig. 1), IPA scatter will be large. Runup forecasts can be improved with more accurate h(x), perhaps from observations and/or modeling (e.g., equilibrium Ludka et al. 2015) based on historical profiles. The bound wave and $E_{IG}=0$ energy boundary conditions used here can be improved using an approximate, empirical formula (including phase coupling) based on PUV observations in 8-15m depth.

An underlying assumption is that, given incident wave at the offshore boundary and the beach profile, 1D SWASH runup simulations are sufficiently accurate to inform overtopping warnings at Imperial Beach. Lidar observations at Imperial Beach support this assumption. Scatter in 1D SWASH simulations, for the same incident sea-swell waves, is caused by uncertainties in bathymetry and incident infragravity waves. For use in a local flood warning system, (https://climateadapt.ucsd.edu/imperialbeach/forecast/), the relationship between incident wave energy spectra E(f) and SWASH-modeled shoreline water levels is approximated with IPA (integrated power law approximation). The fit to SWASH runup estimates is better with IPA than with the commonly used bulk parameterizations using deep water wave height $H_0$ and deep water wavelength $L_0$ (Hunt 1961; Stockdon et al. 2006). However, an IPA using $H_0 L_0$ scaling performs well and is essentially an extension of (Hunt 1961; Stockdon et al. 2006) bulk formulae to spectra.

The range of bathymetries and wave conditions for which 1D SWASH model, and the corresponding IPA, are applicable are unknown. Calibration and validation are integral components of improved predictive skill. Many beaches, however, lack the detailed historical spectral wave and bathymetry data required by the IPA. At locations without these data, local calibration to bulk wave statistics is likely the optimal approach. Future validation with observations, as well as uncertainty quantification, will aid in IPA application to other flood-prone sites.

Appendices

Appendix 1: Runup threshold depths

Model and lidar runup statistics are sensitive to the depth threshold $\delta$, above set at 10 cm, as in Fiedler et al. (2015). Video-based measurements, such as those used in S06, do not explicitly define a threshold. Using the phase-averaged XBeach model, Stockdon et al. (2014) found modeled wave setup decreased approximately linearly 2 cm to every 1 cm increase in $\delta$ on an intermediate beach in high waves.

The IB storm SWASH model results were evaluated at $\delta$ =3, 5, 10 and 15 cm. Holding the $\delta = 3$ cm line as the baseline, we find swash (combined $S_{IG}$ and $S_{SS}$, squares in Fig. 11) shows less than 5% change (equivalent to $\sim$5 cm) for $\delta$ varying from 3 to 15 cm. Setup on the steeper lidar bathymetry ($\beta = 0.12$) decreases approximately 1 cm for every 1 cm increase in the runup threshold depth. Using $\delta =10$ cm instead of $\delta =3$ cm reduces modeled setup by an average of 14%. On the slightly less steep eroded profile ($\beta = 0.08$), setup differences are more pronounced; using $\delta =15$ cm instead of $\delta =3$ cm leads to an average 35% reduction in “measured” setup. For both h(x), setup differences between different $\delta$ exhibit a small increase dependent on magnitude of total run-up, such that larger setup equates to larger differences.

Fig. 11

Mean SWASH model percent difference ($100 \times (\delta _{n}-\delta _3)/\delta _3$) of setup (open circles) and S/2 (filled squares), relative to $\delta =3$ cm versus $\delta$ (5, 10, and 15 cm) for foreshore beach slopes $\beta _f = 0.12$ (blue), and 0.08 (red)

Using $\delta$ = 3 cm changes the parameters (Eqs. 10–12) to

$$\begin{aligned} R_{2\%,G}= & {} 0.31 \int _{SS} E(f)^{0.35} f^{-1.0} df\nonumber \\&+ 2 \left[ 0.24\, \beta _f^2 \int _{SS} E(f)^{0.30} f^{-2.35} df + 0.11 \int _{SS} E(f)^{0.85} f^{-0.8} df\right] ^{1/2}, \end{aligned}$$

(16)

with an rmse of 21.6 cm and $R^2= 0.81$. Using the $\delta$= 3 cm threshold with the parameterization created for the 10 cm runup line yields an rmse of 28.5 cm and $R^2= 0.68$.

Appendix 2: Reference equations

Tuned S06, using the MOPS storm-wave climatology and representative bathymetries (Fig. 1c):

$$\begin{aligned} R_{2\%} = 1.1\left( 0.160\beta _f(H_0L_0)^{1/2} + \frac{[H_0L_0(0.330\beta _f^2+0.0051)]^{1/2}}{2}\right) . \end{aligned}$$

(17)

IPA, $H_0L_0$ form:

$$\begin{aligned} R_{2\%,G}= & {} 0.27 \int _{SS} E(f)^{0.25} f^{-1} df\nonumber \\&+ 2\left[ \int _{SS} E(f)^{0.5} f^{-2} df \left( 0.60 \beta _f^2 + 0.010 \right) \right] ^{1/2}. \end{aligned}$$

(18)

IPA, optimized form:

$$\begin{aligned} R_{2\%,G}= & {} 0.21 \int _{SS} E(f)^{0.45} f^{-1} df\nonumber \\&+ 2 \left[ {0.99 \beta _f^2 \int _{SS} E(f)^{0.45} f^{-1.85} df + 0.15 \int _{SS} E(f)^{0.9} f^{-0.65} df}\right] ^{1/2}. \end{aligned}$$

(19)