Abstract
The uniformization and hyperbolization transformations formulated by Bonk et al. in “Uniformizing Gromov Hyperbolic Spaces”, Astérisque, vol 270 (2001), dealt with geometric properties of metric spaces. In this paper we consider metric measure spaces and construct a parallel transformation of measures under the uniformization and hyperbolization procedures. We show that if a locally compact roughly starlike Gromov hyperbolic space is equipped with a measure that is uniformly locally doubling and supports a uniformly local p-Poincaré inequality, then the transformed measure is globally doubling and supports a global p-Poincaré inequality on the corresponding uniformized space. In the opposite direction, we show that such global properties on bounded locally compact uniform spaces yield similar uniformly local properties for the transformed measures on the corresponding hyperbolized spaces. We use the above results on uniformization of measures to characterize when a Gromov hyperbolic space, equipped with a uniformly locally doubling measure supporting a uniformly local p-Poincaré inequality, carries nonconstant globally defined p-harmonic functions with finite p-energy. We also study some geometric properties of Gromov hyperbolic and uniform spaces. While the Cartesian product of two Gromov hyperbolic spaces need not be Gromov hyperbolic, we construct an indirect product of such spaces that does result in a Gromov hyperbolic space. This is done by first showing that the Cartesian product of two bounded uniform domains is a uniform domain.
Similar content being viewed by others
1 Introduction
Studies of metric space geometry usually consider two types of synthetic (i.e. axiomatic) negative curvature conditions: Alexandrov curvature (known as CAT(\(-1\)) spaces) and Gromov hyperbolicity. While the Alexandrov condition governs both small and large scale behavior of triangles, the Gromov hyperbolicity governs only the large scale behavior. As such, the Gromov hyperbolicity was eminently suited to the study of hyperbolic groups, see e.g. Gromov [24], Coornaert–Delzant–Papadopoulos [20] and Ghys–de la Harpe [23], while Bridson–Haefliger [17] gives an excellent overview of both notions of curvature.
Since the ground-breaking work of Gromov [24], the notion of Gromov hyperbolicity has found applications in other parts of metric space analysis as well. In [14, Theorem 1.1], Bonk, Heinonen and Koskela gave a link between quasiisometry classes of locally compact roughly starlike Gromov hyperbolic spaces and quasisimilarity classes of locally compact bounded uniform spaces. In Buyalo–Schroeder [19] it was shown that every complete bounded doubling metric space is the visual boundary of a Gromov hyperbolic space, see also Bonk–Saksman [15].
While none of the above mentioned studies, involving Gromov hyperbolic spaces and uniform domains, considered how measures transform on such spaces (see also e.g. Buckley–Herron–Xie [18] and Herron–Shanmugalingam–Xie [31]), analytic studies on metric spaces require measures as well. Although [15] does consider function spaces on certain Gromov hyperbolic spaces, called hyperbolic fillings, these function spaces are associated with just the counting measure on the vertices of such hyperbolic fillings and so do not lend themselves to more general Gromov hyperbolic spaces. Similar studies were undertaken in Bonk–Saksman–Soto [16] and Björn–Björn–Gill–Shanmugalingam [8].
In this paper we seek to remedy this gap in the literature on analysis in Gromov hyperbolic spaces. Thus the primary focus of this paper is to construct transformations of measures under the uniformization and hyperbolization procedures, and to demonstrate how analytic properties of the measure are preserved by them. This does not seem to have been considered elsewhere. The analytic properties of interest here are the doubling property and the Poincaré inequality, assumed either globally on the uniform spaces, or uniformly locally (i.e. for balls up to some fixed radius) on the Gromov hyperbolic spaces. As trees are the quintessential models of Gromov hyperbolic spaces, the results in this paper are motivated in part by the results in [8].
The following is our main result, combining Theorems 4.9 and 6.2. Here, \(z_0\in X\) is a fixed uniformization center and \(\varepsilon _0(\delta )\) is as in Bonk–Heinonen–Koskela [14], see later sections for relevant definitions.
Theorem 1.1
Assume that (X, d) is a locally compact roughly starlike Gromov \(\delta \)-hyperbolic space equipped with a measure \(\mu \) which is doubling on X for balls of radii at most \(R_0\), with a doubling constant \(C_d\). Let \(X_\varepsilon =(X,d_\varepsilon )\) be the uniformization of X given for \(0<\varepsilon \le \varepsilon _0(\delta )\) by
with the infimum taken over all rectifiable curves \(\gamma \) in X joining x to y. Also let
Then the following are true:
-
(a)
\(\mu _\beta \) is globally doubling both on \(X_\varepsilon \) and its completion
 .
. -
(b)
If \(\mu \) supports a p-Poincaré inequality for balls of radii at most \(R_0\), then \(\mu _\beta \) supports a global p-Poincaré inequality both on \(X_\varepsilon \) and
 .
.
Along the way, we also show that if the assumptions hold with some value of \(R_0\) then they hold for any value of \(R_0\) at the cost of enlarging \(C_d\), see Proposition 3.2 and Theorem 5.3.
We also obtain the following corresponding result for the hyperbolization procedure, see Propositions 7.3 and 7.4.
Theorem 1.2
Let \((\Omega ,d)\) be a locally compact bounded uniform space, equipped with a globally doubling measure \(\mu \). Let k be the quasihyperbolic metric on \(\Omega \), given by
where \(d_\Omega (x)={{\,\mathrm{dist}\,}}(x,\partial \Omega )\) and the infimum is taken over all rectifiable curves \(\gamma \) in \(\Omega \) connecting x to y. For \(\alpha >0\) we equip the corresponding Gromov hyperbolic space \((\Omega ,k)\) with the measure \(\mu ^\alpha \) given by \(\mathrm{{d}}\mu ^\alpha =d_\Omega (\,\cdot \,)^{-\alpha }\,\mathrm{{d}}\mu \). Let \(R_0 >0\).
Then the following are true:
-
(a)
\(\mu ^\alpha \) is doubling on \((\Omega ,k)\) for balls of radii at most \(R_0\).
-
(b)
If \(\mu \) supports a global p-Poincaré inequality, then \(\mu ^\alpha \) supports a p-Poincaré inequality for balls of radii at most \(R_0\).
We use Theorem 1.1 to study potential theory on locally compact roughly starlike Gromov hyperbolic spaces, equipped with a locally uniformly doubling measure supporting a uniformly local Poincaré inequality. In particular, we characterize when the finite-energy Liouville theorem holds on such spaces, i.e. when there exist no nonconstant globally defined p-harmonic functions with finite p-energy. The characterization is given in terms of the nonexistence of two disjoint compact sets of positive p-capacity in the boundary of the uniformized space, see Theorem 10.5. This characterization complements our results in [12].
As already mentioned, an in-depth study of locally compact roughly starlike Gromov hyperbolic spaces, as well as links between them and bounded locally compact uniform domains, was undertaken in the seminal work Bonk–Heinonen–Koskela [14]. They showed [14, the discussion before Proposition 4.5] that the operations of uniformization and hyperbolization are mutually opposite:
-
A uniformization followed by a hyperbolization takes a given locally compact roughly starlike Gromov hyperbolic space X to a roughly starlike Gromov hyperbolic space which is biLipschitz equivalent to X, see [14, Proposition 4.37]. (Note that in [14] “quasiisometric” means biLipschitz.)
-
A hyperbolization of a bounded locally compact uniform space \(\Omega \), followed by a uniformization, returns a bounded uniform space which is quasisimilar to \(\Omega \), see [14, Proposition 4.28].
Here, a homeomorphism \(\Phi :X\rightarrow Y\) between two noncomplete metric spaces is quasisimilar if it is \(C_x\)-biLipschitz on every ball \(B(x,c_0 {{\,\mathrm{dist}\,}}(x,\partial X))\), for some \(0<c_0<1\) independent of x, and there exists a homeomorphism \(\eta :[0,\infty )\rightarrow [0,\infty )\) such that for each distinct triple of points \(x,y,z\in X\),
It was also shown in [14, Theorem 4.36] that two roughly starlike Gromov hyperbolic spaces are biLipschitz equivalent if and only if any two of their uniformizations are quasisimilar.
We continue the study of Gromov hyperbolic spaces in this spirit by considering pairs of Gromov hyperbolic spaces in Sect. 8. Note that the Cartesian product of two Gromov hyperbolic spaces need not be Gromov hyperbolic, as demonstrated by \({\mathbf {R}}\times {\mathbf {R}}\), which is not a Gromov hyperbolic space even though \({\mathbf {R}}\) is. On the other hand, in Sect. 8 we obtain the following result, see Proposition 8.3 for a more precise result.
Proposition 1.3
Let \((\Omega ,d)\) and \((\Omega ',d')\) be two bounded uniform spaces. Then \(\Omega \times \Omega '\) is a bounded uniform space with respect to the metric
We use this, together with the results of [14], to construct an indirect product \(X\times _\varepsilon Y\) of two Gromov hyperbolic spaces which is also Gromov hyperbolic, see Sect. 8. In this section we also study properties of such product hyperbolic spaces. For a fixed Gromov \(\delta \)-hyperbolic space X, there is a whole family of uniformizations \(X_\varepsilon \), one for each \(0<\varepsilon \le \varepsilon _0(\delta )\). As mentioned above, \(X_{\varepsilon }\) is quasisimilar to \(X_{\varepsilon '}\) when \(0<\varepsilon ,\varepsilon '\le \varepsilon _0(\delta )\).
On the other hand, we show in Proposition 8.5 that the canonical identity mapping between \(X\times _\varepsilon Y\) and \(X\times _{\varepsilon '} Y\) is never biLipschitz if \(\varepsilon \ne \varepsilon '\), and it is even possible that the two indirect products are not even quasiisometric. Here, a map \(\Phi :Z\rightarrow W\) is a quasiisometry (also called, perhaps more accurately, rough quasiisometry as in [14] and [8]) if there are \(C>0\) and \(L\ge 1\) such that the C-neighborhood of \(\Phi (Z)\) contains W and for all \(z,z'\in Z\),
It is not difficult to show that visual boundaries of quasiisometric locally compact roughly starlike Gromov hyperbolic spaces are quasisymmetric, see e.g. Bridson–Haefliger [17, Theorem 3.22]. We take advantage of this to show the quasiisometric nonequivalence of two indirect products of the hyperbolic disk and \({\mathbf {R}}\), see Example 8.7.
The broad organization of the paper is as follows. Background definitions and preliminary results are given in Sects. 2 and 3, while the definition of Poincaré inequalities is given in Sect. 5. The main aims in Sects. 4 and 6 are to deduce parts (a) and (b), respectively, of Theorem 1.1. The dual transformation of hyperbolization, via the quasihyperbolic metric (1.1), is discussed in Sect. 7, where also Theorem 1.2 is shown. The above sections fulfill the main goal of this paper, and form a basis for comparing the potential theories on Gromov hyperbolic spaces and on uniform spaces.
The remaining sections are devoted to applications of the results obtained in the preceding sections. In Sect. 8 we construct and study the indirect product, providing a family of new Gromov hyperbolic spaces from a pair of Gromov hyperbolic spaces. The subsequent sections are devoted to the impact of uniformization and hyperbolization procedures on nonlinear potential theory. In Sect. 9 we discuss Newton–Sobolev spaces and p-harmonic functions, and then in Sect. 10 we show that under certain natural conditions, the class of p-harmonic functions is preserved under the uniformization and hyperbolization procedures. In this final section, we also characterize which Gromov hyperbolic spaces with bounded geometry support the finite-energy Liouville theorem for p-harmonic functions.
In the beginning of each section, we list the standing assumptions for that section in italicized text; in Sects. 2 and 4 these assumptions are given a little later.
2 Gromov Hyperbolic Spaces
A curve is a continuous mapping from an interval. Unless stated otherwise, we will only consider curves which are defined on compact intervals. We denote the length of a curve \(\gamma \) by \(l_\gamma =l(\gamma )\), and a curve is rectifiable if it has finite length. Rectifiable curves can be parametrized by arc length \(\mathrm{{d}}s\).
A metric space \(X=(X,d)\) is L-quasiconvex if for each \(x,y\in X\) there is a curve \(\gamma \) with end points x and y and length \(l_\gamma \le L d(x,y)\). X is a geodesic space if it is 1-quasiconvex, and \(\gamma \) is then a geodesic from x to y. We will consider a related metric, called the inner metric, given by
where the infimum is taken over all curves \(\gamma \) from x to y. If (X, d) is quasiconvex, then d and \(d_{{{\,\mathrm{in}\,}}}\) are biLipschitz equivalent metrics on X. The space X is a length space if \(d_{{{\,\mathrm{in}\,}}}(x,y)=d(x,y)\) for all \(x,y\in X\). By Lemma 4.43 in [5], arc length is the same with respect to d and \(d_{{{\,\mathrm{in}\,}}}\), and thus \((X,d_{{{\,\mathrm{in}\,}}})\) is a length space. A metric space is proper if all closed bounded sets are compact. A proper length space is necessarily a geodesic space, by Ascoli’s theorem or the Hopf–Rinow theorem below. To avoid pathological situations, all metric spaces in this paper are assumed to contain at least two points.
We denote balls in X by \(B(x,r)=\{y \in X: d(y,x) <r\}\) and the scaled concentric ball by \(\lambda B(x,r)=B(x,\lambda r)\). In metric spaces it can happen that balls with different centers and/or radii denote the same set. We will however adopt the convention that a ball comes with a predetermined center and radius. Similarly, when we say that \(x \in \gamma \) we mean that \(x=\gamma (t)\) for some t. If \(\gamma \) is noninjective, this t may not be unique, but we are always implicitly referring to a specific such t.
Theorem 2.1
(Hopf–Rinow theorem) If X is a complete locally compact length space, then it is proper and geodesic.
This version is a generalization of the original theorem, see e.g. Gromov [25, p. 9] for a proof.
Definition 2.2
A complete unbounded geodesic metric space X is Gromov hyperbolic if there is a hyperbolicity constant \(\delta \ge 0\) such that whenever [x, y], [y, z] and [z, x] are geodesics in X, every point \(w\in [x,y]\) lies within a distance \(\delta \) of \([y,z]\cup [z,x]\).
The ideal Gromov hyperbolic space is a metric tree, which is Gromov hyperbolic with \(\delta =0\). A metric tree is a tree where each edge is considered to be a geodesic of unit length.
Definition 2.3
An unbounded metric space X is roughly starlike if there are some \(z_0\in X\) and \(M>0\) such that whenever \(x\in X\) there is a geodesic ray \(\gamma \) in X, starting from \(z_0\), such that \({{\,\mathrm{dist}\,}}(x,\gamma )\le M\). A geodesic ray is a curve \(\gamma :[0,\infty ) \rightarrow X\) with infinite length such that \(\gamma |_{[0,t]}\) is a geodesic for each \(t > 0\).
If X is a roughly starlike Gromov hyperbolic space, then the roughly starlike condition holds for every choice of \(z_0\), although M may change.
Definition 2.4
A nonempty open set \(\Omega \varsubsetneq X\) in a metric space X is an A-uniform domain, with \(A\ge 1\), if for every pair \(x,y\in \Omega \) there is a rectifiable arc length parametrized curve \(\gamma : [0,l_\gamma ] \rightarrow \Omega \) with \(\gamma (0)=x\) and \(\gamma (l_\gamma )=y\) such that \(l_\gamma \le A d(x,y)\) and
where
The curve \(\gamma \) is said to be an A-uniform curve. A noncomplete metric space \((\Omega ,d)\) is A-uniform if it is an A-uniform domain in its completion.
A ball B(x, r) in a uniform space \(\Omega \) is a subWhitney ball if \(r \le c_0 d_\Omega (x)\), where \(0<c_0<1\) is a predetermined constant. We will primarily use \(c_0=\frac{1}{2}\).
The completion of a locally compact uniform space is always proper, by Proposition 2.20 in Bonk–Heinonen–Koskela [14]. Unlike the definition used in [14], we do not require uniform spaces to be locally compact.
It follows directly from the definition that an A-uniform space is A-quasiconvex. One might ask if the uniformity assumption in Proposition 2.20 in [14] can be replaced by a quasiconvexity assumption, i.e. if the completion of a locally compact quasiconvex space is always proper, however the following example shows that this can fail even if the original space is geodesic. Thus the uniformity assumption in Proposition 2.20 in [14] is really crucial.
Example 2.5
Let
equipped with the \(\ell ^1\)-metric. Then X is a bounded locally compact geodesic space which is not totally bounded, and thus has a nonproper completion.
We assume from now on that X is a locally compact roughly starlike Gromov \(\delta \)-hyperbolic space. We also fix a point \(z_0 \in X\) and let M be the constant in the roughly starlike condition with respect to \(z_0\).
By the Hopf–Rinow Theorem 2.1, X is proper. The point \(z_0\) will serve as a center for the uniformization \(X_\varepsilon \) of X. Following Bonk–Heinonen–Koskela [14], we define
and, for a fixed \(\varepsilon >0\), the uniformized metric \(d_\varepsilon \) on X as
and the infimum is taken over all rectifiable curves \(\gamma \) in X joining x to y. Note that if \(\gamma \) is a compact curve in X, then \(\rho _\varepsilon \) is bounded from above and away from 0 on \(\gamma \), and in particular \(\gamma \) is rectifiable with respect to \(d_\varepsilon \) if and only if it is rectifiable with respect to d.
The set X, equipped with the metric \(d_\varepsilon \), is denoted by \(X_\varepsilon \). We let  be the completion of \(X_\varepsilon \), and let
be the completion of \(X_\varepsilon \), and let  . When writing e.g. \(B_\varepsilon \), \({{\,\mathrm{diam}\,}}_\varepsilon \) and \({{\,\mathrm{dist}\,}}_\varepsilon \) the \(\varepsilon \) indicates that these notions are taken with respect to
. When writing e.g. \(B_\varepsilon \), \({{\,\mathrm{diam}\,}}_\varepsilon \) and \({{\,\mathrm{dist}\,}}_\varepsilon \) the \(\varepsilon \) indicates that these notions are taken with respect to  . The length of the curve \(\gamma \) with respect to \(d_\varepsilon \) is denoted by \(l_\varepsilon (\gamma )\), and arc length \(\mathrm{{d}}s_\varepsilon \) with respect to \(d_\varepsilon \) satisfies
. The length of the curve \(\gamma \) with respect to \(d_\varepsilon \) is denoted by \(l_\varepsilon (\gamma )\), and arc length \(\mathrm{{d}}s_\varepsilon \) with respect to \(d_\varepsilon \) satisfies
It follows that \(X_\varepsilon \) is a length space, and thus also  is a length space. By a direct calculation (or
[14, (4.3)]),
is a length space. By a direct calculation (or
[14, (4.3)]),  . Note that as a set, \(\partial _\varepsilon X\) is independent of \(\varepsilon \) and depends only on the Gromov hyperbolic structure of X, see e.g.
[14, Sect. 3]. The notation adopted in
[14] is \(\partial _G X\).
. Note that as a set, \(\partial _\varepsilon X\) is independent of \(\varepsilon \) and depends only on the Gromov hyperbolic structure of X, see e.g.
[14, Sect. 3]. The notation adopted in
[14] is \(\partial _G X\).
The following important theorem is due to Bonk–Heinonen–Koskela [14].
Theorem 2.6
There is a constant \(\varepsilon _0=\varepsilon _0(\delta )>0\) only depending on \(\delta \) such that if \(0 < \varepsilon \le \varepsilon _0(\delta )\), then \(X_\varepsilon \) is an A-uniform space for some A depending only on \(\delta \), and  is a compact geodesic space.
is a compact geodesic space.
If \(\delta =0\), then \(\varepsilon _0(0)\) can be chosen arbitrarily large.
In the proof below we recall the relevant references from [14] and specify the dependence on \(\delta \).
Proof
By Proposition 4.5 in
[14] there is \(\varepsilon _0(\delta )>0\) such that if \(0< \varepsilon \le \varepsilon _0(\delta )\), then \(X_\varepsilon \) is an A-uniform space for some A depending only on \(\delta \). As \(X_\varepsilon \) is bounded, it follows from Proposition 2.20 in
[14] that  is a compact length space, which by Ascoli’s theorem or the Hopf–Rinow Theorem 2.1 is geodesic.
is a compact length space, which by Ascoli’s theorem or the Hopf–Rinow Theorem 2.1 is geodesic.
The bound \(\varepsilon _0(\delta )\) in Proposition 4.5 in [14] is only needed for the Gehring–Hayman lemma to be true, see [14, Theorem 5.1]. If \(\delta =0\), then any curve from x to y contains the unique geodesic [x, y] as a subcurve. From this the Gehring–Hayman lemma follows directly without any bound on \(\varepsilon \). Note that in this case it also follows that a curve in \(X=X_\varepsilon \) is simultaneously a geodesic with respect to d and \(d_\varepsilon \). \(\square \)
We recall, for further reference, the following key estimates from [14].
Lemma 2.7
( [14, Lemma 4.10]) There exists a constant \(C(\delta )\ge 1\) such that for every \(0<\varepsilon \le \varepsilon _0=\varepsilon _0(\delta )\) and all \(x,y\in X\),
Lemma 2.8
( [14, Lemma 4.16]) Let \(\varepsilon >0\). If \(x\in X\), then
where \(C_0=2e^{\varepsilon M}-1\). In particular, \(\varepsilon d_\varepsilon (x) \simeq \rho _\varepsilon (x)\), and \(x\rightarrow \partial _\varepsilon X\) with respect to \(d_\varepsilon \) if and only if \(d(x,z_0)\rightarrow \infty \).
Note that one may choose \(C_0 = 2e^{\varepsilon _0 M}-1\) for it to be independent of \(\varepsilon \), provided that \(0<\varepsilon \le \varepsilon _0\).
Corollary 2.9
Assume that \(0 < \varepsilon \le \varepsilon _0(\delta )\). Let \(x,y\in X\). If \(\varepsilon d(x,y)\ge 1\) then
where the comparison constants depend only on \(\delta \), M and \(\varepsilon _0\).
Proof
Since \(\varepsilon d(x,y)\ge 1\), (2.2) can be written as
where the comparison constants depend only on \(\delta \). Moreover, (2.3) gives
with comparison constants depending only on M and \(\varepsilon _0\). Dividing (2.4) by the last two formulas, and using the definition of \((x|y)_{z_0}\) concludes the proof. \(\square \)
We now wish to show that subWhitney balls in the uniformization \(X_\varepsilon \) are contained in balls of a fixed radius with respect to the Gromov hyperbolic metric d of X.
Theorem 2.10
For all \(0<\varepsilon \le \varepsilon _0(\delta )\), \(x\in X\) and \(0<r\le \tfrac{1}{2} d_\varepsilon (x)\), we have
where \(C_1=e^{-(1+\varepsilon M)}\) and \(C_2=2e(2e^{\varepsilon M}-1)\). If \(d_\varepsilon (x,y)< C_1d_\varepsilon (x)/2C_2\), then
Remark 2.11
As in Lemma 2.8, the constants \(C_1\) and \(C_2\) obtained for \(\varepsilon _0\) will do for \(\varepsilon <\varepsilon _0\) as well. The proof also shows that the condition \(0<r\le \tfrac{1}{2} d_\varepsilon (x)\) can be replaced by \(0<r\le c_0 d_\varepsilon (x)\) for any fixed \(0<c_0<1\), but then \(C_1\) and \(C_2\) also depend on \(c_0\) and get progressively worse as \(c_0\) approaches 1.
Proof
Assume that \(y\in B(x,C_1r/\rho _\varepsilon (x))\) and let \(\gamma \) be a d-geodesic from x to y. The assumption \(r\le \tfrac{1}{2} d_\varepsilon (x)\) and (2.3) then imply that for all \(z\in \gamma \),
The triangle inequality then yields \(d(z,z_0)\ge d(x,z_0)-d(x,z) \ge d(x,z_0)-1/\varepsilon e\) and hence
From this and (2.5) it readily follows that
To see the other inclusion, assume that \(d_\varepsilon (x,y)<r \le \tfrac{1}{2} d_\varepsilon (x)\) and let \(\gamma _\varepsilon \) be a geodesic curve in  connecting x to y. Then for all \(z\in \gamma _\varepsilon \), we have by the triangle inequality that
connecting x to y. Then for all \(z\in \gamma _\varepsilon \), we have by the triangle inequality that
in particular \(\gamma _\varepsilon \subset X_\varepsilon \). It now follows from (2.3) that
where \(C_2\) is as in the statement of the theorem. This implies that
and hence \(B_\varepsilon (x,r) \subset B(x,C_2r/\rho _\varepsilon (x))\).
Finally, if \(d_\varepsilon (x,y)<C_1d_\varepsilon (x)/2C_2\), then from the last inclusion above we see that \(y\in B(x,C_1s/\rho _\varepsilon (x))\) with \(s=\tfrac{1}{2}d_\varepsilon (x)\). Therefore we can apply (2.6) and (2.7) to obtain the last claim of the lemma. \(\square \)
In this paper, the letter C will denote various positive constants whose values may change even within a line. We write \(Y \lesssim Z\) if there is an implicit constant \(C>0\) such that \(Y \le CZ\), and analogously \(Y > rsim Z\) if \(Z \lesssim Y\). We also use the notation \(Y \simeq Z\) to mean \(Y \lesssim Z \lesssim Y\). We will point out how the comparison constants depend on various other constants related to the metric measure spaces under study.
3 Doubling Property
In the rest of this paper, we will continue to assume that X is a locally compact roughly starlike Gromov hyperbolic space. For general definitions and some results, we will assume that Y is a metric space equipped with a Borel measure \(\nu \).
Just as for X, we will denote the metric on Y by d, and balls in Y by B(x, r), but it should always be clear from the context in which space these concepts are taken.
Definition 3.1
A Borel measure \(\nu \), defined on a metric space Y, is globally doubling if
whenever \(x\in Y\) and \(r>0\). If this holds only for balls of radii \(\le R_0\), then we say that \(\nu \) is doubling for balls of radii at most \(R_0\), and also that \(\nu \) is uniformly locally doubling.
The following result shows that the last condition is independent of \(R_0\), provided that Y is quasiconvex. Without assuming quasiconvexity this is not true as shown by Example 3.3 below.
Proposition 3.2
Assume that Y is L-quasiconvex and that \(\nu \) is doubling on Y for balls of radii at most \(R_0\), with a doubling constant \(C_d\). Let \(R_1>0\). Then \(\nu \) is doubling on Y for balls of radii at most \(R_1\) with a doubling constant depending only on \(R_1/R_0\), L and \(C_d\).
Example 3.3
Let \(X=([0,\infty ) \times \{0,1\}) \cup (\{0\} \times [0,1])\) equipped with the Euclidean distance and the measure \(\mathrm{{d}}\mu =w\, d{\mathcal {L}}^1\), where \({\mathcal {L}}^1\) is the Lebesgue measure and
Then X is a connected nonquasiconvex space and \(\mu \) is doubling for balls of radii at most \(R_0\) if and only if \(R_0 \le \frac{1}{2}\). This shows that the quasiconvexity assumption in Proposition 3.2 cannot be dropped.
Before proving Proposition 3.2 we deduce the following lemmas. In particular, Lemma 3.5 covers Proposition 3.2 under the extra assumption that Y is a length space, but with better control of the doubling constant than what is possible in general quasiconvex spaces.
Lemma 3.4
Assume that \(\nu \) is doubling on Y for balls of radii at most \(R_0\), with a doubling constant \(C_d\). Then every ball B of radius \(r\le \tfrac{7}{4}R_0\) can be covered by at most \(C_d^7\) balls with centers in B and radius \(\frac{1}{7} r\).
Proof
Find a maximal pairwise disjoint collection of balls \(B_j\) with centers in B and radii \(\tfrac{1}{14}r\). Note that for each j,
The doubling property then implies that
From this and the pairwise disjointness of all \(B_j\) we thus obtain
i.e. there are at most \(C_d^7\) such balls. As the balls \(2B_j\) cover B, we are done. \(\square \)
Lemma 3.5
Assume that Y is a length space and that \(\nu \) is doubling on Y for balls of radii at most \(R_0\), with a doubling constant \(C_d\). Let n be a positive integer. Then the following are true:
-
(a)
If \(x,x'\in Y\), \(0<r\le R_0\) and \(d(x,x')< nr\), then
$$\begin{aligned} \nu (B(x',r)) \le C_d^n \nu (B(x,r)). \end{aligned}$$ -
(b)
Every ball B of radius nr, with \(r\le \tfrac{1}{4} R_0\), can be covered by at most \(C_d^{7(n+4)/6}\) balls of radius r, \(n=1,2, \ldots \)
In particular, for any \(R_1>0\), \(\nu \) is doubling on Y for balls of radii at most \(R_1\) with a doubling constant depending only on \(R_1/R_0\) and \(C_d\).
Proof
(a) Connect x and \(x'\) by a curve of length \(l_\gamma < nr\). Along this curve, we can find balls \(B_j\) of radius r, \(j=0,1,\ldots ,n\), such that \(B_0=B(x,r)\), \(B_n=B(x',r)\) and \(B_j\subset 2B_{j-1}\). An iteration of the doubling property gives the desired estimate.
(b) Assume that \(\varphi (n)\) is the smallest number such that each ball B(x, nr) is covered by \(\varphi (n)\) balls \(B_j\) of radius r. As Y is a length space, the balls \(7B_j\) cover \(B(x,(n+6)r)\). Using Lemma 3.4, each \(7B_j\) can in turn be covered by at most \(C_d^7\) balls of radius r, which implies that \(\varphi (n+6)\le C_d^{7} \varphi (n)\). Since \(\varphi (1)=1\) and \(\varphi \) is nondecreasing, the statement follows by induction. \(\square \)
Proof of Proposition 3.2
We will use the inner metric \(d_{{{\,\mathrm{in}\,}}}\), defined in (2.1), and denote balls with respect to \(d_{{{\,\mathrm{in}\,}}}\) by \(B_{{{\,\mathrm{in}\,}}}\). It follows from the inclusions
together with a repeated use of the doubling property for metric balls, that \(\nu \) is doubling for inner balls of radii at most \(R_0\). As \((X,d_{{{\,\mathrm{in}\,}}})\) is a length space, it thus follows from Lemma 3.5 that \(\nu \) is doubling for inner balls of radii at most \(LR_1\). Hence, using the inclusions (3.1) again, \(\nu \) is doubling for metric balls of radii at most \(R_1\). \(\square \)
4 The Measure \(\mu _\beta \) is Globally Doubling on \(X_\varepsilon \)
Standing assumptions for this section will be given after Example 4.3.
Given a uniformly locally doubling measure \(\mu \) on the Gromov hyperbolic space X, we wish to obtain a globally doubling measure on its uniformization \(X_\varepsilon \). We do so as follows.
Definition 4.1
Assume that X is a locally compact roughly starlike Gromov hyperbolic space equipped with a Borel measure \(\mu \), and that \(z_0 \in X\).
Fix \(\beta >0\), and set \(\mu _\beta \) to be the measure on \(X=X_\varepsilon \) given by
We also extend this measure to  by letting
by letting  .
.
Our aim in this section is to show that \(\mu _\beta \) is a globally doubling measure on  , under suitable assumptions (see Theorem 4.9).
, under suitable assumptions (see Theorem 4.9).
Bonk–Heinonen–Koskela [14, Theorem 1.1] showed that there is a kind of duality between Gromov hyperbolic spaces and bounded uniform domains, see the introduction for further details. Here we also equip these spaces with measures. The following examples illustrate what happens in a simple case.
Example 4.2
The Euclidean real line \(X={\mathbf {R}}\) is Gromov hyperbolic, because it is a metric tree. Since \(\delta =0\), any \(\varepsilon >0\) is allowed in the uniformization process, by Theorem 2.6. Setting \(z_0=0\), we now determine what \(X_\varepsilon \) is. For \(x,y\in {\mathbf {R}}\), the uniformized metric is given by
With \(y=0\) we get \(d_\varepsilon (x,0)=(1-e^{-\varepsilon |x|})/\varepsilon \). Hence the map \(\Phi :X_\varepsilon \rightarrow (-1/\varepsilon ,1/\varepsilon )\) given by
is an isometry, identifying \(X_\varepsilon \) with the open interval \((-1/\varepsilon ,1/\varepsilon )\).
However, when X is equipped with the Lebesgue measure \({\mathcal {L}}^1\), the measure \(\mu _\beta \) is not the Lebesgue measure on \((-1/\varepsilon ,1/\varepsilon )\). To determine \(\mu _\beta \), note that it is absolutely continuous with respect to the Lebesgue measure \({\mathcal {L}}^1\) on the interval \((-1/\varepsilon ,1/\varepsilon )\). So we compute the Radon–Nikodym derivative of \(\mu _\beta \) with respect to \({\mathcal {L}}^1\). By symmetry, it suffices to consider \(x>0\). Then
Substituting \(\Phi (x)=z\) in the above, we get
where \(d_\varepsilon (z)=1/\varepsilon -z\) is the distance from \(\Phi (x)=z\ge 0\) to the boundary \(\{\pm 1/\varepsilon \}\) of \(\Phi (X_\varepsilon )\).
Similarly, if \(X={\mathbf {R}}\) is equipped with a weighted measure
then as in (4.1),
The following example reverses the procedure in Example 4.2.
Example 4.3
The interval \(X=(-1,1)\) is a uniform domain and so, by Theorem 3.6 in Bonk–Heinonen–Koskela [14], it becomes a Gromov hyperbolic space when equipped with the quasihyperbolic metric k. The quasihyperbolic metric is for \(0\le y<z<1\) given by
cf. Sect. 7. With \(z_0=0\), by symmetry, we have \(k(z,z_0)=\log (1/(1-|z|))\) for \(z \in X\). Hence we consider the map \(\Psi :(-1,1)\rightarrow {\mathbf {R}}\) given by
and see that \(\Psi \) is an isometry between the Gromov hyperbolic space (X, k) and the Euclidean line \({\mathbf {R}}\). By Example 4.2 with \(\varepsilon =1\), the uniformization of \({\mathbf {R}}\) gives back the Euclidean interval \((-1,1)\).
We wish to find a measure \(\mu \) on \((X,k)={\mathbf {R}}\) such that the weighted measure \(\mu _\beta \) given by Definition 4.1 becomes the Lebesgue measure on \((-1,1)\). In view of (4.2) with \(\varepsilon =1\) and \(\Phi =\Psi ^{-1}\), \(\mu \) is given by \(\mathrm{{d}}\mu (x)=w(x)\,\mathrm{d}{\mathcal {L}}^1(x)\), where
In the rest of this section, we assume that X is a locally compact roughly starlike Gromov \(\delta \)-hyperbolic space equipped with a measure \(\mu \) which is doubling on X for balls of radii at most \(R_0\), with a doubling constant \(C_d\). We also fix a point \(z_0 \in X\), let M be the constant in the roughly starlike condition with respect to \(z_0\), and assume that
Finally, we let \(X_\varepsilon \) be the uniformization of X with uniformization center \(z_0\).
In specific cases one may want to consider how to optimally choose \(R_0\), and the corresponding \(C_d\), in the formula for \(\beta _0\). The factor \(\frac{17}{3}\) comes from various estimates leading up to the proof of Proposition 4.7, and is not likely to be optimal. The following example shows however that it is not too far from optimal and that it cannot be replaced by any constant \(<1\).
Example 4.4
Let X be the infinite regular K-ary metric tree, equipped with the Lebesgue measure \(\mu \), as in Björn–Björn–Gill–Shanmugalingam [8, Sect. 3]. Since it is a tree, any \(\varepsilon >0\) is allowed for uniformization.
If \(C_d(R)\) is the optimal doubling constant for radii \(\le R\), then a straightforward calculation shows that
and thus we are allowed, in this paper, to use any
In this specific case, it was shown in [8, Corollary 3.9] that \(\mu _\beta \) is globally doubling and supports a global 1-Poincaré inequality on \(X_\varepsilon \) whenever \(\beta > \log K\). For \(\beta \le \log K\), \(\mu _\beta (X_\varepsilon )= \infty \) and \(\mu _\beta \) cannot possibly be globally doubling on the bounded space \(X_\varepsilon \).
The following lemma gives us an estimate of \(\mu _\beta (B)\) for subWhitney balls B.
Lemma 4.5
Let \(x\in X\) and \(0<r\le \tfrac{1}{2} d_\varepsilon (x)\). Then
with comparison constants depending only on M, \(\varepsilon \), \(C_d\), \(R_0\) and \(\beta \).
Proof
By Lemma 2.8, we have for all \(y\in B_\varepsilon (x,r)\),
Moreover, Theorem 2.10 implies that
This yields
and similarly, \(\mu _\beta (B_\varepsilon (x,r)) > rsim \rho _\beta (x) \mu (B(x,C_1 r/\rho _\varepsilon (x))\). Finally, Lemma 3.5 shows that the last two balls in X have measure comparable to \(\mu (B(x,r/\rho _\varepsilon (x))\), which concludes the proof. \(\square \)
Remark 4.6
Lemma 4.5 implies that if \(\mu _\beta \) is globally doubling on \(X_\varepsilon \) then \(\mu \) is uniformly locally doubling on X, i.e. the converse of Theorem 1.1 (a) holds. Indeed, if \(0<r\le \frac{1}{4e\varepsilon }\) and \(x\in X\), then \(2r\rho _\varepsilon (x) \le \tfrac{1}{2} d_\varepsilon (x)\), by (2.3). Lemma 4.5, with r replaced by \(2r\rho _\varepsilon (x)\) and \(r\rho _\varepsilon (x)\), respectively, then gives
Similar arguments, combined with the arguments in the proof of Lemma 6.1, show that if \(\mu _\beta \) also supports a global p-Poincaré inequality on \(X_\varepsilon \) or  then \(\mu \) supports a uniformly local p-Poincaré inequality on X, i.e. the converse of Theorem 1.1 (b) holds.
then \(\mu \) supports a uniformly local p-Poincaré inequality on X, i.e. the converse of Theorem 1.1 (b) holds.
We shall now estimate \(\mu _\beta (B)\) for balls B centered at \(\partial _\varepsilon X\) in terms of the (essentially) largest Whitney ball contained in B. The existence of such balls is given by Lemma 4.8 below.
Proposition 4.7
Let \(\xi \in \partial _\varepsilon X\) and \(0<r\le 2{{\,\mathrm{diam}\,}}_\varepsilon X_\varepsilon \). Assume that \(a_0>0\) and \(z \in X\) are such that \(B_\varepsilon (z,a_0r)\subset B_\varepsilon (\xi ,r)\) and \(d_\varepsilon (z)\ge 2a_0 r\). Then,
where the comparison constants depend only on \(\delta \), M, \(\varepsilon \), \(C_d\), \(R_0\), \(\beta \) and \(a_0\).
Proof
For \(n=1,2,\ldots \) , define the boundary layers
Corollary 2.9 implies that for every \(x\in A_n\), either \(\varepsilon d(x,z)<1\) or
and hence \(\varepsilon d(x,z) < n+C\), where C depends only on \(\delta \), M, \(\varepsilon \) and \(a_0\).
Using Lemma 3.5 (b), we can thus cover each layer \(A_n\subset B(z,(n+C)/\varepsilon )\) by \(N_n\lesssim C_d^{14n/3\varepsilon R_0}\) balls \(B_{n,j}\) with centers in \(B(z,(n+C)/\varepsilon )\) and radius \(R_0\). Since \(X_\varepsilon \) is geodesic, Lemma 3.5 (a) implies that each of these balls satisfies
Moreover, as in (4.4) we see that \(\rho _\beta (z) = \rho _\varepsilon (z)^{\beta /\varepsilon } \simeq (\varepsilon d_\varepsilon (z))^{\beta /\varepsilon } \simeq (\varepsilon r)^{\beta /\varepsilon }\) and
It thus follows that
and hence for \(\beta >\beta _0=17(\log C_d)/3R_0\),
Since \(a_0 r\le \tfrac{1}{2} d_\varepsilon (z)\), Lemma 4.5 implies that
By (2.3) we see that
and hence, by the doubling property for \(\mu \) on X,
\(\square \)
The following lemma shows how to pick z and \(a_0\) in Proposition 4.7.
Lemma 4.8
Let \(0<a_0< a:=\min \{\tfrac{1}{8},\frac{1}{6A}\}\), where \(A=A(\delta )\) is as in Theorem 2.6. Then for every  and every \(0<r\le 2{{\,\mathrm{diam}\,}}_\varepsilon X_\varepsilon \) we can find a ball \(B_\varepsilon (z,a_0 r) \subset B_\varepsilon (x,r)\) such that \(d_\varepsilon (z)\ge 2a_0r\).
and every \(0<r\le 2{{\,\mathrm{diam}\,}}_\varepsilon X_\varepsilon \) we can find a ball \(B_\varepsilon (z,a_0 r) \subset B_\varepsilon (x,r)\) such that \(d_\varepsilon (z)\ge 2a_0r\).
Proof
First, assume that \(x\in X_\varepsilon \). By Theorem 2.6, there is an A-uniform curve \(\gamma \) from x to \(z_0\), parametrized by arc length \(\mathrm{{d}}s_\varepsilon \). If \(l_\varepsilon (\gamma ) \ge \tfrac{2}{3}r\) then for \(z=\gamma (\tfrac{1}{3}r)\) we have
Thus, any \(a_0\le \frac{1}{6A}\) will do in this case. If \(l_\varepsilon (\gamma ) < \tfrac{2}{3}r \), then letting \(z=z_0\) yields
and for \(a_0 \le \tfrac{1}{8}\),
This proves the lemma for \(x\in X_\varepsilon \). For \(x\in \partial _\varepsilon X\) and any \(0<a_0<a\), choose \(r'=a_0r/a\) and \(x'\in X_\varepsilon \) sufficiently close to x so that, with the corresponding z,
\(\square \)
Lemma 4.5 and Proposition 4.7 can be summarized in the following result, which roughly says that in \((X_\varepsilon ,\mu _\beta )\), the measure of every ball is comparable to the measure of the (essentially) largest Whitney ball contained in it.
Theorem 4.9
The measure \(\mu _\beta \) is globally doubling on  .
.
Moreover, with \(a_0\) and z provided by Lemma 4.8, we have for every  and \(0<r\le 2{{\,\mathrm{diam}\,}}_\varepsilon X_\varepsilon \),
and \(0<r\le 2{{\,\mathrm{diam}\,}}_\varepsilon X_\varepsilon \),
where the comparison constants depend only on \(\delta \), M, \(\varepsilon \), \(C_d\), \(R_0\), \(\beta \) and \(a_0\).
It follows directly that \(\mu _\beta \) is globally doubling also on \(X_\varepsilon \). The optimal doubling constants are the same, by Proposition 3.3 in Björn–Björn [7].
Proof
We start by proving the measure estimate (4.6). As \(a_0 r\le \tfrac{1}{2} d_\varepsilon (z)\), Lemma 4.5 applied to \(B_\varepsilon (z,a_0 r)\) implies that
If \(0<r\le \tfrac{1}{2} d_\varepsilon (x)\) then by (4.4), (4.5) and Lemma 2.8,
Lemma 3.5 then implies that
and another application of Lemma 4.5, this time to \(B_\varepsilon (x,r)\), proves (4.6) in this case.
If \(r\ge \tfrac{1}{2} d_\varepsilon (x)\) then \(B_\varepsilon (x,r) \subset B_\varepsilon (\xi ,3r)\) for some \(\xi \in \partial _\varepsilon X\). Proposition 4.7 (with \(a_0\) replaced by \(\frac{1}{3} a_0\)) then implies
which together with (4.7) proves (4.6) also in this case.
To conclude the doubling property, use the Whitney ball \(B_\varepsilon (z,a_0 r)\) for both \(B_\varepsilon (x,r)\) and \(B_\varepsilon (x,2r)\), with constants \(a_0\) and \(a'_0=\frac{1}{2} a_0\), respectively. Since
we have by (4.6), first used with \(a_0'\) and then with \(a_0\),
\(\square \)
We conclude this section with an estimate of the lower and upper dimensions for the measure \(\mu _\beta \) at \(\partial _\varepsilon X\).
Lemma 4.10
Let

Then for all \(\xi \in \partial _\varepsilon X\) and all \(0<r\le r'\le 2{{\,\mathrm{diam}\,}}_\varepsilon X_\varepsilon \),

with comparison constants depending only on \(\delta \), M, \(\varepsilon \), \(C_d\), \(R_0\), \(\beta \) and the constant \(a_0\) from Theorem 2.6.
Note that  , because \(\beta > \beta _0\), where \(\beta _0\) is as in (4.3).
, because \(\beta > \beta _0\), where \(\beta _0\) is as in (4.3).
Proof
Proposition 4.7 and Lemma 4.8 imply that there are \(z,z' \in X\) such that
where
From Corollary 2.9 we conclude that if \(\varepsilon d(z,z') \ge 1\) then
and hence \(d(z,z') \le \frac{1}{\varepsilon }(C+\log (r'/r))\) holds regardless of the value of \(d(z,z')\). Lemma 3.5 (a) with \(n = \lceil d(z,z')/R_0 \rceil \) (the smallest integer \(\ge d(z,z')/R_0\)) then implies that
which together with (4.8) proves the first inequality in the lemma. The second inequality follows similarly by interchanging z and \(z'\) in (4.9). \(\square \)
5 Upper Gradients and Poincaré Inequalities
We assume in this section that \(1 \le p<\infty \) and that \(Y=(Y,d,\nu )\) is a metric space equipped with a complete Borel measure \(\nu \) such that \(0<\nu (B)<\infty \) for all balls \(B \subset Y\).
We follow Heinonen and Koskela [29] in introducing upper gradients as follows (in [29] they are referred to as very weak gradients).
Definition 5.1
A Borel function \(g:Y \rightarrow [0,\infty ]\) is an upper gradient of an extended real-valued function u on Y if for all arc length parametrized curves \(\gamma : [0,l_{\gamma }] \rightarrow Y\),
where we follow the convention that the left-hand side is considered to be \(\infty \) whenever at least one of the terms therein is \(\pm \infty \). If g is a nonnegative measurable function on Y and if (5.1) holds for p-almost every curve (see below), then g is a p -weak upper gradient of u.
We say that a property holds for p-almost every curve if it fails only for a curve family \(\Gamma \) with zero p-modulus, i.e. there is a Borel function \(0\le \rho \in L^p(Y)\) such that \(\int _\gamma \rho \,\mathrm{{d}}s=\infty \) for every curve \(\gamma \in \Gamma \). The p-weak upper gradients were introduced in Koskela–MacManus [34]. It was also shown therein that if \(g \in L^p_{\mathrm{loc}}(Y)\) is a p-weak upper gradient of u, then one can find a sequence \(\{g_j\}_{j=1}^\infty \) of upper gradients of u such that \(\Vert g_j-g\Vert _{L^p(Y)} \rightarrow 0\).
If u has an upper gradient in \(L^p_{\mathrm{loc}}(Y)\), then it has a minimal p-weak upper gradient \(g_u \in L^p_{\mathrm{loc}}(Y)\) in the sense that for every p-weak upper gradient \(g \in L^p_{\mathrm{loc}}(Y)\) of u we have \(g_u \le g\) a.e., see Shanmugalingam [37] (or [5] or [30]). The minimal p-weak upper gradient is well-defined up to a set of measure zero.
Definition 5.2
Y (or \(\nu \)) supports a global p-Poincaré inequality if there exist constants \(\lambda \ge 1\) (called dilation) and \(C_{\mathrm{PI}}>0\) such that for all balls \(B \subset Y\), all bounded measurable functions u on Y and all upper gradients g of u,

where  .
.
If this holds only for balls B of radii \(\le R_0\), then we say that \(\nu \) supports a p-Poincaré inequality for balls of radii at most \(R_0\), and also that Y (or \(\nu \)) supports a uniformly local p-Poincaré inequality.
Multiplying bounded measurable functions by suitable cut-off functions and truncating integrable functions shows that one may replace “bounded measurable” by “integrable” in the definition. On the other hand, the proofs of [30, Lemma 8.1.5 and Theorem 8.1.53] show that (5.2) can equivalently be required for all (not necessarily bounded) measurable functions u on \(\lambda B\) and all upper (or p-weak upper) gradients g of u. See also [5, Proposition 4.13], [30, Theorem 8.1.49], Hajłasz–Koskela [26, Theorem 3.2], Heinonen–Koskela [29, Lemma 5.15] and Keith [32, Theorem 2] for further equivalent versions.
Theorem 5.3
Assume that \(\nu \) is doubling and supports a p-Poincaré inequality, both properties holding for balls of radii at most \(R_0\). Also assume that Y is L-quasiconvex and that \(R_1 >0\).
Then \(\nu \) supports a p-Poincaré inequality, with dilation constant L, for balls of radii at most \(R_1\).
The proof below can be easily adapted to show that the same is true for so-called (q, p)-Poincaré inequalities. The following examples show that the quasiconvexity assumption cannot be dropped even if one assumes that \(\nu \) is globally doubling, and that one cannot replace L in the conclusion by the dilation constant in the assumed p-Poincaré inequality, nor any fixed multiple of it.
Example 5.4
Let \(X=([0,\infty ) \times \{0,1\}) \cup (\{0\} \times [0,1])\) equipped with the Euclidean distance and the Lebesgue measure \({\mathcal {L}}^1\). Then X is a connected nonquasiconvex space and \({\mathcal {L}}^1\) is globally doubling on X. However, \({\mathcal {L}}^1\) supports a p-Poincaré inequality on X, \(p \ge 1\), for balls of radii at most \(R_0\) if and only if \(R_0 \le 1\). In this case one can choose the dilation constant \(\lambda =1\). This shows that the quasiconvexity assumption in Theorem 5.3 cannot be dropped.
Example 5.5
For \(a \ge 1\), let \(X=([0,a] \times \{0,1\}) \cup (\{0\} \times [0,1])\), equipped with the Euclidean distance and the Lebesgue measure \({\mathcal {L}}^1\). Then X is a connected \((2a+1)\)-quasiconvex space and \({\mathcal {L}}^1\) is globally doubling on X. In this case, \({\mathcal {L}}^1\) supports a p-Poincaré inequality on X, \(p \ge 1\), for balls of radii at most \(R_0\) for any \(R_0>0\), with the optimal dilation
This shows that the dilation constant L in the conclusion of Theorem 5.3 cannot in general be replaced by the dilation constant in the p-Poincaré inequality assumed for balls \(\le R_0\), nor any fixed multiple of it.
Proof of Theorem 5.3
The arguments are similar to the proof of Theorem 4.4 in Björn–Björn [6]. Let \(C_d\), \(C_{\mathrm{PI}}\) and \(\lambda \) be the constants in the doubling property and the p-Poincaré inequality for balls of radii \(\le R_0\). Let B be a ball of radius \(r_B\le \tfrac{5}{2} LR_1=:R_2\). We can assume that \(r_B>R_0\).
First, note that the conclusions in the first paragraph of the proof in [6] with \(B_0=B\), \(\sigma =L\), \(r'=R_0/\lambda \) and \(\mu \) replaced by \(\nu \), follow directly from our assumptions, without appealing to Lemma 4.7 nor Proposition 4.8 in [6]. This and the use of Lemma 3.4 explains why there is no need to assume properness here.
By Lemma 3.5, \(\nu \) is doubling for balls of radii \(\le 7LR_2\), with doubling constant \(C_d'\), depending only on \(C_d\) and \(LR_2/R_0\). Hence, using Lemma 3.4, we can cover B by at most \((C_d')^{7\lceil \log _7 (R_2/r')\rceil }\) balls \(B'_j\) with radius \(r'\). Their centers can then be connected by L-quasiconvex curves. As in the proof of [6, Theorem 4.4], we then construct along these curves a chain \(\{B_j\}_{j=1}^N\) of balls of radius \(r'\), covering B and with a uniform bound on N. It follows that the constant \(C''\) in the proof of [6, Theorem 4.4] only depends on \(C_d\), \(C_{\mathrm{PI}}\), \(\lambda \), L and \(R_2/R_0\). Thus we conclude from the last but one displayed formula in the proof of [6, Theorem 4.4] (with \(B_0=B\)) that \(\nu \) supports a p-Poincaré inequality for balls of radii at most \(R_2\), with dilation 2L.
That we can replace 2L by L now follows from [6, Theorem 5.1], provided that we decrease the bound on the radii to \(R_1\). \(\square \)
6 Poincaré Inequality on \(X_\varepsilon \)
In this section, we assume that X is a locally compact roughly starlike Gromov \(\delta \)-hyperbolic space equipped with a Borel measure \(\mu \). We also fix a point \(z_0 \in X\), let M be the constant in the roughly starlike condition with respect to \(z_0\), and assume that
Finally, we let \(X_\varepsilon \) be the uniformization of X with uniformization center \(z_0\).
The following lemma shows that the p-Poincaré inequality holds for \(\mu _\beta \) on sufficiently small subWhitney balls in \(X_\varepsilon \). Recall that \(\beta _0= (17\log C_d)/3R_0\) as in (4.3).
Lemma 6.1
Assume that \(\mu \) is doubling, with constant \(C_d\), and supports a p-Poincaré inequality, with constants \(C_{\mathrm{PI}}\) and \(\lambda \), both properties holding for balls of radii at most \(R_0\). Let \(\beta > \beta _0\).
Then there exists \(c_0>0\), depending only on \(\delta \), M, \(\varepsilon \), \(R_0\) and \(\lambda \), such that for all \(x\in X_\varepsilon \) and all \(0<r\le c_0 d_\varepsilon (x)\), the p-Poincaré inequality for \(\mu _\beta \) holds on \(B_\varepsilon =B_\varepsilon (x,r)\), i.e. for all bounded measurable functions u and upper gradients \(g_\varepsilon \) of u on \(X_\varepsilon \) we have

where \(\tau =C_2\lambda /C_1\), with \(C_1\) and \(C_2\) from Theorem 2.10, and C depends only on \(\delta \), M, \(\varepsilon \), \(C_d\), \(R_0\), \(\beta \), \(\lambda \) and \(C_{\mathrm{PI}}\).
Proof
Theorem 2.10 shows that if \(c_0\le C_1/2C_2\lambda \) then
Moreover, as in (4.4) we have for all \(y\in \tau B_\varepsilon \),
Hence, by Theorem 4.9, all the balls in (6.1) have comparable \(\mu _\beta \)-measures, as well as comparable \(\mu \)-measures.
Let u be a bounded measurable function on \(X_\varepsilon \), or equivalently on X, and let \(g_\varepsilon \) be an upper gradient of u on \(X_\varepsilon \). Since the arc length parametrization \(\mathrm{{d}}s_\varepsilon \) with respect to \(d_\varepsilon \) satisfies \(\mathrm{{d}}s_\varepsilon = \rho _\varepsilon \,\mathrm{{d}}s\), we conclude that for all compact rectifiable curves \(\gamma \) in \(X_\varepsilon \),
and thus \(g:= g_\varepsilon \rho _\varepsilon \) is an upper gradient of u on X. (Note that a compact curve in X is rectifiable with respect to d if and only if it is rectifiable with respect to \(d_\varepsilon \).) If \(c_0\le R_0\varepsilon /C_2 (2e^{\varepsilon _0M}-1)\), then by Lemma 2.8,
and thus the p-Poincaré inequality holds on B. Using (6.2) we then obtain

Finally, a standard argument based on the triangle inequality makes it possible to replace \(u_{B,\mu }\) on the left-hand side by \(u_{B_\varepsilon ,\mu _\beta }\). \(\square \)
Bonk–Heinonen–Koskela [14, Sect. 6] proved that if \(\Omega \) is a locally compact uniform space equipped with a measure \(\mu \) such that \((\Omega ,\mu )\) is uniformly Q-Loewner in subWhitney balls, then \(\Omega \) is globally Q-Loewner, where \(Q>1\). If \(\mu \) is locally doubling with \(\mu (B(x,r)) > rsim r^Q\) whenever B(x, r) is a subWhitney ball, then the local Q-Loewner condition is equivalent to an analogous local Q-Poincaré inequality, see [29, Theorems 5.7 and 5.9].
We have shown above that the measure \(\mu _\beta \) on the uniformized space \(X_\varepsilon \) is globally doubling and supports a p-Poincaré inequality for subWhitney balls. Following the philosophy of [14, Theorem 6.4], the next theorem demonstrates that the p-Poincaré inequality is actually global on \(X_\varepsilon \).
Theorem 6.2
Assume that \(\mu \) is doubling and supports a p-Poincaré inequality on X, both properties holding for balls of radii at most \(R_0\). Let \(\beta > \beta _0\) and \(\lambda >1\).
Then \(\mu _\beta \) is globally doubling and supports a global p-Poincaré inequality on  with dilation 1, and on \(X_\varepsilon \) with dilation \(\lambda \).
with dilation 1, and on \(X_\varepsilon \) with dilation \(\lambda \).
If \(X_\varepsilon \) happens to be geodesic, then it follows from the proof below that we can choose the dilation constant \(\lambda =1\) also on \(X_\varepsilon \).
Proof
The global doubling property follows from Theorem 4.9, both on \(X_\varepsilon \) and  . Since \(X_\varepsilon \) is a length space and Lemma 6.1 shows that the p-Poincaré inequality on \(X_\varepsilon \) holds for subWhitney balls, the global p-Poincaré inequality on \(X_\varepsilon \), with dilation \(\lambda >1\), follows from the following proposition. Moreover, as
. Since \(X_\varepsilon \) is a length space and Lemma 6.1 shows that the p-Poincaré inequality on \(X_\varepsilon \) holds for subWhitney balls, the global p-Poincaré inequality on \(X_\varepsilon \), with dilation \(\lambda >1\), follows from the following proposition. Moreover, as  is geodesic, the global p-Poincaré inequality on
is geodesic, the global p-Poincaré inequality on  , with dilation 1, also follows from the following proposition. \(\square \)
, with dilation 1, also follows from the following proposition. \(\square \)
Proposition 6.3
Let \((\Omega ,d)\) be a bounded A-uniform space equipped with a globally doubling measure \(\nu \), which supports a p-Poincaré inequality for all subWhitney balls corresponding to some fixed \(0<c_0<1\). Assume that \(\Omega \) is L-quasiconvex. Then \(\nu \) supports a global p-Poincaré inequality on \(\Omega \) with dilation L.
If moreover the completion \({\overline{\Omega }}\) is \(L'\)-quasiconvex, then \(\nu \), extended by \(\nu (\partial \Omega )=0\), supports a global p-Poincaré inequality on \({\overline{\Omega }}\) with dilation \(L'\).
Recall that \(\Omega \) is always A-quasiconvex by the A-uniformity condition, but that L may be smaller than A. Also, \({\overline{\Omega }}\) is always L-quasiconvex, but it is possible to have \(L'<L\).
Proof
Let \(x_0\in \Omega \), \(0<r\le 2{{\,\mathrm{diam}\,}}\Omega \) and \(B_0=B(x_0,r)\) be fixed. The balls in this proof are with respect to \(\Omega \). It is well known, and easily shown using the arguments in the proof of Lemma 4.8, that uniform spaces satisfy the corkscrew condition, i.e. there exists \(a_0\) (independent of \(x_0\) and r) and z such that \(d_\Omega (z)\ge 2a_0r\) and \(B(z,a_0r)\subset B_0\), cf. Björn–Shanmugalingam [13, Lemma 4.2]. With \(c_0\) as in the assumptions of the proposition, let
Since \(\Omega \) is A-uniform, [13, Lemma 4.3] with \(\rho _0=r_0\) and \(\sigma =1/c_0\) provides us for every \(x\in B_0\) with a chain
of balls connecting the ball \(B_{0,0} := B(z,r_0)\) to x as follows:
-
(a)
For all i and j we have \(m_i \le Ar/r_0 = 8A^2/a_0 c_0\),
$$\begin{aligned} 4r_i \le c_0 d_\Omega (x_{i,j}) \quad \text {and} \quad d(x_{i,j},x) \le 2^{-i}A d(x,z) < 2^{-i}Ar. \end{aligned}$$ -
(b)
For large i, we have \(m_i=0\) and the balls \({B_{i,0}}\) are centered at x.
-
(c)
The balls are ordered lexicographically, i.e. \({B_{i,j}}\) comes before \(B_{i',j'}\) if and only if \(i<i'\), or \(i=i'\) and \(j<j'\). If \(B^*\) denotes the immediate successor of \(B\in \mathcal{B}_x\) then \(B \cap B^*\) is nonempty.
Let u be a bounded measurable function on \(\Omega \) and g be an upper gradient of u in \(\Omega \). If \(x\in B_0\) is a Lebesgue point of u then
where \(u_{B} = u_{B,\nu }\) and similarly for other balls. Moreover, \(B^*\subset 3B\) and
As \(3r_i \le c_0 d_\Omega (x_{i,j})\) and the radii of B and \(B^*\) differ by at most a factor 2, an application of the p-Poincaré inequality on 3B shows that

where \(r_B\) is the radius of B and \(\lambda \) is the dilation constant in the assumed p-Poincaré inequality for subWhitney balls. The difference \(|u_{3B} - u_{B}|\) is estimated in the same way. Hence, inserting these estimates into (6.4),

We now wish to estimate the measure of level sets of the function \(x\mapsto |u(x)-u_{B_{0,0}}|\) in \(B_0\). Assume that \(|u(x)-u_{B_{0,0}}| \ge t\) and write \(t= C_\alpha N t \sum _{i=0}^{\infty } 2^{-i\alpha }\), where \(\alpha \in (0,1)\) will be chosen later, and \(N\le 1+Ar/R_0 = 1+8A^2/a_0 c_0 \) is the maximal number of balls in \(\mathcal{B}_x\) with the same radius. Then

Hence, there exists \(B_x = B(x_{i,j},r_i) \in \mathcal{B}_x\) such that

We have \(2^{-i} = r_i/r_0 = 8 Ar_i/a_0 c_0 r\), and inserting this into the last inequality yields

As \(\nu \) is globally doubling, there exists \(s>0\) independent of \(B_x\) such that
see e.g. [5, Lemma 3.3] or [30, (3.4.9)]. Hence

and choosing \(\alpha \in (0,1)\) so that \(\theta := 1- (1-\alpha )p/s \in (0,1)\), we obtain
Let \(E_t = \{x \in B_0: |u(x)-u_{B_{0,0}}| \ge t\}\) and \(F_t\) be the set of all points in \(E_t\) which are Lebesgue points of u. The global doubling property of \(\nu \) guarantees that a.e. x is a Lebesgue point of u, see Heinonen [27, Theorem 1.8]. By the above, for every \(x\in F_t\) there exists \(B_x \in \mathcal{B}_x\) satisfying (6.5). Note also that by construction of the chain, we have \(x\in B'_x:=8(a_0 c_0)^{-1} A^2 B_x\). The balls \(\{B'_x\}_{x\in F_t}\), therefore cover \(F_t\). The 5-covering lemma (Theorem 1.2 in Heinonen [27]) provides us with a pairwise disjoint collection \(\{\lambda {B'_{x_i}}\}_{i=1}^{\infty }\) such that the union of all balls \(5\lambda {B'_{x_i}}\) covers \(F_t\). Then the balls \(3\lambda {B_{x_i}}\subset \lambda {B'_{x_i}}\) are also pairwise disjoint and the global doubling property of \(\nu \), together with (6.5), yields
where \(\Lambda \) depends only on A, \(\lambda \), \(a_0\) and \(c_0\). Lemma 4.22 in Heinonen [27], which can be proved using the Cavalieri principle, now implies that

and a standard argument based on the triangle inequality allows us to replace \(u_{B_{0,0}}\) by \(u_{B_0}\).
Since \(\Omega \) is L-quasiconvex, it follows from [5, Theorem 4.39] that the dilation \(\Lambda \) in the obtained global p-Poincaré inequality can be replaced by L.
Finally, by Proposition 7.1 in Aikawa–Shanmugalingam [1] (or the proof above applied within \({\overline{\Omega }}\) and with \(x_0 \in {\overline{\Omega }}\)), \(\nu \) supports a global p-Poincaré inequality, where, again using [5, Theorem 4.39], the dilation constant can be chosen to be \(L'\). \(\square \)
7 Hyperbolization
We assume in this section that \((\Omega ,d)\) is a noncomplete L-quasiconvex space which is open in its completion \({\overline{\Omega }}\), and let \(\partial \Omega \) be its boundary within \({\overline{\Omega }}\).
We define the quasihyperbolic metric on \(\Omega \) by
\(\mathrm{{d}}s\) is the arc length parametrization of \(\gamma \), and the infimum is taken over all rectifiable curves in \(\Omega \) connecting x to y. It follows that \((\Omega ,k)\) is a length space. Balls with respect to the quasihyperbolic metric k will be denoted by \(B_k\).
Even though our main interest is in hyperbolizing uniform spaces, the quasihyperbolic metric makes sense in greater generality. In fact, the results in this section hold also if we let \(\Omega \varsubsetneq Y\) be an L-quasiconvex open subset of a (not necessarily complete) metric space Y and the quasihyperbolic metric k is defined using \(d_\Omega (x)={{\,\mathrm{dist}\,}}(x,Y \setminus \Omega )\).
If \(\Omega \) is a locally compact uniform space, then Theorem 3.6 in Bonk–Heinonen–Koskela [14] shows that the space \((\Omega ,k)\) is a proper geodesic Gromov hyperbolic space. Moreover, if \(\Omega \) is bounded, then \((\Omega ,k)\) is roughly starlike.
As described in the introduction, the operations of uniformization and hyperbolization are mutually opposite, by Bonk–Heinonen–Koskela [14, the discussion before Proposition 4.5].
Lemma 7.1
Let \(x,y \in \Omega \). Then the following are true:
Moreover,
If \(\Omega \) is A-uniform it is possible to get an upper bound similar to the one in (7.1) also when \(d(x,y) \le \frac{1}{2} d_\Omega (x)\), albeit with a little more complicated expression for the constant. As we will not need such an estimate, we leave it to the interested reader to deduce such a bound.
Proof
Without loss of generality we assume that \(x \ne y\).
Assume first that \(d(x,y) \le d_\Omega (x)\). Let \(\gamma :[0,l_\gamma ] \rightarrow \Omega \) be a curve from x to y. All curves in this proof will be arc length parametrized rectifiable curves in \(\Omega \). Then \(l_\gamma \ge d(x,y)\) and
Taking infimum over all such \(\gamma \) shows that \(k(x,y) \ge d(x,y)/2d_\Omega (x)\).
Suppose next that \(d(x,y) \ge d_\Omega (x)\). Let \(\gamma :[0,l_\gamma ] \rightarrow \Omega \) be a curve from x to y. Then \(l_\gamma \ge d(x,y) \ge d_\Omega (x)\) and
Taking infimum over all such \(\gamma \) shows that \(k(x,y) \ge \tfrac{1}{2}\).
Assume finally that \(d(x,y) \le d_\Omega (x)/2L\). As \(\Omega \) is L-quasiconvex, there is a curve \(\gamma :[0,l_\gamma ] \rightarrow \Omega \) from x to y with length \(l_\gamma \le L d(x,y) \le \frac{1}{2} d_\Omega (x)\). Then
The ball inclusions now follow directly from this. \(\square \)
We shall now equip \((\Omega ,k)\) with a measure determined by the original measure \(\mu \) on \(\Omega \). As before, for the results in this section it will be enough to assume that \(\Omega \) is quasiconvex.
Definition 7.2
Let \(\Omega \) be equipped with a Borel measure \(\mu \). For measurable \(A\subset \Omega \) and \(\alpha >0\), let
Proposition 7.3
Assume that \(\mu \) is globally doubling in \((\Omega ,d)\) with doubling constant \(C_\mu \). Then \(\mu ^\alpha \) is doubling for \(B_k\)-balls of radii at most \(R_0=\frac{1}{8}\), with doubling constant \(C_d=4^\alpha C_\mu ^m\), where \(m=\lceil \log _2 8L \rceil \).
Moreover, if \(R_1 >0\), then \(\mu ^\alpha \) is doubling for \(B_k\)-balls of radii at most \(R_1\).
Proof
Let \(x \in \Omega \), \(r \le \frac{1}{8}\), \(B_k=B_k(x,r)\) and \(B=B(x,r d_\Omega (x))\). By Lemma 7.1,
and hence, again using Lemma 7.1,
As \((\Omega ,k)\) is a length space, Lemma 3.5 shows that \(\mu ^\alpha \) is doubling for \(B_k\)-balls of radii at most \(R_1\) for any \(R_1>0\). \(\square \)
Proposition 7.4
Assume that \((\Omega ,d)\) is equipped with a globally doubling measure \(\mu \) supporting a global p-Poincaré inequality with dilation \(\lambda \) and \(p \ge 1\). Let \(\alpha >0\) and \(R_1>0\). Then \((\Omega ,k)\), equipped with the measure \(\mu ^\alpha \), supports a p-Poincaré inequality for balls of radii at most \(R_1\) with dilation L and the other Poincaré constant depending only on L, \(R_1\) and the global doubling and Poincaré constants.
Proof
Let u be a bounded measurable function on \(\Omega \) and \(\hat{g}\) be an upper gradient of u with respect to k. Since the arc length parametrization \(\mathrm{{d}}s_k\) with respect to k satisfies
we conclude that
and thus \(g(z):= \hat{g}(z)/d_\Omega (z)\) is an upper gradient of u with respect to d, see the proof of Lemma 6.1 for further details.
Next, let \(x\in \Omega \), \(0<r\le R_0:=1/8\lambda L\), \(B_k=B_k(x,r)\) and \(B=B(x,2r d_\Omega (x))\). We see, by Lemma 7.1, that
where all the above balls have comparable \(\mu \)-measures, as well as comparable \(\mu ^\alpha \)-measures. Note that \(d_\Omega (z) \simeq d_\Omega (x)\) for all \(z \in 4\lambda L B_k\). Thus,

A standard argument based on the triangle inequality makes it possible to replace \(u_{B,\mu }\) on the left-hand side by \(u_{B_k,\mu ^\alpha }\), and thus Y supports a p-Poincaré inequality for balls of radii \(\le R_0\), with dilation \(4\lambda L\). The conclusion now follows from Theorem 5.3. \(\square \)
Remark 7.5
Let X be a Gromov hyperbolic space, equipped with a measure \(\mu \), and consider its uniformization \(X_\varepsilon \), together with the measure \(\mu _\beta \), \(\beta >0\), as in Definition 4.1. With \(\alpha =\beta /\varepsilon \), it is then easily verified that the pull-back to X of the measure \((\mu _\beta )^\alpha \), defined on the hyperbolization \((X_\varepsilon ,k)\) of \(X_\varepsilon \), is comparable to the original measure \(\mu \).
8 An Indirect Product of Gromov Hyperbolic Spaces
We assume in this section that X and Y are two locally compact roughly starlike Gromov \(\delta \)-hyperbolic spaces. We fix two points \(z_X \in X\) and \(z_Y \in Y\), and let M be a common constant for the roughly starlike conditions with respect to \(z_X\) and \(z_Y\). We also assume that \(0 < \varepsilon \le \varepsilon _0(\delta )\) and that \(z_X\) and \(z_Y\) serve as centers for the uniformizations \(X_\varepsilon \) and \(Y_\varepsilon \).
In general, the Cartesian product \(X\times Y\) of two Gromov hyperbolic spaces X and Y need not be Gromov hyperbolic; for example, \({\mathbf {R}}\times {\mathbf {R}}\) is not Gromov hyperbolic. In this section, we shall construct an indirect product metric on \(X\times Y\) that does give us a Gromov hyperbolic space, namely we set \(X\times _\varepsilon Y\) to be the Gromov hyperbolic space \((X_\varepsilon \times Y_\varepsilon ,k)\). To do so, we first need to show that the Cartesian product of two uniform spaces, equipped with the sum of their metrics, is a uniform domain. This can be proved using Theorems 1 and 2 in Gehring–Osgood [22] together with Proposition 2.14 in Bonk–Heinonen–Koskela [14], but this would result in a highly nonoptimal uniformity constant. We instead give a more self-contained proof that also yields a better estimate of the uniformity constant for the Cartesian product.
Example 8.1
Recall that the uniformization \({\mathbf {R}}_\varepsilon \) of the hyperbolic 1-dimensional space \({\mathbf {R}}\) is isometric to \((-\tfrac{1}{\varepsilon },\tfrac{1}{\varepsilon })\), see Example 4.2. Hence, for all \(\varepsilon >0\), \({\mathbf {R}}_\varepsilon \times {\mathbf {R}}_\varepsilon \) is a planar square region, which is biLipschitz equivalent to the planar disk. Thus also its hyperbolization \({\mathbf {R}}\times _\varepsilon {\mathbf {R}}\) is biLipschitz equivalent to the hyperbolic disk, which is the model 2-dimensional hyperbolic space.
Lemma 8.2
Let \((\Omega ,d)\) be a bounded A-uniform space. Then for every pair of points \(x,y\in \Omega \) and for every L with \(d(x,y)\le L \le {{\,\mathrm{diam}\,}}\Omega \), there exists a curve \(\gamma \subset \Omega \) of length
connecting x to y and such that for all \(z\in \gamma \),
where \(\gamma _{x,z}\) and \(\gamma _{z,y}\) are the subcurves of \(\gamma \) from x to z and from z to y, respectively.
Proof
Choose \(x_0\in \Omega \) such that \(d_\Omega (x_0) \ge \tfrac{4}{5} \sup _{z\in \Omega } d_\Omega (z)\). Then for all \(z\in \Omega \), with \(\gamma _{z,x_0}\) being an A-uniform curve from z to \(x_0\), and \(z'\) its midpoint,
Hence \({{\,\mathrm{diam}\,}}\Omega \le 5A d_\Omega (x_0)\). Now, let \(x,y\in \Omega \) and L be as in the statement of the lemma. Let \(\gamma _{x,x_0}\) be an A-uniform curve from x to \(x_0\). We shall distinguish two cases:
-
1.
If \(L\le 5Al(\gamma _{x,x_0})\) then let \(\hat{\gamma }_x\) be the restriction of \(\gamma \) to [0, L/10A] and \(\hat{x}=\gamma (L/10A)\) be its new endpoint.
-
2.
If \(L\ge 5Al(\gamma _{x,x_0})\) then let \(\gamma _x\) be the restriction of \(\gamma \) to \([0,\tfrac{1}{2} l(\gamma _{x,x_0})]\) and \(\hat{x}=\gamma (\tfrac{1}{2} l(\gamma _{x,x_0}))\) be its new endpoint. Note that
$$\begin{aligned} d_\Omega (\hat{x}) \ge d_\Omega (x_0) - \frac{l(\gamma _{x,x_0})}{2} \ge \frac{{{\,\mathrm{diam}\,}}\Omega }{5A} - \frac{L}{10A} \ge \frac{L}{10A}. \end{aligned}$$Choose a curve \(\gamma '\) of length L/10A, which starts and ends at \(\hat{x}\). Then for all \(z\in \gamma '\),
$$\begin{aligned} d_\Omega (z) \ge d_\Omega (\hat{x}) - \frac{L}{20A} \ge \frac{L}{20A}. \end{aligned}$$Thus, concatenating \(\gamma '\) to \(\gamma _x\) we obtain a curve \(\hat{\gamma }_x\) from x to \(\hat{x}\) of length
$$\begin{aligned} \frac{L}{10A} \le l(\hat{\gamma }_x) \le \frac{L}{5A} \end{aligned}$$(8.2)and such that for all \(z\in \hat{\gamma }_x\),
$$\begin{aligned} d_\Omega (z) \ge \frac{1}{\max \{4,A\}} l(\hat{\gamma }_{x,z}) \ge \frac{1}{4A} l(\hat{\gamma }_{x,z}), \end{aligned}$$(8.3)where \(\hat{\gamma }_{x,z}\) is the part of \(\hat{\gamma }_x\) from x to z. The curve \(\hat{\gamma }_x\), obtained in case 1, clearly satisfies (8.2) and (8.3) as well.
A similar construction, using an A-uniform curve from y to \(x_0\), provides us with a curve \(\hat{\gamma }_y\) from y to \(\hat{y}\), satisfying (8.2) and (8.3) with x replaced by y.
Now, let \(\tilde{\gamma }\) be a uniform curve from \(\hat{x}\) to \(\hat{y}\) and let \(\gamma \) be the concatenation of \(\hat{\gamma }_x\) with \(\tilde{\gamma }\) and \(\hat{\gamma }_y\) (reversed). Since \(d(\hat{x},\hat{y}) \le d(x,y) + 2L/5A \le (1+2/5A)L\), we see that
and the right-hand side inequality in (8.1) holds, while the left-hand side follows from (8.2).
To prove the second property, in view of (8.3), it suffices to consider \(z\in \tilde{\gamma }\). Without loss of generality, assume that the part \(\tilde{\gamma }_{\hat{x},z}\) of \(\tilde{\gamma }\) from \(\hat{x}\) to z has length at most \(\tfrac{1}{2} l(\tilde{\gamma })\). Note that (8.3), applied to the choice \(z=\hat{x}\), gives
Again, we distinguish two cases.
1. If \(\tfrac{1}{2} d_\Omega (\hat{x})\ge l(\tilde{\gamma }_{\hat{x},z})\) then by (8.4),
and hence we obtain that
where \(\gamma _{x,z}\) is the part of \(\gamma \) from x to z.
2. On the other hand, if \(\tfrac{1}{2} d_\Omega (\hat{x})\le l(\tilde{\gamma }_{\hat{x},z})\) then by (8.4) again,
We conclude that
\(\square \)
Proposition 8.3
Let \((\Omega ,d)\) and \((\Omega ',d')\) be two bounded uniform spaces, with diameters and uniformity constants D, \(D'\), A and \(A'\), respectively. Then \(\widetilde{\Omega }=\Omega \times \Omega '\) is also a bounded uniform space with respect to the metric
with uniformity constant
Proof
The boundedness is clear. Let \(\tilde{x}=(x,x')\) and \(\tilde{y}=(y,y')\) be two distinct points in \(\widetilde{\Omega }\), and let
Note that
We use Lemma 8.2 to find curves \(\gamma \subset \Omega \) and \(\gamma '\subset \Omega '\), connecting x to y and \(x'\) to \(y'\), respectively, of lengths
and such that for all \(z\in \gamma \),
where \(\gamma _{x,z}\) and \(\gamma _{z,y}\) are the parts of \(\gamma \) from x to z and from z to y, respectively; similar statements holding true for \(z'\in \gamma '\) and \(A'\). Note that \(\Lambda >0\) since \(\tilde{x}\ne \tilde{y}\). Hence \(L,L'>0\) and, by (8.7), the curves \(\gamma \) and \(\gamma '\) are nonconstant.
Next, assuming that \(\gamma \) and \(\gamma '\) are arc length parametrized, we show that the curve
is an \(\tilde{A}\)-uniform curve in \(\widetilde{\Omega }\) connecting \(\tilde{x}\) to \(\tilde{y}\). To see this, note that we have by the definition (8.5) of \(\tilde{d}\) that for all \(0\le s\le t \le 1\), using (8.7) and then (8.6),
In particular, \(\tilde{\gamma }\) has the correct length. Since
we see that for all \(\tilde{\gamma }(t)=(z,z')\) with \(0 \le t \le \frac{1}{2}\), using (8.8) and then (8.7),
and similarly \(d_\Omega (z') \ge \Lambda D' t/80(A')^3\). Thus, using (8.7) for the last inequality,
As a similar estimate holds for \(\frac{1}{2} \le t \le 1\), we see that \(\tilde{\gamma }\) is indeed an \(\tilde{A}\)-uniform curve.
\(\square \)
We next see that the projection map \(\pi :X\times _\varepsilon Y\rightarrow X\) given by \(\pi ((x,y))=x\) is Lipschitz continuous.
Proposition 8.4
The above-defined projection map \(\pi :X\times _\varepsilon Y\rightarrow X\) is \((C/\varepsilon )\)-Lipschitz continuous, with C depending only on \(\varepsilon _0\) and M.
Proof
Since \(X\times _\varepsilon Y\) is geodesic, it suffices to show that \(\pi \) is locally \((C/\varepsilon )\)-Lipschitz with C independent of the locality. With \(C_1=e^{-(1+\varepsilon M)}\) and \(C_2=2e(2e^{\varepsilon M}-1)\) as in Theorem 2.10, for \((x,y)\in X\times Y\) let
The last part of Theorem 2.10 together with Lemma 2.8 then gives
with comparison constants depending only on \(\varepsilon _0\) and M.
Let \(k_\varepsilon \) denote the quasihyperbolic metric on \(\Omega :=X_\varepsilon \times Y_\varepsilon \). Note that since both \(X_\varepsilon \) and \(Y_\varepsilon \) are length spaces, so is \(\Omega \). As \(C_2/C_1 >2e\), we see that
and thus (7.1) in Lemma 7.1 with \(L=e\) yields
It follows that
\(\square \)
Next, we shall see how \(X\times _\varepsilon Y\) compares to \(X\times _{\varepsilon ^\prime }Y\).
Proposition 8.5
Let \(0< \varepsilon ' < \varepsilon \le \varepsilon _0(\delta )\). The canonical identity maps
are Lipschitz continuous. More precisely, there is a constant \(C'\), depending only on \(\varepsilon _0\) and M, such that \(\Phi \) is \((C'\varepsilon '/\varepsilon )\)-Lipschitz while \(\Psi \) is \(C'\)-Lipschitz.
Moreover, neither \(\Phi ^{-1}\) nor \(\Psi ^{-1}\) is Lipschitz continuous.
Proof
We first consider \(\Phi \). Since \(X\times _\varepsilon Y\) is geodesic, it suffices to show that \(\Phi \) is locally \((C'\varepsilon '/\varepsilon )\)-Lipschitz with \(C'\) independent of the locality. As in the proof of Proposition 8.4, for \((x,y)\in X\times Y\) and \(C_1, C_2\) from Theorem 2.10, let
Theorem 2.10 then gives
Let \(\tilde{d}_\varepsilon \), \(\tilde{d}_{\varepsilon '}\), \(k_\varepsilon \) and \(k_{\varepsilon '}\) denote the product metrics as in (8.5) and the quasihyperbolic metrics on \(X_\varepsilon \times Y_\varepsilon \) and \(X_{\varepsilon '}\times Y_{\varepsilon '}\) respectively. As in (8.9), we conclude that
Without loss of generality we assume that \(\rho _\varepsilon (x)\le \rho _\varepsilon (y)\), and then using Lemma 2.8,
in which case we also have that
Therefore, using (8.10),
with a similar statement holding true for \(\varepsilon '\). Since
we conclude from (8.11) that
which proves the Lipschitz continuity of \(\Phi \).
We now compare the product uniform domains \(X_\varepsilon \times Y_\varepsilon \) and \(X_{\varepsilon ^\prime }\times Y_{\varepsilon ^\prime }\). With \((x,y), (x',y') \in X\times Y\) as in the first part of the proof, we have by (8.10) and the assumption \(0<\varepsilon '<\varepsilon \) that
which proves the Lipschitz continuity of \(\Psi \). On the other hand, choosing \(y=y'=z_Y\), with \(\rho _\varepsilon (z_Y)=1\), gives
Since \(\varepsilon ' <\varepsilon \), letting \(d(x,z_X)\rightarrow \infty \) and so \(\rho _\varepsilon (x)\rightarrow 0\) shows that \(\Psi ^{-1}\) is not Lipschitz.
To show that \(\Phi ^{-1}\) is not Lipschitz, let \(x_j\in X\) be such that \(\rho _\varepsilon (x_j)\rightarrow 0\) (and equivalently, \(\rho _{\varepsilon '}(x_j)\rightarrow 0\)) as \(j\rightarrow \infty \). With \(C(\delta )\) as in (2.2) and \(C_1,C_2\) as in Theorem 2.10, for \(j=1,2,\ldots \) we choose \(y_j\in Y\) such that
This is possible since Y is geodesic. Then, for sufficiently large j, we have \( \varepsilon d(z_Y,y_j) \le 1 \) and hence by (2.2),
Since also \(\rho _\varepsilon (x_j) \le 1 = \rho _\varepsilon (z_Y)\), we thus conclude from (8.11), with the choice \(x=x'=x_j\), \(y=z_Y\) and \(y'=y_j\), that
with a similar statement holding also for \(\varepsilon '\). This shows that
i.e. \(\Phi ^{-1}\) is not Lipschitz. \(\square \)
Remark 8.6
If \(X=Y={\mathbf {R}}\) then, according to Example 8.1, all the indirect products \({\mathbf {R}}\times _\varepsilon {\mathbf {R}}\) are mutually biLipschitz equivalent. However, Proposition 8.5 shows that this equivalence cannot be achieved by the canonical identity map \(\Phi \).
By Theorem 1.1 in Bonk–Heinonen–Koskela [14], \(\Phi \) is biLipschitz if and only if \(\Psi \) is a quasisimilarity. Note that \(X_\varepsilon \) and \(X_{\varepsilon ^\prime }\) are quasisymmetrically equivalent by [14], and so are \(Y_\varepsilon \) and \(Y_{\varepsilon ^\prime }\). On the other hand, products of quasisymmetric maps need not be quasisymmetric, as exhibited by the Rickman rug \(([0,1],d_{{{\,\mathrm{Euc}\,}}})\times ([0,1], d_{{{\,\mathrm{Euc}\,}}}^\alpha )\) for \(0<\alpha <1\), see Bishop–Tyson [2, Remark 1, Sect. 5] and DiMarco [21, Sect. 1]. This seems to happen whenever one of the component spaces has dimension 1 and the other has dimension larger than 1.
Example 8.7
Let X be the unit disk in \({\mathbf {R}}^2\), equipped with the Poincaré metric k, making it a Gromov hyperbolic space. Let \(Y=(-1,1)\) be equipped with the quasihyperbolic metric (and so it is isometric to \({\mathbf {R}}\), see Examples 4.2 and 4.3). For both X and Y we can choose \(\varepsilon =1\), resulting in \(X_1\) being the Euclidean unit disk and \(Y_1\) being the Euclidean interval \((-1,1)\). Thus \(X_1\times Y_1\) is a solid 3-dimensional Euclidean cylinder, with boundary made up of \({\mathbf {S}}^1\times [-1,1]\) together with two copies of the disk.
Choosing \(0<\varepsilon <1\), we instead obtain \(X_\varepsilon \) and \(Y_\varepsilon \), with \(Y_\varepsilon \) isometric to the Euclidean interval \((-1/\varepsilon ,1/\varepsilon )\), see Example 4.2. The boundary of \(X_\varepsilon \times Y_\varepsilon \) is made up of two copies of \(X_\varepsilon \) together with \(Z\times [-1/\varepsilon ,1/\varepsilon ]\), where Z is the \(\varepsilon \)-snowflaking of \({\mathbf {S}}^1\), which results in Z being biLipschitz equivalent to a generalized von Koch snowflake loop.
If \(X\times _\varepsilon Y\) were biLipschitz equivalent to \(X\times _1 Y\), then \(Z\times [-1/\varepsilon ,1/\varepsilon ]\) would be quasisymmetrically equivalent to a 2-dimensional region in \(\partial (X_1\times Y_1)\), which is impossible as pointed out before this example.
9 Newtonian Spaces and p-Harmonic Functions
We assume in this section that \(1 \le p<\infty \) and that \(Y=(Y,d,\nu )\) is a metric space equipped with a complete Borel measure \(\nu \) such that \(0<\nu (B)<\infty \) for all balls \(B \subset Y\).
For proofs of the facts stated in this section we refer the reader to Björn–Björn [5] and Heinonen–Koskela–Shanmugalingam–Tyson [30].
Following Shanmugalingam [36], we define a version of Sobolev spaces on Y.
Definition 9.1
For a measurable function \(u:Y\rightarrow [-\infty ,\infty ]\), let
where the infimum is taken over all upper gradients g of u. The Newtonian space on Y is
In this paper we assume that functions in \(N^{1,p}(Y)\) are defined everywhere (with values in \([-\infty ,\infty ]\)), not just up to an equivalence class in the corresponding function space. This is important in Definition 5.1, to make sense of g being an upper gradient of u. The space \(N^{1,p}(Y)/{\sim }\), where \(u \sim v\) if and only if \(\Vert u-v\Vert _{N^{1,p}(Y)}=0\), is a Banach space and a lattice. For a measurable set \(E\subset Y\), the Newtonian space \(N^{1,p}(E)\) is defined by considering \((E,d|_E,\nu |_E)\) as a metric space in its own right. We say that \(f \in N^{1,p}_{\mathrm{loc}}(\Omega )\), where \(\Omega \) is an open subset of X, if for every \(x \in \Omega \) there exists \(r_x>0\) such that \(B(x,r_x)\subset \Omega \) and \(f \in N^{1,p}(B(x,r_x))\). The space \(L^p_{\mathrm{loc}}(\Omega )\) is defined similarly.
Definition 9.2
The (Sobolev) capacity of a set \(E\subset Y\) is the number
where the infimum is taken over all \(u\in N^{1,p}(Y) \) such that \(u=1\) on E.
A property is said to hold quasieverywhere (q.e.) if the set of all points at which the property fails has \({C_p}\)-capacity zero. The capacity is the correct gauge for distinguishing between two Newtonian functions. If \(u \in N^{1,p}(Y)\), then \(u \sim v\) if and only if \(u=v\) q.e. Moreover, if \(u,v \in N^{1,p}_{\mathrm{loc}}(Y)\) and \(u= v\) a.e., then \(u=v\) q.e.
We will also need the variational capacity.
Definition 9.3
Let \(\Omega \subset Y\) be open. Then
The variational capacity of \(E\subset \Omega \) with respect to \(\Omega \) is
where the infimum is taken over all \(u \in N^{1,p}_0(\Omega )\) such that \(u=1\) on E.
The following lemma provides us with a sufficient condition for when a set has positive capacity, in terms of Hausdorff measures. It is similar to Proposition 4.3 in Lehrbäck [35], but the dimension condition for s is weaker here and is only required for \(x\in E\). For the reader’s convenience, we provide a complete proof. We will use Lemma 9.4 to deduce Proposition 10.10.
Lemma 9.4
Let \((Y,d,\nu )\) be a complete metric space equipped with a globally doubling measure \(\nu \) supporting a global p-Poincaré inequality. Let \(E\subset Y\) be a Borel set of positive \(\kappa \)-dimensional Hausdorff measure and assume that for some \(C,s,r_0>0\),
Then \({C_p^Y}(E)>0\) whenever \(p>s-\kappa \).
Note that if (9.1) holds for some \(r_0\), then it holds with \(r_0=1\), although C may change.
Proof
By the regularity of the Hausdorff measure, there is a compact set \(K \subset E\) with positive \(\kappa \)-dimensional Hausdorff measure. Assume that \({C_p^Y}(K)=0\). Then also the variational capacity \({{\,\mathrm{cap}\,}}_p^Y(K,B)=0\) for every ball \(B\supset K\). By splitting K into finitely many pieces if necessary, and shrinking B, we can assume that \(\nu (2B\setminus B)>0\).
As \({{\,\mathrm{cap}\,}}_p^Y(K,B)=0\), it follows from [5, Theorem 6.19] that there are
with upper gradients \(g_k\) such that \(u_k=1\) on K, \(0 \le u_k \le 1\) on Y and
We can assume that \(r_0\le {{\,\mathrm{dist}\,}}(K,Y\setminus B)\) and set \(r_j=2^{-j}r_0\), \(j=0,1,\ldots \) . For a fixed \(x\in K\), consider the balls \(B_j=B(x,r_j)\). A standard telescoping argument, using the doubling property of \(\nu \) together with the p-Poincaré inequality, then shows that for a fixed k and \(u:=u_k\),

Because u vanishes outside B and \(\nu (2B\setminus B)>0\), we see that

Moreover,
where \(r_B\) stands for the radius of B. Since \(u(x)=1\), we conclude that for sufficiently large k, independently of \(x\in K\),
where \(\tau =1-(s-\kappa )/p>0\). Inserting this into (9.2) and comparing the sums, we see that for each \(x\in K\) there exists a ball \(B_x=B_{j(x)}\) centered at x and with radius \(r_x= r_{j(x)}\) such that
because of the assumption (9.1). Using the 5-covering lemma, we can out of the balls \(\lambda B_x\) choose a countable pairwise disjoint subcollection \(\lambda {\widehat{B}}_j\), \(j=1,2,\ldots \) , with radii \(\hat{r}_j\), so that \(K\subset \bigcup _{j=1}^\infty 5\lambda {\widehat{B}}_j\). Hence using (9.3) we obtain
showing that the \(\kappa \)-dimensional Hausdorff content (and thus also the corresponding measure) is zero. This causes a contradiction, which concludes the proof. \(\square \)
Definition 9.5
Assume that Y is complete. Let \(\Omega \subset Y\) be open. Then \(u \in N^{1,p}_{\mathrm{loc}}(\Omega )\) is p-harmonic in \(\Omega \) if it is continuous and
This is one of several equivalent definitions in the literature, see Björn [3, Proposition 3.2 and Remark 3.3] (or [5, Proposition 7.9 and Remark 7.10]). In particular, multiplying \(\varphi \) by suitable cut-off functions shows that the inequality in (9.4) can equivalently be required for all \(\varphi \in N^{1,p}_0(\Omega )\) with bounded support.
If \(\nu \) is locally doubling and supports a local p-Poincaré inequality then every \(u\in N^{1,p}_{\mathrm{loc}}(\Omega )\) satisfying (9.4) can be modified on a set of zero capacity to become continuous, and thus p-harmonic, see Kinnunen–Shanmugalingam [33, Theorem 5.2]. Moreover, it follows from [33, Corollary 6.4] that p-harmonic functions obey the strong maximum principle, i.e. if \(\Omega \) is connected, then they cannot attain their maximum in \(\Omega \) without being constant.
Definition 9.6
A metric space Y is locally annularly quasiconvex around a point \(x_0\) if there exist \(\Lambda \ge 2\) and \(r_0>0\) such that for every \(0<r\le r_0\), each pair of points \(x,y \in B(x_0,2r)\setminus B(x_0,r)\) can be connected within \(B(x_0,\Lambda r)\setminus B(x_0,r/\Lambda )\) by a curve of length at most \(\Lambda d(x,y)\).
Lemma 9.7
Let Y be a complete metric space equipped with a globally doubling measure \(\nu \) supporting a global p-Poincaré inequality. Assume that a connected open set \(\Omega \subset Y\) is locally annularly quasiconvex around \(x_0\in \Omega \), with parameters \(\Lambda \) and \(r_0 < {{\,\mathrm{dist}\,}}(x_0,Y \setminus \Omega )/2\Lambda \). Let u be a p-harmonic function in \(\Omega \setminus \{x_0\}\). Then for every \(0<r\le r_0\),
where C depends only on \(\Lambda \) and the global doubling and Poincaré constants.
Here \({{\,\mathrm{dist}\,}}(x_0,\varnothing )\) is considered to be \(\infty \).
Remark 9.8
Under the assumptions of Lemma 9.7 and the additional assumption that \(r < \frac{1}{4} {{\,\mathrm{diam}\,}}Y\), the sum in (9.5) is, by e.g. [5, Proposition 6.16], comparable to
where the last inequality follows from Lemma 2.6 in Heinonen–Kilpeläinen–Martio [28] whose proof applies verbatim also in the metric space setting. Thus if \({{\,\mathrm{cap}\,}}_p^Y(\{x_0\},B(x_0,r))\) is positive, then the above sum is finite.
Proof of Lemma 9.7
We can assume that \(r_0 < \frac{1}{2} {{\,\mathrm{diam}\,}}\Omega \). For \(0<\rho \le r_0\), we can find \(x,y \in B(x_0,2\rho )\setminus B(x_0,\rho )\) so that
Let \(\gamma \) be a curve in the annulus \(B(x_0,\Lambda \rho )\setminus B(x_0,\rho /\Lambda )\) provided by the annular quasiconvexity. Along this curve, we can find a chain of balls \(\{B_j\}_{j=1}^{N}\) of radius \(\rho /4\lambda \Lambda \), such that N is bounded by a constant depending only on \(\Lambda \) and the dilation \(\lambda \) from the p-Poincaré inequality, and
Using Lemma 4.1 in Björn–Björn–Shanmugalingam [12], we thus get that
Since \(\nu \) is globally doubling, we have \(\nu (B_j)\simeq \nu (B(x_0,\rho ))\) and so by (9.6) and the uniform bound on N,
Hölder’s inequality, together with the last estimate applied to \(\rho =r_k=2^{-k}r\) then yields
where \(A_k=B(x_0,2\Lambda r_k) \setminus B(x_0,r_k/2\Lambda )\). These annuli have clearly bounded overlap depending only on \(\Lambda \), and so (9.5) follows. \(\square \)
The following lemma will be used when proving Theorem 10.5.
Lemma 9.9
Let \((\Omega ,d)\) be an A-uniform space and \(a\in \partial \Omega \). Then \({\overline{\Omega }}\setminus \{a\}\) is locally annularly quasiconvex around a with \(\Lambda =4A\).
Proof
Let \(r>0\) and assume that \(x,y\in \Omega \cap B(a,2r) \setminus B(a,\frac{1}{2} r)\). Let \(\gamma \) be an arc length parametrized A-uniform curve joining x to y. Since \(l_\gamma \le A d(x,y)\le 4Ar\), we have \(\gamma \subset B(a,(2+2A)r)\). Now, if \(\tfrac{1}{4} r\le t\le l_\gamma -\tfrac{1}{4} r\), then
Similarly, if \(d(x,\gamma (t))<\tfrac{1}{4} r\) or \(d(y,\gamma (t))<\tfrac{1}{4} r\) then \(d(a,\gamma (t)) > \tfrac{1}{4} r\). In both cases it follows that \(\gamma \cap B(a,\tfrac{1}{4} r)=\varnothing \), and the lemma is proved under the assumption that \(x,y\in \Omega \).
Finally, if \(x,y\in {\overline{\Omega }}\cap B(a,2r) \setminus B(a,r)\) with \(x \ne y\), then we find
By the definition of uniform space, \(\Omega \) is A-quasiconvex, and hence so is \({\overline{\Omega }}\). Join \(x'\) to \(y'\) by a curve \(\gamma \) as in the first part of the proof. Concatenating \(\gamma \) with the A-quasiconvex curves, joining x to \(x'\) and \(y'\) to y, gives a suitable curve \(\tilde{\gamma }\) with length
which concludes the proof. \(\square \)
10 p-Harmonic Functions on X and \(X_\varepsilon \)
In this section, we assume that X is a locally compact roughly starlike Gromov \(\delta \)-hyperbolic space equipped with a complete Borel measure \(\mu \) such that \(0<\mu (B)<\infty \) for all balls \(B \subset X\). We also fix a point \(z_0 \in X\), let M be the constant in the roughly starlike condition with respect to \(z_0\), and assume that
Finally, we let \(X_\varepsilon \) be the uniformization of X with uniformization center \(z_0\). When discussing the uniformization \(X_\varepsilon \), and in particular  , it will always be assumed to be equipped with \(\mu _\beta \) for the \(\beta \) given above.
, it will always be assumed to be equipped with \(\mu _\beta \) for the \(\beta \) given above.
In this section we shall see that with suitable choices of p, \(\varepsilon \) and \(\beta \) satisfying \(\beta =p \varepsilon \), each p-harmonic function on the unbounded Gromov hyperbolic space \((X,d,\mu )\) transforms into a p-harmonic function on the bounded space \((X_\varepsilon ,d_\varepsilon ,\mu _\beta )\). This fact will make it possible to characterize, under uniformly local assumptions, when there are no nonconstant p-harmonic functions with finite p-energy on X, i.e. when the finite-energy Liouville theorem holds. A function u has finite p-energy with respect to \((X,d,\mu )\) if \(\int _X g_u^p \,\mathrm{{d}}\mu <\infty \).
In the setting of complete metric spaces, equipped with a globally doubling measure supporting a global p-Poincaré inequality, it was shown in Björn–Björn–Shanmugalingam [12, Theorem 1.1] that the finite-energy Liouville theorem holds on X whenever X is either annularly quasiconvex around a point or
The focus of this section will be to consider the finite-energy Liouville theorem for Gromov hyperbolic spaces under uniformly local assumptions.
Proposition 10.1
Let \(\Omega \subset X\) be open and \(u: \Omega \rightarrow [-\infty ,\infty ]\) be measurable. Then the following are true:
-
(a)
With \(g_u\) and \(g_{u,\varepsilon }\) denoting the minimal p-weak upper gradients of u with respect to \((d,\mu )\) and \((d_\varepsilon ,\mu _\beta )\), respectively, we have
$$\begin{aligned} g_{u,\varepsilon }(x)=g_u(x) e^{\varepsilon d(x,z_0)} \end{aligned}$$(10.1)and
$$\begin{aligned} \int _\Omega g_u(x)^p\,\mathrm{{d}}\mu (x) = \int _\Omega g_{u,\varepsilon }(x)^p e^{(\beta -p\varepsilon )d(x,z_0)}\,\mathrm{{d}}\mu _\beta (x). \end{aligned}$$(10.2) -
(b)
\(N^{1,p}_{\mathrm{loc}}(\Omega ,d,\mu )= N^{1,p}_{\mathrm{loc}}(\Omega ,d_\varepsilon ,\mu _\beta )\).
-
(c)
If \(\Omega \) is bounded, then \(N^{1,p}(\Omega ,d,\mu )= N^{1,p}(\Omega ,d_\varepsilon ,\mu _\beta )\), as sets and with comparable norms (depending only on \(\varepsilon \), \(\beta \), p and \(\Omega \)).
Remark 10.2
At first glance it would seem that the minimal p-weak upper gradient \(g_{u,\varepsilon }\) of u would also depend on the ambient measure \(\mu _\beta \), but because of the local nature of minimal weak upper gradients and by the fact that the weight \(x\mapsto e^{-\beta d(x,z_0)}\) is locally bounded away from both 0 and \(\infty \), it follows that \(g_{u,\varepsilon }\) indeed does not depend on the choice of \(\beta \), see the proof below.
Proof of Proposition 10.1
Clearly, (b) follows directly from (c). To prove (a) and (c), we conclude from (6.3) that \(g_\varepsilon (x):=g(x) e^{\varepsilon d(x,z_0)}\) is an upper gradient of u with respect to \(d_\varepsilon \) if and only if g is an upper gradient of u with respect to d. Since p-weak upper gradients can be approximated by upper gradients, both in the \(L^p\)-norm and also pointwise almost everywhere with respect to \(\mu \) and (equivalently) \(\mu _\beta \), this identity holds also for p-weak upper gradients. In particular, (10.1) and (10.2) hold, which proves part (a).
If \(\Omega \) is bounded, we also have that \(\mu \) and \(\mu _\beta \) are comparable on \(\Omega \), which implies that
with comparison constants depending on \(\beta \) and \(\Omega \). Together with (10.2), this implies that \(u \in N^{1,p}(\Omega ,d,\mu )\) if and only if \(u \in N^{1,p}(\Omega ,d_\varepsilon ,\mu _\beta )\), with comparable norms. \(\square \)
Remark 10.3
The proof of Proposition 10.1 also shows that even if \(\Omega \) is not bounded then for \(\beta \ge p\varepsilon \),
and thus \( N^{1,p}(\Omega ,d,\mu ) \subset N^{1,p}(\Omega ,d_\varepsilon ,\mu _\beta ). \)
Proposition 10.4
Let \(\Omega \subset X\) be open. If \(p=\beta /\varepsilon >1\), then a function \(u: \Omega \rightarrow {\mathbf {R}}\) is p-harmonic in \(\Omega \) with respect to \((d,\mu )\) if and only if it is p-harmonic in \(\Omega \) with respect to \((d_\varepsilon ,\mu _\beta )\). Moreover, its p-energy is the same in both cases, i.e.
Proof
By Proposition 10.1 (b), \(u\in N^{1,p}_{\mathrm{loc}}(\Omega ,d,\mu )\) if and only if \(u\in N^{1,p}_{\mathrm{loc}}(\Omega ,d_\varepsilon ,\mu _\beta )\). Let \(\varphi \) be a function with bounded support in X. Then \(\varphi \in N^{1,p}_0(\Omega ,d,\mu )\) if and only if \(\varphi \in N^{1,p}_0(\Omega ,d_\varepsilon ,\mu _\beta )\). Thus (10.2), together with a similar identity for the minimal p-weak upper gradients of \(u+\varphi \), shows that
It then follows from the discussion after Definition 9.5 that u is p-harmonic with respect to \((d,\mu )\) if and only if it is p-harmonic with respect to \((d_\varepsilon ,\mu _\beta )\). Moreover, (10.3) follows directly from (10.2). \(\square \)
Theorem 10.5
Assume that \(\mu \) is doubling and supports a p-Poincaré inequality, both properties holding for balls of radii \({\le }\) \(R_0\). Assume that \(\beta > \beta _0\) and \(p=\beta /\varepsilon >1\). Then the following are equivalent:
-
(a)
There exists a nonconstant p-harmonic function on \((X,d,\mu )\) with finite p-energy, i.e. the finite-energy Liouville theorem fails for X.
-
(b)
There are two disjoint compact sets \(K_1,K_2 \subset \partial _\varepsilon X\) with positive
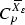 capacity.
capacity.
After proving the theorem we will give some illustrating examples. But first, before proving the theorem, we will provide several useful characterizations of the second condition (b). The characterization (e), applied to the restriction of  to the boundary \(\partial _\varepsilon X\), will be used in the proof of Theorem 10.5.
to the boundary \(\partial _\varepsilon X\), will be used in the proof of Theorem 10.5.
Lemma 10.6
Let Z be a separable metric space, and \({{\,\mathrm{Cap}\,}}(\,\cdot \,)\) be a monotone, countably subadditive set-function with values in \([0,\infty )\), defined for all subsets of Z. Assume that for each Borel set \(E \subset Z\),
where the supremum is taken over all compact subsets \(K \subset E\).
Define the support of \({{\,\mathrm{Cap}\,}}\) as
Then the following are equivalent:
-
(a)
There are two disjoint compact sets \(K_1,K_2 \subset Z\) such that \({{\,\mathrm{Cap}\,}}(K_1)>0\) and \({{\,\mathrm{Cap}\,}}(K_2)>0\).
-
(b)
There is a Borel set \(E \subset Z\) such that \({{\,\mathrm{Cap}\,}}(E)>0\) and \({{\,\mathrm{Cap}\,}}(Z \setminus E)>0\).
-
(c)
There is an open set \(G \subset Z\) such that \({{\,\mathrm{Cap}\,}}(G)>0\) and \({{\,\mathrm{Cap}\,}}(Z \setminus G)>0\).
-
(d)
The support \({{\,\mathrm{supp}\,}}{{\,\mathrm{Cap}\,}}\) contains at least two points.
-
(e)
\({{\,\mathrm{Cap}\,}}\) is not concentrated to one point, i.e. \({{\,\mathrm{Cap}\,}}(Z \setminus \{a\})>0\) for each \(a \in Z\).
If Y is equipped with a globally doubling measure \(\nu \) supporting a global p-Poincaré inequality and \(p>1\), then \({C_p^Y}\) is a Choquet capacity, by [5, Theorem 6.11], and thus satisfies the assumptions above. Hence the assumptions are also satisfied for any restriction of \({C_p^Y}\) to any closed subset of Y as well. Example 6.6 in [5] shows that (10.4) can fail if \(p=1\).
The assumption (10.4) is only needed to establish the equivalence of (a) and (b). On the other hand, separability is only used to deduce the identity (10.5) below, which in turn is used to show the equivalence of (b)–(e).
Proof
We start by showing that
To this end, for each \(x \in Z \setminus {{\,\mathrm{supp}\,}}{{\,\mathrm{Cap}\,}}\) there is \(r_x>0\) so that \({{\,\mathrm{Cap}\,}}(B(x,r_x))=0\). As Z is Lindelöf (which for metric spaces is equivalent to separability, see e.g. [5, Proposition 1.5]), we can write \(Z \setminus {{\,\mathrm{supp}\,}}{{\,\mathrm{Cap}\,}}\) as a countable union of such balls, each of which has zero capacity. Hence the countable subadditivity shows that (10.5) holds.
Now we are ready to prove the equivalences of (a)–(e).
(b)  (a) By (10.4) there are \(K_1 \subset E\) and \(K_2 \subset Z \setminus E\) such that \({{\,\mathrm{Cap}\,}}(K_1)>0\) and \({{\,\mathrm{Cap}\,}}(K_2)>0\).
(a) By (10.4) there are \(K_1 \subset E\) and \(K_2 \subset Z \setminus E\) such that \({{\,\mathrm{Cap}\,}}(K_1)>0\) and \({{\,\mathrm{Cap}\,}}(K_2)>0\).
(a)  (c)
(c)  (b) These implications are trivial.
(b) These implications are trivial.
(b)  (e) Let \(a \in Z\). If \(a \in E\), then \({{\,\mathrm{Cap}\,}}(Z \setminus \{a\}) \ge {{\,\mathrm{Cap}\,}}(Z \setminus E)>0\). Similarly, if \(a \notin E\), then \({{\,\mathrm{Cap}\,}}(Z \setminus \{a\}) \ge {{\,\mathrm{Cap}\,}}(E)>0\).
(e) Let \(a \in Z\). If \(a \in E\), then \({{\,\mathrm{Cap}\,}}(Z \setminus \{a\}) \ge {{\,\mathrm{Cap}\,}}(Z \setminus E)>0\). Similarly, if \(a \notin E\), then \({{\,\mathrm{Cap}\,}}(Z \setminus \{a\}) \ge {{\,\mathrm{Cap}\,}}(E)>0\).
(e)  (d) As \({{\,\mathrm{Cap}\,}}(Z \setminus \{a\})>0\) for each \(a \in Z\), it follows from (10.5) that \({{\,\mathrm{supp}\,}}{{\,\mathrm{Cap}\,}}\) is nonempty. Let \(a \in {{\,\mathrm{supp}\,}}{{\,\mathrm{Cap}\,}}\). As again \({{\,\mathrm{Cap}\,}}(Z \setminus \{a\})>0\), and (10.5) holds, there is \(b \in {{\,\mathrm{supp}\,}}{{\,\mathrm{Cap}\,}}\setminus \{a\}\).
(d) As \({{\,\mathrm{Cap}\,}}(Z \setminus \{a\})>0\) for each \(a \in Z\), it follows from (10.5) that \({{\,\mathrm{supp}\,}}{{\,\mathrm{Cap}\,}}\) is nonempty. Let \(a \in {{\,\mathrm{supp}\,}}{{\,\mathrm{Cap}\,}}\). As again \({{\,\mathrm{Cap}\,}}(Z \setminus \{a\})>0\), and (10.5) holds, there is \(b \in {{\,\mathrm{supp}\,}}{{\,\mathrm{Cap}\,}}\setminus \{a\}\).
(d)  (c) Let \(a,b \in {{\,\mathrm{supp}\,}}{{\,\mathrm{Cap}\,}}\), \(a \ne b\), and then let \(G=B(a,\frac{1}{2} d(a,b))\). Thus \({{\,\mathrm{Cap}\,}}(G)>0\) as \(a \in {{\,\mathrm{supp}\,}}{{\,\mathrm{Cap}\,}}\), while \({{\,\mathrm{Cap}\,}}(Z \setminus G) \ge {{\,\mathrm{Cap}\,}}(B(b,\frac{1}{2} d(a,b)))>0\) since \(b \in {{\,\mathrm{supp}\,}}{{\,\mathrm{Cap}\,}}\). \(\square \)
(c) Let \(a,b \in {{\,\mathrm{supp}\,}}{{\,\mathrm{Cap}\,}}\), \(a \ne b\), and then let \(G=B(a,\frac{1}{2} d(a,b))\). Thus \({{\,\mathrm{Cap}\,}}(G)>0\) as \(a \in {{\,\mathrm{supp}\,}}{{\,\mathrm{Cap}\,}}\), while \({{\,\mathrm{Cap}\,}}(Z \setminus G) \ge {{\,\mathrm{Cap}\,}}(B(b,\frac{1}{2} d(a,b)))>0\) since \(b \in {{\,\mathrm{supp}\,}}{{\,\mathrm{Cap}\,}}\). \(\square \)
Proof of Theorem 10.5
By Theorem 6.2, the uniformized space \((X_\varepsilon ,d_\varepsilon ,\mu _\beta )\), as well as its closure  , supports a global p-Poincaré inequality and \(\mu _\beta \) is globally doubling. Moreover,
, supports a global p-Poincaré inequality and \(\mu _\beta \) is globally doubling. Moreover,  is complete. It thus follows from
[5, Theorem 6.11], that
is complete. It thus follows from
[5, Theorem 6.11], that  is a Choquet capacity, and in particular satisfies the assumptions in Lemma 10.6, and so does its restriction to \(\partial _\varepsilon X\).
is a Choquet capacity, and in particular satisfies the assumptions in Lemma 10.6, and so does its restriction to \(\partial _\varepsilon X\).
(b)  (a) Let \(f(x):= {{\,\mathrm{dist}\,}}_\varepsilon (x,K_1)\). Since
(a) Let \(f(x):= {{\,\mathrm{dist}\,}}_\varepsilon (x,K_1)\). Since  is bounded, we have
is bounded, we have  and hence there exists a p-harmonic function u in \(X_\varepsilon \) such that \(u-f\in N^{1,p}_0(X_\varepsilon )\), see Shanmugalingam
[37, Theorem 5.6] (or
[5, Theorem 8.28 and Definition 8.31]). The function u is denoted \(H_pf\) in Björn–Björn–Shanmugalingam
[10] (and Hf in
[5]). By the Kellogg property (
[10, Theorem 3.9] or
[5, Theorem 10.5]), we have \(\lim _{X_\varepsilon \ni y\rightarrow x} u(y) = f(x)\) on \(\partial _\varepsilon X\), except possibly for a set of zero
and hence there exists a p-harmonic function u in \(X_\varepsilon \) such that \(u-f\in N^{1,p}_0(X_\varepsilon )\), see Shanmugalingam
[37, Theorem 5.6] (or
[5, Theorem 8.28 and Definition 8.31]). The function u is denoted \(H_pf\) in Björn–Björn–Shanmugalingam
[10] (and Hf in
[5]). By the Kellogg property (
[10, Theorem 3.9] or
[5, Theorem 10.5]), we have \(\lim _{X_\varepsilon \ni y\rightarrow x} u(y) = f(x)\) on \(\partial _\varepsilon X\), except possibly for a set of zero  -capacity. Consequently, as \(f= 0\) on \(K_1\), \(f>0\) on \(K_2\) and both \(K_1\) and \(K_2\) have positive
-capacity. Consequently, as \(f= 0\) on \(K_1\), \(f>0\) on \(K_2\) and both \(K_1\) and \(K_2\) have positive  -capacity, u must be nonconstant on \(X_\varepsilon \).
-capacity, u must be nonconstant on \(X_\varepsilon \).
Proposition 10.4 implies that \(u\in N^{1,p}_{\mathrm{loc}}(X,d,\mu ) \) is p-harmonic in X with respect to \((d,\mu )\) as well, and from (10.2) with \(\beta =p\varepsilon \) it follows that
\(\lnot \) (b)  \(\lnot \) (a) By Lemma 10.6, there is \(a \in \partial _\varepsilon X\) such that
\(\lnot \) (a) By Lemma 10.6, there is \(a \in \partial _\varepsilon X\) such that  . The capacity of \(\{a\}\) can be zero or positive.
. The capacity of \(\{a\}\) can be zero or positive.
Let u be a p-harmonic function in \((X,d,\mu )\) with finite p-energy. Then u is also p-harmonic on \((X_\varepsilon ,d_\varepsilon ,\mu _\beta )\) with finite p-energy, by Proposition 10.4. Applying the global p-Poincaré inequality to the ball \(B_\varepsilon (x_0,2{{\,\mathrm{diam}\,}}_\varepsilon X)\cap X_\varepsilon =X_\varepsilon \), with an arbitrary \(x_0\in X\), shows that \(u\in N^{1,p}(X_\varepsilon )\), cf. [5, Proposition 4.13 (d)].
If \(\partial _\varepsilon X\) has zero  -capacity then it is removable for p-harmonic functions in \(N^{1,p}(X_\varepsilon )\), by Theorem 6.2 in Björn
[4] (or
[5, Theorem 12.2]). Hence, an extension of u is p-harmonic on the compact connected set
-capacity then it is removable for p-harmonic functions in \(N^{1,p}(X_\varepsilon )\), by Theorem 6.2 in Björn
[4] (or
[5, Theorem 12.2]). Hence, an extension of u is p-harmonic on the compact connected set  and is thus constant by the strong maximum principle.
and is thus constant by the strong maximum principle.
Finally, assume that  . Then \(E:=\partial _\varepsilon X\setminus \{a\}\) has zero capacity and is thus removable for p-harmonic functions in \(N^{1,p}(X_\varepsilon )\), by
[4, Theorem 6.2] (or
[5, Theorem 12.2]). Since \(u\in N^{1,p}(X_\varepsilon )\), it follows that an extension of u is p-harmonic in the open set
. Then \(E:=\partial _\varepsilon X\setminus \{a\}\) has zero capacity and is thus removable for p-harmonic functions in \(N^{1,p}(X_\varepsilon )\), by
[4, Theorem 6.2] (or
[5, Theorem 12.2]). Since \(u\in N^{1,p}(X_\varepsilon )\), it follows that an extension of u is p-harmonic in the open set  . By Lemma 9.9, we know that \(X_\varepsilon \cup E\) is annularly quasiconvex at a. Since
. By Lemma 9.9, we know that \(X_\varepsilon \cup E\) is annularly quasiconvex at a. Since  , it is also true that
, it is also true that  if \(\rho < \frac{1}{4} {{\,\mathrm{diam}\,}}_\varepsilon X_\varepsilon \), by e.g.
[5, Proposition 6.16]. Moreover,
if \(\rho < \frac{1}{4} {{\,\mathrm{diam}\,}}_\varepsilon X_\varepsilon \), by e.g.
[5, Proposition 6.16]. Moreover,  is connected. Thus Lemma 9.7, together with the remark after it, implies that for sufficiently small \(r>0\),
is connected. Thus Lemma 9.7, together with the remark after it, implies that for sufficiently small \(r>0\),
Since  , the last integral tends to 0 as \(r\rightarrow 0\) and we conclude that
, the last integral tends to 0 as \(r\rightarrow 0\) and we conclude that  exists. In particular, u is bounded on the compact set
exists. In particular, u is bounded on the compact set  . Finally, the strong maximum principle for p-harmonic functions on
. Finally, the strong maximum principle for p-harmonic functions on  shows that u must be constant on
shows that u must be constant on  . \(\square \)
. \(\square \)
Example 10.7
(Continuation of Example 4.2.) We have \(C_d=2\), and all choices of \(R_0\) are acceptable. Hence any \(\varepsilon ,\beta >0\) are allowed. Fixing \(\varepsilon >0\) and \(1<p<\infty \) and choosing \(\beta =p\varepsilon \), we see that the weight in (4.1) becomes
By considering the functions
for which \(\Vert u_j\Vert _{N^{1,p}(X_\varepsilon ,\mu _\beta )} \rightarrow 0\), as \(j \rightarrow \infty \), we see that  .
.
Note that \({\mathbf {R}}\) does not admit any nonconstant p-harmonic function with finite p-energy.
Example 10.8
Consider \(X={\mathbf {R}}\times [-1,1]\), which is a Gromov hyperbolic space when equipped with the Euclidean metric. We equip X with a weighted measure
such that \((X,\mu )\) is uniformly locally doubling and supports a uniformly local p-Poincaré inequality. Fixing \(z_0=(0,0)\), the uniformization with \(\varepsilon =1\) gives a uniform domain \(X_1\) such that \(\partial _1X\) consists of two points.
To understand the potential theory and geometry of \(X_1\) near these two points, consider \(z=(x,y)\in X\) such that \(x\gg 1\). Then, with \(d_1\) denoting the uniformized metric on \(X_1\), we have
Here by \(d_1(z,z_0)\approx 1-e^{-x}\) we mean that \(d_1(z,z_0)/(1-e^{-x})\rightarrow 1\) as \(x\rightarrow \infty \). Thus, near the two boundary points, \(X_1\) is (biLipschitz equivalent to) the diamond region in \({\mathbf {R}}^2\) with corners \((\pm 1,0)\) and \((0,\pm 1)\). The two boundary points of \(X_1\) are  .
.
Let \(\beta =p >1\) and let \(\mu _\beta \) be the weighted measure on \(X_1\), given by Definition 4.1. By Theorem 10.5, X supports a nonconstant p-harmonic function with finite p-energy if and only if both boundary points  have positive
have positive  -capacity. By Björn–Björn–Lehrbäck
[9, Proposition 5.3],
-capacity. By Björn–Björn–Lehrbäck
[9, Proposition 5.3],  if and only if
if and only if

for some (all) sufficiently small \(r_0\), where the balls  are with respect to the metric \(d_1\). By the global doubling property of \(\mu _\beta \) we see that
are with respect to the metric \(d_1\). By the global doubling property of \(\mu _\beta \) we see that

In view of (2.3), each of these annuli is (roughly) the image of a rectangular region with fixed size and at distance approximately \(\log (1/r)\) from the base point \(z_0\). Letting \(Q(t)=[t-1,t+1]\times [-1,1]\), we therefore have

Since \(e^{-\beta x} \simeq r^\beta \) on \(Q(\log (1/r))\), we therefore conclude that  if and only if
if and only if
or equivalently,
An analogous condition holds for  .
.
Note that when \(w\equiv 1\), both (10.6) and its analogue for  fail, showing that the unweighted strip \({\mathbf {R}}\times [-1,1]\) satisfies the finite-energy Liouville theorem. This special case was obtained in Björn–Björn–Shanmugalingam
[12] by a more direct method, without the use of uniformization.
fail, showing that the unweighted strip \({\mathbf {R}}\times [-1,1]\) satisfies the finite-energy Liouville theorem. This special case was obtained in Björn–Björn–Shanmugalingam
[12] by a more direct method, without the use of uniformization.
Remark 10.9
The weighted Euclidean real line \(({\mathbf {R}},\mu )\), where \(\mathrm{{d}}\mu =w\,\mathrm{{d}}x\) is uniformly locally doubling and supports a uniformly local p-Poincaré inequality, can be treated similarly and we obtain that \(({\mathbf {R}},\mu )\) supports nonconstant p-harmonic functions with finite energy if and only if a condition similar to (10.6) holds on it:
In [12], this question was studied by different methods and under local assumptions on w. It follows from the results in Björn–Björn–Shanmugalingam [11] on local \(A_p\) weights, that the condition
obtained in [12], is equivalent to (10.7) under the local assumptions on w.
We end the paper with the following result which is a direct consequence of Theorem 6.2 together with Lemmas 4.10 and 9.4. In combination with Theorem 10.5, it provides a sufficient condition for the existence of nonconstant p-harmonic functions on \((X,d,\mu )\) with finite p-energy. Note that the Hausdorff dimension depends only on \(\varepsilon \), \(C_d\) and \(R_0\), but not on \(\beta \) or p.
Proposition 10.10
Assume that \(\mu \) is doubling and supports a p-Poincaré inequality, both properties holding for balls of radii at most \(R_0\). Let \(\beta > \beta _0\). Assume that the Borel set \(E\subset \partial _\varepsilon X\) has positive \(\kappa \)-dimensional Hausdorff measure for some \(\kappa >(\log C_d)/\varepsilon R_0\). If \(p=\beta /\varepsilon \ge 1\), then  .
.
References
Aikawa, H., Shanmugalingam, N.: Carleson-type estimates for \(p\)-harmonic functions and the conformal Martin boundary of John domains in metric measure spaces. Michigan Math. J. 53, 165–188 (2005)
Bishop, C., Tyson, J.T.: Locally minimal sets for conformal dimension. Ann. Acad. Sci. Fenn. Math. 26, 361–373 (2001)
Björn, A.: A weak Kellogg property for quasiminimizers. Comment. Math. Helv. 81, 809–825 (2006)
Björn, A.: Removable singularities for bounded \(p\)-harmonic and quasi(super)harmonic functions on metric spaces. Ann. Acad. Sci. Fenn. Math. 31, 71–95 (2006)
Björn, A., Björn, J.: Nonlinear Potential Theory on Metric Spaces. EMS Tracts in Mathematics, vol. 17. European Math. Soc, Zürich (2011)
Björn, A., Björn, J.: Local and semilocal Poincaré inequalities on metric spaces. J. Math. Pures Appl. 119, 158–192 (2018)
Björn, A., Björn, J.: Poincaré inequalities and Newtonian Sobolev functions on noncomplete metric spaces. J. Differ. Equ. 266, 44–69 (2019)
Björn, A., Björn, J., Gill, J., Shanmugalingam, N.: Geometric analysis on Cantor sets and trees. J. Reine Angew. Math. 725, 63–114 (2017)
Björn, A., Björn, J., Lehrbäck, J.: Volume growth, capacity estimates, \(p\)-parabolicity and sharp integrability properties of \(p\)-harmonic Green functions (In preparation)
Björn, A., Björn, J., Shanmugalingam, N.: The Dirichlet problem for \(p\)-harmonic functions on metric spaces. J. Reine Angew. Math. 556, 173–203 (2003)
Björn, A., Björn, J., Shanmugalingam, N.: Locally \(p\)-admissible measures on \({\mathbb{R}}\). J. Funct. Anal. 278, 108344 (2020)
Björn, A., Björn, J., Shanmugalingam, N.: The Liouville theorem for \(p\)-harmonic functions and quasiminimizers with finite energy. To appear in Math Z. https://doi.org/10.1007/s00209-020-02536-2
Björn, J., Shanmugalingam, N.: Poincaré inequalities, uniform domains and extension properties for Newton-Sobolev functions in metric spaces. J. Math. Anal. Appl. 332, 190–208 (2007)
Bonk, M., Heinonen, J., Koskela, P.: Unifomizing Gromov Hyperbolic Spaces. Astérisque, vol. 270 (2001)
Bonk, M., Saksman, E.: Sobolev spaces and hyperbolic fillings. J. Reine Angew. Math 737, 161–187 (2018)
Bonk, M., Saksman, E., Soto, T.: Triebel-Lizorkin spaces on metric spaces via hyperbolic fillings. Indiana Univ. Math. J. 67, 1625–1663 (2018)
Bridson, M., Haefliger, A.: Metric Spaces of Non-positive Curvature. Grundlehren der mathematischen Wissenschaften 319. Springer, Berlin (1999)
Buckley, S., Herron, D., Xie, X.: Metric space inversions, quasihyperbolic distance, and uniform spaces. Indiana Univ. Math. J. 57, 837–890 (2008)
Buyalo, S., Schroeder, V.: Elements of Asymptotic Geometry. EMS Monographs in Mathematics, vol. 3. European Math. Soc, Zürich (2007)
Coornaert, M., Delzant, T., Papadopoulos, A.: Géométrie et théorie des groupes. Lecture Notes in Math, vol. 1441. Springer, Berlin (1990)
DiMarco, C.: Fractal curves and rugs of prescribed conformal dimension. Topol. Appl. 248, 117–127 (2018)
Gehring, F.W., Osgood, B.G.: Uniform domains and the quasihyperbolic metric. J. Anal. Math. 36, 50–74 (1979)
Ghys, É., de la Harpe, P.: Espaces métriques hyperboliques, in Sur les groupes hyperboliques d’après Mikhael Gromov (Bern, 1988). Progress Math. 83, 27–45 (1990)
Gromov, M.: Hyperbolic groups, in Essays in Group Theory. Math. Sci. Res. Inst. Publ. 8, 75–263 (1987)
Gromov, M.: Metric Structures for Riemannian and Non-Riemannian Spaces. Progress in Math, vol. 152. Birkhäuser, Boston, MA (1999)
Hajłasz, P., Koskela, P.: Sobolev met Poincaré. Mem. Am. Math. Soc. 145, 688 (2000)
Heinonen, J.: Lectures on Analysis on Metric Spaces. Springer, New York (2001)
Heinonen, J., Kilpeläinen, T., Martio, O.: Nonlinear Potential Theory of Degenerate Elliptic Equations, 2nd edn. Dover, Mineola, NY (2006)
Heinonen, J., Koskela, P.: Quasiconformal maps in metric spaces with controlled geometry. Acta Math. 181, 1–61 (1998)
Heinonen, J., Koskela, P., Shanmugalingam, N., Tyson, J.T.: Sobolev Spaces on Metric Measure Spaces. New Mathematical Monographs, vol. 27. Cambridge Univ. Press, Cambridge (2015)
Herron, D., Shanmugalingam, N., Xie, X.: Uniformity from Gromov hyperbolicity. Illinois J. Math. 52, 1065–1109 (2008)
Keith, S.: Modulus and the Poincaré inequality on metric measure spaces. Math. Z. 245, 255–292 (2003)
Kinnunen, J., Shanmugalingam, N.: Regularity of quasi-minimizers on metric spaces. Manuscr. Math. 105, 401–423 (2001)
Koskela, P., MacManus, P.: Quasiconformal mappings and Sobolev spaces. Studia Math. 131, 1–17 (1998)
Lehrbäck, J.: Neighbourhood capacities. Ann. Acad. Sci. Fenn. Math. 37, 35–51 (2012)
Shanmugalingam, N.: Newtonian spaces: An extension of Sobolev spaces to metric measure spaces. Rev. Mat. Iberoam. 16, 243–279 (2000)
Shanmugalingam, N.: Harmonic functions on metric spaces. Illinois J. Math. 45, 1021–1050 (2001)
Acknowledgements
Open access funding provided by Linköping University. The discussions leading to this paper started in 2013, while the authors were visiting Institut Mittag-Leffler. They continued during the parts of 2017 and 2018 when N. S. was a guest professor at Linköping University, partially funded by the Knut and Alice Wallenberg Foundation, and during the parts of 2019 when A. B. and J. B. were Taft Scholars at the University of Cincinnati. The authors would like to thank these institutions for their kind support and hospitality. A.B. and J.B. were partially supported by the Swedish Research Council grants 2016-03424 and 621-2014-3974, respectively. N.S. was partially supported by the NSF grants DMS-1500440 and DMS-1800161. The authors would also like to thank Xining Li for a fruitful discussion on annular quasiconvexity leading to Lemma 9.9.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Dedicated to Pekka Koskela and the late Juha Heinonen on their 59th birthdays.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Björn, A., Björn, J. & Shanmugalingam, N. Bounded Geometry and p-Harmonic Functions Under Uniformization and Hyperbolization. J Geom Anal 31, 5259–5308 (2021). https://doi.org/10.1007/s12220-020-00477-0
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s12220-020-00477-0
Keywords
- Bounded geometry
- Doubling measure
- Finite-energy Liouville theorem
- Gromov hyperbolic space
- Hyperbolization
- Metric space
- p-harmonic function
- Poincaré inequality
- Quasihyperbolic metric
- Uniform space
- Uniformization





 .
. .
.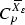 capacity.
capacity.