Hostname: page-component-8448b6f56d-42gr6 Total loading time: 0 Render date: 2024-04-20T04:02:50.043Z Has data issue: false hasContentIssue false
  • English
  • Français

ON GILP’S GROUP-THEORETIC APPROACH TO FALCONER’S DISTANCE PROBLEM

Part of: Classical measure theory Discrete geometry

Published online by Cambridge University Press:  28 July 2020

HAN YU
HAN YU*
Affiliation:
Department of Pure Mathematics and Mathematical Statistics, University of Cambridge, CB3 0WB, UK, e-mail: hy351@cam.ac.uk
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper, we follow and extend a group-theoretic method introduced by Greenleaf–Iosevich–Liu–Palsson (GILP) to study finite points configurations spanned by Borel sets in 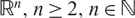$\mathbb{R}^n,n\geq 2,n\in\mathbb{N}.$ We remove a technical continuity condition in a GILP’s theorem in [Revista Mat. Iberoamer31 (2015), 799–810]. This allows us to extend the Wolff–Erdogan dimension bound for distance sets to finite points configurations with k points for $k\in\{2,\dots,n+1\}$ forming a $(k-1)$ -simplex.

MSC classification

Primary: 28A80: Fractals
Secondary: 52C10: Erdős problems and related topics of discrete geometry 52C15: Packing and covering in $2$ dimensions 52C35: Arrangements of points, flats, hyperplanes
Type
Research Article
Information
Glasgow Mathematical Journal , Volume 63 , Issue 3 , September 2021 , pp. 547 - 562
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author(s), 2020. Published by Cambridge University Press on behalf of Glasgow Mathematical Journal Trust

References

Du, X., Guth, L., Ou, Y., Wang, H., Wilson, B. and Zhang, R., Weighted restriction estimates and application to Falconer distance set problem, preprint,arXiv:1802.10186, to appear in Amer. J. Math. (2018).Google Scholar
Du, X. and Zhang, R., Sharp $L^2$ estimates of the Schrödinger maximal function in higher dimensions, Ann. Math.(2) 189 (2019), 837–861.CrossRefGoogle Scholar
Elekes, G. and Sharir, M., Incidences in three dimensions and distinct distances in the plane, in Proceedings 26th ACM Symposium on Computational Geometry (2010), 413–422.CrossRefGoogle Scholar
Erdogan, B., A bilinear Fourier extension problem and applications to the distance set problem, Int. Math. Res. Not. 23 (2005), 1411–1425.CrossRefGoogle Scholar
Falconer, K., Fractal geometry: Mathematical foundations and applications (Wiley, Hoboken, New Jersey, 2004).Google Scholar
Fraser, J., Howroyd, D. and Yu, H., Dimension growth for iterated sumsets, Math. Z. 293 (2019), 1015–1042.CrossRefGoogle Scholar
Greenleaf, A., Iosevich, A., Liu, B. and Palsson, E., A group-theoretic viewpoint on Erdös-Falconer problems and the Mattila integral, Revista Mat. Iberoamer 31(3) (2015), 799–810.CrossRefGoogle Scholar
Guth, L., Polynomial methods in combinatorics (American Mathematical Society, Providence, Rhode Island, 2016).CrossRefGoogle Scholar
Guth, L., Iosevich, A., Ou, Y-M. and Wang, H., On Falconer’s distance set problem in the plane, Invent. Math. 219 (2020), 779–830.CrossRefGoogle Scholar
Guth, L. and Katz, N., On the Erdös distances problem in the plane, Ann. Math.(2) 181 (2015), 155–190.CrossRefGoogle Scholar
Keleti, T. and Shmerkin, P., New bounds on the dimensions of planar distance sets, Geom. Funct. Anal. 29 (2020), 1886–1948.CrossRefGoogle Scholar
Mattila, P., Geometry of sets and measures in Euclidean spaces: Fractals and rectifiability, Cambridge Studies in Advanced Mathematics (Cambridge University Press, Cambridge, UK, 1999).Google Scholar
Mattila, P., Fourier analysis and Hausdorff dimension, Cambridge Studies in Advanced Mathematics (Cambridge University Press, Cambridge, UK, 2015).Google Scholar
Orponen, T., On the distance sets of Ahlfors-David regular sets, Adv. Math. 307 (2017), 1029–1045.CrossRefGoogle Scholar
Shmerkin, P., On the Hausdorff dimension of pinned distance sets, Israel J. Math. 230 (2019), 949–972.CrossRefGoogle Scholar
Wolff, T., Recent work connected with the Kakeya problem, Prospects in Mathematics (American Mathematical Society, Providence, 1996).Google Scholar
Wolff, T., Decay of circular means of Fourier transforms of measures, Int. Math. Res. Not. 10 (1996), 547–567.Google Scholar
Yu, H., Dimensions of triangle sets, Mathematika 65(2) (2019), 311–332.CrossRefGoogle Scholar