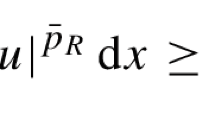On the Uniqueness of Minimizers for a Class of Variational Problems with Polyconvex Integrand

Abstract

We prove existence and uniqueness of minimizers for a family of energy functionals that arises in Elasticity and involves polyconvex integrands over a certain subset of displacement maps. This work extends previous results by Awi and Gangbo to a larger class of integrands. We are interested in Lagrangians of the form $L(A,u)=f(A)+H(\det A)-F\cdot u$. Here the strict convexity condition on $f$ and $H$ have been relaxed to a convexity condition. Meanwhile, we have allowed the map $F$ to be non-degenerate. First, we study these variational problems over displacements for which the determinant is positive. Second, we consider a limit case in which the functionals are degenerate. In that case, the set of admissible displacements reduces to that of incompressible displacements which are measure preserving maps. Finally, we establish that the minimizer over the set of incompressible maps may be obtained as a limit of minimizers corresponding to a sequence of minimization problems over general displacements provided we have enough regularity on the dual problems. We point out that these results do not rely on the direct methods of the calculus of variations.

Appendix

1.1 A.1 Proof of Lemma 3.4

We will prove Lemma 3.4 through two lemmas. The results of the first lemma can be found in Lemma 4.3 of [2]. We give here a sketch of the proof for the convenience of the reader.

Lemma A.1

Assume that$\mathbf{(A2)}$holds. Consider a lower semicontinuous function$l:\mathbb{R}^{d} \to \bar{\mathbb{R}}$such that$\inf_{\bar{\varLambda }}l>-\infty$; $l$is finite on$\varLambda$and$l \equiv +\infty$on$\mathbb{R}^{d} \setminus \bar{\varLambda }$. Set$k= l^{\#}$and let$w\in \mathbb{R}^{d}$. Then:

• 1. There exist$\bar{u}\in \bar{\varLambda }$and$\bar{t}>0$such that

  $$ k( w ) =-\bar{t}l(\bar{u})-H(\bar{t})-\bar{u}\cdot w. $$

  (A.1)

  Moreover, $\bar{u}$and$\bar{t}$satisfy$\bar{u}\in \partial k( w)$and$H'(\bar{t})+l(\bar{u})=0$.

• 2. If$k$is differentiable at$w$then$\bar{u}$and$\bar{t}$are uniquely determined by$\bar{u}=\nabla k(w)$and$\bar{t}=(H')^{-1}(-l( \bar{u}))$.

Proof

(1.) We have

$$ k(w)=\sup \bigl\{ u\cdot w-l(u)t-H(t):u\in \bar{\varLambda },t>0\bigr\} . $$

(A.2)

Consider a maximizing sequence $\{(u_{n},t_{n})\}_{n=1}^{\infty }$ in (A.2). As $0\in \varLambda$, we may assume without loss of generality that

$$\begin{aligned} u_{n}w-l(u_{n})t_{n}-H(t_{n}) &\geq 0\cdot w-l(0)-H(1) \end{aligned}$$

for $n\geq 1$. It follows that

$$\begin{aligned} |w|r^{*}+l(0)+H(1) &\geq \Bigl(\inf_{\bar{\varLambda }}l \Bigr)t_{n}+H(t_{n}) \end{aligned}$$

for $n\geq 1$. In light of the growth condition on $H$ in (A2) there exists a positive real number $\alpha$ such that $\{t_{n}\}_{n=1}^{\infty }\subset [\alpha ,\alpha ^{-1}]$. As $\varLambda$ is bounded, we may assume without loss of generality that the sequence $\{(u_{n},t_{n})\}_{n=1}^{\infty }$ converges to some $(\bar{u},\bar{t})\in \bar{\varLambda }\times [\alpha ,\alpha ^{-1}]$. We next use the lower semicontinuity of $H$ and $l$ to deduce that

$$ k(w)= \bar{u}\cdot w-l(\bar{u})\bar{t}-H(\bar{t}). $$

(A.3)

Note that $k(w)\geq \bar{u}\cdot w-l(\bar{u})t-H( t) \text{ for all }t>0$. In view of (A.3), it follows that $g: (0, \infty )\to \mathbb{R}$ defined by $g(t)=\bar{u}\cdot w-l(\bar{u})t-H( t)$ admits a maximum at $\bar{t}$. As $g$ is differentiable at $\bar{t}$, we have $g'(\bar{t})=0$, that is, $l(\bar{u})+H'( \bar{t})=0$. Next, observe that $k(z)\geq \bar{u}\cdot z-l(\bar{u}) \bar{t}-H( \bar{t}) \text{ for all }z\in \mathbb{R} ^{d}$. In light of the convexity of $k$ we have that $\bar{u}\in \partial k(w)$.

(2.) Assume that $k$ is differentiable at $w$. Then, $\bar{u}$ is uniquely determined as $\bar{u}=\nabla k (w)$. As $H'(\bar{t})=-l_{0}(\bar{u})$ and $H'$ is a bijection, we obtain that $\bar{t}$ is also uniquely determined as $\bar{t}=(H')^{-1}(-l(\bar{u}))$. □

The second lemma which is inspired by Lemma 4.4 in [2] is the following:

Lemma A.2

Assume that$\mathbf{(A2)}$holds. Consider a lower semicontinuous function$l_{0}:\mathbb{R}^{d} \to \bar{\mathbb{R}}$such that$\inf_{\bar{\varLambda }}l_{0}>-\infty$; $l_{0}$is finite on$\varLambda$and$l_{0}\equiv +\infty$on$\mathbb{R}^{d} \setminus \bar{ \varLambda }$. Set$k_{0}= ({l_{0}})^{\#}$. Let$\hat{l}\in C_{b}( \mathbb{R}^{d} )$and let$1\geq \epsilon >0$. Define$l_{\epsilon }=l _{0}+\epsilon \hat{l}$and$k_{\epsilon }={ (l_{\epsilon } )} ^{\#}$. Let$v\in \mathbb{R}^{d}$be such that$k_{0}$is differentiable at$v$.

• 1. There exists a constant$M$independent of$v$and$\epsilon$such that

  $$ \biggl\vert \frac{k_{\epsilon }(v)-k_{0}( v ) }{\epsilon } \biggr\vert \leq M. $$

  (A.4)

• 2. We have

  $$ \lim_{\epsilon \rightarrow 0 } \frac{k_{\epsilon }(v)-k_{0}( v ) }{ \epsilon }=- t_{0}\hat{l}(u_{0}). $$

  (A.5)

Proof

Note that the map $l_{\epsilon }=l_{0}+\epsilon \hat{l}$ is bounded below by $m-|\hat{l}|_{\infty }$. As $k_{\epsilon }={ (l _{\epsilon } )}^{\#}$ and $k_{0}={ (l_{0} )}^{\#}$, Lemma A.1 ensures that there exist $t_{0}, t_{\epsilon }>0$ and $u_{0}, u_{\epsilon }\in \bar{\varLambda }$ such that

$$ k_{\epsilon }(v)=u_{\epsilon }v-l(u_{\epsilon })t_{\epsilon }-H(t_{ \epsilon }) $$

and

$$ k_{0}(v)=u_{0} v-l(u_{0})t_{0}-H(t_{0}). $$

We then have

$$ k_{\epsilon }(v) =-\epsilon \hat{l}(u_{\epsilon })t_{\epsilon }+u_{ \epsilon }v-l_{0}(u_{\epsilon })t_{\epsilon }-H(t_{\epsilon }) \leq - \epsilon \hat{l}(u_{\epsilon })t_{\epsilon }+k_{0}(v) $$

(A.6)

and

$$ k_{0}(v)=\epsilon \hat{l}(u_{0})t_{0} +u_{0} v-l_{\epsilon }(u_{0})t _{0}-H(t_{0})\leq \epsilon \hat{l}(u_{0})t_{0} +k_{\epsilon }(v). $$

(A.7)

We combine (A.6) and (A.7) to get

$$ -\hat{l}(u_{0})t_{0}\leq \frac{(k_{\epsilon }(v)- k_{0}(v))}{\epsilon }\leq -\hat{l}(u_{\epsilon })t_{\epsilon }. $$

(A.8)

Using again Lemma A.1 we have

$$ t_{\delta }= \bigl(H'\bigr)^{-1}\bigl( l_{\delta }(u_{\delta })\bigr),\quad u_{\delta } \in \partial k_{\delta }(v),\ \delta \in \{0,\epsilon \}. $$

As $l_{\delta }$ is bounded below by $m-|l|_{\infty }$, we use the fact that $H'$ is a continuous and strictly increasing bijection from $(0,\infty )$ to ℝ to deduce that $t_{\delta }$ is bounded above by $M_{1}>0$ given by $M_{1}:=(H')^{-1}(-m+|\hat{l}|_{\infty })$. This bound on $t_{\delta }$ combined with (A.8) yields a constant $M:=|\hat{l}|_{\infty }(H')^{-1}(-m+| \hat{l}|_{\infty })$ such that (A.4) holds. As a result $\lim_{\epsilon \to 0^{+}}k_{\epsilon }(v)=k_{0}(v)$. Next, let $\{e_{n}\}_{n=1}^{\infty }\subset (0,1]$ converging to 0 such that $\limsup_{\epsilon \to 0} \hat{l}(u_{\epsilon })t_{\epsilon }= \lim_{n\to \infty }\hat{l}(u _{e_{n}} )t_{e_{n}}$. Without loss of generality, we may assume that $\{u _{e_{n}}\}_{n=1}^{\infty }$ converges to some $\bar{u}\in \bar{\varLambda }$ and $\{ t _{e_{n}}\} _{n=1}^{\infty }$ converges to $\bar{t} \in [0,M_{1}]$. Exploiting the lower semicontinuity of $l_{0}$, $\hat{l}$ and $H$, we get:

$$\begin{aligned} k_{0}(v) &=\lim_{n\to \infty } k_{e_{n}}(v) \\ &=\lim_{n\to \infty } u_{e_{n}}v-l_{e_{n}}(u_{e_{n}})t_{e_{n}}-H(t _{e_{n}}) \\ &\leq \bar{u} v-l_{0}(\bar{u})\bar{t}-H(\bar{t}) \\ &\leq k_{0}(v). \end{aligned}$$

It follows that $k_{0}(v)=\bar{u} v-l_{0}(\bar{u})\bar{t}-H(\bar{t})$. As $k_{0}$ is differentiable at $v$, we have $t_{0}=\bar{t}$ and $u_{0}=\bar{u}$. We use (A.8), the definition of $\{e_{n}\}_{n=1}^{\infty }$, the convergence of $\{u _{e_{n}}\}_{n=1} ^{\infty }$ and $\{ t _{e_{n}}\}_{n=1}^{\infty }$ to obtain

$$ -t_{0}\hat{l}(u_{0})\leq \liminf _{\epsilon \to 0}-t_{\epsilon } \hat{l}(u_{\epsilon })\leq \limsup_{\epsilon \to 0}-t_{\epsilon } \hat{l}(u_{\epsilon })= \lim_{n\to \infty }-t_{e_{n}}\hat{l}(u_{e_{n}})=-t _{0}\hat{l}(u_{0}). $$

(A.9)

As a result, $\lim_{\epsilon \to 0}-t_{\epsilon }\hat{l}(u_{\epsilon })=-t_{0}\hat{l}(u_{0})$. We invoke one more time Eq. (A.8) to obtain (A.5). □

1.2 A.2 Some Properties of the Legendre Transform

We have the following lemma which is similar to Lemma 3.4 but uses the Legendre transform instead of the $(\cdot )^{\#}$ operator.

Lemma A.3

Consider a lower semicontinuous function$l_{0}:\mathbb{R}^{d} \to \bar{ \mathbb{R}}$such that$\inf_{\bar{\varLambda }}l_{0}>-\infty$; $l_{0}$is finite on$\varLambda$and$l_{0}\equiv +\infty$on$\mathbb{R}^{d} \setminus \bar{\varLambda }$. Set$k_{0}= ({l_{0}})^{*}$.

• 1. There exists a measurable map$T_{0}:\mathbb{R}^{d} \to \mathbb{R} ^{d}$such that$k_{0}(v)=v\cdot T_{0}(v)-l_{0}(T_{0}(v))$for all$v\in \mathbb{R}^{d}$and$T_{0}(v)=\nabla k_{0}(v)$whenever$k_{0}$is differentiable at$v\in \mathbb{R}^{d}$.

• 2. Let$\hat{l}\in C_{b}(\mathbb{R}^{d} )$and let$1\geq \epsilon >0$. Define$l_{\epsilon }=l_{0}+\epsilon \hat{l}$and$k_{\epsilon }= { (l_{\epsilon } )^{*}}$.

  • (a) For all$v\in \mathbb{R}^{d}$we have:

    $$ \biggl\vert \frac{k_{\epsilon }(v)-k_{0}( v ) }{\epsilon } \biggr\vert \leq | \hat{l}|_{\infty }. $$

  • (b) For$\epsilon \in (0,1)$, there exists a map$T_{\epsilon }: \mathbb{R}^{d} \to \mathbb{R}^{d}$satisfying for all$v\in \mathbb{R}^{d}$: $k_{\epsilon }(v)=vT_{\epsilon }(v)-l_{\epsilon }(T _{\epsilon }(v))$. When$k_{0}$is differentiable at$v\in \mathbb{R}^{d}$, we have$\lim_{\epsilon \to 0}T_{\epsilon }(v)= \nabla k_{0}(v)$and

    $$ \lim_{\epsilon \rightarrow 0 } \frac{k_{\epsilon }(v)-k_{0}( v ) }{ \epsilon }=- t_{0} \hat{l}\bigl(\nabla k_{0}(v)\bigr). $$

Proof

(1.) Let $v\in \mathbb{R}^{d}$. We have

$$ k_{0}(v)=\sup \bigl\{ uv-l_{0}(u): u\in \mathbb{R}^{d}\bigr\} =\sup \bigl\{ uv-l_{0}(u): u\in \bar{ \varLambda }\bigr\} . $$

We use the lower semicontinuity of $l_{0}$ and the compactness of $\bar{\varLambda }$ to deduce that there exists $\bar{u}\in \varLambda$ such that $k_{0}(v)=\bar{u} v-l_{0}(\bar{u})$. We have $k_{0}(w)-( \bar{u}w-l_{0}(\bar{u}))\geq 0$ for all $w\in \mathbb{R}^{d}$ while $k_{0}(v)-(\bar{u}v-l_{0}(\bar{u}))= 0$. Since $k_{0}$ is convex, we deduce that $\bar{u} \in \partial k_{0}(v)$.

Next, for $v\in \mathbb{R}^{d}$, define

$$ \varGamma (v)=\bigl\{ u\in \bar{\varLambda }:k_{0}(v)=uv-l_{0}(u) \bigr\} . $$

Assume $\{u_{n}\}_{n\in \mathbb{N}}\subset \mathbb{R}^{d}$ converges to $u$; $\{v_{n}\}_{n\in \mathbb{N}}\subset \mathbb{R}^{d}$ converges to $v$ and for all $n\in \mathbb{N}$, one has $u_{n}\in \varGamma (v_{n})$. Then $u\in \varGamma (v)$. Indeed, one has

$$ k_{0}(v)\leq \liminf_{n\to \infty }k_{0}(v_{n})= \liminf_{n\to \infty } \bigl(u_{n}v_{n}-l_{0}(u_{n}) \bigr)\leq uv-l_{0}(u)\leq k_{0}(v). $$

Therefore, $uv-l_{0}(u)=k_{0}(v)$ and $u\in \varGamma (v)$. As a result, the multifunction $\varGamma :\mathbb{R}^{d} \rightrightarrows \mathbb{R}^{d}$ is closed and nonempty valued. By the Measurable Selection Theorem [14, Corollary 14.6], there exists a measurable map $T_{0}:\mathbb{R}^{d}\to \mathbb{R}^{d}$ such that for all $v\in \mathbb{R}^{d}$, one has $T_{0}(v)\in \varGamma (v)$. That is $k_{0}(v)=vT_{0}(v)-l_{0}(T_{0}(v))$. As $T(v)\in \varGamma (v)\subset \partial k_{0}(v)$, we also have $T_{0}=\nabla k_{0}$ almost everywhere.

(2.) For $\epsilon >0$, $l_{\epsilon }$ is bounded below and satisfies the hypothesis on $l_{0}$. Let $k_{\epsilon }=l_{\epsilon }^{*}$ and consider a map $T_{\epsilon }$ satisfying for all $v\in \mathbb{R} ^{d}$: $k_{\epsilon }(v)=vT_{\epsilon }(v)-l_{\epsilon }(T_{\epsilon }(v))$ as given by part 1.). We have for $v\in \mathbb{R}^{d}$:

$$ k_{\epsilon }(v)=vT_{\epsilon }(v)-l_{\epsilon } \bigl(T_{\epsilon }(v)\bigr)=- \epsilon \hat{l}\bigl(T_{\epsilon }(v) \bigr)+vT_{\epsilon }(v)-l_{0}\bigl(T_{\epsilon }(v)\bigr) \leq -\epsilon \hat{l}\bigl(T_{\epsilon }(v)\bigr)+k_{0}(v). $$

(A.10)

Similarly, for $v\in \mathbb{R}^{d}$ we have

$$ k_{0}(v)=vT_{0}(v)-l_{0} \bigl(T_{0}(v)\bigr)=\epsilon \hat{l}\bigl(T_{0}(v) \bigr)+vT_{0}(v)-l _{\epsilon }\bigl(T_{0}(v)\bigr) \leq \epsilon \hat{l}\bigl(T_{0}(v)\bigr)+k_{\epsilon }(v). $$

(A.11)

We combine (A.10) and (A.11) to get

$$ -\hat{l}\bigl(T_{0}(v)\bigr)\leq \frac{k_{\epsilon }(v)-k_{0}(v)}{\epsilon } \leq -\hat{l}\bigl(T_{\epsilon }(v)\bigr), $$

(A.12)

which leads to

$$ \biggl\vert \frac{k_{\epsilon }(v)-k_{0}(v)}{\epsilon } \biggr\vert \leq | \hat{l}|_{\infty }. $$

(A.13)

Consider a sequence $\{\epsilon _{n}\}_{n}$ converging to 0. The sequence $\{T_{\epsilon _{n}}(v)\}_{n}$ is bounded so we may find a subsequence $\{\epsilon '_{n}\}_{n}$ of $\{\epsilon _{n}\}_{n}$ such that the sequence $\{T_{\epsilon '_{n}}(v)\}_{n}$ converges to $u\in \bar{\varLambda }$. We then have:

$$ k_{0}(v)=\lim_{n\to \infty }k_{\epsilon _{n}'}(v)= \lim_{n\to \infty } \bigl(vT_{\epsilon _{n}'}(v)-l_{\epsilon _{n}} \bigl(T_{\epsilon _{n}'}(v)\bigr) \bigr) \leq vu-l_{0}(u)\leq k_{0}(v). $$

(A.14)

We use (A.14) to obtain $k_{0}(v)=vu-l_{0}(u)$ and thus $u=\nabla k_{0}(v)$ as $k_{0}$ is differentiable at $v$. It follows that $\lim_{\epsilon \to 0}T_{\epsilon }(v)= \nabla k_{0}(v)$. We use Eq. (A.12) and the continuity of $\hat{l}$ to obtain

$$ \lim_{\epsilon \rightarrow 0 } \frac{k_{\epsilon }(v)-k_{0}( v ) }{ \epsilon }=- t_{0} \hat{l}\bigl(\nabla k_{0}(v)\bigr). $$

 □