Pressure-driven flow in a thin pipe with rough boundary

Abstract

Stationary incompressible Newtonian fluid flow governed by external force and external pressure is considered in a thin rough pipe. The transversal size of the pipe is assumed to be of the order $\varepsilon$, i.e., cross-sectional area is about $\varepsilon ^{2}$, and the wavelength in longitudinal direction is modeled by a small parameter $\mu$. Under general assumption $\varepsilon ,\mu \rightarrow 0$, the Poiseuille law is obtained. Depending on $\varepsilon ,\mu$-relation ($\varepsilon \ll \mu$, $\varepsilon /\mu \sim \mathrm {constant}$, $\varepsilon \gg \mu$), different cell problems describing the local behavior of the fluid are deduced and analyzed. Error estimates are presented.

1 Introduction

Laminar fluid flow through pipes appears in various applications (blood circulation, heating/cooling processes, etc.). Experimental studies of the pipe flow go back to 1840s when Poiseuille [32, 33] established the relationship between the volumetric efflux rate of fluid from the tube, the driving pressure differential, the tube length and the tube diameter. The distinction between laminar, transitional and turbulent regimes for fluid flows was done by Stokes [37] and later was popularized by Reynolds [34]. In 1886, he also obtained limit equations similar to Poiseuille’s law but for flows in thin films [35]. In further experiments done by Nikuradse in 1933 [27], it was shown that “...for small Reynolds numbers there is no influence of wall roughness on the flow resistance” and since then for many years, the roughness phenomenon has been traditionally taken into account only in case of turbulent flow [2, 12, 38, 40]. However, in 2000s his experiments were reassessed [17, 18] and the importance of considering roughness effects for laminar flows was emphasized [14]. By means of classical analysis, different geometries were analyzed, e.g., detailed velocity and pressure profiles for flows with small Reynolds’ numbers in sinusoidal capillaries were obtained numerically in [16]; for creeping flow in pipes of varying radius [36], pressure drop was estimated by using a stream function method; in [39], the Stokes flow through a tube with a bumpy wall was solved through a perturbation in the small amplitude of the three-dimensional bumps.

There are several mathematical approaches to analyze thin pipe flow, e.g., asymptotic expansions with variations (see [20] for the case of helical pipes and [28] for an extended overview of such methods) and two-scale convergence [1, 19, 26] adapted for thin structures in [22] (see also [23, 25, 29]). The same techniques appear in analysis of thin film flows ( [3, 4, 11, 24]), where involving surface roughness effects are often connected to problems in sliding or rolling contacts [7, 31]. For the case of flow in curved pipes, we refer the reader to [13, 21, 30].

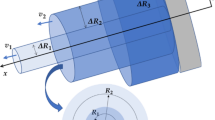
The present paper studies Stokes flow in a $\mu$-periodic rough pipe $\Omega ^{\varepsilon \mu }$ of thickness $\varepsilon$ with $x_{3}$-length L and an arbitrary transversal geometry, i.e., the representative volume of $\Omega ^{\varepsilon \mu }$ is a cylinder ${\textit{\textbf{Q}}}^{\varepsilon \mu }$ of length $\mu$ and arbitrary cross section with the area of order $O(\varepsilon ^{2})$.

We assume that the flow is governed by two factors—an external volume force f imposed all over $\Omega ^{\varepsilon \mu }$ and an external pressure $p^{b}$ acting on both ends of the pipe. The standard no-slip boundary condition is imposed on the walls of the pipe, whereas a Neumann stress boundary condition involving the external pressure $p^{b}$ is applied on its ends. The similar case of pressure-governed flow in helical pipes is considered in [20].

As all laminar flows in tubes, the asymptotic flow as $\varepsilon ,\mu \rightarrow 0$ in $\Omega ^{\varepsilon \mu }$ satisfies the one-dimensional Poiseuille law. Due to the choice of Neumann boundary condition for the original Stokes problem, the asymptotic limit satisfies Dirichlet boundary condition for the pressure.

The scalar parameter k appearing in Poiseuille’s law [see (2)] corresponds to geometrical part of Darcy’s friction factor. Depending on mutual $\varepsilon ,\mu$-rate, three cases are obtained:

HRTP:

—homogeneously rough thin pipe is characterized by $\varepsilon (\mu )\ll \mu$. The corresponding factor $k=k^{0}$ is built on the solution of the parameterized 2D Laplace equation.

PRTP:

—proportionally rough thin pipe is described by the rate $\varepsilon (\mu )/\mu \sim \lambda$, where $\lambda >0$ corresponds to the proportions of transverse size and longitudinal length of ${\textit{\textbf{Q}}}^{\varepsilon \mu }$. The factor $k=k^{\lambda }$ is derived through the solution of 3D Stokes cell problem in (1, 1)-scaled representative volume ${\textit{\textbf{Q}}}^{\varepsilon \mu }$.

ROTP:

—rapidly oscillating thin pipe satisfies $\varepsilon (\mu )\gg \mu$. The flow occurs only in non-rough region of the pipe, and the limit parameter $k=k^{\infty }$ comes from 2D Laplace equation for a fixed domain.

Analogous problems for the flow in thin films are studied by Amirat and Simon [3] and also in series of works by Bayada et al. (see [4,5,6]), where Reynolds, Stokes and high-frequency roughness regimes as thin film analogues of HRTP, PRTP and ROTP were established and analyzed. Moreover, the equations for HRTP approximation were rigorously proven by means of two-scale convergence technique in [9].

2 Problem formulation

2.1 Geometry

For each $z\in [0,1]$, we denote by $Q(z)(\subset {\mathbb {R}}^{2})$ a bounded domain such that a family $\{Q(z)\}_{z\in (0,1)}$ forms a smooth (actually Lipschitz) pipe ${\textit{\textbf{Q}}}\subset {\mathbb {R}}^{3}$ with the cylindrical (longitudinal) axis z:

$$\begin{aligned} {\textit{\textbf{Q}}}=\{(y,z)\in {\mathbb {R}}^{2}\times {\mathbb {R}}; z\in (0,1),y\in Q(z)\} \end{aligned}$$

with boundaries

$$\begin{aligned} \varvec{\gamma }_{N}= & {} \{(y,z)\in {\mathbb {R}}^{2}\times {\mathbb {R}}; z\in \{0,1\},y\in Q(z)\}, \\ \varvec{\gamma }_{D}= & {} \{(y,z)\in {\mathbb {R}}^{2}\times {\mathbb {R}}; z\in (0,1),y\in \partial Q(z)\} \end{aligned}$$

(Fig. 1b) In order for the fluid to pass through the pipe, we assume that there exists $\alpha >0$ such that the distance $d(\partial Q(z),(0,0,z))>\alpha$ for all $z\in [0,1]$. Let also

$$\begin{aligned} Q_{\min }=\{y\in {\mathbb {R}}^{2}; y\in \mathrm {int}(Q(z))\;\forall z\in [0,1]\}, \end{aligned}$$

where $\mathrm {int}(X)$ denotes the interior of a set X, and ${\textit{\textbf{Q}}}_{\min }$ is the largest straight pipe of cross section $Q_{\min }$ that is contained in ${\textit{\textbf{Q}}}$:

$$\begin{aligned} {\textit{\textbf{Q}}}_{\min }=Q_{\min }\times (0,1)\subset {\textit{\textbf{Q}}}. \end{aligned}$$

In addition, we impose the periodicity condition $Q(0)=Q(1)$ that allows us to extend ${\textit{\textbf{Q}}}$ smoothly along its longitudinal z-axis to infinitely long pipe $\overline{{\textit{\textbf{Q}}}}$ as follows:

$$\begin{aligned} \overline{{\textit{\textbf{Q}}}}=\{(y,\zeta )\in {\mathbb {R}}^{2+1}; \zeta \in {\mathbb {R}},y\in Q(z), z\in [0,1), z=\zeta \mathrm {mod}{\mathbb {Z}}\}. \end{aligned}$$

Fig. 1

Geometry of the pipe: a pipe $\Omega ^{\varepsilon \mu }$, b representative volume ${\textit{\textbf{Q}}}$

For small parameters $\mu ,\varepsilon \ll 1$, we define a smooth rough pipe $\Omega ^{\varepsilon \mu }$ of the length L (Fig. 1a):

$$\begin{aligned} \Omega ^{\varepsilon \mu }=\{x\in {\mathbb {R}}^{3}; x_{3}=\mu z\in (0,L), (x_{1},x_{2})=\varepsilon y\in \varepsilon Q(x_{3})=Q(x_{3}+\mu {\mathbb {Z}})\} \end{aligned}$$

with the boundary $\partial \Omega ^{\varepsilon \mu }=\Gamma ^{\varepsilon \mu }_{N}\cup \Gamma ^{\varepsilon \mu }_{D}$, where

$$\begin{aligned} \Gamma ^{\varepsilon \mu }_{N}= & {} \{x\in {\mathbb {R}}^{3}; x_{3}\in \{0,L\}, (x_{1},x_{2})\in \varepsilon Q(x_{3})\}, \\ \Gamma ^{\varepsilon \mu }_{D}= & {} \{x\in {\mathbb {R}}^{3}; x_{3}\in (0,L), (x_{1},x_{2})\in \partial (\varepsilon Q(x_{3}))\}. \end{aligned}$$

2.2 Notation for differential operators

For convenience’ sake in this section, we introduce all specific notation that will be used further. Thus, for variables $x=(x_{1},x_{2},x_{3})\in {\mathbb {R}}^{3}$, $y=(y_{1},y_{2})\in {\mathbb {R}}^{2}$, $z\in [0,1]$ and parameters $\varepsilon ,\mu ,\lambda >0$ we define the following differential operators:

$$\begin{aligned} \begin{array}{ll} \nabla _{y}=\left( \frac{\partial }{\partial y_{1}}, \frac{\partial }{\partial y_{2}}, 0\right) ,&{} \quad \Delta _{y}=\frac{\partial ^{2}}{\partial y_{1}^{2}}+\frac{\partial ^{2}}{\partial y_{1}^{2}}, \\ \nabla _{x_{3}}=\left( 0,0,\frac{\partial }{\partial x_{3}}\right) ,&{} \quad \Delta _{x_{3}}=\frac{\partial ^{2}}{\partial x_{3}^{2}}, \\ \nabla _{\varepsilon }=\frac{1}{\varepsilon }\nabla _{y}+\nabla _{x_{3}},&{} \quad \Delta _{\varepsilon }=\frac{1}{\varepsilon ^{2}}\Delta _{y}+\Delta _{x_{3}}. \\ \nabla _{z}=\left( 0,0,\frac{\partial }{\partial z}\right) ,&{} \quad \Delta _{z}=\frac{\partial ^{2}}{\partial z^{2}}, \\ \nabla _{\lambda }=\frac{1}{\lambda }\nabla _{y}+\nabla _{z},&{} \quad \Delta _{\lambda }=\frac{1}{\lambda ^{2}}\Delta _{y}+\Delta _{z}. \end{array} \end{aligned}$$

2.3 Problem statement

We consider the Stokes equations for incompressible Newtonian fluid:

$$\begin{aligned} \left\{ \begin{array}{lll} -\nabla P^{\varepsilon \mu }+\eta \Delta U^{\varepsilon \mu }+f=0&{}\quad \text {in }\Omega ^{\varepsilon \mu } &{}\text {(a)}\\ \nabla \cdot U^{\varepsilon \mu } =0 &{}\quad \text {in }\Omega ^{\varepsilon \mu }&{} \text {(b)}\\ (-P^{\varepsilon \mu }I+2\eta e(\nabla U^{\varepsilon \mu })){\hat{n}} =-p^{b}~{\hat{n}} &{}\quad \text {on }\Gamma ^{\varepsilon \mu }_{N} &{} \text {(c)}\\ U^{\varepsilon \mu } =0 &{}\quad \text {on }\Gamma ^{\varepsilon \mu }_{D} &{} \text {(d)} \end{array}\right. , \end{aligned}$$

(1)

where $2e(\nabla U^{\varepsilon \mu })=\nabla U^{\varepsilon \mu }+\left( \nabla U^{\varepsilon \mu }\right) ^{t}$, $\eta$ is fluid’s viscosity and f and $p^{b}$ are external volume force and boundary pressure correspondingly. We assume that the force $f=(0,0,f)$ acts only in longitudinal $x_{3}$-direction and both f and $p^{b}$ depend only on variable $x_{3}$—such limitation excludes circular or re-entrant flow in the vicinity of $\Gamma ^{\varepsilon \mu }_{N}$.

3 Main result

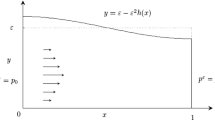
Under the assumption of small $\varepsilon$, $\mu$, the solution $(U^{\varepsilon \mu }, P^{\varepsilon \mu })$ of (1) can be approximated in terms of asymptotic expansions by an effective flow $(u^{\lambda },p^{\lambda })$ satisfying the one-dimensional Poiseuille’s law:

$$\begin{aligned} \left\{ \begin{array}{ll} \nabla _{x_{3}}\left( k^{\lambda }\left( \nabla _{x_{3}}p^{\lambda }-f\right) \right) =0,&{}\quad \text {in}\;(0,L)\\ u^{\lambda }=-\frac{1}{\eta }k^{\lambda }\left( \nabla _{x_{3}} p^\lambda -f\right) &{}\quad \text {in}\;(0,L)\\ p^{\lambda }=p^{b},\qquad &{}\quad \text {on}\;\{0,L\} \end{array}\right. , \end{aligned}$$

(2)

(see also Fig. 2) where parameter $\lambda \sim \varepsilon (\mu )/\mu$ represents mutual $\varepsilon ,\mu$-rate and thus even by letting $\varepsilon ,\mu \rightarrow 0$ can take high values, i.e., $\lambda \in [0,\infty ]$.

Fig. 2

Velocity approximation

The scalar parameter $k^{\lambda }\ge 0$ arising in (2) takes the micro-geometry of the pipe into account and is built on the solutions of cell problems that depend on mutual $\varepsilon ,\mu$-ratio.

• PRTP (Proportionally rough thin pipe) In proportional regime, $0<\lambda <\infty$, the expression for $k^{\lambda }$ has the form

  $$\begin{aligned} k^{\lambda } = \frac{1}{|{\textit{\textbf{Q}}}|}\int \limits _{{\textit{\textbf{Q}}}}W_{3}~\mathrm{d}y~\mathrm{d}z, \end{aligned}$$

  (3)

  where $W_{3}$ is the third velocity component of the solution (W, q) for the Stokes problem in a 3D unit cell ${\textit{\textbf{Q}}}$ governed by the unit force $e_{3}=(0,0,1)$

  $$\begin{aligned} \left\{ \begin{array}{ll} -\frac{1}{\lambda }\nabla _{\lambda }q+\Delta _{\lambda }W+\frac{1}{\lambda ^{2}}e_{3}=0&{}\quad \text {in }{\textit{\textbf{Q}}}\\ \nabla _{\lambda }\cdot W =0 &{}\quad \text {in }{\textit{\textbf{Q}}}\\ W =0 &{}\quad \text {on }\varvec{\gamma }_{D} \end{array}\right. \end{aligned}$$

  (4)

• HRTP (Homogeneously rough thin pipe) For the very thin regime, $\lambda =0$, the coefficient $k^{0}$ can be expressed as follows:

  $$\begin{aligned} k^{0}=\frac{1}{|{\textit{\textbf{Q}}}|}\left( \int \limits _{0}^{1}\frac{1}{a(z)}~\mathrm{d}z\right) ^{-1}, \end{aligned}$$

  (5)

  where

  $$\begin{aligned} a(z)=\int \limits _{Q(z)}\phi (y,z)~\mathrm{d}y \end{aligned}$$

  and $\phi$ is the solution of the 2D Laplace equation for z-parameterized, $z\in (0,1)$, domain Q(z):

  $$\begin{aligned} \left\{ \begin{array}{ll} -\Delta _{y}\phi =1&{}\quad \text {in }Q(z)\\ \phi =0 &{}\quad \text {on }\partial Q(z).\\ \end{array}\right. \end{aligned}$$

  (6)

• ROTP (Rapidly oscillating thin pipe) In the very rough regime, $\lambda =\infty$, the flow takes place only in the non-rough part of the pipe. In other words, the microstructure of the roughness can be ignored. This regime is characterized by the factor $k^{\infty }$

  $$\begin{aligned} k^{\infty } = \frac{1}{|{\textit{\textbf{Q}}}|}\int \limits _{Q_{\min }}W_{3}~\mathrm{d}y \end{aligned}$$

  (7)

  that is built on the solution of 2D Laplace equation for a fixed domain $Q_{\min }$:

  $$\begin{aligned} \left\{ \begin{array}{ll} -\Delta _{y}W_{3}=1&{}\quad \text {in }Q_{\mathrm {min}}\\ W_{3} =0 &{}\quad \text {on }\partial Q_{\min }.\\ \end{array}\right. \end{aligned}$$

  (8)

Remark 3.1

Let us note that in case of periodic pipe $\Omega ^{\varepsilon \mu }$ (see Sect. 2.1), the parameter $k^{\lambda }$, $\lambda \in [0,\infty ]$, is constant with respect to the longitudinal coordinate $x_{3}$. It allows to simplify the Poiseuille law (2) and obtain an explicit expression for the approximated pressure:

$$\begin{aligned} p^{\lambda }=\frac{p^{b}(L)-p^{b}(0)-\int \limits _{0}^{L}f~\mathrm{d}z}{L}z+\int \limits _{0}^{z}f~\mathrm{d}z+p^{b}(0). \end{aligned}$$

However, the analysis provided below can be applied for more general geometries which allow nontrivial dependence $k^{\lambda }=k^{\lambda }(x_{3})$, $x_{3}\in (0,L)$. The geometrical notation and corresponding results are presented in “Appendix I.”

Remark 3.2

As one can see, by starting from Neumann condition (1c) for the original Stokes problem we come up with Dirichlet pressure condition in the limit equation (2). Such switching in boundary conditions (and in opposite order) is observed also in context of flows in porous media [1, 10] and thin domains [9].

Remark 3.3

Instead of (1), one can also consider the full Navier–Stokes system. As it is expected for laminar flows, the inertial term does not affect the analysis and the approximation results above would still be valid.

4 Asymptotic expansions

4.1 Rescaling $\Omega ^{\varepsilon \mu }\rightarrow \Omega ^{\mu }$

First of all, in order to get rid of $\varepsilon$ from geometry of the pipe, we change variables $(x_{1},x_{2})\rightarrow (y_{1},y_{2})=(x_{1}/\varepsilon ,x_{2}/\varepsilon )$ and get

$$\begin{aligned} \left\{ \begin{array}{lll} -\nabla _{\varepsilon }p^{\varepsilon \mu }+\eta \Delta _{\varepsilon } u^{\varepsilon \mu }+f=0 &{}\quad \text {in }\Omega ^{\mu } &{} \text {(a)}\\ \nabla _{\varepsilon }\cdot u^{\varepsilon \mu } =0 &{} \quad \text {in }\Omega ^{\mu } &{} \text {(b)}\\ (-p^{\varepsilon \mu }I+2\eta e(\nabla _{\varepsilon } u^{\varepsilon \mu })){\hat{n}} =-p^{b}~{\hat{n}} &{}\quad \text {on }\Gamma ^{\mu }_{N} &{} \text {(c)}\\ u^{\varepsilon \mu } =0 &{}\quad \text {on }\Gamma ^{\mu }_{D} &{} \text {(d)} \end{array}\right. , \end{aligned}$$

(9)

where $\Omega ^{\mu }=\Omega ^{1\mu }$, $\Gamma ^{\mu }_{N,D}=\Gamma ^{1\mu }_{N,D}$ and

$$\begin{aligned} u^{\varepsilon \mu }(y,x_{3})&=U^{\varepsilon \mu }(\varepsilon y,x_{3}), \\ p^{\varepsilon \mu }(y,x_{3})&=P^{\varepsilon \mu }(\varepsilon y,x_{3}). \end{aligned}$$

4.2 Proportional case $\varepsilon =\lambda \mu$

Assume that

$$\begin{aligned} \begin{aligned} u^{\varepsilon \mu }(y,x_{3})&=\sum \limits _{i=2}^{\infty }\mu ^{i}\lambda ^{i}u^{i}\left( y,\frac{x_{3}}{\mu },x_{3}\right) , \\ p^{\varepsilon \mu }(y,x_{3})&=\sum \limits _{i=0}^{\infty }\mu ^{i}\lambda ^{i}p^{i}\left( y,\frac{x_{3}}{\mu },x_{3}\right) , \end{aligned} \end{aligned}$$

(10)

and let $z=x_{3}/\mu$. Since the geometry of the pipe becomes to be 1-periodic in z, we assume the same behavior for functions $p^{i}$, $i=0,\ldots ,\infty$, $u^{j}$, $j=2,\ldots ,\infty$.

By substituting (10) into (9) and collecting terms with the same powers of $\lambda$, we get the following:

• (1) Momentum equation From (9a), one can extract

  $$\begin{aligned} \mu ^{-1}:&\quad -\nabla _{\lambda }p^{0}=0, \end{aligned}$$

  (11)
  $$\begin{aligned} \mu ^{0}:&\quad -\frac{1}{\lambda ^{2}}\nabla _{x_{3}}p^{0}-\frac{1}{\lambda }\nabla _{\lambda }p^{1}+\eta \Delta _{\lambda }u^{2}+\frac{1}{\lambda ^{2}}f=0. \end{aligned}$$

  (12)

• (2) Mass equation Equation (9b) gives

  $$\begin{aligned} \mu ^{1}:&\quad \nabla _{\lambda }\cdot u^{2}=0, \end{aligned}$$

  (13)
  $$\begin{aligned} \mu ^{2}:&\quad \frac{1}{\lambda }\nabla _{x_{3}}\cdot u^{2}+\nabla _{\lambda }\cdot u^{3}=0. \end{aligned}$$

  (14)

• (3) Neumann condition Equation (9c) gives

  $$\begin{aligned}&\mu ^{0}:\quad p^{0}~{\hat{n}}=p^{b}~{\hat{n}}. \end{aligned}$$

  (15)

• (4) Dirichlet condition Equation (9d) gives

  $$\begin{aligned} u^{i}=0\qquad \text {for all}\quad i\ge 2. \end{aligned}$$

  (16)

4.2.1 Analysis of equations

• Macro-pressure $p^{0}$ Equation (11) provides

  $$\begin{aligned} p^{0}=p^{0}(x_{3}). \end{aligned}$$

  (17)

  By adding the boundary condition (15), we get

  $$\begin{aligned} p^0\big |_{0,L}=p^{b}\big |_{0,L}. \end{aligned}$$

  (18)

• Two-pressure problem Higher-order terms (see (12), (13) and (16)) constitute the system for $(p^{0}, p^{1}, u^{2})$:

  $$\begin{aligned} \left\{ \begin{array}{lll} -\frac{1}{\lambda ^{2}}\nabla _{x_{3}}p^{0}-\frac{1}{\lambda }\nabla _{\lambda }p^{1}+\eta \Delta _{\lambda }u^{2}+\frac{1}{\lambda ^{2}}f=0&{}\quad \text {in }{\textit{\textbf{Q}}}\times (0,L) &{} \text {(a)}\\ \nabla _{\lambda }\cdot u^{2} =0 &{}\quad \text {in }{\textit{\textbf{Q}}}\times (0,L) &{} \text {(b)}\\ u^{2} =0 &{}\quad \text {on }\varvec{\gamma }_{D}\times (0,L) &{} \text {(c)} \end{array}\right. \end{aligned}$$

  (19)

  Due to the linearity of Problem (19), one can write

  $$\begin{aligned} \begin{array}{lll} u^{2}&{}=&{}1/\eta \left( \nabla _{x_{3}}p^{0}-f\right) W,\\ p^{1}&{}=&{}\left( \nabla _{x_{3}}p^{0}-f\right) q, \end{array} \end{aligned}$$

  (20)

  where (W, q) is the 1-periodical in z-direction solution of the cell problem [compare with (4)]:

  $$\begin{aligned} \left\{ \begin{array}{ll} -\frac{1}{\lambda }\nabla _{\lambda }q+\Delta _{\lambda }W+\frac{1}{\lambda ^{2}}e_{3}=0&{}\quad \text {in }{\textit{\textbf{Q}}}\\ \nabla _{\lambda }\cdot W =0 &{}\quad \text {in }{\textit{\textbf{Q}}}\\ W =0 &{}\quad \text {on }\varvec{\gamma }_{D} \end{array}\right. \end{aligned}$$

  Here, $e_{3}=(0,0,1)$—the unit vector in z-direction.

• Poiseuille’s law System (2) for renamed functions

  $$\begin{aligned} \left\{ \begin{array}{rcl} p^{\lambda }&{}=&{}p^{0}\\ u^{\lambda }&{}=&{}\int \limits _{{\textit{\textbf{Q}}}}u^{2}~\mathrm{d}y~\mathrm{d}z \end{array} \right. \end{aligned}$$

  together with expression (3) for $k^{\lambda }$-factor is obtained by integrating (14) over ${\textit{\textbf{Q}}}$ and using equations (16), (20) together with z-periodicity assumption for $u^{2}$.

4.3 Homogeneously rough thin pipe

The case $\varepsilon \ll \mu$ corresponds to considering the limit $\lambda =\varepsilon /\mu \rightarrow 0$. Thus, we start with the cell problem (4) and look for the its solution (W, q) in the form

$$\begin{aligned} \begin{aligned} W(y,z)&=\sum \limits _{i=0}^{\infty }\lambda ^{i}W^{i}\left( y,z\right) , \\ q(y,z)&=\sum \limits _{i=-2}^{\infty }\lambda ^{i}q^{i}\left( y,z\right) . \end{aligned} \end{aligned}$$

(21)

Substituting the expansions into (4) gives the following series of equations with different powers of parameter $\lambda$.

4.3.1 Momentum equation

$$\begin{aligned}&\lambda ^{-2}:\quad -\nabla _{y}q^{-2}=0, \end{aligned}$$

(22)

$$\begin{aligned}&\lambda ^{-1}:\quad -\left( \nabla _{y}q^{-1}+\nabla _{z}q^{-2}\right) =0. \end{aligned}$$

(23)

The equations above imply

$$\begin{aligned} q^{-2}=\mathrm {const},\qquad q^{-1}=q^{-1}(z). \end{aligned}$$

The next order terms satisfy

$$\begin{aligned} \lambda ^{0}:&\quad -\left( \nabla _{y}q^{0}+\nabla _{z}q^{-1}\right) +\Delta _{y}W^{0}+e_{3}=0. \end{aligned}$$

(24)

4.3.2 Mass equation

It gives in addition

$$\begin{aligned} \lambda ^{-1}:&\quad \nabla _{y}\cdot W^{0}=0, \end{aligned}$$

(25)

$$\begin{aligned} \lambda ^{0}:&\quad \nabla _{y}\cdot W^{1}+\nabla _{z}\cdot W^{0}=0. \end{aligned}$$

(26)

4.3.3 Analysis of equations

Let’s consider a weak formulation of (24) with a smooth function $\varphi$, $\varphi =0$ on $\varvec{\gamma }_{D}$, as a test function:

$$\begin{aligned} \int \limits _{{\textit{\textbf{Q}}}}q^{0}\nabla _{y}\cdot \varphi +q^{-1}\nabla _{z}\cdot \varphi -\nabla {y}W^{0}:\nabla _{y}\varphi +e_{3}\cdot \varphi ~\mathrm{d}y~\mathrm{d}z=0. \end{aligned}$$

For $\varphi =(\varphi _{1},\varphi _{2},0)$ such that $\nabla _{y}\cdot \varphi =0$ in ${\textit{\textbf{Q}}}$, it reads as

$$\begin{aligned} \int \limits _{{\textit{\textbf{Q}}}}\nabla _{y}W^{0}:\nabla _{y}\varphi ~\mathrm{d}y~\mathrm{d}z=0. \end{aligned}$$

By taking $\varphi _{i}=W^{0}_{i}$, $i=1,2$, we obtain

$$\begin{aligned} \nabla _{y} W^{0}_{1}=\nabla _{y} W^{0}_{2}=0 \end{aligned}$$

that together with boundary conditions $W^{i}=0$ on $\varvec{\gamma }_{D}$, $i=0,1,\ldots$, implies

$$\begin{aligned} W^{0}_{1,2}=0. \end{aligned}$$

Thus (see (24)), $q^{0}=q^{0}(z)$ and the lowest order nontrivial terms $(q^{-1},W^{0}_{3})$ satisfy

$$\begin{aligned} -\frac{d q^{-1}}{\mathrm{d}z}+\Delta _{y}W^{0}_{3}+1&= 0, \end{aligned}$$

(27)

$$\begin{aligned} \int \limits _{Q(z)}\nabla _{z}\cdot W^{0}~\mathrm{d}y&= 0. \end{aligned}$$

(28)

The velocity solution $W^{0}_{3}$ of (27) can be written as

$$\begin{aligned} W^{0}_{3}=\left( 1-\frac{dq^{-1}}{\mathrm{d}z}\right) \phi , \end{aligned}$$

(29)

where $\phi$ is the solution of (6). Substituting (29) into (28) gives

$$\begin{aligned} \int \limits _{Q(z)}\frac{\partial }{\partial z}\left( 1-\frac{dq^{-1}}{\mathrm{d}z}\right) \phi (y,z)~\mathrm{d}y=0. \end{aligned}$$

Since $\phi =0$ on $\partial Q(z)$, the last equation is equivalent to

$$\begin{aligned} \frac{d}{d z}\left( \left( 1-\frac{dq^{-1}}{\mathrm{d}z}\right) a(z)\right) =0\qquad \text {with}\; a(z)=\int \limits _{Q(z)}\phi (y,z)~\mathrm{d}y. \end{aligned}$$

(30)

Integration of (30) gives

$$\begin{aligned} q^{-1}=C_{1}\int \limits _{0}^{z}\frac{1}{a(z)}~\mathrm{d}z-z+C_{2}, \end{aligned}$$

where by periodicity assumption $q^{-1}(0)=q^{-1}(1)$

$$\begin{aligned} C_{1} =\left( \int \limits _{0}^{1}a^{-1}(z)~\mathrm{d}z\right) ^{-1}. \end{aligned}$$

Finally,

$$\begin{aligned} W^{0}_{3}(y,z)=\left( 1-\frac{dq^{-1}}{\mathrm{d}z}\right) \phi =\frac{1}{\int \limits _{0}^{1}\frac{1}{a(z)}~\mathrm{d}z}\frac{\phi (y,z)}{a(z)} \end{aligned}$$

and [compare with (5)]

$$\begin{aligned} k^{0}=\frac{1}{|{\textit{\textbf{Q}}}|}\int \limits _{{\textit{\textbf{Q}}}}W^{0}_{3}~\mathrm{d}y~\mathrm{d}z= \frac{1}{|{\textit{\textbf{Q}}}|} \left( \int \limits _{0}^{1}\frac{1}{a(z)}~\mathrm{d}z\right) ^{-1}. \end{aligned}$$

4.4 Rapidly oscillating thin pipe

The fact that in ROTP limit the flow occurs only in no-rough region is expected from a physical point of view. However, its mathematical justification is not trivial and can be of a particular interest.

The case $\varepsilon \gg \mu$ corresponds to $\lambda =\mu /\varepsilon \rightarrow 0$. So, we replace $\lambda \rightarrow 1/\lambda$ in (4):

$$\begin{aligned} \left\{ \begin{array}{lll} -\left( \nabla _{y}+\frac{1}{\lambda }\nabla _{z}\right) q+\left( \Delta _{y}+\frac{1}{\lambda ^{2}}\Delta _{z}\right) W+e_{3}=0&{}\quad \text {in }{\textit{\textbf{Q}}}&{} \text {(a)}\\ \left( \lambda \nabla _{y}+\nabla _{z}\right) \cdot W =0 &{}\quad \text {in }{\textit{\textbf{Q}}}&{} \text {(b)}\\ W =0 &{}\quad \text {on }\varvec{\gamma }_{D}&{} \text {(c)} \end{array}\right. \end{aligned}$$

(31)

and look for (W, q) in the form of (21) with respect to $\lambda =\mu /\varepsilon$.

Substituting (21) into (31) gives

$$\begin{aligned} \left\{ \begin{array}{lll} -\sum \limits _{i=-2}^{\infty }\left( \lambda ^{i}\nabla _{y}+\lambda ^{i-1}\nabla _{z}\right) q^{i}+\sum \limits _{i=0}^{\infty }\left( \lambda ^{i}\Delta _{y}+\lambda ^{i-2}\Delta _{z}\right) W^{i}+e_{3}=0&{}\quad \text {in }{\textit{\textbf{Q}}}&{} \text {(a)}\\ \sum \limits _{i=0}^{\infty }\left( \lambda ^{i+1}\nabla _{y}+\lambda ^{i}\nabla _{z}\right) \cdot W^{i} =0 &{}\quad \text {in }{\textit{\textbf{Q}}}&{} \text {(b)}\\ W^{i} =0 &{}\quad \text {on }\varvec{\gamma }_{D}&{} \text {(c)} \end{array}\right. \end{aligned}$$

(32)

4.4.1 Momentum equation

From (32a), we get

$$\begin{aligned} \lambda ^{-3}:&\quad -\nabla _{z}q^{-2}=0, \end{aligned}$$

(33)

$$\begin{aligned} \lambda ^{-2}:&\quad -\nabla _{y}q^{-2}-\nabla _{z}q^{-1}+\Delta _{z}W^{0}=0, \end{aligned}$$

(34)

$$\begin{aligned} \lambda ^{-1}:&\quad -\nabla _{y}q^{-1}-\nabla _{z}q^{0}+\Delta _{z}W^{1}=0, \end{aligned}$$

(35)

$$\begin{aligned} \lambda ^{0}:&\quad -\nabla _{y}q^{0}-\nabla _{z}q^{1}++\Delta _{y}W^{0}+\Delta _{z}W^{2}+e_{3}=0. \end{aligned}$$

(36)

4.4.2 Mass equation

Equation (32b) gives in addition

$$\begin{aligned} \lambda ^{0}:&\quad \nabla _{z}\cdot W^{0}=0, \end{aligned}$$

(37)

$$\begin{aligned} \lambda ^{1}:&\quad \nabla _{y}\cdot W^{0}+\nabla _{z}\cdot W^{1}=0, \end{aligned}$$

(38)

$$\begin{aligned} \lambda ^{2}:&\quad \nabla _{y}\cdot W^{1}+\nabla _{z}\cdot W^{2}=0. \end{aligned}$$

(39)

4.4.3 Analysis of equations

• (i) Equation (33) implies $q^{-2}=q^{-2}(y)$.

• (ii) The next order terms satisfy (34) and (37). Equation (37) implies

  $$\begin{aligned} W^{0}_{3}=W^{0}_{3}(y),\qquad q^{-1}=q^{-1}(y). \end{aligned}$$

  By multiplying (34) by $\varphi (y,z)=\left( \varphi _{1},\varphi _{2},0\right)$, such that $\varphi =0$ on $\varvec{\gamma }_{D}$, 1-periodical with respect to z, and integrating over ${\textit{\textbf{Q}}}$ we get

  $$\begin{aligned} 0=\int \limits _{{\textit{\textbf{Q}}}}-\nabla _{y}q^{-2}\cdot \varphi +\Delta _{z}W^{0}\cdot \varphi ~\mathrm{d}y~\mathrm{d}z= \int \limits _{{\textit{\textbf{Q}}}}q^{-2}\nabla _{y}\cdot \varphi -\nabla _{z}W^{0}:\nabla _{z}\varphi ~\mathrm{d}y~\mathrm{d}z. \end{aligned}$$

  The expression above is valid in all Lipschitz domains (such that the divergence theorem holds). Now, let us consider $\varphi _{1,2}=W^{0}_{1,2}$ and take into account (38). It gives us the following:

  $$\begin{aligned}&0=\int \limits _{{\textit{\textbf{Q}}}}q^{-2}\nabla _{y}\cdot W^{0}-|\nabla _{z}W^{0}|^{2}~\mathrm{d}y~\mathrm{d}z= \int \limits _{{\textit{\textbf{Q}}}}-q^{-2}\nabla _{z}\cdot W^{1}-|\nabla _{z}W^{0}|^{2}~\mathrm{d}y~\mathrm{d}z\\&\quad =\int \limits _{{\textit{\textbf{Q}}}}\nabla _{z}q^{-2}\cdot W^{1}-|\nabla _{z}W^{0}|^{2}~\mathrm{d}y~\mathrm{d}z= \int \limits _{{\textit{\textbf{Q}}}}-|\nabla _{z}W^{0}|^{2}~\mathrm{d}y~\mathrm{d}z \end{aligned}$$

  (since $q^{-2}$ does not depend on z). It implies

  $$\begin{aligned} W^{0}=W^{0}(y) \end{aligned}$$

  that together with (34) additionally gives

  $$\begin{aligned} q^{-2}=const. \end{aligned}$$

  Moreover, if we consider $y\notin Q_{\min }$ and z-line passing through the point y, we obtain that the constant (in z) velocity $W^{0}$ has to be zero at points of intersection with the boundary $\varvec{\gamma }_{D}$ that means

  $$\begin{aligned} W^{0}=0\qquad \text {in}\;{\textit{\textbf{Q}}}/{\textit{\textbf{Q}}}_{\min }. \end{aligned}$$

  Since $W^{0}$ is a function of y only, (38) provides that $\partial W^{1}_{3}/\partial z$ depends also only on y. By periodicity assumption, we get that $\partial W^{1}_{3}/\partial z$ must be zero then and thus

  $$\begin{aligned} W^{1}_{3}=W^{1}_{3}(y),\qquad \nabla _{y}\cdot W^{0}=0. \end{aligned}$$

• (iii) The next couple to consider is (35), (39). This system can be analyzed in the same way as at step (ii). Below, we provide the summary of results obtained:

  $$\begin{aligned} \begin{array}{ll} q^{-2,-1}=const&{}\\ q^{0}=q^{0}(y)&{}\\ W^{0,1}=W^{0,1}(y)&{}\\ \nabla _{y}\cdot W^{0,1}=0&{}\\ W^{0,1}=0,&{}\quad y\notin Q_{\min }\\ W^{2}_{3}=W^{2}_{3}(y).&{} \end{array} \end{aligned}$$

  (40)

• (iv) Finally, we come to equation (36) that involves the force term $e_{3}$. By integrating it over ${\textit{\textbf{Q}}}$ with a test function $\varphi$ such that $\varphi =0$ on $\varvec{\gamma }_{D}$ and 1-periodic in z, we get

  $$\begin{aligned}&0=\int \limits _{{\textit{\textbf{Q}}}}\left( -\nabla _{y}q^{0}-\nabla _{z}q^{1}+\Delta _{y}W^{0}+\Delta _{z}W^{2}+e_{3}\right) \cdot \varphi ~\mathrm{d}y~\mathrm{d}z\\&=\int \limits _{{\textit{\textbf{Q}}}}-\nabla _{y}q^{0}\cdot \varphi +q^{1}\nabla _{z}\cdot \varphi -\nabla _{z}W^{2}:\nabla _{z}\varphi +\left( \Delta _{y}W^{0}+e_{3}\right) \cdot \varphi ~\mathrm{d}y~\mathrm{d}z. \end{aligned}$$

  (as before the expression above is valid in all Lipschitz domains, i.e., such that divergence theorem holds) By choosing $\varphi =\varphi (y)$ such that $\varphi =0$ outside of $Q_{\min }$, we get

  $$\begin{aligned} \int \limits _{{\textit{\textbf{Q}}}_{\min }}\left( -\nabla _{y}q^{0}+\Delta _{y}W^{0}+e_{3}\right) \cdot \varphi ~\mathrm{d}y~\mathrm{d}z= \int \limits _{Q_{\min }}\left( -\nabla _{y}q^{0}+\Delta _{y}W^{0}+e_{3}\right) \cdot \varphi ~\mathrm{d}y. \end{aligned}$$

  That is a weak formulation of

  $$\begin{aligned} -\nabla _{y}q^{0}+\Delta _{y}W^{0}+e_{3}\qquad \text {in}\;Q_{\min }. \end{aligned}$$

  (41)

  By taking $\varphi =(W^{0}_{1}, W^{0}_{2},0)$, we gain

  $$\begin{aligned} \int \limits _{Q_{\min }}|\nabla _{y}(W^{0}_{1}, W^{0}_{2},0)|^{2}~\mathrm{d}y=0 \end{aligned}$$

  that together with Friedrichs’ inequality implies

  $$\begin{aligned} W^{0}_{1,2}\equiv 0. \end{aligned}$$

  Thus, (41) can be rewritten as

  $$\begin{aligned} -\Delta _{y}W^{0}_{3}=1\qquad \text {and}\qquad \nabla _{y}q^{0}=0 \end{aligned}$$

  that completes analysis and leads to expressions (7), (8).

Remark 4.1

The same results (5), (6) ((7), (8)) for the limit case HRTP (ROTP) can also be obtained by modeling $\varepsilon ,\mu$-relation in (9) as $\varepsilon =\mu ^{2}$ ($\mu =\varepsilon ^{2}$ correspondingly) and considering $(u^{\varepsilon \mu }, p^{\varepsilon \mu })$ as series with respect to $\mu$ ($\varepsilon$) only.

5 Model example

To illustrate the results above numerically, we consider sinusoidal pipes $\Omega ^{\varepsilon \mu }$ with representative volume ${\textit{\textbf{Q}}}$:

$$\begin{aligned} {\textit{\textbf{Q}}}=\{(y,z)\in {\mathbb {R}}^{3},\;|y|<a\cos (2\pi z)+b,\;z\in (0,1)\}, \end{aligned}$$

(42)

where $b>a>0$, $a+b=1$, and circular cross section Q(z)

$$\begin{aligned} Q(z)=\{y\in {\mathbb {R}}^{2},\;|y|<R(z)=a\cos (2\pi z)+b\} \end{aligned}$$

(43)

of variable radius $R_{\min }<R<R_{\max }$. The maximal value of R is preserved to be 1 ($R_{\max }=1$), whereas $R_{\min }$ takes values $R_{\min }=0.4, 0.5, 0.6$. (Fig. 3 and Table 1).

Fig. 3

Elementary volume ${\textit{\textbf{Q}}}$: a 3D view, b XY view, c) YZ view, d) ZX view

Table 1 Volume $|{\textit{\textbf{Q}}}|$ for different $R_{\min }$, a and b

Table 2 Values of $k^{\lambda }$ for different radii $R_{\min }$

For each value of $R_{\min }$, all three cases ($\varepsilon /\mu =0$, $\varepsilon /\mu \in (0,\infty )$, $\mu /\varepsilon =0$) are considered.

• PRTP case is calculated by means of FEM software COMSOL Multiphysics, and the values for the friction factor $k^{\lambda }$ are presented in Table 2.

• HRTP In this case, the coefficient $k^{0}$ is built on the solution of (6) that for circular Q(z) (see (43)) has the form:

  $$\begin{aligned} \phi =-\frac{1}{4}\left( |y|^{2}-R^{2}(z)\right) . \end{aligned}$$

  Thus,

  $$\begin{aligned} k^{0}=\frac{1}{|{\textit{\textbf{Q}}}|}\left( \int \limits _{0}^{1} \frac{1}{a(z)}~\mathrm{d}z\right) ^{-1}=\frac{1}{4\left( a^{2}+2b^{2}\right) }\left( \int \limits _{0}^{1}\frac{1}{ R^{4}(z)}~\mathrm{d}z\right) ^{-1} \end{aligned}$$

  has the following values (see Table 3).

• ROTP The flow occurs only in the region

  $$\begin{aligned} {\textit{\textbf{Q}}}_{\min }=Q_{\min }\times (0,1),\qquad Q_{\min }=\{y\in {\mathbb {R}}^{2},\;|y|<R_{\min }\}. \end{aligned}$$

  The velocity $W_{3}$ is the solution of (8):

  $$\begin{aligned} W_{3}=-\frac{1}{4}\left( |y|^{2}-R_{\min }^{2}\right) , \end{aligned}$$

  and according to (7),

  $$\begin{aligned} k^{\infty } = \frac{\pi }{8|{\textit{\textbf{Q}}}|}(b-a)^{4}=\frac{(b-a)^{4}}{4\left( a^{2}+2b^{2}\right) } \end{aligned}$$

  (see also Table 3).

Table 3 $k^{0}$ and $k^{\infty }$ for different values of $R_{\min }$

Fig. 4

HRTP limit

Fig. 5

ROTP limit

The comparison between intermediate PRTP and limit cases HRTP and ROTP is presented in Figures 4 and 5, and x-axis is chosen as $1/\lambda =\mu /\varepsilon$ due to better resolution of the graph. As one can see from Fig. 4, the curves $k^{\lambda }=k^{\lambda }(1/\lambda )$ for all values of $R_{\min }$ have $\log$ shapes and fast rate of convergence $k^{\lambda }\rightarrow k^{0}$. According to Fig. 5, $k^{\lambda }$ allows the linear approximation for $1/\lambda \in (0,1)$ and the corresponding convergence $k^{\lambda }\rightarrow k^{\infty }$ has a linear rate in this region.

6 Justification of the result

The approximation results stated in Sect. 3 are obtained by using asymptotic series with respect to small parameters $\varepsilon$, $\mu$. This analysis is a formal method and needs to be combined with other techniques in order to make conclusions mathematically rigorous.

It is known [8, 15] that the Stokes system (1) allows the unique solution $(U^{\varepsilon \mu }, P^{\varepsilon \mu })$. In this section, we provide a priori estimates for $(U^{\varepsilon \mu }, P^{\varepsilon \mu })$ and error estimates for its approximation $(\varepsilon u^{2}, p^{0}+\varepsilon p^{1})$ (see (19)).

Both, a priori and error estimates are based on two main methods:

• the Korn inequality

  $$\begin{aligned} \Vert v\Vert _{2}\leqslant \varepsilon K\Vert e(\nabla v)\Vert _{2},\qquad v,e(\nabla v)\in L^{2}(\Omega ^{\varepsilon \mu }),\;v=0\text { on }\Gamma ^{\varepsilon \mu }_{D}, \end{aligned}$$

  (44)

  that establishes the relation between $L^{2}$-norms of a function and the symmetric part of its gradient;

• the Bogovskiǐ operator $B: \nabla \cdot v\mapsto [v]$ that recovers (as an equivalence class) an original function $v\in L^{2}(\Omega ^{\varepsilon \mu })$, $v=0$ on $\Gamma ^{\varepsilon \mu }_{D}$, from its $L^{2}$-divergence $\nabla \cdot v$ and provides the estimate

  $$\begin{aligned} \Vert v\Vert _{2}\leqslant \varepsilon ^{-1}B\Vert \nabla \cdot v\Vert _{2}. \end{aligned}$$

  (45)

Both constants $K,B>0$ are independent on $\varepsilon , \mu$. Moreover, the estimate (45) in case of functions $v=(v_{1},v_{2},0)$ can be improved to

For more details and proofs of (44), (45), we refer the reader to Theorems 4.1 and 4.3 in [9] where general thin domains are considered. The case of the rough pipe $\Omega ^{\varepsilon \mu }$ can be reduced to one in [9] by extending arguments. More precise, due to no-slip boundary condition (1d) one can always prolong $U^{\varepsilon \mu }$ by zero to any straight pipe $\Omega ^{\varepsilon }=\varepsilon Y\times (0,L)$ containing $\Omega ^{\varepsilon \mu }$. Here, $Y\subset {\mathbb {R}}^{2}$ is a sufficiently big circle (or square) such that $Y\supset Q(x_{3})$ for any $x_{3}\in (0,L)$. The comments on Inequality ($45^{\prime }$) can be found in Appendix II (see p. 22).

6.1 A priori estimates

There exists a constant $C>0$ independent of parameters $\varepsilon$, $\mu$ such that the following estimates

$$\begin{aligned} \frac{1}{\varepsilon ^{2}}\Vert U^{\varepsilon \mu }\Vert _{2}+\frac{1}{\varepsilon }\Vert \nabla U^{\varepsilon \mu }\Vert _{2}+\Vert P^{\varepsilon \mu }\Vert _{2}\leqslant C|\Omega ^{\varepsilon \mu }|^{1/2} \end{aligned}$$

are valid for the solution $\left( U^{\varepsilon \mu },P^{\varepsilon \mu }\right)$ of (1). The estimates above are proved in [9] (see Theorem 4.2, 4.5) for any smooth enough thin domain $\Omega ^{\varepsilon }$. The proof is also valid for the rough pipe $\Omega ^{\varepsilon \mu }$ due to no-slip condition on the rough surface.

As one can see, these estimates for $U^{\varepsilon \mu }$, $P^{\varepsilon \mu }$ do not depend on $\mu$ and give corresponding orders of convergence for Problem (1) to System (2) with respect to the pipe thickness $\varepsilon$.

6.2 Errors problem statement

After rescaling in (19) to the original variables $(y,z,x_{3})\rightarrow \left( x_{1}/\varepsilon ,x_{2}/\varepsilon , x_{3}/\mu , x_{3}\right)$ and subtracting it from (1), one gets the following system

$$\begin{aligned} \left\{ \begin{array}{lll} -\nabla p_{\mathrm {err}}+\eta \Delta u_{\mathrm {err}}+f^{\varepsilon }=0&{}\quad \text {in }\Omega ^{\varepsilon \mu } &{} \text {(a)}\\ \nabla \cdot u_{\mathrm {err}} =h^{\varepsilon } &{}\quad \text {in }\Omega ^{\varepsilon \mu } &{} \text {(b)}\\ (-p_{\mathrm {err}}I+2\eta e(\nabla u_{\mathrm {err}})){\hat{n}} =-g^{\varepsilon }~{\hat{n}} &{}\quad \text {on }\Gamma ^{\varepsilon \mu }_{N} &{} \text {(c)}\\ u_{\mathrm {err}} =0 &{}\quad \text {on }\Gamma ^{\varepsilon \mu }_{D} &{} \text {(d)} \end{array}\right. \end{aligned}$$

(46)

for the error functions

$$\begin{aligned} u_{\mathrm {err}}(x)&=U^{\varepsilon \mu }(x)- \varepsilon ^{2} u^{2}\left( \frac{x_{1}}{\varepsilon },\frac{x_{2}}{\varepsilon }, \frac{x_{3}}{\mu }, x_{3}\right) , \\ p_{\mathrm {err}}(x)&=P^{\varepsilon \mu }(x)-p^{0}(x_{3})-\varepsilon p^{1}\left( \frac{x_{1}}{\varepsilon },\frac{x_{2}}{\varepsilon }, \frac{x_{3}}{\mu }, x_{3}\right) . \end{aligned}$$

Here,

$$\begin{aligned} \begin{array}{lll} f^{\varepsilon }&{}=&{}\varepsilon ^{2}\eta \Delta _{x_{3}}u^{2}-\varepsilon \nabla _{x_{3}}p^{1}\\ h^{\varepsilon }&{}=&{}-\varepsilon ^{2}\nabla _{x_{3}}\cdot u^{2}\\ g^{\varepsilon }&{}=&{}2\varepsilon ^{2}\eta \nabla _{x_{3}}\cdot u^{2}=-2\eta h^{\varepsilon }. \end{array} \end{aligned}$$

(47)

Note that all derivatives in expressions for $f^{\varepsilon }, h^{\varepsilon }, g^{\varepsilon }$ are taken with respect to unscaled $x_{3}$ only and do not affect cell functions W, q constituting $u^{2}$ and $p^{1}$ (see (20)).

For any test function v such that $\nabla \cdot v=0$ in $\Omega ^{\varepsilon \mu }$ and $v=0$ on $\Gamma ^{\varepsilon \mu }_{D}$, the divergence theorem provides the following weak formulation of (46)

$$\begin{aligned} 2\eta \int \limits _{\Omega ^{\varepsilon \mu }}e(\nabla u_{\mathrm {err}}):e(\nabla v)~\mathrm{d}x= \int \limits _{\Omega ^{\varepsilon \mu }}j^{\varepsilon }\cdot v~\mathrm{d}x, \end{aligned}$$

(48)

with $j^{\varepsilon }=-\nabla g^{\varepsilon }+f^{\varepsilon }-\eta \nabla h^{\varepsilon }$ as a source term. Since the functions $u^{2}, p^{1}$ on the right-hand side of (47) are independent of $\varepsilon$ and $\mu$, the next norm estimate holds:

$$\begin{aligned} \Vert j^{\varepsilon }\Vert _{2}\leqslant \Vert f^{\varepsilon }\Vert _{2}+\Vert \nabla h^{\varepsilon }\Vert _{2}+ \Vert \nabla g^{\varepsilon }\Vert _{2}\leqslant \varepsilon C|\Omega ^{\varepsilon \mu }|^{1/2}. \end{aligned}$$

(49)

6.3 Error estimates

Now, let us estimate the $L^{2}$-norm of $u_{\mathrm {err}}$. For this, we take the difference $v=u_{\mathrm {err}}-\varphi$ where $\varphi$ is such that

$$\begin{aligned} \nabla \cdot \varphi =\nabla \cdot u_{\mathrm {err}}=h^{\varepsilon },\qquad \varphi =0 \;\text {on}\;\Gamma ^{\varepsilon \mu }_{D}, \end{aligned}$$

as a test function in (48):

$$\begin{aligned} 2\eta \int \limits _{\Omega ^{\varepsilon \mu }} |e(\nabla U)|^{2}\mathrm{d}x= \int \limits _{\Omega ^{\varepsilon \mu }}j^{\varepsilon }\cdot (U-\varphi )~\mathrm{d}x+2\eta \int \limits _{\Omega ^{\varepsilon \mu }}e(\nabla U):e(\nabla \varphi )~\mathrm{d}x. \end{aligned}$$

Using the Young inequality in the last term leads us to

$$\begin{aligned} \eta \int \limits _{\Omega ^{\varepsilon \mu }} |e(\nabla U)|^{2}\mathrm{d}x\leqslant \int \limits _{\Omega ^{\varepsilon \mu }}j^{\varepsilon }\cdot (U-\varphi )~\mathrm{d}x+ \eta \Vert e(\nabla \varphi )\Vert ^{2}_{2}. \end{aligned}$$

(50)

The further application of Hölder, Korn (44) and Young inequalities allows the following:

$$\begin{aligned} \int \limits _{\Omega ^{\varepsilon \mu }}j^{\varepsilon }\cdot (U-\varphi )~\mathrm{d}x\leqslant & {} \Vert j^{\varepsilon }\Vert _{2}\Vert (U-\varphi )\Vert _{2}\leqslant \varepsilon K\Vert j^{\varepsilon }\Vert _{2}\Vert e(\nabla (U-\varphi ))\Vert _{2} \\\leqslant & {} \varepsilon K\Vert j^{\varepsilon }\Vert _{2}\left( \Vert e(\nabla U)\Vert _{2}+\Vert e(\nabla \varphi )\Vert _{2}\right) \\\leqslant & {} \frac{\varepsilon ^{2}K^{2}}{2\eta }\Vert j^{\varepsilon }\Vert ^{2}_{2}+\frac{\eta }{2}\Vert e(\nabla U)\Vert ^{2}_{2}+ \varepsilon K\Vert j^{\varepsilon }\Vert _{2}\Vert e(\nabla \varphi )\Vert _{2}\\\leqslant & {} \frac{\varepsilon ^{2}K^{2}}{2`\eta }\Vert j^{\varepsilon }\Vert ^{2}_{2}+\frac{\eta }{2}\Vert e(\nabla U)\Vert ^{2}_{2}+ \frac{\varepsilon ^{2}K^{2}}{2}\Vert j^{\varepsilon }\Vert ^{2}_{2}+\frac{1}{2}\Vert e(\nabla \varphi )\Vert ^{2}_{2}. \end{aligned}$$

The last estimate implies the next inequality for (50)

$$\begin{aligned} \frac{\eta }{2} \int \limits _{\Omega ^{\varepsilon \mu }} |e(\nabla U)|^{2}\mathrm{d}x\leqslant \varepsilon ^{2} C_{1}\Vert j^{\varepsilon }\Vert ^{2}_{2}+ C_{2}\Vert e(\nabla \varphi )\Vert ^{2}_{2} \end{aligned}$$

(51)

with $C_{1}=K^{2}(1+\eta )/2\eta$, $C_{2}=(\eta +1/2)$.

Equation (49) provides $\Vert j^{\varepsilon }\Vert _{2}\leqslant \varepsilon C|\Omega ^{\varepsilon \mu }|^{1/2}$. To estimate the $\varphi$-term in (51), Inequality ($45^{\prime }$) can be used—it is enough to show that there exists $\varphi =(\varphi _{1},\varphi _{2},0)$ such that

$$\begin{aligned} \nabla \cdot \varphi =h^{\varepsilon }=-\varepsilon ^{2}\nabla _{x^{3}}\cdot u^{2}=-\varepsilon ^{2}\left( p^{0,\prime }-f\right) ^{\prime }W_{3}. \end{aligned}$$

This can be done due to the properties of the cell problem (4). Indeed, $\nabla _{\lambda }\cdot W=0$ in (4) provides

$$\begin{aligned} \nabla _{\lambda }\cdot \left( \int W_{1}~\mathrm{d}z,\int W_{2}~\mathrm{d}z,0\right) =-\int \frac{\partial W_{3}}{\partial z} \mathrm{d}z=-W_{3}. \end{aligned}$$

That gives us $\nabla \cdot \varphi =h^{\varepsilon }$ for $\varphi =(\varphi _{1},\varphi _{2},0)$:

$$\begin{aligned} \varphi _{1,2}(x)=\varepsilon ^{2}\left( p^{0,\prime }(x_{3})-f(x_{3})\right) ^{\prime } \int \limits _{0}^{x_{3}/\mu } W_{1,2}\left( \frac{x_{1}}{\varepsilon },\frac{x_{2}}{\varepsilon },z\right) ~\mathrm{d}z,\quad x\in \Omega ^{\varepsilon \mu }. \end{aligned}$$

The condition $\varphi =0$ on $\Gamma ^{\varepsilon \mu }_{D}$ follows from $W_{1,2}=0$ on $\varvec{\gamma }_{D}$ (see (4)).

Finally, we obtain the following estimate for (51):

$$\begin{aligned} \Vert e(\nabla u_{\mathrm {err}})\Vert _{2}\leqslant \varepsilon ^{2}C|\Omega ^{\varepsilon \mu }|^{1/2}, \end{aligned}$$

which together with the Korn inequality (44) implies also

$$\begin{aligned} \Vert u_{\mathrm {err}}\Vert _{2}\leqslant \varepsilon \Vert e(\nabla u_{\mathrm {err}})\Vert _{2}\leqslant \varepsilon ^{3}C|\Omega ^{\varepsilon \mu }|^{1/2}, \end{aligned}$$

(52)

where the constant C is independent of $\varepsilon$ and $\mu$.

To obtain the pressure estimates, we define $p_{\mathrm {err}}$ through the functional F by orthogonality:

$$\begin{aligned} \int \limits _{\Omega ^{\varepsilon \mu }}p_{\mathrm {err}}\nabla \cdot v~\mathrm{d}x=\langle F, v\rangle =\int \limits _{\Omega ^{\varepsilon \mu }}2\eta e(\nabla u_{\mathrm {err}}):e(\nabla v)- j^{\varepsilon }\cdot v~\mathrm{d}x. \end{aligned}$$

for any test function v such that $v=0$ on $\Gamma ^{\varepsilon \mu }_{D}$.

By using the Korn inequality (44), one can show

$$\begin{aligned} \left| \langle F, v\rangle \right|\leqslant & {} 2\eta \Vert e(\nabla u_{\mathrm {err}})\Vert _{2}\Vert e(\nabla v)\Vert _{2}+ \Vert j^{\varepsilon }\Vert _{2}\Vert v\Vert _{2}\\\leqslant & {} 2\eta \Vert e(\nabla u_{\mathrm {err}})\Vert _{2}\Vert e(\nabla v)\Vert _{2}+\varepsilon K\Vert j^{\varepsilon }\Vert _{2}\Vert e(\nabla v)\Vert _{2}= \varepsilon ^{2} C\Vert e(\nabla v)\Vert _{2} \end{aligned}$$

that due to (45) implies the estimate for the pressure $p_{\mathrm {err}}$:

$$\begin{aligned} \Vert p_{\mathrm {err}}\Vert _{2}\leqslant \varepsilon C|\Omega ^{\varepsilon \mu }|^{1/2} \end{aligned}$$

(53)

with C independent of $\varepsilon , \mu$. For the complete discussion regarding the last estimate, we refer the reader to Theorem 4.5 in [9], where the analogous result for thin domains is obtained and the detailed calculations are presented.

Together Eqs. (52) and (53) constitute the error estimates. The errors obtained are of the higher orders with respect to $\varepsilon$:

$$\begin{aligned} U^{\varepsilon \mu }-u^{2} \sim {\mathcal {O}}(\varepsilon ^{3})&\qquad \left( \text {whereas}\right. U^{\varepsilon \mu }, u^{2} \left. \sim {\mathcal {O}}(\varepsilon ^{2})\right) , \\ P^{\varepsilon \mu }-p^{0} \sim {\mathcal {O}}(\varepsilon )&\qquad \left( \text {whereas}\right. P^{\varepsilon \mu }, p^{0} \left. \sim {\mathcal {O}}(1)\right) \end{aligned}$$

and do not depend on $\mu$. To improve them further, the next terms in asymptotic expansions need to be considered.

Appendices

Appendix I

In this section, we will comment on the general case $k^{\lambda }=k^{\lambda }(z)$ as it was mentioned in Remark 3.1.

1.1 $x_{3}$-depending geometry

First, we introduce a straight pipe $\Omega ^{\varepsilon \mu }$ that is quasi-periodical in longitudinal direction, i.e., in addition to z-periodicity its geometry has a non-periodic global $x_{3}$-trend. For that purpose on par with the condition $Q(0)=Q(1)$ (see Sect. 2.1), we assume some $x_{3}$-dependence of y-cross section Q as follows:

Let f be a $2\times 2$ diagonal functional matrix with smooth components $f_{i}=f_{i}(x_{3})$, $i=1,2$, that are bounded from 0, i.e.,

$$\begin{aligned} f=\left( \begin{array}{cc}f_{1}&{}0\\ 0&{}f_{2}\end{array}\right) \qquad \text {and}\quad \forall x_{3}\in [0,L]\qquad f_{i}(x_{3})>a,\;i=1,2, \end{aligned}$$

for some positive parameter a.

By $[fQ]=[fQ](x_{3},z)$, we denote the following y-cross section of the pipe:

$$\begin{aligned} y\in [fQ](x_{3},z)\;\text {if and only if}\;f^{-1}y=\left( \frac{y_{1}}{f_{1}(x_{3})},\frac{y_{2}}{f_{2}(x_{3})}\right) \in Q(z),\;z\in [0,1], \end{aligned}$$

where Q(z) is as in Sect. 2.1. By analogy with ${\textit{\textbf{Q}}}$ (see Sect. 2.1),

$$\begin{aligned} {[}f{\textit{\textbf{Q}}}]=[f{\textit{\textbf{Q}}}](x_{3})=\{(y,z)\in {\mathbb {R}}^{2+1}; z\in (0,1),f^{-1}y\in Q(x_{3},z)\} \end{aligned}$$

has as its bounds

$$\begin{aligned} {[}f\varvec{\gamma }]_{N}=\{(y,z)\in {\mathbb {R}}^{2+1}; z\in \{0,1\},f^{-1}y\in Q(z)\}, \\ {[}f\varvec{\gamma }]_{D}=\{(y,z)\in {\mathbb {R}}^{2+1}; z\in (0,1),f^{-1}y\in \partial Q(z)\}. \end{aligned}$$

The minimal region

$$\begin{aligned} {[}fQ]_{\min }=[fQ]_{\min }(x_{3})=\{y\in {\mathbb {R}}^{2}; f^{-1}y\in \mathrm {int}(Q(z))\;\forall z\in [0,1]\} \end{aligned}$$

and $[f{\textit{\textbf{Q}}}]_{\min }$ is the largest pipe of cross section $[fQ]_{\min }=[fQ]_{\min }(x_{3})$ that is contained in $[f{\textit{\textbf{Q}}}]$.

For small parameters $\mu ,\varepsilon \ll 1$, we define a smooth rough pipe $\Omega ^{\varepsilon \mu }$ of the length L:

$$\begin{aligned} \Omega ^{\varepsilon \mu }=\{x\in {\mathbb {R}}^{3}; x_{3}=\mu z\in (0,L), (x_{1},x_{2})=\varepsilon y\in \varepsilon [fQ](x_{3},z)\} \end{aligned}$$

with the boundary $\partial \Omega ^{\varepsilon \mu }=\Gamma ^{\varepsilon \mu }_{N}\cup \Gamma ^{\varepsilon \mu }_{D}$, where

$$\begin{aligned} \Gamma ^{\varepsilon \mu }_{N}= & {} \{x\in {\mathbb {R}}^{3}; x_{3}\in \{0,L\}, (x_{1},x_{2})\in \varepsilon [fQ](x_{3},z)\}, \\ \Gamma ^{\varepsilon \mu }_{D}= & {} \{x\in {\mathbb {R}}^{3}; x_{3}\in (0,L), (x_{1},x_{2})\in \partial (\varepsilon [fQ](x_{3},z))\}. \end{aligned}$$

1.2 Reformulation of cell problems

The more general geometry of $\Omega ^{\varepsilon \mu }$ introduced above does not affect the analysis done in Sect. 4 and the main “global” result; the Poiseuille law expressed by System (2) is still valid (see also Fig. 2 in Sect. 3). However, since newly introduced “cells” $[f{\textit{\textbf{Q}}}]$ become depending on the global variable $x_{3}$, all expressions that are related to “micro”-structure of $\Omega ^{\varepsilon \mu }$ ((3),(5),(7), etc.) and stated in Sect. 3 need to be reformulated with replacing Q-domains by their [fQ]-analogues. For the sake of completeness, the corresponding changes are provided below.

• PRTP The factor $k^{\lambda }$ is calculated as

  $$\begin{aligned} k^{\lambda }=k^{\lambda }(x_{3}) = \frac{1}{|[f{\textit{\textbf{Q}}}]|}\int \limits _{[f{\textit{\textbf{Q}}}]}W_{3}~\mathrm{d}y~\mathrm{d}z, \end{aligned}$$

  for $W_{3}$—the third component of W in

  $$\begin{aligned} \left\{ \begin{array}{ll} -\frac{1}{\lambda }\nabla _{\lambda }q+\Delta _{\lambda }W+\frac{1}{\lambda ^{2}}e_{3}=0&{}\quad \text {in }[f{\textit{\textbf{Q}}}]\\ \nabla _{\lambda }\cdot W =0 &{}\quad \text {in }[f{\textit{\textbf{Q}}}]\\ W =0 &{}\quad \text {on }[f\varvec{\gamma }]_{D} \end{array}\right. \end{aligned}$$

• HRTP limit value $k^{0}$ is represented by

  $$\begin{aligned} k^{0}=k^{0}(x_{3})=\frac{1}{|[f{\textit{\textbf{Q}}}]|}\left( \int \limits _{0}^{1}\frac{1}{a(z,x_{3})}~\mathrm{d}z\right) ^{-1}, \end{aligned}$$

  where

  $$\begin{aligned} a(z,x_{3})=\int \limits _{[fQ](x_{3},z)}\phi (y,z)~\mathrm{d}y \end{aligned}$$

  and $\phi$ comes from

  $$\begin{aligned} \left\{ \begin{array}{ll} -\Delta _{y}\phi =1&{}\quad \text {in }[fQ](x_{3},z)\\ \phi =0 &{}\quad \text {on }\partial [fQ](x_{3},z).\\ \end{array}\right. \end{aligned}$$

• ROTP As before, the flow does not come into $[f{\textit{\textbf{Q}}}]/[f{\textit{\textbf{Q}}}]_{\min }$ and

  $$\begin{aligned} k^{\infty }=k^{\infty }(x_{3}) = \frac{1}{|[f{\textit{\textbf{Q}}}]|}\int \limits _{[fQ]_{\min }}W_{3}~\mathrm{d}y, \end{aligned}$$

  where $W_{3}$ satisfies

  $$\begin{aligned} \left\{ \begin{array}{ll} -\Delta _{y}W_{3}=1&{}\quad \text {in }[fQ]_{\mathrm {min}}\\ W_{3} =0 &{}\quad \text {on }\partial [fQ]_{\min }.\\ \end{array}\right. \end{aligned}$$

Appendix II

Here, we discuss the estimate ($45^{\prime }$). Without going into details about (45) (which can be found in Appendix B of [9]), we point out that the proof is based on a simple rescaling $(y,x_{3})\rightarrow (x_{1}/\varepsilon ,x_{2}/\varepsilon , x_{3})$ of a unit pipe $\Omega$ to its thin version $\Omega ^{\varepsilon }$ and the factor $\varepsilon ^{-1}$ appearing on the right-hand side of (45) is caused only by $\varepsilon ^{-2}$ in the inequality

$$\begin{aligned} \frac{1}{|\Omega ^{\varepsilon }|}\Vert \nabla (S^{\varepsilon }v)\Vert ^{2}_{L^2(\Omega ^{\varepsilon })}\leqslant \varepsilon ^{-2} \frac{1}{|\Omega |}\Vert \nabla v\Vert ^{2}_{L^{2}(\Omega )} \end{aligned}$$

(54)

for the gradient norm of the scaling operator $S^{\varepsilon }: L^{2}(\Omega )\rightarrow L^{2}(\Omega ^{\varepsilon })$

$$\begin{aligned} (S^{\varepsilon }v)(x)&= \left( \varepsilon v_{1}\left( \frac{x_{1}}{\varepsilon }, \frac{x_{2}}{\varepsilon }, x_{3}\right) ,\varepsilon v_{2}\left( \frac{x_{1}}{\varepsilon }, \frac{x_{2}}{\varepsilon }, x_{3}\right) , v_{3}\left( \frac{x_{1}}{\varepsilon }, \frac{x_{2}}{\varepsilon }, x_{3}\right) \right) . \\ \end{aligned}$$

Thus, to prove ($45^{\prime }$) is enough to show that (54) can be improved in case $v_{3}=0$.

Indeed, for $y_{1,2}=x_{1,2}/\varepsilon$ one can write

$$\begin{aligned} \nabla (S^{\varepsilon }v)(x)= \left( \begin{array}{ccc} \frac{\partial v_{1}}{\partial y_{1}} &{} \frac{\partial v_{1}}{\partial y_{2}}&{} \varepsilon \frac{\partial v_{1}}{\partial x_{3}}\\ \frac{\partial v_{2}}{\partial y_{1}} &{} \frac{\partial v_{2}}{\partial y_{2}}&{} \varepsilon \frac{\partial v_{2}}{\partial x_{3}}\\ 0 &{} 0 &{} 0 \\ \end{array} \right) \left( \frac{x_{1}}{\varepsilon },\frac{x_{2}}{\varepsilon },x_{3}\right) \end{aligned}$$

and thus

$$\begin{aligned} |\nabla (S^{\varepsilon }v)(x)|=\sum \limits _{i,j=1,2}\left| \frac{\partial v_{i}}{\partial y_{j}}\right| ^{2}\left( \frac{x_{1}}{\varepsilon },\frac{x_{2}}{\varepsilon },x_{3}\right) +\varepsilon ^{2}\sum \limits _{i=1,2}\left| \frac{\partial v_{i}}{\partial x_{3}}\right| ^{2} \left( \frac{x_{1}}{\varepsilon },\frac{x_{2}}{\varepsilon },x_{3}\right) . \end{aligned}$$

After integration over $\Omega ^{\varepsilon \mu }$, one gets a better version of (54):

$$\begin{aligned} \frac{1}{|\Omega ^{\varepsilon }|}\Vert \nabla (S^{\varepsilon }v)\Vert ^{2}_{L^2(\Omega ^{\varepsilon })}\leqslant \frac{1}{|\Omega |}\Vert \nabla v\Vert ^{2}_{L^{2}(\Omega )}, \end{aligned}$$

that allows to gain one more $\varepsilon$ in (45) and obtain ($45^{\prime }$).