The static deformation of the asymmetric Japanese bow: modelling bow asymmetries with the elastica theory

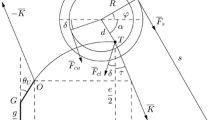
Abstract

The static deformation of symmetric bow limbs has been widely studied in the last century. However, asymmetries in shape and length which correspond to a more realistic situation, have not been thoroughly investigated. Here, we report a model for asymmetric bows based on the elastica theory and solved numerically by the Runge–Kutta method. We apply the model to describe the large asymmetric deformation which occurs in the Japanese bow, currently employed in the Japanese martial art of Kyūdō. We compare the model with experimental data acquired from a modern glass-fiber bow and a traditional bamboo bow, different in shape and construction. The model provides accurate results in predicting the deformation and the total energy stored in the bows, as long as the bending stiffness of the limbs is correctly reproduced. The energy is reproduced with an error within 1% and the unbraced and drawn shapes are reproduced with an RMSE of few millimeters compared to the length of $\sim \,2.2\,\hbox {m}$ of the bows. We investigate the influence of the grip position on the bow strength and shape which is not possible using classic symmetric models. At the end we show the possibility to analyze the bow design and potential failures by computing the bending stress extracted from the solution of the model. This study provides a further development with respect to the existing bow models by including the effect of the limb’s asymmetries in the static performances of the bows. The model for asymmetric limbs can bring important contributions for the design of the bows, reconstruction of ancient bows as well as to study the influence of the asymmetries on the targeting performance in modern competitive archery.

Appendices

Appendix 1: Contribution of the limb’s components to the bending stiffness

The final strength of the bows is directly related to the bending stiffness. By using Eq. (28) we calculated the contribution of the limb’s components to W(s), excluding the string stopper close the limb tip, as shown in Fig. 12. The calculated average percentage contributions $W^{\%}$ are the following; albeit rather simple calculation, we can get an insight of the role played by the layers of the limbs. In case of the GF bow, the upper fiberglass sheet accounts for $W^{\%}_{f1} \simeq 36\%$, the lower sheet for $W^{\%}_{f2} \simeq 35\%$ and the wood core for $W^{\%}_{w} = 29\%$. In the B bow, uchidake, todake, higo and sobagi contribute for $W^{\%}_{u} \simeq 49.5\%, W^{\%}_{t} \simeq 46\%, W^{\%}_{h} \simeq 3.3\%$ and $W^{\%}_{s} \simeq 1.2\%$ respectively. In both the bows, the major contribution comes from the external layers. In Fig. 12a, the trend of the contributions for the GF bow is linked to the thickness of the wood core which decreases from the grip to the limb tips, whereas the thickness of the fiberglass is kept constant at 1 mm. For the B bow in Fig. 12b, the external bamboo layers are thicker (4-5 mm) with their thickness constant along the limbs and since they are the furthest parts from the centroid of the cross-section, contribute together more than 90%. Contrary to what is traditionally believed in Japanese bow manufacturing, according to these results the main function of the core would be to add thickness for increasing the inertia of the outer parts rather than giving a direct contribution to the bow strength. The function of higo, usually cut from the low-density internal part of bamboo culm responsible for absorbing compression, could be the damping of bow vibrations.

Fig. 12

Percentage contribution of the cross-section parts to W(s). a GF bow: wood core $W^{\%}_{w}$, belly (back) side fiberglass sheets $W^{\%}_{f1(2)}$. b B bow: uchidake (belly) $W^{\%}_{u}$, todake (back) $W^{\%}_{t}$, higo core $W^{\%}_{h}$ and lateral sobagi strips $W^{\%}_{s}$ (Color figure online)

A confirmation of the percentage contributions of W(s) can be done by using the simple three-layer structure of the sandwich beam theory [25, 26]. By using Eq. (28), the stiffness of a rectangular sandwich limb of width w, with a core of thickness c and two external skins of thickness t, can be written as

$$\begin{aligned} W_{sw}=W_{c} + W_{f}=E_{c}\frac{wc^{3}}{12}+E_{f}\left[ \frac{wt^{3}}{6} + \frac{wt(c+t)^{2}}{2}\right] , \end{aligned}$$

(35)

where $W_{c}$ and $W_{f}$ represent the stiffness of the core and faces respectively. $E_{c}$ and $E_{f}$ are the Young moduli of the core and faces. To derive Eq. (35), we used the second-moment of area of a rectangular element about its centroid written as

$$\begin{aligned} I_{r}=\frac{wd^{3}}{12} , \end{aligned}$$

(36)

where $d = t, c$ is the thickness of the single layers. Note that in Eq. (35), $W_{sw}$ varies as the cube of the thicknesses ($c^{3}, t^{3}$) by Eq. (36) and it varies as the square of the distance of the outer layers from the centroid $(c+t)$/2 by Eq. (28). We now define normalized stiffness terms as ${\overline{W}} = 12 \cdot W/(Ewc^{3})$. If we take three layers of the same thickness $t = c$ and material $E_{c} = E_{f} = E$, we get for the core and the skins ${\overline{W}}_{c} = 1$ and ${\overline{W}}_{f} = 26$. This means a contribution of 3.7% for the core and 96.3% for the external layers; this case resembles well the B bow. Similarly to the case of the GF bow, if the outer skins have $E_{c} = E$ and $E_{f} = 4E$ and $t = c/10$, it follows that ${\overline{W}}_{c} = 1$ and ${\overline{W}}_{f} = 364/125 \sim 2.912$. This means a contribution of 25.6% for the core and 74.4% for the faces. To conclude, regardless the yield stress of materials or strength-to-weight ratio problems, the thickness of the limb and stiff parts placed externally are the main contributors to the stiffness; light and less stiff parts instead should be used as the core of the limb.

Appendix 2: Traditional rules for bow manufacturing

In this section, we want to briefly comment on using the asymmetric model, the design of the bamboo bow according to traditional manufacturing rules. Traditionally, for a fixed bow length L and construction rules of a bow-maker, the strength of bamboo bows was evaluated by measuring the maximum thickness of the limb above the grip, which is located in correspondence of a bamboo node of the belly side. This operation was called “Bu Ai”, from the Japanese measurement units (1 bu = 3 mm) [31] and it is used even nowadays as reference quantity during the bow construction. As expected by Eq. (32) of the linear beam theory, the greater changes in the final strength of the bow are due to thickness variations of the limbs. This has been widely discussed e.g. in Refs. [5, 21, 45]. Looking at the second-moment of inertia of a beam with rectangular cross-section shown in Eq. (36), in the same way the stiffness of the bow limb depends linearly on the width and varies as the cube of the thickness. Hence, small variations of the thickness can produce large variations in the bending stiffness. The same dependence exists for the trapezoidal cross-section [24]. For this reason, it would be reasonable to judge the strength of the bamboo bow with the Bu Ai criterion, according to the grip thickness.

Fig. 13

Bow force $F_{b}$ calculated at $b = 0.90$ m, $b_{f} = 0.145 \,\hbox {m}$ for a bow with length $L\simeq 2.25$ m and $c_{D}\simeq 0.38$ at different initial curvatures u and grip thicknesses $t_{G}$, taking $E_{b} = 16 \,\hbox {GPa}$. The arrow indicates the curves for increasing u, from the bottom: $u = 9 \,\hbox {cm}$, 11.8 cm, 14 cm, 17.4 cm, 19.3 cm, 22 cm. The inset shows the rough cross-section created for the calculations

To analyze the dependence of the bow strength on the limb thickness, we construct a fictitious bending stiffness for the limbs based on the following construction rules. As shown in the inset of Fig. 13, for simplicity we choose the shape of a rough bamboo bow which is not tapered in a trapezoidal cross-section yet. The thicknesses $t_{T}$ and $t_{U}$ of the external ($\textit{todake}$) and internal ($\textit{uchidake}$) bamboo sheets are usually fixed around 4 mm and 5 mm and cut from a bamboo culm with a radius of 4–5 cm or greater; for the calculation we set a radius of $R = 4 \,\hbox {cm}$. Different bow strengths can be obtained by changing the thickness of the core $t_{C}$ constituted by bamboo strips (${higo}$) with a total width of $w_{C} = 16 \,\hbox {mm}$ and lateral wood strips (${sobagi}$). Excluding the rigid string stopper of the limb tip, we reduce $t_{C}$ linearly from the grip to the limb tip about 3 mm. The maximum width of the finished bow at the grip is usually fixed around $w_{G}= 27 \,\hbox {mm}$ and decreases 3 mm to the tip.

However, a second variable to consider is the initial curvature of the bow, which has been previously shown as a determinant factor for its static performance [5]. In particular, the curvature of the bamboo bow is not strictly fixed since it can vary according to environmental conditions, so we introduced it as a second variable. In Japanese archery, the information about the curvature or $\textit{urazori}$ is evaluated as the height of the recurve of the unbraced bow. Similarly, here we calculate u as the difference between the x-coordinates of the grip (belly side) and limb tips when the tips of the upper and lower limbs have the same final x-coordinates. Figure 13 shows the calculated strength of the bow at full draw ($b = 0.90 \,\hbox {m}$) for increasing grip thickness $t_{G}$ and curvature u. The Young moduli of the materials used in the B bow was used in the calculations. As input of the initial curvatures we used real shapes of different unbraced bows, ensuring with the model that the characteristic shape of the bows at full draw was preserved. Now we fit the simulated curves with a power function $A(u)\cdot t_{G}^{B(u)}$, and we derive the equation for estimating the bow force $F_{b}$ as

$$\begin{aligned} F_{b}(u,t_{G})=(0.04951u+2.27)\cdot t_{G}^{3.563} , \end{aligned}$$

(37)

where u and $t_{G}$ are expressed in cm and the force is calculated in kgf. As shown in Fig. 13, in a range of $t_{G} = 1.2-1.8$ cm, $F_{b}$ changes in a range of $\sim$ 5–27 kgf. From Eq. (37) we can note that with respect to the linear beam theory, $F_{b}$ varies slightly more than the cube of the thickness. For a fixed $t_{G}$, the force increases linearly with the curvature in a range of $u = 9-22$ cm. However, due the high variability of bamboo and its elasto-plastic behavior, these calculations must be taken just as a qualitative investigation and precise quantitative calculations need to be performed according to the characteristics of the bamboo (e.g. aging, density, treatment) employed in the bow.