Abstract
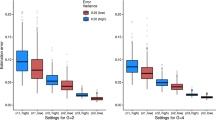
With the emergence of numerical sensors in many aspects of everyday life, there is an increasing need in analyzing multivariate functional data. This work focuses on the clustering of such functional data, in order to ease their modeling and understanding. To this end, a novel clustering technique for multivariate functional data is presented. This method is based on a functional latent mixture model which fits the data into group-specific functional subspaces through a multivariate functional principal component analysis. A family of parsimonious models is obtained by constraining model parameters within and between groups. An Expectation Maximization algorithm is proposed for model inference and the choice of hyper-parameters is addressed through model selection. Numerical experiments on simulated datasets highlight the good performance of the proposed methodology compared to existing works. This algorithm is then applied to the analysis of the pollution in French cities for 1 year.









Similar content being viewed by others
References
Akaike H (1974) A new look at the statistical model identification. IEEE Tran Autom Control 9:716–723
Basso RM, Lachos VH, Cabral CRB, Ghosh P (2010) Robust mixture modeling based on scale mixtures of skew-normal distributions. Comput Stat Data Anal 54(12):2926–2941
Berrendero J, Justel A, Svarc M (2011) Principal components for multivariate functional data. Comput Stat Data Anal 55:2619–263
Biernacki C, Celeux G, Govaert G (2000) Assessing a mixture model for clustering with the integrated completed likelihood. IEEE Trans PAMI 22:719–725
Birge L, Massart P (2007) Minimal penalties for Gaussian model selection. Probab Theory Relat Fields 138:33–73
Bongiorno EG, Goia A (2016) Classification methods for hilbert data based on surrogate density. Comput Stat Data Anal 99(C):204–222
Bouveyron C, Jacques J (2011) Model-based clustering of time series in group-specific functional subspaces. Adv Data Anal Classif 5(4):281–300
Bouveyron C, Come E, Jacques J (2015) The discriminative functional mixture model for the analysis of bike sharing systems. Ann Appl Stat 9(4):1726–1760
Bouveyron C, Celeux G, Murphy T, Raftery A (2019) Model-based clustering and classification for data science: with applications in R. Statistical and probabilistic mathematics. Cambridge University Press, Cambridge
Byers S, Raftery AE (1998) Nearest-neighbor clutter removal for estimating features in spatial point processes. J Am Stat Assoc 93(442):577–584
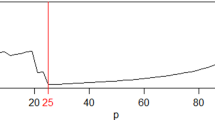
Cattell R (1966) The scree test for the number of factors. Multivar Behav Res 1(2):245–276
Chen L, Jiang C (2016) Multi-dimensional functional principal component analysis. Stat Comput 27:1181–1192
Chiou J, Chen Y, Yang Y (2014) Multivariate functional principal component analysis: a normalization approach. Stat Sin 24:1571–1596
Chiou JM, Li PL (2007) Functional clustering and identifying substructures of longitudinal data. J R Stat Soc Ser B Stat Methodol 69(4):679–699
Dempster A, Laird N, Rubin D (1977) Maximum likelihood from incomplete data via the EM algorithm. J R Stat Soc 39(1):1–38
Ferraty F, Vieu P (2003) Curves discrimination: a nonparametric approach. Comput Stat Data Anal 44:161–173
Gallegos MT, Ritter G (2005) A robust method for cluster analysis. Ann Stat 33(1):347–380
Gallegos MT, Ritter G (2009) Trimming algorithms for clustering contaminated grouped data and their robustness. Adv Data Anal Classif 3:135–167
Hennig C, Coretto P (2007) The noise component in model-based cluster analysis. Springer, Berlin, pp 127–138
Ieva F, Paganoni AM (2016) Risk prediction for myocardial infarction via generalized functional regression models. Stat Methods Med Res 25:1648–1660
Ieva F, Paganoni A, Pigoli D, Vitelli V (2013) Multivariate functional clustering for the morphological analysis of ECG curves. J R Stat Soc Series C (Appl Stat) 62(3):401–418
Jacques J, Preda C (2013) Funclust: a curves clustering method using functional random variable density approximation. Neurocomputing 112:164–171
Jacques J, Preda C (2014a) Functional data clustering: a survey. Adv Data Anal Classif 8(3):231–255
Jacques J, Preda C (2014b) Model based clustering for multivariate functional data. Comput Stat Data Anal 71:92–106
James G, Sugar C (2003) Clustering for sparsely sampled functional data. J Am Stat Assoc 98(462):397–408
Kayano M, Dozono K, Konishi S (2010) Functional cluster analysis via orthonormalized Gaussian basis expansions and its application. J Classif 27:211–230
Petersen KB, Pedersen MS (2012) The matrix cookbook. http://www2.imm.dtu.dk/pubdb/p.php?3274, version 20121115
Preda C (2007) Regression models for functional data by reproducing kernel hilbert spaces methods. J Stat Plan Inference 137:829–840
R Core Team (2017) R: a language and environment for statistical computing. R foundation for statistical computing, Vienna, Austria, https://www.R-project.org/
Ramsay JO, Silverman BW (2005) Functional data analysis, 2nd edn. Springer series in statistics. Springer, New York
Rand WM (1971) Objective criteria for the evaluation of clustering methods. J Am Stat Assoc 66(336):846–850
Saporta G (1981) Méthodes exploratoires d’analyse de données temporelles. Cahiers du Bureau universitaire de recherche opérationnelle Série Recherche 37–38:7–194
Schwarz G (1978) Estimating the dimension of a model. Ann Stat 6(2):461–464
Singhal A, Seborg D (2005) Clustering multivariate time-series data. J Chemom 19:427–438
Tarpey T, Kinateder K (2003) Clustering functional data. J Classif 20(1):93–114
Tokushige S, Yadohisa H, Inada K (2007) Crisp and fuzzy k-means clustering algorithms for multivariate functional data. Comput Stat 22:1–16
Traore OI, Cristini P, Favretto-Cristini N, Pantera L, Vieu P, Viguier-Pla S (2019) Clustering acoustic emission signals by mixing two stages dimension reduction and nonparametric approaches. Comput Stat 34(2):631–652
Yamamoto M (2012) Clustering of functional data in a low-dimensional subspace. Adv Data Anal Classif 6:219–247
Yamamoto M, Terada Y (2014) Functional factorial k-means analysis. Comput Stat Data Anal 79:133–148
Yamamoto M, Hwang H (2017) Dimension-reduced clustering of functional data via subspace separation. J Classif 34:294–326
Zambom AZ, Collazos JA, Dias R (2019) Functional data clustering via hypothesis testing k-means. Comput Stat 34(2):527–549
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflicts of interest
The authors declare that they have no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
We would like to thank the LabCom ’CWD-VetLab’ for its financial support. The LabCom ’CWD-VetLab’ is financially supported by the Agence Nationale de la Recherche (Contract ANR 16-LCV2-0002-01).
Appendix: Proofs
Appendix: Proofs
1.1 Proof of Proposition 1
where \(z_{ki}{=}1\) if \(x_i\) belongs to the cluster k and \(z_{ki}=0\) otherwise. \(f(x_i,\theta _k)\) is a Gaussian density, with parameters \(\theta _k=\{\mu _k,\Sigma _k\}\). So the complete log-likelihood is written:
For the \([a_{kj}b_kQ_kd_k]\) model, we have:
Let \(n_k=\sum _{i=1}^nz_{ki}\) be the number of curves within cluster k, the complete log-likelihood is then written:
The quantity \((x_i-\mu _k)^tQ_k\Delta _k^{-1}Q_k^t(x_i-\mu _k)\) is a scalar, so it is equal to it trace:
Well \(tr([(x_i-\mu _k)^tQ_k]\times [\Delta _k^{-1}Q_k^t(x_i-\mu _k)])=tr([\Delta _k^{-1}Q_k^t(x_i-\mu _k)]\times [(x_i-\mu _k)^tQ_k])\), consequently:
where \(C_k=\frac{1}{n_k}\sum _{i=1}^{n}z_{ki}(x_i-\mu _k)^t(x_i-\mu _k)\) is the empirical covariance matrix of the kth element of the mixture model. The \(\Delta _k\) matrix is diagonal, so we can write:
where \(q_{kj}\) is jth column of \(Q_k\). Finally,
1.2 Proof of Proposition 2
But, \(\Sigma _k=Q_k\Delta _k Q_k^t\) and \(Q_k^tQ_k=I_R\), hence:
Let \(Q_k=\tilde{Q_k}+\bar{Q_k}\) where \(\tilde{Q_k}\) is the \(R\times R\) matrix containing the \(d_k\) first columns of \(Q_k\) completed by zeros and where \(\bar{Q_k}=Q_k-\tilde{Q_k}\). Notice that \(\tilde{Q_k}\Delta _k^{-1}\bar{Q_k^t}=\bar{Q_k}\Delta _k^{-1}\tilde{Q_k^t}=O_p\) where \(O_p\) is the null matrix. So,
Hence,
With definitions \(\tilde{Q_k}[\tilde{Q_k^t}\tilde{Q_k}]=\tilde{Q_k}\) and \(\bar{Q_k}[\bar{Q_k^t}\bar{Q_k}]=\bar{Q_k}\), we can rephrase \(H_k(x)\) as:
We define \(\mathcal {D}_k=\tilde{Q_k}\Delta _k^{-1}\tilde{Q_k^t}\) and the norm \(||.||_{\mathcal {D}_k}\) on \(\mathbb {E}_k\) such as \(||x||_{\mathcal {D}_k}=x^t\mathcal {D}_kx\). So, on one hand:
On the other hand:
Consequently,
Knowing \(P_k\), \(P_k^{\bot }\) and \(||\mu _k-P_k^{\bot }||^2=||x-P_k(x)||^2\), we have:
Moreover, \(log|\Sigma _k|=\sum _{j=1}^{d_k}log(a_{kj})+(R-d_k)log(b_k)\). Finally,
1.3 Proof of Proposition 3
Parameter\(Q_{k}\) We have to maximise the log-likelihood under the constraint \(q_{kj}^tq_{kj}=1\), which is equivalent to looking for a saddle point of the Lagrange function:
where \(\omega _{kj}\) are Lagrange multiplier. So we can write:
Therefore, the gradient of \(\mathcal {L}\) in relation to \(q_{kj}\) is:
As a reminder, when W is symmetric, then \(\frac{\partial }{\partial x}(x-s)^TW(x-s)=2W(x-s)\) and \(\frac{\partial }{\partial x}(x^Tx)=2x\) (cf. Petersen and Pedersen (2012)), so:
where \(\sigma _{kj}\) is the jth diagonal term of matrix \(\Delta _k\).
So,
\(q_{kj}\) is the eigenfunction of \(W^{1/2}C_kW^{1/2}\) which match the eigenvalue \(\lambda _{kj}=\frac{\omega _{kj}\sigma _{kj}}{\eta _k}=W^{1/2}C_kW^{1/2}\). We can write \(q_{kj}^tq_{kl}=0\) if \(j\ne l\). So the log-likelihood can be written:
we substitute the equation \(\sum _{j=d_k+1}^R\lambda _{kj}=tr(W^{1/2}C_kW^{1/2})-\sum _{j=1}^{d_k}\lambda _{kj}\):
In order to minimize \(-2l(\theta )\) compared to \(q_{kj}\), we minimize the quantity \(\sum _{k=1}^K\eta _k\sum _{j=1}^{d_k}\lambda _{kj}(\frac{1}{a_{kj}}-\frac{1}{b_k})\) compared to \(\lambda _{kj}\). Knowing that \((\frac{1}{a_{kj}}-\frac{1}{b_k})\le 0, \forall j=1,\ldots ,d_k,\)\(\lambda _{kj}\) has to be as high as feasible. So, the jth column \(q_{kj}\) of matrix Q is estimated by the eigenfunction associated to the jth highest eigenvalue of \(W^{1/2}C_kW^{1/2}\).
Parameter\(a_{kj}\) As a reminder \((ln(x))'=\frac{x'}{x}\) and \((\frac{1}{x})'=-\frac{1}{x^2}\). The partial derivative of \(l(\theta )\) in relation to \(a_{kj}\) is:
The condition \(\frac{\partial l(\theta )}{\partial a_{kj}}=0\) is equivalent to:
Parameter\(b_k\) The partial derivative of \(l(\theta )\) in relation to \(b_{k}\) is:
But,
so:
The condition \(\frac{\partial l(\theta )}{\partial b_{k}}=0\) is equivalent to:
Rights and permissions
About this article
Cite this article
Schmutz, A., Jacques, J., Bouveyron, C. et al. Clustering multivariate functional data in group-specific functional subspaces. Comput Stat 35, 1101–1131 (2020). https://doi.org/10.1007/s00180-020-00958-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00180-020-00958-4