On the Bayesian Analysis of Constant-Stress Life Test Model Under Type-Ii Censoring

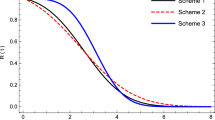
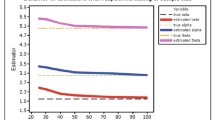
In this article, a constant-stress partially accelerated life test model of high reliability products and materials with type-II censored data from the linear failure rate distribution is considered. Two different methods of estimation likelihood and Bayesian are used to estimate the unknown parameters of the model. The maximum likelihood estimates of the model parameters are obtained using the Newton–Raphson technique. The posterior means and posterior variances are derived under the squared error loss function using Lindley’s approximation procedure. The advantages of this approximation are discussed. Monte Carlo simulations are made for comparing and evaluating the performance of the proposed methods of estimation.

Appendix

The derivation of posterior means and posterior variances: the used model contains three parameters. That is, m = 3. Let the subscripts 1, 2, and 3 refer to β, α, and θ, respectively. It is hard to obtain the posterior moments analytically. Therefore, using Lindley’s expansion, the posterior mean (i.e., Bayesian estimator under squared-error loss function) and the posterior variance of β are given, respectively, in the form:

$$ {\upbeta}^{\ast }=E\left(\upbeta | data\right)=\left[\upbeta -\left(\frac{\upsigma_{11}}{\upbeta}+\frac{\upsigma_{12}}{\uptheta}+\frac{\upsigma_{13}}{\upalpha}\right)+\frac{1}{2}\left({\upsigma}_{11}{E}_1+{\upsigma}_{12}{E}_2+{\upsigma}_{13}{E}_3\right)\right]\downarrow \Theta $$

(4)

and

$$ \operatorname{var}\left(\upbeta | data\right)=E\left({\upbeta}^2|y\right)-{\left({\upbeta}^{\ast}\right)}^2={\upsigma}_{11}-{\left[\left(\frac{\upsigma_{11}}{\upbeta}+\frac{\upsigma_{12}}{\uptheta}+\frac{\upsigma_{13}}{\upalpha}\right)-\frac{1}{2}\left({\upsigma}_{11}{E}_1+{\upsigma}_{11}{E}_2+{\upsigma}_{13}{E}_3\right)\right]}^2\downarrow \Theta . $$

(5)

Similarly, for the shape parameter α, the posterior mean and the posterior variance are given by

$$ {\upalpha}^{\ast }=E\left(\upalpha | data\right)=\left[\upalpha -\left(\frac{\upsigma_{31}}{\upbeta}+\frac{\upsigma_{32}}{\uptheta}+\frac{\upsigma_{33}}{\upalpha}\right)+\frac{1}{2}\left({\upsigma}_{31}{E}_1+{\upsigma}_{32}{E}_2+{\upsigma}_{33}{E}_3\right)\right]\downarrow \Theta, $$

(6)

$$ \operatorname{var}\left(\upalpha | data\right)={\upsigma}_{13}-{\left[\left(\frac{\upsigma_{31}}{\upbeta}+\frac{\upsigma_{32}}{\uptheta}+\frac{\upsigma_{33}}{\upalpha}\right)-\frac{1}{2}\left({\upsigma}_{31}{E}_1+{\upsigma}_{32}{E}_2+{\upsigma}_{33}{E}_3\right)\right]}^2\downarrow \Theta . $$

(7)

Applying the same technique, the posterior mean and posterior variance of the scale parameter θ take the following form:

$$ {\uptheta}^{\ast }=E\left(\uptheta | data\right)=\left[\uptheta -\left(\frac{\upsigma_{21}}{\upbeta}+\frac{\upsigma_{22}}{\uptheta}+\frac{\upsigma_{23}}{\upalpha}\right)+\frac{1}{2}\left({\upsigma}_{21}{E}_1+{\upsigma}_{22}{E}_2+{\upsigma}_{23}{E}_3\right)\right]\downarrow \Theta $$

(8)

and

$$ \operatorname{var}\left(\uptheta | data\right)={\upsigma}_{22}-{\left[\left(\frac{\upsigma_{21}}{\upbeta}+\frac{\upsigma_{22}}{\uptheta}+\frac{\upsigma_{23}}{\upalpha}\right)-\frac{1}{2}\left({\upsigma}_{21}{E}_1+{\upsigma}_{22}{E}_2+{\upsigma}_{23}{E}_3\right)\right]}^2\downarrow \Theta, $$

(9)

where

$$ {E}_1=\sum \limits_{i,j}{\upsigma}_{ij}{L}_{ij1}^{(3)},\kern1em {E}_2=\sum \limits_{i,j}{\upsigma}_{ij}{L}_{ij2}^{(3)},\kern1em {E}_3=\sum \limits_{i,j}{\upsigma}_{ij}{L}_{ij3}^{(3)}, $$

for i, j = 1, 2, 3, σ_ij are the elements of the inverse of the asymptotic Fisher-information matrix of the ML estimators of β, θ, and α in the case of type-II censored data, while i, j = 1, 2, 3, ${L}_{ijk}^{(3)}$ are the third derivatives of the natural logarithm of the likelihood function in type-II censoring.

To compute the posterior means and the posterior variances of β, θ, and α derived before, both second and third derivatives of the natural logarithm of the likelihood function given in (2) must be obtained.

The second derivatives can be derived via the following equations:

$$ {\displaystyle \begin{array}{c}\frac{\partial^2\ln L}{\partial {\upalpha}^2}=-\sum \limits_{i=1}^{n\left(1-\uppi \right)}{\updelta}_{u_i}\left[\frac{1}{{\left(\upalpha +\uptheta {t}_i\right)}^2}\right]-{\upbeta}^2\sum \limits_{j=1}^{n\uppi}{\updelta}_{a_j}\left[\frac{1}{{\left(\upalpha \upbeta +{\uptheta \upbeta}^2{x}_j\right)}^2}\right],\\ {}\frac{\partial^2\ln L}{\mathrm{\partial \upalpha \partial \uptheta }}=\frac{\partial^2\ln L}{\mathrm{\partial \uptheta \partial \upalpha }}=-\sum \limits_{i=1}^{n\left(1-\uppi \right)}{\updelta}_{u_i}\left[\frac{t_i}{{\left(\upalpha +\uptheta {t}_i\right)}^2}\right]-{\upbeta}^3\sum \limits_{j=1}^{n\uppi}{\updelta}_{a_j}\left[\frac{1}{{\left(\upalpha \upbeta +{\uptheta \upbeta}^2{x}_j\right)}^2}\right],\\ {}\frac{\partial^2\ln L}{\mathrm{\partial \upalpha \partial \upbeta }}=\frac{\partial^2\ln L}{\mathrm{\partial \upbeta \partial \upalpha }}=\sum \limits_{j=1}^{n\uppi}{\updelta}_{a_j}\left[\frac{-\left({\uptheta \upbeta}^2{x}_j\right)}{{\left(\upalpha \upbeta +{\uptheta \upbeta}^2{x}_j\right)}^2}-{x}_j\right]+P\left({n}_a-n\uppi \right),\\ {}\frac{\partial^2\ln L}{\partial {\uptheta}^2}=-\sum \limits_{i=1}^{n\left(1-\uppi \right)}{\updelta}_{u_i}\left[\frac{t_i^2}{{\left(\upalpha +\uptheta {t}_i\right)}^2}\right]-{\upbeta}^4\sum \limits_{j=1}^{n\uppi}{\updelta}_{a_j}\left[\frac{x_j^2}{{\left(\upalpha \upbeta +{\uptheta \upbeta}^2{x}_j\right)}^2}\right],\\ {}\frac{\partial^2\ln L}{\mathrm{\partial \uptheta \partial \upbeta }}=\frac{\partial^2\ln L}{\mathrm{\partial \upbeta \partial \uptheta }}=\sum \limits_{j=1}^{n\uppi}{\updelta}_{a_j}\left[\frac{-\left({\upalpha \upbeta}^2{x}_j\right)}{{\left(\upalpha \upbeta +{\uptheta \upbeta}^2{x}_j\right)}^2}-\upbeta {x}_j^2\right]+\upbeta {P}^2\left({n}_a-n\uppi \right),\\ {}\frac{\partial^2\ln L}{\partial {\upbeta}^2}=\sum \limits_{j=1}^{n\uppi}{\updelta}_{a_j}\left[\frac{-\left({\upalpha}^2+2\upalpha \uptheta \upbeta {x}_j+2{\left(\uptheta \upbeta {x}_j\right)}^2\right)}{{\left(\upalpha \upbeta +{\uptheta \upbeta}^2{x}_j\right)}^2}-\uptheta {x}_j^2\right]+\uptheta {P}^2\left({n}_a-n\uppi \right).\end{array}} $$

For the third derivatives, they are given as follows:

$$ {\displaystyle \begin{array}{c}{L}_{111}^{(3)}=\frac{\partial^3\ln L}{\partial {\upbeta}^3}=\sum \limits_{j=1}^{n\uppi}{\updelta}_{a_j}\left(\frac{2\left({\upalpha}^2+2\upalpha \uptheta \upbeta {x}_j+2{\uptheta}^2{\upbeta}^2{x}_j^2\right)\left(\upalpha +2\uptheta \upbeta {x}_j\right)-\left(\upalpha \upbeta +{\uptheta \upbeta}^2{x}_j\right)\left(2\upalpha \uptheta {x}_j+4{\uptheta}^2\upbeta {x}_j^2\right)}{{\left(\upalpha \upbeta +{\uptheta \upbeta}^2{x}_j\right)}^3}\right),\\ {}{L}_{222}^{(3)}=\frac{\partial^3\ln L}{\partial {\upalpha}^3}=\sum \limits_{i=1}^{n\left(1-\uppi \right)}{\updelta}_{u_i}\left(\frac{2}{{\left(\upalpha +\uptheta {t}_i\right)}^3}\right)+\sum \limits_{j=1}^{n\uppi}{\updelta}_{a_j}\left(\frac{2{\upbeta}^3}{{\left(\upalpha \upbeta +{\uptheta \upbeta}^2{x}_j\right)}^3}\right),\\ {}{L}_{333}^{(3)}=\frac{\partial^3\ln L}{\partial {\uptheta}^3}=\sum \limits_{i=1}^{n\left(1-\uppi \right)}{\updelta}_{u_i}\left(\frac{2{t}_i^3}{{\left(\upalpha +\uptheta {t}_i\right)}^3}\right)+\sum \limits_{j=1}^{n\uppi}{\updelta}_{a_j}\left(\frac{2{\left({\upbeta}^2{x}_j\right)}^3}{{\left(\upalpha \upbeta +{\uptheta \upbeta}^2{x}_j\right)}^3}\right),\\ {}{L}_{112}^{(3)}={L}_{211}^{(3)}={L}_{121}^{(3)}=\frac{\partial^3\ln L}{\partial {\upbeta}^3\mathrm{\partial \upalpha }}=\frac{\partial }{\mathrm{\partial \upbeta }}\left(\frac{\partial^2\ln L}{\mathrm{\partial \upbeta \partial \upalpha }}\right)=\sum \limits_{j=1}^{n\uppi}{\updelta}_{a_j}\left(\frac{2\left({\uptheta}^2{\upbeta}^3{x}_j^2\right)}{{\left(\upalpha \upbeta +{\uptheta \upbeta}^2{x}_j\right)}^3}\right),\\ {}{L}_{113}^{(3)}={L}_{311}^{(3)}={L}_{131}^{(3)}=\frac{\partial^3\ln L}{\partial {\upbeta}^2\mathrm{\partial \uptheta }}=\frac{\partial }{\mathrm{\partial \upbeta }}\left(\frac{\partial^2\ln L}{\mathrm{\partial \upbeta \partial \uptheta }}\right)=\sum \limits_{j=1}^{n\uppi}{\updelta}_{a_j}\left(\frac{-2\left({\upalpha \uptheta \upbeta}^3{x}_j^2\right)}{{\left(\upalpha \upbeta +{\uptheta \upbeta}^2{x}_j\right)}^3}-{x}_j^2\right)+{P}^2\left({n}_a-n\uppi \right),\\ {}{L}_{221}^{(3)}={L}_{122}^{(3)}={L}_{212}^{(3)}=\frac{\partial^3\ln L}{\partial {\upalpha}^2\mathrm{\partial \upbeta }}=\frac{\partial }{\mathrm{\partial \upalpha }}\left(\frac{\partial^2\ln L}{\mathrm{\partial \upalpha \partial \upbeta }}\right)=\sum \limits_{j=1}^{n\uppi}{\updelta}_{a_j}\left(\frac{2{\uptheta \upbeta}^3{x}_j}{{\left(\upalpha \upbeta +{\uptheta \upbeta}^2{x}_j\right)}^3}\right),\\ {}{L}_{331}^{(3)}={L}_{133}^{(3)}={L}_{313}^{(3)}=\frac{\partial^3\ln L}{\partial {\uptheta}^2\mathrm{\partial \upbeta }}=\frac{\partial }{\mathrm{\partial \uptheta }}\left(\frac{\partial^2\ln L}{\mathrm{\partial \uptheta \partial \upbeta }}\right)=\sum \limits_{j=1}^{n\uppi}{\updelta}_{a_j}\left(\frac{-2{\upalpha \uptheta \upbeta}^4{x}_j^2}{{\left(\upalpha \upbeta +{\uptheta \upbeta}^2{x}_j\right)}^3}\right),\\ {}{L}_{223}^{(3)}={L}_{322}^{(3)}={L}_{232}^{(3)}=\frac{\partial^3\ln L}{\partial {\upalpha}^2\mathrm{\partial \uptheta }}=\frac{\partial }{\mathrm{\partial \upalpha }}\left(\frac{\partial^2\ln L}{\mathrm{\partial \upalpha \partial \uptheta }}\right)=\sum \limits_{i=1}^{n\left(1-\uppi \right)}{\updelta}_{u_i}\left(\frac{2{t}_i}{{\left(\upalpha +\uptheta {t}_i\right)}^3}\right)+\sum \limits_{j=1}^{n\uppi}{\updelta}_{a_j}\left(\frac{2{\upbeta}^4{x}_j}{{\left(\upalpha \upbeta +{\uptheta \upbeta}^2{x}_j\right)}^3}\right),\\ {}{L}_{332}^{(3)}={L}_{233}^{(3)}={L}_{323}^{(3)}=\frac{\partial^3\ln L}{\partial {\uptheta}^2\mathrm{\partial \upalpha }}=\frac{\partial }{\mathrm{\partial \uptheta }}\left(\frac{\partial^2\ln L}{\mathrm{\partial \uptheta \partial \upalpha }}\right)=\sum \limits_{i=1}^{n\left(1-\uppi \right)}{\updelta}_{u_i}\left(\frac{2{t}_i^2}{{\left(\upalpha +\uptheta {t}_i\right)}^3}\right)+\sum \limits_{j=1}^{n\uppi}{\updelta}_{a_j}\left(\frac{2{\upbeta}^5{x}_j^2}{{\left(\upalpha \upbeta +{\uptheta \upbeta}^2{x}_j\right)}^3}\right),\\ {}{L}_{123}^{(3)}={L}_{321}^{(3)}={L}_{231}^{(3)}={L}_{312}^{(3)}={L}_{213}^{(3)}={L}_{132}^{(3)}=\frac{\partial^3\ln L}{\mathrm{\partial \upalpha \partial \uptheta \partial \upbeta }}=\frac{\partial }{\mathrm{\partial \upbeta }}\left(\frac{\partial^2\ln L}{\mathrm{\partial \upalpha \partial \uptheta }}\right)=\sum \limits_{j=1}^{n\uppi}{\updelta}_{a_j}\left(\frac{{\uptheta \upbeta}^4{x}_j^2-{\upalpha \upbeta}^3{x}_j}{{\left(\upalpha \upbeta +{\uptheta \upbeta}^2{x}_j\right)}^3}\right).\end{array}} $$