Abstract
We study the consumption and portfolio decisions by incorporating mortality risk and altruistic factor in the classical model of Merton (Rev Econ Stat 51:247–257, 1969; J Econ Theory 3:373–413, 1971) and Yaari (Rev Econ Stud 32(2):137–150, 1965). We find that besides the present-biased preference, the process of updating mortality information may be another underlying cause of dynamically time-inconsistent consumption behavior. We use the game-theoretic approach to obtain the extended Hamilton–Jacobi–Bellman equation. Furthermore, we obtain the closed-form solution for the logarithmic utility and explore comparative statics and implications for dynamic behavior. We present numerical results for the power utility that shows the sophisticated individual enjoys higher expected discounted utility than the naive. Our analytical solution enables us to generate a set of testable predictions that are consistent with existing empirical evidence. In particular, we show that for a moderate range of expected investment return, individuals will exhibit a “hump-shaped” consumption pattern, as widely documented in the empirical literature.



Similar content being viewed by others
Notes
The bequest in our model is in the form of a consumption stream instead of a lump sum inheritance. The assumption of an inherited consumption stream can be justified by the increasing use of trust funds, which guarantee beneficiaries, such as the heirs, a steady stream of cash flows akin to the consumption stream in our model.
The individual’s optimal consumption and investment solutions are time inconsistent in the sense that they do not follow the Bellman optimality principle.
Compared with the exponential discounting, hyperbolic discounting increases the instantaneous consumption rate, but does not affect the share of wealth invested in the risky asset.
Approximately 80% of the capital held by households is inherited [41]. Kuehlwein [42] shows that elderly households value bequests as highly as their own consumption. De Nardi [18] shows that the bequest motive is quantitatively important in explaining the wealth accumulation behavior of the richest in Sweden.
\(D(t,\tau )\) of Eq. (10) is similar in form to the expectation of the stochastic hyperbolic discount function, proposed by Harris and Laibson [33]. However, \(\pi (y)\) in Harris and Laibson [33] is constant. The experiments in McClure et al. [48] also show that when making an inter-temporal decision, the brain has two decision systems. The discount rate of the decision system responsible for discounting the far future utility is lower than the that of the decision system responsible for discounting the near future utility.
“Appendix A” gives the definition for a time varying discount function.
Gul and Pesendorfer [29] propose an alternative approach to model time-consistent preference suggesting that temptation but not preference change might be the cause of dynamically inconsistent behavior. Miao [51] adopts the Gul-Pesendorfer approach to solve the problem of the optimal option exercise by dynamic programming technique.
“Appendix A” gives the definition of non-stationarity.
If the hazard rate of death is constant, the discount function reflects only the time preference and the problem is the same as Ekeland and Pirvu [23], Ekeland and Lazrak [25], Ekeland et al. [24], Marín-Solano and Navas [46], Zou et al. [68], in which the solution depends only on the initial wealth.
\(\Gamma (\cdot )\) is the gamma function that satisfies \(\Gamma (\eta )=\int _0^\infty y^{\eta -1}e^{-y}dy\).
Basak and Chabakauri [4] show that the optimal consumption policies are time inconsistent in their mean-variance model because of the adjustment of the variance term.
We could also argue the time-consistent consumption and portfolio rules based on a more complex characterization of utility, for example, Epstein-Zin-Weil (EZW) recursive preferences utility functions [22, 65], which separate risk aversion from the elasticity of intertemporal substitution of consumption. Although EZW preferences have been useful in explaining the behavior of financial markets, we cannot obtain closed-form analytical solutions.
For the actual functional form of A(t) and B(t), please see “Appendix E”.
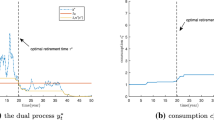
\(c^*_t(\tau )\) is the optimal instantaneous consumption rate at time \(\tau \) from the perspective of time t and \(c^*_\tau (\tau )\) is the actual instantaneous consumption rate at time \(\tau \) for a naive Bayesian individual.
Because of the individual’s finite lifetime, her wealth will be inherited by her heirs after her death, with the death time denoted by S. Following Merton [49], we assume that the bequest function takes the form of \(H(S,w(S))=\xi ^b\frac{(w(S))^{1-b}}{1-b}\), which means \(V(S,w(S))=\beta H(S,w(S))\) and \(H(S)=\beta \xi ^b\), where \(\xi =\frac{b}{\rho -(1-b)(r+\frac{a^2}{2b{\bar{\sigma }}^2})}\). Therefore, \(\lim _{t\rightarrow \infty }h(t)=\beta \xi ^b\).
o(1) is infinitesimal and \(\lim _{\epsilon \rightarrow 0}\frac{o(1)}{\epsilon }\)=0.
To be specific, this equilibrium strategy is also a weak and regular equilibrium strategy. Readers are referred to He and Jiang [37] for detailed discussions of the weak and regular strategy.
It is necessary to use a numerical solution to analyze the dynamic behavior with a power utility function. We omit it here for the sake of brevity. The non-linear integro-differential Eq. (28) is similar to those (Equation 42) in Zou et al. [68]. Readers are referred to Zou et al. [68] for the numerical analysis.
For the sake of brevity, we do not repeat these assumptions verbatim in the following proposition statements.
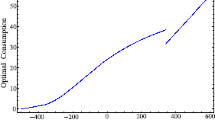
The consumption amount \({\hat{C}}(t)\) = \({\hat{c}}(t){\hat{w}}(t)\) is the product of the instantaneous consumption rate and wealth.
We show that \(\frac{1}{\rho }>\int _t^{\infty }e^{-\lambda (y^{\gamma }-t^{\gamma })}e^{-\rho (y-t)} dy\). By letting \(y-t=m\), we have
$$\begin{aligned}&\int _t^{\infty }e^{-\lambda (y^{\gamma }-t^{\gamma })}e^{-\rho (y-t)} dy\\&\quad =\int _0^{\infty }e^{-\lambda ((m+t)^{\gamma }-t^{\gamma })}e^{-\rho m} dm\\&\quad<\int _0^{\infty }e^{-\lambda \gamma t^{\gamma }m}e^{-\rho m} dm\\&\quad =\frac{1}{\lambda \gamma t^\gamma +\rho }\\&\quad <\frac{1}{\rho } \end{aligned}$$The third strict inequality holds because \((m+t)^{\gamma }-t^{\gamma }>\gamma t^{\gamma }m\) for \(\gamma >1\), \(m>0\) and \(t>0\).
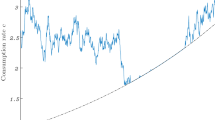
Since the life expectancy E[T] is \({(\frac{1}{\lambda })}^{\frac{1}{\gamma }}\Gamma (1+\frac{1}{\gamma })\), E[T] decreases with the parameter \(\lambda \). Eq. (33) implies that a shorter lifetime is associated with an increasing instantaneous consumption rate and therefore a longer expected lifespan is associated with a decreasing instantaneous consumption rate. Since E[T] is not monotonic with the parameter \(\gamma \), we do not explore the comparative statics of the time-consistent instantaneous consumption rate with regard to the parameter \(\gamma \) on the time-consistent instantaneous consumption rate, \({\hat{c}}(t)\).
i.e., \(\frac{\partial {\bar{t}}}{\partial R}>0\), \(\frac{\partial {\bar{t}}}{\partial \beta }>0\), where \({\bar{t}}\) is the duration of the period for which the individual is a net saver and \({\bar{t}}\) is defined as the solution to \(R=\frac{1}{(1-\beta )\int _t^\infty e^{-\lambda (y^\gamma -t^\gamma )}e^{-\rho (y-t)}dy+\frac{\beta }{\rho }}\).
The life expectancy is \((\frac{1}{\lambda })^{\frac{1}{\gamma }}\Gamma (1+\frac{1}{\gamma })=\Gamma (1.5)=0.8862\).
References
Angeletos, G.M., Laibson, D., Repetto, A., Tobacman, J., Weinberg, S.: The hyperbolic consumption model: calibration, simulation, and empirical evaluation. J. Econ. Perspect. 15(3), 47–68 (2001)
Akerlof, G.A.: Procrastination and obedience. Am. Econ. Rev. 81(2), 1–19 (1991)
Azfar, O.: Rationalizing hyperbolic discounting. J. Econ. Behav. Organ. 38(2), 245–252 (1999)
Basak, S., Chabakauri, G.: Dynamic mean-variance asset allocation. Rev. Financ. Stud. 23(8), 2970–3016 (2010)
Bommier, A.: Portfolio choice under uncertain lifetime. J. Public Econ. Theory 12(1), 57–73 (2010)
Barro, R.J.: Ramsey meets Laibson in the neoclassical growth model. Q. J. Econ. 114(4), 1125–1152 (1999)
Bagliano, F.C., Fugazza, C., Nicodano, G.: Optimal life-cycle portfolios for heterogeneous workers. Rev. Finance 18(6), 2283–2323 (2014)
Björk, T., Murgoci, A.: A general theory of Markovian time inconsistent stochastic control problems. SSRN:1694759 (2010)
Björk, T., Murgoci, A.: A theory of Markovian time-inconsistent stochastic control in discrete time. Finance Stoch. 18(3), 545–592 (2014)
Björk, T., Murgoci, A., Zhou, X.Y.: Mean-variance portfolio optimization with state-dependent risk aversion. Math. Finance 24(1), 1–24 (2014)
Björk, T., Khapko, M., Murgoci, A.: On time-inconsistent stochastic control in continuous time. Finance Stoch. 21(2), 331–360 (2017)
Beshears, J., Choi, J.J., Laibson, D., Madrian, B.C.: Does aggregated returns disclosure increase portfolio risk taking? Rev. Financ. Stud. 30(6), 1971–2005 (2017)
Chang, F.R.: Stochastic Optimization in Continuous Time. Cambridge University Press, Cambridge (2004)
Chen, S., Fu, R., Wedge, L., Zou, Z.: Non-hyperbolic discounting and dynamic preference reversal. Theor. Decis. 86(2), 283–302 (2019)
Chen, H., Ju, N., Miao, J.: Dynamic asset allocation with ambiguous return predictability. Rev. Econ. Dyn. 17(4), 799–823 (2014a)
Chen, S., Li, Z., Zeng, Y.: Optimal dividend strategies with time-inconsistent preferences. J. Econ. Dyn. Control 46, 150–172 (2014b)
Cocco, J.F., Gomes, F.J., Maenhout, P.J.: Consumption and portfolio choice over the life cycle. Rev. Financ. Stud. 18(2), 491–533 (2005)
De Nardi, M.: Wealth inequality and intergenerational links. Rev. Econ. Stud. 71(3), 743–768 (2004)
DellaVigna, S., Malmendier, U.: Contract design and self control: theory and evidence. Q. J. Econ. 119(2), 353–402 (2004)
Ekeland, I., Lazrak, A.: Being serious about non-commitment: subgame perfect equilibrium in continuous time. arXiv:math/0604264v1 (2006)
Ekeland, I., Karp, L., Sumaila, R.: Equilibrium resource management with altruistic overlapping generations. J. Environ. Econ. Manag. 70, 1–16 (2015)
Epstein, L.G., Zin, S.E.: Substitution, risk aversion and the temporal behavior of consumption and asset returns: an empirical analysis. J. Polit. Econ. 99(2), 263–286 (1991)
Ekeland, I., Pirvu, T.A.: Investment and consumption without commitment. Math. Financ. Econ. 2(1), 57–86 (2008)
Ekeland, I., Mbodji, O., Pirvu, T.A.: Time-consistent portfolio management. SIAM J. Financ. Math. 3(1), 1–32 (2012)
Ekeland, I., Lazrak, A.: The golden rule when preferences are time-inconsistent. Math. Financ. Econ. 4(1), 29–55 (2010)
Frederick, S., Loewenstein, G., O’Donoghue, T.: Time discounting and time preference: a critical review. J. Econ. Literat. 40(2), 351–401 (2002)
Gollier, C.: The Economics of Risk and Time. MIT Press, Cambridge (2001)
Gong, L.T., Smith, W., Zou, H.F.: Consumption and Risk with hyperbolic discounting. Econ. Lett. 96(2), 153–160 (2007)
Gul, F., Pesendorfer, W.: Temptation and self-control. Econometrica 69(6), 1403–1435 (2001)
Green, L., Myerson, J.: Exponential versus hyperbolic discounting of delayed outcomes: risk and waiting time. Am. Zool. 36(4), 496–505 (1996)
Grenadier, S.R., Wang, N.: Investment under uncertainty and time-inconsistent preferences. J. Financ. Econ. 84(1), 2–39 (2007)
Gourinchas, P.O., Parker, J.A.: Consumption over the life cycle. Econometrica 70(1), 47–89 (2002)
Harris, C., Laibson, D.: Instantaneous gratification. Q. J. Econ. 128(1), 205–248 (2013)
Halevy, Y.: Time consistency: stationarity and time invariance. Econometrica 83(1), 335–352 (2015)
Halevy, Y.: Diminishing Impatience: Disentangling Time Preference from Uncertain Lifetime, unpublished working paper, Department of Economics, University of British Columbia (2005)
Halevy, Y.: Strotz meets allais: diminishing impatience and the certainty effect. Am. Econ. Rev. 98(3), 1145–1162 (2008)
He, X.D., Jiang, Z.: On the Equilibrium Stragegies for Time-Inconsistent Problems in Continuous Time. Available at SSRN: https://ssrn.com/abstract=3308274 or https://doi.org/10.2139/ssrn.3308274 (2019)
Huang, Y.J., Zhou, Z.: Strong and Weak Equilibria for Time-Inconsistent Stochastic Control in Continuous Time. Available at arXiv:1809.09243v3 (2019)
Karp, L.: Non-constant discounting in continuous time. J. Econ. Theory 132(1), 557–568 (2007)
Koopmans, T.C.: Stationary ordinal utility and impatience. Econometrica 28(2), 287–309 (1960)
Kotlikoff, L.J., Summers, L.H.: The role of intergenerational transfers in aggregate capital accumulation. J. Polit. Econ. 89(4), 706–732 (1981)
Kuehlwein, M.: Life-cycle and altruistic theories of saving with lifetime uncertainty. Rev. Econ. Stat. 75(1), 38–47 (1993)
Kinari, Y., Ohtake, F., Tsutsui, Y.: Time discounting: declining impatience and interval effect. J. Risk Uncertain. 39(1), 87–112 (2009)
Laitner, J.: Secular changes in wealth inequality and inheritance. Econ. J. 111(474), 691–721 (2001)
Marín-Solano, J., Navas, J.: Non-constant discounting in finite horizon: the free terminal time case. J. Econ. Dyn. Control 33(3), 666–675 (2009)
Marín-Solano, J., Navas, J.: Consumption and portfolio rules for time-inconsistent investors. Eur. J. Oper. Res. 201(3), 860–872 (2010)
McClure, S.M., Laibson, D., Loewenstein, G., Cohen, J.D.: Separate neural systems value immediate and delayed monetary rewards. Science 306(5695), 503–507 (2004)
McClure, S.M., Ericson, K.M., Laibson, D., Loewenstein, G., Cohen, J.D.: Time discounting for primary rewards. J. Neurosci. 27(21), 5796–5804 (2007)
Merton, R.C.: Lifetime portfolio selection under uncertainty: the continuous-time case. Rev. Econ. Stat. 51, 247–257 (1969)
Merton, R.C.: Optimum consumption and portfolio rules in a continuous-time model. J. Econ. Theory 3, 373–413 (1971)
Miao, J.: Option exercise with temptation. Econ. Theor. 34(3), 473–501 (2008)
O’Donoghue, T., Rabin, M.: Doing it now or later. Am. Econ. Rev. 89(1), 103–124 (1999)
O’Donoghue, T., Rabin, M.: Present bias: lessons learned and to be learned. Am. Econ. Rev. 105(5), 273–279 (2015)
Palacios-Huerta, I., Pérez-Kakabadse, A.: Consumption and portfolio rules with stochastic hyperbolic discounting, unpublished working paper, London School of Economics, London, UK (2013)
Phelps, E.S., Pollak, R.A.: On second-best national saving and game-equilibrium growth. Rev. Econ. Stud. 35(2), 185–199 (1968)
Read, D.: Is time-discounting hyperbolic or subadditive? J. Risk Uncertain. 23(1), 5–32 (2001)
Read, D., Roelofsma, P.H.: Subadditive versus hyperbolic discounting: a comparison of choice and matching. Organ. Behav. Hum. Decis. Process. 91(2), 140–153 (2003)
Strotz, R.H.: Myopia and inconsistency in dynamic utility maximization. Rev. Econ. Stud. 23(3), 165–180 (1955)
Sozou, P.D.: On hyperbolic discounting and uncertain hazard rates. Proc. R. Soc. Lond. (Ser. B-Biol. Sci.) 265(1409), 2015–2020 (1998)
Scholten, M., Read, D.: Discounting by intervals: a generalised model of intertemporal choice. Manag. Sci. 52(9), 1424–1436 (2006)
Thaler, R.H., Shefrin, H.M.: An economic theory of self-control. J. Polit. Econ. 89(2), 392–406 (1981)
Weibull, W.: A statistical distribution function of wide applicability. J. Appl. Mech. 18(3), 293–297 (1951)
Wang, C., Wang, N., Yang, J.: A unified model of entrepreneurship dynamics. J. Financ. Econ. 106(1), 1–23 (2012)
Wei, J., Li, D., Zeng, Y.: Robust Optimal consumption-investment strategy with non-exponential discounting. J. Ind. Manag. Optim. 16(1), 207–230 (2018)
Weil, P.: Nonexpected utility in macroeconomics. Q. J. Econ. 105(1), 29–42 (1990)
Yaari, M.E.: Uncertain lifetime, life insurance, and the theory of the consumer. Rev. Econ. Stud. 32(2), 137–150 (1965)
Yong, J.: Time-inconsistent optimal control problems and the equilibrium HJB equation. Math. Control Relat. Fields 2(3), 271–329 (2012)
Zou, Z., Chen, S., Wedge, L.: Finite horizon consumption and portfolio decisions with stochastic hyperbolic discounting. J. Math. Econ. 52, 70–80 (2014)
Acknowledgements
We thank Rong Tang for his detailed comments on the paper. We also thank Frank Riedel (the editor) and the anonymous referee for helpful comments.
Funding
Funding was provided by National Natural Science Foundation of China (Grant Nos. 71221001, 804 71790593, 71501065 and 71850012), Natural Science Foundation of Hunan (Grant No. 2019JJ50082), Science and Technology Development Center of the Ministry of Education (Grant No. 2019J01020) and Major Program of the National Social Science Foundation of China (Grant No.18ZDA092).
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix A
Define \(MRS_t(t'+\tau _1,t'+\tau _2)\) as the marginal rate of substitution of utility at \(t'+\tau _1\) for utility at \(t'+\tau _2\) from the perspective of time t, \(t'+\tau _1>t\), \(\tau _2>\tau _1\), where \(MRS_t(t'+\tau _1,t'+\tau _2)=\frac{D(t,t'+\tau _2)}{D(t,t'+\tau _1)}\). Following Halevy [35] and Frederick et al. [26], we term this marginal rate of substitution as time discounting-the value at \(t'+\tau _1\) of receiving a unit utility at \(t'+\tau _2\) from the perspective of time t. According to Read [56], Read and Roelofsma [57], Scholten and Read [60], Kinari et al. [43] and Halevy [35], in the case when the perspective of time is current, i.e. \(t=0\), if an individual’s marginal rate of substitution \(MRS_0(t'+\tau _1,t'+\tau _2)\) increases with \(t'\), the individual is characterized by increasing patience, which is commonly called hyperbolic discounting.
For a wear-out individual characterized by the Weibull distribution with a constant pure time preference, i.e., the hazard rate of death is \(\pi (\tau )=\lambda \gamma \tau ^{\gamma -1}\) and the pure time preference factor is \(\rho \), then the discount function
where \(\gamma >1\).
From the definition \(MRS_0(t'+\tau _1,t'+\tau _2)\) and Eq. (A1), we have
Therefore,
where
From Eq. (A3), we can see that \((1-\beta )e^{-\lambda (t'+\tau _2)^\gamma -\lambda (t'+\tau _1)^\gamma } [(t'+\tau _1)^{\gamma -1}-(t'+\tau _2)^{\gamma -1}]\) is less than zero; \(\beta [e^{-\lambda (t'+\tau _1)^\gamma }(t'+\tau _1)^{\gamma -1}-e^{-\lambda (t'+\tau _2)^{\gamma }}(t'+\tau _2)^{\gamma -1}]\) is less than zero when \(t'\) is sufficiently large. As the time \(t'\) increases, \(g(t')\) is first less than zero and then eventually greater than zero. Therefore, from Eq. (A2), as time \(t'\) increases, the marginal rate of substitution \(MRS_0(t'+\tau _1,t'+\tau _2)\) first decreases and then increases. Hence, by the definition of the hyperbolic discounting, Eq. (10) is not a hyperbolic discount function since it does not monotonically increases with \(t'\).
Halevy [34] first formally define stationarity and time invariance. We use the concept of marginal rate of substitution to define them, an equivalent way to Halevy’s [34] (see Chen et al. [14]). A preference is stationary if and only if at any fixed decision time, the marginal rate of substitution over two future rewards depends only on the time distance and reward difference between these two alternatives, i.e., \(MRS_{t} (t+\Delta _1, t+\Delta _2) = MRS_{t} (t'+\Delta _1, t'+\Delta _2)\). Since \(MRS_{0}(t'+\tau _1,t'+\tau _2)\) first decreases and then increases as time \(t'\) increases, the discount function of Eq. (10) is non-stationary.
A preference is time invariant if and only if the marginal rate of substitution of any two future two rewards with the same time distance and reward difference does not change long as the time distance between the decision time and rewards remains the same, i.e., \(MRS_{t}(t+\Delta _1, t+\Delta _2) = MRS_{t'}(t'+\Delta _1, t'+\Delta _2)\). Since the hazard rate of death is non-constant, we can see that \(MRS_0(\tau _1,\tau _2)\ne MRS_t(t+\tau _1,t+\tau _2)\) for \(t>0\). Therefore, the discount function of Eq. (10) is time varying.
Appendix B
If the individual does not care about her bequests, then \(\beta =0\) and the optimization problem of Eq. (3) becomes
s.t. Eq. (2) and the initial condition (s, w(s)).
Define \(\{c_t^*(\tau ),\alpha _t^*(\tau )\}\), \(0\le t\le s\le \tau \) as the optimal consumption and portfolio choices and the value function is Q(t, s, w(s)), then
Furthermore, the value functions Q(0, s, w(s)) and Q(t, s, w(s)) satisfy the following equation
Equation (B2) can be written as
By the Taylor expansion, we have
From Eq. (B6), the optimal instantaneous consumption rate \(c_0^*(s)\) and \(c_t^*(s))\) must satisfy
and
The optimal instantaneous consumption rate is time consistent if and only if \(c_0^*(s)=c_t^*(s)\) for \(0<t\le s\). Therefore, from Eqs. (B7)–(B8), we have
From Eq. (B3), we obtain Eq. (B9).
By same analysis, the optimal instantaneous portfolio rule is also time consistent.
Appendix C
We first show that
and then use Eq. (C1) to show that the planned optimal instantaneous consumption rate is time inconsistent.
By the definition of marginal rate of substitution \(MRS_{t}(\tau _1,\tau _2)\), we have
Therefore,
since \(\Omega '(t)<0\) and \(\Omega (\tau _2)<\Omega (\tau _1)\).
Assume that \(c_0^*(\tau )\) is the optimal instantaneous consumption rate and \(w_0(\tau )\) is the wealth at time \(\tau \) from the perspective of time 0, then
Equation (C1) implies that
Equations (C2)–(C3) imply that
Therefore,
Equation (C4) implies that the planned optimal instantaneous consumption rate \(c_0^*(\tau )\) from the perspective of time 0 is not optimal from the perspective of time t and the individual will increase her welfare by deviating from it.
Since \(u'(\cdot )>0\) and \(u''(\cdot )<0\), the individual increases her welfare by raising the instantaneous consumption rate at \(\tau _1\) and lowering the instantaneous consumption rate at \(\tau _2\) until
Therefore, when an individual can re-optimize, she has an incentive to deviate from her ex-ante plan and increase the instantaneous consumption rate, i.e., \(c_\tau ^*(\tau )>c_t^*(\tau )>c_0^*(\tau )\), where \(\tau \ge s\ge t>0\).
Appendix D
Since
we have
where
and \({\hat{c}}(\tau )\) is the solution of Eq. (D2) and \({\hat{w}}(\tau )\) is the corresponding Markovian state.
From Eq. (D2), we have
From Eq. (D4), we have
From Eq. (2), \(w(t+\epsilon )\) satisfies the following equation
where \(\mu (t,c(t),\alpha (t))=\alpha (t)aw(t)+rw(t)-c(t)w(t)\). From Eq. (D6), we have
Combining Eqs. (D5) and (D7) and letting \(\epsilon \rightarrow 0\), we obtain
where
and \({\hat{c}}(t)\) satisfies Eq. (D8) and \({\hat{w}}(t)\) is the corresponding Markovian state.
Thus, the HJB equation of problem (15) subject to Eq. (2) is Eqs. (D8)–(D9) with the following boundary condition:
Appendix E
Since \(V(t,w(t))=A(t)\ln w(t)+B(t)\), we have
Thus, from Eq. (21), we obtain
and the corresponding Markovian state trajectory becomes
Substituting Eq. (E1) into Eq. (22), we obtain
From Eq. (E2), we have
Hence
Substituting Eq. (E5) into Eq. (E3), K(t, w(t)) can be expressed as
Substituting Eqs. (E1) and (E6) into Eq. (21), we obtain
Because Eq. (E7) must hold for every t and w(t), A(t) satisfy the following ordinary differential equation:
We solve Eq. (E8) and obtain
From Eqs. (E1) and (E9), we obtain the consumption rate determined by Eqs. (21)–(24)
Appendix F
Since \(V(t,w(t))=h(t)\frac{(w(t))^{1-b }}{1-b}\), we have
Therefore, from Eq. (21), we have
and the corresponding state trajectory becomes
Substituting Eq. (F1) into Eq. (22), we obtain
From Eq. (F2), we have
Substituting Eq. (F4) into Eq. (F3), K(t, w(t)) can be expressed as
Substituting Eqs. (F1) and (F5) into Eq. (21), we obtain
Because of the individual’s finite lifetime, her wealth will be inherited by her heirs after her death, the death time denoted by S. Following in Merton [49], we assume that the bequest function takes the form of \(H(S,w(S))=\xi ^b\frac{(w(S))^{1-b}}{1-b}\), which means \(V(S,w(S))=\beta H(S,w(S))\) and \(H(S)=\beta \xi ^b\), where \(\xi >0\). Therefore, \(\lim _{t\rightarrow \infty }h(t)=\beta \xi ^b\).
Appendix G
For any consumption and portfolio rules \(\varphi (\tau ,w(\tau ))=(\alpha (\tau ),c(\tau ))\), we denote
and
Denote \(U^{t,w(t),\varphi }(\tau ,w(\tau ))\) as the discounted instantaneous utility when the initial condition is (t, w(t)) and the individual follows the strategy \(\varphi \), where
Denote \({\bar{u}}^{t,w(t),x}(\tau ,w(\tau ))\) as the expected discounted instantaneous utility when the individual follows the strategy \({\hat{\varphi }}\) and the wealth at time \(\tau \) is \(w(\tau )\), where
Consider a function \(\xi ^x(\tau ,w(\tau ))\) for \(\tau \in [t,x]\) and \(w(\tau )\in (0,\infty )\), where \(\xi ^x(\tau ,w(\tau ))\) has continuous first-order partial derivatives with \(\tau \in [t,x]\) and \(w(\tau )\in (0,\infty )\) and a continuous second-order partial derivative with \(x\in (0,\infty )\), and denote these derivatives as \(\frac{\partial \xi ^x(\tau ,w(\tau ))}{\partial \tau }\), \(\frac{\partial \xi ^x(\tau ,w(\tau ))}{\partial w}\), and \(\frac{\partial ^2\xi ^x(\tau ,w(\tau ))}{\partial w^2}\), respectively. For any \(\xi ^x(\tau ,w(\tau ))\), denote
where \( \tau \in [t,x]\), \(w(\tau )\in (0,\infty )\).
Following the same argument as in Lemma 3 in He and Jiang [37], for the logarithmic utility function and the power utility function, we have
where
and o(1) is infinitesimal and \(\lim _{\epsilon \rightarrow 0}\frac{o(1)}{\epsilon }=0\).
(1) The logarithmic utility function
For the logarithmic utility function, \({\hat{\varphi }}=({\hat{c}}(t),{\hat{\alpha }}(t))\) is the solution of Eqs. (21)–(24), where
Denote \({\hat{w}}(\tau )\) as the above Markovian state of consumption and portfolio rules. From Eqs. (2) and (G8), we have
From Eq. (G9), we have
Denote \(w^{\epsilon }(\tau )\) as the Markovian state of consumption and portfolio rules \(\varphi _{t,\epsilon ,\varsigma }(\tau ,w(\tau ))\), which is defined in Eq. (17), \(\tau \ge t\). If the individual follows the strategy \(\varphi _{t,\epsilon ,\varsigma }\), the state trajectory \(w^{\epsilon }(\tau )\) becomes
From Eqs. (G4) and (G10), for the logarithmic utility function, we have
From Eq. (G3), we have
From Eqs. (G1), (G2), (G5) and (G12), it is easy to see that
From Eq. (G14), we have
From Eqs. (G7), (G13) and (G15), we have
Since both \({\hat{\alpha }}(t)\) and \({\hat{c}}(t)\) are constant, it is straightforward to see the maximum \(\Gamma ^{{\hat{\varphi }}}(t,w(t),\varsigma )\le 0\). Furthermore, \(\Gamma ^{{\hat{\varphi }}}(t,w(t),\varsigma )=0\) if and only if \({\hat{\varphi }}(t,w(t))\equiv \varsigma (t,w(t))\).
From the above analysis, for the logarithmic utility function, the strategy \({\hat{\varphi }}(t,w(t))\) determined by Eqs. (21)–(24) satisfies Eq. (19) and thus is an equilibrium strategy, i.e.,
for any sufficiently small \(\epsilon \).
Furthermore, following the same argument as in Theorem 1 in He and Jiang [37], the strategy is a weak and regular equilibrium strategy.
(2) The Power utility function
For the power utility function, \({\hat{\varphi }}=({\hat{c}}(t),{\hat{\alpha }}(t))\) is the solution of Eqs. (21)–(24),
where h(t) satisfies the following non-linear integro-differential equation
and \(\lim _{t\rightarrow \infty }h(t)=\beta \xi ^b\)
Denote \({\hat{w}}(\tau )\) as the above Markovian state of consumption and portfolio rules. From Eqs. (2) and (G17), we have
and therefore
Denote \(w^{\epsilon }(\tau )\) as the Markovian state of consumption and portfolio rules \(\varphi _{t,\epsilon ,\varsigma }(\tau ,w(\tau ))\), which is defined in Eq. (17), \(\tau \ge t\). If the individual follows the strategy \(\varphi _{t,\epsilon ,\varsigma }\), the state trajectory \(w^{\epsilon }(\tau )\) becomes
From Eqs. (G4) and (G20), for the power utility function, we have
From Eq. (G3), we have
From Eqs. (G1), (G2), (G5), (G17) and (G22), it is easy to see that
From Eq. (G24), we have
Denote \(f(t)=\int _t^\infty D(t,x)(h(x))^{1-\frac{1}{b}}\exp \left[ (1-b)\int _t^x(\frac{a^2}{2b{\bar{\sigma }}^2}+r-(h(y))^{-\frac{1}{b}})dy\right] dx\). It is easy to see that f(t) satisfies Eq. (28) and \(\lim _{t\rightarrow \infty }f(t)=\beta \xi ^b\). Therefore, \(f(t)\equiv h(t)\) and Eq. (G25) becomes
From Eqs. (G7), (G23) and (G26), we have
Since both \({\hat{\alpha }}(t)\) and \({\hat{c}}(t)\) are constant, it is straightforward to see the maximum \(\Gamma ^{{\hat{\varphi }}}(t,w(t),\varsigma )\le 0\). Furthermore, \(\Gamma ^{{\hat{\varphi }}}(t,w(t),\varsigma )=0\) if and only if \({\hat{\varphi }}(t,w(t))\equiv \varsigma (t,w(t))\).
From the above analysis, for the power utility function, the strategy \({\hat{\varphi }}(t,w(t))\) determined by Eqs. (21)–(24) satisfies Eq. (19) and thus is an equilibrium strategy, i.e.,
for any sufficiently small \(\epsilon \).
Furthermore, following the same argument as in Theorem 1 in He and Jiang [37], the strategy is a weak and regular equilibrium strategy.
Appendix H
We prove \(\frac{\partial {\hat{c}}(t)}{\partial t}>0\) and \({\hat{c}}(t)=\frac{1}{(1-\beta )\int _t^{\infty }e^{-\lambda (x^\gamma -t^\gamma )}e^{-\rho (x-t)} dx+\frac{\beta }{\rho }}\rightarrow \frac{\rho }{\beta }\) as \(t\rightarrow \infty \) and \(\gamma >1\). From Eq. (26), we have
By defining \(x=t+y\), from Eq. (H1), we have
The second strict inequality holds because \((t+y)^\gamma -\tau ^\gamma > \gamma t^{\gamma -1}y\) for \(\gamma >1\), \(y>0\) and \(t>0\).
We second show \({\hat{c}}(t)\rightarrow \frac{\rho }{\beta }\). Define \(x=t+y\), then
where the first inequality holds because \( (t+y)^\gamma -t^\gamma > \gamma t^{\gamma -1}y \) for \(\gamma >1\), \(y>0\) and \(t>0\). Since \(\frac{1-\beta }{\lambda \gamma t^{\gamma -1}+\rho }+\frac{\beta }{\rho }\rightarrow \frac{\beta }{\rho }\) as \(t\rightarrow \infty \) and \(\gamma >1\), we have
Appendix I
From Eqs. (E1), (E2) and (E10) in “Appendix E”, the average budget constraint equation is
where \({\bar{w}}(t)=\frac{E_t[dw]}{dt}\) and \(R=\frac{a^2}{{\bar{\sigma }}^2}+r\).
Differentiating Eq. (I1) and from Eq. (34), we obtain
Equation (I2) shows that the expected growth rate of wealth is a decreasing function of time. Therefore, if \(R<{\hat{c}}(0)\), the individual plans to disinvest, i.e., she plans to consume more than her expected income.
If \({\hat{c}}(0)<R<\frac{\rho }{\beta }\), she plans to increase her wealth for \(0<t<{\bar{t}}\) and then disinvests her wealth at an expected rate \(R-{\hat{c}}(t)\) for \(t>{\bar{t}}\), where \({\bar{t}}\) is defined as the solution to
If \(R>\frac{\rho }{\beta }\), she plans to grow her wealth.
Appendix J
From Eq. (E2) in “Appendix E”,
Therefore, from Eq. (J1), the average budget equation for \({\hat{C}}(t)\) is
where \(\bar{{\hat{C}}}(t)=\frac{E_t[d\bar{{\hat{C}}}(t)]}{dt}\).
From “Appendix I”, if \(R<{\hat{c}}(0)\), the individual plans to decrease her expected consumption amount. If \({\hat{c}}(0)<R<\frac{\rho }{\beta }\), she plans to increase her expected consumption amount for \(0<t<{\bar{t}}\), and then decreases her expected consumption amount at an expected rate \(R-{\hat{c}}(t)\) for \(t>{\bar{t}}\), where \({\bar{t}}\) is defined as the solution to
If \(R>\frac{\rho }{\beta }\), she plans to increase her expected consumption amount.
Appendix K
Define \(\{c_t^*(\tau ),\alpha _t^*(\tau )\}\), \(0\le t\le \tau \), as the optimal consumption rate and the portion of risky asset from the perspective of the naive individual at time t with the initial condition \((\tau ,w(\tau ))\). The value function is therefore, \(Q(t,\tau ,w(\tau ))\). By the same analysis as in “Appendix B”, the corresponding HJB equation is
We conjecture the value function to be \(Q(t,\tau ,w(\tau ))=\psi (t,\tau )\frac{w^{1-b}}{1-b}\). From Eq. (K1), we can see that
where
and \( q=\frac{1-b}{b}(r+\frac{a^2}{2b{\bar{\sigma }}^2}) \). Notice that \(\lim _{\tau \rightarrow \infty }\psi (t,\tau )=0\), which means that the expected discounted utility generated from the wealth in the far future \(w(\tau )\) is zero from the perspective of the present because of discounting. Another boundary condition is \(\lim _{\tau \rightarrow \infty }\psi (\tau ,\tau )=\beta \xi ^b\). Footnote (22) shows the \(\xi \) and \(\lim _{\tau \rightarrow \infty }\psi (\tau ,\tau )=\beta \xi ^b\).
The optimal consumption policies \((c^*_t(\tau ),\alpha ^*_t(\tau ))\) will not be implemented at time \(\tau \) and the actual consumption and portfolio rules are
where
Following the method in Yong’s [67] and Wei et al. [64], we derive the actual expected discounted utility \({\bar{Q}}(t,\tau ,w(\tau ))\) following the consumption policies given by Eqs. (K4)–(K5),
Equation (K6) can be written as
By the Taylor expansion, we have
We conjecture the expected discounted utility to be \({\bar{Q}}(t,\tau ,w(\tau ))=\phi (t,\tau )\frac{w^{1-b}}{1-b}\) and therefore
From Eqs. (K4), (K9) and (K10), we have
Thus,
and
and \(\lim _{\tau \rightarrow \infty }\phi (t,\tau )=0\) and \(\lim _{\tau \rightarrow \infty }\phi (\tau ,\tau )=\beta \xi ^b\).
Rights and permissions
About this article
Cite this article
Chen, S., Fu, R., Wedge, L. et al. Consumption and portfolio decisions with uncertain lifetimes. Math Finan Econ 14, 507–545 (2020). https://doi.org/10.1007/s11579-020-00263-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11579-020-00263-0
Keywords
- Time inconsistency
- Equilibrium strategies
- Uncertain lifetime
- Consumption and portfolio choices
- Non-hyperbolic discounting