1 Introduction

An accurate estimate of geomechanical properties of rocks is crucial for almost any form of design and analysis in geomechanical projects. The strength and deformation behavior of rocks have been studied by many authors Xiong et al. (2019), Yang et al. (2016), Zhao et al. (2017), Ranjith et al. (2004), Rahimi and Nygaard (2018), Davarpanah et al. (2019) and Berezovski and Ván (2017). Among these properties modulus of elasticity (E), modulus of rigidity (G) and bulk modulus (K) are the basic parameters used in rock engineering. There are two common methods to calculate the moduli: destructive and non-destructive procedures. In the destructive one, moduli are calculated from the stress–strain curves of the rock material. This is characteristic of the modulus of elasticity. For the non-destructive one, the most common method is an ultrasonic test, measuring both longitudinal and shear wave velocities.

Measuring the longitudinal and shear wave velocities, the dynamic elastic material parameters for isotropic and ideal elastic rocks are calculated with the help of the following formula (Martinez-Martinez et al. 2012):

$$E_{dyn} = \frac{{\rho V_{s}^{2} \left( {3V_{P}^{2} - 4V_{S}^{2} } \right)}}{{V_{P}^{2} - V_{S}^{2} }}$$
(1)
$$\vartheta_{dyn} = \frac{{V_{P}^{2} - 2V_{S}^{2} }}{{2\left( {V_{P}^{2} - V_{S}^{2} } \right)}}$$
(2)
$$G_{dyn} = \frac{{E_{dyn} }}{{2\left( {1 + \vartheta_{dyn} } \right)}}$$
(3)
$$K_{dyn} = \frac{{E_{dyn} }}{{3\left( {1 - 2\vartheta_{dyn} } \right)}}$$
(4)

where Edyn = dynamic modulus of elasticity, GPa, Gdyn = dynamic modulus of rigidity, GPa, Kdyn = dynamic bulk modulus, GPa, \({\text{J}}_{\text{dynamic}} = {\text{dynamic}}\;{\text{Poisso's}}\;{\text{ratio}}\), \(\rho = {\text{density}},\frac{\text{g}}{{{\text{cm}}^{ 3} }}\),\(V_{S} = {\text{shearvelocity}},\;{\text{km/s}}\), \(V_{P} = {\text{longitudinal}}\;{\text{infinite}}\;{\text{medium}}\;{\text{velocity}},{\text{km/s}}\).

The Young’s modulus obtained from the compression (destructive) test is called the static elastic modulus (Estat). The International Society for Rock Mechanics (ISRM) suggests three standard methods for its determination (Ulusay and Hudson 2007). They are as followings:

  • Tangent Young’s modulus Etan—at fixed percentage of ultimate stress. This is defined as the slope of a line tangent to the stress–strain curve at a fixed percentage of the ultimate strength (Fig. 1a);

    Fig. 1
    figure 1

    a Tangent Young’s modulus Etan, b Average Young’s modulus Eav, c Secant Young’s modulus Esec

    Full size image

  • Average Young’s modulus Eav—of the straight-line part of a curve. The elastic modulus is defined as the slope of the straight-line part of the stress–strain curve for the given test (Fig. 1b);

  • Secant Young’s modulus Esec—at a fixed percentage of ultimate stress. It is defined as the slope of the line from the origin (usually point (0; 0)) to some fixed percentage of ultimate strength, usually 50% (Fig. 1c). In this paper, the secant static modulus has been calculated following ASTM D 3148-69 (1996).

The difference between dynamic (\(E_{dyn}\)) and static (\(E_{stat}\)) Young’s Modulus for rocks has been addressed widely in rock engineering (van Heerden 1977; Lama and Vutukuri 1978; Barton 2006). Ratios for \(E_{dyn}\)/\(E_{stat}\) are typically in the range from 1 to 2 (Eissa and Kazi 1988).

Generally, the dynamic modulus of elasticity is slightly higher than the static value (Zhang 2006; Stacey et al. 1987; Al-Shayea 2004; Ide 1936; Kolesnikov 2009; Vanheerden 1987). The discrepancies between the dynamic and static elastic moduli have been widely attributed to microcracks and pores in the rocks. Figure 2 shows the ratio of dynamic elastic modulus to static elastic modulus compiled by Stacey et al. (1987). The ratio varies between about 1 and 3.

Fig. 2
figure 2

(Stacey et al. 1987)

Comparison of static and dynamic elastic modulus

Full size image

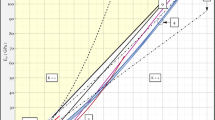
In other research (Martinez-Martinez et al. 2012) conducted a laboratory experiment on ten different carbonate rocks quarried in Spain and received the following diagram (Fig. 3). As shown, for the majority of cases dynamic (\(E_{dyn}\)) Young’s Modulus is higher than static (\(E_{stat}\)) Young’s Modulus.

Fig. 3
figure 3

(Martinez–Martinez et al. 2012)

Relationship between Edyn and Estat in the studied samples. The straight red line corresponds to the ideal ratio \(\frac{{E_{dyn} }}{{E_{stat} }}\) = 1.

Full size image

The rocks consist of homogeneous limestones, low anisotropic travertines, limestones and dolostones with abundant stylolites, veins and fissures. Ultrasonic waves were measured using non-polarised Panametric transducers (1 MHz), a precise ultrasonic device consisting of signal emitting– receiving equipment and an oscilloscope (TDS 3012BTektronix) (Martinez-Martinez et al. 2012) (Fig. 4).

Fig. 4
figure 4

Plot of the relationship between the measured static and dynamic modulus of elasticity (Estat = a Edyn − b)

Full size image

Types of rocks are denoted below the picture and can be described as following. Blanco Alconera (BA): white crystalline limestone. Piedra de Colmenar (PdC): grey and white lacustrine fossiliferous limestone (99% calcite). Travertino Amarillo (TAm): porous layered limestone Travertino Rojo (TR): porous layered limestone. Gris Macael (GM): grey calcite marble.Blanco Tranco (BT): white homogeneous calcite marble. Amarillo Triana (AT): yellow dolomite marble.Crema Valencia (CV): cream micritic limestone (99% calcite). Rojo Cehegín (RC): micritic limestone. Marrón Emperador (ME): brown brecciated dolostone.

2 Empirical relationships between dynamic and static Young’s modulus

There are several relationships between the static and dynamic Young’s moduli (Belikov et al. 1970; King 1983; Eissa and Kazi 1988; McCann and Entwisle 1992; Eissa and Kazi 1988; Christaras et al. 1994; Nur and Wang 1999; Brotons et al. 2014, 2016; Małkowskia et al. 2018). These equations can be divided into the following groups:

  • Linear

  • Non-linear: Logarithmic (power-law) and polynomial

2.1 Linear relationships

Up to now, several linear relationships have been established between the dynamic and the static Young’s modulus. The following form was used:

$$E_{stat} = aE_{dyn} {-}b$$
(5)

where a and b are material parameters. These values are summarized in Table 1.

Table 1 Linear relationship between static (Estat) and dynamic (Edyn) modulus (Estat = a Edyn – b)
Full size table

2.2 Non-linear relationships

Some published papers use a logarithmic relationship. Analyzing the measured data, they suggest the following formula between the dynamic and the static Young’s modulus:

$$\log_{10} E_{stat} = c\log_{10} \left( {\rho_{bulk} E_{dyn} } \right) \, {-}d$$
(6)

The values of Estat, and Edyn are expressed in GPa while that of ρbulk in g/cm3. Here c and d are material constants (the published values are summarized in Table 2).

Table 2 Relationship between static (Estat) and dynamic (Edyn) Young’s modulus log10 Estat = c log10(ρbulkEdyn) – d
Full size table

These equations can be rewritten to the following form:

$$E_{stat} = \alpha E_{dyn}^{\beta }$$
(7)

where the parameters are presented in Table 3.

Table 3 Relationship between static (Estat) and dynamic (Edyn) Young’s modulus Estat = α Eβdyn
Full size table

The power-law relation (7) was suggested in other researches, too (see Table 4). E.g. according to the data of Ohen (2003). the dynamic Young’s modulus is about 18 times the static Young’s modulus (Peng and Zhang 2007).

Table 4 Relationship between static (Estat) and dynamic (Edyn) Young’s modulus
Full size table

From ultrasonic test data of 600 core samples in the Gulf of Mexico, Lacy (1997) obtained the following polynomial correlation for sandstones (Peng and Zhang 2007):

$$E_{stat} = \, eE_{dyn}^{2} + \, fE_{dyn}$$
(8)

A similar connection exists for shales and sedimentary rocks (Horsrud 2001; see Table 5).

$$E_{stat} = \, 0.0428E_{dyn}^{2} + \, 0.2334E_{dyn}$$
(9)
Table 5 Relationship between static (Estat) and dynamic (Edyn) Young’s modulus \(E_{stat} = eE_{dyn}^{2} + fE_{dyn}\)
Full size table

3 Data analysis

For this study, 40 samples of different types of rocks from the literature were analyzed (Lama and Vutukuri 1978). Data were classified according to rock types and the relationship between dynamic and static constants was investigated in Table 6. Also, the histogram of investigated parameters is shown in Fig. 5.

Table 6 Static and dynamic deformation constants of studied rocks
Full size table
Fig. 5
figure 5

Histogram of investigated parameters

Full size image

According to Fig. 6, there is a linear regression between static and dynamic modulus of elasticity for all studied rocks, giving R2 = 0.89. More precisely, Fig. 7 shows the relationship between static and dynamic modulus of elasticity based on rock types. As it is shown, for igneous rocks there is a linear correlation that gives the value of R2 = 0.95, for sedimentary rocks the value is R2 = 0.90 and for metamorphic rocks, the value is R2 = 0.70. Similarly, Fig. 8 illustrates the correlation between static and dynamic modulus of rigidity for all samples, giving R2 = 0.89. Figure 9 demonstrates the relationship between static and dynamic modulus of rigidity based on rock types.

Fig. 6
figure 6

Relationship between static and dynamic modulus of elasticity for all rocks

Full size image
Fig. 7
figure 7

Relationship between static and dynamic modulus of elasticity based on rock types

Full size image
Fig. 8
figure 8

Relationship between static and dynamic modulus of rigidity for all rocks

Full size image
Fig. 9
figure 9

Relationship between static and dynamic modulus of rigidity based on rock types

Full size image

As it is clear, for igneous rocks the value of R2 = 0.96, for sedimentary rocks the value of R2 = 0.91 and for metamorphic rocks the value of R2 = 0.63. Figure 10 exhibits the linear correlation between static and dynamic bulk modulus for all studied rocks, giving R2 = 0.77. Figure 11 shows the relationship between static and dynamic bulk modulus with respect to rock types. As can be seen, for igneous rock the value of R2 = 0.77, for sedimentary rocks the value of R2 = 0.38 and for metamorphic rocks, the value of R2 = 0.87. The results are summarised in Tables 7, 8, 9.

Fig. 10
figure 10

Relationship between static and dynamic bulk modulus for all rocks

Full size image
Fig. 11
figure 11

Relationship between static and dynamic bulk modulus based on rock types

Full size image
Table 7 Linear regression between static and dynamic deformation constants (Estat = a Edyn – b)
Full size table
Table 8 Power regression between static and dynamic deformation constants \(\left( {E_{stat} = \alpha E_{dyn}^{\beta } } \right)\)
Full size table
Table 9 Logarithmic regression between static and dynamic deformation constants (log10 Estat = c log10(ρbulk Edyn) – d)
Full size table

Our achieved results in Fig. 12, with previously published correlations, are illustrated in Fig. 13. It can be concluded that the formulas well fit the data.

Fig. 12
figure 12

Linear and non-linear achieved correlations for all rock types

Full size image
Fig. 13
figure 13

Previously published correlations

Full size image

According to our analysis, with respect to different published linear correlations between static modulus of elasticity (Estat) and dynamic modulus of elasticity (Edyn), a relationship with high correlation (R2 = 0.91) was observed between a and b parameters as it is shown in Fig. 14. It should be stated that data published by McCann & Entwisle (1992) for Crystalline rocks were not included in this analysis. The reason is that by applying their equation, the amount of correlation decreases from (R2 = 0.91) to (R2 = 0.57). It might be related to the link between the crystallized structure of rock and wave propagation.

Fig. 14
figure 14

Relationship between a and b constants

Full size image

4 Results and discussion

In this research, the basic geomechanical properties of different types of rocks were measured and analyzed. The results show that there is a good correlation between static and dynamic elasticity modulus, rigidity modulus and bulk modulus. Regarding the relationships between static and dynamic modulus of elasticity, the best correlation found to be nonlinear logarithmic and power regression with the value of (R2 = 0.91). Similarly, Brotons et al. (2014, 2016) established the nonlinear correlation between static and dynamic elastic modulus of different types of rocks with the value of R2 = 0.99. Eissa and Kazi (1988) carried out similar research and discovered that the best correlation was to be nonlinear with the value of R2 = 0.92. On the other hand, some other researchers adopted the linear correlation as well-fitted regression line (Belikov et al. 1970) for Granite with R2 = 0.92, (King 1983) for Igneous and metamorphic rocks with R2 = 0.82, (McCann and Entwisle 1992) for crystalline rocks with R2 = 0.82, (Christaras et al. 1994) for all types of rocks with R2 = 0.99, (Nur and Wang 1999) for all types of rocks with R2 = 0.8). Nevertheless, in the present study, we established the linear correlations for igneous rocks with R2 = 0.95, for sedimentary rocks with R2 = 0.90 and for metamorphic rocks with R2 = 0.69. Considering the relationship between static and dynamic modulus of rigidity, the best correlation observed was nonlinear logarithmic regression with giving the value of (R2 = 0.97); when it comes to bulk modulus, the best correlation was linear with the value of (R2 = 0.77). According to rock types, for igneous rock, the best correlation between static and dynamic modulus of elasticity (E) was nonlinear logarithmic and power ones with the value of (R2 = 0.96); However, King (1983) found that the best correlation was linear for igneous-metamorphic rocks with the value of (R2 = 0.82). For sedimentary rocks, the best correlation was linear with the value of (R2 = 0.88) and for metamorphic rocks was nonlinear logarithmic and power with the value of (R2 = 0.93). For igneous rocks, the best correlation between static and dynamic modulus of rigidity (G) was nonlinear logarithmic with the value of (R2 = 0.96); for sedimentary rocks was nonlinear logarithmic with the value of (R2 = 0.98); for metamorphic rocks was nonlinear logarithmic with the value of (R2 = 0.99). For igneous rocks, the best correlation between static and dynamic bulk modulus (K) was nonlinear logarithmic with the value of (R2 = 0.88); for sedimentary rocks was linear with the value of (R2 = 0.38); for metamorphic rocks was nonlinear logarithmic with (R2 = 0.98). These values demonstrate an interesting finding that there is a higher correlation between static and dynamic constants in igneous rocks rather than sedimentary and metamorphic rocks except for bulk modulus. Also, based on an analysis of previously obtained linear correlations between static and dynamic modulus of elasticity in Table 1, there is a good logarithmic correlation between constant parameters (a, b). Interestingly enough, our achieved result as shown in Fig. 14 fits well with previously published results with high correlation R2 = 0.91. It means the static modulus of elasticity depends on the dynamic modulus only with a one-parameter formula:

$$E_{stat} = \, \left( {0.135 \, \ln \left( b \right) \, + 0.78} \right){-}b,\;{\text{where}}\;b\;{\text{is}}\;{\text{rock}}\;{\text{type - dependent}}\;{\text{parameter}} .$$

Additionally, for a more accurate comparison, root-mean-square (χ) errors between the dynamic and static elastic modulus was calculated as:

$$\chi \left( m \right) = \sqrt {\frac{{\mathop \sum \nolimits_{j = 1}^{n} \left[ {\varPi_{obs\left( j \right)} - \varPi_{cal\left( j \right)} } \right]^{2} }}{n - 1}}$$
(10)

where \(\varPi_{obs\left( j \right)}\) is the observed value of a parameter in the jth sample, here is the modulus of elasticity (E), \(\varPi_{cal\left( j \right)}\) is the calculated value of a parameter in the jth sample, j = 1, 2,…,n, is the number of tested samples. Based on our analyses we received the following correlation,

$$\log_{10} E_{stat} = \, 1.37 \, \log_{10} \left( {\rho_{bulk} E_{dyn} } \right) \, {-} \, 1.32, \, R^{2} = 0.91,\chi = \, 10.52$$
$$E_{stat} = 0.164E_{dyn}^{1.373} , \, R^{2} = 0.91,\chi = 11.58$$
$$E_{stat} = \, 0.89E_{dyn} {-} \, 5.26, \, R^{2} = 0.89,\chi = 13.17$$

The difference between dynamic and static elastic moduli is highly associated with mineralogical differences, differences in grain/crystal size, differences in porosity. A deviation of dynamic elastic modulus from static elastic modulus can be attributed to the presence of fractures, cracks, cavities and planes of weakness and foliation (Al-Shayea 2004; Guéguen and Palciauskas 1994). In other words, as the number of discontinuities increase, the lower value of Young’s modulus and the higher discrepancy between static and dynamic values are expected. The most crucial petrographic parameter that influences the deformation behavior of rock is porosity. The trend observed in porous rocks was that the static elastic modulus was inversely proportional to porosity (Brotons et al. 2016; Garcia-del-Cura et al. 2012). However, Crystalline rocks exhibit lower values of elastic moduli due to the fact that their porous system is constituted by a dense microcrack network. That is, crystalline rocks act as non-continuous solid, while porous rocks with interparticle porosity behave as a more continuous solid due to the presence of cement and matrix between grains. The effect of mineralogy on elastic moduli of rocks have been studied by several authors and found to be much less than other factors such as porosity and crystal size (Heap and Faulkner 2008; Palchik and Hatzor 2002). Regarding the effect of grain size on the elastic modulus of nanocrystalline, with the decrease of grain size, the elastic modulus decreases (Kim and Bush 1999; Chaim 2004; Zhang and Tahmasebi 2019; Tugrul and Zarif 1999).

It is worth mentioning that more detailed material models beyond ideal elasticity give an exact relationship between the elastic and static moduli. Notably, the observed relations can be explained in a universal thermodynamic framework where internal variables are characterizing the structural changes (Asszonyi et al. 2015; Berezovski and Ván 2017). The difference of dynamic and elastic moduli is natural in this framework as it is clear from the corresponding dispersion relation and related laboratory experiments (Barnaföldi et al. 2017; Ván et al. 2019) These constitutive models are based only on universal principles of thermodynamics, are independent of particular mechanisms and are successful in characterizing rheological phenomena in rocks including and beyond simple creep and relaxation. This is in accordance with the difficulty for finding a very detailed quantitative mesoscopic mechanism for the dynamics of dissipative phenomena in rocks as well.

5 Conclusion

Generally, the performance difference between the linear and power-law formulas was small, the linear relationship fitted well the data. Therefore, considering also the possibility of one parameter formulation, given in (11), the linear relationship between dynamic and static elastic moduli is suitable for rock engineering. It was expected, that the modulus of rigidity and bulk modulus, as original theoretical Lamé parameters, would correlate better. However, the correlation between the static and dynamic Young modulus (R2 = 0.89) is as good as for the other ones (R2 = 0.89 and 0.77), in spite of the fact that the Young’s modulus is a composite parameter. The reason could be the uncertainty in the Poisson ration measurements and also the difference in rock types for the bulk modulus measurements is remarkable. It is worth mentioning that thermodynamic principles more detailed material models beyond ideal elasticity give detailed relationships between the elastic and static moduli in general. Particularly, the observed relations can be explained in a universal thermodynamic framework where internal variables are characterizing the structural changes in the rock.